Matrices & Determinants Questions and Answers

likely to turn around look menacingly at me and say Prove it What she or he really wants is to be convinced of my statement by some evidence In this case it would probably be a big physical push Convincing evidence is also what the world asks for before accepting a scientist s predictions or a historian s claims In the same way if you want a mathematical statement to be accepted as true you would need to provide mathematically acceptable evidence to support it This means that you would need to show that the statement is universally true And this would be done in the form of a logically valid argument Definition An argument in mathematics or logic is a finite sequence of statements P P p such that p A P A A p p Each statement in the sequence except the last one i e pi for i 1 n is called a premise or an assumption or a hypothesis The final statement p is called the conclusion Let s consider an example of an argument that shows that a given statement is true Example 1 Give an argument to show that the mathematical statement For any two sets A and B An BCA is true Solution One argument could be the following Let x be an arbitrary element of AnB Then X E A and x E B by definition of n Therefore x A This is true for every x in An B Therefore AnBC A by definition of C The argument in Example 1 has a peculiar nature The truth of each of tho 4 premises and of its conclusion follows from the truth of the earlier premises in it Of course we start by assuming that the first statement is true Then assuming the definition of intersection the second statement is true Tlic third one is true whenever the second one is true because of the properties of logical implication The fourth statement is truc whenever the first three arc true because of the definition and properties of the term for all And finally the last statement is true whenever all the earlier ones are In this way we have shown that the given statcinent is true In other words we have proved the given statement as the following definitions show Definitions We say that a proposition p follows logically from propositions P P2 and Pn if p must be true whenever P P2 Pn are true i e P AP A AP p Here note the use of the implication arrow For any two propositions r and s rs denotes s is true whenever r is true Note that using the contrapositive this also denotes r is false whenever s is false Thus rs and rs are different except when both r and s are true or both are false A proof of a proposition p is a mathematical argument consisting of a sequence of statements P P2 Pn from which p logically follows So p is the conclusion of this argument The statement that is proved to be true is called a theorem Sometimes as you will see in Sec 2 3 3 instead of showing that a statement p is true we try to prove that it is false i e that p is true Such a proof is

called a disproof of p In the next section you will read about some ways of disproving a statement Sometimes it happens that we feel a certain statement is true but we don t succeed in proving it It may also happen that we can t disprove it Such statements are called conjectures If and when a conjecture is proved it would be called a theorem If it is disproved then its negative will be a theorem In this context there s a very famous conjecture which was made by a mathematician Goldbach in 1742 He stated that For every n E N if n is even arid n 2 then n is the sum of two primes To this day no one has been able to prove it or disprove it To disprove it several people have been hunting for an example for which the statement is not truc i e an even number 1 2 such that h cannot be written as the sum of two prime numbers Now as you have seen a mathematical proof of a statement consists of one or more premises These premises could be of four types i a proposition that has been proved earlier e g to prove that the complex roots of a polynomial in R x occur in pairs we use tlie division algorithm or ii a proposition that follows logically from the earlier the proof as you have seen in Example 1 or iii a mathematical fact that has never been proved but is universally accepted as true e g two points determine a line Such a fact is called an axiom or a ppstulate Dositions given in iv the definition of a mathematical term e g assuming the definition of C in the proof of AnBCA You will come across more examples of each type while doing the following exercises and while going through proofs in this course and other courses El Write down an example of a theorem and its proof of at least 4 steps taken from school lcvcl algebra At each step indicate which of tlie four types of premise it is E2 Is every statement a theorem Why So far we have spoken about valid or acceptable arguments Now let us see an example of a sequence of statements that will not Sorm a valid argument Consider the following sequence If Maya sees the movie she won t finish her homework Maya won t finish her homework Therefore Maya sees the movie Looking at the argument can you say whether it is valid or not Intuitively you may feel that the argument isn t valid But is there a formal logical tool that you can apply to checlr if your intuition is correct What about truth tables Let s see The given argument is of the form pa q P where p Maya sees the movie and q Maya won t finish her homework J M

Solution A good way of disproving it is to look for a counterexample that is a pair of real numbers a and b for which a b2 but a b Can you think of such a pair What about a 1 and b 1 They serve the purpose In fact there are infinitely many counterexamples Why Now an exercise E12 Disprove the following statements by providing a suitable counterexample i VxEZ x N ii x y n x y Vn N x yeZ iii f N N is 1 1 iff f is onto Hint To disprove p q it is enough to prove that p q is false or qp is false There are some other strategies of proof like a constructive proof which you will come across in the appendix to Unit 11 and in other mathematics courses We shall not discuss this method here Other proof related adjectives that you will come across are vacuous and trivial A vacuous proof makes use of the fact that if p is false then p q is true regardless of the truth value of q So to vacuously prove pq all we need to do is to show that p is false For instance suppose we want to prove that If n n 1 for n Z then n 0 Since n n 1 is false for every ne Z the given statement is vacuously true or true by default Similarly a trivial proof of p q is one based on the fact that if q is true then pq is true regardless of the truth value of p So for example If n n 1 for n E Z then n 1 n is trivially true since n 1 nVnEZ The truth value of the hypothesis which is false in this example does not come into the picture at all Here s a chance for you to think up such proofs now E13 Give one example each of a vacuous proof and a trivial proof And now let us study a very important technique of proof for statements that are of the form p n n N 2 4 PRINCIPLE OF INDUCTION In a discussion with some students the other day one of them told me very cynically that all Indian politicians are corrupt I asked him how he had reached such a conclusion As an argument he gave me instances of several politicians all of whom were known to be corrupt What he had done was to formulate his general opinion of politicians on the basis of several particular instances This is an example of inductive logic a process of reasoning by which general rules are discovered by the observation of several individual

7 of such a pair What about a 1 and b 1 They serve the purpose In fact there are infinitely many counterexamples Why Now an exercise E12 Disprove the following statements by providing a suitable counterexample i VxEZ x N ii x y n x y Vn N x y Z iii f N N is 1 1 iff f is onto Hint To disprove p q it is enough to prove that p q is false or qp is false There are some other strategies of proof like a constructive proof which you will come across in the appendix to Unit 11 and in other mathematics courses We shall not discuss this method here Other proof related adjectives that you will come across are vacuous and trivial A vacuous proof makes use of the fact that if p is false then p q is true regardless of the truth value of q So to vacuously prove p q all we need to do is to show that p is false For instance suppose we want to prove that If n n 1 for n Z then n 0 Since n n 1 is false for every ne Z the given statement is vacuously true or true by default Similarly a trivial proof of p q is one based on the fact that if q is true then p q is true regardless of the truth value of p So for example If n n 1 for n E Z then n 1 n is trivially true since n 1 nVnEZ The truth value of the hypothesis which is false in this example does not come into the picture at all Here s a chance for you to think up such proofs now E13 Give one example each of a vacuous proof and a trivial proof And now let us study a very important technique of proof for statements that are of the form p n n N 2 4 PRINCIPLE OF INDUCTION In a discussion with some students the other day one of them told me very cynically that all Indian politicians are corrupt I asked him how he had reached such a conclusion As an argument he gave me instances of several politicians all of whom were known to be corrupt What he had done was to formulate his general opinion of politicians on the basis of several particular instances This is an example of inductive logic a process of reasoning by which general rules are discovered by the observation of several individual cases Inductive reasoning is used in all the sciences including mathematics But in mathematics we use a more precise form

1 2 3 n 1 division of vernier scale n division of main scale 5 one Vemier division n 1 main scale division 1 Least count 1 M S D 1 V D n 1M S D n 1M S adding i and ii Mg V For an object placed at infinity the image after first refraction will be formed at v 462 462 by R 1 The image after second refraction will be found at H3 H2 H3 H2 V V R HgR bbg jy R Therefore focal length will be s Hy 2 1 Rhc 7 2 hv 2 1 3RC SOLUTIONS Mg py R Z 42 Loss in K E of the gas where n number of moles If its temperature change by AT Then n RAT nm v mv AT 3R V v sincsti v cos cxtj n 1 AE nm f

Two narrow cylindrical pipes A and B have the same length Pipe A is open at both ends and is filled with a monoatomic gas of molar mass M Pipe B is open at opne end and closed at the other end and is filled with a diatomic gas of molar mass M Both gases are at the same temperature a If the frequency of the second harmonic of the fundamental mode in Pipe Als equal to the frequency of the third harmonic of the fundamental mode in pipe B determine the value of M MB b Now the opeen end to pipe B is also closed so that the pipe is closed at both ends Find the ratio of the fundamental frequency in pipe A to that in pipe B 3 2 A cubical box of side 1 meter contains hellum gas atomic weight 4 at a pressure of 100N m During an observation time of 1 second an atom travelling with the root mean square speed parallel to one of the edges of the cube was found to make 500 hits with a particular wall wolthout any collision with other atoms Take R J mol K andk 1 38x10 J K a Evaluate the temperature of the gas b Evaluate the average kinetic energy per atom c Evaluate the total mass of helulm gas in the box A uniform solld cylinder of density 0 8 g cm floats in equilibrium in a combination of two non mixing liquids A and B with its axis vertical The densities of the liquids A and B are 0 7 g cm and 1 2 g cm respectively The height of liquid A is h 1 2 cm The length of the part of the cylinder Immersed in liquid B Ish 0 8 cm a Find the total force exerted by liquid A on the cylinder air A thin uniform wire AB of length 1m an unknown resistance X and a resistance of 1202 are connected by thick conducting strips as shown in A B 2 1 2 b Find h the length of the part of teh cylinder in air c The cylinder is depressed in such a way that is top surface is just below the upper surface of liquid A and is then released Find the acceleration of the cylinder immediately after it is released 1 2 2 ha 120

10 A proton and an alpha particle after being accelerated through same potential difference enter a uniform magnetic field the direction of which is perpendicular to their velocities Find the ratio of radii of the circular paths of the two particles 1 A solid sphere of radius R is floating in a liquid of density p with half of its volume submerged If the sphere is slightly pushed and released it starts performing simple harmonic motion Find the frequency of these oscillations 12 An object is approaching a thin convex lens of focal length 0 3 m with a speed of 0 01 m s Find the magnitudes of the rates of change of position and lateral magnification of image when the object is at a distance of 0 4 m from the lens 13 Draw the circuit for experimental verification of Ohm s using a source of variable D C voltage a main resistance of 10022 two galvanometers and two resistances of values 10 and 10 respectively Clearly show the positions of the voltmeter and the ammeter 14 A cube of coefficient of linear expansion a is floating in a bath containing a liquid of coefficient of volume expansiony When the temperature is raised by AT the depth upto which the cube is submerged in the liquid remains the same Find the relation between o and Y showing all the steps 15 One end of a rod of length L and cross sectional area A is kept in a fumace of temperature T The other end of the rod is kept at a temperature T The thermal conductivity of the material of the rod is K and emissivity of the rod is e It is given that T T AT where AT T T being the temperature of the surroundings If AT T T find the proportionality constant Consider that heat is lost only by radiation at the end where the temperature of the rod is T 16 Two blocks A and B of equal masses are released from an inclined plane of inclination 45 at t 0 Both the blocks are initially at rest The coefficient of kinetic friction between block A and the inclined plane is 02 while it is 19 In the circuit shown A and B are two cells of same emf E but different internal resistances r and r r r respectively Find the value of R such that the potential difference across the terminals of cell A is zero a long time after the key K is closed Pumace 0 3 for block B Initially the block A is 2m behind the block B When and where their front faces will come in a line Take g 10 m s 17 Wavelengths belonging to Balmer series lying in the range of 450 nm to 750 nm were used to eject photoelectrons from a metal surface whose work function is 2 0 eV Find in eV the maximum kinetic energy of the emitted photoelectrons Take hc 1242 eV nm 18 In a Young s double slit experiment two wavelengths of 500 nm and 700 nm were used What is the minimum distance from the central maximum where their maximas coincide again Take D d 10 Symbols have their usual meanings minumay 0 In a LR series circuit a sinusoidal voltage V V sin oot is applied VA It is given that L 35mH R 112 V V 220V 00 2m 50Hz and 1121 Mo anhyd 1 06 Lenina OPCHR

2 1 ol On solving the lines we get S R points S 2 k k R k k Two lines intersect at Q 1 1 1 2 ol Solutions to IIT JEE 2005 Mains Paper Memory based Mathematics A line passes through the point P h k is parallel to the x axis It forms a triangle with the lines y x x y 2 of area 4h then find the locus of P 1 3 Area of the AQRS x2 k 1 QS QR SR 4h k 1 locus is the pair of straight lines A cricket player in his career plays n match and scores total no of If he scores k 2 runs in k match where 1 k n Find n Let S be the total scores in his career plays n matches S 241 SO n 20 1 n 1 8 But S 2 1 2 n as given 2 2 n 2 2 n 2 so n 7 Ans 4x y 1 Ans 22 4 2n 22 2n 4 n 1x2 n 2 4 runs 132 21 9 9 probability that he is reaching office late if he takes car scooter bus or train is probability that he has travelled by car if he reaches office in time Ramesh goes to office either by car scooter bus or train probability of which being and respectively and 2 40 and respectively Find the 2

1 MATHEMATICS Find the centre and radius of the circle formed by all the points represented by z x iy satisfyin k k 1 where a and are constant complex numbers given b the relation z BI a a B B iB 2 If 5 6 6 4 are four distinct vectors satisfying the conditions axb xd and ax bxd then prov that ab cd c bd 3 is an integer where n is a positive integer 4 If M is a 3x3 matrix where M M I and det M 1 then prove that det M 1 0 Using permutation or otherwise prove that 5 If y x 3 116 cosx cos 1 sin 8 that 0 de then find lin 7 If f 1 1 R and f 0 dy 5 T is a parallelopiped in which A B C and D are vertices of one face And the face just above has corresponding vertices A B C D T is now compressed to S with face ABCD remaining sam and A B C D shifted to A B C D in S The volume of parallelopiped S is reduced to 90 of T Prove that locus of A is a plane af and f 0 0 Find the value of 1 a 1 cos give n at x x EG If P x 51x 2323x45x 1035 using Rolle s theorem prove that atleast one root lie between 451 100 46 9 A plane is parallel to two lines whose direction ratios are 1 0 1 and 1 1 0 and it contain the point 1 1 1 If it cuts co ordinate axis at A B C Then find the volume of the tetrahedro OABC 10 If A and B are two independent events prove that P AUB P AB SP C where C is an ever defined that exactly one of A and B occurs x 1 y 3 11 A curve passes through 2 0 and the slope of tangent at point P x y equals the equation of the curve and area enclosed by the curve and the x axis in the fourth quadrant 12 A circle touches the line 2x 3y 1 0 at the point 1 1 and is orthogonal to the circle whic has the line segment having end points 0 1 and 2 3 as the diameter

Physics If n division of main scale coincides with n 1 divisions of vernier scale Given one main scale division is equal to a units Find the least count of the vernier Find the focal length of the lens shown in the figure The radii of curvature of both the surfaces are equal to R A particle of mass m moving in a circular path of radius R with a constant speed v is located at point 2R 0 at time t 0 and a man starts moving with a velocity v along the ve y axis from origin at time t 0 Calculate the linear momentum of the particle w r t the man as a function of time Hi H H Frequency of a photon emitted due to transition of electron of a certain element from L to K shell is found to be 4 2 x 10 Hz Using Moseley s law find the atomic number of the element given that the Rydberg s constant R 1 1 x 10 m R An insulated container containing mono atomic gas of molar mass m is moving with a velocity ve If the container is suddenly stopped find the change in temperature How a battery is to be connected so that the shown rheostat will behave like a potential divider Also indicate the points about which output can be taken Charges q and q are located at the corners of a cube of side a as shown in the figure Find the work done to separate the charges to infinite distance He H He A tuning fork of frequency 480 Hz resonates with a tube closed at one end of length 18 cm and diameter 5 cm in fundamental mode Calculate velocity of sound in air D ww R 44 A radioactive sample emits n 8 particles in 2 sec In next 2 sec it emits 0 75 n particle what is the mean life of the sample In a photoelectric experiment set up photons of energy 5 eV falls on the cathode having work function 3 eV a If the saturation current is i 4 A for intensity 10 W m then plot a graph between anode potential and current h Also draw a graph

a32a33 Cofactor of a21 A 1 M 1 a 2a33a 3 a Remark Expanding the determinant A in Example 21 along R a2 2 1 1 A 1 a 1 a32 86 911 1 2 a A a 2A 2 a13A 3 where A is cofactor of a 11 12 sum of product of elements of R with their corresponding cofactors Similarly A can be calculated by other five ways of expansion that is along R R C C and C Hence A sum of the produ of elements of any row or column with their corresponding cofactors MATHEMATICS Note If elements of a row or column are multiplied with cofactors of any other row or column then their sum is zero For example A a A 1 a 2 A22 a13 A23 a12 913 a32 6 0 5 Solution We have M M 2 1 1 all a12 a13 a11 a12 a13 a31 932 933 Similarly we can try for other rows and columns M 3 M M 2 M 3 a23 a33 5 16 64 1 II 12 33 943 a33 4 and verify that a A3 a 2 A32 a 3 A33 0 31 2 a 12 Example 11 Find minors and cofactors of the elements of the determinant 2 3 5 5 921 923 a31 a33 1 2 10 4 Rationalised 2023 24 7 21 2 RT 0 since R and R are identical a21 922 1 3 a3 a31 932 9 1 a13 a31 933 30 0 30 a12933 a13a32 we have 4 a 13 14 5 19 10 3 13 1 3 0 20 20 A 1 20 20 42 4 46 A 1 2 46 46 a11 a12 a31 a32 1 2 19 19 A23 1 3 13 13 perance

Remarks i Since area is a positive quantity we always take the absolute value of the determinant in 1 ii If area is given use both positive and negative values of the determinant for calculation iii The area of the triangle formed by three collinear points is zero Example 6 Find the area of the triangle whose vertices are 3 8 4 2 and 5 1 Solution The area of triangle is given by 38 A 4 5 This gives 2 1 1 1 3 2 1 8 4 5 1 4 10 61 2 1 3 72 14 Example 7 Find the equation of the line joining A 1 3 and B 0 0 using determinants and find k if D k 0 is a point such that area of triangle ABD is 3sq units Solution Let P x y be any point on AB Then area of triangle ABP is zero Why So 1 0 0 2 1 3 y Rationalised 2023 24 X This gives which is the equation of required line AB Also since the area of the triangle ABD is 3 sq units we 3 1 10 0 13 y 3x 0 or y 3x k 0 0 3k 3 i e k F 2 2 EXERCISE 4 2 DETERMINANTS 83 iii 2 3 3 2 1 8 e reputished 1 Find area of the triangle with vertices at the point given in each of the following i 1 0 6 0 4 3 ii 2 7 1 1 10 8 2 Show that points A a b c B b c a C c a b are collinear 3 Find values of k if area of triangle is 4 sq units and vertices are i k 0 4 0 0 2 ii 2 0 0 4 0 k 4 i Find equation of line joining 1 2 and 3 6 using determinants ii Find equation of line joining 3 1 and 9 3 using determinants 5 If area of triangle is 35 sq units with vertices 2 6 5 4 and k 4 Then k is

In the previous chapter we have studied inverse of a matrix In this section we shall discuss the condition for existence of inverse of a matrix To find inverse of a matrix A i e A we shall first define adjoint of a matrix 4 5 1 Adjoint of a matrix n Definition 3 The adjoint of a square matrix A a is defined as the transpose of the matrix A where A is the cofactor of the element a Adjoint of the matrix A is denoted by adj A 1 n y Let 88 a11 912 913 A 9 1 922 923 a31 32 33 Hence MATHEMATICS A11 A12 A13 Then adj A Transpose of A21 A22 A23 A31 A32 A33 Rationalised 2023 24 3 Example 12 Find adj A for A 4 Solution We have A 4 A 1 A 3 A 2 2 Let Remark For a square matrix of order 2 given by adj A AA 42 A22 1 adj A A of The adj A can also be obtained by interchanging a a 2 and a212 i e anl a21 911 912 921 a22 where I is the identity matrix of order n Verification A11 A21 A31 A12 A22 A32 A13 A23 A33 a12 Change sign Interchange We state the following theorem without proof Theorem 1 If A be any given square matrix of order n then a11 912 a13 A 921 922 923 then adj A A adj A adj A A A I A21 a a 12 3 and by changing signs Autished All A21 A31 A12 A22 A32

using minors and cofactors Definition 1 Minor of an element a of a determinant is the determinant obtained by deleting its ith row and jth column in which element a lies Minor of an element a IS denoted by M ij Remark Minor of an element of a determinant of order n n 2 is a determinant of order n 1 1 2 3 Example 8 Find the minor of element 6 in the determinant A 4 5 6 8 Solution Since 6 lies in the second row and third column its minor 1 M23 3 8 14 6 obtained by deleting R and C in A is defined by Definition 2 Cofactor of an element denoted A 1 M where M is minor Example 9 Find minors and cofactors of all the elements of the determinant Solution Minor of the element Here a 1 So M Minor of a 3 M 2 Minor of the element a 2 4 M 1 Minor of the element a21 2 M 2 Minor of the element a 1 Now cofactor of a is A So A 1 M 1 3 3 A 2 1 2 M 1 4 4 A 1 1 M 1 2 2 A 2 1 2 M 2 1 1 1 Minor of a M Minor of a M Rationalised 2023 24 Example 10 Find minors and cofactors of the elements a a in the determinant a11 912 a13 a23 a31 a32 a33 Solution By definition of minors and cofactors we have 922 a23 a32 933 a22 a33a23 a32 Cofactor of a A 1 M A22 A33 A23 a32 11 11 11 a12 A 921 922 is given by a13 a a a 3 A32 21 DETERMINANTS 85 ed

5 Graph f x x and g x x 4

A matrix is said to be a column matrix if it has only one column 3 For example A 1 1 2 In general A a mx is a column matrix of order m 1 ii Row matrix 1 A matrix is said to be a row matrix if it has only one row For example B J1x4 In general B b x is a row matrix of order 1 n ii Square matrix 40 For example A is a column matrix of order 4 1 2 A matrix in which the number of rows are equal to the number of columns is said to be a square matrix Thus an m n matrix is said to be a square matrix if m n and is known as a square matrix of order n 4 MATHEMATICS 5 23 3 1 0 3 3 2 1 3 v Scalar matrix In general A a mxm Note If A a is a square matrix of order n then elements entries a a is a row matr 1 3 are said to constitute the diagonal of the matrix A Thus if A 2 4 3 5 Then the elements of the diagonal of A are 1 4 6 is a square matrix of order 3 is a square matrix of order m For example A 4 B Rationalised 2023 24 of order 1 2 3 respectively 1 olished iv Diagonal matrix A square matrix B b mxm is said to be a diagonal matrix if all its non diagonal elements are zero that is a matrix B b xm is said to be a diagonal matrix if b 0 when i j y 1 1 0 0 C 0 20 0 03 b 0 when i j y 1 1 6 a nn he are diagonal matrices A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal that is a square matrix B b nxn is said to be a scalar matrix

This means that rate of change of P with respect to x depends on the quantity s b which is the difference of selling price and the variable cost of each product Thus in order to gain profit this should be positive and to get large gains we need to produce large quantity of the product and at the same time try to reduce the variable cost Example 7 Let a tank contains 1000 litres of brine which contains 250 g of salt per litre Brine containing 200 g of salt per litre flows into the tank at the rate of 25 litres per minute and the mixture flows out at the same rate Assume that the mixture is kept uniform all the time by stirring What would be the amount of salt in the tank at any time t Solution Step 1 The situation is easily identifiable Step 2 Let y y t denote the amount of salt in kg in the tank at time t in minutes after the inflow outflow starts Further assume that y is a differentiable function When t 0 i e before the inflow outflow of the brine starts y 250 g x 1000 250 kg Note that the change in y occurs due to the inflow outflow of the mixture Now the inflow of brine brings salt into the tank at the rate of 5 kg per minute as 25 x 200 g 5 kg and the outflow of brine takes salt out of the tank at the rate of 25 or 206 00 4 1000 Thus the rate of change of salt with respect to t is given by dy Why dt or or 40 kg per minute as at time t the salt in the tank is MATHEMATICS Therefore dt 40 ax 1 1 40 e This gives a mathematical model for the given problem Step 3 Equation 1 is a linear equation and can be easily solved The solution of 1 is given by ye 200 e where c is the constant of integration Note that when t 0 y 250 Therefore 250 200 C or C 50 Then 2 reduces to y 200 50 1 40 t y 40 y 5 Rationalised 2023 24 y 200 50 e 40 200 Ce C or y t 50 1 40 e 40 1000 ERT kg 40 1 published 4

Linear Linear programming can be used in a variety of situations In most of the business or economical situation resources will be limited The problem there will be to make use of the available resources in such a way that to maximise the production or to minimize the expenditure These datas can be formulated as linear programming models The objective of the linear programming problem is to maximize the profit and minimize the total cost inng Froblem The LPP is to determine the values of the decision variables such that all the constraints are satisfied and gives the maximum or minimum value for the objective function The maximum or minimum value of the objective function is called an Optimum value Formulation of LPP resources The formulation of any situation to a LPP is based on the following guidelines 1 Identification of decision variables 2 Formation of objective function which is to be either maximize or minimize 3 The various constraints involved due to the limited availability of Mathematical Formulation of LPP The general form of LPP is as follows Max or Min z C x C X Cnxn Subject to a 1x A 2X2 nxn b a21x1 a22x2 a2nxn b am1x1 am 2x2 amn n bm x 0 V

Suppose there are n jobs J1J2Jn which are to be processed in two machines say M and M in order M M M first and M next Let tij be the processing time for ith job in jih machine The list of jobs along with their processing times can be summarized as in the following table Jobs Processing time in M Processing time in M J t11 t21 J t12 above t22 Let x2j be the time for which the machine M remains idle after completing the j 1 th job and before starting jth job A job is assigned to machine My first and after it has been completely processed in machine M it is assigned to the machine M If the machine M is not free at any moment for processing a particular job then that job has to wait in a waiting line for its turn on the machine M In other words passing is not allowed Hence machine My will always be busy and will process the n jobs one by one After processing all the n jobs the machine My remains idle until all the n jobs are completed in the machine M However M may remain idle after the completion of some of the m jobs and before starting the next job The sequencing problem is to minimize the total idle time of the second machine M Jn tin 32 tzn Hence the total idle time for machine M is E 1X2j Thus the sequencing problem is to minimize E1 X2 The total elapsed time T is given by T Processing time idle time i e T Ej 1t2j j 1 X2j Here some of the x2 may be zeros We observe that E 1 t2 is constant Hence minimizing T is equivalent to minimizing j1 X2j Algorithm to find the optimum sequence for n jobs in 2 machines Step 1 List the jobs along with their processing times in a table as given Step 2 Find the minimum tij t2j for all j 1 2 n Step 3 If the smallest processing time is for the first machine M then place the corresponding job in the first available position in the sequence If it is for the second machine M then place the corresponding job in the last available position in the sequence Step 4 If there is a tie in the minimum of all the processing times then there arises three cases Case i Minimum among all processing times is same for the two machines i e minimum t j t2j t t2s then place the rth job in the first available position in the sequence and the sth job in the last available position in the sequence Case ii If the tie is for the minimum among the processing times tij on machine M only then place the jobs arbitrarily one after the other in the last available positions in the sequence Case iii If the tie is for the minimum among the processing times t2j on machine M only then place the jobs arbitrarily one after the other in the last available positions in the sequence Stan 5 Remove the assigned jobs from the table If the table becomes

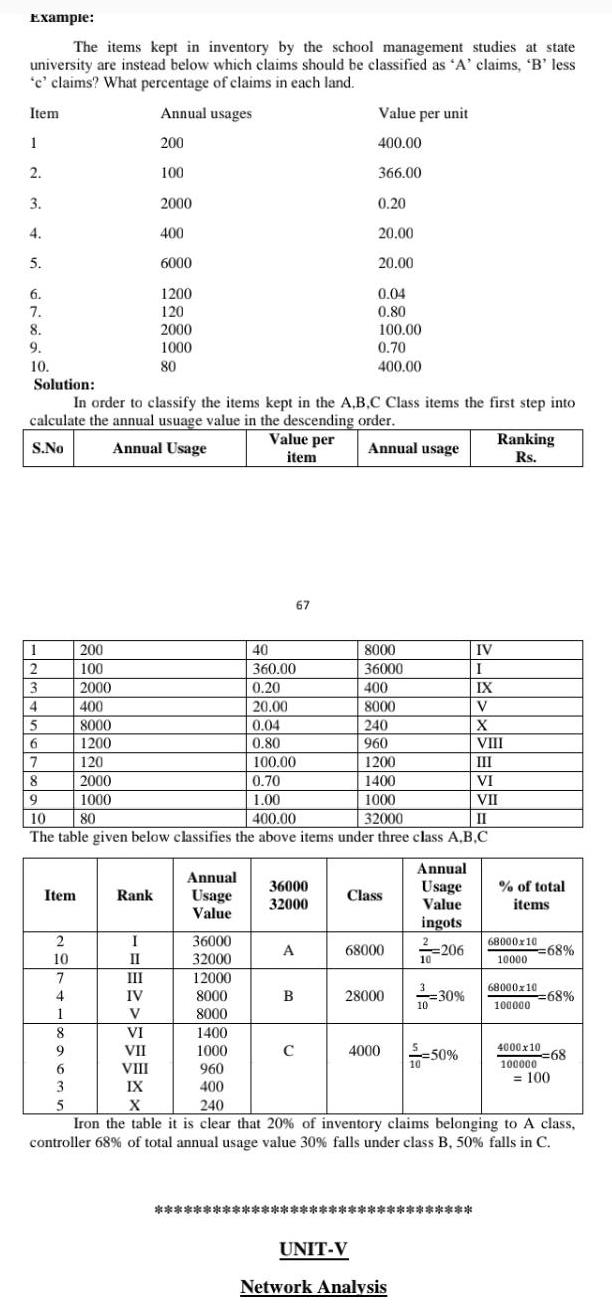
Example The items kept in inventory by the school management studies at state university are instead below which claims should be classified as A claims B less c claims What percentage of claims in each land Item Annual usages 1 200 2 3 4 5 6 7 8 9 10 Item 2 10 7 4 1 8 9 200 100 2000 400 8000 1200 120 2000 1000 6 3 5 Solution In order to classify the items kept in the A B C Class items the first step into calculate the annual usuage value in the descending order Value per item Annual Usage S No Annual usage Rank 100 I II 2000 400 6000 1200 120 2000 1000 80 III IV V 1 40 2 360 00 3 0 20 400 4 20 00 8000 5 0 04 240 6 0 80 960 7 100 00 1200 8 0 70 1400 9 1 00 1000 10 80 400 00 32000 The table given below classifies the above items under three class A B C Annual Usage Value 36000 32000 12000 8000 8000 1400 1000 960 400 36000 32000 A 67 B Value per unit 400 00 C 366 00 0 20 20 00 20 00 0 04 0 80 100 00 0 70 400 00 8000 36000 Class UNIT V 68000 28000 Annual Usage Value ingots 206 10 3 10 Network Analysis 30 4000 50 10 IV VI VII VIII IX X 240 Iron the table it is clear that 20 of inventory claims belonging to A class controller 68 of total annual usage value 30 falls under class B 50 falls in C Ranking Rs I IX V X VIII III VI VII II of total items 68000x10 10000 68000x10 100000 68 68 4000x10 10000068 100

The various paths are 1 2 3 Job 1 2 The critical path is 1 2 3 5 8 and 1 6 7 8 The project duration is 36 days Variance of the critical path 4 16 16 36 Exercises 1 A project consists of 12 jobs Draw a project network and determine the critical path 2 3 2 4 3 4 3 5 4 6 5 8 Activity 1 2 1 3 3 5 3 4 4 6 5 6 6 7 6 8 7 8 8 9 Duration 2 7 3 3 5 3 5 1 2 4 5 8 1 2 3 5 8 1 6 7 8 2 Consider the following project whose activities along with PERT time estimates the optimistic time a most likely time m and the pessimistic time b are given as follows a days 12 7 4 36 12 6 9 6 4 8 Job 6 7 75 6 10 7 9 8 9 9 10 m days 14 10 6 Duration 23 36 36 40 15 8 12 10 5 10 Duration 8 4 4 1 7 b days 21 16 10 60 24 12 18 15 7 14

10 Prove that the logarithmic function is increasing on 0 11 Prove that the function fgiven by f x x x 1 is neither strictly increasing nor decreasing on 1 1 TU 12 Which of the following functions are decreasing on 0 2 A cos x B cos 2x C cos 3x D tan x 13 On which of the following intervals is the function fgiven by f x x 00 sin x 1 decreasing A 0 1 D None of these 14 For what values of a the function f given by f x x ax 1 ncreasing on 1 2 15 Let I be any interval disjoint from 1 1 Prove that the function f given by 1 f x x is increasing on I X 16 Prove that the function fgiven by f x log TC TU B TC C 0 2 2 decreasing on 160 increasing on TC T TU 2 37 3 2 a Ge MATHEMATICS 17 Prove that the function fgiven by f x log cos x is decreasing on 0 0 7 ar is increasing on thenERPo 0 1 18 Prove that the function given by f x x 3x 3x 100 is increasing in R 19 The interval in which y x e is increasing is A B 2 0 C 2 Rationalised 2023 24 and D 0 2 6 4 Maxima and Minima In this section we will use the concept of derivatives to calculate the maximum or minimum values of various functions In fact we will find the turning points of the graph of a function and thus find points at which the graph reaches its highest or and lowest locally The knowledge of such points is very useful in sketching the graph of a given function Further we will also find the absolute maximum and absolute minimum of a function that are necessary for the solution of many applied problems Let us consider the following problems that arise in day to day life 1 The profit from a grove of orange trees is given by P x ax bx where a b are constants and x is the number of orange trees per acre How many trees per acre will maximise the profit ii A ball thrown into the air from a building 60 metres high travels along a path

X C Now let c be a real number such that c 0 Then f c c Also lim f x lim x c X C X C Since lim f x f c f is continuous is continuous at all points Example 8 Discuss the continuity of the function f given by f x x x 1 Solution Clearly fis defined at every real number c and its value at c is c c 1 We also know that fis a continuous function Thus lim f x f c and hence fis continuous at every real number This means X C Solution Fix any non zero real number c we have 1 1 Example 9 Discuss the continuity of the function f defined by f x x 0 X lim x x 1 c c 1 X C explanatory lim f x lim X C X f x X C X 1 Also since for c 0 f c we have lim f x f c and hence fis continuous X C at every point in the domain off Thus fis a continuous function 1 1 3 333 Rationalised 2023 24 0 3 0 2 5 We take this opportunity to explain the concept of infinity This we do by analysing 1 X the function f x near x 0 To carry out this analysis we follow the usual trick of finding the value of the function at real numbers close to 0 Essentially we are trying to find the right hand limit of fat 0 We tabulate this in the following Table 5 1 Table 5 1 0 3 0 2 0 1 10 0 01 10 5 10 100 10 0 001 10 10 f x 13 333 1000 10 10 We observe that as x gets closer to 0 from the right the value of f x shoots up higher This may be rephrased as the value of f x may be made larger than any given number by choosing a positive real number very close to 0 In symbols 1 lim f x x 0 to be read as the right hand limit of f x at 0 is plus infinity We wish to emphasise that is NOT a real number and hence the right hand limit of fat 0 does not exist as a real number Similarly the left hand limit of f The following table is self hed C real numbers Hence f CONTINUITY AND DIFFERENTIABILITY 109 Table 5 2 0 may be fou 10 10 10 10 3 10 10 2 10

function defined by wherever the limit exists is defined to be the derivative off The derivative of fis d dy denoted by f x or f x or if y f x by or y The process of finding dx dx derivative of a function is called differentiation We also use the phrase differentiate f x with respect to x to mean find f x 3 The following rules were established as a part of algebra of deriva 1 ut v u v 2 uv u v uv Leibnitz or product rule lim h 0 120 u v uv wherever v 0 Quotient rule The following table gives a list of derivatives of rtain standard functions Table 5 3 its answer If lim h 0 f x 2 I f x f c h f c h f x lim h 0 Therefore MATHEMATICS sec x Whenever we defined derivative we had put a caution provided the limit exists Now the natural question is what if it doesn t The question is quite pertinent and so is f c h f c does not exist we say that f is not differentiable at c h In other words we say that a function f is differentiable at a point c in its domain if both are finite and equal A function is said to be differentiable in an interval a b if it is differentiable at every point of a b As in case of continuity at the end points a and b we take the right hand limit and left hand limit which are nothing but left hand derivative and right hand derivative of the function at a and b respectively Similarly a function is said to be differentiable in an interval a b if it is differentiable at every point of a b f x h f x h and lim h 0 But for x c we have sin x f c h f c h lim X C COS X Rationalised 2023 24 f x f c lim f x f c X C f x f c X C Theorem 3 If a function f is differentiable at a point c then it is also continuous at that point Proof Since f is differentiable at c we have blish C COS X lim X C sin x f x f c X C f c 560 3 x c f x f c X C tan x x c COT ed

Example 18 Prove that the function defined by f x tan x is a continuous function Solution The function f x tan x sin x COS X TU that cos x 0 i e x 2n 1 2 We have just proved that both sine and cosine functions are continuous Thus tan x being a quotient of two continuous functions is continuous wherever it is defined This is defined for all real numbers such An interesting fact is the behaviour of continuous functions with respect to composition of functions Recall that if fand g are two real functions then fog x f g x is defined whenever the range of g is a subset of domain off The following theorem stated without proof captures the continuity of composite functions Theorem 2 Suppose fand g are real valued functions such that fog is defined at c If g is continuous at c and if fis continuous at g c then fog is continuous at c The following examples illustrate this theorem Example 19 Show that the function defined by f x sin x is a continuous function Solution Observe that the function is defined for every real number The function f may be thought of as a composition g o h of the two functions g and h where g x sin x and h x x Since both g and h are continuous functions by Theorem 2 it can be deduced that fis a continuous function Example 20 Show that the function f defined by f x 11 x x where x is any real number is a continuous function Solution Define 116 MATHEMATICS h 1 x x 1 x x f x In Example 7 we have seen that h is a continuous function Hence g being a sum of a polynomial function and the modulus function is continuous But then f being a composite of two continuous functions is continuous g x 1 x x and h by h x x for all real x Then hog x h g x Rationalised 2023 24 EXERCISE 5 1 1 Prove that the function f x 5x 3 is continuous at x 0 at x 3 and at x 5 2 Examine the continuity of the function f x 2x 1 at x 3 3 Examine the following functions for continuity a f x x 5 b f x 1 x 5 x 5

Teration 8 Show that the relation R in the set A 1 2 3 4 5 given by R a b ab is even is an equivalence relation Show that all the elements of 1 3 5 are related to each other and all the elements of 2 4 are related to each other But no element of 1 3 5 is related to any element of 2 4 9 Show that each of the relation R in the set A x Z 0 x 12 given by i R a b a b is a multiple of 4 ii R a b a b is an equivalence relation Find the set of all elements relate 10 Give an example of a relation Which is elle 1 Symmetric but neither reflexive nor transitive ii Transitive but neither reflexive nor symmetric iii Reflexive and symmetric but not transitive iv Reflexive and transitive but not symmetric v Symmetric and transitive but not reflexive 11 Show that the relation R in the set A of points in a plane given by R P Q distance of the point P from the origin is same as the distance of the point Q from the origin is an equivalence relation Further show that the set of all points related to a point P 0 0 is the circle passing through P with origin as centre 12 Show that the relation R defined in the set A of all triangles as R T T T is similar to T is equivalence relation Consider three right angle triangles T with sides 3 4 5 T with sides 5 12 13 and T with sides 6 8 10 Which triangles among T T and T are related ollec 13 Show that the relation R defined in the set A of all polygons as R P P P and P have same number of sides is an equivalence relation What is the set of all elements in A related to the right angle triangle T with sides 3 4 and 5 1 in each case 14 Let L be the set of all lines in XY plane and R be the relation in L defined as R L L L is parallel to L Show that R is an equivalence relation Find the set of all lines related to the line y 2x 4 Rationalised 2023 24 11 RELATIONS AND FUNCTIONS 7 15 Let R be the relation in the set 1 2 3 4 given by R 1 2 2 2 1 1 4 4 1 3 3 3 3 2 Choose the correct answer A R is reflexive and symmetric but not transitive B R is reflexive and transitive but not symmetric C R is symmetric and transitive but not reflexive D R is an equivalence relation 16 Let R be the relation in the set Ngiven by R a b a b 2 b 6 Choose the correct answer A 2 4 ER B 3 8 R C 6 8 R D 8 7 R 1 3 Types of Functions The notion of a function along with some special functions like identity function constant function polynomial function rational function modulus function signum function etc along with their graphs have been given in Class XI

What is AL 1 Draw any Why better to use wuring the lengt 4 FAB DE WO Exercise 5 1 ying in between A BC a AC s AB Note A that AC bele disadvantage in ervation 200 p between hut oder veget ay ABC Mre the length of All three points and AC mpang Ine segments that aru whle Venty whether the mid poid SHE mad poet of AC and is the m where A B C D on a straight ine say why A of Bo R D the mid point of AC D where A B C C07 uth that Buch Draw ve triangles and measure the sides Checke each case tsunof the length any he desi is the mid point of raight line say why All mast 309 id 1209 0 10 2 Where will the hand of a clock of a revolus a starts at 12 and make d starts at 2 and makes starts at 5 and makes a revolutions dockwise ution clock d starts at 5 and minesofaolution dockwise and make Nouth and Should ir this What part you stand facing la st ant tu the south and sum clock and tum Exercise 5 2 4 1001 tWhat fraction of a clockaine revolution does the four E How many right hand of a clock tum through when it goes from 710 58103 une full revolution specify dockwise of a lon Why noth evolution have you tume h Land Find the number of night angles uned through y hour hand dock when it gowe from 1355 028 wou and tum D north and tum ckase to fo west and tum to west id south and sam to north intiff in 1266 to weat wise to nas NURAY wit the hour hand of a clock stop fi i om 6 and tans through 1 night angle on and tuma through 2 right angles 0 from 10 and tums through 3 right angles 7 and tuma through 2 straight angles Exercise 5 3 DRO shes ange Clanuly each tight we than one outh more 1 Write down the measu a some acute angies some obtuse aigles hall noon ution blowing for eve walton of Exercise 5 4 What is the measure of a right ang70straight angle 2 Say True or The measure of an acute angle 90 b The measure of an abuse angle 30 fet The measure of a refox ange 180 da sight The measure of one complete revoto 360 e Itin A3 and mc 30 thn m CA mc Give at least two examples of nach 4 Messu the angles given below using the protractor and writs down the measure Wichangs Fland that mere Measure of ap L From these anges which has larger me Ea and then countem by meaning them 7 4 Menu ofangels Fin the banks with a ghaght 4 Ann whose messus is less than that of a Ito An angin whose measure is greater than that of a i An angle whose measures the sum of the of two night ang When the sum of the me res of two anges in that a When the sum of the measures of two gles is that s straight angis and if one of them is acute other should be then Find the First mure of the angle shown in each figurs mate with your eyes and then find the actual

A perpendicular line segment All that passes through the mid point of another linea called the perpendicular bisector of PQ Classification of Triangles You know now that a portion covered by three line segments is called a triangle Look at adjoining figures of triangles in the first fig a three sides are equal in the second Some Special Quadrilaterals b two of the sides are equal But in the third fig c all three sides are unequal Here are some special quadrilaterals Square A equal sides b 4 right angles 4 WI GA 4 In the same way in fig d triangle has all three acute angles fig e contains a right angle and triangle has an obtuse angle Hence all triangles can be named on the basis of measurement of sides or angles Types of Triangles at the Basis of Sides 0 A triangle that has all three its sides unequal is called a scalerie triangle Fig c A triangle that has two of its sides equal is called isosceles triangle Fig b i A triangle that has all three sides are equal is called equilateral triangle Fig a Types of Triangles at the Basis of Angles 1 If each of a triangle is less than 90 then the triangle is called an acute angled triang Fig d i If any one angle in a triangle is right angle ie of 90 then the triangle is called a angled triangle Fig e i If any one angle in a triangle is an obtuse is larger than then the triangle is an obtuse angled triangle fig f Quadrilaterals A polygon made of four straight edges and four corners vertices is called a quadrilateral Given polygon ABCD is a quadrilateral as it has four 0 Sides AB BC CD DA i Angles ZA ZB ZC ZD i Vertices A B C D When you look around yourself you find many quadrilateral figures in your daily life Examples Your study table on which you study and acquire knowledge the picture frame which your picture looks attractive bedsheet which you use to have a sound sleep or a kite alla in the quadrilateral shape 52 Properties of a Square a Diagonals of square are equal b Diagonals of square are perpendicular to each other c Diagonals bisect each other i Rectangle X a 2 pairs of opposite equal sides b 4 night angles Properties of Rectangle a Opposite sides of a rectangle are equal and parallel b Diagonals of a rectangle are equal e Diagonals of a rectangle bisect each other ii Khombus a 4 equal sides b Opposite sides are parallel c Opposite angles are equal Properties of Rhombus A Opposite angles of a rhombus are equal 6 The diagonals of a shombus are perpendicular bisector of each other iv Parallelogram a 2 pairs of opposite equal sides b Opposite siden are parallel c Opposite angles are equal Properties of a Parallelogram a Opposite sides of a parallelogram are equal b Opposite angles of a parallelogram are equal c Diagonals of a parallelogram bisect each other Do You Know Square is a special kindvof parallelogram

n s 1 p sp n E 0 1 p s p 1 Sp N s 1 p 1 This queueing modrl with limited waiting room is valuable because of its relevance to many real situations and the fact that changes may be made to its properties by adjusting the number of servers or the capacity of the waiting room However while poission arrivals are common in practice negative exponential service times are less so and it is the second assumption in the system MIMs that limits its usefulness Example A supermarket has two girls ringing up stales at the counters If the service time for each customer is exponential with mean 4 minutes and if people arrive in a poission fashion at the counter at the rate of 10 per hour then calculate Solution a The probability of having to wait for service b The expected percentage of idle time for each girl c If a customer has to wait find the expected length of his waiting time a Probability of having to wait for service is P W 0 Po s 1 p 1 6 s s 2 Now compute Po 1 n 0 52 16 0 5 p s sp n sp s n n s 1 P n 0 2 1 3 2 1 3 1 2 3 4 9 2x2 31 1 2 Thusprob W 0 21 1 3 1 6 b The fraction of the time the service remains busy is given by p us 1 3 2 1 3 1 3 Theefore the fraction of the time thee service remains idle is 1 1 3 2 3 67 nearly c W W 0 3 minutes

The following table gives the activities in a construction project and other relevant information Activity Duration Days i ii iii Solution L 0 E 0 Activity 1 2 1 3 2 3 20 25 10 Draw the network for the project 3 4 4 5 Duration 20 0 1 3 25 0 III 2 3 10 20 2 4 12 20 6 30 10 Find the critical path and the project duration Find the total float for each activity 1 2 Activity 1 2 1 3 1 4 2 5 3 6 L 20 E 20 3 E 30 L 30 The critical path is 1 2 3 4 5 The project duration is 46 days Solution T EST 36 Problem 2 A project has the following time schedule Time in months 2 2 1 4 8 75 20 70 EFT 20 25 30 32 36 46 i Construct the network ii Find the total float for each activity iii 2 4 12 E 36 L 36 LST 0 5 20 24 30 36 Find the critical path and the project duration L 11 E 6 Activity 3 7 4 6 5 8 6 9 7 8 8 9 3 4 6 LFT 20 30 30 36 36 46 5 E 46 L 46 L 12 E 11 4 5 10 TF 0 5 0 4 0 0 Time in months 5 3 1 5 4 3 70

NANA t The total cost per year C Q G Cs QC D GO Differenhating w r to Q We get dQ t d CA Q 2D doz Total ordering cost total inventory carrying cost C s C Gis always posture Q 0 is given by Q 2DG C For this value of Q CA Q in minimum toQus Q dQ 2DG 55 2DG C CA O 2DG When Q G This ordering quantity is denoted by Q t 56 time

Solution Job 1 2 7 8 2 3 3 5 5 8 6 7 4 5 2 4 1 6 The various paths are 1 2 1 6 2 3 2 4 TE 1 2 3 3 5 4 5 6 7 5 8 7 8 3 TD Tp 4Tm The critical path is 1 2 3 5 8 The project duration is 36 days Variance of the critical path 4 16 4 1 25 6 42 6 7 108 6 18 84 6 14 66 6 11 24 6 4 66 6 11 42 6 7 30 6 5 36 6 6 3 2 6 2 5 3 1 2 3 5 8 1 2 4 5 8 1 6 7 8 3 1 4 73 5 SD Tp 2 4 4 2 1 4 2 1 2 6 Problem 4 The following table lists the jobs of a network with their time estimates Job Optimistic Duration days Most Likely 6 5 7 12 5 11 6 9 4 19 To Variance 16 16 4 1 16 4 1 4 Duration 36 23 35 Pessimistic HHGBHS 15 14 30 17 15 27 7 28 72

vausvAI The objective function is maximization so the resulting LPP becomes Max z 5x 3x 0x3 0x4 0x5 subject to X x2 x3 2 5x 2x x 10 3x1 8x2 x5 12 x 20 Vi 1 2 5 The initial basic feasible solution is obtained by putting x x2 0 in the reformulated form of LPP and we get x3 2 x4 10 x5 12 Starting Simplex Table 000 CB XB 5 0 0 1 X3 2 Y3 X4 10 Y4 5 X5 12 Y5 2 First Iteration CB 72 CBi Yij B1 Z G Z C YB XB X 2 X4 0 X5 6 New Pivot equation old equation pivot element Z 0 72 CBi Xij j 1 2 9 5 C YB Y 1 Y 0 Ys 0 5 5 0 Y 5 Y 1 2 8 0 3 1 3 5 5 2 7 3 Y 3 Y 1 0 0 0 0 1 5 3 5 5 0 Y3 0 Y3 Hence an optimal basic feasible solution is obtained Solution is x 2 x 0 and Max z 10 Exercise 0 1 0 0 0 0 1 0 0 0 0 Y 0 Y 0 0 1 0 0 0 0 1 0 0 1 Solve the following LPP using simplex method Min z x 3x2 2x3 subject to 3x1 x2 2x3 7 0 Y 0 Y Ratio 2 2 4 XBi Yir 2x 4x2 12 4x 3x2 8x3 10 and x 0 Vi 1 2 3 2 Solve the following LPP using simplex method

The objective function is converted to maximisation objective function The resulting LPP becomes Max z 12x 20x 0x3 0x4 Mx5 Mx subject to 6x1 8x2x3 x5 100 7x1 12x2x4 x6 120 xi 20 Vi The initial basic feasible solution is obtained by putting x x x3 X4 0 in the reformulated form of LPP and we get x5 100 x6 120 Starting Simplex Table CB M M M 20 XB X5 100 Y X6 120 Y6 n First Iteration Z CBiYij j 1 Z G 12 20 CB XB X5 20 Y5 X 10 Y Second Iteration C YB Y CB XB X 15 X 5 4 n z CBt Yij Z Gj 72 12 6 7 13M G 12 YB Y 13M 20 4 3 7 12 4M 3 1 3 C YB Y 1 Y 0 z CBiY ij 7 1 4 G 12 Y 12 0 4M 3 35 3 20 0 1 20 8 12 20M 9 Y 20M 20 0 20 Y 0 20 Y 0 1 20 0 Y3 1 0 M M ol 0 Y3 1 0 M M 0 Y3 3 4 7 16 14 14 0 Y 0 1 M M 10 0 Y4 2 3 1 12 2M 5 5 3 2M 5 5 3 1 0 M 0 Y4 7 3 0 5 12 7 3 Hence an optimal basic feasible solution is obtained Solution is x 15 x 5 4 and Max z 205 M M Ratio Y5 Y5 1 0 M Y6 0 1 M 0 M Ratio 0 XBi Yir 12 5 10 XBi Yir 15 120 7

The initial basic feasible solution is obtained by putting x x x3 X4 0 in the reformulated form of LPP and we get x5 900 x6 1200 Starting Simplex Table CB M M CB First Iteration M 60 CB 80 60 XB X5 900 Ys 20 X6 1200 Y 40 60M z CBi Yij j 1 Z Gj XB X 300 X 30 Second Iteration C 5 72 C YB 72 z CBi Yij 1 Z G Y Y6 Y C YB z CBiYij 1 Z G 60 Y 60M 60 0 0 1 60 60 Y XB X 20 Y 0 X 15 Y 1 60 Y 60 0 11 30 30 60M 80 60M 80 15 3 4 Y 80 Y 15M 45 0 15M 35 80 Y 1 0 80 12 0 Y3 Y 1 0 M 0 M M 1 0 M M 0 0 Y3 1 15 1 20 7 3 0 1 M Y3 Y4 7 3 HHH 0 lo M 2 3 2 M 2 3 2 1 3 Hence an optimal basic feasible solution is obtained Solution is x 15 x 20 and Max 2 2500 M M Ys 1 0 1 M M 0 Y4 1 30 1 20 1 3 0 1 2 1 1 40 0 0 M Y5 M Y 0 0 Ratio Ratio XBi Yir 20 40 45 30 XBi Yir

vausva The objective function is maximization so the resulting LPP becomes Max z 5x 3x 0x3 0x4 0x subject to x x2 x3 2 5x 2x x 10 3x1 8x2 x5 12 x 0 Vi 1 2 5 The initial basic feasible solution is obtained by putting x x2 0 in the reformulated form of LPP and we get x3 2 x4 10 x5 12 Starting Simplex Table 000 CB XB 5 0 0 1 X3 2 Y3 X4 10 Y4 5 X5 12 Y5 2 First Iteration CB 72 CBi Yij B1 Z G Z C YB XB X 2 X4 0 X5 6 New Pivot equation old equation pivot element Z 0 72 CBi Xij j 1 2 9 5 C YB Y 1 Y 0 Ys 0 5 5 0 Y 5 Y 1 2 8 0 3 1 3 5 5 2 7 3 Y 3 Y 1 0 0 0 0 1 5 3 5 5 0 Y3 0 Y3 Hence an optimal basic feasible solution is obtained Solution is x 2 x 0 and Max z 10 Exercise 0 1 0 0 0 0 1 0 0 0 0 Y 0 Y 0 0 1 0 0 0 0 1 0 0 1 Solve the following LPP using simplex method Min z x 3x2 2x3 subject to 3x1 x2 2x3 7 0 Y 0 Y Ratio 2 2 4 XBi Yir 2x 4x2 12 4x 3x2 8x3 10 and x 0 Vi 1 2 3 2 Solve the following LPP using simplex method

7 Which of the following phenomena of light are involved in the formation of a rainbow A Refraction B Dispersion C Internal reflection Only one correct answer A A and B only B B and C only C D A and C only Review All A B and C 0

is a px p symmetric matrix with spectral decomposition A FAIT where diag A show that det A tr A

1 point Consider the matrix 0 A Answer 7 x 368 15T 3 3 x 9 x 9 and let B be a matrix similar to A i e B is of the form SAS for some nonsingular matrix S Find all possible values of a so that det B 0 Separate multiple values by a comma

1 point Find the determinant of the matrix M and use the adjoint method to find M det M 2 2x 6 2x 4x x 1 x 2x 10 6x 20 12x M 18881 0 0 3 3x

given the graph of the function y f x evaluate F 1 Given the graph of the function y f x evaluate f 1 undefined 02

Multiply the monomials 4a7 2a 4a7 2a Simplify your answer Use integers or fractions for any numbers in the

Divide Express your answer in standard form 4 2 i 4 2 i 11

3 Write the point slope form of the equation of the line through the given point with the given slope 9 8 through 3 2 slope 2 A y 2 2 x 3 B y 3 x 2 C y 3 x 2 D y 3 x 2 9 through 2 5 slope A y 2 x 5 B y 2 x 5 C y 2 x 5 D y 5 x 2 Write the point slope form of the equation of the line through the given points 10 through 5 1 and 5 1 11 11 through 1 3 and 0 3 A 0 x 5 A y 1 6 x 3 B y 1 x 5 B y 3 6 x 1 C y 1 x 5 D y 1 3 x 5 C y 3 x 1 6 D y 1 6 x 3 3 2

36 MATHEMATICS respectively Similarly in the second arrangement the entries in the first row represent the number of notebooks possessed by Radha Fauzia and Simran respectively The entries in the second row represent the number of pens possessed by Radha Fauzia and Simran respectively An arrangement or display of the above kind is called a matrix Formally we define matrix as Definition 1 A matrix is an ordered rectangular array of numbers or functions The numbers or functions are called the elements or the entries of the matrix We denote matrices by capital letters The following are some examples of matrices 2 5 A 0 5 3 6 B 3 5 3 2 i 3 Jou 1 7 5 N a 12 a22 m2 SUNNI In the above examples the horizontal lines of elements are said to constitute rows of the matrix and the vertical lines of elements are said to constitute columns of the matrix Thus A has 3 rows and 2 columns B has 3 rows and 3 columns while C has 2 rows and 3 columns 3 2 1 Order of a matrix A matrix having m rows and n columns is called a matrix of order m n or simply m n matrix read as an m by n matrix So referring to the above examples of matrices we have A as 3 x 2 matrix B as 3 x 3 matrix and C as 2 x 3 matrix We observe that A has 3 x 2 6 elements B and C have 9 and 6 elements respectively In general an m xn matrix has the following rectangular array C A 13 aj A23 x cosx sinx 2 or A almx 1 i m l j n i jEN n Thus the 7th row consists of the elements a consists of the elements a az azamj 1 x Rationalised 2023 24 am Azn in mn mxn a2 a3 ain while the 7th column In general a is an element lying in the 7th row and jth column We can also call it as the i j th element of A The number of elements in an m n matrix will be equal to mn MATRICES 37 Note In this chapter 1 We shall follow the notation namely A a to indicate that A is a matrix of order mx n

This new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order Thus if A 2 3 matrix Then we define A B Example 6 911 912 913 921 922 923 is a 2 x 3 matrix and B and is given by A B In general if A a and B b are two matrices of the same order say m n Then the sum of the two matrices A and B is defined as a matrix C c a b for all possible values of i and j 3 1 1 Since A B are of the same order 2 3 0 and B she a 1 b a 2 b 2 a21 b 1 a22 b 2 2 3 1 5 1 1 2 2 15 3 3 0 defined For example if A 2 51 2 3 b b2 b 3 b 1 b22 23 6 a 3 b 3 a23 b 3 is another 3 Therefore addition of A and B is defined 1 2 123 01 Note 1 We emphasise that if A and B are not of the same order then A B is not 13 3 B 1 then A B is not defined 2 We may observe that addition of matrices is an example of binary operation on the set of matrices of the same order 3 4 2 Multiplication of a matrix by a scalar Now suppose that Fatima has doubled the production at a factory A in all categories refer to 3 4 1

iii Write the elements a3 a21 a332 a242 a23 2 If a matrix has 24 elements what are the possible orders it can have What if it has 13 elements 3 If a matrix has 18 elements what are the possib orders it can have What if it has 5 elements 4 Construct a 2 2 matrix A i j 2 5 Construct a 3 x 4 matrix whose elements are given by 1 aj 1 X 1 a ii a 2i j 6 Find the values of x y and z from the following equations 4 3 1 A x 35 3 a whose elements are given by 5 2 3x Z 7 Find the value of a b c and d from the equation a b 2a c 30 4 0 5 2a b 3c d 8 A am is a square matrix if n A m n B m n ii y 7 x y 2 5 z xy Rationalised 2023 24 0 y 2 4 62 58 Factory at A Boys Girls 13 C m n D None of these 9 Which of the given values of x and y make the following pair of matrices equal 3x 7 x 8 y 1 iii aij D x y present B Not possible to find 2 2 Boys 2 C y 7 x 3 3 3 10 The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is A 27 B 18 C 81 Factory at B i 2j 2 x y z x Z y z MATRICES Girls II 3 4 Operations on Matrices In this section we shall introduce certain operations on matrices namely addition of matrices multiplication of a matrix by a scalar difference and multiplication of matrices 5 3 4 1 Addition of matrices Suppose Fatima has two factories at places A and B Each factory produces sport shoes for boys and girls in three different price categories labelled 1 2 and 3 The quantities produced by each factory are represented as matrices given below 43

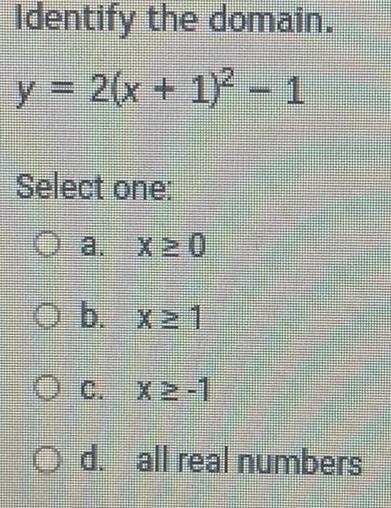
Identify the domain y 2 x 1 2 1 Select one O a x 20 O b x 21 O c x2 1 O d all real numbers

4 The height of a firework at a 4th of July celebration can be modeled by a quadratic function Suppose the firework is launched from a platform thre feet off the ground at a velocity of 96 feet per second Use h t 16t vt ho a Write a function to represent the situation b Show steps to find the vertex and describe its meaning in context

Consider the systems of equations below from previous exercises for each system write it as Ax b and then try to perform LU factorization on A note this means the b portion of the augemented matrix you Should not include 3x2 6x3 6X4 4X5 5 3X 7x2 8x3 5x4 8x5 9 3x1 9x2 12X3 9x4 6Xs 15 b 2x y 2 180 X 3y 27 300 2x 27 240