Matrices & Determinants Questions and Answers

Algebra
Matrices & DeterminantsUse the fundamental identities to fully simplify cos x sin x csc x Enclose arguments of functions in parentheses For example sin 2x cos x sin x csc x FOT
Algebra
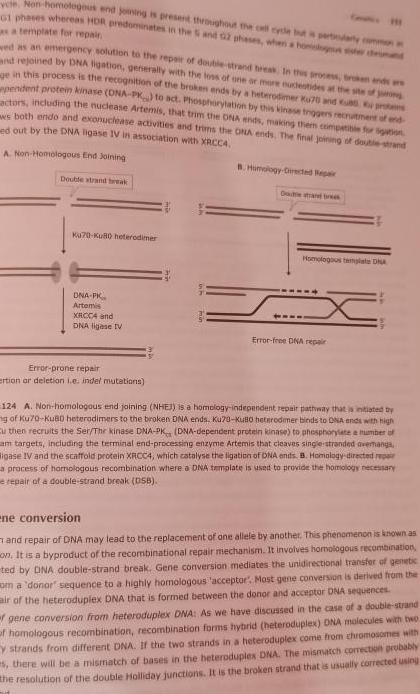
Matrices & Determinantsvete Non homologous end Soming is present throughout the cell cycle but is particularly common G1 phases whereas HDR predominates in the 5 and 12 phases when a homloy sister druand as a template for repair ed as an emergency solution to the repair of double strand breas In this process broken andre and rejoined by DNA ligation generally with the loss of one or more nucleotides at the site of ge in this process is the recognition of the broken ends by a heterodimer Ku70 and usu pro pendent protein kinase DNA PK to act Phosphorylation by this kinase trggers recruitment of end actors including the nuclease Artemis that trim the DNA ends making the compatible for gation s both endo and exonuclease activities and trims the ONA ends The final joining of double strand ed out by the DNA ligase IV in association with XRCC4 A Non Homologous End Joining Double strand break Ku70 Ku80 heterodimer DNA PK Artemis XRCCA and DNA ligase IV Error prone repair Ertion or deletion i e indel mutations B Himology Directed Repair Homologous template D x Error free DNA repair 124 A Non homologaus end joining NHEI is a homology independent repair pathway that is initiated by g of Ku70 Ku80 heterodimers to the broken DNA ends Ku70 KUBo heterodimer binds to ONA ends with high Cu then recruits the Ser The kinase DNA PK DNA dependent protein kinase to phosphorylate a number of am targets including the terminal end processing enzyme Artemis that cleaves single stranded avemangs ligase IV and the scaffold protein XRCC4 which catalyse the ligation of DNA ends B Homology directed repair a process of homologous recombination where a DNA template is used to provide the homology necessary e repair of a double strand break DSB ene conversion and repair of DNA may lead to the replacement of one allele by another This phenomenon is known as on It is a byproduct of the recombinational repair mechanism It involves homologous recombination ted by DNA double strand break Gene conversion mediates the unidirectional transfer of genetic om a donor sequence to a highly homologous acceptor Most gene conversion is derived from the air of the heteroduplex DNA that is formed between the donor and acceptor DNA sequences f gene conversion from heteroduplex DNA As we have discussed in the case of a double strand of homologous recombination recombination forms hybrid heteroduplex DNA malecules with two y strands from different DNA If the two strands in a heteroduplex come from chromosomes with s there will be a mismatch of bases in the heteroduplex DNA The mismatch correction probably the resolution of the double Holliday junctions It is the broken strand that is usually corrected using

Algebra
Matrices & Determinants9 Show that if the first and second columns of the 3x3 determinant in number 8 interchanged the value of the determinant changes sign
Algebra
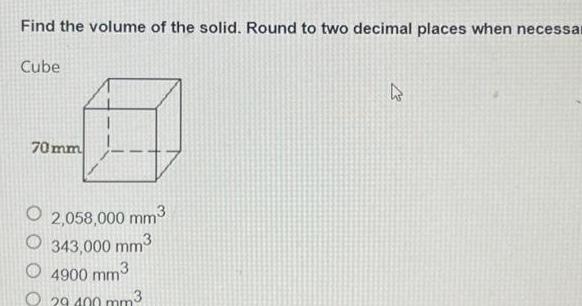
Matrices & DeterminantsFind the volume of the solid Round to two decimal places when necessar Cube 70mm 2 058 000 mm 343 000 mm3 4900 mm 29 400 mm3 4
Algebra
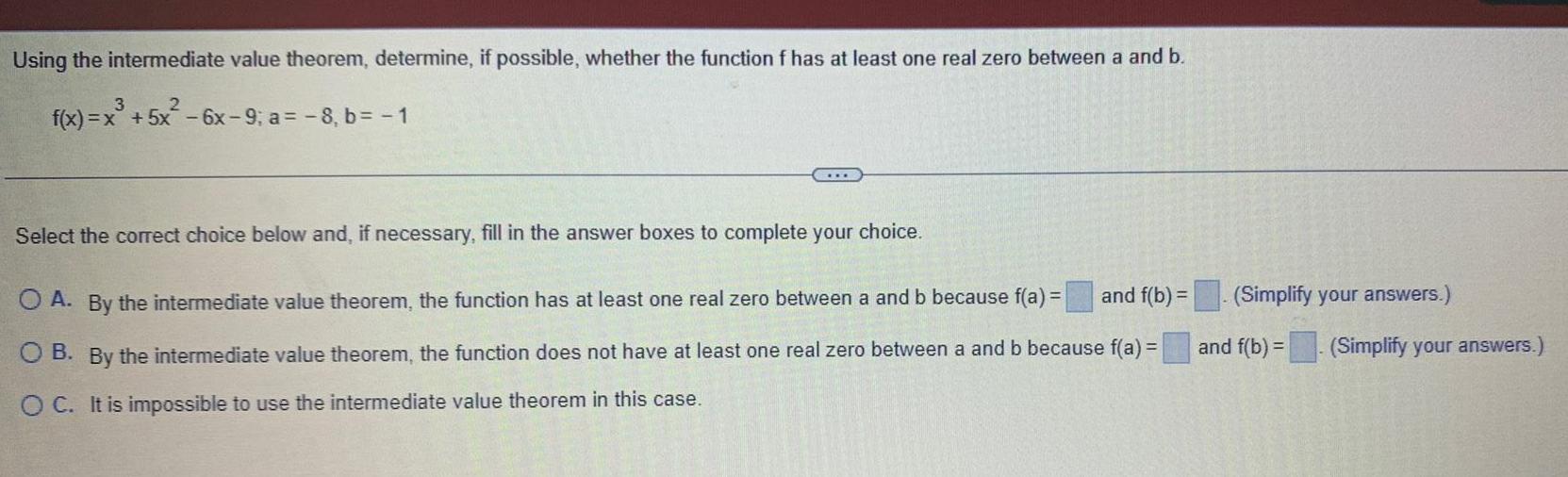
Matrices & DeterminantsUsing the intermediate value theorem determine if possible whether the function f has at least one real zero between a and b 3 2 f x x 5x 6x 9 a 8 b 1 Select the correct choice below and if necessary fill in the answer boxes to complete your choice and f b O A By the intermediate value theorem the function has at least one real zero between a and b because f a O B By the intermediate value theorem the function does not have at least one real zero between a and b because f a O C It is impossible to use the intermediate value theorem in this case Simplify your answers and f b Simplify your answers

Algebra
Matrices & Determinants20 Solve the following equation for x 25 ln x 4ln x Express numbers in exact form Use symbolic notation and fractions where need

Algebra
Matrices & Determinants60 The terminal velocity for an object dropped near the surface of Earth is the maximum downward velocit by the falling object For a man of average size the terminal velocity is about 176 feet per second It is f velocity v in feet per second t seconds into his fall before he opens his parachute is given by v 176 1 0 75 How long does it take the skydiver to achieve 99 of terminal velocity Give your answer to the nearest second Macmillan Learnir

Algebra
Matrices & Determinantswe know that the range of the principal value branch of sin 7 5 sin Example 2 Find the principal value of cot cot 1 2 Solution Let cot Therefore principal alue of sin 2 57 732 3 1 sin 7 sec 3 cot y 2 3 Fy Then 1 77 33 A T 11 tan 1 cos 13 If sin x y then A 0 y n cot Co 57 We know that the range of principal value branch of cot is 0 and er Find the principal values of the following 9 4 tan 3 DE OU Hence principal value of cot 10 cosec 2 Find the values of the following 1 2 2 cos 5 cos B EXERCISE 2 1 cot x 7 cot 7 3 8 cot 3 C 0 y 14 tan 3 sec 2 is equal to sin Rationalised 2023 24 TU 3 3 2 3 1 2 D 3 cosec 2 6 tan 1 9 cos B Isys1 2 TU INVERSE TRIGONOMETRIC FUNCTIONS 27 12 cos 2 3 V CORT EN T 22 2 11 12 2 sin 2 3 and 1 ublished

Algebra
Matrices & Determinantsrestricted to any of the intervals etc is bijective 2 2 2 2 2 2 and its range is R Thus tan can be defined as a function whose domain is R and range could be any of the intervals intervals give different branches of the function tan The branch with range is called the principal value branch of the function tan We thus have tan R The graphs of the function y tan x and y tan x are given Y y tan x intervals T 2 3 3 17 19 4 2 2 2 2 2 2 T T T 3 2 NCER X Rationalised 2023 24 and so on These 2 1 TC T Fig 2 5 i ii 2 3T 2 T 2 O 12 TC 2 2 Y y tan x republished Fig 2 5 i Fig 2 5 ii We know that domain of the cot function cotangent function is the set x x R and x n n Z and range is R It means that cotangent function is not defined for integral multiples of If we restrict the domain of cotangent function to 0 then it is bijective with and its range as R In fact cotangent function restricted to any of the intervals 0 0 2 etc is bijective and its range is R Thus cot can be defined as a function whose domain is the R and range as any of the X INVERSE TRIGONOMETRIC FUNCTIONS 25 2 ete These intervals give different branches of the

Algebra
Matrices & Determinants90 70 75 Suppose Fatima wants to know the total production of sport shoes in each price category Then the total production In category 1 for boys 80 90 for girls 60 50 In category 2 for boys 75 70 for girls 65 55 In category 3 for boys 90 75 for girls 85 75 80 90 This can be represented in the matrix form as 75 70 90 75 1 2 3 44 MATHEMATICS 80 75 90 60 65 85 911 912 913 Thus if A 921 922 923 1 2 3 Rationalised 2023 24 Example 6 Given A This new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order 2x3 matrix Then we define A B is a 2 3 matrix and B 31 2 3 0 a b a 2 b 2 a21 b 1 a22 b 2 and B 50 55 75 2 5 60 50 65 55 85 75 2 3 In general if A a and B b are two matrices of the same order say m n Then the sum of the two matrices A and B is defined as a matrix C c c a b for all possible values of i and j where b b2 b13 b21 b2 a 3 b 3 a23 b 3 b23 is another 45 Since A B are of the same order 3 Therefore addition of A and B is defined and is given by 12 55 1 255 1 1 2 6 1 1 5 07

Algebra
Matrices & DeterminantsSupport Fatiila has two latiunits at places A allu D Each factory products spont shoes for boys and girls in three different price categories labelled 1 2 and 3 The quantities produced by each factory are represented as matrices given below 44 Boys 80 75 90 Suppose Fatima wants to know the total production of sport shoes in each price category Then the total production In category 1 for boys 80 90 for girls 60 50 In category 2 for boys 75 70 for girls 65 55 In category 3 for boys 90 75 for girls 85 75 80 90 This can be represented in the matrix form as 75 70 90 75 1 2 3 MATHEMATICS Factory at A In general if A 2x3 matrix Then we define A B Girls 60 65 85 Example 6 Given A A B 9 1 912 913 Thus if A is a 2 x 3 matrix and B 921 922 923 This new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order Rationalised 2023 24 2 2 31 Since A B are of the same order and is given by 1 2 3 2 3 0 2 3 1 5 1 1 1 5 1 1 3 3 0 Factory at B Boys 90 70 75 Then the sum of the two matrices A and B is defined as a matrix C c a b for all possible values of i and j a and B b are two matrices of the same order say m n where defined For example if A a b a 2 b 2 a21 b 1 a22 b22 and B 2 5 1 2 3 B 1 0 2 3 Girls 50 55 75 60 50 65 55 85 75 2 3 1 5 0 1 0 2 6 b b 2 b13 b 1 b22 b 3 a 3 b 3 a23 b 3 1 2 3 1 10 1 Therefore addition of A and B is defined is another Note 1 We emphasise that if A and B are not of the same order then A B is not use then A B is not defined

Algebra
Matrices & Determinantssin We know that the range of the principal value branch of sin is 1 1 TU 4 cot Example 2 Find the principal value of cot Solution Let cot y Then 3 Therefore principal value of sin 1 sin meno 7 sec cot y Find the principal values of the following 1 2 cot 3 3 We know that the range of principal value branch of cot is 0 and 2 1 Hence principal value of cot 9 4 tan 3 2 3 A T 11 tan 1 cos 13 If sin x y then A 0 y n cot 1 2 10 cosec 2 Find the values of the following 2 cos 5 cos EXERCISE 2 1 B Cop sin C 0 y n 14 tan 3 sec 2 is equal to cot 8 cot 3 3 3 2 er 2 Rationalised 2023 24 11 12 D EN IS IS 3 cosec 2 6 tan 1 2 3 INVERSE TRIGONOMETRIC FUNCTIONS 27 9 cos T B 1 120 2 T 12 cos CERT p I 1 2 2 11 2 2 sin 11 2 w 5 and 2 ublished 2 3 Properties of Inverse Trigonometric Functions In this section we shall prove some important properties of inverse trigonometric functions It may be mentioned here that these results are valid within the principal
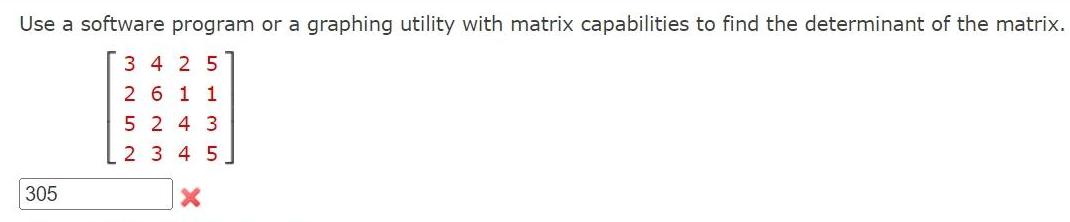
Algebra
Matrices & DeterminantsUse a software program or a graphing utility with matrix capabilities to find the determinant of the matrix 34 25 26 11 305 5243 2 3 4 5 X
Algebra
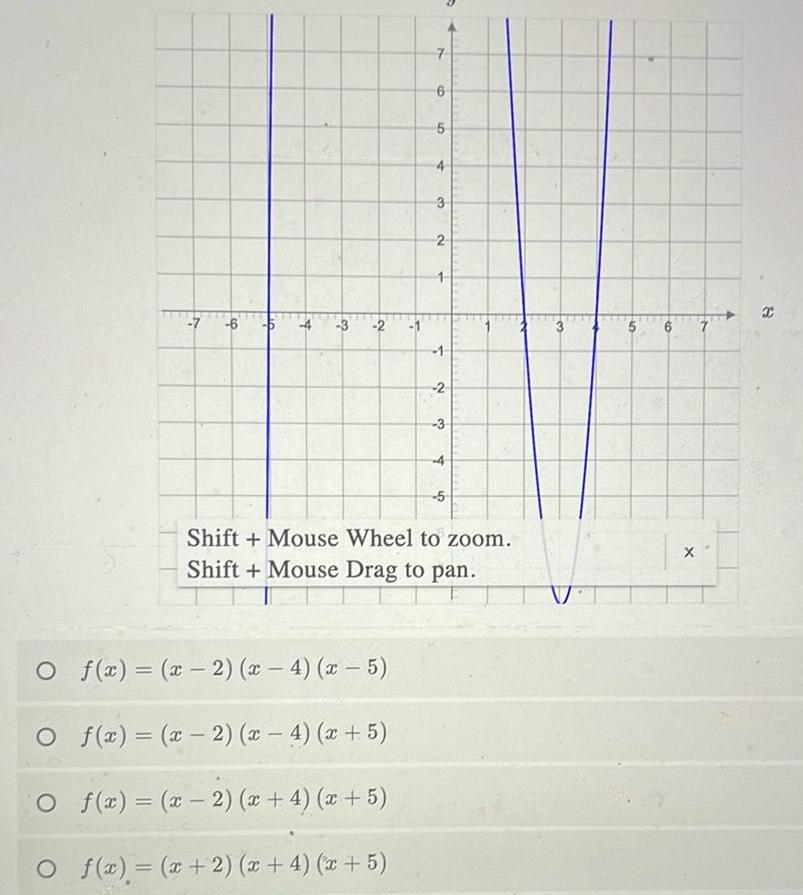
Matrices & DeterminantsO O 6 10 3 2 f x x 2 x 4 x 5 f x x 2 x 4 x 5 7 O f x x 2 x 4 x 5 O f x x 2 x 4 x 5 6 5 4 3 2 1 1 2 3 Shift Mouse Wheel to zoom Shift Mouse Drag to pan 4 5 V S 6 X X

Algebra
Matrices & Determinants9 Given a set P of P R P 1 x x x 1 2x a Use the Wronskian to show that P is a basis for P R Page 2

Algebra
Matrices & DeterminantsDefinition A graph in which any two distinct points are adjacent is called a complete graph A complete graph with p vertices is denoted by K K K K K Fig 1 8 Note The number of edges of a complete graph K is p C 2 Ks 5 NULL GRAPH Definition A graph G whose edge set is empty is called a null graph or a totally disconnected graph
Algebra
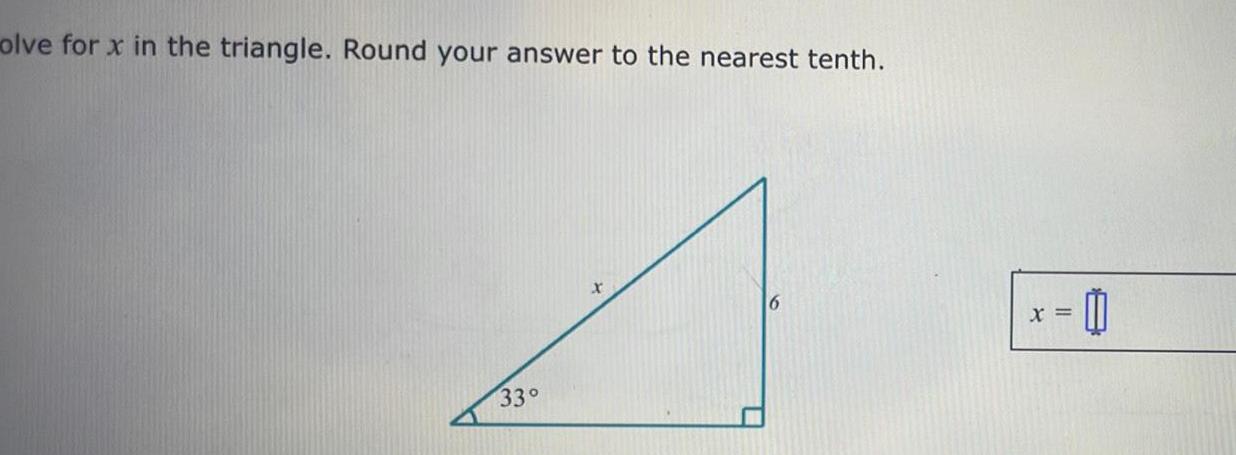
Matrices & Determinantsolve for x in the triangle Round your answer to the nearest tenth 33 6 X

Algebra
Matrices & DeterminantsSolve the system of equations by the method of your choice 5x y 3 20x 4y 7

Algebra
Matrices & DeterminantsGiven below is the principal owed on a student loan last month the annual interest rate and the way the minimum monthly payment is computed Find this month s minimum payment due Method for Calculating Minimum Monthly Payment finance charge 40 1 5 of principal Principal 23 700 Annual Rate 9 This month s minimum payment is Round to the nearest cent as needed CLIXE
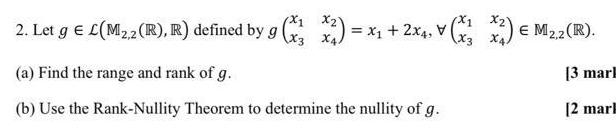
Algebra
Matrices & Determinants2 Let g L M2 2 R R defined by g x x x 2x4 x x2 M 2 R E M2 2 3 mark 2 marl a Find the range and rank of g b Use the Rank Nullity Theorem to determine the nullity of g

Algebra
Matrices & DeterminantsThe function f t 1 5t 16 9 can be used to estimate the yearly sales of soccer equipment in billions of dollars as a function of time where t is the number of years after 1982 Determine the amount of sales made in the year 1991 28 9 Billion 16 9 Billion 1 5 Billion 30 4 Billion

Algebra
Matrices & Determinants3 Lucy is a dressmaker In of an hour she can sew she sew each day if she works 8 hours per day of a dress How many dresses will

Algebra
Matrices & DeterminantsSubtract 3 80 3 125 3 80 3 125 Simplify your answer Type your answer in the form a bi Type an exact answer using radicals as
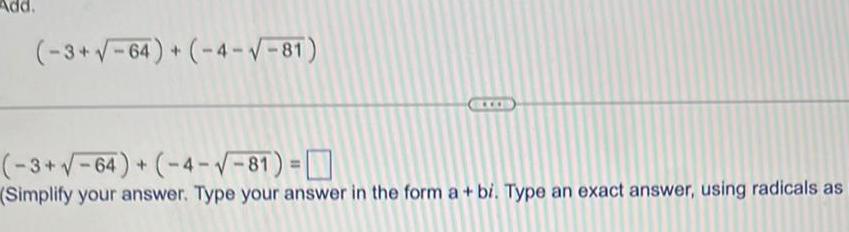
Algebra
Matrices & Determinants3 64 4 81 3 64 4 81 Simplify your answer Type your answer in the form a bi Type an exact answer using radicals as

Algebra
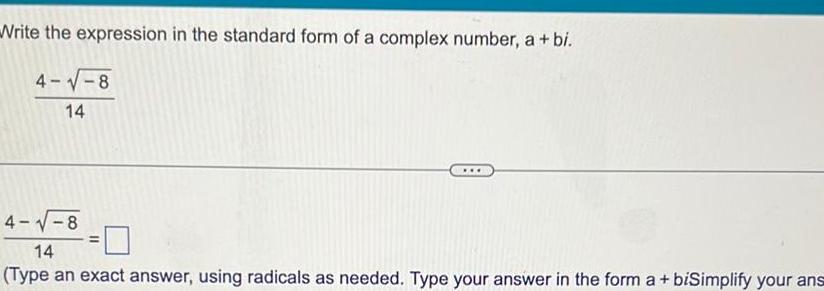
Matrices & DeterminantsWrite the expression in the standard form of a complex number a bi 4 8 14 4 8 14 Type an exact answer using radicals as needed Type your answer in the form a biSimplify your ans

Algebra
Matrices & DeterminantsMultiply 3i 2 8i 3i 2 8i Type your answer in the form a biUse integers or fractions for any numbers in the
Algebra
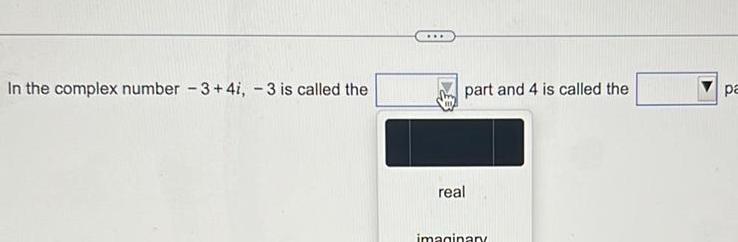
Matrices & DeterminantsIn the complex number 3 4i 3 is called the part and 4 is called the real imaginary pa

Algebra
Matrices & DeterminantsExpress in terms of i 343 343 Simplify your answer Type your answer in the form a bi
Algebra
Matrices & DeterminantsGraph the quadratic function f x x 5 4 Give the a vertex b axis c domain and d range a The vertex is

Algebra
Matrices & DeterminantsWhat does Descartes rule of signs tell you about the possible number of positive real zeros and the possible number of negative real zeros of the function f x 2x5 5x x 5 The possible number of positive real zeros is Use a comma to separate answers as needed and the possible number of negative real zeros is

Algebra
Matrices & DeterminantsAbout the sequence x keZ we have the following a 1 EBx b for each t to b te b MKk b x 0 x 0 te t b t b k 20 k 1 c xk Z is uniformly Cauchy on t b t b verification of these properties is left for the reader We consider the uniform limit of the sequence x to 8 to 8 B x b C which is given by x t lim x 1 1 t b to b Thus x t lim x f s x s ds 5 8 8 de 1 2 x lim ff s x s ds x j Finally the validity of this integral equation has the following two implications X f x f s x s ds x 0 xo x f f s lim x s ds x ff s x s ds fo Thus the function tx 1 satisfying the integral equation x 1 x f f s x s ds for all 1 t b t b dt lim f s x s ds 0 ff s x s ds f t X t This now proves that the curve X 1 8 4 82 thus obtained is a solution of the initial value problem
Algebra
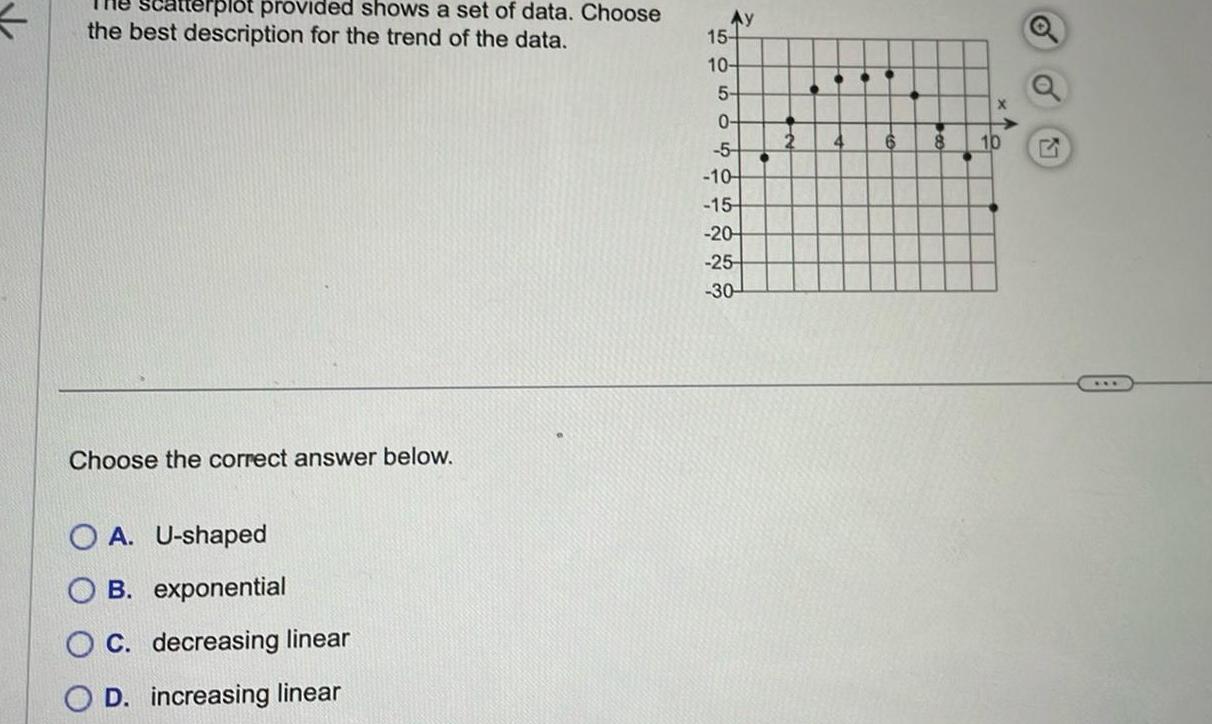
Matrices & DeterminantsThe atterplot provided shows a set of data Choose the best description for the trend of the data Choose the correct answer below OA U shaped OB exponential OC decreasing linear OD increasing linear 15 10 5 0 5 10 15 20 25 30 O 4 8 10
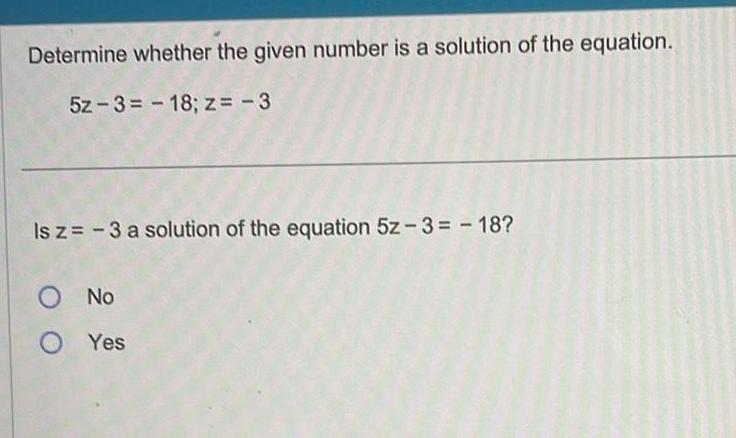
Algebra
Matrices & DeterminantsDetermine whether the given number is a solution of the equation 5z 3 18 z 3 Is z 3 a solution of the equation 5z 3 18 O No OYes
Algebra
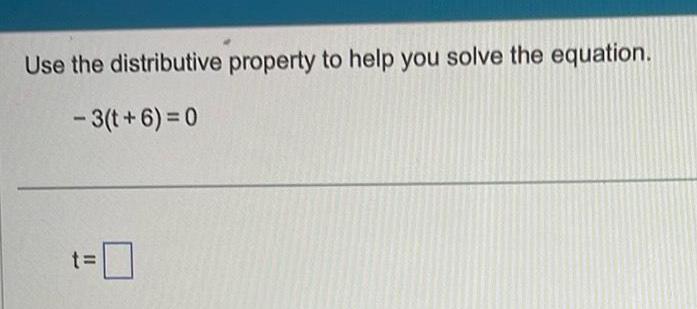
Matrices & DeterminantsUse the distributive property to help you solve the equation 3 t 6 0 11
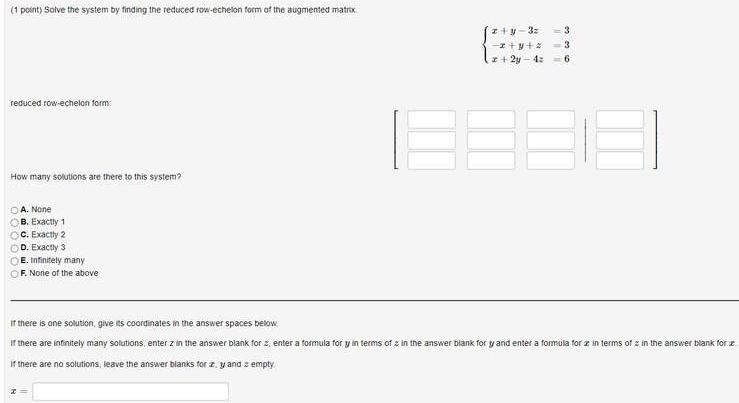
Algebra
Matrices & Determinants1 point Solve the system by finding the reduced row echelon form of the augmented matrix reduced row echelon form How many solutions are there to this system OA None B Exactly 1 OC Exactly 2 D Exactly 3 E Infinitely many F None of the above z y 3z x y z x 2y 4 6 a ww 3 3 If there is one solution give its coordinates in the answer spaces below If there are infinitely many solutions enter z in the answer blank for z enter a formula for y in terms of in the answer blank for y and enter a formula for a in terms of in the answer blank for z If there are no solutions leave the answer blanks for z y and empty

Algebra
Matrices & DeterminantsProblem 6 Consider the following matrix A and let B A Find b31 b32 and b33 i e find the entries in the third row of A 1 1 TT 42 1 2
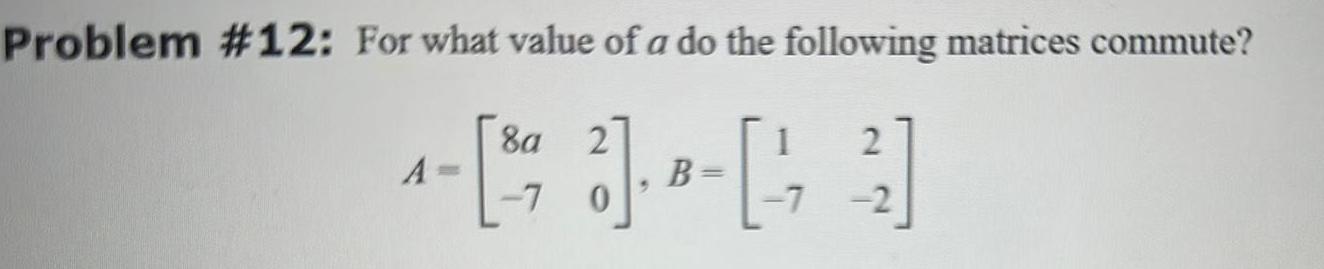
Algebra
Matrices & DeterminantsProblem 12 For what value of a do the following matrices commute 8a 1 4 123 23 A 7 0 7

Algebra
Matrices & Determinantsoblem 10 Let A and B be nxn matrices Which of the following statements are always true i AB A B ii If the homogeneous system Ax 0 has infinitely many solutions then A is not invertible iii If AB AC then B C A ii and iii only B i and iii only C iii only D all of them E ii only F none of them G i and ii only H i only
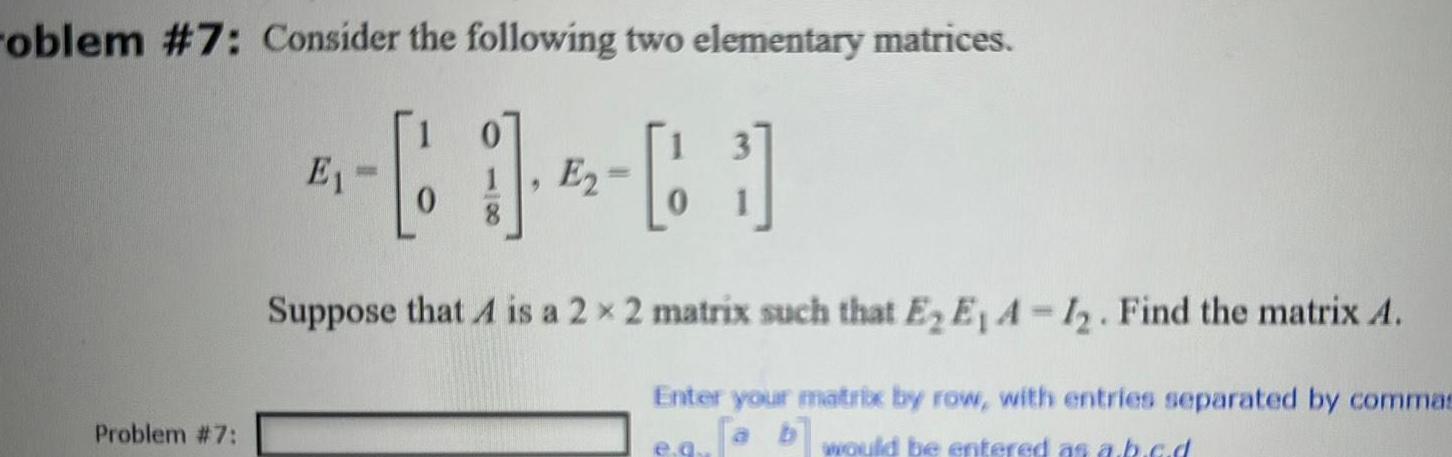
Algebra
Matrices & Determinantsoblem 7 Consider the following two elementary matrices 1 6 E2 0 Problem 7 E1 Suppose that A is a 2 x 2 matrix such that E E A 1 Find the matrix A Enter your matrix by row with entries separated by commas a b would be entered as a k a d e q
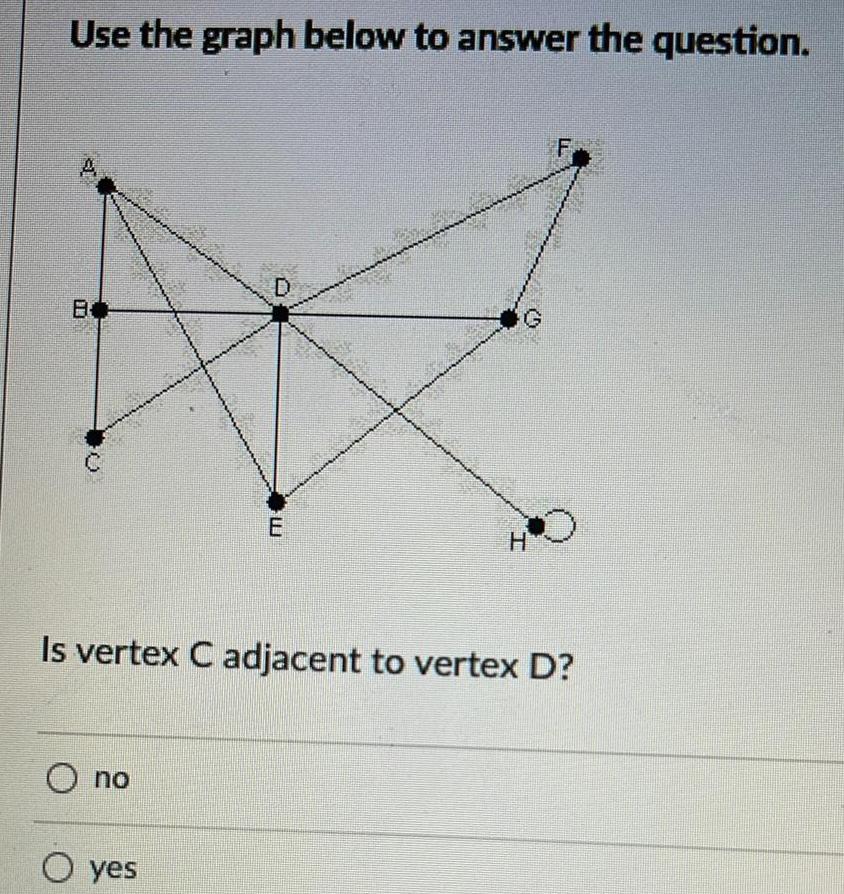
Algebra
Matrices & DeterminantsUse the graph below to answer the question A O no E O yes mannk H Is vertex C adjacent to vertex D F
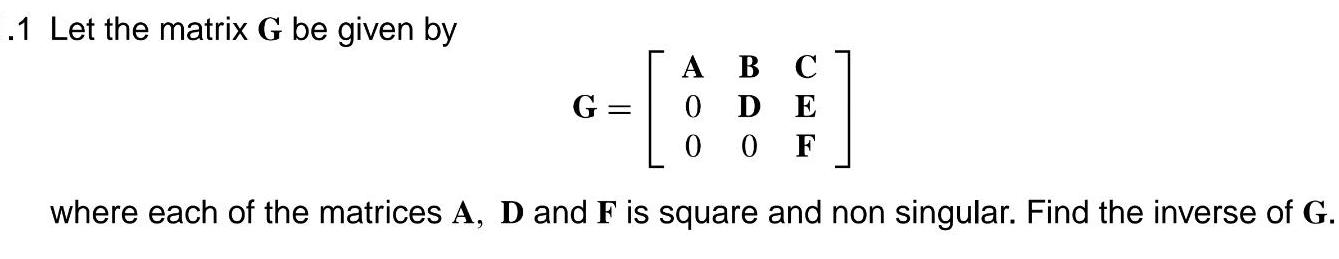
Algebra
Matrices & Determinants1 Let the matrix G be given by G A B C 0 D E 00F where each of the matrices A D and F is square and non singular Find the inverse of G

Algebra
Matrices & DeterminantsIn 1833 in the case of Barron v Baltimore the Supreme Court reasoned that the whole thrust of the Bill of Rights was O directed exclusively at restraining state power directed at restraining federal and state power equally O advisory in nature directed at neither the national government nor the states O directed exclusively at restraining the power of the national government O only a hortatory and not a mandatory document at the state level

Algebra
Matrices & DeterminantsMATHEMATICS Proposition 3 Let x J n y J be two solutions of the initial value problem dx f t x x t x dt then x 1 y 1 for all tJnJ Proof Recall that both x and y being solutions of the initial value problem satisfy the integral equations on their domain intervals x 1 x f s x s ds y 1 x f s y s ds Therefore x 1 y t ffs x s f s y s ds which implies x 1 y 1 0 s x s f s y s 0 SK x s y s for all 12 Applying Gronwalls result with A 0 we get 0 x 1 y 1 0 for all 1 1 This gives the desired equality x t y t for all tJJ Towards the uniqueness of the solution of the initial value problem 3 we consider all the solutions of the initial value problem 3 Let the totality of them be denoted by J XEA the solutions x being thus indexed by a suitable indexing set A Above we have verified that any two solutions say x and x are equal on the overlap of their domains Therefore we patch together all the solutions to get a maximal solution is the solution defined on the largest open interval It is obtained as follows Let J U J A clearly Jis an open sub internal of I with x J and all the solutions x patch up to get a solution x J of the initial value problem

Algebra
Matrices & Determinantsa b Xx 1 x 0 5 1E t b t b k20 c x keZ is uniformly Cauchy on t b t b verification of these properties is left for the reader We consider the uniform limit of the sequence x to 8 to 8B x b C which is given by x t lim x 1 1E1 b t b x 1 B x b for each te to b t b MK k 1 Thus x t lim xo 1 2 F 8 8 89 ds f s x x lim ff s x s ds x lim f s x s ds E xXx 4 ff s lim x s ds x f f s x s ds Thus the function tx 1 satisfying the integral equation Finally the validity of this integral equation has the following two implications x dx dt x 1 x ff s f s x s ds for all 1 t b t b that is X t x f s 4 d 0 f s x s ds x 0 xo j f s x s ds f t X t This now proves that the curve X 1 8 1 82 thus obtained is a solution of the initial value problem 2 3 UNIQUENESS OF A SOLUTION 20 We prove an inequality which will lead us to the uniqueness of the solutions Let Proposition 2 Gronwall s Inequality f a b 0 g a b 000 be continuous functions and A 0 a constant satisfying ft A Chapter 2 Systmes of First Order ODE g de ffs gs ds for all te ab Then ft A e Proof First we assume A 0 and put ht A S te ab Then ht 0 for all 1 a b and h t f t g t h t g t for all te a b fsgs ds for all Salt for all 16 ab Integrating this inequality over at
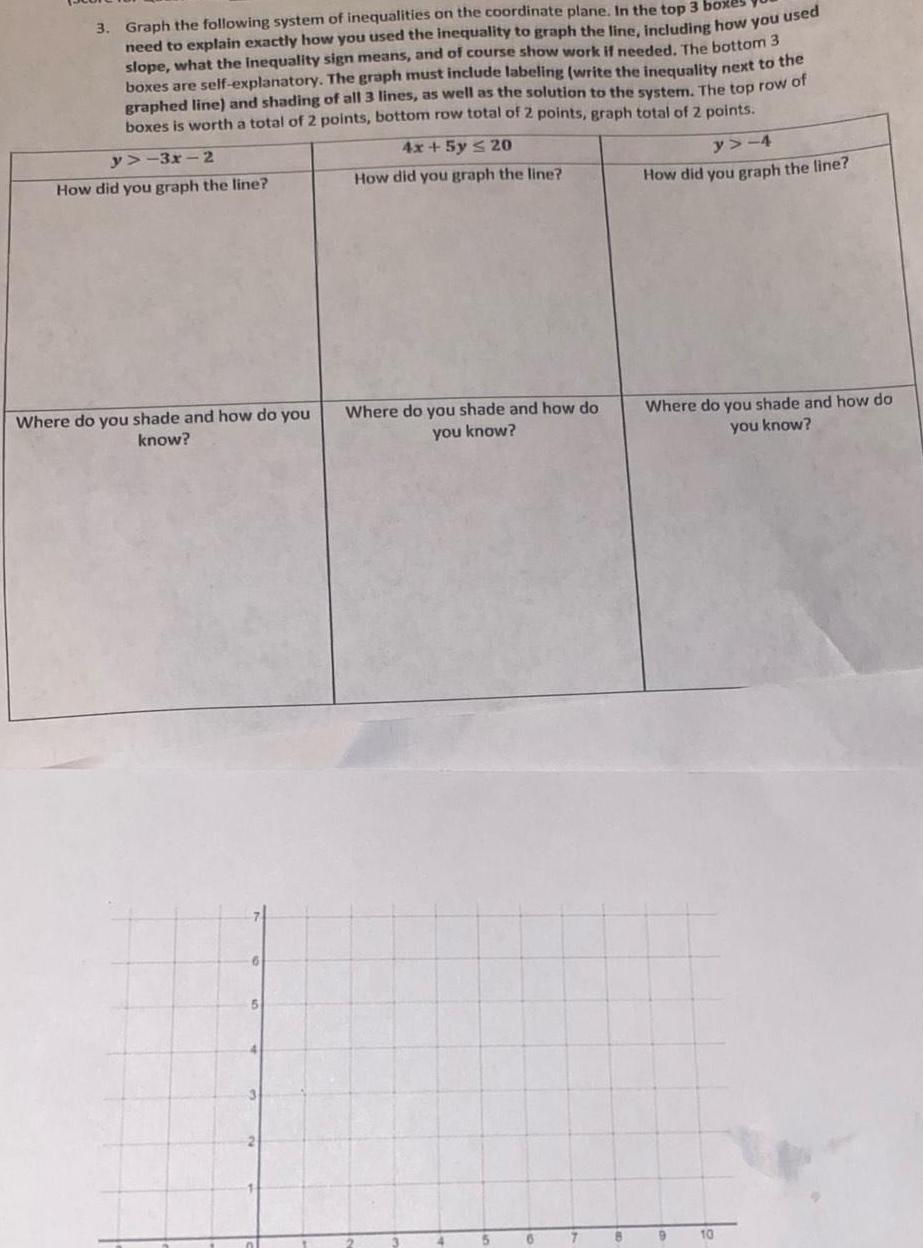
Algebra
Matrices & Determinants3 Graph the following system of inequalities on the coordinate plane In the top 3 boxe need to explain exactly how you used the inequality to graph the line including how you used slope what the inequality sign means and of course show work if needed The bottom 3 boxes are self explanatory The graph must include labeling write the inequality next to the graphed line and shading of all 3 lines as well as the solution to the system The top row of boxes is worth a total of 2 points bottom row total of 2 points graph total of 2 points 4x 5y 20 How did you graph the line y 3x 2 How did you graph the line Where do you shade and how do you know 5 Where do you shade and how do you know 6 8 y 4 How did you graph the line Where do you shade and how do you know 9 10

Algebra
Matrices & Determinants1 2 x lim k no xo f f s lim x s ds x f f s x s ds fo Thus the function tx 1 satisfying the integral equation x 1 x dx dr 500 Finally the validity of this integral equation has the following two implications X 1 x ff s x s ds 0 d dts x f s x s ds for all 1 t b t b f s x s ds f s x s ds x 0 x 1 S lim f s x s ds 11 f s x s ds f 1 X t This now proves that the curve X 1 8 82 thus obtained is a solution of the initial value problem 2 3 UNIQUENESS OF A SOLUTION 20 We prove an inequality which will lead us to the uniqueness of the solutions fi A e Proposition 2 Let Gronwall s Inequality f a b 0 g a b 0x be continuous functions and A 0 a constant satisfying PESA Ss s gs ds for all tea b Then Chapter 2 Systmes of First Order ODE for all te a b Proof First we assume A 0 and put ht A Sf a te a b Then ht 0 for all 1 a b and ht f t g t h t g t fsgs ds for all

Algebra
Matrices & Determinants8 A construction manager is planning to build a ramp for wheelchair access to a building entrance The ramp will be in the shape of a right angled triangle The height of the building entrance from the ground is 5 feet and the desired slope of the ramp should not exceed a 1 12 ratio i e for every 1 unit of vertical rise there should be 12 units of horizontal run a Calculate the length of the ramp the hypotenuse of the right angled triangle that meets the 1 12 slope requirement C 4 4 5A 60 60 52 C 60 2 Ft b If the construction manager has limited space and can only build the ramp to a maximum length of 15 feet determine the maximum allowable height for the building entrance while still meeting the 1 12 slope requirement 15 60 2 60 2 15 5 X 1 25 F X 6 X 60 2 15