Permutations and Combinations Questions and Answers
Algebra
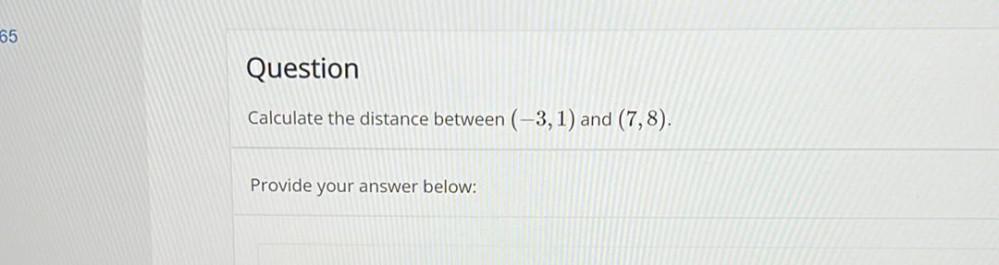
Permutations and CombinationsCalculate the distance between (-3, 1) and (7,8). Provide your answer below:
Algebra
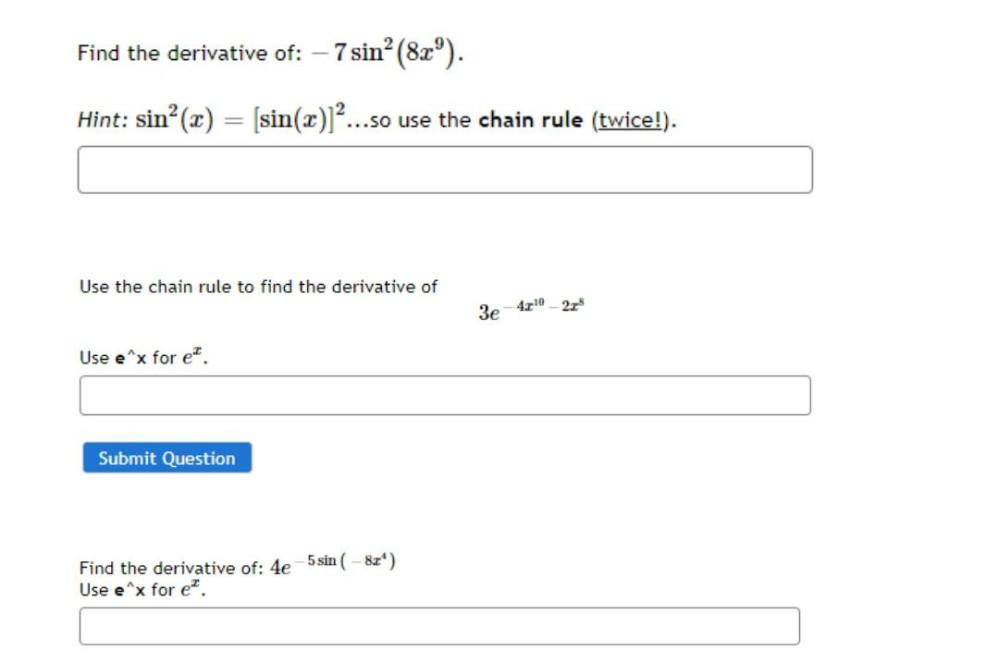
Permutations and CombinationsFind the derivative of: -7 sin² (8x⁹).
Use the chain rule to find the derivative of
3e^(-4x¹⁰-2x⁸)
Find the derivative of: 4e^(-5sin(-8x⁴))

Algebra
Permutations and CombinationsFind the accumulated present value of an investment over a 9 year period if there is a continuous money flow of $12,000 per year and the interest rate is 1.7% compounded continuously.

Algebra
Permutations and CombinationsSolve the initial value problem.
y"'-4y"-4y' +16y=0; y(0) = 5, y'(0)=-6, y''(0)=20
The solution is y(t) = ____

Algebra
Permutations and CombinationsAn island is located 31 miles N37°11'W of a city. A freighter in distress radios its position as N15°33'E of the island and N12°26'W of the city. How far is the freighter from the city?

Algebra
Permutations and CombinationsFind the present value of a continuous income stream F(t)=40+5t, where t is in years and F is in thousands of dollars per year, for 10 years, if money can earn 2.5% annual interest, compounded continuously. Calculate your integral using Desmos or other technology
Algebra
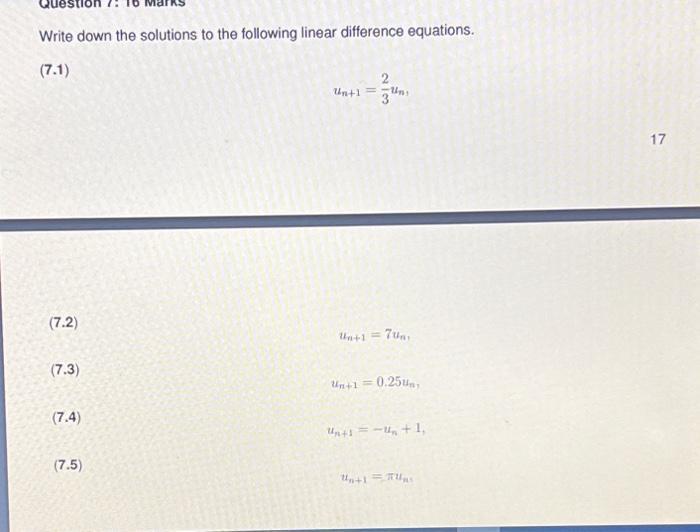
Permutations and CombinationsWrite down the solutions to the following linear difference equations.
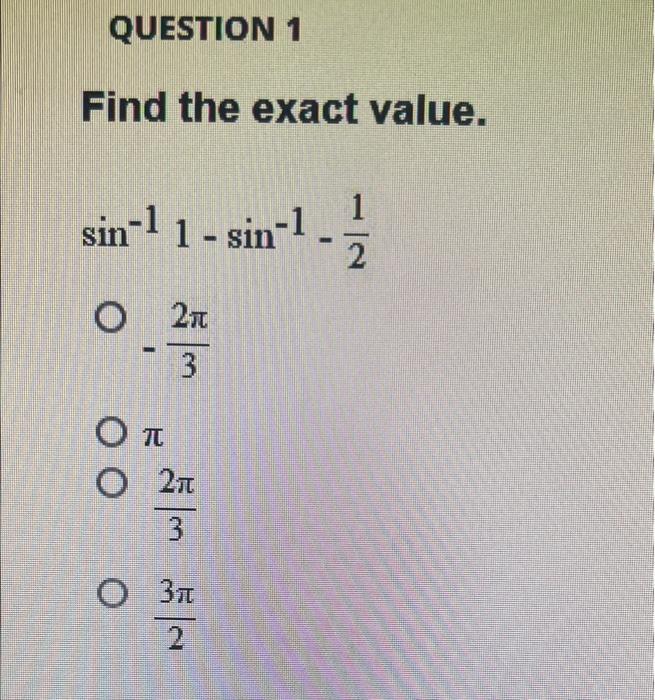
Algebra
Permutations and CombinationsFind the exact value.
sin-¹(1-sin-¹- (1/2))
-(2π/3)
π
(2π/3)
3π/2

Algebra
Permutations and CombinationsTickets for a recent concert cost $20 for adults and $12 for kids. Total attendance for the concert was 840 and total ticket sales were $12,496. How many of each ticket type were sold?

Algebra
Permutations and CombinationsProve that if 5 points are chosen from the interior of an equilateral triangle whose one side is 2 units, then there are at least two points which are at most 1 unit apart.

Algebra
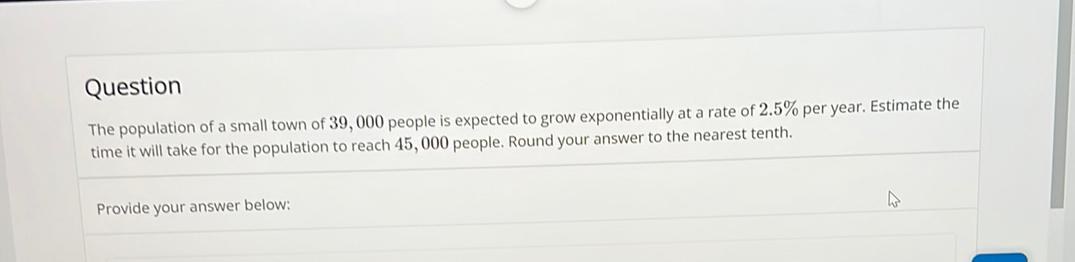
Permutations and CombinationsThe population of a small town of 39,000 people is expected to grow exponentially at a rate of 2.5% per year. Estimate the time it will take for the population to reach 45,000 people. Round your answer to the nearest tenth.
Algebra
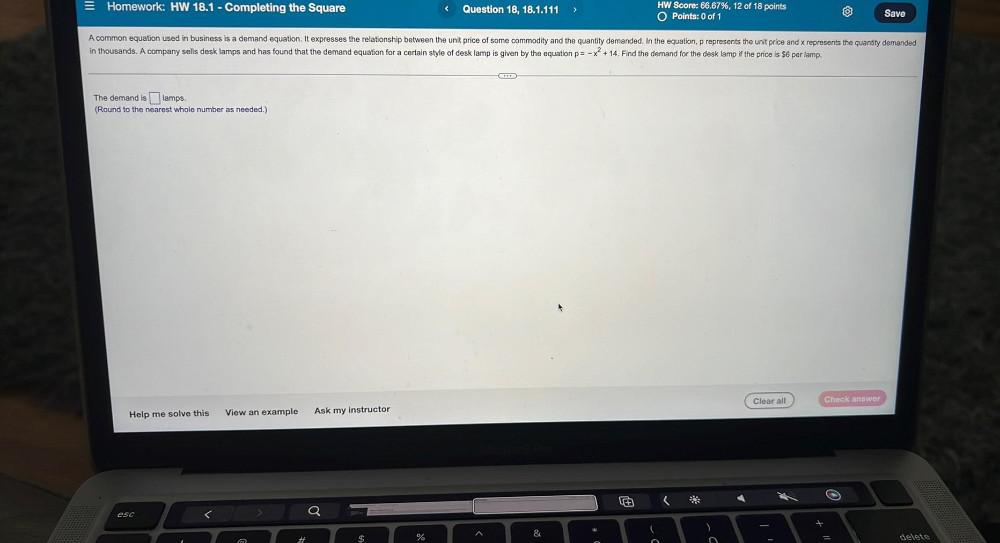
Permutations and CombinationsA common equation used in business is a demand equation. It expresses the relationship between the unit price of some commodity and the quantity demanded. In the equation, p represents the unit price and x represents the quantity demanded in thousands. A company sells desk lamps and has found that the demand equation for a certain style of desk lamp is given by the equation p= -x² +14. Find the demand for the desk lamp if the price is $6 per lamp.
.
Algebra
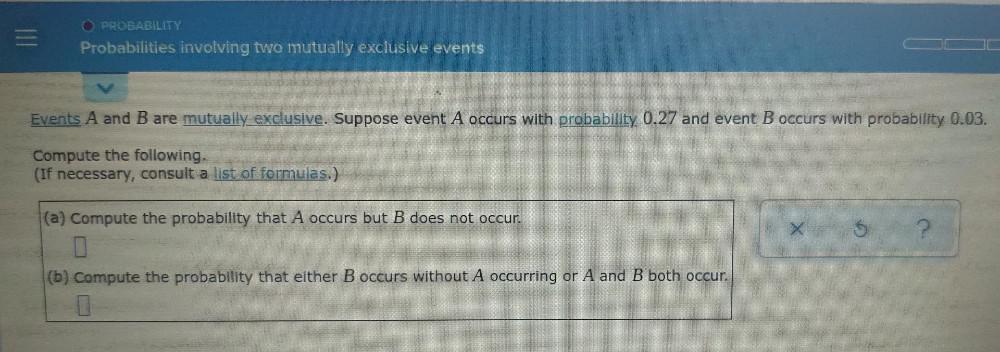
Permutations and CombinationsEvents A and B are mutually exclusive. Suppose event A occurs with probability 0.27 and event B occurs with probability 0.03.
Compute the following.
(a) Compute the probability that A occurs but B does not occur.
(b) Compute the probability that either B occurs without A occurring or A and B both occur.
Algebra
Permutations and CombinationsKara invested her $54, 000 bonus in an account earning 6.7% annual interest that is compounded continuously. How long will it take the account to triple in value? Round your answer to the nearest tenth.

Algebra
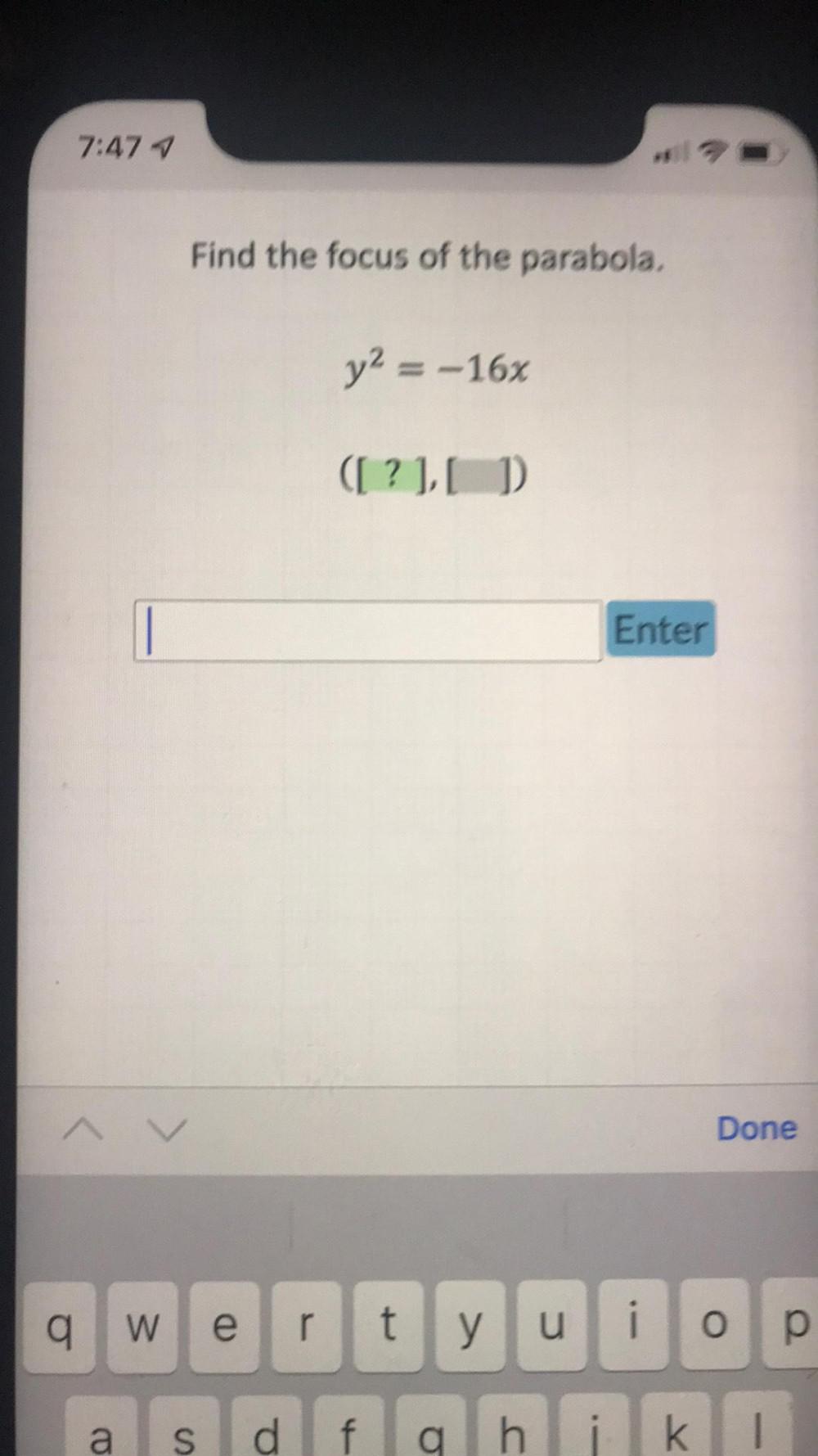
Permutations and CombinationsThe rectangular coordinates of a point are given. Find the polar coordinates of each point in (r,θ) form.
A. (-4,4√3)
Use the appropriate conversion rules to write the coordinates of this point in polar (r,θ) form.
B.(0,7)
Use the appropriate conversion rules to write the coordinates of this point in polar (r,θ) form.
Algebra
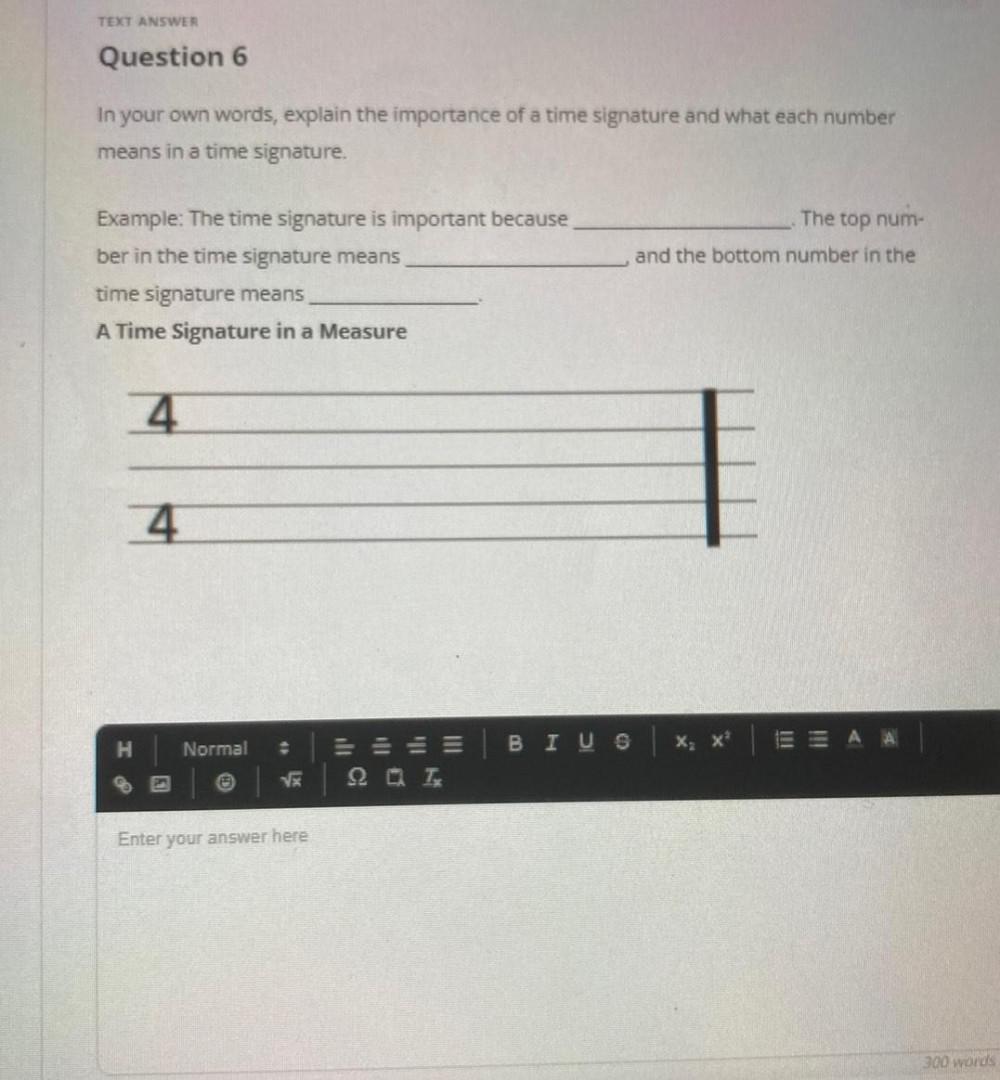
Permutations and CombinationsIn your own words, explain the importance of a time signature and what each number means in a time signature. Example: The time signature is important because The top number in the time signature means and the bottom number in the time signature means A Time Signature in a Measure

Algebra
Permutations and CombinationsIn Exercises 11-12, show that the matrices are orthogonal with respect to the standard inner product on M₂₂.
11. U = 2 1 , V = -3 0
-1 3 0 2
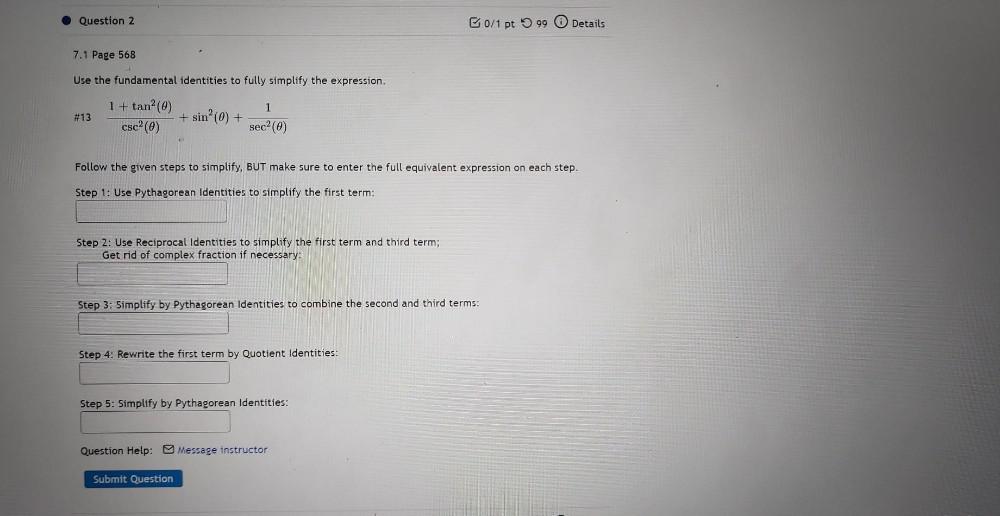
Algebra
Permutations and CombinationsUse the fundamental identities to fully simplify the expression.
# 13 1 + tan² (θ)/csc² (θ)+ sin² (0) +1/ sec² (θ)
Follow the given steps to simplify, BUT make sure to enter the full equivalent expression on each step.
Step 1: Use Pythagorean Identities to simplify the first term:
Step 2: Use Reciprocal Identities to simplify the first term and third term;
Get rid of complex fraction if necessary:
Step 3: Simplify by Pythagorean Identities to combine the second and third terms:
Step 4: Rewrite the first term by Quotient Identities:
Step 5: Simplify by Pythagorean Identities:
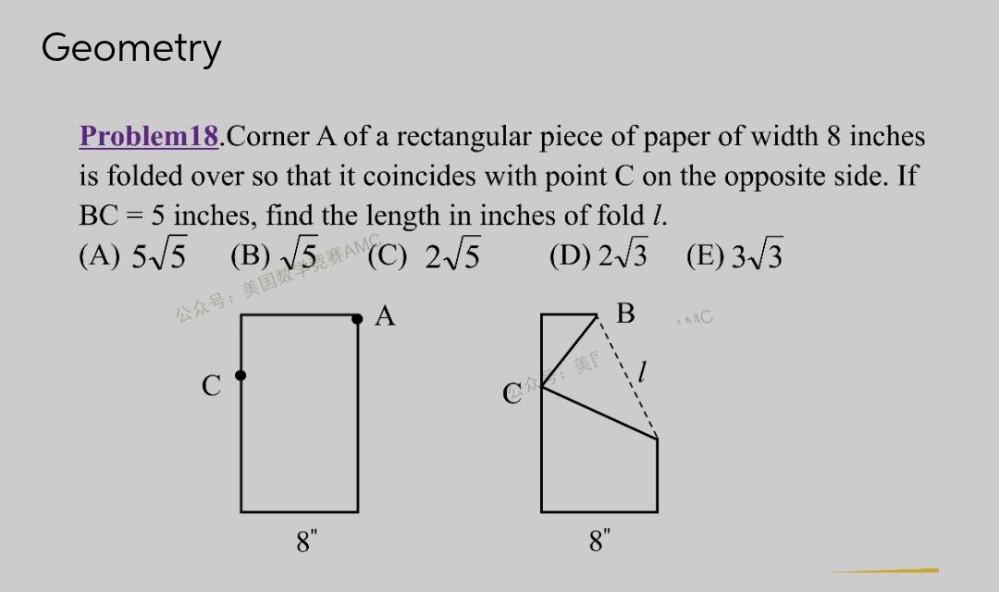
Algebra
Permutations and CombinationsCorner A of a rectangular piece of paper of width 8 inches is folded over so that it coincides with point C on the opposite side. If C = 5 inches, find the length in inches of fold 7.
(A) 5√5
(C) 2√5
(D) 2√3
(E) 3√3

Algebra
Permutations and CombinationsSuppose a triangle has a side c = π/2. Prove
cos C=cos A cos B
Compare this with the Spherical Pythagorean Theorem.

Algebra
Permutations and CombinationsThomas would like to get employee of the month at his job, Grandview Movie Theater for two months in a row. There are only 5 employees that work at the theater with him, so the probability that he is an employee of the month is 20% in March and 20% in April. What is the probability that his is an employee of the month for both March and April? Show your work.

Algebra
Permutations and CombinationsThe probability of Gregor scoring an A on his Geography test (event A) is 0.90, and the probability of Candace scoring an A on her Geography test (event B) is 0.85. The probability of both of them scoring an A on the test is 0.765. Given this information, are events A and B dependent or independent? Show your work.
Algebra
Permutations and CombinationsThere are 8 people that would like to receive tickets for the orchestra concert, but there are only 3 tickets. If you are someone that would like a ticket, what is the probability that you will be chosen? (order doesn't matter - you don't care if you are chosen 1st, 2nd, or 3rd and repetition is not allowed - you can't be chosen twice.)

Algebra
Permutations and CombinationsAt Choo Choo Mike's toy store, there are 100 toys that are randomly selected. Out of those 100, 12 of them are defective. What is the probability if you randomly choose three toys that two of them are defective? Show your work.
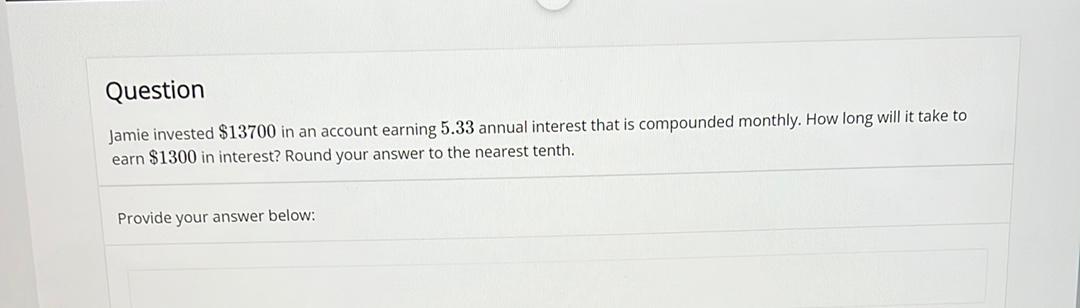
Algebra
Permutations and CombinationsJamie invested $13700 in an account earning 5.33 annual interest that is compounded monthly. How long will it take to earn $1300 in interest? Round your answer to the nearest tenth.
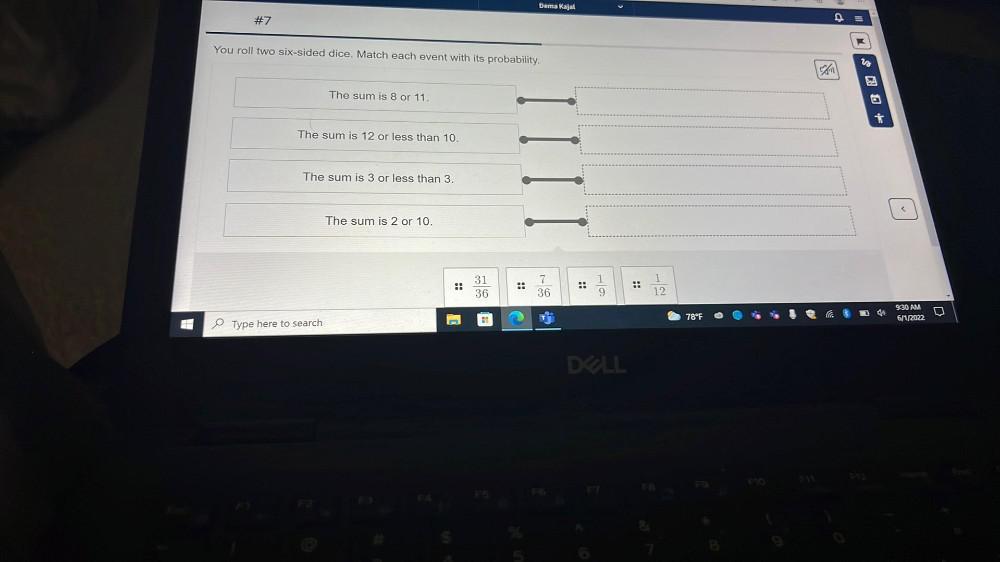
Algebra
Permutations and CombinationsYou roll two six-sided dice. Match each event with its probability.
The sum is 8 or 11.
The sum is 12 or less than 10.
The sum is 3 or less than 3.
The sum is 2 or 10.
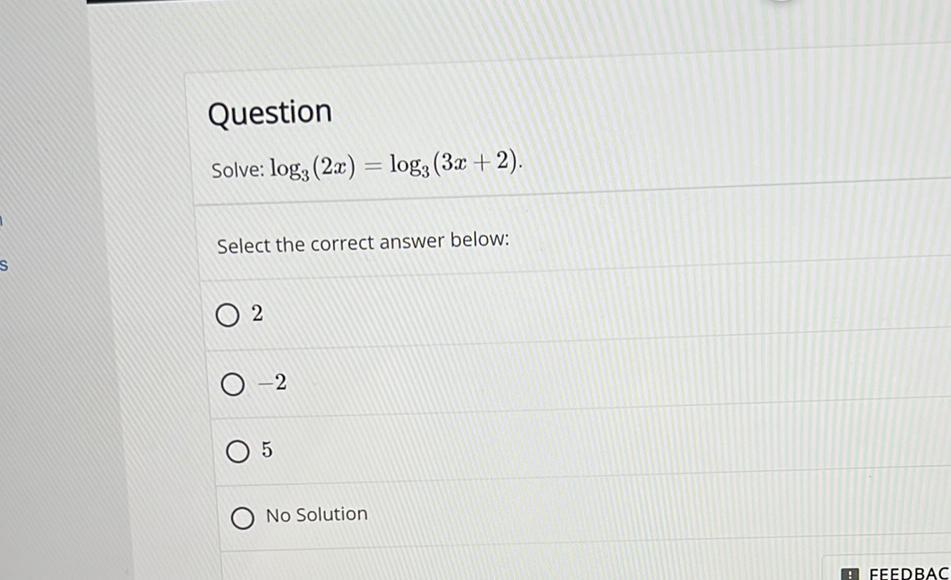
Algebra
Permutations and CombinationsSolve: log₃(2x) = log₃(3x + 2).
Select the correct answer below:
2
-2
5
No Solution


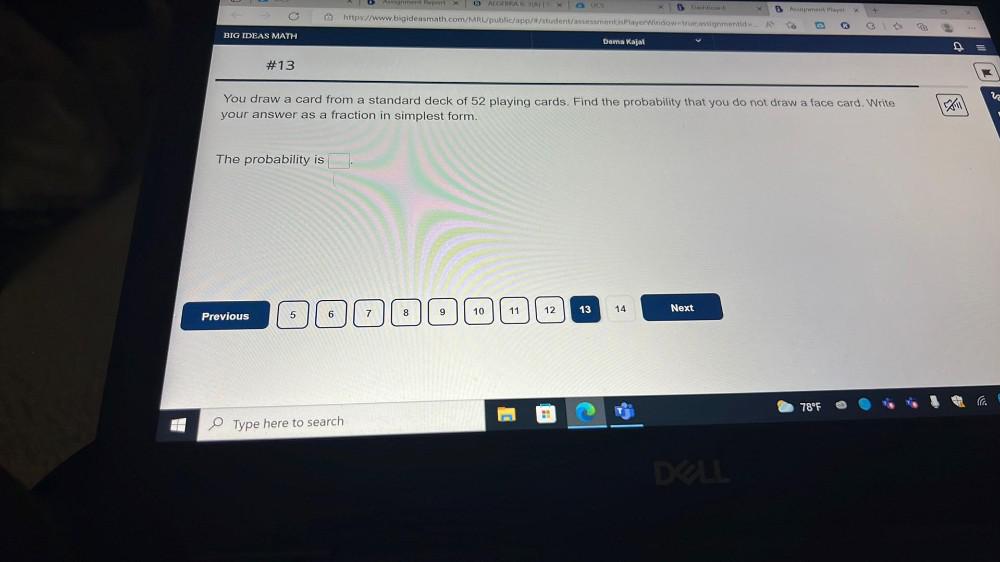
Algebra
Permutations and CombinationsYou draw a card from a standard deck of 52 playing cards. Find the probability that you do not draw a face card. Write your answer as a fraction in simplest form.
The probability is __________________

Algebra
Permutations and CombinationsFor the given linear systems in reduced row echelon form. Solve the system and decided x and y,
x-2z = 5
y+z=2

Algebra
Permutations and CombinationsIn how many ways can 12 people be chosen from a group of 20? (in this example, repetition not allowed because you can't choose the same person twice, and order doesn't matter because when you group people, the order in which you chose them is not important. They are all part of the same group.) Show your work.
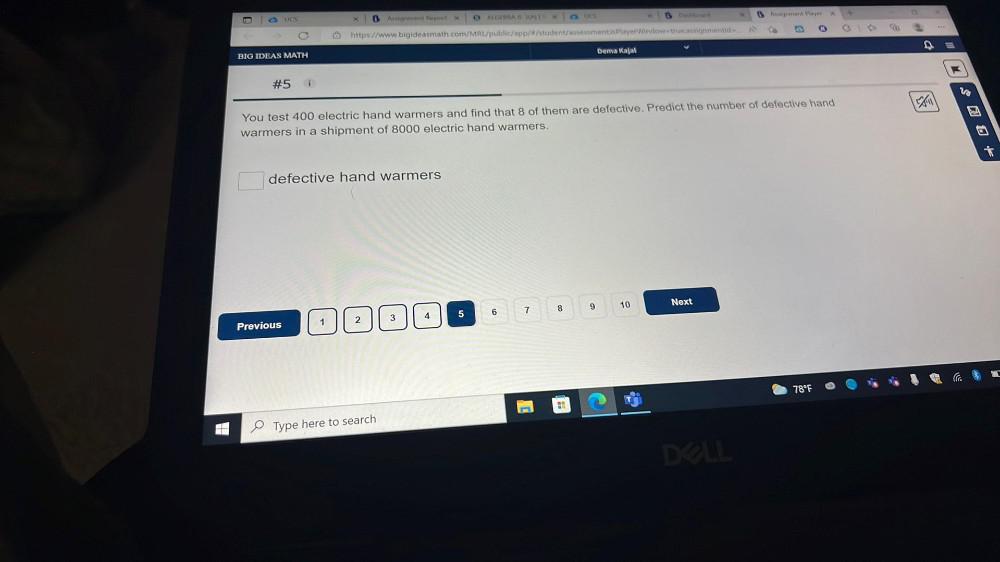
Algebra
Permutations and CombinationsYou test 400 electric hand warmers and find that 8 of them are defective. Predict the number of defective hand warmers in a shipment of 8000 electric hand warmers.
_____defective hand warmers

Algebra
Permutations and CombinationsConsider the following polynomial expression:
4x⁵ - 16x² + 13x⁸
What is the degree of the polynomial and the leading coefficient?
a) Degree = & Leading coefficient = 4
b) Degree = 8 Leading coefficient = 13
c) Degree = 5 Leading coefficient = 4
d) Degree = 5 Leading coefficient = 13

Algebra
Permutations and CombinationsSolve each problem, where t, ω, r. 0. s & v are defined as
Find θ if t = 3 and ω=2π/3 radians per sec
Find v if r= 3 m and ω =2π/3 radians per sec
Finds x if v= 3π in per sec and t = 4 sec

Algebra
Permutations and CombinationsFind the coefficient of the 6th term of the expanded binomial, (2c – d)¹².
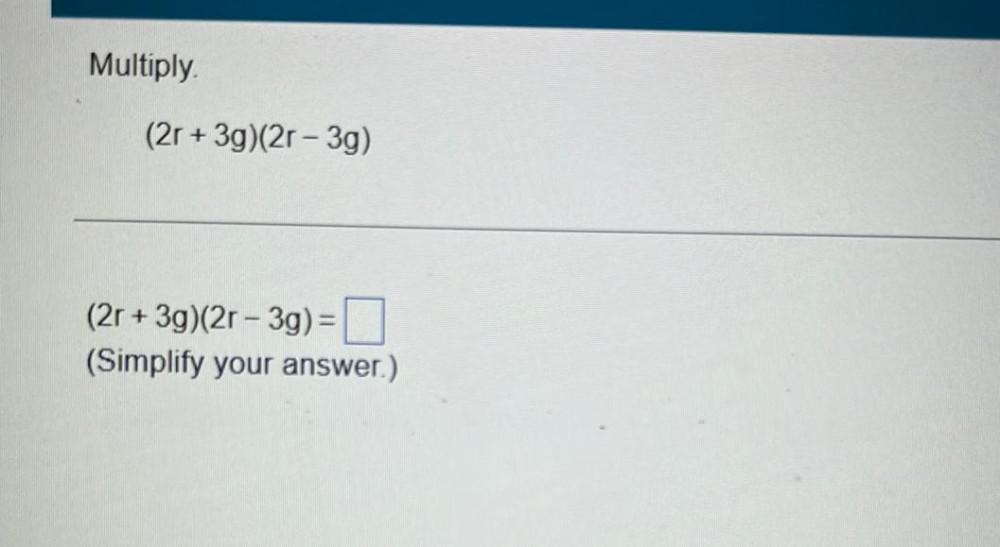
Algebra
Permutations and CombinationsMultiply (2r + 3g)(2r - 3g)
(2r+ 3g)(2r - 3g) =?(Simplify your answer.)

Algebra
Permutations and CombinationsA private college reports:
70% of incoming freshmen attended public schools.
75% of public school students who enroll as freshmen eventually graduate.
90% of other freshmen eventually graduate.
Based on the probabilities given, what percent of freshmen eventually graduate?
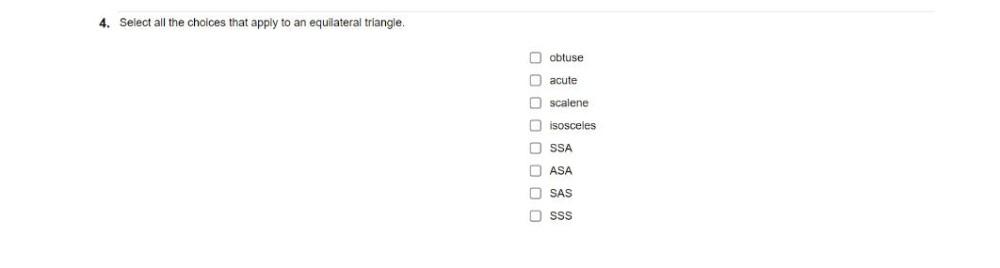
Algebra
Permutations and CombinationsSelect all the choices that apply to an equilateral triangle.
obtuse
acute
scalene
isosceles
SSA
ASA
SAS
sss
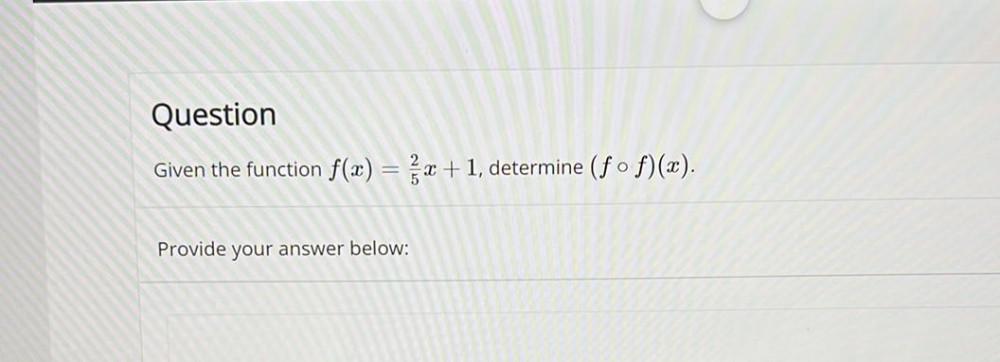

Algebra
Permutations and Combinationsfind the formula of all possible combinations using 5 numbers that will equal 147. The numbers to use is 1-69.You cannot reuse a number.
Algebra
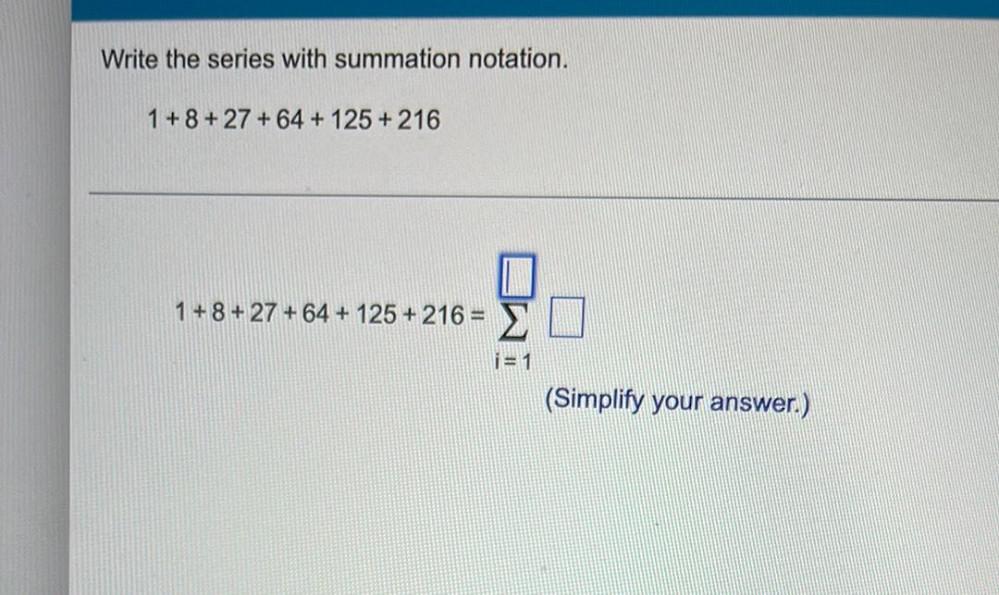
Permutations and CombinationsWrite the series with summation notation.
1+8+27 +64 +125 +216
1+8+27 +64 + 125 +216 =i=1Σ?
(Simplify your answer.)

Algebra
Permutations and CombinationsFind the canonical link function for the generalised linear model with probability mass function
P(Y = y) = (μ^(y/φ)/φ) e^(-μ/φ)/(y/φ)! = 0, φ,2φ,3φ,...
where is μ the parameter of interest.

Algebra
Permutations and CombinationsIn terms of the tangent of a positive acute angle, what is the expression for tan ( 10π/7) ?

Algebra
Permutations and CombinationsA = {5'x : x is even and 4 ≤ x ≤ 15}. Rewrite A in roster notation.