Permutations and Combinations Questions and Answers

Algebra
Permutations and CombinationsGiven the functions defined by f(x) = 8x³ + 5 and g(x) = ∛(x - 5), find (g o f)(x).
Algebra
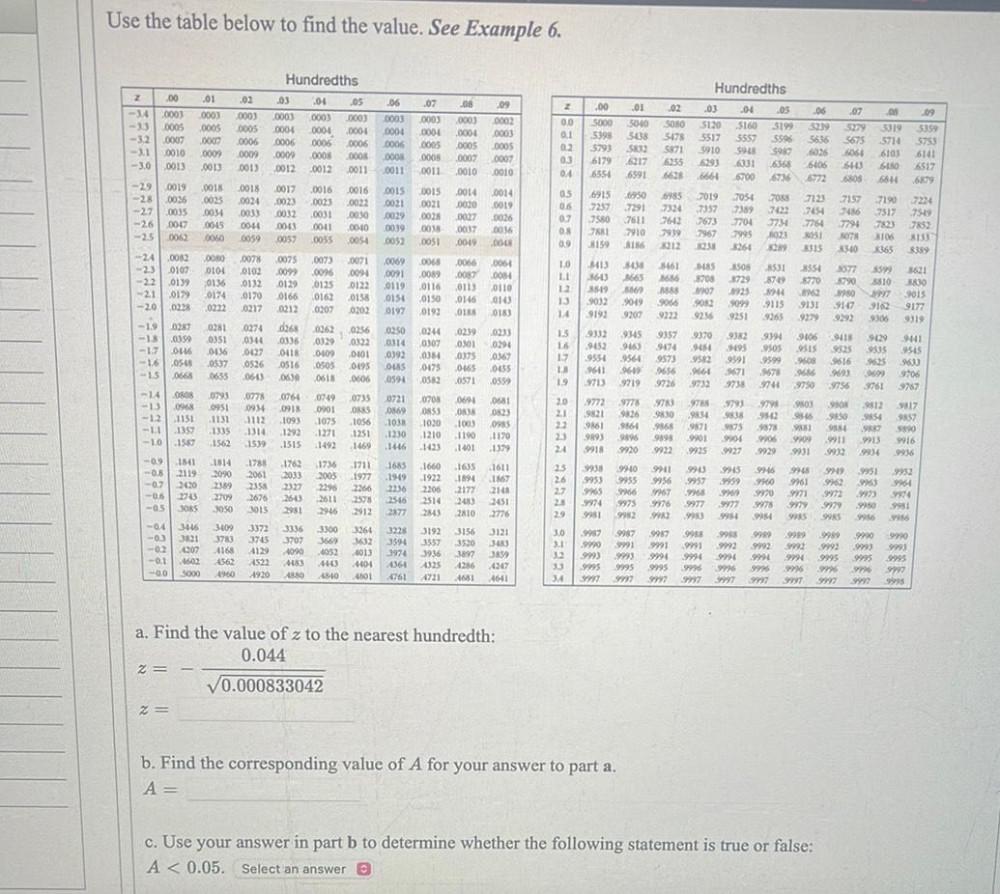
Permutations and CombinationsUse the z table below to find the value.
a). Find the value of z to the nearest hundredth:
z =0.044/√0.000833042
b). Find the corresponding value of A for your answer to part a.
c). Use your answer in part b to determine whether the following statement is true or false:
A < 0.05.
Algebra
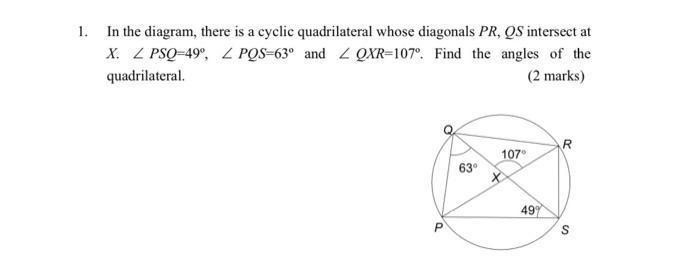
Permutations and CombinationsIn the diagram, there is a cyclic quadrilateral whose diagonals PR, QS intersect at X. ∠ PSQ=49°, ∠ PQS=63° and ∠ QXR=107°. Find the angles of the quadrilateral.
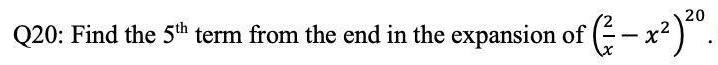

Algebra
Permutations and CombinationsThe distance between school and home is 8 km and home and playground is 7 km. Find the distance between school and ground in meters.
7000
8000
14000
15000

Algebra
Permutations and CombinationsGraph the system
x^2 + y^2 ≤ 5
x + 3y < -5
Label the intersections and solution region.
Algebra
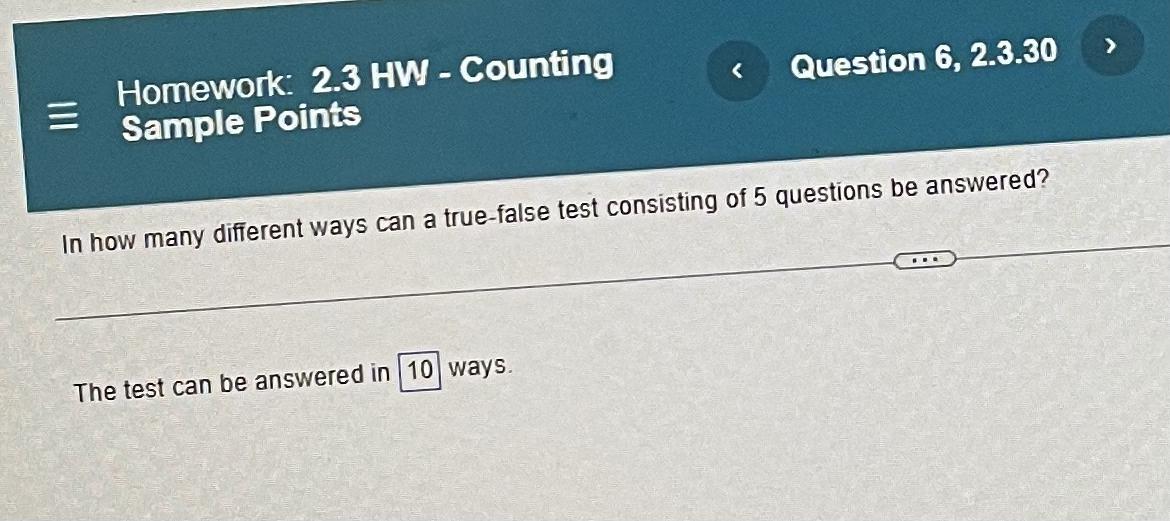
Permutations and CombinationsIn how many different ways can a true-false test consisting of 5 questions be answered?

Algebra
Permutations and Combinations(a) How many distinct permutations can be made from the letters of the word CANOE?
(b) How many of these permutations start with the letter O?
(a) There are ____ distinct permutations. (Type a whole number.)
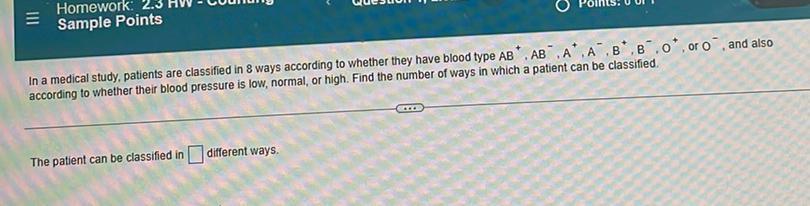
Algebra
Permutations and CombinationsIn a medical study, patients are classified in 8 ways according to whether they have blood type AB+,AB‾, A+ .A‾ .B+ .B‾.O+, or O‾, and also according to whether their blood pressure is low, normal, or high. Find the number of ways in which a patient can be classified.

Algebra
Permutations and CombinationsThe graph of f(x) = e^x−2+ 3 will have:
A) asymptote at x = 3, and contains the point (0,1/e^2+3)
B) asymptote at y = 0, and contains the point (0, 1)
C) asymptote at y = 3, and contains the point (2,4)
D) asymptote at x =5, and contains the point (0,1/e^2+3)
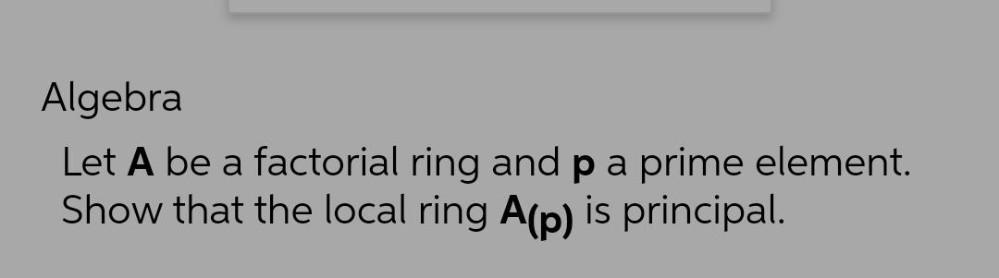
Algebra
Permutations and CombinationsLet A be a factorial ring and p a prime element. Show that the local ring A(p) is principal.

Algebra
Permutations and CombinationsNow set each derivative equal to zero and solve the system of equations for L and W.
-(29,160/L²)+ 5W = 0
-(29,160/W²)+5L = 0
(L,W) = ?
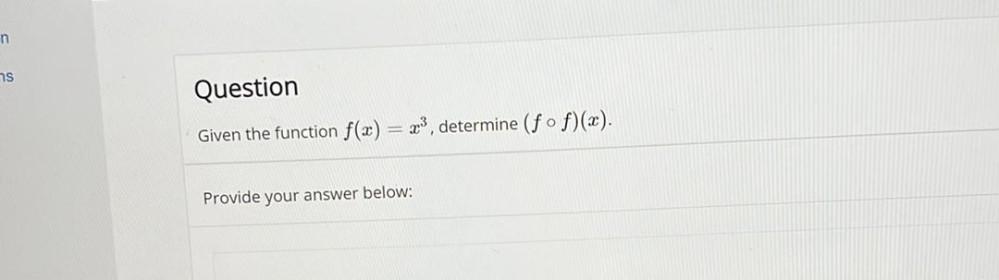
Algebra
Permutations and CombinationsGiven the function f(x) = x³, determine (f∘f)(x).
Provide your answer below:
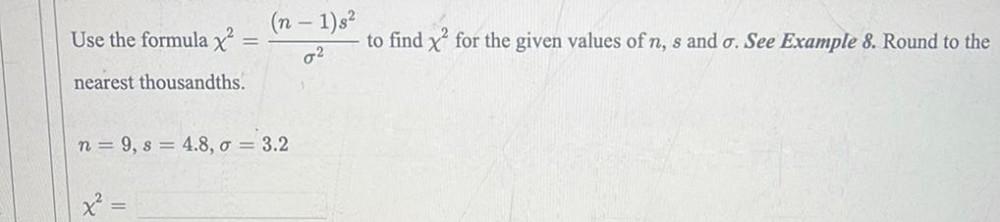
Algebra
Permutations and CombinationsUse the formula x² =(n-1) s²/σ² to find x² for the given values of n, s and σ. Round to the nearest thousandths.
n = 9, s = 4.8, σ= 3.2
x²=?

Algebra
Permutations and CombinationsSelect all the choices that apply to ∆ ABC with: ∠B=110°, ∠A=∠C, AC = 50.
obtuse
acute
scalene
isosceles
ASA
AAS
SSA
SAS

Algebra
Permutations and CombinationsSolve the non-linear Differential Equation y"=-eʸ : y=f(x) by explicitly following these steps: (Note: u=f(y), w=f(u) so use the chain rule as necessary)
Find x+D wrt z= √(C²-2u) by way of integration wrt u, where D is the constant of integration wrt.x

Algebra
Permutations and CombinationsFind the 1st and 2nd derivative of any polynomial of the 5th order (as given in the class) using the forward, central, and backward finite difference method!

Algebra
Permutations and CombinationsAbby, Ben, Charles, and Daniel are on a boat. The boat hit a reef and one-by-one each person fell out of the boat. In how many different orders could these passengers fall off the boat?

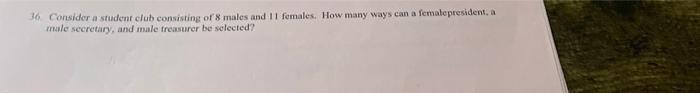
Algebra
Permutations and CombinationsConsider a student club consisting of 8 males and 11 females. How many ways can a femalepresident, a male secretary, and male treasurer be selected?
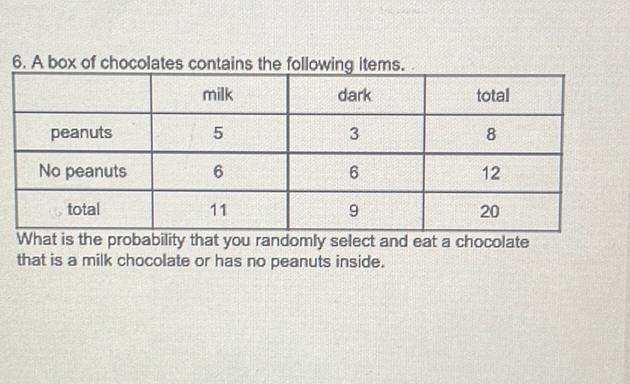
Algebra
Permutations and CombinationsA box of chocolates contains the following items.
milk dark total
peanuts 5 3 8
No peanuts 6 6 12
total 11 9 20
What is the probability that you randomly select and eat a chocolate that is a milk chocolate or has no peanuts inside.

Algebra
Permutations and CombinationsThe loudness of a sound is related to the logarithm of the ratio of the measured intensity, I, to a reference intensity, I. The loudness, L, of a sound is measured in decibels, dB, and can be determined using the formula L = 10log10 (I/Io)). If the intensity of the sound of a rocket launching is 4500 times that of a jet engine and the rocket has a loudness of 170 dB, then the loudness of the jet engine, to the nearest decibel, is
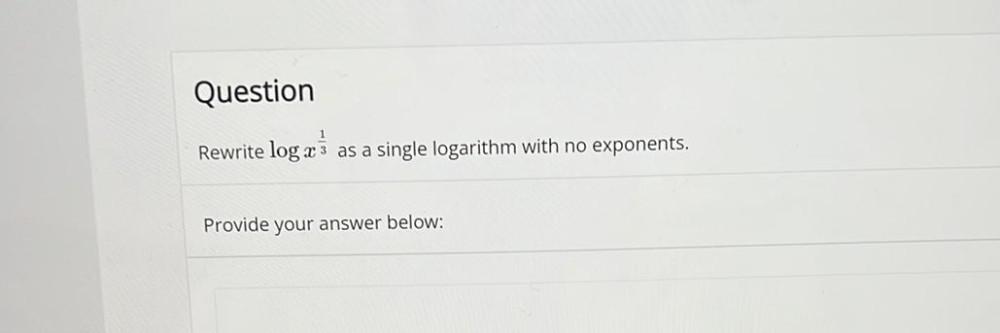

Algebra
Permutations and Combinations1. Suppose we want to know the probability that a student will choose a Water at random.
Beverage Boys Girls Total
Water 27 34 61
Lemonade 5 25 30
Soda 35 6 41
total 67 65 132
What is the probability that a student will choose a water? Show your work. Answer should be a percent to the tenth spot.
2. What is the probability that the student is a boy and chooses water? Answer should be a percent to the tenth spot.
3. Suppose we want to know the probability that a student chosen at random will be a boy and have a beverage choice is Lemonade. From the table: P(GPA Boy/Lemonade) Is this dependant or independent?
4. Now let's look at the probability that a student is a girl and chooses Soda. Answer is a percent and to the tenth of a percent. This would be dependant or independant?

Algebra
Permutations and CombinationsFind the X-Valites CIF any) at which the function f(x) = x+2/x²+6x78 is not continuous. Which of the discontinvities are removable?
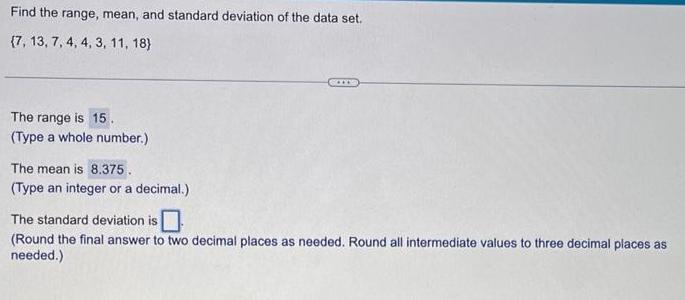
Algebra
Permutations and CombinationsFind the range, mean, and standard deviation of the data set.
(7, 13, 7, 4, 4, 3, 11, 18)
The range is
(Type a whole number.)
The mean is
(Type an integer or a decimal.)
The standard deviation is
(Round the final answer to two decimal places as needed. Round all intermediate values to three decimal places as needed.)

Algebra
Permutations and CombinationsFrom the top of a 20 m lighthouse, the angles of depression to two ships, the Acadian and the Bounty, are 52° and 63° respectively. If the angle between the ships is 120°, how far apart are they?
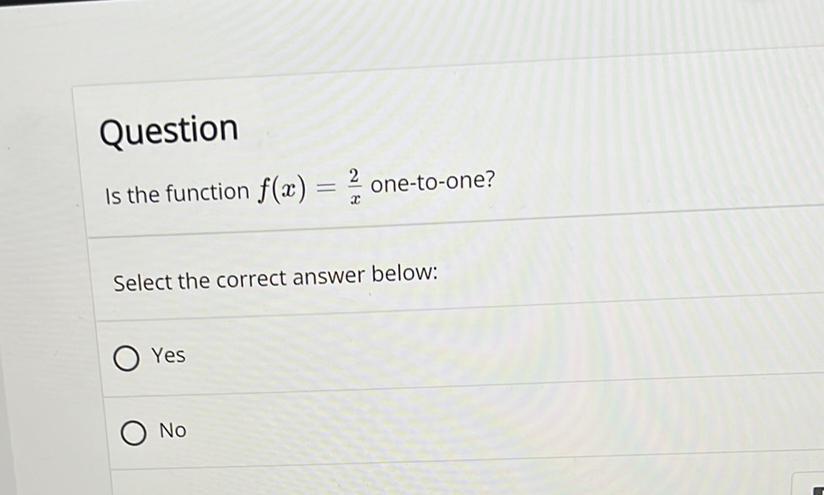
Algebra
Permutations and CombinationsIs the function f(x) = 2/x one-to-one?
Select the correct answer below:
a) Yes
B) No
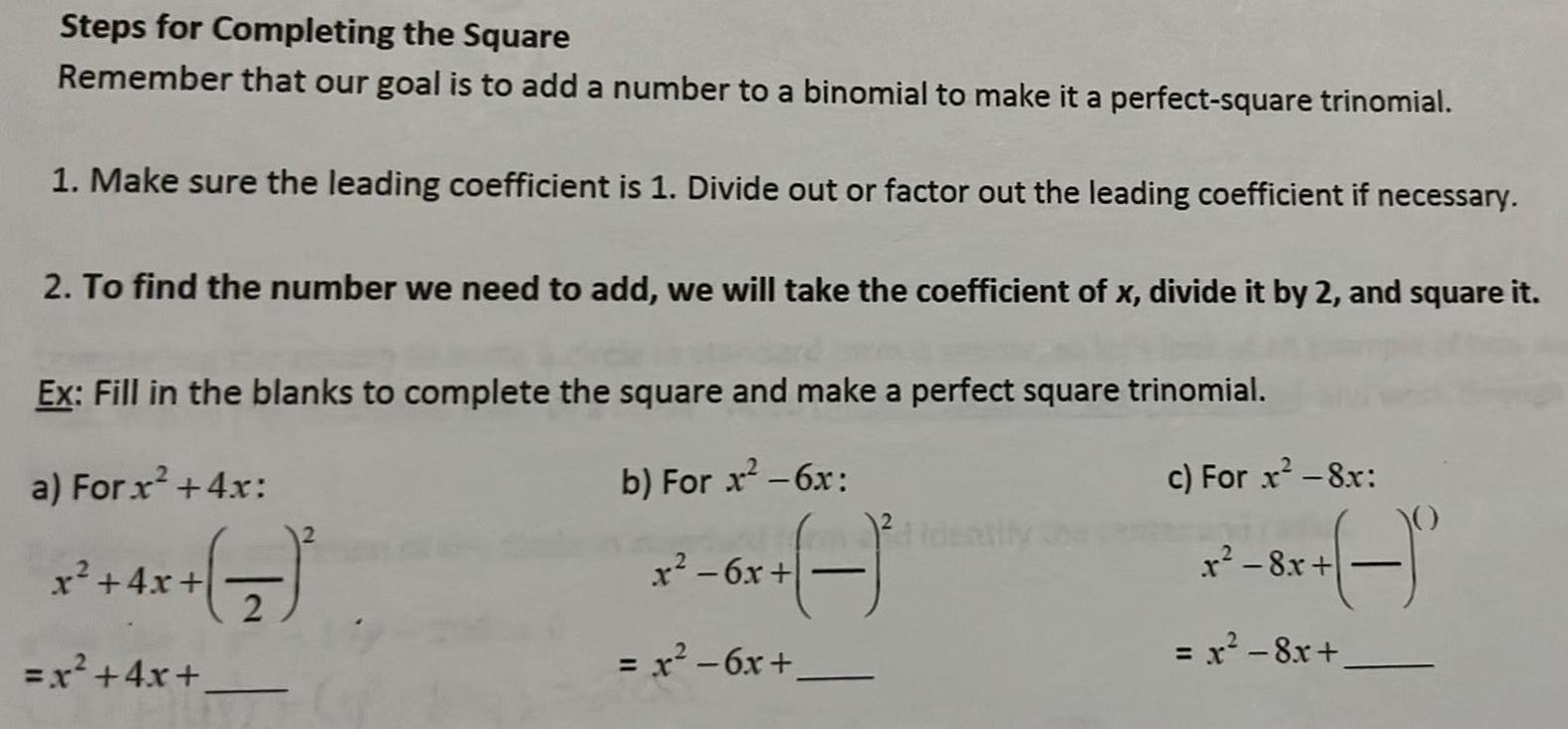
Algebra
Permutations and CombinationsRemember that our goal is to add a number to a binomial to make it a perfect-square trinomial.
1. Make sure the leading coefficient is 1. Divide out or factor out the leading coefficient if necessary.
2. To find the number we need to add, we will take the coefficient of x, divide it by 2, and square it.
Ex: Fill in the blanks to complete the square and make a perfect square trinomial.


Algebra
Permutations and CombinationsIf money is invested in an account earning 3.3% annual interest that is compounded continuously, how long will it take the amount to double? Round your answer to the nearest tenth. Provide your answer below:
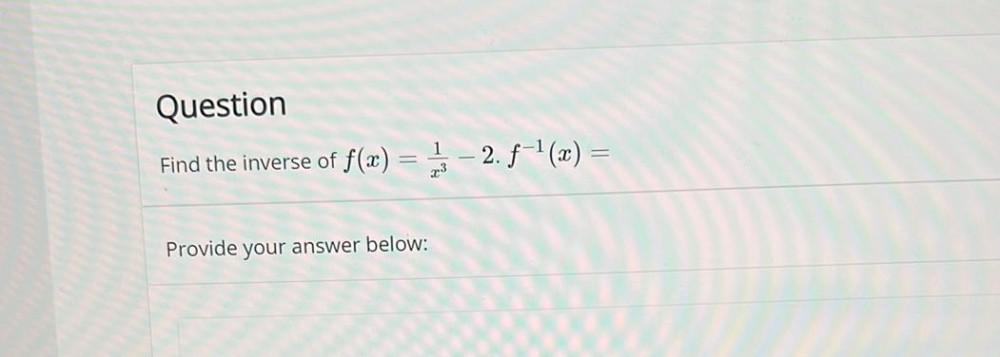
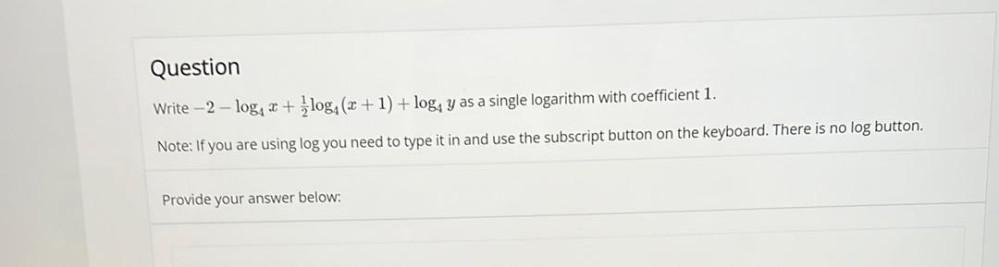
Algebra
Permutations and CombinationsWrite -2 - log₄x +(1/2)log₄(x + 1) + log₄y as a single logarithm with coefficient 1.
Note: If you are using log you need to type it in and use the subscript button on the keyboard. There is no log button.
Provide your answer below:______________

Algebra
Permutations and CombinationsLet H be a transitive permutation group in S con- taining an n-cycle and a transposition. Then prove that H = S.

Algebra
Permutations and CombinationsIf sin (θ)=2/3 and θ is in the 2nd quadrant, find cos(θ)
cos(θ) =
Enter your answer as a reduled radical. Enter √12 as 2sqrt(3).
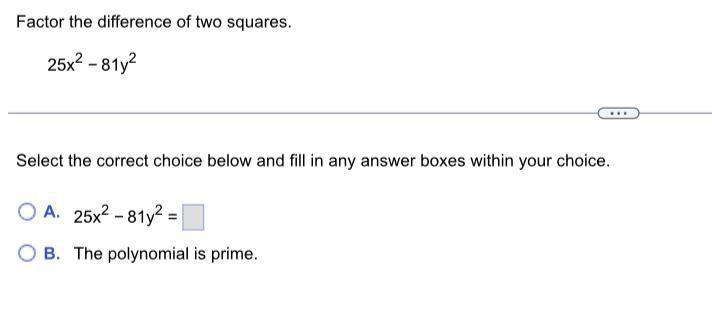
Algebra
Permutations and CombinationsFactor the difference of two squares.
25x²-81y²
Select the correct choice below and fill in any answer boxes within your choice.
A. 25x²-81y² =_______
B. The polynomial is prime.
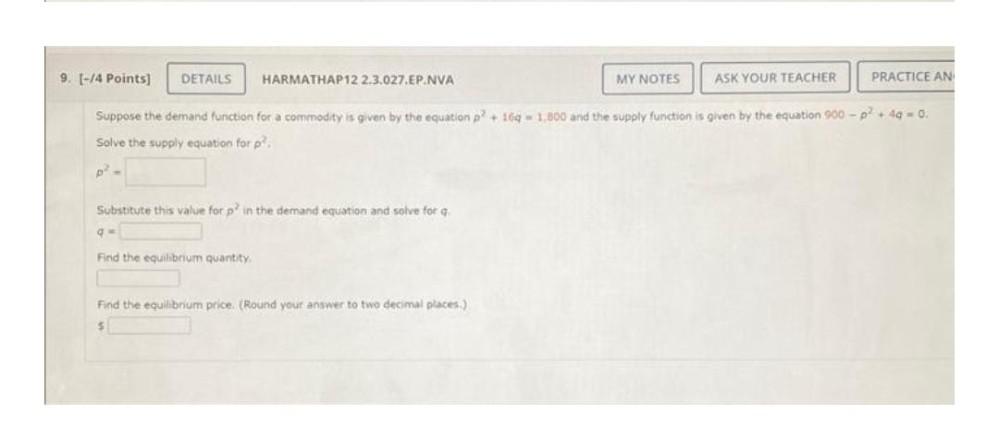
Algebra
Permutations and CombinationsSuppose the demand function for a commodity is given by the equation p² + 16q =1,800 and the supply function is given by the equation
900-p² + 4q = 0.
Solve the supply equation for p².
p²=__________
Substitute this value for p² in the demand equation and solve for q.
q=__________
Find the equilibrium quantity.
__________
Find the equilibrium price. (Round your answer to two decimal places)
$____________
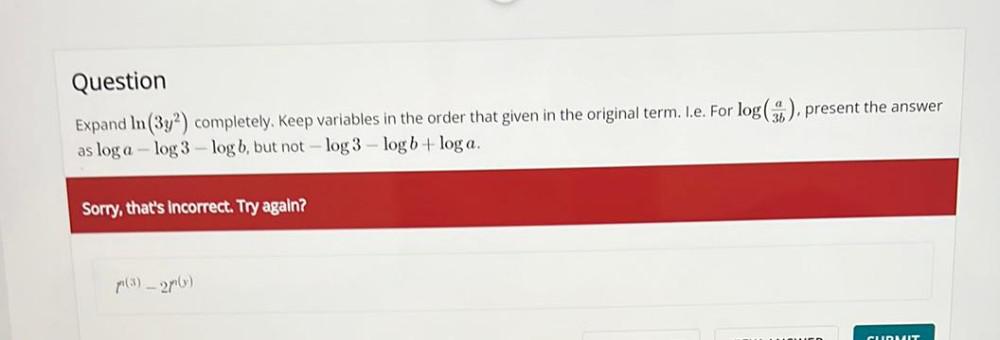
Algebra
Permutations and CombinationsExpand In (3y²) completely. Keep variables in the order that given in the original term. I.e. For log(a/3b), present the answer as log a-log 3-logb, but not - log 3-log b + log a.
r(³)-2r(y)

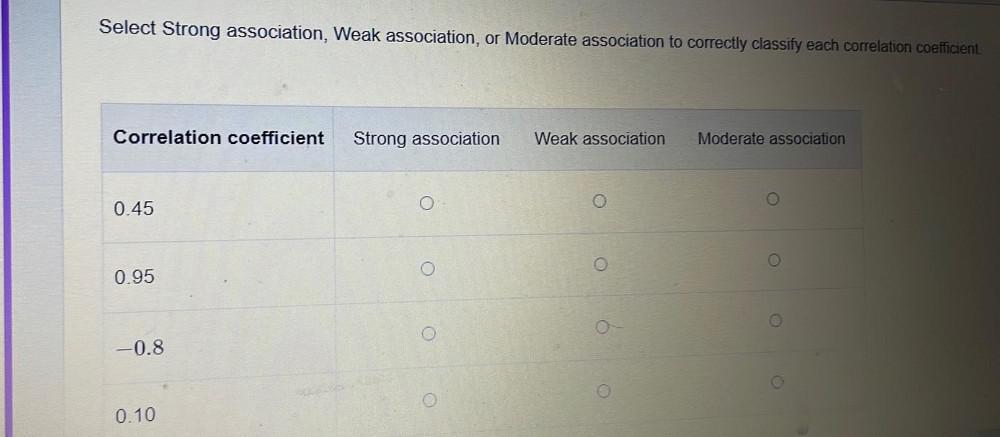
Algebra
Permutations and CombinationsSelect Strong association, Weak association, or Moderate association to correctly classify each correlation coefficient.
Correlationcoefficient Strongassociation Weakassociation Moderate association
0.45
0.95
-0.8
0.10

Algebra
Permutations and CombinationsIn the 2010 census, the population of state A in thousands was 4,792, State B was 2,991, and State C was 4,551. Apportion 15 representative seats to
these three states. Assign the seats using the Hamilton apportionment method
The representation includes
members from State A.
...
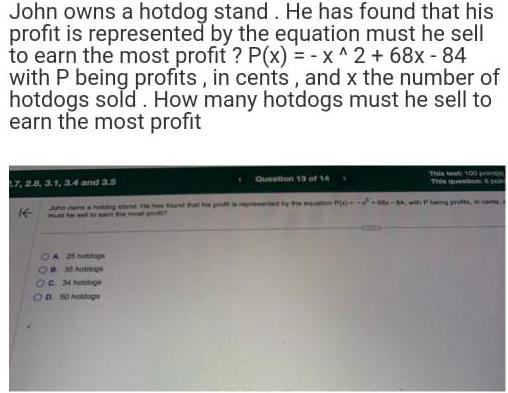
Algebra
Permutations and CombinationsJohn owns a hotdog stand. He has found that his profit is represented by the equation must he sell to earn the most profit? P(x) = -x^2 +68x-84 with P being profits, in cents, and x the number of hotdogs sold. How many hotdogs must he sell to earn the most profit

Algebra
Permutations and CombinationsUse Cramer's Rule to solve (if possible) the system of linear equations. (If not possible, enter IMPOSSIBLE.)
18x₁ + 12x₂= 25
30x₁ +24x₂ = 47

Algebra
Permutations and Combinations(Solving for a specified variable, equations of lines) When writing the equation of a line in college algebra, we will start with the point-slope form of line, y - y₁ = m(x-x₁), and we will solve it for y to write it in
slope-intercept-form, y = mx + b. Substitute the given point and slope into the point-slope form and then solve for y so your equation is in slope-intercept form.
a) x₁ = 2, y₁ = 3, m = 4
b) x₁ = 5, y₁ = -5, m = -2
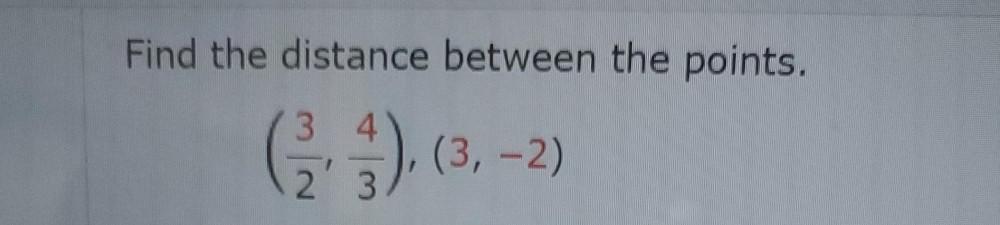
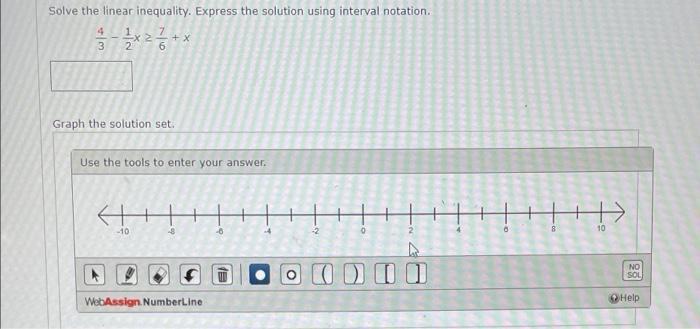
Algebra
Permutations and CombinationsSolve the linear inequality. Express the solution using interval notation.
(4/3) - (1/2)x ≥ (7/6) +x
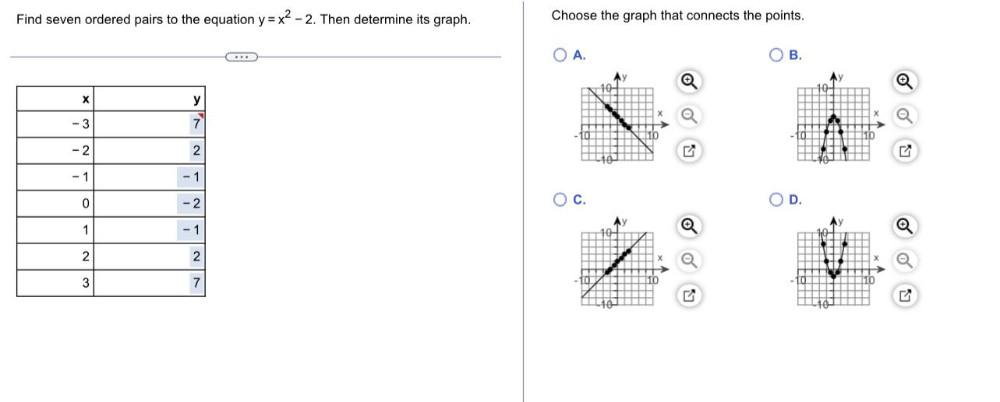
Algebra
Permutations and CombinationsFind seven ordered pairs to the equation y=x²-2. Then determine its graph.

Algebra
Permutations and CombinationsThe population of wolves in a wildlife reserve can be modelled by the function f(x) = (1000 + 600x)/(10 + 0.6x), where f(x) is the population of wolves, and x is the number of years since the population was introduced. In the context of this model, what does the vertical asymptote represent?
(a) Nothing; the vertical asymptotes are irrelevant in all contexts.
(b) Nothing; the vertical asymptote is outside the domain.
(c) The maximum number of wolves that can survive in the reserve at any given time.
(d) The time at which the wolves began living in the reserve.
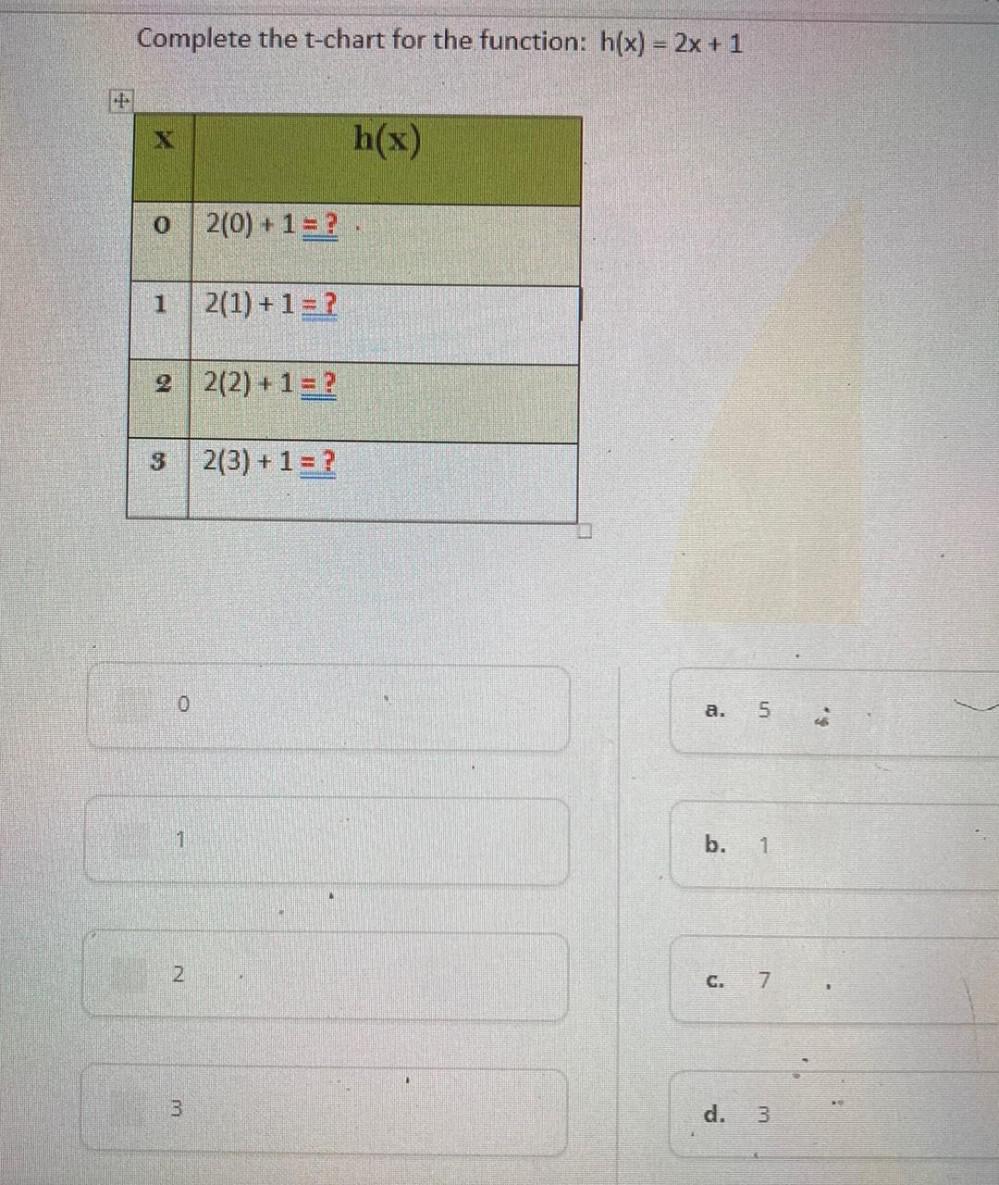
Algebra
Permutations and CombinationsComplete the t-chart for the function: h(x) = 2x + 1
x h(x)
0 2(0)+1=?
1 2(1) + 1 = ?
2 2(2) + 1 = ?
3 2(3)+1 = ?
a. 5
b. 1
C. 7
d. 3

Algebra
Permutations and CombinationsUse the fact that the diameter of the largest particle that can be moved by a stream varies approximately directly as the square of the velocity of the stream.
A stream with a velocity of 1/5 mile per hour can move coarse sand particles about 0.07 inch in diameter. Approximate the velocity required to carry particles 0.2 inch in diameter. (Round your answer to two decimal places.)