Permutations and Combinations Questions and Answers
Algebra
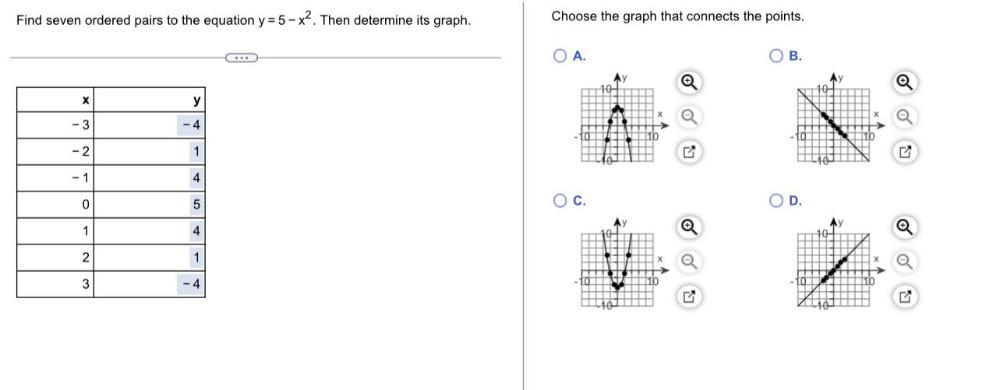
Permutations and CombinationsFind seven ordered pairs to the equation y = 5 - x². Then determine its graph.
x y
-3 -4
-2 1
-1 4
0 5
1 4
2 1
3 -4
Choose the graph that connects the points.

Algebra
Permutations and CombinationsFor x ∈ (3/7, ∞), use only the definition of increasing or decreasing function to determine if the f(x) = 1/3 - 5/(7(√7x - 3))is increasing or decreasing.

Algebra
Permutations and CombinationsEvery day at Thomas's house they buy a baguette of bread that has the shape of a cylinder with a height of 45 cm and a radius of 5 cm joined with two hemispheres. What are the dimensions of the bread bag in the shape of a right circular cylinder where the bread can be packed in such a way that there is the least amount of space left over?

Algebra
Permutations and CombinationsFind seven ordered pairs to the equation y = 5-x². Then determine its graph.
X y
- 3 ____
Algebra
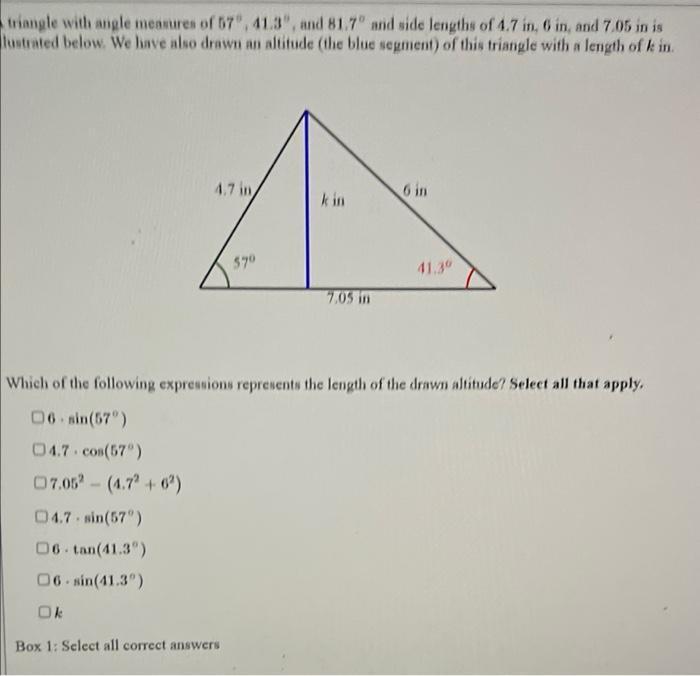
Permutations and CombinationsWhich of the following expressions represents the length of the drawn altitude? Select all that apply.
(A) 6 * sin(57°)
(B) 4.7 * cos(57°)
(C) 7.05² - (4.7² + 6²)
(E) 4.7 * sin(57°)
(F) 6 * tan(41.3°)
(G) 6 * sin(41.3°)
(H) k

Algebra
Permutations and CombinationsFind the exact value of cos (7π/12)
a) 1-√3/2√2
b) √3+1/√2
c) √3-1/2√2
d) √3+1/2√2

Algebra
Permutations and CombinationsWrite the expression in simplest form.
√300
a. 100√3
b. 3√10
c. 150
d. 10√3

Algebra
Permutations and CombinationsRewrite and simplify log₁₀₀x as a logarithm with base ten.
a) (1/2)log₁₀x
b) 2log₁₀x
c) 2x
d) log₁₀2x

Algebra
Permutations and CombinationsThe board of directors of a company knows that the probability that the carbon emission from the company's manufacturing permissible level is 30%. A consultant is hired to use a carbon footprint calculator to test for the emission What is the probability that the manufacturing unit has carbon emission beyond the permissible is exceeding the of this test is said to be 85%. level. The accuracy emission level and the test predicts this?
Algebra
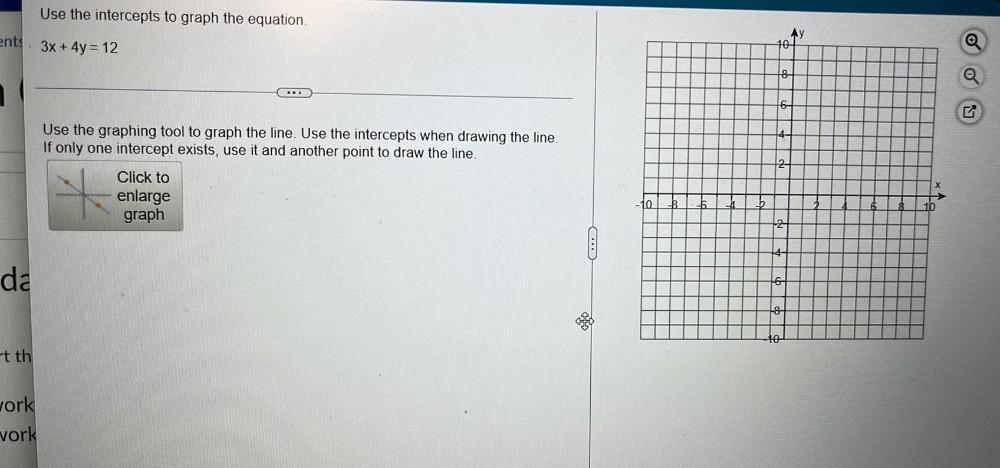
Permutations and CombinationsUse the intercepts to graph the equation.
3x+4y=12
Use the graphing tool to graph the line. Use the intercepts when drawing the line.
If only one intercept exists, use it and another point to draw the line.
Algebra
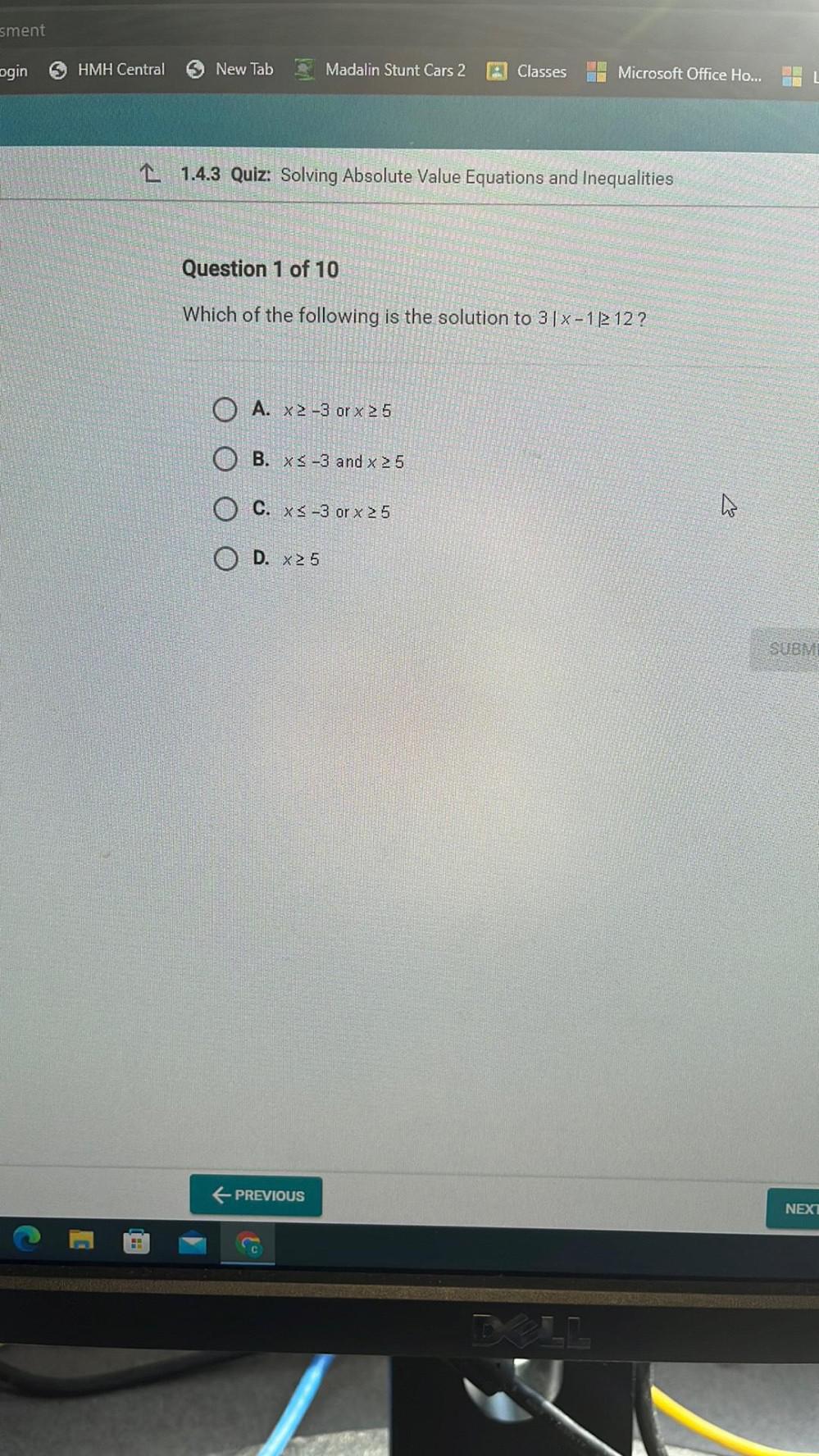
Permutations and CombinationsWhich of the following is the solution to 3|x-1|≥12?
A. x≥-3 or x ≥5
B. x ≤3 and x ≥ 5
C. x≤3 or x≥5
D. x≥5
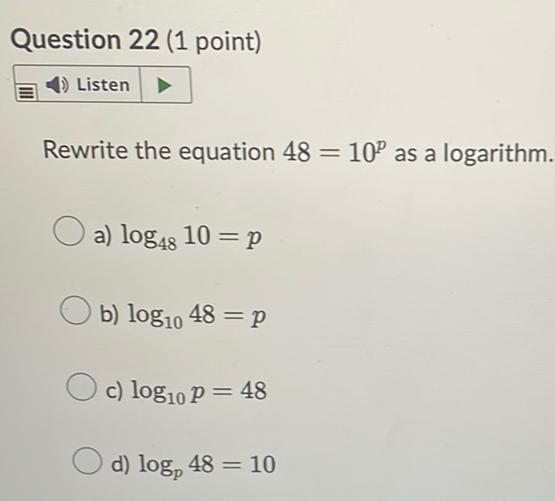
Algebra
Permutations and CombinationsRewrite the equation 48 = 10ᵖ as a logarithm.
a) log₄₈10 = p
b) log₁₀48 = p
c) log₁₀p = 48
d) log_p 48 = 10

Algebra
Permutations and CombinationsA total of 270 tickets were sold for the school play. They were either adult tickets or student tickets. The number of student tickets sold was two times the number of adult tickets sold. How many adult tickets were sold?
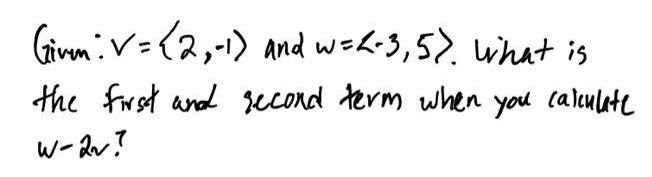
Algebra
Permutations and CombinationsGiven : V = <2,-1> and w=<-3,5>. What is
the first and second term when you calculate
w-2v?

Algebra
Permutations and CombinationsYou have 7 balls that are each a different color of the rainbow. In how many distinct ways can these balls be ordered? Show your work.

Algebra
Permutations and CombinationsElise sells cupcakes and brownies. Her cupcakes cost $1.50 each and she sold
$45.75 worth of brownies. Write an equation to determine how many cupcakes she sold if she made a total of $143.25.

Algebra
Permutations and CombinationsLast year there were 450 students in a soccer league. This year, participation increased by 64%. How many more children joined the league this year?
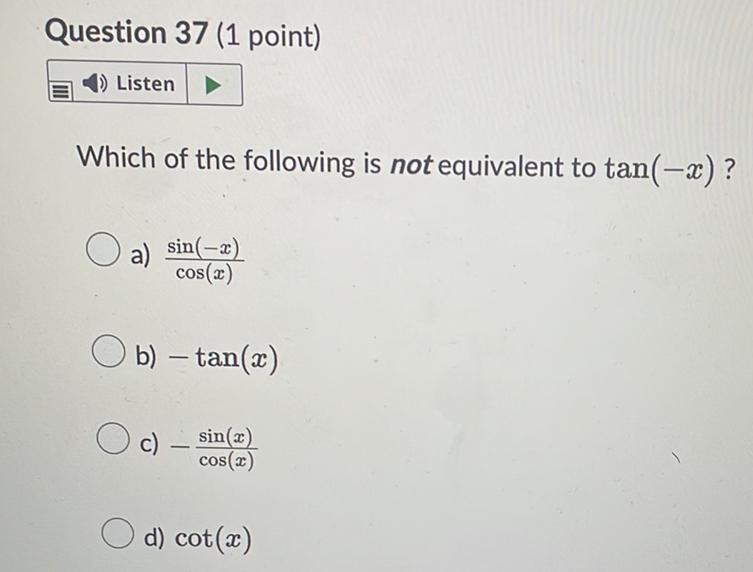
Algebra
Permutations and CombinationsWhich of the following is not equivalent to tan(-x)?
a)sin(-x)/cos(x)
b)-tan(x)
c)-sin(x)/cos(x)
d) cot(x)

Algebra
Permutations and CombinationsThere are 1,400 individuals in a school. Staff make up 4%. How many staff
members are at the school?

Algebra
Permutations and CombinationsYou have 6 different colored balloons. In how many distinct ways can the balloons be ordered Select one:
O a. 720
O b. 365
O C. 5040
O d. 120

Algebra
Permutations and Combinations1,200 students registered for an art camp. 945 students showed up. Calculate the percent error.

Algebra
Permutations and CombinationsWhich of the following could be the artist's rendition graph of
f(x) = log 4/3 (x+3)-2

Algebra
Permutations and Combinations30 people are running for an office to be chosen randomly. You plan to use a 6-sided dice and a spinner. How many sections need to be on the spinner so each person has their own shape and number?
Select one:
a. 8
b. 6
c. 5
d. 24
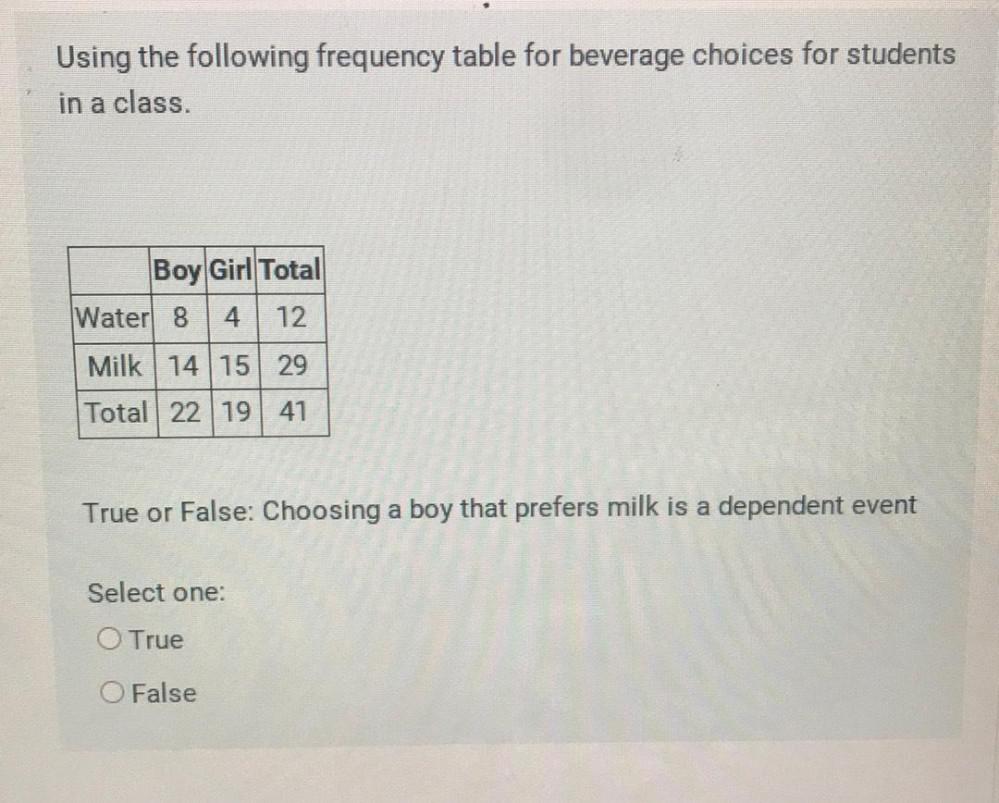
Algebra
Permutations and CombinationsUsing the following frequency table for beverage choices for students in a class.
Boy Girl Total
Water 8 4 12
Milk 14 15 29
Total 22 19 41
True or False: Choosing a boy that prefers milk is a dependent event
Select one:
True
False
Algebra
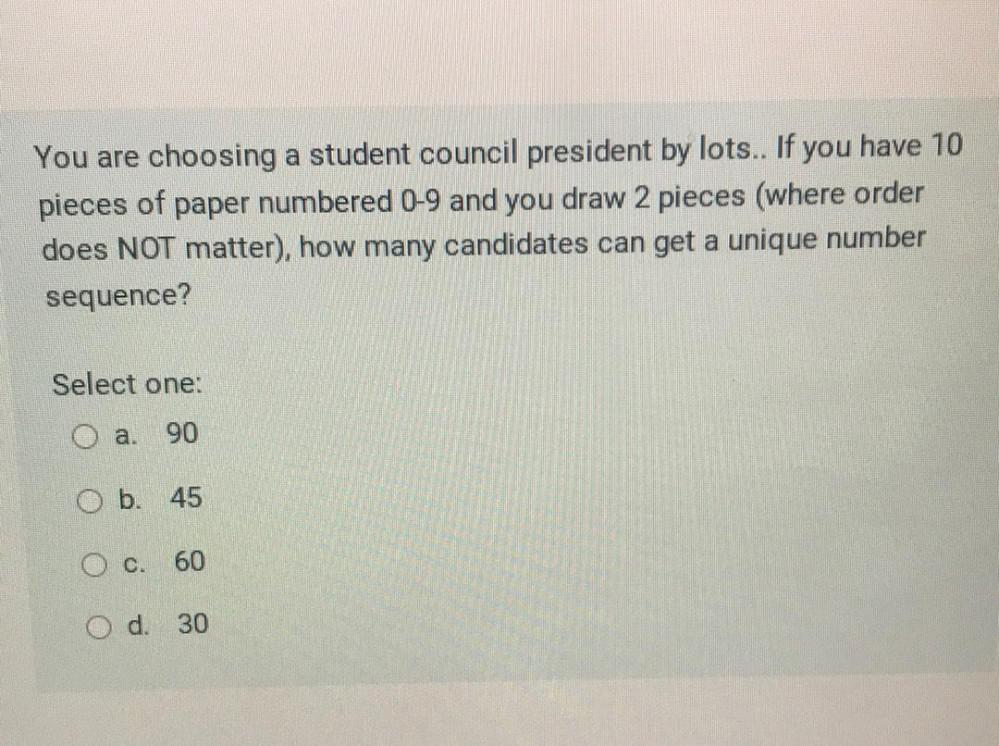
Permutations and CombinationsYou are choosing a student council president by lots.. If you have 10 pieces of paper numbered 0-9 and you draw 2 pieces (where order does NOT matter), how many candidates can get a unique number sequence?
a. 90
b. 45
c. 60
d. 30
Algebra
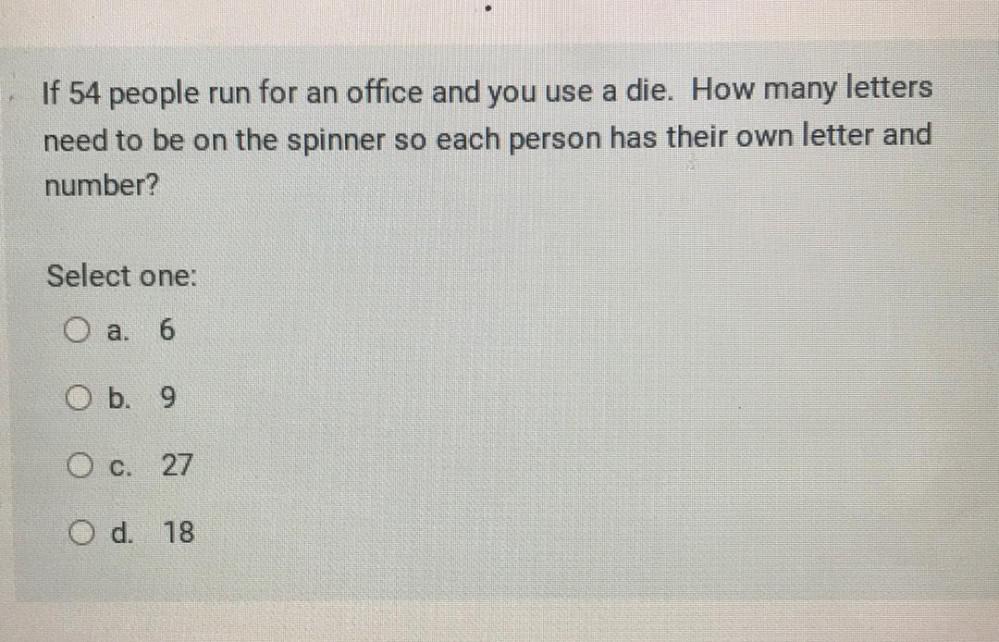
Permutations and CombinationsIf 54 people run for an office and you use a die. How many letters need to be on the spinner so each person has their own letter and number?
Select one:
a. 6
b. 9
c. 27
d. 18
Algebra
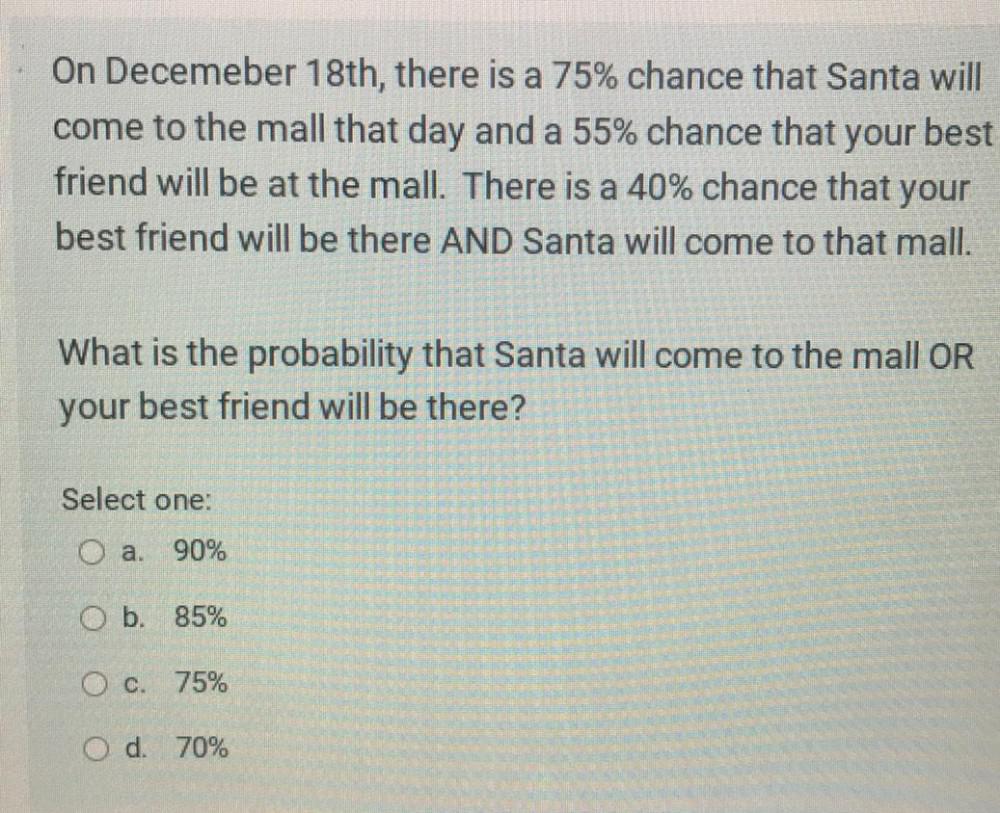
Permutations and CombinationsOn December 18th, there is a 75% chance that Santa will
come to the mall that day and a 55% chance that your best
friend will be at the mall. There is a 40% chance that your
best friend will be there AND Santa will come to that mall.
What is the probability that Santa will come to the mall OR
your best friend will be there?
Select one:
a. 90%
b. 85%
c. 75%
d. 70%

Algebra
Permutations and CombinationsYou play a game that requires rolling a six-sided die then randomly choosing a colored card from a deck containing 3 red cards, 7 blue cards,
and 7 yellow cards. Find the probability that you will roll a 5 on the die and then choose a yellow card.
(a) 7/17
(b) 7/102
(c) 1/6
(d) 1/17
Algebra
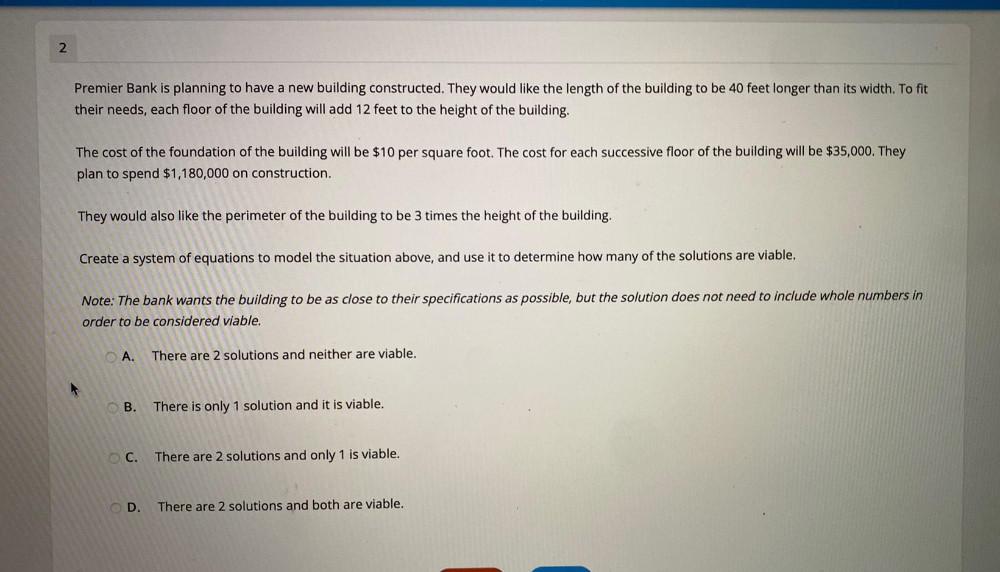
Permutations and CombinationsPremier Bank is planning to have a new building constructed. They would like the length of the building to be 40 feet longer than its width. To fit
their needs, each floor of the building will add 12 feet to the height of the building. The cost of the foundation of the building will be $10 per square foot. The cost for each successive floor of the building will be $35,000. They plan to spend $1,180,000 on construction. They would also like the perimeter of the building to be 3 times the height of the building. Create a system of equations to model the situation above, and use it to determine how many of the solutions are viable. Note: The bank wants the building to be as close to their specifications as possible, but the solution does not need to include whole numbers in
order to be considered viable.
A. There are 2 solutions and neither are viable..
B. There is only 1 solution and it is viable.
C. There are 2 solutions and only 1 is viable.
D. There are 2 solutions and both are viable.

Algebra
Permutations and CombinationsAt a sandwich shop, 61% of customers buy a drink with their sandwich. Only 26% of customers buy a drink and chips with their sandwich. What is the probability that a customer who buys a drink also buys chips?
a about 42.6%
b 87%
c about 2.3%
d 35%
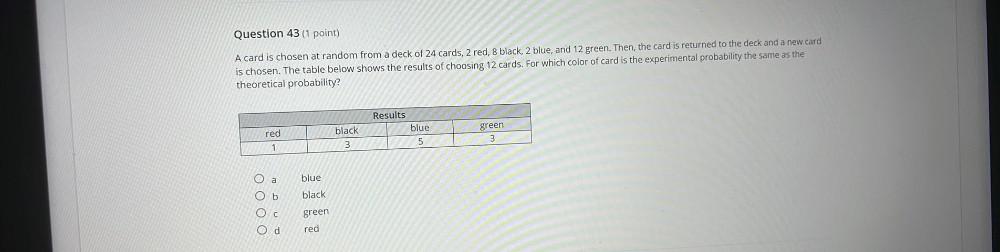
Algebra
Permutations and CombinationsA card is chosen at random from a deck of 24 cards, 2 red, 8 black, 2 blue, and 12 green. Then, the card is returned to the deck and a new card is chosen. The table below shows the results of choosing 12 cards. For which color of card is the experimental probability the same as the theoretical probability?
Results
red black blue green
1 3 5 3
a) blue
b) black
c) green
d) red
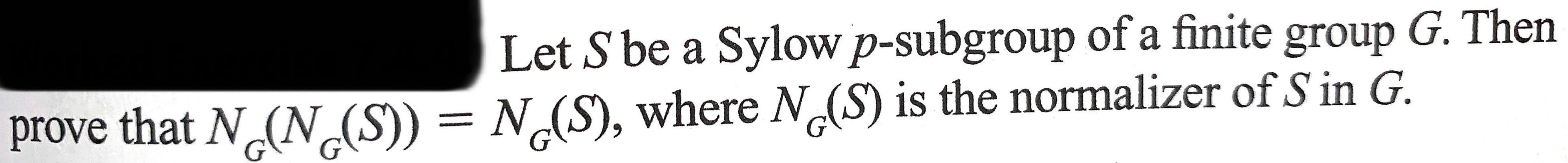
Algebra
Permutations and CombinationsLet S be a Sylow p-subgroup of a finite group G. Then prove that Nċ(N(S)) = N(S), where N(S) is the normalizer of S in G.


Algebra
Permutations and CombinationsSolve the system.
x+y=7
y+z=8
x-z = -1
Is the system inconsistent, dependent or does it have 1 solution?

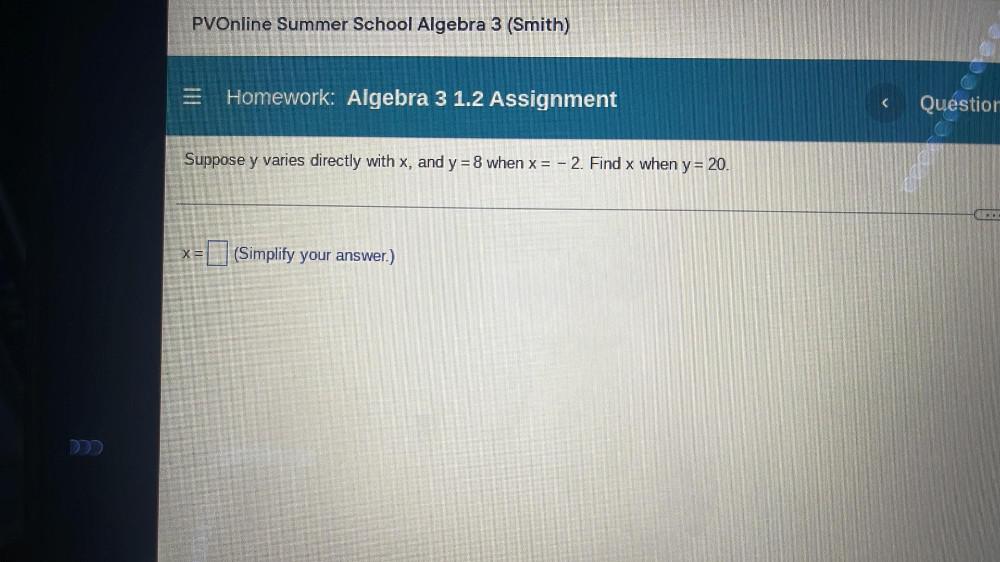
Algebra
Permutations and CombinationsSuppose y varies directly with x, and y = 8 when x = -2. Find x when y = 20.
x =
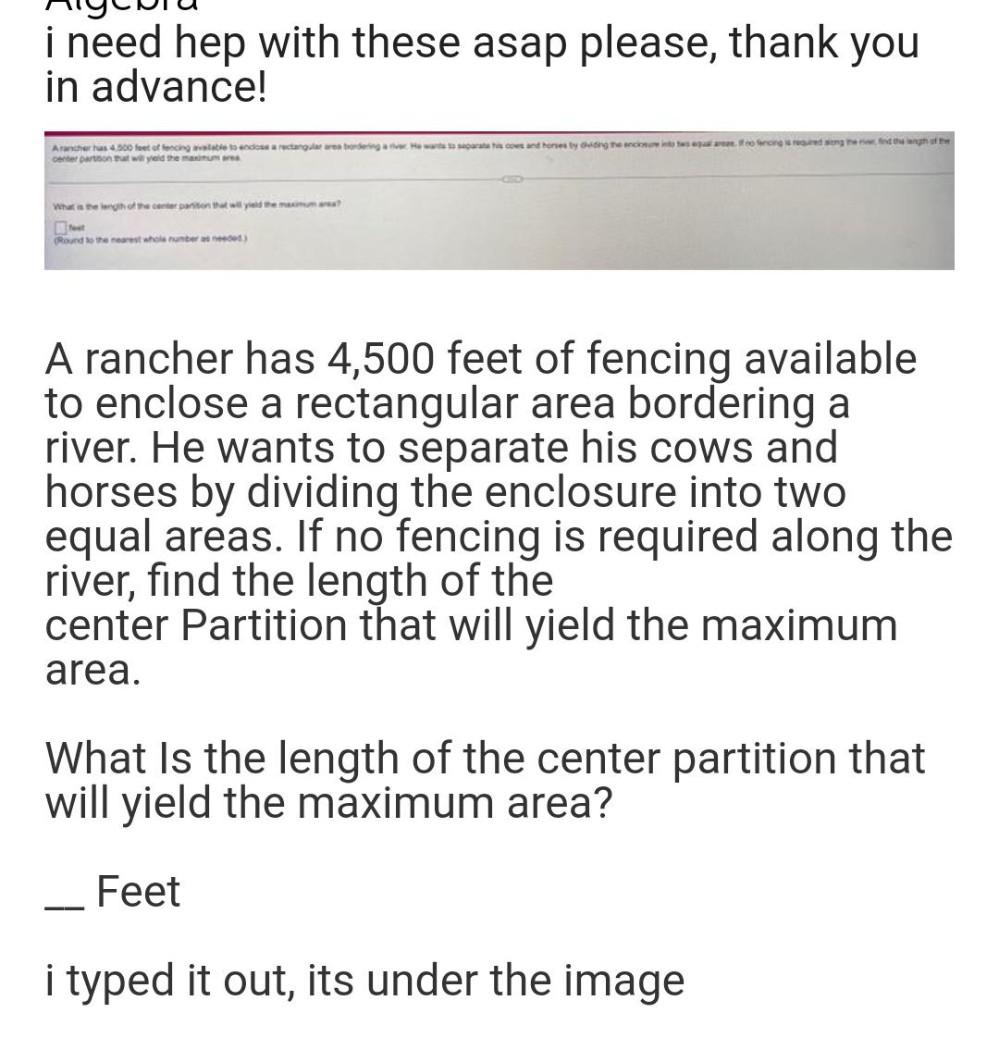
Algebra
Permutations and CombinationsA rancher has 4,500 feet of fencing available to enclose a rectangular area bordering a river He wants to separate his cows and horses by hiding the enclosure into two equal areas. If no fencing is required along the find the length of the center partition that will yield the maximum area. What is the length of the center partition that will yield the maximum area? (Round to the nearest whole number as needed)

Algebra
Permutations and CombinationsDefine S(h)= -f(x + 2h) + 4f(x+h)-3f(x)/2h
(a) Show that
f'(x) - S(h) = c₁h² + c₂h³ + c3h² + ...

Algebra
Permutations and CombinationsFind the coordinate of the midpoint of the line segment that joins the two given points.
(6, 3) and (-2, - 5)

Algebra
Permutations and CombinationsLet p and 2p + 1 be prime numbers and z is an integer. Are these nonlinear
Diophantine equation have an integer solution? In what form?
a. p¹ +(2p + 1)¹ = z²
b. p¹ +(2p + 1)² = z²
c. p² + (2p+1)¹ = z²
d. p¹ +(2p + 1)³ = z²
e. p² + (2p + 1)² = z²
f. p³ +(2p+1)¹ = z²
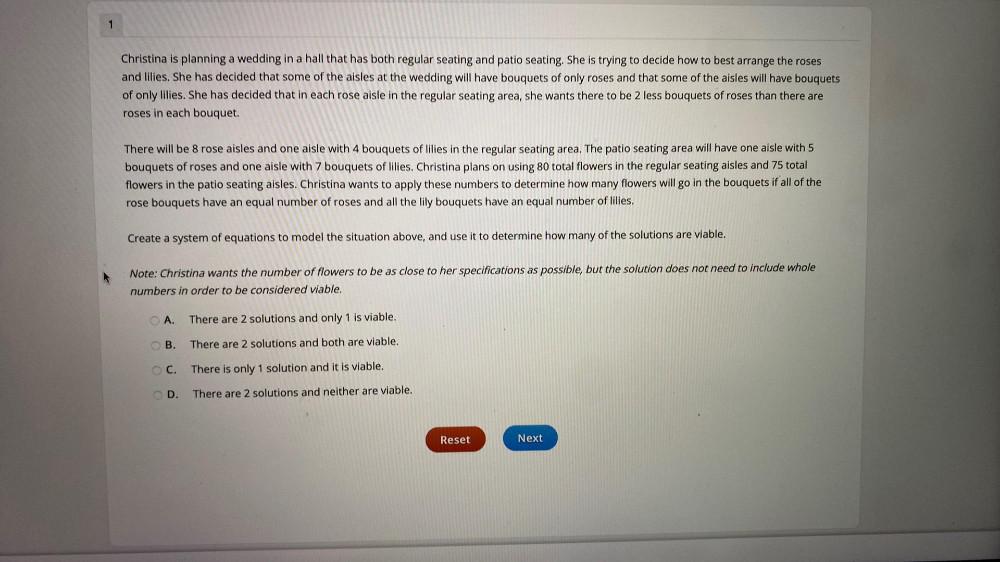
Algebra
Permutations and CombinationsChristina is planning a wedding in a hall that has both regular seating and patio seating. She is trying to decide how to best arrange the roses and lilies. She has decided that some of the aisles at the wedding will have bouquets of only roses and that some of the aisles will have bouquets of only lilies. She has decided that in each rose aisle in the regular seating area, she wants there to be 2 less bouquets of roses than there are roses in each bouquet. There will be 8 rose aisles and one aisle with 4 bouquets of lilies in the regular seating area. The patio seating area will have one aisle with 5 bouquets of roses and one aisle with 7 bouquets of lilies. Christina plans on using 80 total flowers in the regular seating aisles and 75 total flowers in the patio seating aisles. Christina wants to apply these numbers to determine how many flowers will go in the bouquets if all of the rose bouquets have an equal number of roses and all the lily bouquets have an equal number of lilies. Create a system of equations to model the situation above, and use it to determine how many of the solutions are viable. Note: Christina wants the number of flowers to be as close to her specifications as possible, but the solution does not need to include whole numbers in order to be considered viable.
A. There are 2 solutions and only 1 is viable.
B. There are 2 solutions and both are viable.
C. There is only 1 solution and it is viable.
D. There are 2 solutions and neither are viable.
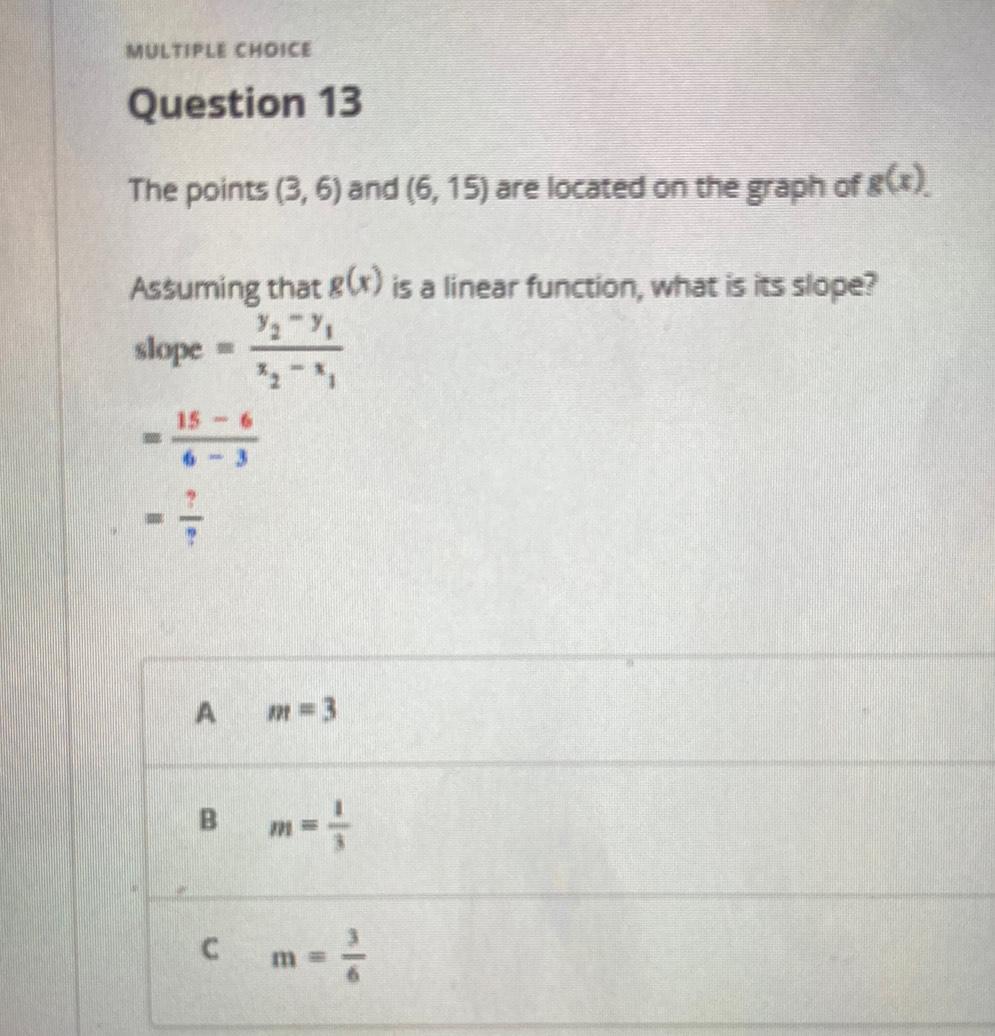
Algebra
Permutations and CombinationsThe points (3,6) and (6, 15) are located on the graph of g(x).
Assuming that g(x) is a linear function, what is its slope?
slope= (y₂-y₁)/(x₂-x₁)
A m=3
B m=1/3
C m=3/6

Algebra
Permutations and CombinationsIf P dollars is deposited in a savings account that pays interest at a rate of r% per year compounded continuously, find the balance after t years.
P = 80, r=3 1/2 , t = 10

Algebra
Permutations and CombinationsA dripping faucet wastes a cup of water if it drips for three minutes. the faucet drips. How long will it take for the faucet to waste 4.5 cups of water? The amount of water wasted varies directly
with the amount of time Show your work or describe how you found your answer.


Algebra
Permutations and CombinationsWrite the equation of the line if the slope = -3/5 and the line passes through (-4, 0). Show your work.
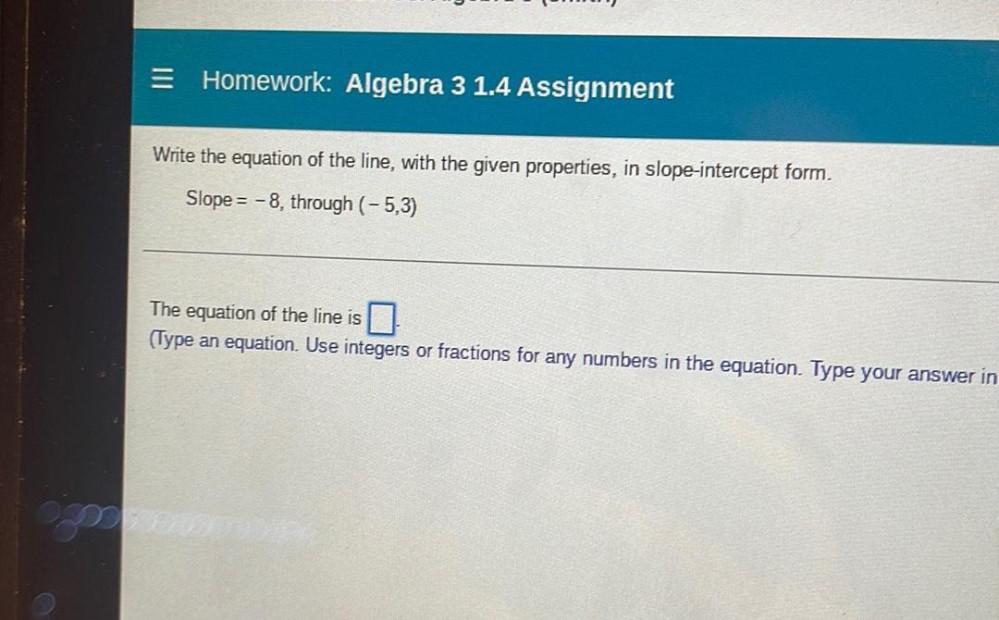
Algebra
Permutations and CombinationsWrite the equation of the line, with the given properties, in slope-intercept form.
Slope=-8, through (-5,3)
The equation of the line is__.
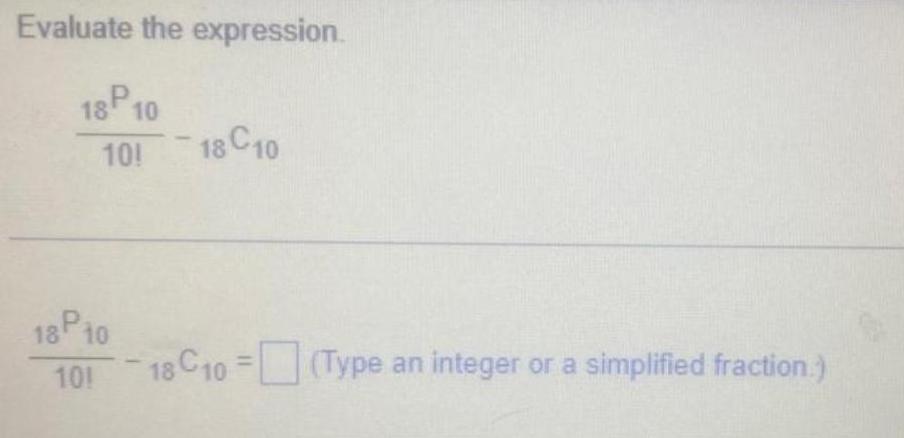
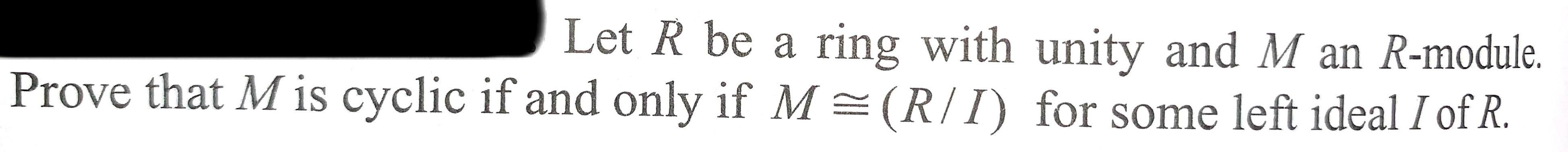
Algebra
Permutations and CombinationsLet R be a ring with unity and M an R-module. Prove that M is cyclic if and only if M = (R/I) for some left ideal I of R.

Algebra
Permutations and CombinationsConsider the system of equations
x₁ + x₂ + x₂ = 2
2x₁ + x₂ - x₂ = 5
x₁ - x₂-3x₂ = 2
Using the inverse of A or otherwise, find the solution x =