Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
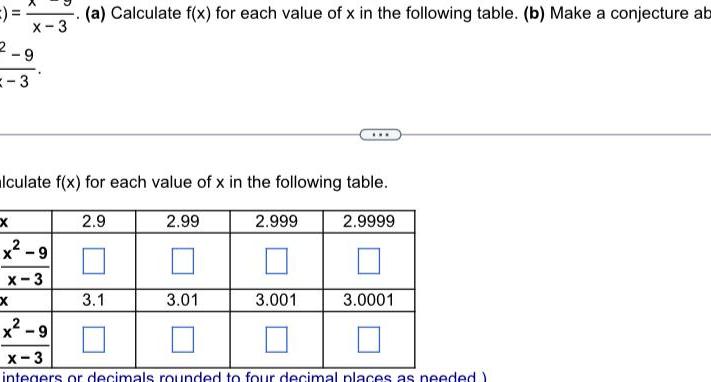
Differential equations3 x X 3 9 Xx lculate f x for each value of x in the following table x 9 x 3 a Calculate f x for each value of x in the following table b Make a conjecture ab 2 9 3 1 2 99 3 01 2 999 3 001 2 9999 3 0001 x 9 x 3 integers or decimals rounded to four decimal places as needed
Calculus
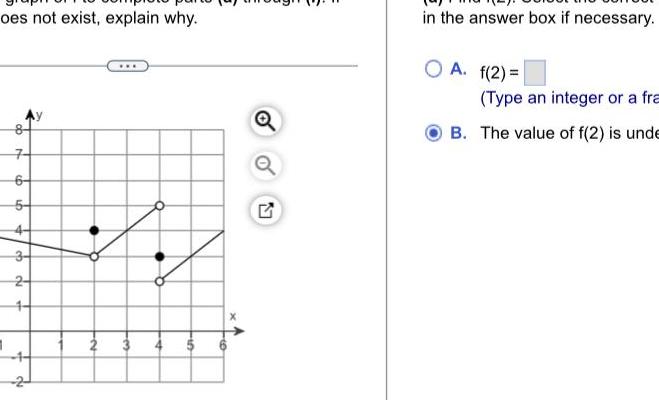
Application of derivativesoes not exist explain why 7 6 5 3 2 1 3 4 10 to S in the answer box if necessary A f 2 Type an integer or a fra B The value of f 2 is unde

Calculus
Vector CalculusHow much work is required to move an object from x 5 to x 9 measured in meters with a constant force of 6 N acting along the x axis If a constant force F displaces an object a distance d in the direction of the force what is the correct relationship to use to calculate the work done OA workforce distance distance force OB work c work force distance force distance OD work The work required is

Calculus
Application of derivativesUse the disk method to find the volume of a solid of revolution around the x axis with other functions Question A solid of revolution is generated by rotating the region between the x axis and the graphs of f x 2e2x x 0 and x ln 9 about the x axis Using the disk method what is the volume of the solid Enter your answer in terms of Sorry that s incorrect Try again 407
Calculus
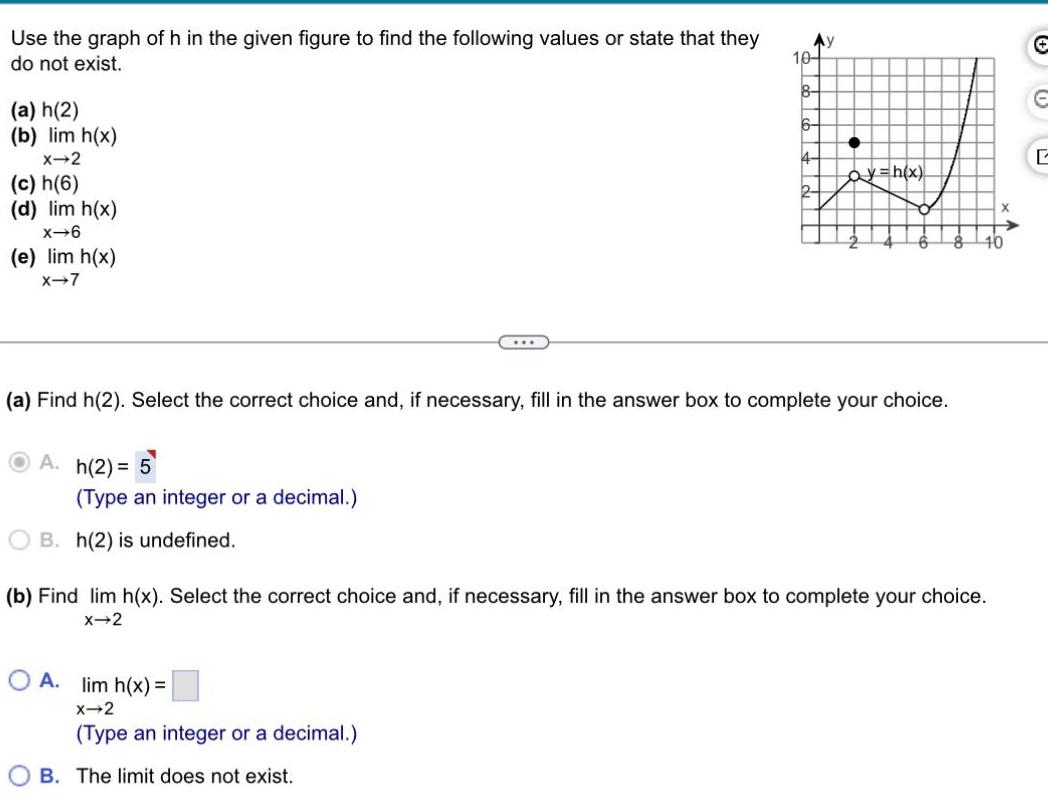
Application of derivativesUse the graph of h in the given figure to find the following values or state that they do not exist a h 2 b lim h x X 2 c h 6 d lim h x x 6 e lim h x X 7 h 2 5 Type an integer or a decimal B h 2 is undefined a Find h 2 Select the correct choice and if necessary fill in the answer box to complete your choice 10 8 OA lim h x X 2 Type an integer or a decimal OB The limit does not exist ay h x b Find lim h x Select the correct choice and if necessary fill in the answer box to complete your choice X 2 X 10 E L

Calculus
Limits & ContinuityA semicircle with diameter PQ sits on an isosceles triangle PQR to form a region shaped like a two dimensional ice cream cone as shown in the figure P 10 cm A 0 B 0 01 R Q 10 cm If A 0 is the area of the semicircle and B 0 is the area of the triangle find A 0 lim 0 0 B 0

Calculus
Application of derivativesCURRENT OBJECTIVE Use the disk method to find the volume of a solid of revolution around the x axis with other functions Question A solid of revolution is generated by rotating the region between the x axis and the graphs of f x 3 2sin x x 37 and x about the x axis Using the disk method what is the volume of the solid Enter your answer in terms of Provide your answer below

Calculus
Definite IntegralsCURRENT OBJECTIVE Determine the volume of a solid by integrating a cross section with a circle or semicircle Question The result of slicing through the center of the solid S is the base described by the ellipse y 1 Cross sections of S perpendicular to the x axis and the elliptical base are circles What is the volume of S Enter your answer in terms of t Provide your answer below

Calculus
Definite IntegralsUse the disk method to find the volume of a solid of revolution around the y axis with a function defined as a function of y Question Define R as the region bounded by the graphs of g y 6 y 1 y 2 y 3 and the y axis Using the disk method what is the volume of the solid of revolution generated by rotating R about the y axis Enter your answer in terms of Provide your answer below
Calculus
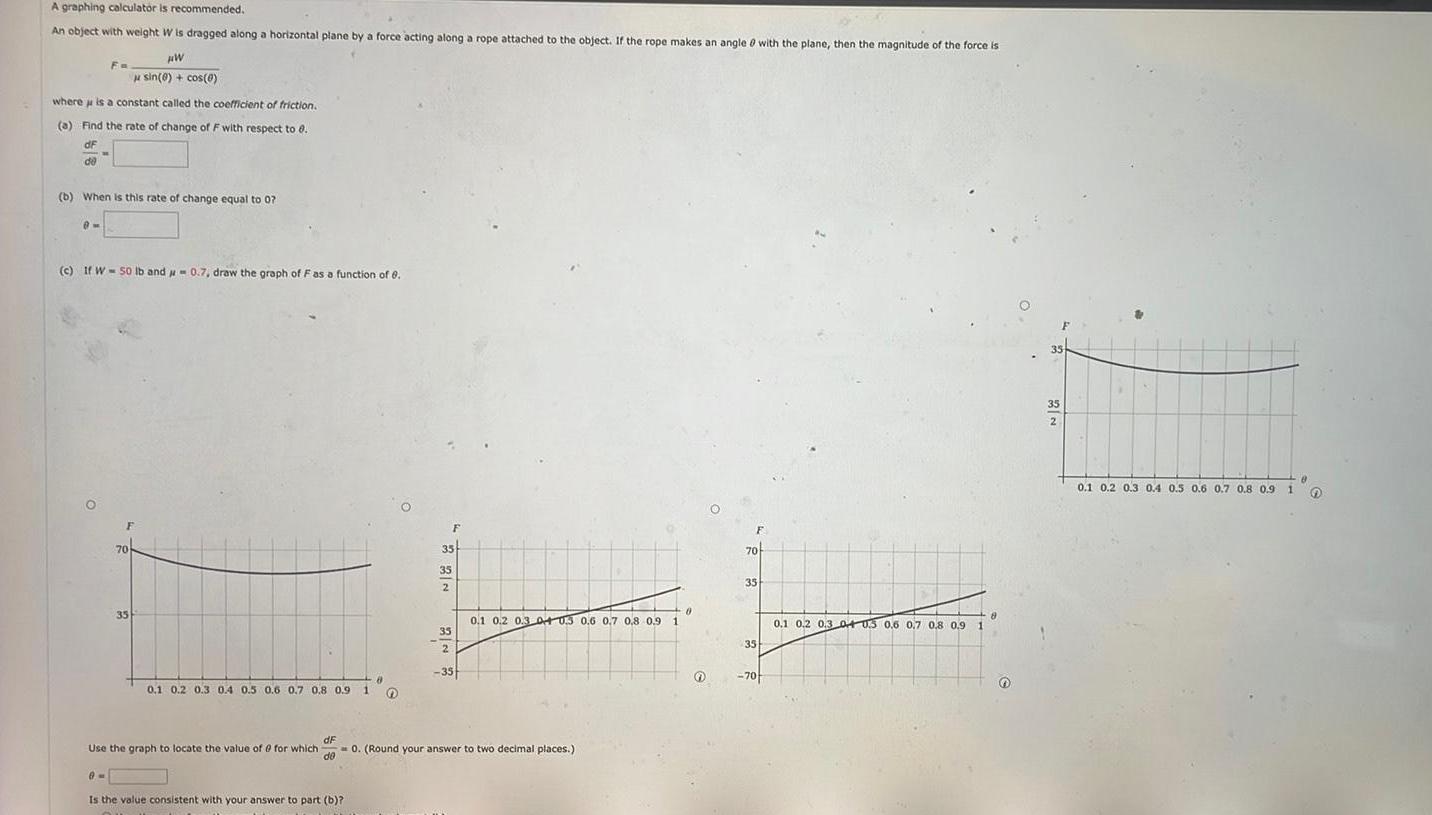
Application of derivativesA graphing calculator is recommended An object with weight W is dragged along a horizontal plane by a force acting along a rope attached to the object If the rope makes an angle with the plane then the magnitude of the force is HW sin 0 cos 0 where is a constant called the coefficient of friction a Find the rate of change of F with respect to 8 dF de Fo b When is this rate of change equal to 07 m c If W 50 lb and 0 7 draw the graph of F as a function of 6 35 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 Use the graph to locate the value of 0 for which dF de 9M Is the value consistent with your answer to part b 1 8 O 35 35 2 35 2 35 0 0 1 0 2 0 3 04 03 0 6 0 7 0 8 0 9 1 0 Round your answer to two decimal places F 70 35 35 70 8 0 1 0 2 0 3 04 03 0 6 0 7 0 8 0 9 1 35 2 N 2 8 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 1

Calculus
DifferentiationThe path r t t i 212 9 j describes motion on the parabola y 2x2 9 Find the particle s velocity and acceleration vectors at t 1 and sketch them as vectors on the curve CIUD The velocity vector at t 1 is v 1 i j Simplify your answer including any radicals Use integers or fractions for any numbers in the expression

Calculus
Differential equationsThe equation r t cos 2t i sin 2t j t20 describes the motion of a particle moving along the unit circle Answer the following questions about the behavior of the particle a Does the particle have constant speed If so what is its constant speed b Is the particle s acceleration vector always orthogonal to its velocity vector c Does the particle move clockwise or counterclockwise around the circle d Does the particle begin at the point 1 0 a Select the correct choice below and fill in any answer boxes w your choice OA The particle s constant speed is OB The particle s speed is not constant

Calculus
Differential equationsThe equation r t 2t 5 1 312 3 j 3t k is the position of a particle in space at time t Find the particle s velocity and acceleration vectors Then write the particle s velocity at t 1 as a product of its speed and direction What is the velocity vector v t 0 0 0 j i
Calculus
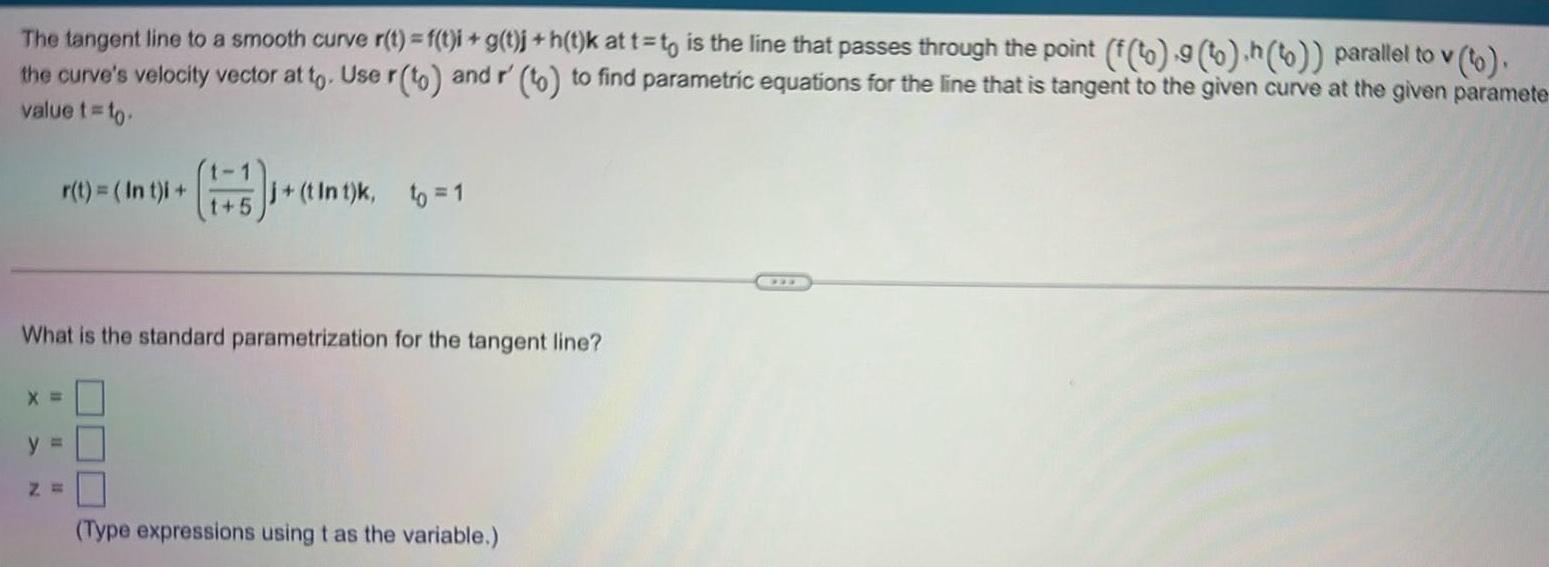
Vector CalculusThe tangent line to a smooth curve r t f t i g t j h t k at t t is the line that passes through the point f to 9 to h to parallel to v to the curve s velocity vector at to Use r to and r to to find parametric equations for the line that is tangent to the given curve at the given paramete value t to r t int i 1 5 tint What is the standard parametrization for the tangent line X y t Int k to 1 Z Type expressions using t as the variable
Calculus
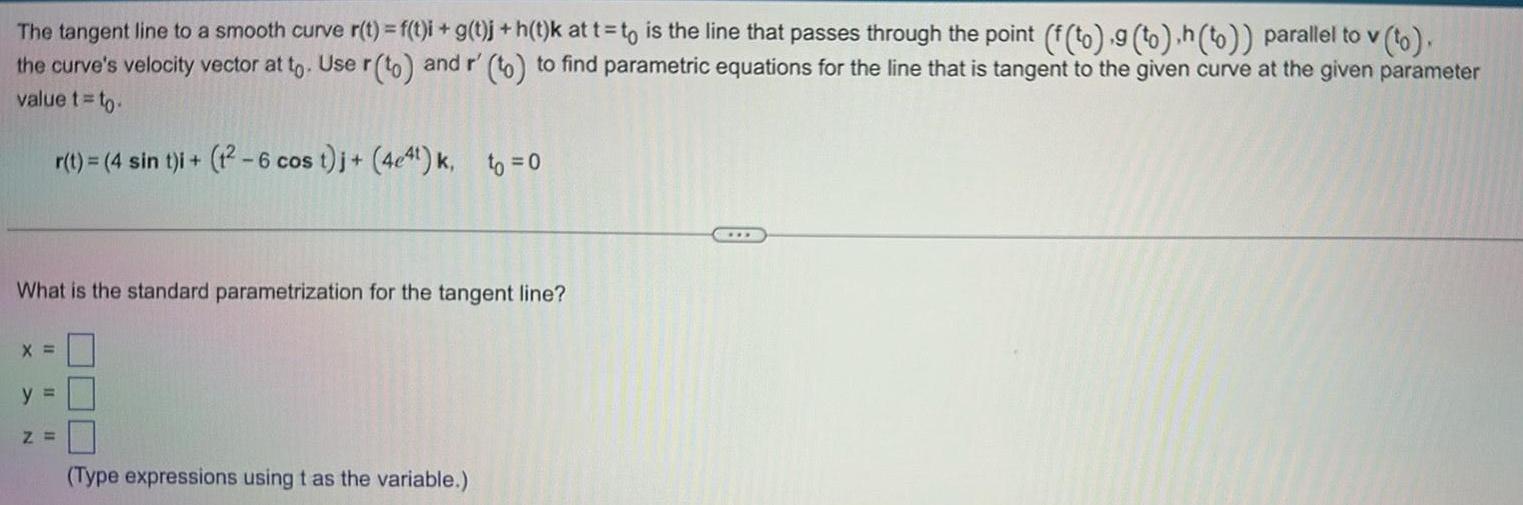
DifferentiationThe tangent line to a smooth curve r t f t i g t j h t k at t to is the line that passes through the point f to 9 to h to parallel to v to the curve s velocity vector at to Use r to and r to to find parametric equations for the line that is tangent to the given curve at the given parameter value t to r t 4 sin t i t 6 cos t j 4e4t k to 0 What is the standard parametrization for the tangent line X y Z Type expressions using t as the variable
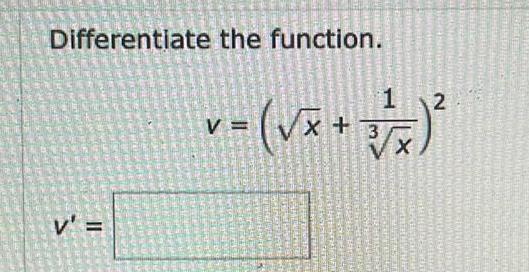
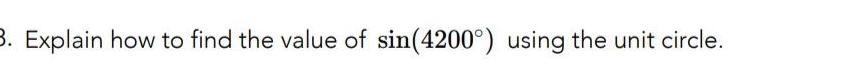

Calculus
Differentiation4 Explain how to use the unit circle to evaluate a trig ratio for an angle with negative measure 2 T For example sin 45 or cos 3

Calculus
Indefinite Integration1 For 0 0 2 name all the angles on the unit circle where cos 0 What do you notice about these angles
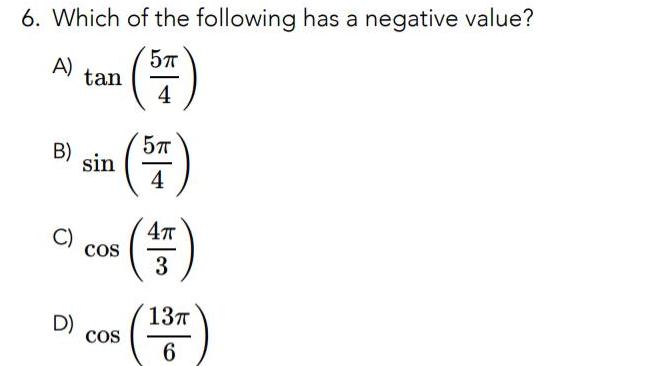
Calculus
Differentiation6 Which of the following has a negative value 57 4 A tan B sin D COS 57 4 COS 47 3 13TT 6


Calculus
Application of derivatives1 Four points and their coordiates are shwon on the unit circle Which value a b c d e f g or h is equal to a sin 3 2 b cos 360 C COS e f c d 0 g h a b
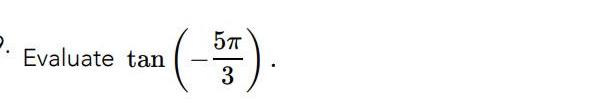
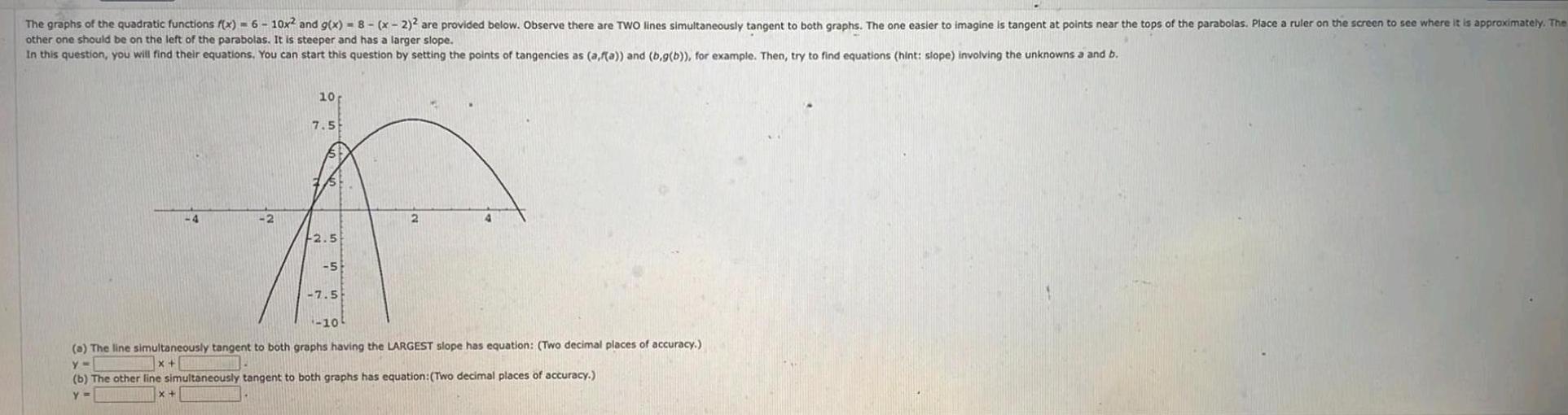
Calculus
Definite IntegralsThe graphs of the quadratic functions f x 6 10x and g x 8 x 2 2 are provided below Observe there are TWO lines simultaneously tangent to both graphs The one easier to imagine is tangent at points near the tops of the parabolas Place a ruler on the screen to see where it is approximately The other one should be on the left of the parabolas It is steeper and has a larger slope In this question you will find their equations You can start this question by setting the points of tangencies as a f a and b g b for example Then try to find equations hint slope involving the unknowns a and b 4 2 10 7 5 F2 5 5 7 5 10 a The line simultaneously tangent to both graphs having the LARGEST slope has equation Two decimal places of accuracy y x b The other line simultaneously tangent to both graphs has equation Two decimal places of accuracy Y x

Calculus
Application of derivatives5 Which angles on the unit circle have a reference angle of Give your answers in radians
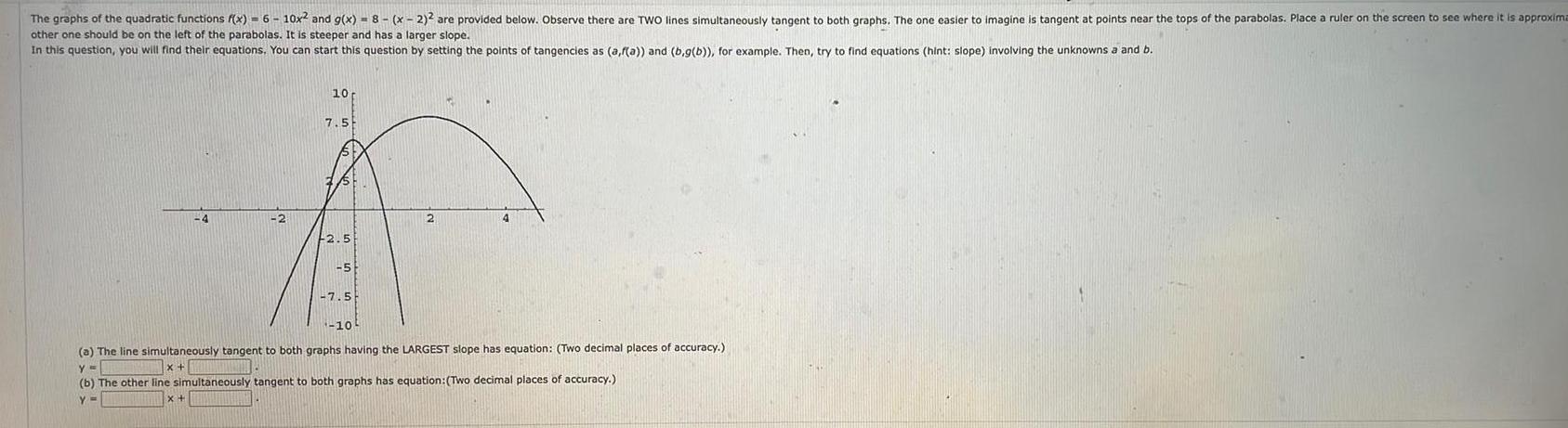
Calculus
Definite IntegralsThe graphs of the quadratic functions f x 6 10x and g x 8 x 2 are provided below Observe there are TWO lines simultaneously tangent to both graphs The one easier to imagine is tangent at points near the tops of the parabolas Place a ruler on the screen to see where it is approxima other one should be on the left of the parabolas It is steeper and has a larger slope In this question you will find their equations You can start this question by setting the points of tangencies as a f a and b g b for example Then try to find equations hint slope involving the unknowns a and b 10 7 5 A 2 2 4 2 5 5 7 5 10 a The line simultaneously tangent to both graphs having the LARGEST slope has equation Two decimal places of accuracy y x b The other line simultaneously tangent to both graphs has equation Two decimal places of accuracy Y x
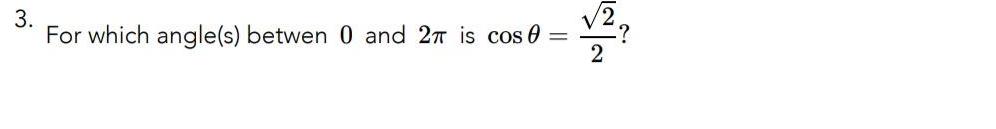

Calculus
Vector CalculusIf each of the following angles were an angle in a triangle how many significant digits would a side in the triangle contain 11 24 13 76 2 4 12 4 3 14 23 45

Calculus
Vector CalculusGive the number of significant digits in each of the following numbers 1 42 3 2 2 05 3 0 76 4 0 84 5 3 5723 6 4 189
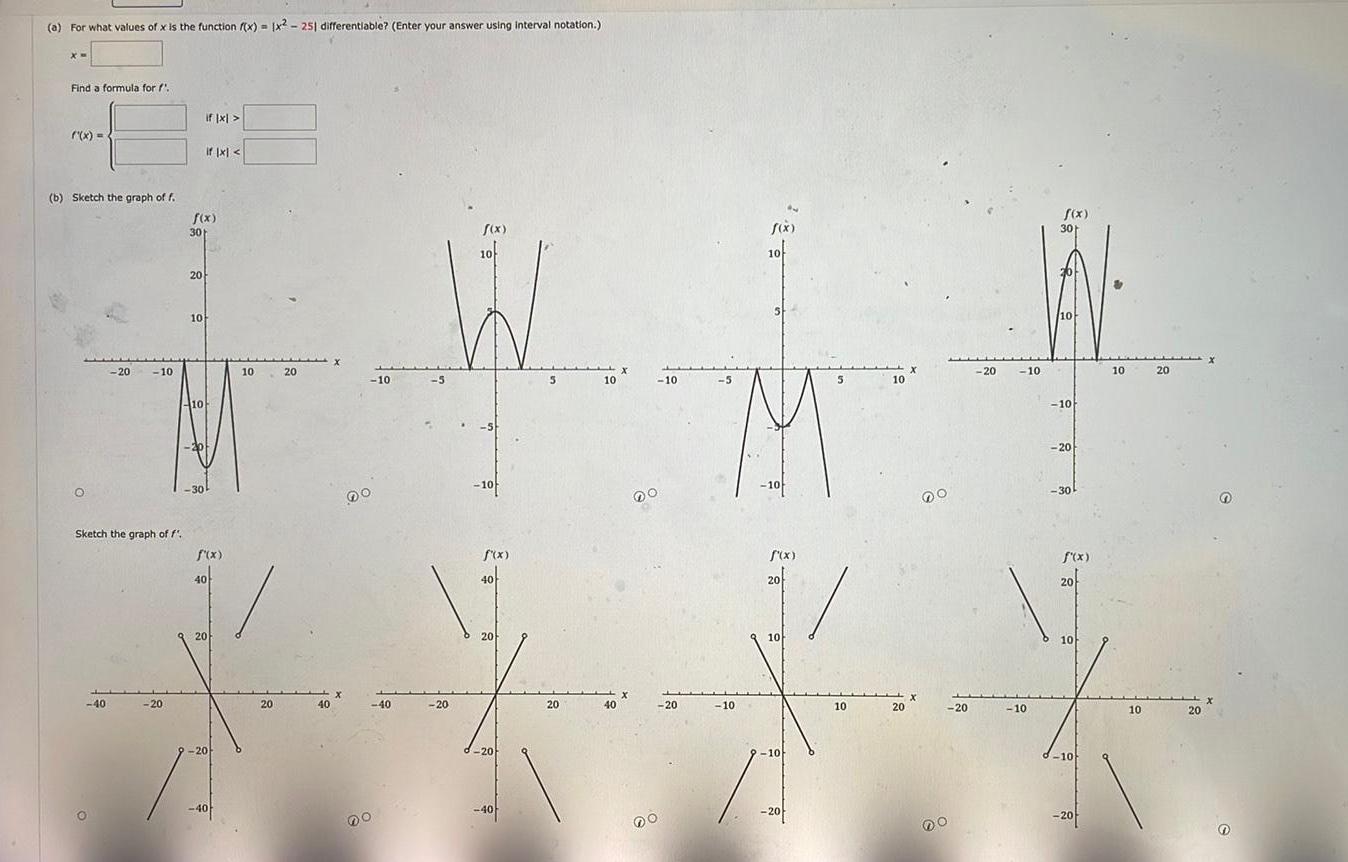
Calculus
Differential equationsa For what values of x is the function f x x2 251 differentiable Enter your answer using interval notation x Find a formula for f x b Sketch the graph of f if x if x f x f x f x 30 10 10 20 10 4 20 10 10 20 10 5 10 10 5 5 10 10 10 10 30k 40 O X 40 DO 40 40 20 X Do 20 20 Sketch the graph of f f x f x f x f x 40 20 40 20 20 20 10 10 X X X Y X 40 20 20 40 20 20 20 10 10 20 10 10 201 20 10 10 20 20 10 DO f x 30 10 10 20 30 10 20 20 20
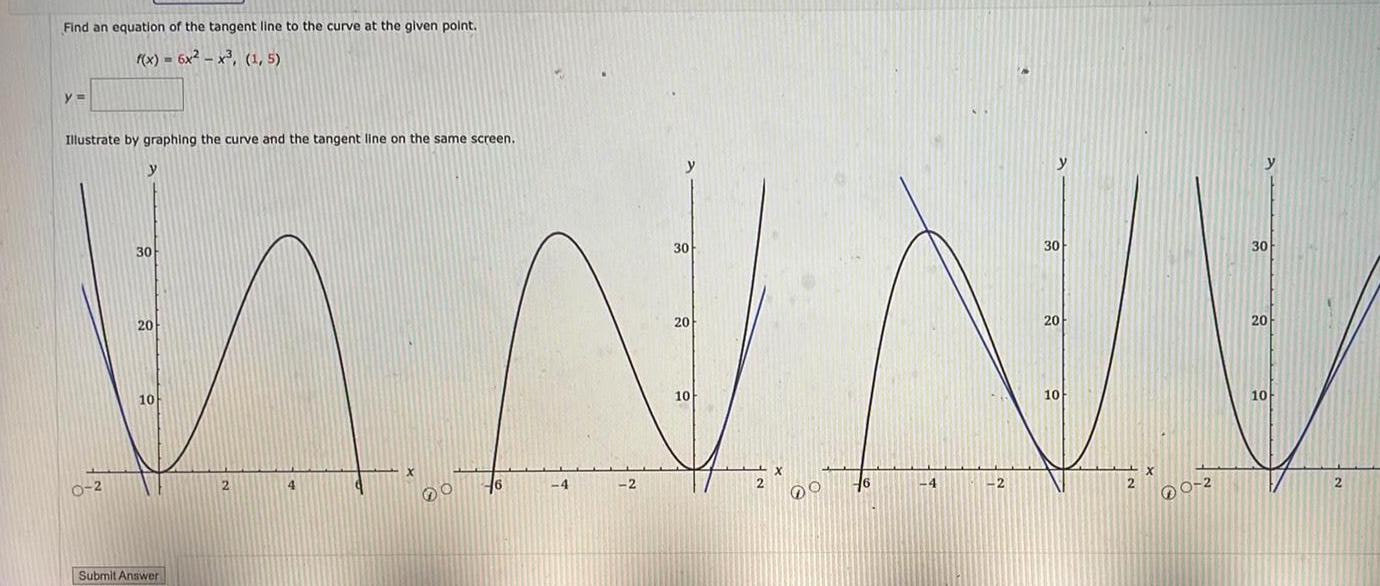
Calculus
Application of derivativesFind an equation of the tangent line to the curve at the given point f x 6x x 1 5 y Illustrate by graphing the curve and the tangent line on the same screen y 0 2 30 20 10 Submit Answer 2 y N N V 4 2 4 2 2 6 O 6 2 0 2
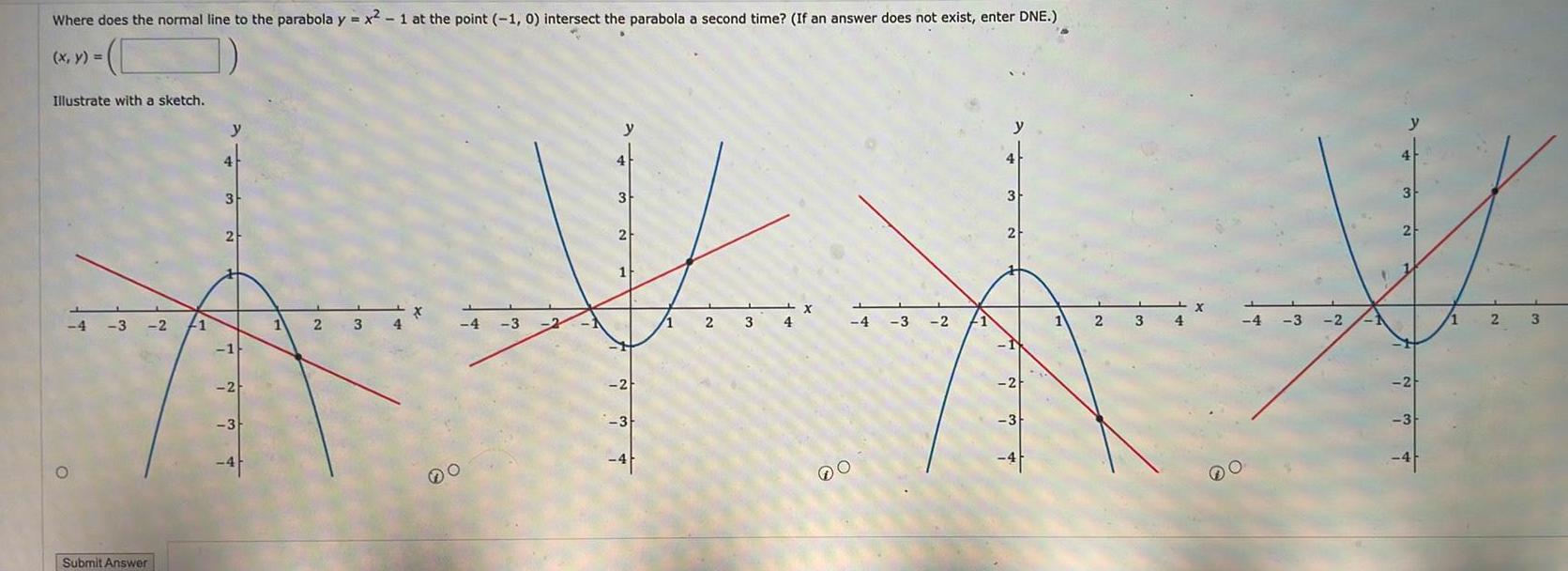
Calculus
Application of derivativesWhere does the normal line to the parabola y x 1 at the point 1 0 intersect the parabola a second time If an answer does not exist enter DNE x y Illustrate with a sketch 4 3 2 Submit Answer 1 y 4 3 2 1 2 3 1 2 3 4 X 4 3 2 y 4 3 2 1 2 3 1 2 3 4 X 4 3 2 41 y 2 2 3 1 2 3 4 X 4 3 2 1 3 2 2 3 1 2 3

Calculus
Application of derivativesIn this problem consider the curve y f x x2 3x 1 a For any real number a the formula for f a b The equation of the tangent line to the curve y f x at the point P a f a is x y c There are two tangent lines to the curve y f x with x intercept 8 The x coordinates of these two points of tangency listed left to right are and

Calculus
Differential equationsFind the first and second derivatives of the function f x 12x 2 4x4 x f x f x 11

Calculus
Definite IntegralsQuestion The result of slicing through the center of the solid S is the base described by the ellipse 1 Cross sections of S perpendicular to the x axis and the elliptical base are rectangles whose height from the base is one fourth its length What is the volume of S Provide your answer below
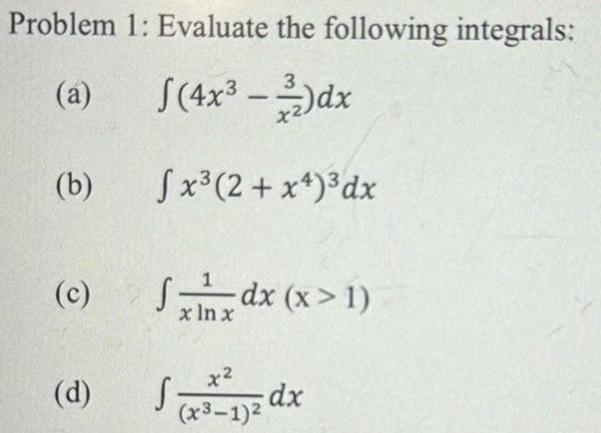
Calculus
DifferentiationProblem 1 Evaluate the following integrals a 4x 3 dx Sx 2 x4 dx b c d 1 Sxx dx x 1 ln x S dx x 1

Calculus
Application of derivativesA car travels up a hill at a constant speed of 41 km h and returns down the hill at a constant speed of 60 km h Calculate the average speed for the round trip Number i 98 7 Units km h
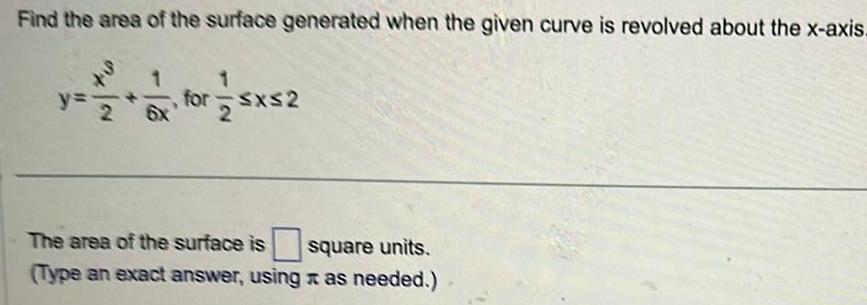
Calculus
Application of derivativesFind the area of the surface generated when the given curve is revolved about the x axis 2 for x 2 The area of the surface is square units Type an exact answer using as needed

Calculus
DifferentiationSuppose a sphere of radius r is sliced by two horizontal planes h units apart as shown Show that the surface area of the resulting zone on the sphere is 2xrh independent of the location of the cutting planes To show that the surface area of the resulting zone of the sphere is 2xrh independent of the location of the cutting planes find the surface area of the zone Orient the sphere so that the planes are vertical as shown in the figure This allows the computations to be done in terms of x Let r represent the radius of the sphere in the problem statement Write the equation of the curve that when revolved about the x axis on the interval r r will result in the sphere given in the problem statement f x

Calculus
Application of derivativesWrite the integral that gives the area of the surface generated when the curve is revolved about the given axis b Use a calculator or software to approximate the surface area y tan x for sxs about the x axis K a Choose the correct answer below x 4 OA 2xx 1 s x 6 x 4 OB 2x tanxV 1 secxdx x 6 x 4 OC 2x XV17 S C X X 2x tanx 1 1 sec xdx x 6 x 4 OD Stan x 6 tan xV 1 sec xdx

Calculus
Definite Integralsa Write the integral that gives the area of the surface generated when the curve is revolved about the given axis b Use a calculator or software to approximate the surface area y 2 cos x for 0 x about the x axis R a Choose the correct answer below x 7 2 2 S 0 x 7 OB 2n S 2 cos x 1 4 sin x dx 0 OA 2n 2 cos x 1 4 sin x dx x 7 OC 2 cos x1 0 2 cos x1 4 sin x dx 7 OD 2 S 2 cos x1 4 cos x dx 0

Calculus
Application of derivativesFind the area of the surface generated when the given curve is revolved about the given a 3 7 9 9 y 4 16 x between the points 4 4 and The surface area is square units Type an exact answer using as needed 2 2 about the y axis

Calculus
Definite Integralsetermine whether the following statements are true and give an explanation or counter example Complete parts a through d below f b a If the curve y f x on the interval a b is revolved about the y axis the area of the surface generated is f a O A False To obtain the surface area integral of f x when it is rotated about the y axis on a b the function y f x must be solved for x in terms of y This yields the function x g y Then the su f b 2ng y 1 g y dy assuming g y is positive on the interval f a f b f a OB area integral becomes 2n y 1 f y dy b True The surface area integral of f x when it is rotated about the x axis on a b is 2 x 1 f x dy To obtain the surface area of the function when it is rotated about the y axis change a limits of integration to f x evaluated at each endpoint and integrate with respect to y This is assuming f y is positive on the interval f a f b
Calculus
Indefinite IntegrationBiologists have noticed that the chirping rate of crickets of a certain species is related to temperature and the relationship appears to be very nearly linear A cricket produces 113 chirps per minute at 70 F and 163 chirps per minute at 80 F a Find a linear equation that models the temperature 7 as a function of the number of chirps per minute N T X b What is the slope of the graph What does it represent The slope means that the temperature in Fahrenheit degrees increases X as rapidly as the number of cricket chirps per minute c If the crickets are chirping at 160 chirps per minute estimate the temperature Round your answer to the nearest whole number OF

Calculus
Definite IntegralsFind the area of the surface generated when the given curve is revolved about the given axis 1 3 1 y 8x for 0 x about the y axis The surface area is square units Type an exact answer using as needed
Calculus
Differential equationsFind the functions and their domains Enter the domains in interval notation g x g x x 5 X x 2 f x x a fog fog x domain b gof gof x domain c fof fof x domain d gog g g x domain
Calculus
Indefinite IntegrationThe surface area A of a right circular cylinder is given by the formula A 2xrh 2xr2 where r is the radius and his height Find the height of a right circular cylinder whose surface area is 80x square centimeters and whose radius in centimeters What is the height of the cylinder cm

Calculus
DifferentiationThe volume of a swimming pool is 2080 cubic feet Assuming that the pool is 16 feet long and 10 feet deep find its width The width is