Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
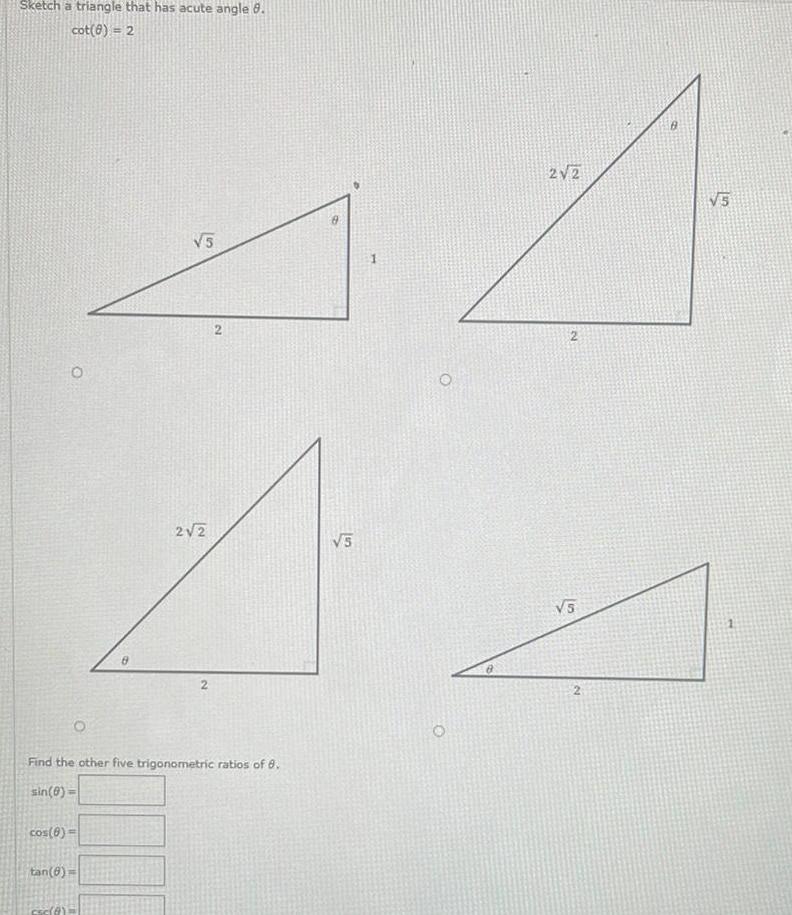
Vector CalculusSketch a triangle that has acute angle 8 cot 8 2 O cos 6 tan 6 5 2 2 Find the other five trigonometric ratios of 8 sin 0 2 8 VS 2 2 2 5 s B 5
Calculus
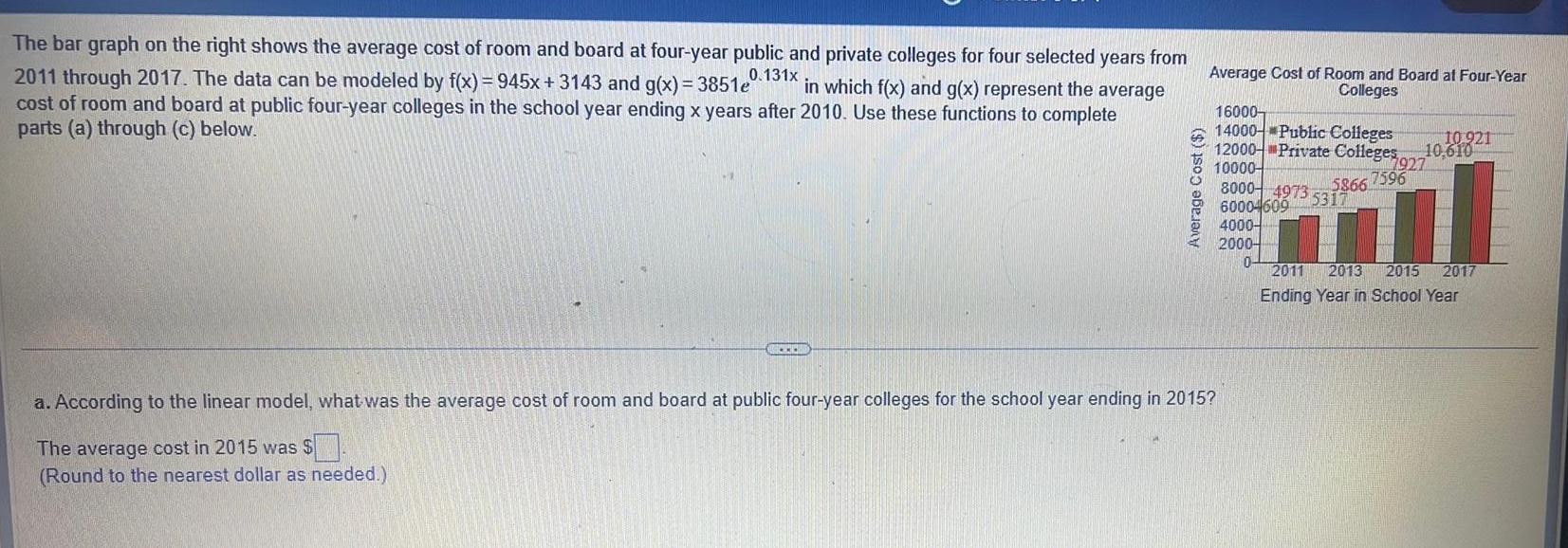
Limits & ContinuityThe bar graph on the right shows the average cost of room and board at four year public and private colleges for four selected years from 2011 through 2017 The data can be modeled by f x 945x 3143 and g x 3851e 0 131x in which f x and g x represent the average cost of room and board at public four year colleges in the school year ending x years after 2010 Use these functions to complete parts a through c below ACCEDI Average Cost Average Cost of Room and Board at Four Year Colleges 16000 14000 Public Colleges 10 921 12000 Private Colleges 10 610 10000 8000 4973 5317 600046095317 a According to the linear model what was the average cost of room and board at public four year colleges for the school year ending in 2015 The average cost in 2015 was Round to the nearest dollar as needed 4000 2000 0 7927 5866 7596 2011 2013 2015 2017 Ending Year in School Year

Calculus
Application of derivativesFind the area of a triangle with the given description Round your answer to one decimal place a triangle with sides of length 5 and 6 and included angle 74
Calculus
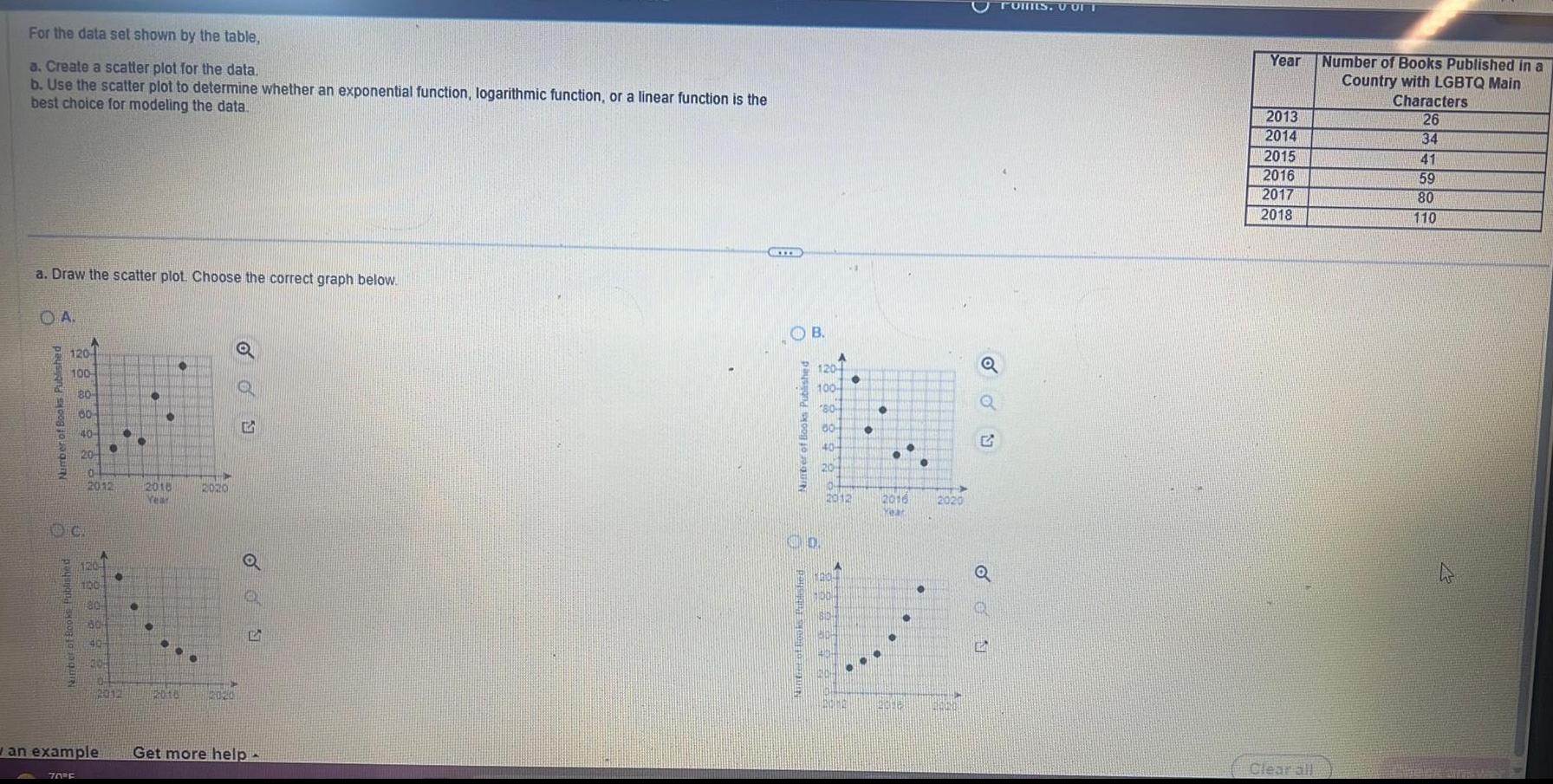
Differential equationsFor the data set shown by the table a Create a scatter plot for the data b Use the scatter plot to determine whether an exponential function logarithmic function or a linear function is the best choice for modeling the data a Draw the scatter plot Choose the correct graph below A Number of Books Published 120 100 Nimber of Books Published A 70 F 80 60 40 20 0 2012 100 80 30 40 2012 2018 Year HIPP 2020 12016 2020 o wan example Get more help CYTE Nimber of Books Published B 1204 100 60 60 40 10 20 10 2012 2016 Year 2020 Q G G TOMES U OFT Year 2013 2014 2015 2016 2017 2018 Clear all Number of Books Published in a Country with LGBTQ Main Characters 26 34 41 59 80 110

Calculus
Limits & ContinuityTwo tugboats that are a 125 ft apart pull a barge as shown If the length of one cable is b 208 ft and the length of the other is c 245 ft find the angle formed by the two cables Round your answer to the neares degree poboboboto b
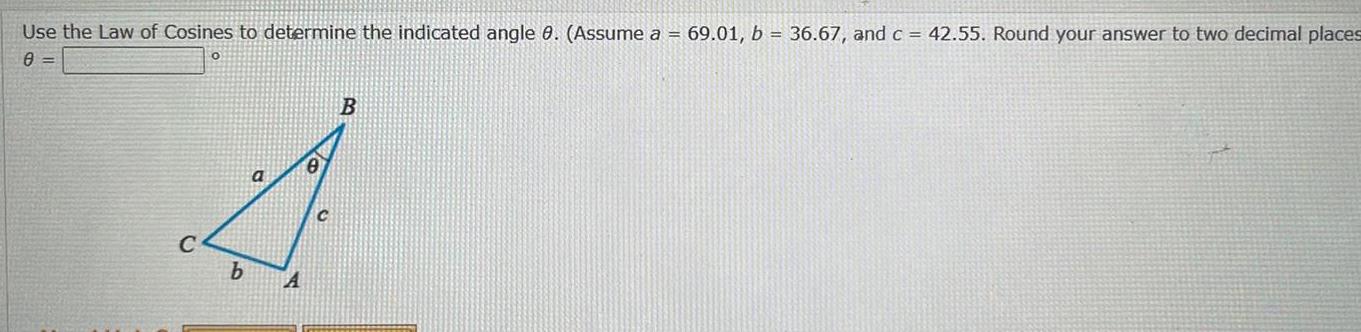
Calculus
Vector CalculusUse the Law of Cosines to determine the indicated angle 0 Assume a 69 01 b 36 67 and c 42 55 Round your answer to two decimal places 0 b A C B

Calculus
Application of derivativesFind the area of the triangle whose sides have the given lengths Round your answer to one decimal place a 6 b 8 C 10 A

Calculus
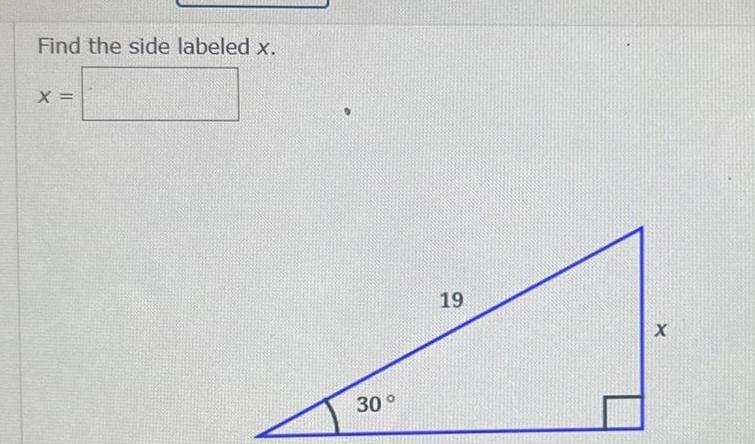
Application of derivativesFind the indicated side x Use either the Law of Sines or the Law of Cosines as appropriate Assume LA 34 and ZC 86 Round your answer to two decimal pl X C B

Calculus
DifferentiationThe differential equation 1EJ The initial conditions Remarks Xlo X dX dt dX dt An da X dr 1 W a A dt f d X to dt 1 MATHEMATICS I Though the independent variable t of the function X t in the ODE 1 is stipulated to range in the interval I we expect the solution t X t of the initial value problems 4 to be defined only on a sub internal J of I with to EJ Indeed we come across concrete cases of the IVP in which a solution exists only on a sub inter J of I and therefore we grant this concession a solution need be defined only on a sub interval J of I II Often the initial conditions are expressed more explicitly in terms of dX the equations xt Xo to W dt da W 1 Let f RR be the function fx 1 x 0 1 x20 di dik 1 for all important special case of the ODE 3 is dX d X d X fx 6 di di di initial value problem f X x o 0 dt in which the function f is independent of the variable t f 0xR x xR R In this case we say that the ODE 6 is autonomous Returning to the initial value problem 5 there are two questions Does the initial value problem 5 admit a solution at all If it does is the solution unique Clearly because fis the main ingredient of the ODE the answer to both of there questions naturally depends on the properties of f especially on its behaviour around the initial condition t WW i e how if varies continuously differentially etc around too WW Following two examples illustrate that answers to both the questions are in general in the negative For this function we consider the first order autonomous case of the dX We contend that this initial value problem has no solution For if there was a solution X J R with OEJ then 0 f 0 1 0 implies that the solution tX t is strictly

Calculus
DifferentiationI Though the independent variable t of the function X t in the ODE 1 is stipulated to range in the interval I we expect the solution X t of the initial value problems 4 to be defined only on a sub internal J of I with to EJ Indeed we come across concrete cases of the IVP in which a solution exists only on a sub inter J of I and therefore we grant this concession a solution need be defined only on a sub interval J of I II Often the initial conditions are expressed more explicitly in terms of dX the equations X to Xo to W dt An important special fX dX dx d X d X di di di case MATHEMATICS di 1 in which the function f is independent of the variable t f 0xR x xR R In this case we say that the ODE 6 is autonomous Let f RR be the function f x 1 x 0 1 x 0 Returning to the initial value problem 5 there are two questions Does the initial value problem 5 admit a solution at all If it does is the solution unique Clearly because fis the main ingredient of the ODE the answer to both of there questions naturally depends on the properties of f especially on its behaviour around the initial condition to Ww i e how if varies continuously differentially etc around X WW Following two examples illustrate that answers to both the questions are in general in the negative Wk 1 of the ODE 3 is 6 For this function we consider the first order autonomous case of the dX initial value problem f X x o 0 dt dX di We contend that this initial value problem has no solution For if there was a solution X J R with OEJ then 0 f 0 1 0 implies that the solution X t is strictly dt monotonic increasing in a neighborhood 8 8 of O On the other hand 1 0 f t for all re 8 0 implies that t X t t is strictly monotonic decreasing in 8 0 Thus if the solution of the above IVP exists then it is strictly monotonic increasing as well as strictly monotonic decreasing This prevents a solution

Calculus
Differentiation0 as k MATHEMATICS This last observation is true because converging te Note that in the inequalities M K 1 10 j 1 MK Kj XI K MK n Kj X 1 x 1 the right hand sides are independent Kj lim x X lim of t and therefore 1 x 1 Ouniformly on to 1 1 as k p being arbitrary This completes the proof of our claim that the sequence x kEZ of functions is uniformly Cauchy on to to 1 X Using this last mentioned property of the sequence xk Z we define a function x 4 1 1x8 x 8 by putting x t lim x 1 t to to 1 The function x thus defined is the uniform limit of the sequence x kEN Therefore we have lim x 1 x 11 x1 x f s X 5 5 1 de ff s x s ds ff s lim x s ds ff s x s ds Kn lim f s x s ds is convergent Finally the identity All the above equations being valid because of the uniform convergence of of x fox on to 1 1 s x s ds t 1 1 1 1 derived above has the following two consequences 1 Differentiation of the identity implies

Calculus
DifferentiationAbout the sequence XKEZ we have the following x 1 EBx b for each 1 to b t b MKk a X 1 1 x 1 k 1 1E10 b t b k 20 c x k Z is uniformly Cauchy on t b t b verification of these properties is left for the reader We consider the uniform limit of the sequence x to 8 to 8 B x b C which is given by tet b t b b Thus x t lim xo kin x t lim x 1 4 00 1 2 x lim ff s x s ds 76 x A f s x s ds S s lim x s ds x ff s x s ds Thus the function rx 1 satisfying the integral equation x 1 x S f s x s ds for all te t b to b Finally the validity of this integral equation has the following two implications 4 x X t xo f s x s ds x 0 xo 50 4 S A dx d 0 af f s x s ds f t X 1 di dt Proposition 2 This now proves that the curve X 1 8 1 82 thus obtained is a solution of the initial value problem 20 2 3 UNIQUENESS OF A SOLUTION lim f s x s ds We prove an inequality which will lead us to the uniqueness of the solutions Gronwall s f a b 0x g a b 0 o be Chapter 2 Systmes of First Order ODE Let Inequality continuous functions and

Calculus
DifferentiationProposition 3 Let x J y J be two solutions of the initial value problem dx f t x x t x dt then x t y t for all 1 JOJ Proof Recall that both x and y being solutions of the initial value problem satisfy the integral equations on their domain intervals x 1 x f s x s ds y t x f s y s ds Therefore x 1 y 1 f s x s f s y s ds which implies x 1 y 1 0 s x s s y s 0 SK x s y s for all 12 Applying Gronwalls result with A 0 we get 0 x 1 y 1 0 for all t t This gives the desired equality x t y t for all 1JJ Towards the uniqueness of the solution of the initial value problem 3 we consider all the solutions of the initial value problem 3 Let the totality of them be denoted by J XEA the solutions x being thus indexed by a suitable indexing set A Above we have verified that any two solutions say x and xx are equal on the overlap JJ of their domains Therefore we patch together all the solutions to get a maximal solution is the solution defined on the largest open interval It is obtained as follows Let J UJ e clearly Jis an open sub internal of I with x J and all the solutions x patch up to get a solution x J of the initial value problem 3

Calculus
DifferentiationProof Let Ix be arbitrary Using openness of IxJ choose 8 0 such that t 8 1 8 x 8 x 8 IXJ Of Now the function is continuous on IxJ and therefore it is x bounded on the compact subset to 8 to 8 x 8 x 8 We consider any constant k 0 with the property 1 0 K K for all tto 8 1 8 and for all xx 8 x 8 x Finally let 1 t 8 1 8 x y in x 8 x 8 be arbitrary By the mean value theorem of differential calculus we have Of fty f t x y x 1 Z x for some z between x and y Therefore 1 350 3053 1 1 2 K yx If t y f t x z Ox Since 1 2 18 1 8 x x 8 x 8 and therefore of 1 Z K t Z K This proves the locally Lipschitz property of f dx Theorem 1 Emil Picard If f 1 J Ris locally Lipschitz then for any to EI x EJ the initial value problem df f t x x to dx has a solution x 8 to 8J for some 8 0 Proof Choose 8 0 such that to 8 1 8 1 8 x 8 J and there exists K 0 for which f 1 x f t y Kx y holds for all t 8 8 x 8 x 8 We choose M 0 such that f 1 x M for all te t 8 1 8 x x 8 x 8 Using the constants 8 0 K 0 M 0 chosen above we choose 18 one more constant 7 satisfying 0 n min KM We define a sequence of functions 1 1 R keZ recursively as follows

Calculus
DifferentiationThis shows that the solutions of the order k ODE 4 can be studied in terms of the solutions of the first order ODE 5 Note that if f of the ODE 4 is continuously differentiable on its domain namely the set IxQxR R then F is continuously differentiable on its own domain consequently the existence and uniqueness result for the first order ODE applies to the initial value problem The solution of which giving the solution of the above initial value problem dt to the system dx dt y X dx di has a unique solution 2 dx dt XoXo fo W di We summarize this observation in the following Theorem 3 If the function f 1xxR x R R is continuously differentiable on its domain of definition then the initial value problem dx dk 1x dx 1 x dr dr 1 condition 3 dx dx dt dt dt y To dy F t y dt 1 The second order ODE dx di dy di dz di Illustrative Examples These examples explain how we obtain a system of first order ODE from a given higher order ODE 10 W d x dr kx Moreover the initial condition xoxo yo gives the initial dx The initial value problem d x 4d x dx dr 10 W dr 1 y x 0 1 31 1 x 1 dt d x dt2 z y 0 2 for the reduced first order system dx x 0 1 0 2 0 3 dt to W 1 Chapter 2 Systmes of First Order ODE kx k being a given constant gives rise reduces to the following system of first order ODE along with the initial conditions 28 42 3ty 1 x 1 z 0 3 The third order system of ODE d x x y dt y x y is equivalent to the following system of first order ODE in 2 2 2 23 24 25 26 35

Calculus
Differential equationsX 1 Solution We have y t 20 1 j 4 s ds 1 Thus x 1 2 2 1 3 0 2 3 ds 2 91 2 1 3 3ds 3 3r 3 3r 191 441 2 3 3 4 1 41 3 0 2 9s ds 4t 3 x 1 34 y 1 9t 3 2 0 3r 2 3 123 91 441 19 91 1 17 2 36 200 3 jx d 31 2 4 9 4 9 6 2 3 62 3 91 191 2 3 2 3 4 4s 35 ds 271 3 4 2 8 27 41 44 m 4 4 91

Calculus
Definite IntegralsFind the volume of the region bounded by the coordinate planes the plane x y 5 and the cylinder y 9z 2 25 2 The volume is Type an exact answer using as needed

Calculus
Limits & Continuity37 50 Horizontal asymptotes Determine lim f x and lim f x x18 8116 for the following functions Then give the horizontal asymptotes of f if any 37 f x 39 f x 41 f x 43 f x 45 f x 47 f x 49 f x 4x 20x 1 6x 9x 8 3x 2 3x 7 x4 5x2 40x5 x 16x4 2x 1 2x4 4x89x4 4x 1 2x 16x6 1 x6 8 4x 3x4 1 38 f x 40 f x 42 f x 44 f x 46 f x 3x 7 x2 5x 12x 3 3x8 2x7 2x 1 3x4 2 6x 1 4x4 3x 1 x 1 2x 1 48 f x x x 9x 50 f x 4x 3x 9x 1
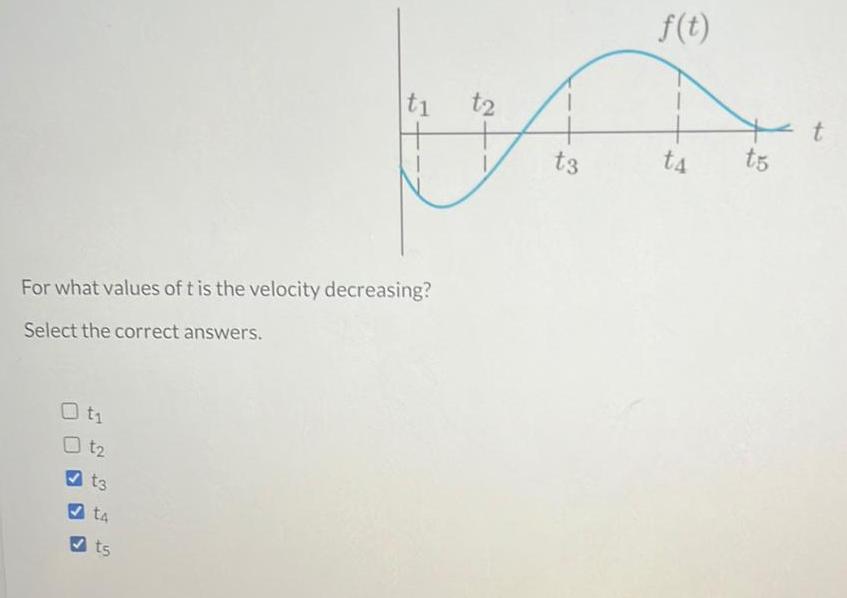
Calculus
DifferentiationFor what values of t is the velocity decreasing Select the correct answers t t2 t3 t4 s ts t t3 f t ta t5 t

Calculus
Limits & Continuity11 37 50 Horizontal asymptotes Determine lim f x and lim f x for the following functions Then give the horizontal asymptotes of f if any 37 f x 39 f x 41 f x 45 f x 47 f x 4x 20x 1 6x 9x 8 3x 2 40x x 43 f x 16x4 2x 3x 7 x4 5x 38 f x 1 2x4 4x8 9x4 4x 1 2x 16x6 1 40 f x 42 f x 44 f x 46 f x 3x 7 x 5x 12x 3 3x8 2x7 2x 1 3x4 2 6x 1 4x4 3x 1 x 1 2x 1 48 f x x x 9x

Calculus
Application of derivatives7 7 Use the fact that the derivative of the function f x is f x X the tangent line to the graph of f x at the point x 9 to find the equation of The equation of the tangent line to the graph of f x at the point x 9 is
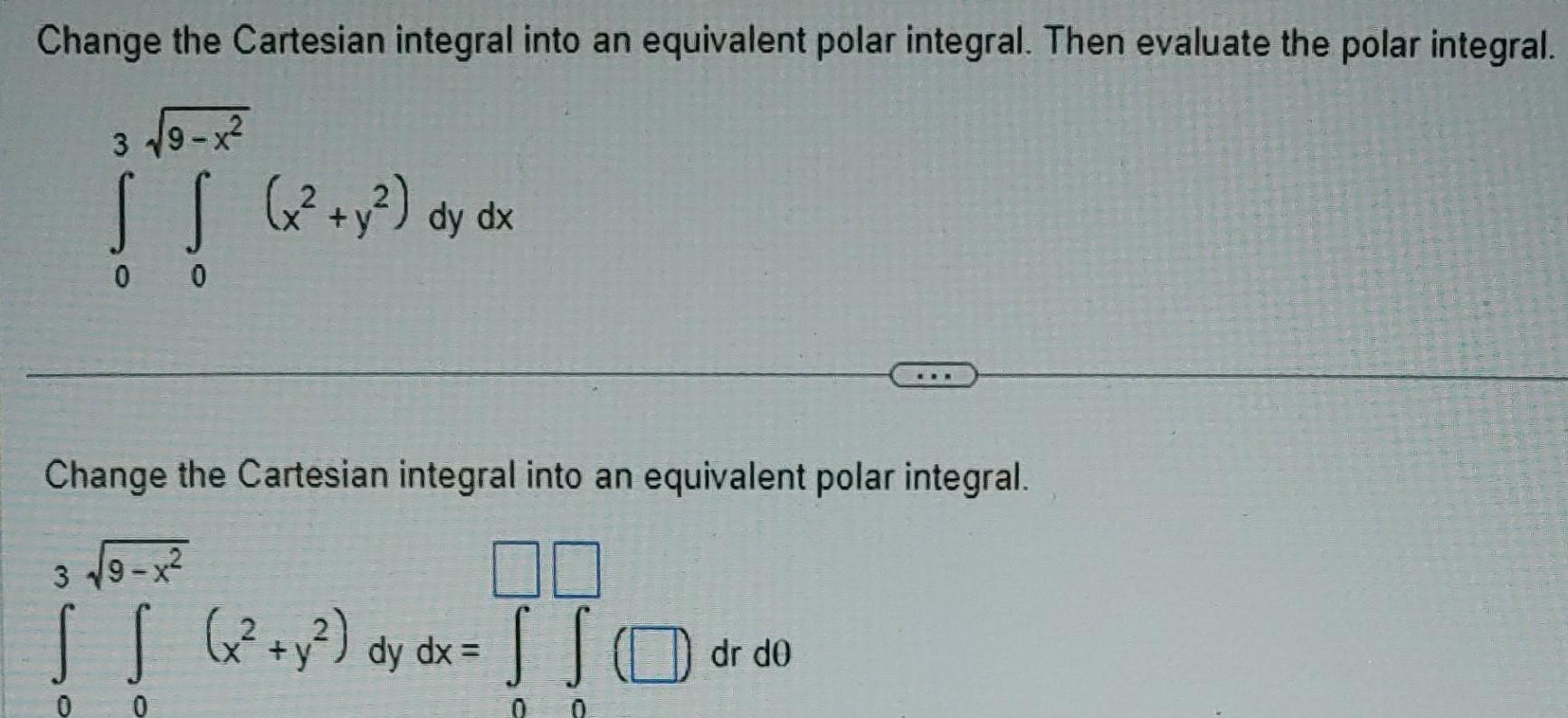
Calculus
Application of derivativesChange the Cartesian integral into an equivalent polar integral Then evaluate the polar integral 3 9 x S S x y dy dx 0 0 Change the Cartesian integral into an equivalent polar integral 3 9 x IT TIC S S x y dy dx 0 dr de
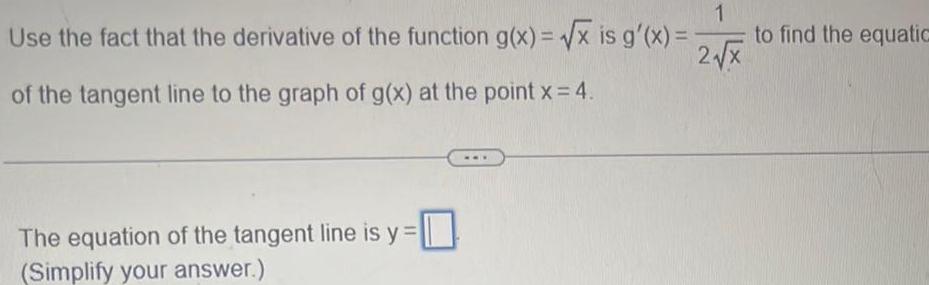
Calculus
Application of derivativesUse the fact that the derivative of the function g x x is g x 1 2 x of the tangent line to the graph of g x at the point x 4 The equation of the tangent line is y Simplify your answer to find the equatic

Calculus
Application of derivativesx 1 Thus y 1 1 91 441 6 2 3 1 91 17 2 6 3 31 8 2 6 HIGHER ORDER ODE 41 271 41 4 16 As mentioned earlier we associate a first order ODE with a order k ODE and try to get information about the solutions of the higher order ODE in terms of those of the associated first order ODE In particular we are interested in a condition on the function f f t X which will di di ensure existence and uniqueness of the initial value problem for the higher order ODE In this article we explain the theory To begin with we consider the ODE dx dx f 1 x dt 4 Together with the initial condition dx MATHEMATICS di We introduce a new variable y 2 where y ranges in 2 and y y ranging in R Next we define F 1x2xRx R R by putting F t y F t Y Y3 f t y Now the given initial value problem for the order k ODE give rise to the following initial value problem in the first order ODE to W 1 dr F t y 5 the initial condition for it being y t x W W Clearly the above first order ODE is actually the following system of first order ODE 27
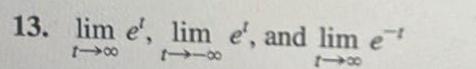
Calculus
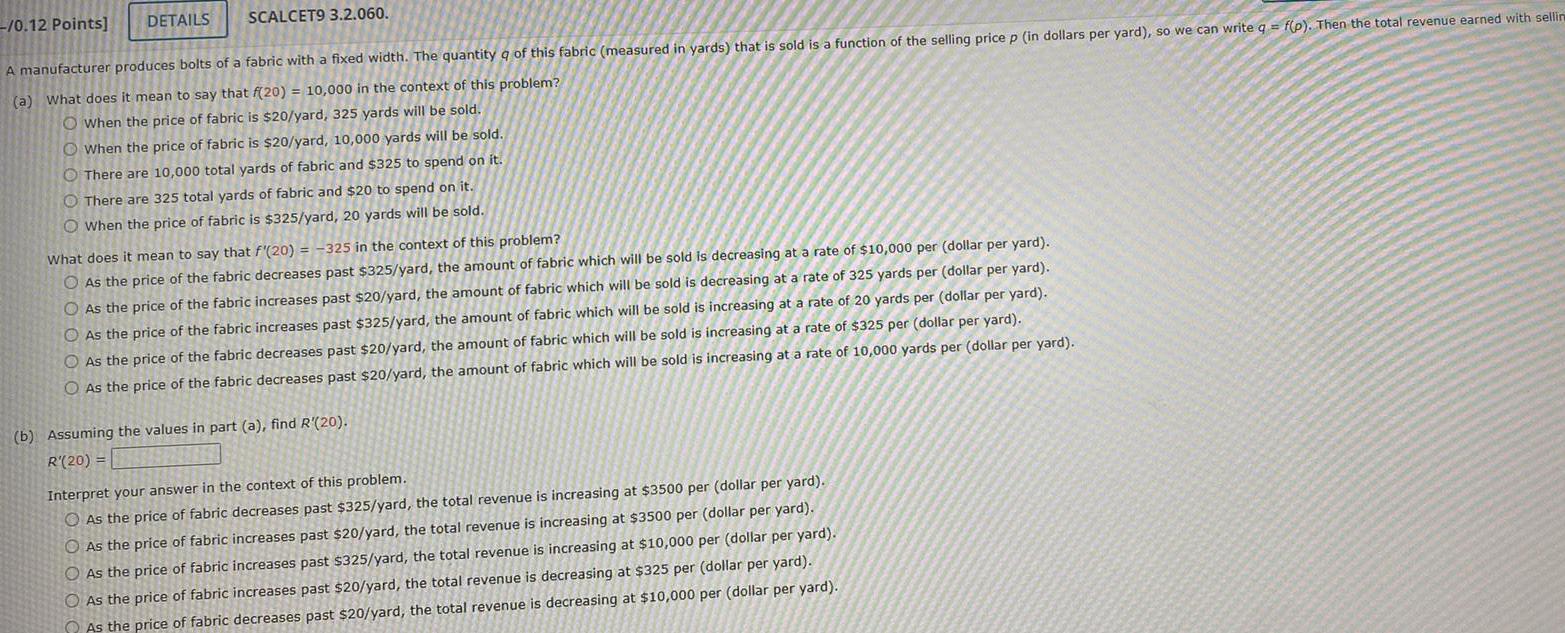
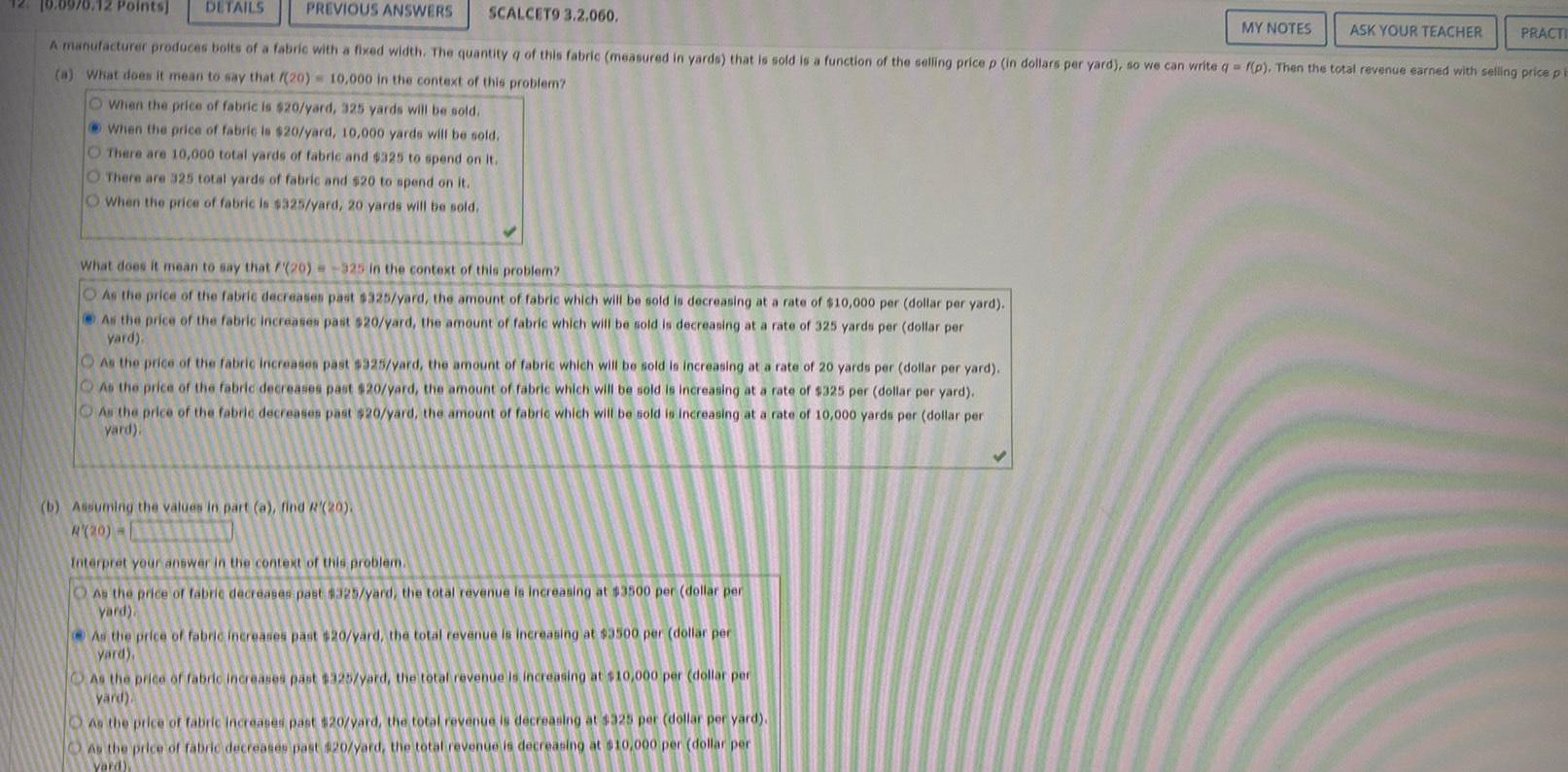
Application of derivatives0 12 Points DETAILS SCALCET9 3 2 060 A manufacturer produces bolts of a fabric with a fixed width The quantity of this fabric measured in yards that is sold is a function of the selling price p in dollars per yard so we can write q f p Then the total revenue earned with sellin a What does it mean to say that f 20 10 000 in the context of this problem O When the price of fabric is 20 yard 325 yards will be sold When the price of fabric is 20 yard 10 000 yards will be sold There are 10 000 total yards of fabric and 325 to spend on it O There are 325 total yards of fabric and 20 to spend on it When the price of fabric is 325 yard 20 yards will be sold What does it mean to say that f 20 325 in the context of this problem O As the price of the fabric decreases past 325 yard the amount of fabric which will be sold is decreasing at a rate of 10 000 per dollar per yard O As the price of the fabric increases past 20 yard the amount of fabric which will be sold is decreasing at a rate of 325 yards per dollar per yard As the price of the fabric increases past 325 yard the amount of fabric which will be sold is increasing at a rate of 20 yards per dollar per yard O As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 325 per dollar per yard O As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 10 000 yards per dollar per yard b Assuming the values in part a find R 20 R 20 Interpret your answer in the context of this problem As the price of fabric decreases past 325 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 20 yard the total revenue is increasing at 3500 per dollar per yard O As the price of fabric increases past 325 yard the total revenue is increasing at 10 000 per dollar per yard O As the price of fabric increases past 20 yard the total revenue is decreasing at 325 per dollar per yard As the price of fabric decreases past 20 yard the total revenue is decreasing at 10 000 per dollar per yard

Calculus
Application of derivativeswith components 8 828 18 x dx 8 2010 x dx Equivalently form we have 18 x dx 18 x dx 182 x dx 1 j de Thus We will use these notations in this article Example 1 Obtain approximate solutions upto of the following initial value problem 2x 3y x 0 1 dx di dy dt Solution t y y 0 2 Thus We have x t 1 y t 2 x 1 1 2 x 8 3y s ds 1 8ds X 1 2 2 s y s ds x 1 0 2 2 2 2 y 1 2 s 8r 1 Next x 1 2x 0 35 404 ds 1 1 8 2 2x 2 s x 1 LY C 11 8 1 2 s y s d 2 3 2 31 2 1 35 2 d 2 3 6 2 21 11 8 1 21 2 6 1 8ds 8t 1 then 3 2 24 written in the columnal and so on 18 x dx Chapter 2 Systmes of First Order ODE Example 2 Obtain approximate solution upto dx tx 1 y x 0 1 dt
Calculus
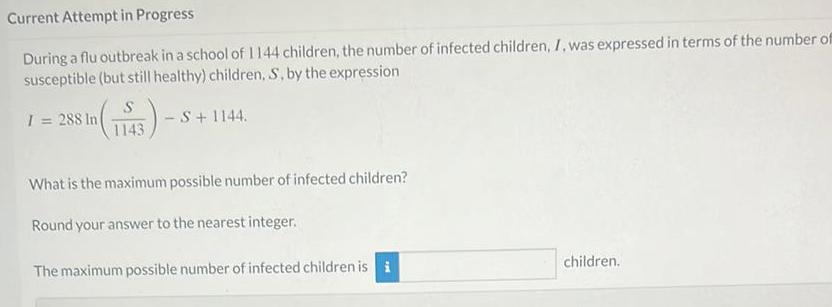
Application of derivativesCurrent Attempt in Progress During a flu outbreak in a school of 1144 children the number of infected children I was expressed in terms of the number of susceptible but still healthy children S by the expression 153 S S 1144 1143 I 288 In What is the maximum possible number of infected children Round your answer to the nearest integer The maximum possible number of infected children is i children
Calculus
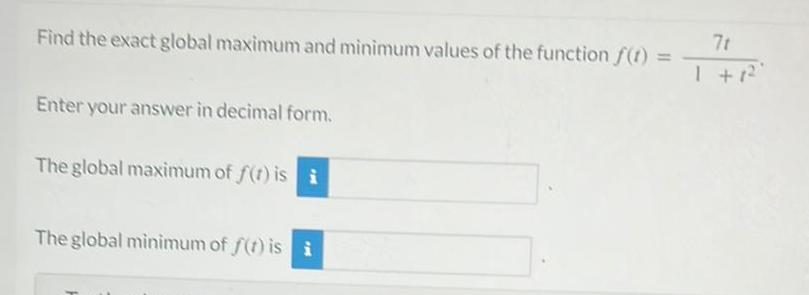
Differential equationsFind the exact global maximum and minimum values of the function f 1 Enter your answer in decimal form The global maximum of f t is i The global minimum of f t is i 7t 1 1
Calculus
Differential equationsPREVIOUS ANSWERS SCALCET9 3 2 060 A manufacturer produces bolts of a fabric with a fixed width The quantity q of this fabric measured in yards that is sold is a function of the selling price p in dollars per yard so we can write q f p Then the total revenue earned with selling price pi a What does it mean to say that 20 10 000 in the context of this problem O When the price of fabric is 20 yard 325 yards will be sold When the price of fabric is 20 yard 10 000 yards will be sold There are 10 000 total yards of fabric and 325 to spend on it 10 0970 12 Points DETAILS O There are 325 total yards of fabric and 20 to spend on it O When the price of fabric is 325 yard 20 yards will be sold What does it mean to say that 20 325 in the context of this problem As the price of the fabric decreases past 325 yard the amount of fabric which will be sold is decreasing at a rate of 10 000 per dollar per yard As the price of the fabric increases past 20 yard the amount of fabric which will be sold is decreasing at a rate of 325 yards per dollar per yard As the price of the fabric increases past 325 yard the amount of fabric which will be sold is increasing at a rate of 20 yards per dollar per yard As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 325 per dollar per yard As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 10 000 yards per dollar per yard b Assuming the values in part a find R 20 R 20 D Interpret your answer in the context of this problem As the price of fabric decreases past 325 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 20 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 325 yard the total revenue is increasing at 10 000 per dollar per yard As the price of fabric increases past 20 yard the total revenue is decreasing at 325 per dollar per yard As the price of fabric decreases past 20 yard the total revenue is decreasing at 10 000 per dollar per Yard MY NOTES ASK YOUR TEACHER PRACTI
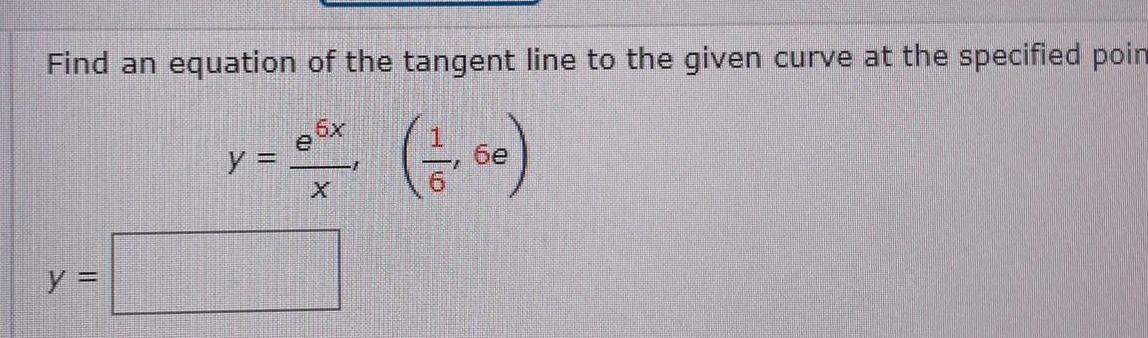
Calculus
Application of derivativesFind an equation of the tangent line to the given curve at the specified poin y ath 1 00 X y

Calculus
Definite Integralsy cosec x 07 201 restrict the domain of secant function to 0 x 0 y see x 0 1 the domain of y secx is the set R x x 2n 1 COS X n Z and range is the set R 1 1 It means that sec secant function assumes all real values except 1 1 and is not defined for odd multiples of 3 If we Y y cosec x Rationalised 2023 24 Fig 2 3 ii then it is one one and onto with its range as the set R 1 1 Actually secant function restricted to any of the 3x intervals 1 0 0 n 2n etc is bijective and its range 3x is R 1 1 Thus sec can be defined as a function whose domain is R 1 1 and range could be any of the intervals 7 0 0 n 2n etc Corresponding to each of these intervals we get different branches of the function sec The branch with range 0 is called the principal value branch of the function sec We thus have R R 1 1 0 x 1 A 2 INVERSE TRIGONOMETRIC FUNCTIONS 23 see 161 The graphs of the functions y sec x and y sec x are given in Fig 2 4 1 ii CERT reptableted y sec x
Calculus
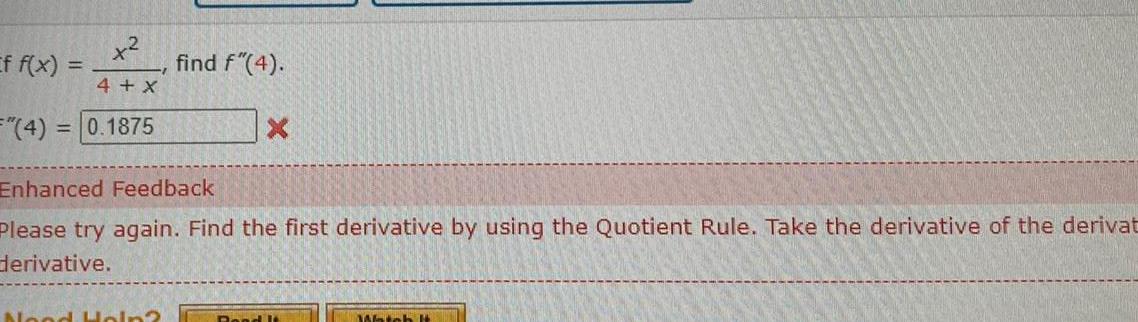
Application of derivativesx 4 X 0 1875 Ef f x 4 find f 4 Enhanced Feedback Please try again Find the first derivative by using the Quotient Rule Take the derivative of the derivat derivative Nood Hain Rond I Watch It


Calculus
Limits & Continuity20 Fifty part time students were asked how many courses they were taking this term The incomplete results are shown in the table below of Courses Frequency 30 15 1 2 3 Relative Frequency Cumulative Relative Frequency 0 6 a Fill in the blanks in the table b What percent of students take exactly two courses c What percent of students take one or two courses d Describe the difference between the Relative Frequency and the Cumulative Relative Frequency columns
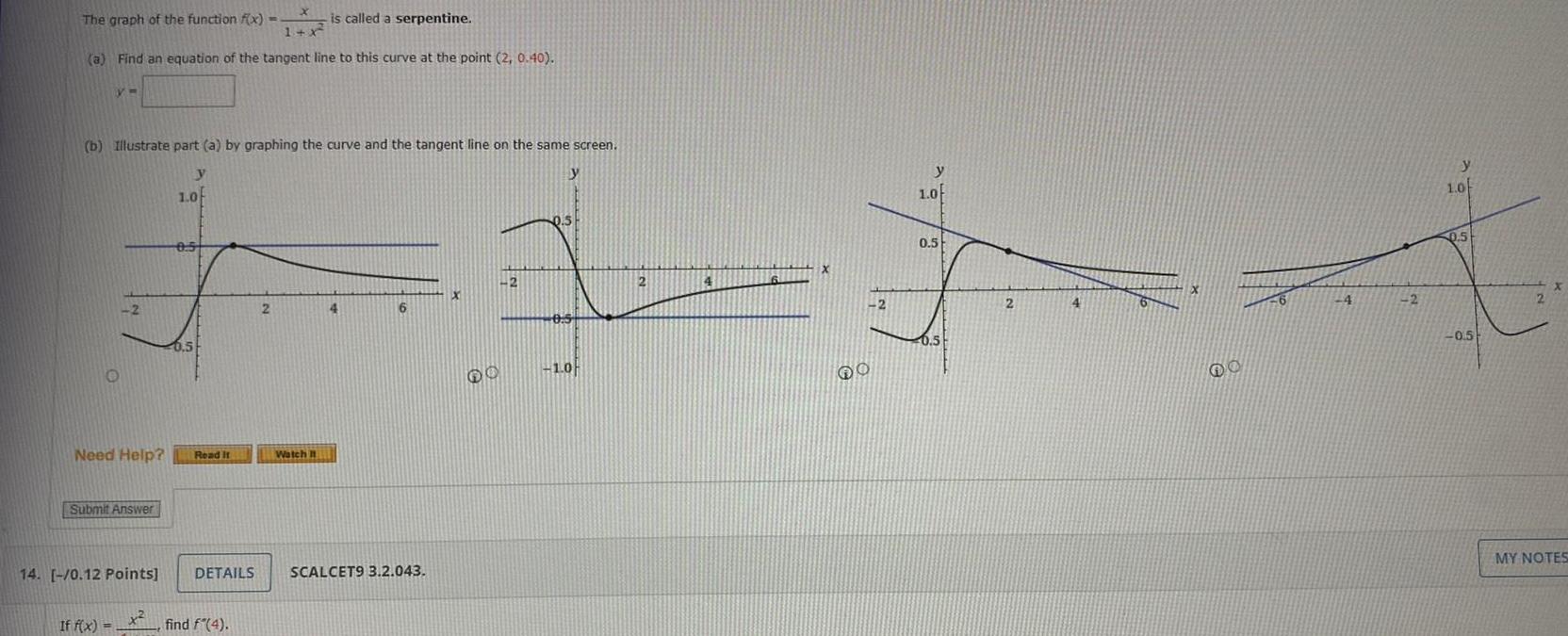
Calculus
Application of derivativesX is called a serpentine 1 x 2 a Find an equation of the tangent line to this curve at the point 2 0 40 The graph of the function f x VW b Illustrate part a by graphing the curve and the tangent line on the same screen y O 2 Need Help Submit Answer If f x 14 0 12 Points 1 0 05 0 5 Read It DETAILS find f 4 2 Watch It 4 6 SCALCET9 3 2 043 60 2 y 0 5 0 5 1 0 2 4 X 60 2 y 1 0 0 5 0 5 2 4 6 x 4 2 y 1 0 0 5 0 5 2 MY NOTES

Calculus
Definite Integrals1 log 3 log x 1 5log x 2 4log x 3 C 4 log x 1 2log x 2 log x 3 C 5 4log x 2 2log x 1 C 8 10 11 12 29 50 5 3 x 2 C 1 x 2 3 x 1 log x 1 log x 1 5 444 20 22 14 3log x 2 C 7 x 2 16 log n 13 log x 1 log 1 x tan x C 18 x 3 log x 1 log x 2 log x 2 C log x log x 1 C x 4 22 B 1 H tan C X 3 MATHEMATICS 3tan 2 1 x cos x sin x C 6 3 e x 2x 2 C log2r C 6 15 log 19 17 log log 4 x 1 x 3 21 Rationalised 2023 24 2 sin x 1 siny blished 23 A EXERCISE 7 6 6 x 1 C 10g c 2 cos3x sin 3x C 4 log x tan x C log x C pe
Calculus
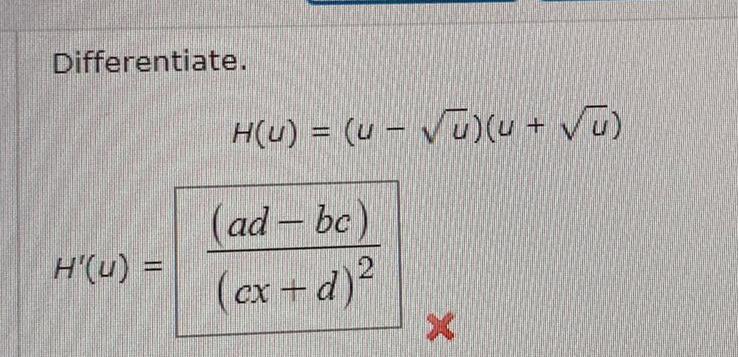
DifferentiationFind equations of the tangent lines to the curve X 1 X 1 that are parallel to the line x 2y 5 Enter your answers as a comma separated list of equations y Need Help Read It
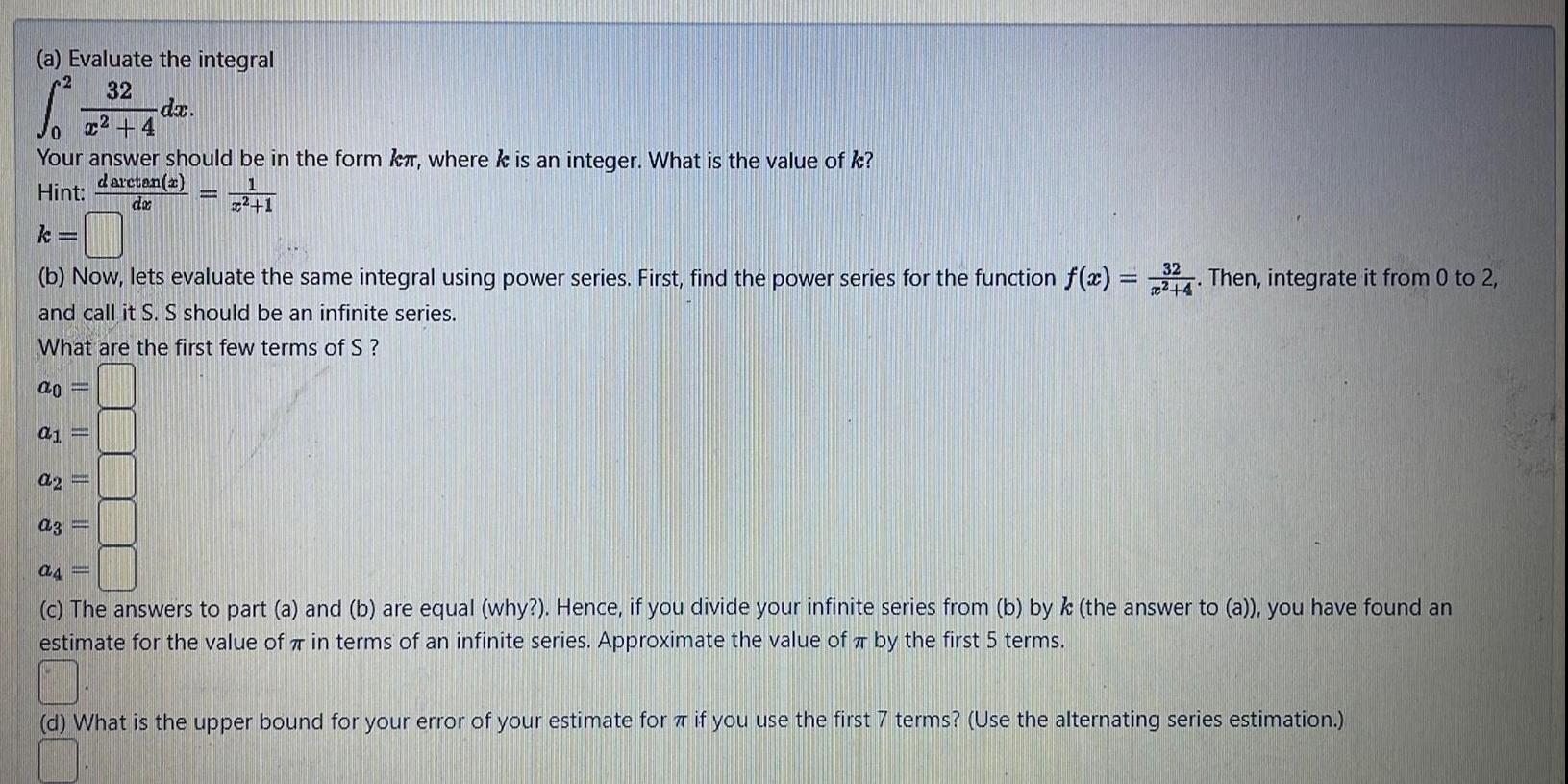
Calculus
Indefinite Integrationa Evaluate the integral 2 32 x 4 0 Your answer should be in the form kr where k is an integer What is the value of k daretan x Hint do ao a1 32 b Now lets evaluate the same integral using power series First find the power series for the function f x 34 Then integrate it from 0 to 2 4 and call it S S should be an infinite series What are the first few terms of S P da a2 a3 1 as c The answers to part a and b are equal why Hence if you divide your infinite series from b by k the answer to a you have found an estimate for the value of 7 in terms of an infinite series Approximate the value of by the first 5 terms d What is the upper bound for your error of your estimate for if you use the first 7 terms Use the alternating series estimation 01 K

Calculus
Definite Integralscollinear Solution Direction ratios of line joining A and B are 1 2 2 3 3 4ie 1 5 7 The direction ratios of line joining B and Care 3 1 8 2 11 3 ie 2 10 14 It is clear that direction ratios of AB and BC are proportional hence AB is parallel to BC But point B is common to both AB and BC Therefore A collinear points B C are EXERCISE 11 1 1 Ifa line makes angles 90 135 45 with the x y axes respectively find its direction cosines 2 Find the direction cosines of a line which makes equal angles with the coordinate axes 3 If a line has the direction ratios 18 12 4 then what are its direction cosines 4 Show that the points 2 3 4 1 2 1 5 8 7 are collinear 5 Find the direction cosines of the sides of the triangle whose vertices are 3 5 4 1 1 2 and 5 5 2 11 3 Equation of a Line in Space We have studied equation of lines in two dimensions in Class XI we shall now study the vector and cartesian equations of a line in space A line is uniquely determined if 1 it passes through a given point and has given direction or i it passes through two given points 11 3 1 Equation of a line through a given point and parallel to a given vector h Let a be the position vector of the given point A with respect to the origin O of the rectangular coordinate system Let be the line which passes through the point A and is parallel to a given vector b Let 7 be the position vector of an arbitrary point P on the line Fig 11 3 382 MATHEMATICS Then AP is parallel to the vector b i e AP b where is some real number But i e Rationalised 2023 24 AP OP 0A 2b 7 a Conversely for each value of the parameter A this equation gives the position vector of a point P on the line Hence the vector equation of the line is given by F a b and a ishd A P Fig 11 3 Pl Y 1 Remark If h ai b ck then a b c are direction ratios of the line and conversely if a b c are direction ratios of a line then b ai bj ck will parallel to the line Here b should not be confused with bl Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z the direction ratios of the line be a b Consider the ates of any point Pbe x y z Then x i y j z k 7 xi y zk b al b ck Substituting these values in 1 and equating the coefficients of 1 and k we get x x a y y b z z kc 2 These are parametric cautions of the line Fliminating the parameter from 2
Calculus
Application of derivativesLet f x 1 8x x x Find the derivative by using the Product Rule f x Find the derivative by multiplying first f x Do your answers agree Yes O No

Calculus
Limits & ContinuityThe function f x 10x ln 1 x is represented as a power series Find the following coefficients in the power series C2 C3 CA C5 Find the radius of convergence R of the series 8 f x Cnz 7 0
Calculus
Application of derivativesSuppose that f 5 1 f 5 4 g 5 3 and g 5 5 Find the following values a fg 5 b c 5 7 5
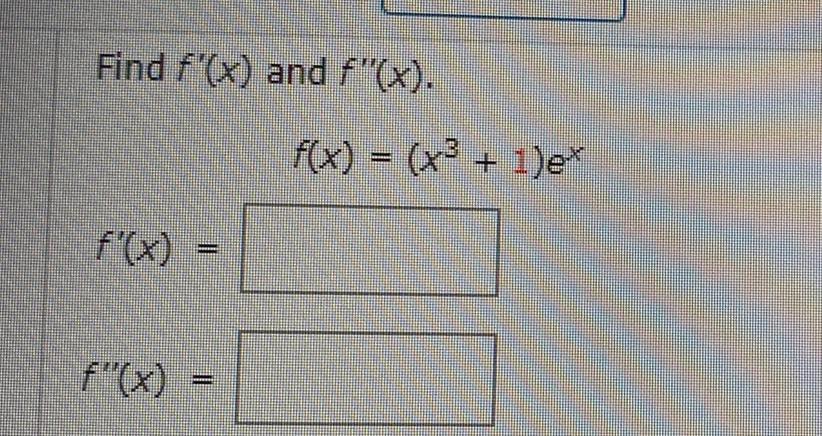
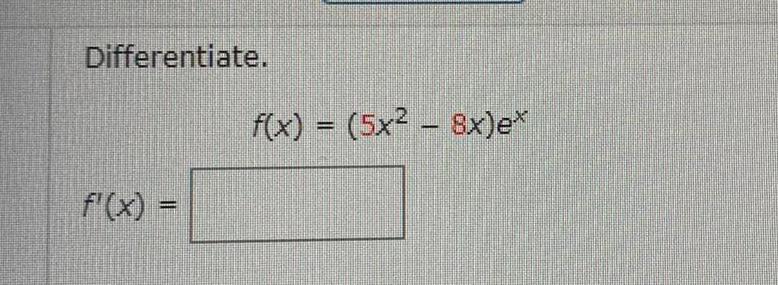

Calculus
Application of derivativesCurrent Attempt in Progress Find all critical points and then use the first derivative test to determine local maxima and minima Check your answers by graphin f x 3x 4x 6 Enter the critical points in increasing order If there is no local maximum or local minimum enter NA X The local maximum is at x The local minimum is at x
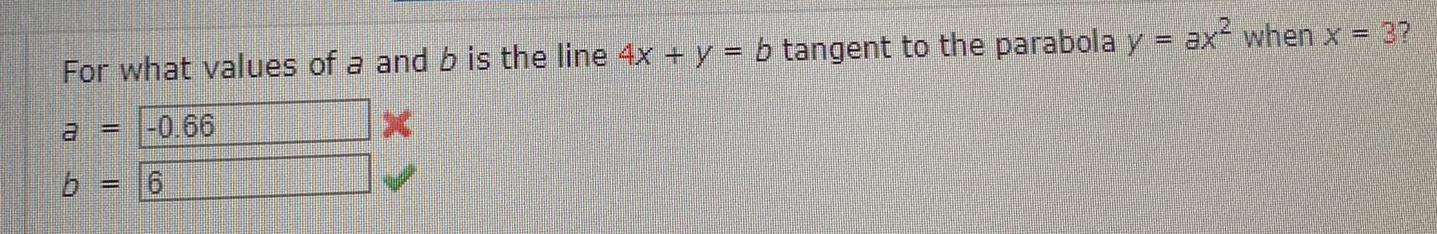
Calculus
DifferentiationFor what values of a and b is the line 4x y b tangent to the parabola y ax when x 3 a 0 66 6

Calculus
Limits & Continuity3 For each of the following functions find all values a in o at which the function is discontinuous if there are any At each such value compute the two one sided limits lim f x and x a In x lim f x x and say what type of discontinuity removable discontinuity jump discontinuity vertical asymptote or other occurs at a If there is a removable discontinuity explain how you could redefine the function at that point to make it continuous a h x b g t ln let 4 c f x COS d g x arctan