Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Differentiation8 12 17 20 1 2est log e C 22 tan 7 4x C 24 log 2sin x 3cos x C 1 21 C 9 x 1 C 10 2log x 1 C x 4 x 8 C 70x n x c log x 1 m 32 26 2sin x C 29 log sin x C C x 1 22 1 37 39 B C 34 2 tanx C x 1 15 log19 4x 1 C 16 18 C cos tan x C sin 2x C NCERT 35 1 log x C sin 4x 10 C 1 13 18 2 3x 30 log 1 cos x C 31 Rationalised 2023 24 19 log e EXERCISE 7 3 sin12r r sin8r si 25 ottone repurushed tan 2x 3 x C 33 1 1 tan x 28 2v1 sinx C 1 1 cos x sin x C C 22 38 D 14 C log cos x sin x C 36 x log x C ANSWERS cos 7x cos x C 441

Calculus
Differential equationsexampie Show that the points collinear Solution Direction ratios of line joining A and B are 1 2 2 3 3 4ie 1 5 7 1 It is clear that direction ratios of AB and BC are proportional hence AB is parallel to BC But point B is common to both AB and BC Therefore A B C are collinear points The direction ratios of line joining B and Care 3 1 8 2 11 3 ie 2 10 14 EXERCISE 11 1 1 If a line makes angles 90 135 45 with the x ya direction cosines 2 Find the direction cosines of a line which makes equal angles with the coordinate axes 3 If a line has the direction ratios 12 4 then what are its direction cosines 4 Show that the points 2 3 4 1 2 1 5 8 7 are collinear 5 Find the direction cosines of the sides of the triangle whose vertices are 3 5 4 1 1 2 and 5 5 2 11 3 Equation of a Line in Space We have studied equation of lines in two dimensions in Class XI we shall now study the vector and cartesian equations of a line in space A line is uniquely determined if 1 it passes through a given point and has given direction or n it passes through two given points 382 11 3 1 Equation of a line through a given point and parallel to a given vector b Let be the position vector of the given point A with respect to the origin O of the rectangular coordinate system Let be the line which passes through the point A and is parallel to a given vector b Let be the position vector of an arbitrary point P on the line Fig 11 3 wish But 1 0 MATHEMATICS Then AP is parallel to the vector b i e APA b where is some real number AP OP DA b 7 Conversely for each value of the parameter A this equation gives the position vector of a point P on the line Hence the vector equation of the line is given by X Rationalised 2023 24 s respectively find its and a 2 Fig 11 3 Y F a b Remark If hai b ck then a b c are direction ratios of the line and conversely if a b c are direction ratios of a line then b al by ck will be the parallel to the line Here b should not be confused with lb Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z and the direction ratios of the line be a b c Consider the coordinates of any point P be x y z Then x t v t thit xitritzk b ai bj ck Substituting these values in 1 and equating the coefficients of i and k we get x x g v v b 2 2 kc 2

Calculus
Differential equations26 8 3 NT 0 C 4 B 8 A 2 A 6 C 0 C 4 A 1 2 8 8 B H 2 tan B C 2 sin 2A 31 D 35 C 39 B 43 D 47 C 51 B 55 B 59 D 63 C 27 m x 1 65 13 FI4 e TL 29 0 2nn 32 D 36 B 40 D 44 C 48 C 52 C 56 A DBD 60 1 4 12 14 3 a 1 2 a 4 66 3 3 8 True 69 False 70 False 2 False 73 True 74 True 6 a iv b i c ii d iii 5 bl 33 C 37 C 41 D 45 B 49 B 53 C 57 B 61 110 8 67 2 71 True 75 True

Calculus
Application of derivatives304 EXEMPLAR PROBLEMS MATHEMATICS 39 C 41 B 45 1 43 C 46 n B 47 AB 48 9 1 2 1 2 49 0 1 2 3 4 5 6 8 50 6 1 5 9 10 ii 1 2 3 5 6 7 9 10 31 AUB 53 True 57 True 38 C 42 B 2 3 2 3 EXERCISE 1 1 1 1 3 2 1 2 3 3 1 3 3 1 1 1 2 1 3 3 1 3 2 3 3 52 1 b ii c ii a iv f v d vi e 55 False 54 False 56 True 58 False 1 1 1 3 3 1 3 3 iv 1 1 1 2 1 3 2 1 2 2 2 3 3 1 i 40 A 44 1 2 0 1 0 2 1 1 1 2 2 1 2 2 i 0 3 1 3 ii 0 2 0 3 0 4 0 5 1 2 1 3 1 4 1 5 11 and h i a 0 and b 2 3 4 5 b 1 4 2 3 3 2 4 1 1 1 1 2 1 3 2 1 2 2 3 1 i 4 5 5 4 5 5 6 Domain of R 0 3 4 5 Range of R 7 Domain of R 1 5 51 and Range of R 1 3 17 8 R 0 8 8 0 0 8 8 0 9 Domain of RR and range of R R U 0 b 10 1 is not a function ii f is a function g is a function iv is a function v is a constant function 11 a 6 1364 4 12 a x 4 b x 4 13 8 x x 2x 2 3 2 3 3 c 13 d 4 e 5 ii f g x 2x alished

Calculus
Definite Integralsdx dt dy dt 2x 1 1 2 xy 3y 1 3 2xy a Find the value for each of the six parameters r1 72 K K2 01 02 b Perform nullcline analysis draw all nullclines draw the arrows in each section and across each nullclines indicating if each population increases or decreases find and label each equilibrium use this sketch to label each equilibria as stable or unstable if possible c Determine the stability of the equilibrium at coexistence neither population is extinct by linearizing around that equilibrium Find the Jacobian the matrix of partial derivatives Evaluate the Jacobian at the equilibria in question Either calculate the eigenvalues of this matrix OR use the trace determinant
Calculus
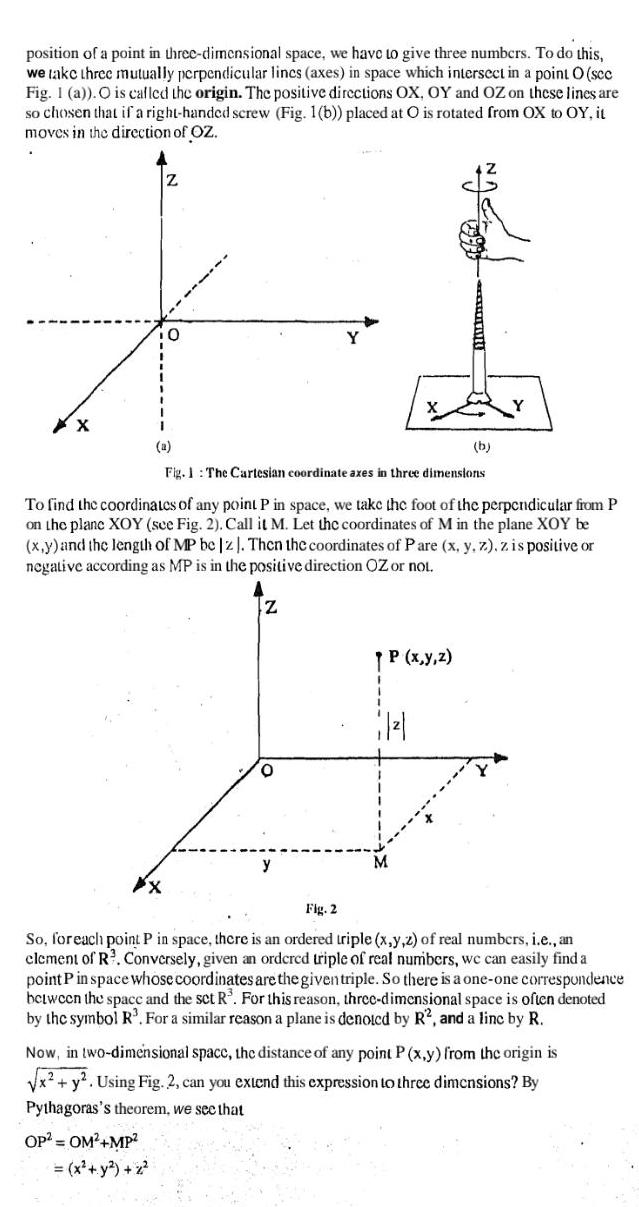
Differentiationposition of a point in three dimensional space we have to give three numbers To do this we take three mutually perpendicular lincs axes in space which intersect in a point O sec Fig 1 a O is called the origin The positive directions OX OY and OZ on these lines are so chosen that if a right handed screw Fig 1 b placed at O is rotated from OX to OY it moves in the direction of OZ XX Z X 0 OP OM MP x y z a Fig 1 The Cartesian coordinate axes in three dimensions To find the coordinates of any point P in space we take the foot of the perpendicular from P on the plane XOY see Fig 2 Call it M Let the coordinates of M in the plane XOY be x y and the length of MP be z Then the coordinates of Pare x y z z is positive or negative according as MP is in the positive direction OZ or not Z O NACE P x y z 662 1 b Fig 2 So for each point P in space there is an ordered triple x y z of real numbers i e an element of R Conversely given an ordcrcd triple of real numbers we can easily find a point P in space whose coordinates are the given triple So there is a one one correspondence between the space and the set R For this reason three dimensional space is often denoted by the symbol R For a similar reason a plane is denoted by R2 and a linc by R Now in two dimensional space the distance of any point P x y from the origin is x y Using Fig 2 can you extend this expression to three dimensions By Pythagoras s theorem we see that

Calculus
Definite IntegralsFind the volume of the solid whose base is the region in the xy plane that is bounded by the parabola y 4 x and the line y 3x while the top of the solid is bounded by the plane z x 8 The volume is units Type an integer or a simplified fraction

Calculus
Definite IntegralsFind the volume of the region bounded above by the paraboloid z x y and below by the triangle enclosed by the x y lines y x x 0 and x y 2 in the xy plane The volume under the paraboloid is Type a simplified fraction

Calculus
Limits & ContinuityTheorem 1 If lim f x L and lim f x M then L M x p x p Proof Suppose LM then I L MI 0 Since lim f x L if we take x p then 38 0 such that Ix pl 8 1 f x LI e Similarly since lim f x M 38 0 such that x p Ix pl 8 lf x MI E If we choose 8 min 8 8 then Ix pl 8 will mean that Ix pl 8 and lx pl 8 In this case we will have both I f x Li e as well as I f x MI E So that IL MI IL f x f x MISI f x LI f x MI That is we get L MI IL MI which is a contradiction Therefore our supposition is wrong Hence L M We now state and prove a theorem whose usefulness will be clear to you in Unit 4 ii lim f x L lim h x X 4 Xa Theorem 2 Let f g and h be functions defined on an interval I containing a except possibly at a Suppose i f x g x Sh x x I a Then lim g x exists and is equal to L x a Proof By the definition of limit given 0 38 0 and 8 0 such that If x LI e for 0 ix al 8 and Ih x LI e for 0 lx al 8 Let 8 min 8 8 Then 0 lx al 8 If x LI e and h x LI E L ESf x SL E and L E h x L E We also have f x g x Sh x x E I a Thus we get 0 1x al 8 L es f x g x Sh x L In other words 0 lx al 8 lg x LI E Therefore lim g x L 2 IL MI Theorem 2 is also called the sandwich theorem or the squeeze theorem because g is being sandwiched between f and h Let us see how this theorem can be used IL MI 2 Example 4 Given that I f x 11 3 x 1 2 xe R can we calculate lim f x x 1 We know that 3 x 1 f x 1 3 x 1 2x This means that 3 x 1 1 f x 3 x 1 1 lim 3 x 1 1 1 lim x Using the sandwich theorem and the fact that 3 x 1 1 we get lim f x 1 31 1 X 1 x 11 In the next section we will look at the limits of the sum product and quotient of functions Theorem 3 Let f and g be two functions such that lim f x and lim g x exist Then x p x p i 2 2 1 Algebra of limits Now that you are familiar with limits Let us state some basic properties of limits Their proofs are beyond the scope of this course ii lim f x g x lim f x lim g x x p x p x p lim f x g x lim f x im 8 x x p Sum rule Product rule

Calculus
DifferentiationFig 2 Look at the graph of f in Fig 2 You will see that when x is small x is also small As x comes closer and closer to er to 0 x also comes closer and closer to zero It is reasonable to expect that lim f x 0 as x 0 Let us prove that this is what happens Take any real number e 0 Then I f x 01 ix i x e Therefore if we choose 8 we get 1 f x Oke whenever 0 1x 01 This gives us lim f x 0 3 2 A useful general rule to prove lim f x Lis to write down f x L and then express it in terms of x a as much as possible Let us now see how to use this rule to calculate the limit in the following examples x 1 Example 2 Let us calculate lim lim 241 12 X is not We know that division by zero is not defined Thus the function f x defined at x 1 But as we have mentioned earlier when we calculate the limit as x approaches I we do not take the value of the function at x 1 Now to obtain x 1 we first note that x 1 x 1 x 1 so that x 1 for x 1 lim x 1 741 Therefore lim As x approaches 1 we can intuitively see that this limit approaches 2 To prove that the limit is 2 we first write f x L x 1 2 x 1 which is itself in the form x a since a 1 in this case Let us take any number e 0 Now 1 x 1 21 E lx 1 E Thus if we choose 8 E in our definition of limit we see that x 1 x 1 8 E if x L1 1x 11 e This shows that lim x 1 2 Hence X41 1 1 X 1 Example 3 Let us prove that lim x 4 13 13 That is we shall prove that e 0 38 0 such that 1 x 4 131 e whenever Ix 3 Here f x L x 4 13 x 9 and x a x 3
Calculus
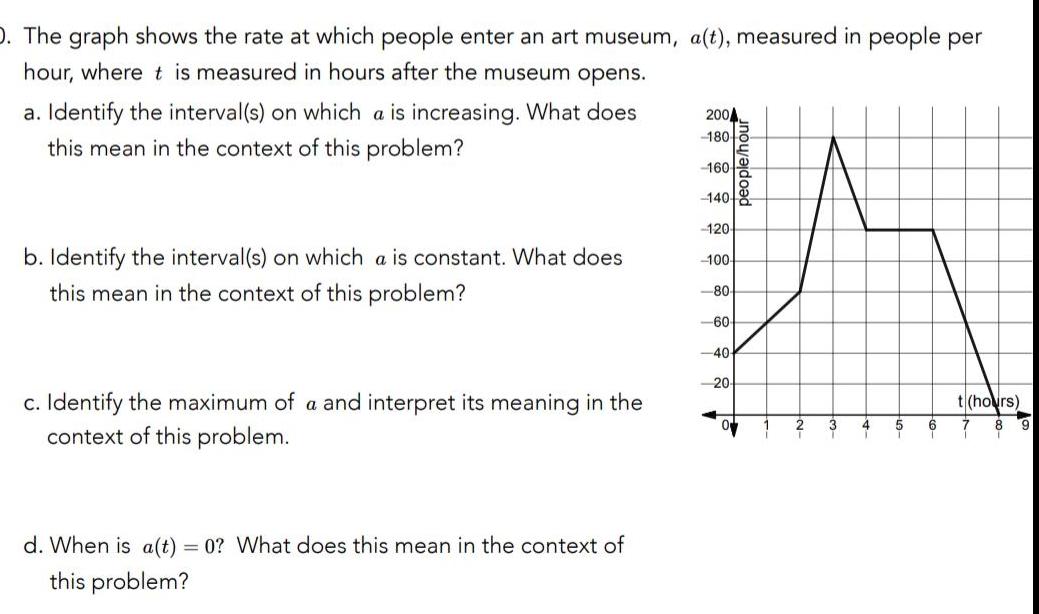
DifferentiationD The graph shows the rate at which people enter an art museum a t measured in people per hour where t is measured in hours after the museum opens a Identify the interval s on which a is increasing What does this mean in the context of this problem b Identify the interval s on which a is constant What does this mean in the context of this problem c Identify the maximum of a and interpret its meaning in the context of this problem d When is a t 0 What does this mean in the context of this problem 2004 180 160 140 120 100 80 60 40 20 people hou 3 4 5 6 t hours 7 8
Calculus
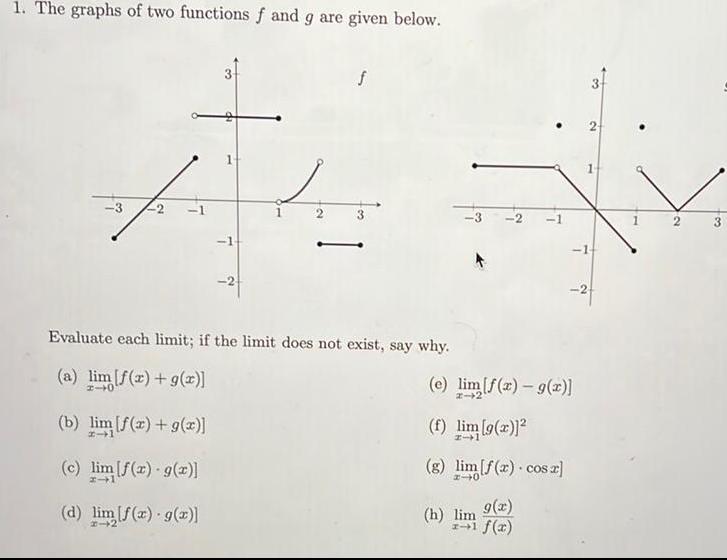
Differentiation1 The graphs of two functions f and g are given below 11 Evaluate each limit if the limit does not exist say why a lim f x g x 40 b lim f x g x c lim f x g x d lim f x g x 14 e lim f x g x f lim 9 2 g lim f x cos z g x h lim f x 2 3
Calculus
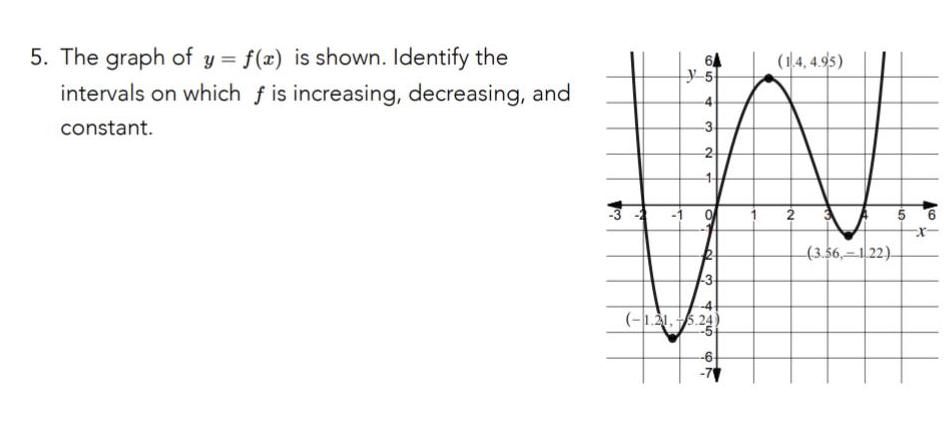
Differentiation5 The graph of y f x is shown Identify the intervals on which f is increasing decreasing and constant 3 y 5 3 2 N 3 1 215 24 6 14 4 95 2 3 56 122 5 6

Calculus
Differentiation9 After doing some market research Crunchy Cookie Inc has found that their profit on cookies after spending amount on advertising can be modeled by P x 5000 1000x 5a Both x and P x are measured in thousands of dollars a What is the most profit that Crunchy Cookie Inc can make b How much would they have to spend on advertising to achieve this result c Is there ever a time when Crunchy Cookie Inc will make no profit Explain why or why not Profit in thousands 55000 50000 45000 E 40000 35000 50 30000 25000 20000 15000 10000 5000 PM 50 Advertising in thousands 100 150 200

Calculus
Differential equations7 Information about a function f x is given in the table f 2 Decreasing 0 x 3 x 3 3 x 5 x 55 x Increasing 11 Increasing 5 a For which value s of e if any does f x have a relative local minimum b For which value s of x if any does f x have a relative local maximum
Calculus
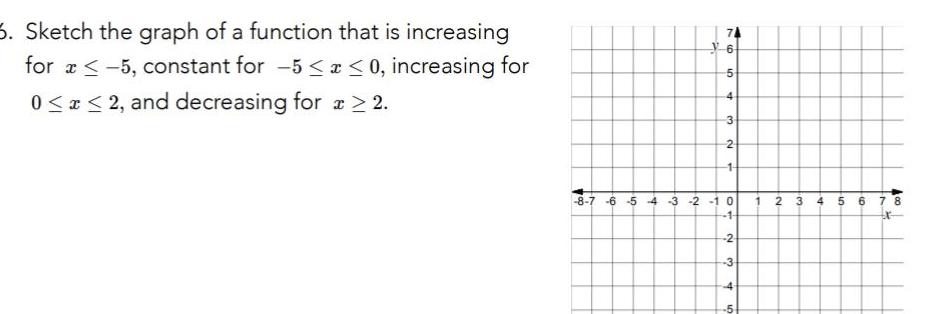
Differentiation5 Sketch the graph of a function that is increasing for a 5 constant for 5 x 0 increasing for 0 x 2 and decreasing for x 2 6 5 4 3 2 1 8 7 6 5 4 3 2 10 1 2 3 4 5 1 2 3 4 5 6 7 8 tr
Calculus
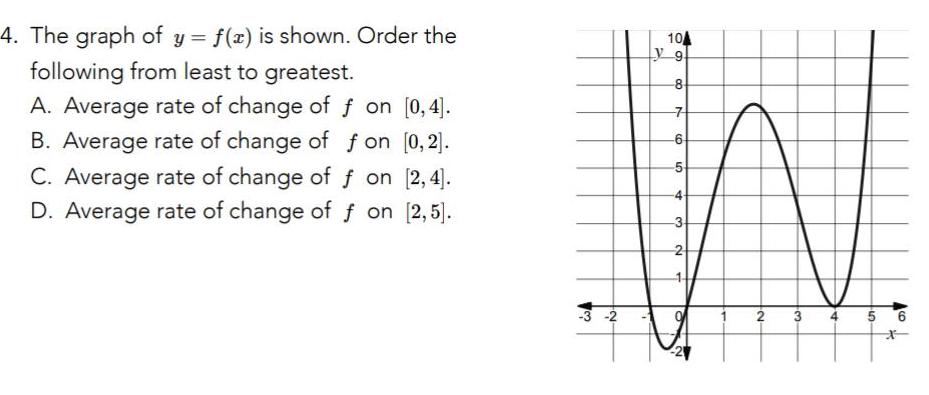
Differentiation4 The graph of y f x is shown Order the following from least to greatest A Average rate of change of f on 0 4 B Average rate of change of fon 0 2 C Average rate of change of f on 2 4 D Average rate of change of on 2 5 w 104 Ly9 8 N 7 6 5 4 3 2 O 2 3 A 5 6 x

Calculus
Application of derivatives8 The value of stock in Chelsea s Chocolate Company increased between 2017 and 2019 then decreased until June of 2020 then started increasing again Which of the following conclusions is true A The value of the stock was at its absolute highest in 2019 B The value of the stock reached a relative maximum in 2019 C The value of the stock reached a relative minimum in 2017 D The value of the stock was at its absolute lowest in June of 2020


Calculus
Differentiation2 The temperature of a mug of hot chocolate t minutes after it is prepared is given by the function H t where H is measured in degrees Fahrenheit Selected values of H t are given below t 0 2 5 10 13 20 H t 170 137 107 83 77 72 Find the average rate of change of the temperature of the hot chocolate between t 0 and t 2 Use proper units in your answer
Calculus
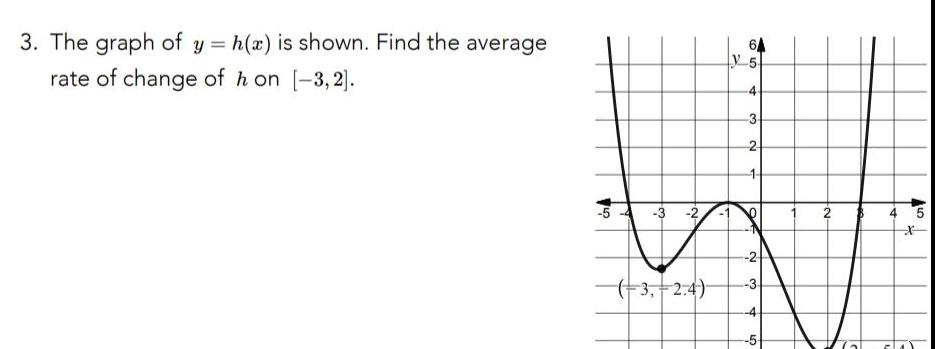
Application of derivatives3 The graph of y h x is shown Find the average rate of change of h on 3 2 3 2 3 2 4 64 5 4 3 2 1 9 N 3 4 5 2

Calculus
Limits & ContinuityFind the point closest to the origin in the line of intersection of the planes y 2z 10 and x y 11 The point closest to the origin is Type an ordered triple

Calculus
Application of derivatives2 2 2 Find the maximum and the minimum values of f x y z 5x 2y 9z on the sphere x y z 110 The maximum value is Simplify your answer
Calculus
Application of derivatives2 Find the points on the surface z xy 9 closest to the origin The points on the surface closest to the origin are Type an ordered triple Use a comma to separate answers as needed

Calculus
Vector CalculusA hummingbird flies 382 m south then turns right and flies 146 m west What is the direction of the

Calculus
Vector CalculusLet A be a vector with magnitude A and components A and Ay In terms of components we can write A Az Ay Consider the following specific case A 52 0 km 84 0 km What is A Provide your answer below

Calculus
Definite IntegralsX Let A be a vector with magnitude A and components A and Ay In terms of components we can write A A Ay Consider the following specific case A 18 0 km 11 0 km What is the direction of A Note Express your answer as an angle measured clockwise from the Provide your answer below direction

Calculus
Differentiation8 12 14 x 4 x 8 C log x 1 m 29 32 17 2 C 18 C 20 log e C 22 tan 7 4x C 4 26 2sin x C 1 m 24 log 2sin x 3cosx C 1 x 1 2 2 37 39 B logsin x C 9 x x 1 C C 15 log19 4x 1 C 16 34 2 tunx C cos ta cos 4 10 2log x 1 C tan x C 13 35 1 log x C NCERT 19 log e e 25 log 1 cos x C 31 1 18 2 3x 33 1 1 tin x 28 2V1 sinx C X tan 2x 3 x C sin x C 1 1 cos x 38 D C C C perda do log cosx sinx C 36 x log x C
Calculus
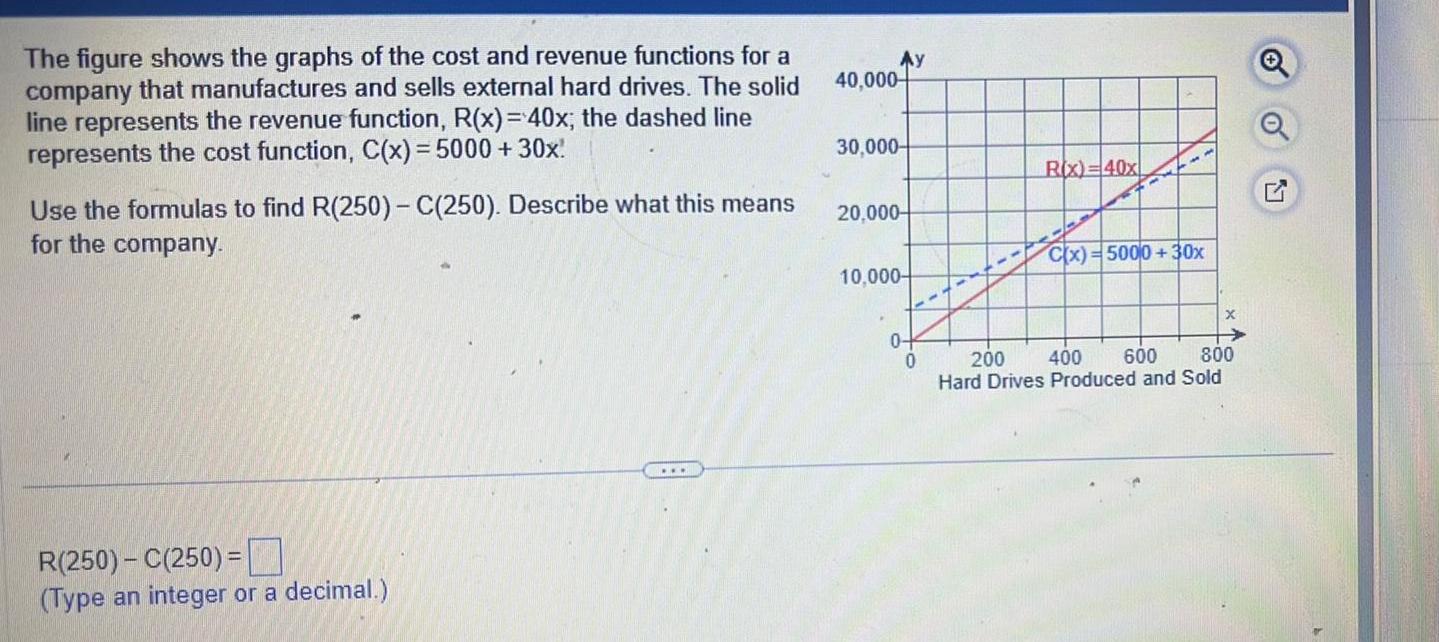
DifferentiationThe figure shows the graphs of the cost and revenue functions for a company that manufactures and sells external hard drives The solid line represents the revenue function R x 40x the dashed line represents the cost function C x 5000 30x Use the formulas to find R 250 C 250 Describe what this means for the company R 250 C 250 Type an integer or a decimal 40 000 Ay 30 000 20 000 10 000 0 0 R x 40x C x 5000 30x X 200 400 600 800 Hard Drives Produced and Sold o

Calculus
DifferentiationDetermine whether 1 0 is a solution of the system 2x 5y 9 3x y 2 Is 1 0 a solution of the system Choose the correct answer below O Yes O No
Calculus
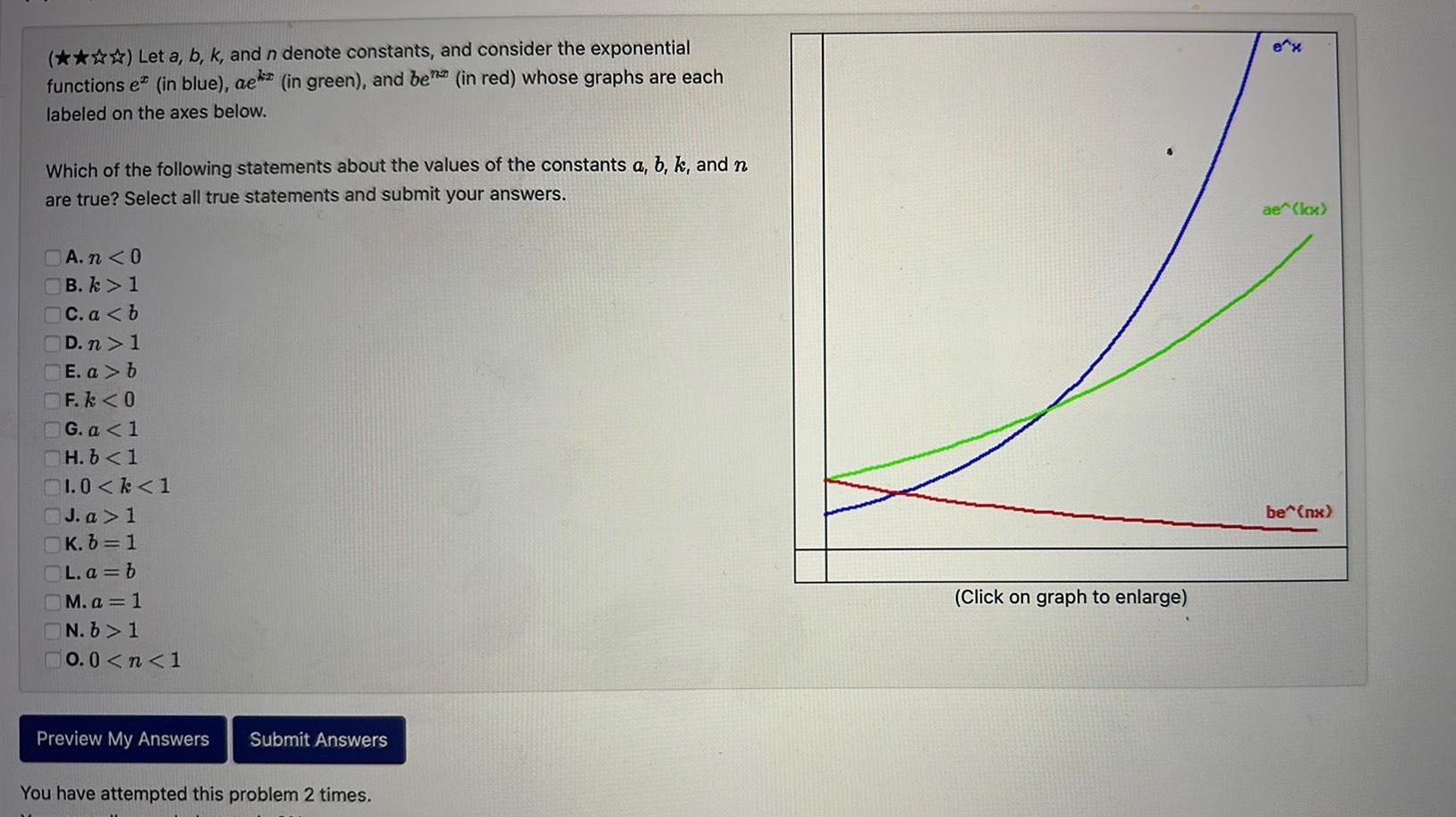
Application of derivativesLet a b k and n denote constants and consider the exponential functions e in blue ae in green and ben in red whose graphs are each labeled on the axes below Which of the following statements about the values of the constants a b k and n are true Select all true statements and submit your answers A n 0 B k 1 C a b D n 1 E a b F k 0 G a 1 H b 1 1 0 k 1 J a 1 K b 1 L a b M a 1 N b 1 0 0 n 1 Preview My Answers Submit Answers You have attempted this problem 2 times Click on graph to enlarge ae kx be nx
Calculus
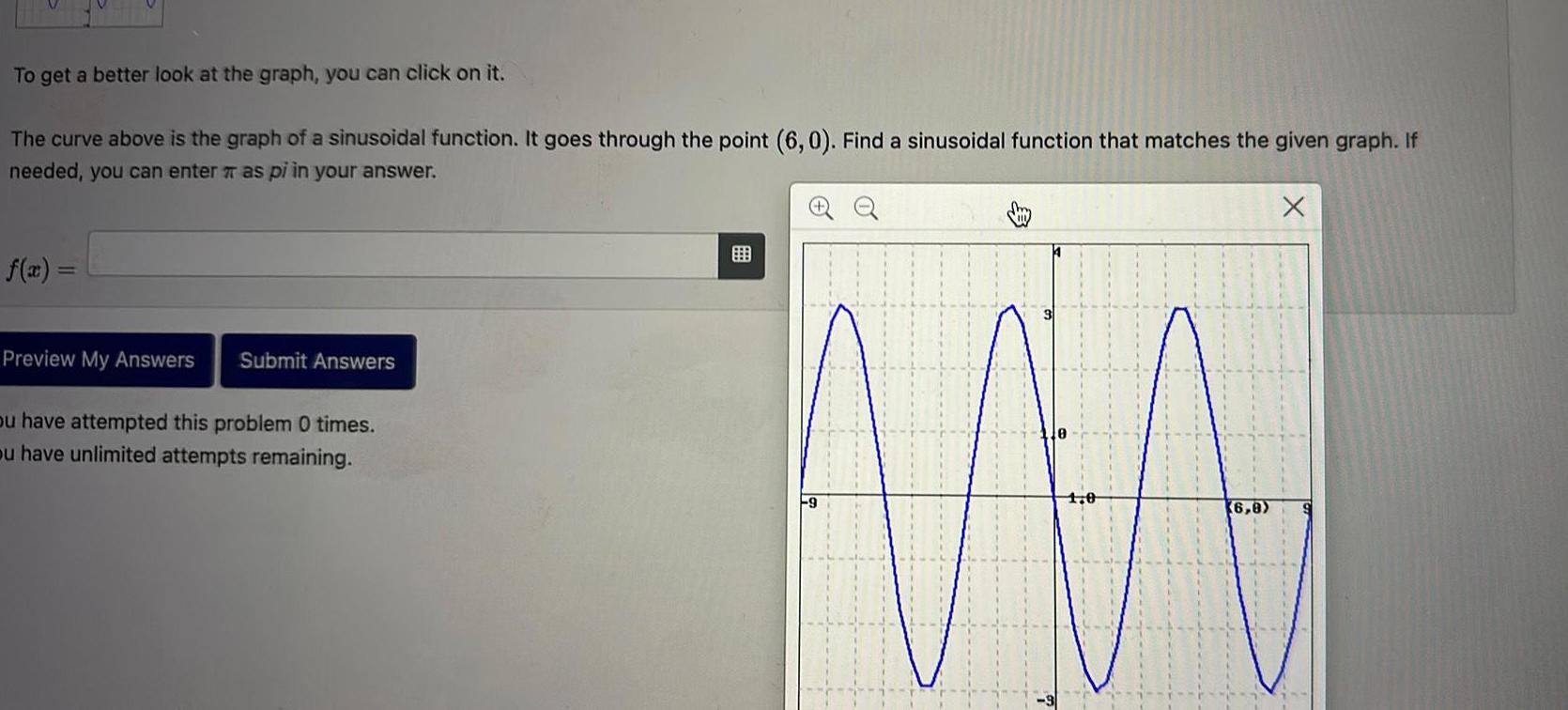
Application of derivativesTo get a better look at the graph you can click on it The curve above is the graph of a sinusoidal function It goes through the point 6 0 Find a sinusoidal function that matches the given graph If needed you can enter as pi in your answer f x Preview My Answers Submit Answers ou have attempted this problem 0 times ou have unlimited attempts remaining 9 6 8 X
Calculus
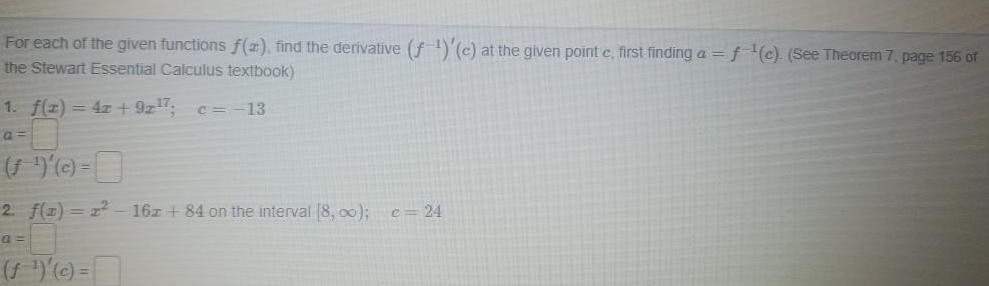
Application of derivativesFor each of the given functions f x find the derivative f c at the given point c first finding a f c See Theorem 7 page 156 of the Stewart Essential Calculus textbook 1 x 4x 9x 7 c 13 c 2 f 1 1 16x 84 on the interval 8 f c c 24
Calculus
Application of derivativesFor each of the given functions f 2 find the derivative f c at the given point c first finding a f c See Theorem 7 page 156 of the Stewart Essential Calculus textbook 1 f x 4z 9x 7 c 13 a f c 2 f 2 x 16z 84 on the interval 8 00 c 24 a f c

Calculus
Differentiation11 tan 2x C 2 2 7 1 log x 1 C 8 log x x a C 9 log tanx tan x 4 C 10 log x 1 x 2x 2 C 6 13 log x 2 3x 2 C 15 logx 4 a b 2 16 2 2x x 3 C 18 log 3x 2x 1 20 x a x b C 6 log x 2 x 1 12 sin 9 19 6 9x 20 og x 2 x 9x 20 C C C 21 x 2x 3 log x 1 x 2x 3 C 22 log x 21 5 76108 1 6 1 2log x 1 C C X Rationalised 2023 24 23 5 x 4x 10 7log x 2 x 4x 10 C 24 B 25 B EXERCISE 7 5 1 log 3 log x 1 5log x 2 4log x 3 C 4 log x 1 2log x 2 log x 3 C 2 log 6 x go to he rept dished ANSWERS pe 443
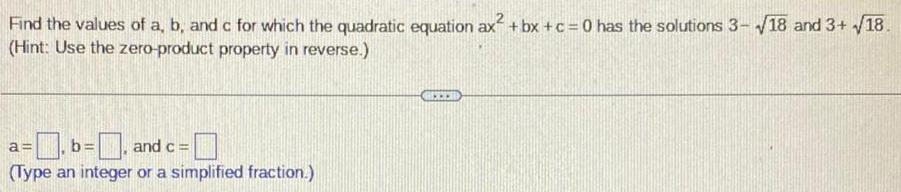
Calculus
Definite IntegralsFind the values of a b and c for which the quadratic equation ax bx c 0 has the solutions 3 18 and 3 18 Hint Use the zero product property in reverse a b and c Type an integer or a simplified fraction

Calculus
Differential equations8 01 2 C 90 x C 10 2log x 1 C 12 14 17 1 Zet C 2e 20 log e C 29 x 4 x 8 C x 0 4 n c log x 1 m 22 tan 7 4x C 24 log 2sinx 3cos x C 26 2sin x C 32 37 C 15 1 3 39 B log sin x x 1 28 18 C 34 2v tanx C 35 cos tan x C I 13 18 2 3x log19 4x 1 C 16 C g cos x sin x C NCERT sin 4x 10 C 6 in 2x C 1 log x C Rationalised 2023 24 19 log e 1 C 30 log 1 cos x C 31 1 cos x otto e repurushed EXERCISE 7 3 sin 12x x sin 8x sin 4x C 8 4 cos 2x 1 cos 2x 1 C 25 tan 2x 3 x C sin x C 4 1 1 tan x 33 28 2 1 sin x C x 1 2 2 C 38 D 36 x log x C log cos x sin x C cos ANSWERS cos 7x cosx C 4 441

Calculus
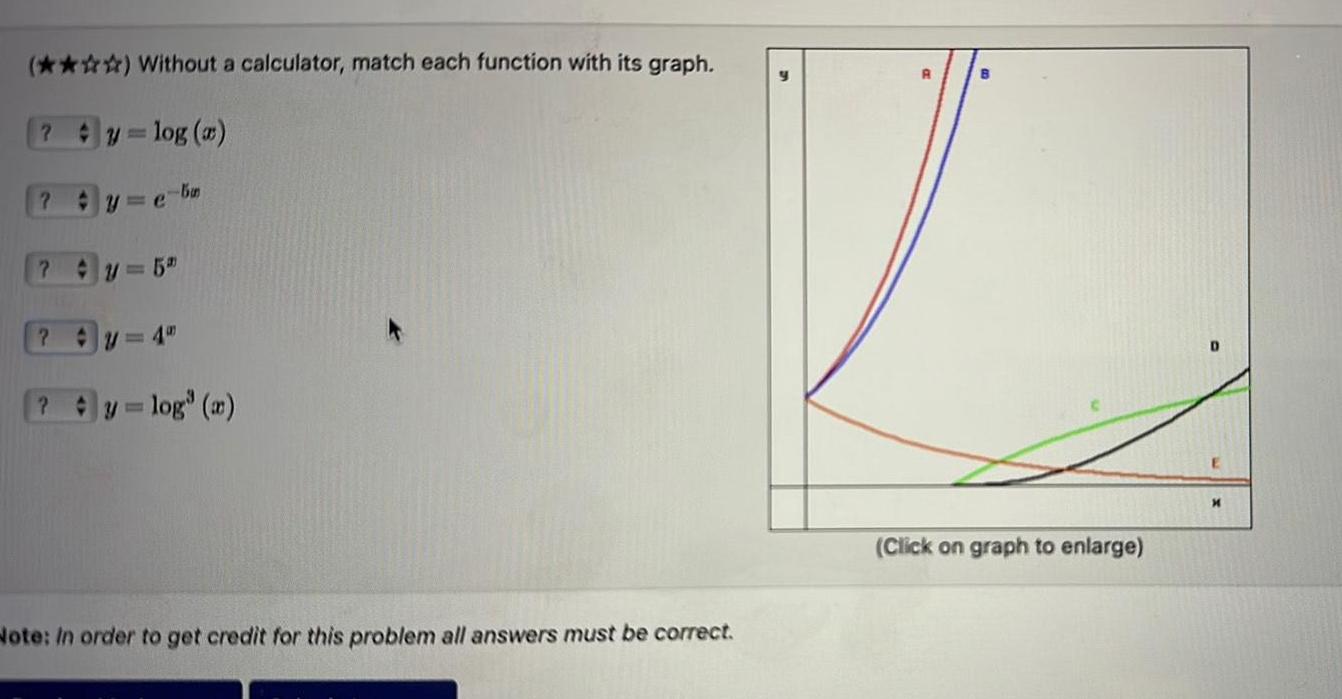
Application of derivativesWithout a calculator match each function with its graph y log x e ba y e 97 5 4 y log a Note In order to get credit for this problem all answers must be correct y Click on graph to enlarge D X
Calculus
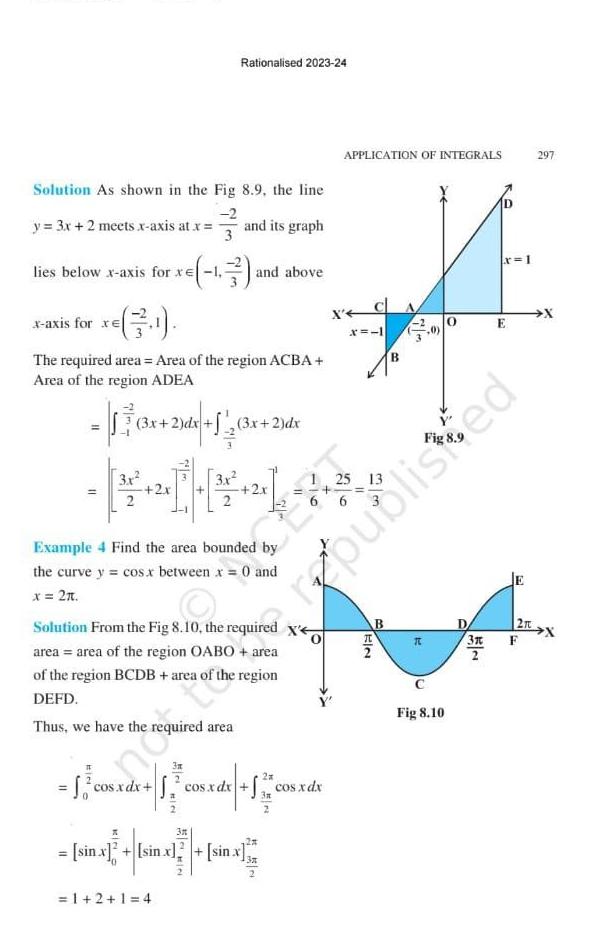
Differential equationsSolution As shown in the y 3x 2 meets x axis at x lies below x axis for xe x axis for xe 3 11 1 The required area Area of the region ACBA Area of the region ADEA 3x 2 dx 3 x Rationalised 2023 24 Fig 8 9 the line 2 and its graph 2 dx 3x 2 dx 1 2 1 4 and above Example 4 Find the area bounded by the curve y cos x between x 0 and x 2t 3n 0 Solution From the Fig 8 10 the required x area area of the region OABO area of the region BCDB area of region DEFD Thus we have the required area 2x cos xdx 1 cos x dx cos xdx cos xdx X sin x sin x sin x sin x APPLICATION OF INTEGRALS X CA 24 6 x 1 EIN B B 3 T 6 Fig 8 10 0 x 1 3x E republisted 1 2rt 297 F

Calculus
Definite IntegralsExample 1 Find the area enclosed by the circle x y a Solution From Fig 8 5 the whole area enclosed by the given circle 4 area of the region AOBA bounded by the curve x axis and the ordinates x 0 and x a as the circle is symmetrical about both x axis and y axis 45 ydx taking vertical strips 4 a x dx Since x y a gives As the region AOBA lies in the first quadrant y is taken as positive Integrating we get the whole area enclosed by the given circle a y 22 to be republish a x a v tu a x 0 sin 1 2 1x x0 sin 1 2 1 a sin y sin Alternatively considering horizontal strips as shown in Fig 8 6 the whole area of the region enclosed by circle X B 0 a 45 xdy 4 y dy Rationalised 2023 24 0 Why Fig 8 5 X APPLICATION OF INTEGRALS b dx A a 0 X dy O Fig 8 6 295 A a 0 ied Example 2 Find the area enclosed by the ellipse Solution From Fig 8 7 the area of the region ABA B A bounded by the ellipse area of the region AOBA in the first quadrant bounded 4 by the curve x axis and the ordinates x 0 x a as the ellipse is symmetrical about both x axis and y axis

Calculus
Differential equationslim Evaluate the Given limit 2x Answer 0 At x 2 the value of the given rational function takes the form 0 lim x 81 x 3 x 3 x 9 lim 2x 5x 3 al x 3 2x 1 x 3 x 9 Question 9 Answer Question 10 lim lim Evaluate the Given limit cx 1 lim 1 2x 1 Answer 3 3 3 9 2 3 1 ax b a 0 b lim cx 1 c 0 1 6x18 7 108 7 Evaluate the Given limit lim Accordingly lim 1 lim 2441 H ax b lim 2 4 At z 1 the value of the given function takes the form 0 Put x so that z 1 as x 1 lim 44 21h lim 13 0
Calculus
Application of derivativesConsider the functions A y x B y x n C y x n where n is an integer greater than 1 n 2 3 4 Which of these functions increases most steeply for values of a greater than 1 Which decreases for large values of x Which of these functions is not defined at x 0 Note In order to get credit for this problem all answers must be correct

Calculus
Definite Integrals440 MATHEMATICS 8 12 17 20 24 29 1 2 C 9 x x 1 C x 4 x 8 C 32 log x 1 m log e e C 22 tan 7 4x C 2e 1 26 2sin x C 39 B C x 1 22 C 15 log19 4x C 16 log 2sin x 3 cos x C log sin x C 18 C x 1 28 14 2 tanx C 35 cos tan x C sin 4x 10 C NCERT 10 2log x 1 C I 13 18 2 3x 30 log 1 cosx C31 1 log x C Rationalised 2023 24 19 log e EXERCISE 7 3 sin 12x x sin 8x sin 4x 25 n2x C 28 2 1 sin x C otto e republished tan 2x 3 x C 33 1 sin x C 1 1 tan x 1 1 cosx C x 1 2 2 38 D C log cos x sin x C 36 x log x C ANSWERS 441

Calculus
Definite Integralsthe Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z and the direction ratios of the line be a b c Consider the coordinates of any point P be x y z Then 7 xi y zk a x i j z k and b al bj ck Substituting these values in 1 and equating the coefficients of i and k we get x x a y y b z z kc 2 These are parametric equations of the line Eliminating the parameter from 2 we get x X 2 4 b This is the Cartesian equation of the line Note If 1 m n are the direction cosines of the line the equation of the line is 2 4 11 m Example 6 Find the vector and the Cartesian equations of the line through the point 5 2 4 and which is parallel to the vector 3 2j 8k Solution We have a Si 2 4k and b 3i 2j 8k cos 8 Rationalised 2023 24 Therefore the vector equation of the line is F 57 23 4k 37 27 8k Now F is the position vector of any point P x y z on the line Therefore xi yj zk 5i 2j 4k 3 2j 8k Eliminating we get 5 3 2 2X j 4 8 k 5y 2 4 8 THREE DIMENSIONAL GEOMETRY 383 which is the equation of the line in Cartesian form 11 4 Angle between Two Lines Let L and L be two lines passing through the origin and with direction ratios a b c and a b c respectively Let P be a point on L and Q be a point on L Consider the directed lines OP and OQ as given in Fig 11 6 Let 8 be the acute angle between OP and OQ Now recall that the directed line segments OP and OQ are vectors with components a b c and a b c respectively Therefore angle 8 between them is given by aa bb cc a b c b c The angle between the lines in terms of sin 8 is given by sin 0 1 cos 0 3 a bb 56 Fig 11 4 resublished Q L

Calculus
Application of derivativesTo say that where A is and B is 5 5 2 is the same as saying is in the closed interval A B
Calculus
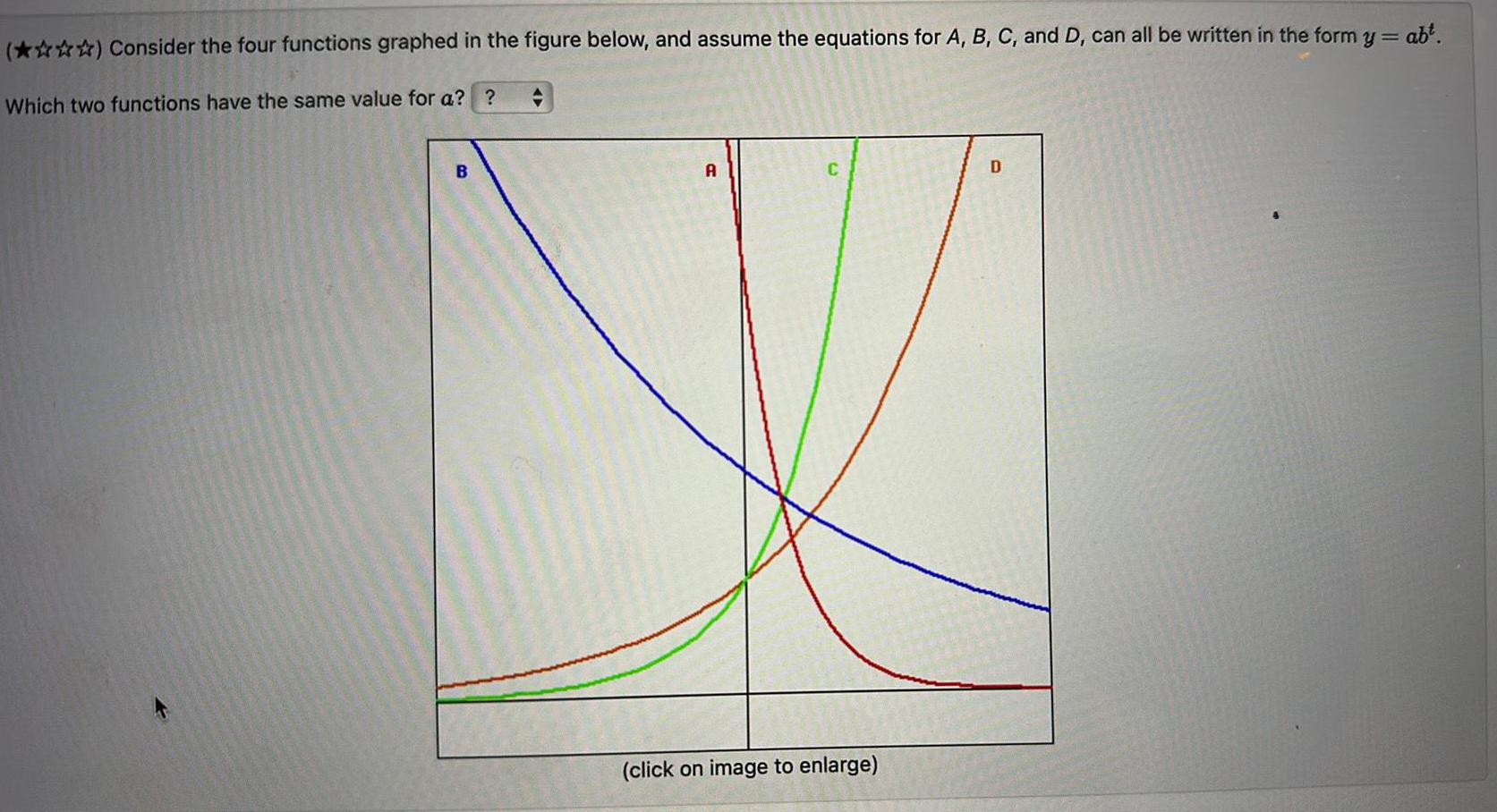
DifferentiationConsider the four functions graphed in the figure below and assume the equations for A B C and D can all be written in the form y abt Which two functions have the same value for a B A click on image to enlarge D

Calculus
Application of derivativesA particle is moving along the curve y 3 4x 1 As the particle passes through the point 2 9 its z coordinate increases at a rate of 3 units per second Find the rate of change of the distance from the particle to the origin at this instant 6

Calculus
DifferentiationLet f x 2x cos 2x f z 4x cos 2x 4x sin 2x f 5 20 cos 10 100 sin 10 2 4 cos 2 16 sin 2x 18x cos 2x f 5 80 sin 10 196 cos 10