Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Vector CalculusGiven the equation y 8x 9 answer the following questions www a If x increases by 1 unit what is the corresponding change in y units b If x decreases by 5 units what is the corresponding change in y units
Calculus
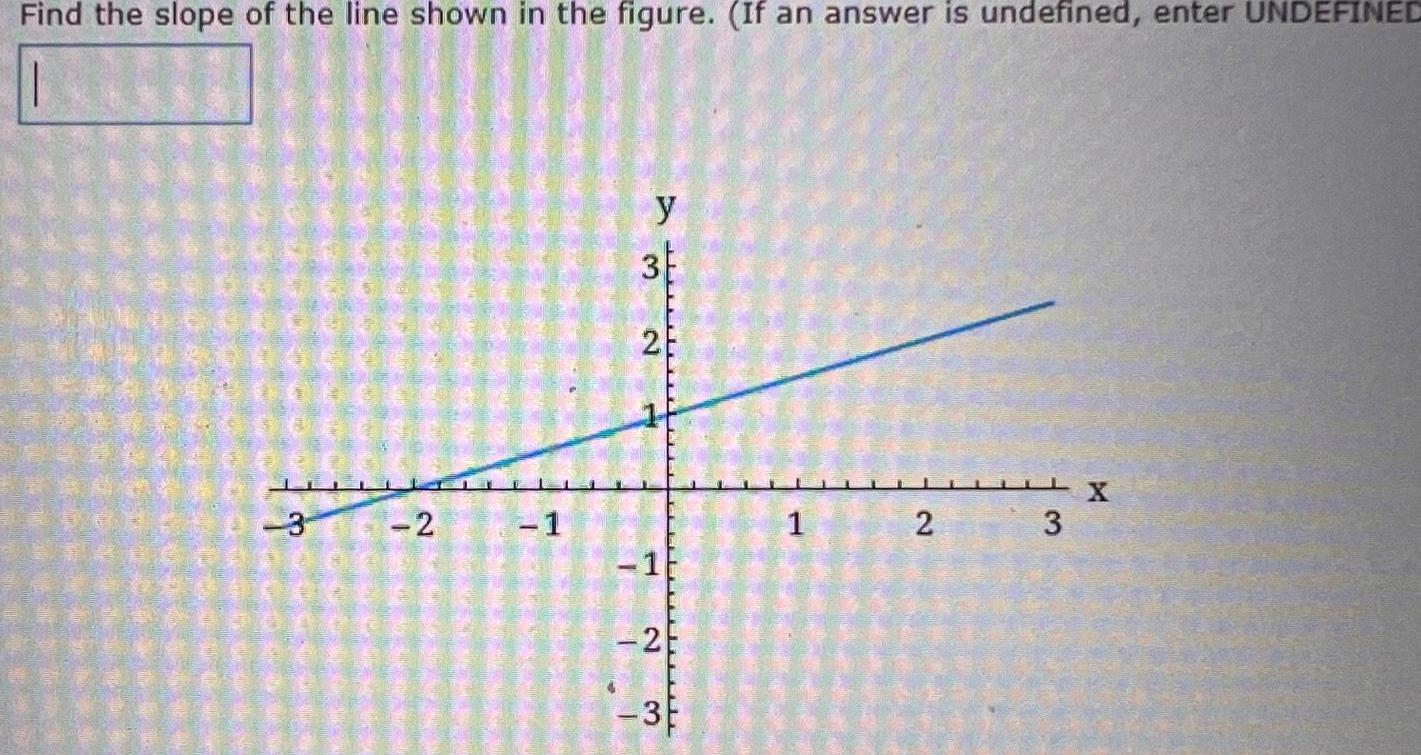
Vector CalculusFind the slope of the line shown in the figure If an answer is undefined enter UNDEFINED 3 2 1 y 3 26 1 25 35 L 1 X 2 3
Calculus
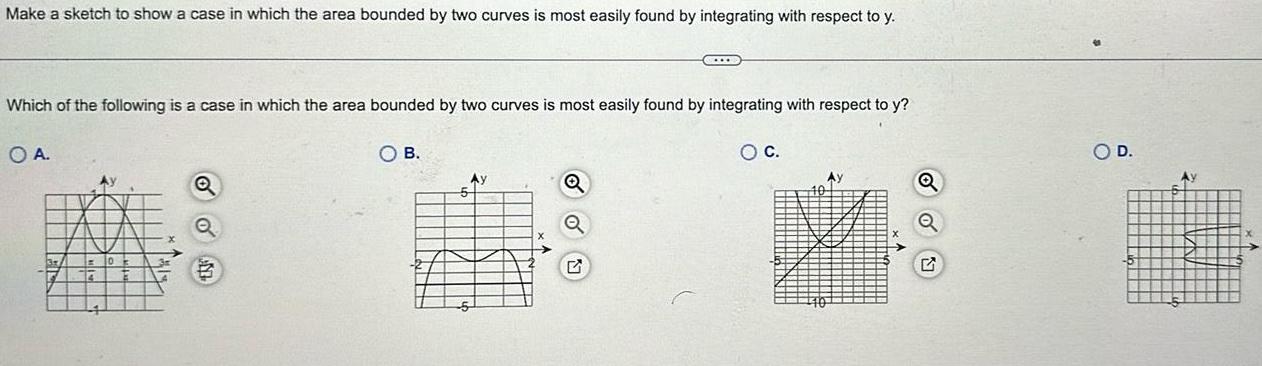
Application of derivativesMake a sketch to show a case in which the area bounded by two curves is most easily found by integrating with respect to y Which of the following is a case in which the area bounded by two curves is most easily found by integrating with respect to y OA OB 5 Ay COL G O C Q O D Ay

Calculus
Differential equationsConsider an object moving along a line with the following velocity and initial position v t 16 1 on 0 5 s 0 3 Determine the position function for 120 using both the antiderivative method and the Fundamental Theorem of Calculus Check for agreement between the two methods To determine the position function for 120 using the antiderivative method first determine how the velocity function and the position function are related Choose the correct answer below OA The position function is the absolute value of the antiderivative of the velocity function OB The position function is the derivative of the velocity function OC The velocity function is the antiderivative of the absolute value of the position function D The position function is the antiderivative of the velocity function Which equation below will correctly give the position function according to the Fundamental Theorem of Calculus b OA s t s 0 v t d Sv t dt a t Sv x dx 0 CELLE OC s 0 s t b OB s t Sv tydt a t Sv x dx 0 D s t s 0 Determine the position function for t20 using both methods Select the correct choice below and fill in the answer box es to complete your choice OA The same function is obtained using each method The position function is s t OB Different functions are obtained using each method The position function obtained using the antiderivative method is s t and the position function obtained using the Fundamental Theo
Calculus
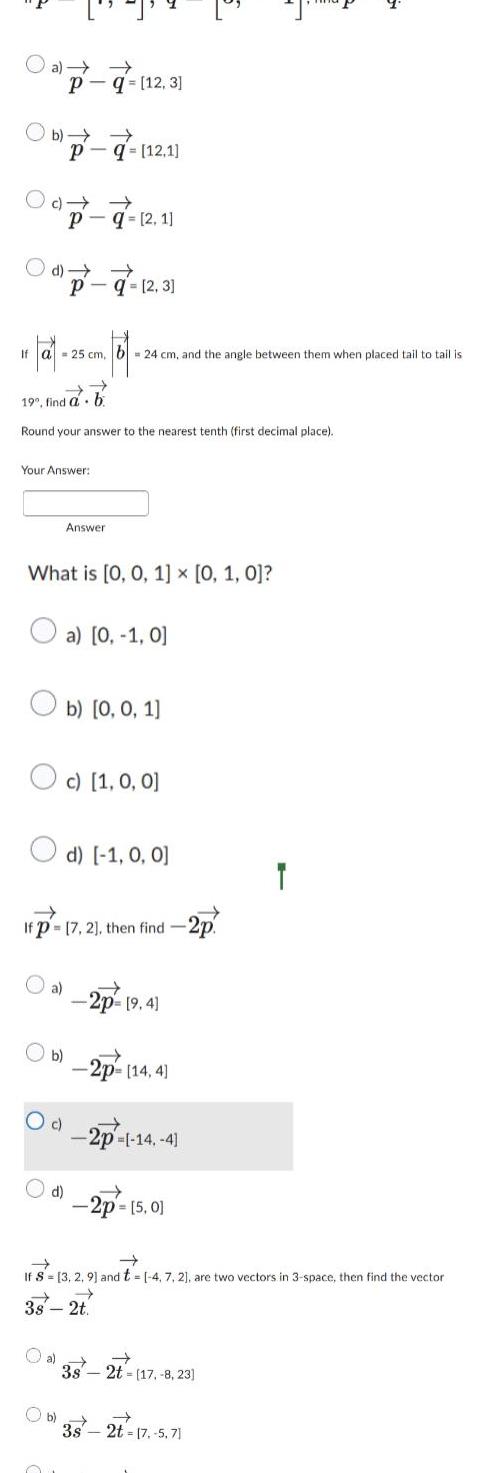
Application of derivativesa Pq 12 3 Ob Pq 12 1 PO d P q 2 3 10 101 102 101 101 If a 25 cm b 24 cm and the angle between them when placed tail to tail is Pq 2 1 19 find a Round your answer to the nearest tenth first decimal place Your Answer b a What is 0 0 1 0 1 0 Ob O c Answer Oc 1 0 0 d a 0 1 0 If p 17 2 then find 2p b 0 0 1 d 1 0 0 2p 9 4 b 2p 14 4 2p 14 4 2p 5 0 If S 3 2 9 and t 4 7 2 are two vectors in 3 space then find the vector 3s 2t 3s 2t 17 8 23 Ob 3s 2t 17 5 71
Calculus
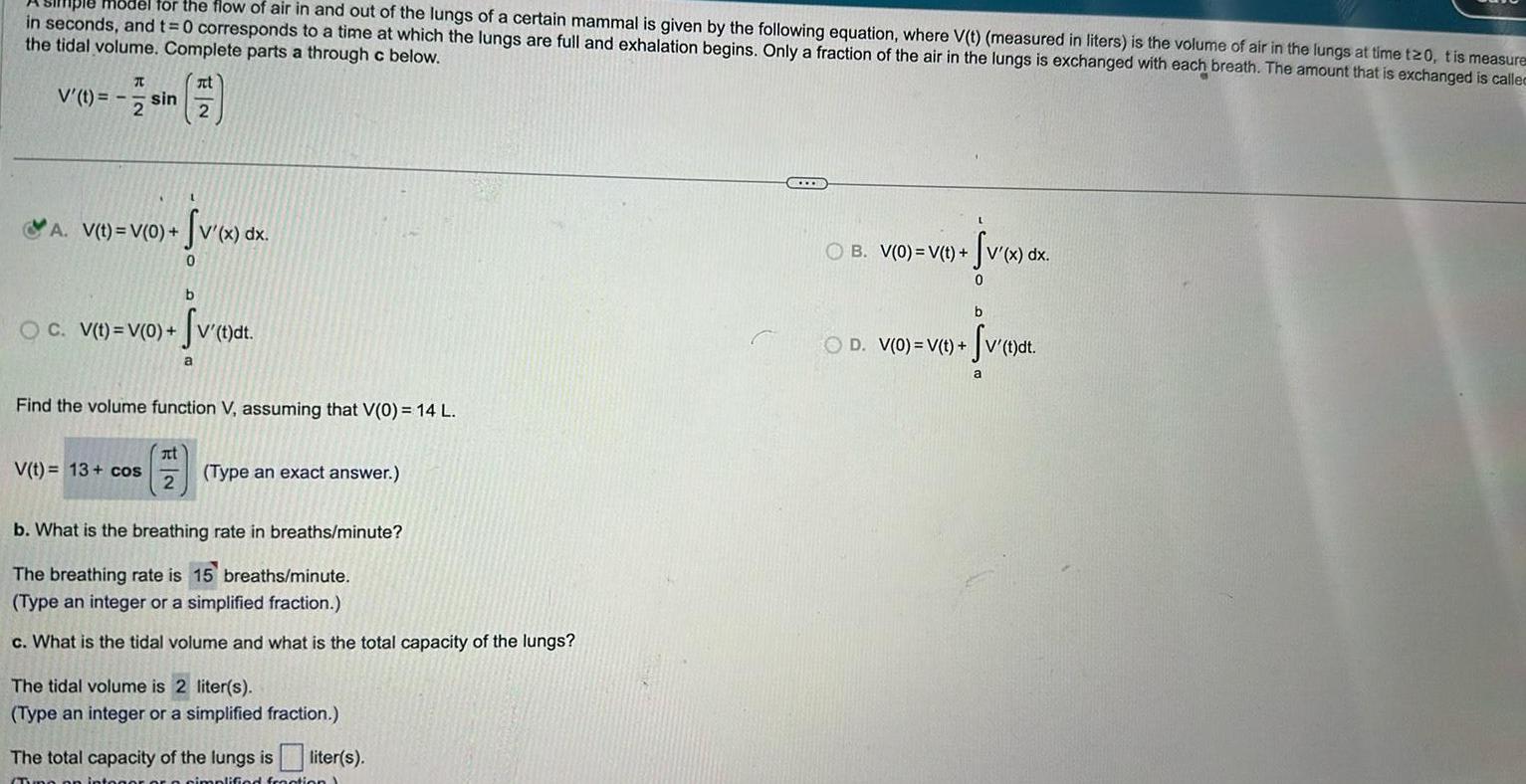
Application of derivativesHiple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t20 tis measures in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below It V sin 7 2 2 A V t V 0 b OC V t V 0 V t dt Svet a v x dx 0 Find the volume function V assuming that V 0 14 L V t 13 cos at 2 Type an exact answer b What is the breathing rate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs The tidal volume is 2 liter s Type an integer or a simplified fraction The total capacity of the lungs is liter s o simplified fraction Sv x dx 0 OB V 0 V t b Sv t dt OD V 0 V t a
Calculus
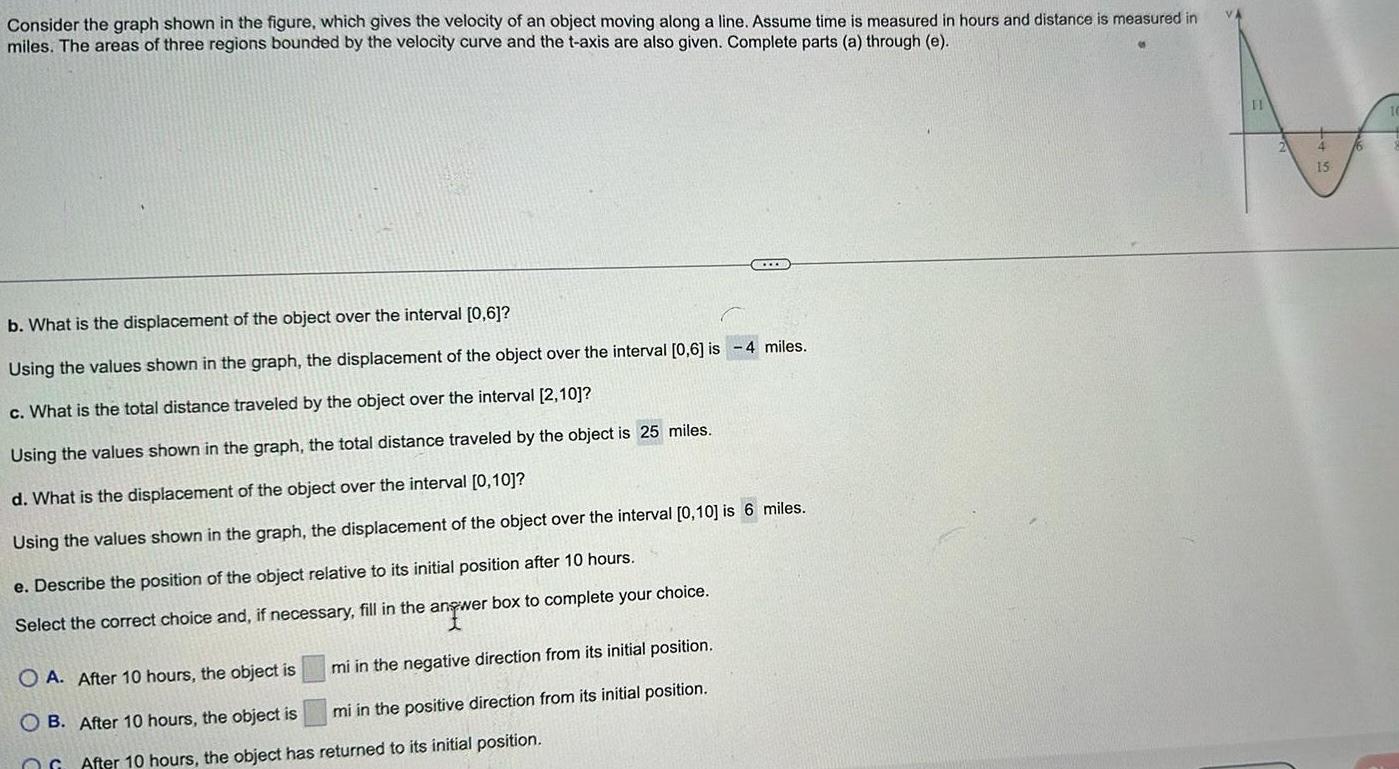
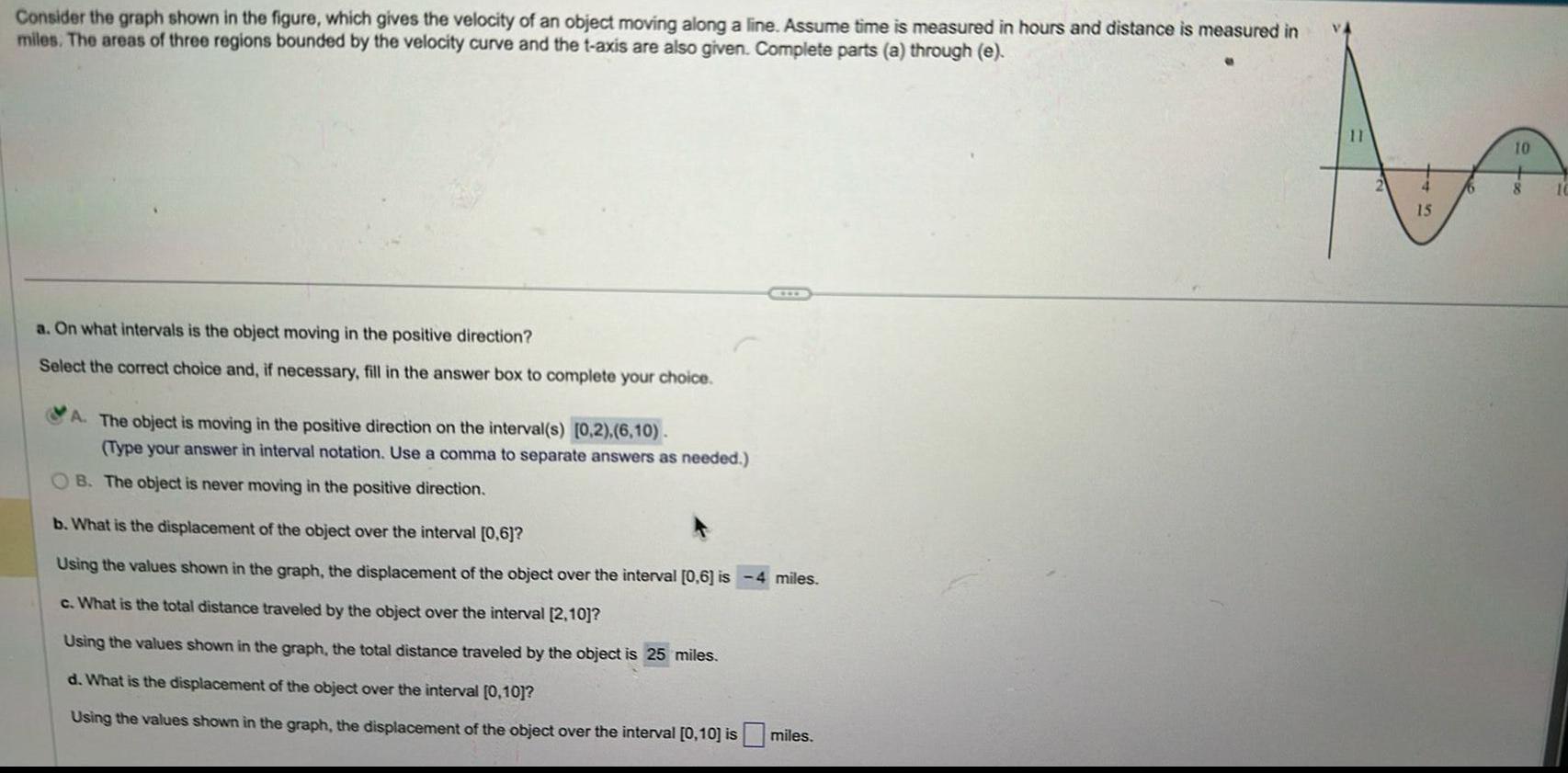
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is 4 miles c What is the total distance traveled by the object over the interval 2 10 Using the values shown in the graph the total distance traveled by the object is 25 miles d What is the displacement of the object over the interval 0 10 Using the values shown in the graph the displacement of the object over the interval 0 10 is 6 miles e Describe the position of the object relative to its initial position after 10 hours Select the correct choice and if necessary fill in the answer box to complete your choice angwe mi in the negative direction from its initial position mi in the positive direction from its initial position CCXXX O A After 10 hours the object is OB After 10 hours the object is After 10 hours the object has returned to its initial position 11 15
Calculus
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e a On what intervals is the object moving in the positive direction Select the correct choice and if necessary fill in the answer box to complete your choice A The object is moving in the positive direction on the interval s 0 2 6 10 Type your answer in interval notation Use a comma to separate answers as needed B The object is never moving in the positive direction b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is 4 miles c What is the total distance traveled by the object over the interval 2 10 Using the values shown in the graph the total distance traveled by the object is 25 miles d What is the displacement of the object over the interval 0 10 Using the values shown in the graph the displacement of the object over the interval 0 10 is miles 11 15 16 10 8 10

Calculus
Vector CalculusA firework is launched into the air from ground level with an initial velocity of 128 ft s If acceleration due to gravity is 16 ft s2 what is the maximum height reached by the firework h t at vt ho 256 ft 512 ft 448 ft 1 024 ft
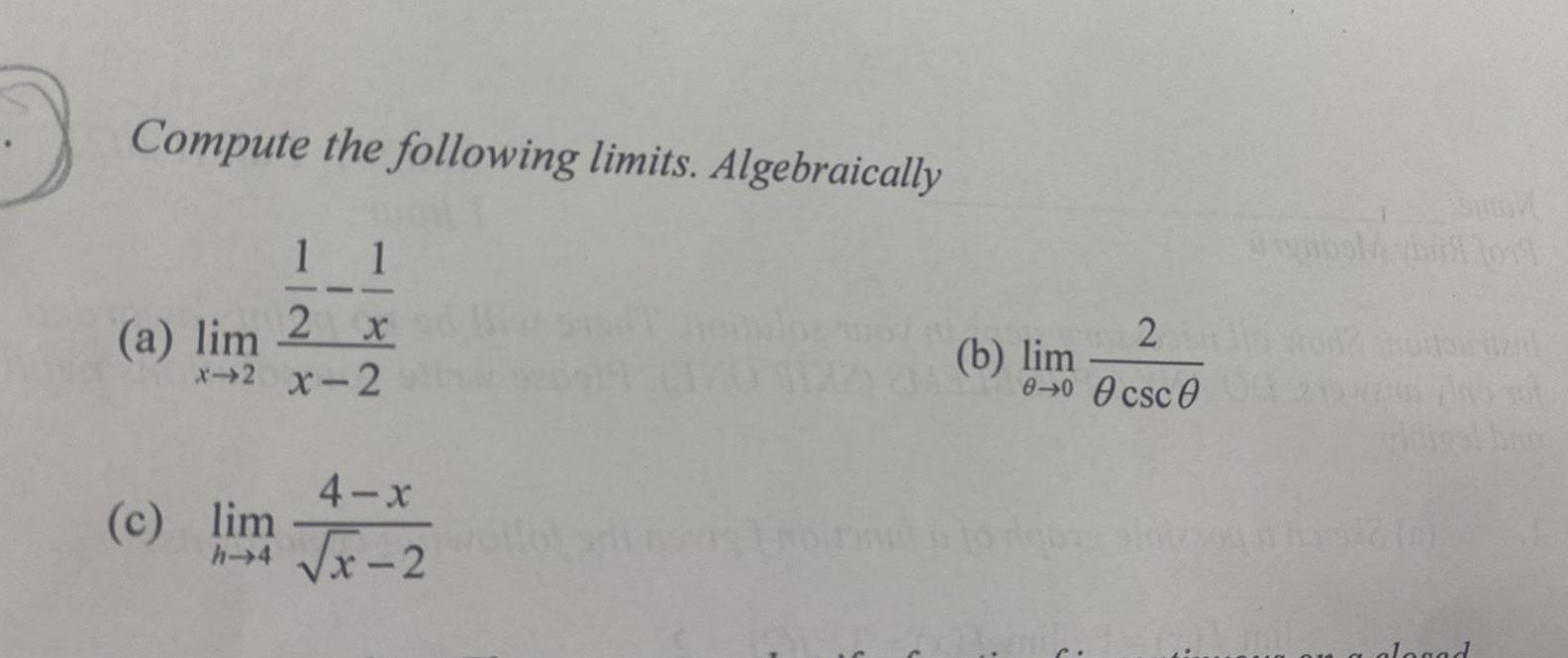
Calculus
DifferentiationCompute the following limits Algebraically 1 1 2 x x 2 X 2 a lim 4 x h 4 x 2 c lim wallot 2 0 0 0csc0 b lim bir 1019 digs brin alogad
Calculus
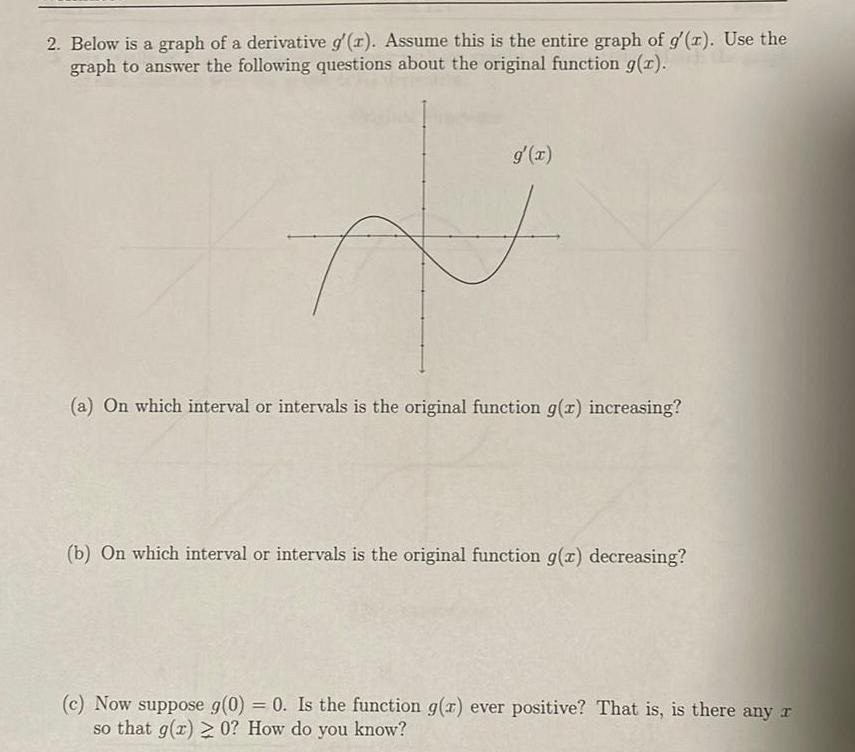
Application of derivatives2 Below is a graph of a derivative g r Assume this is the entire graph of g z Use the graph to answer the following questions about the original function g x g x F a On which interval or intervals is the original function g z increasing b On which interval or intervals is the original function g x decreasing c Now suppose g 0 0 Is the function g z ever positive That is is there any r so that g x 0 How do you know

Calculus
Application of derivativesA company makes two types of biscuits Jumbo and Regular The oven can cook at most 200 biscuits per day Each jumbo biscuit requires 2 oz of flour each regular biscuit requires 1 oz of flour and there is 300 oz of flour available The income from each jumbo biscuit is 0 08 and from each regular biscuit is 0 09 How many of each size biscuit should be made to maximize income What is the maximum income The company should make Type whole numbers jumbo and regular biscuits
Calculus
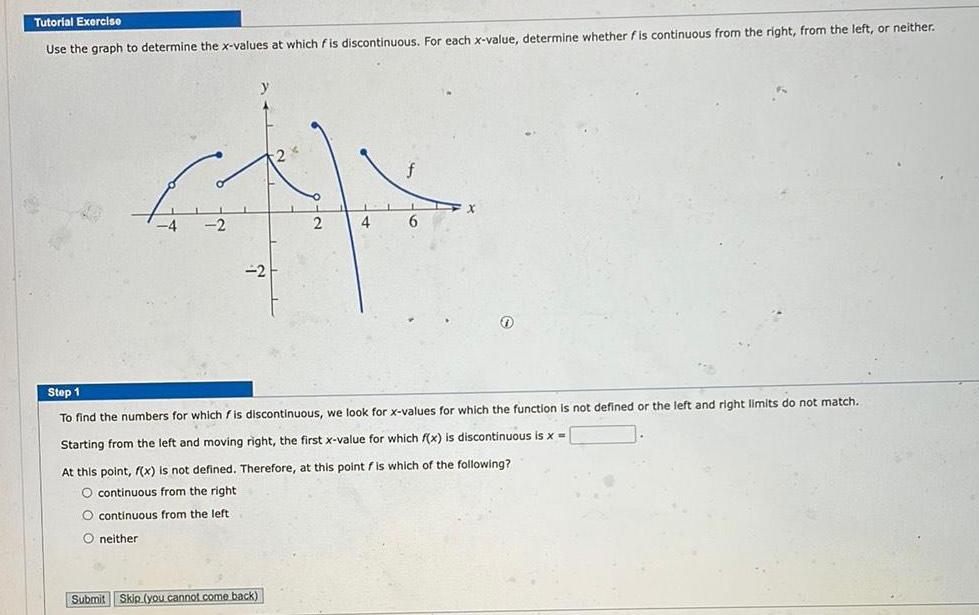
Limits & ContinuityTutorial Exercise Use the graph to determine the x values at which fis discontinuous For each x value determine whether f is continuous from the right from the left or neither 2 2 Submit Skip you cannot come back 4 6 Step 1 To find the numbers for which is discontinuous we look for x values for which the function is not defined or the left and right limits do not match Starting from the left and moving right the first x value for which f x is discontinuous is x At this point f x is not defined Therefore at this point f is which of the following O continuous from the right O continuous from the left O neither
Calculus
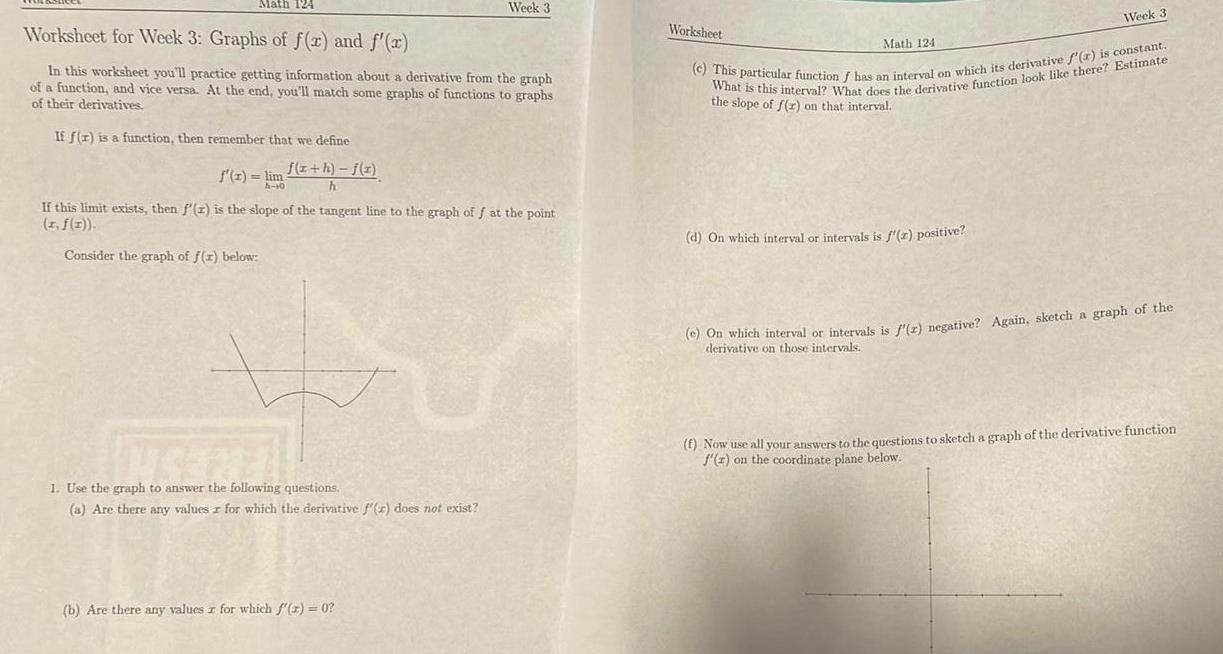
Differential equationsMath 124 Worksheet for Week 3 Graphs of f x and f x In this worksheet you ll practice getting information about a derivative from the graph of a function and vice versa At the end you ll match some graphs of functions to graphs of their derivatives If f r is a function then remember that we define f x h f x h f x lim A 10 Week 3 If this limit exists then f z is the slope of the tangent line to the graph off at the point I f x Consider the graph of f x below UNSERE 1 Use the graph to answer the following questions a Are there any values for which the derivative f x does not exist b Are there any values z for which f x 0 Worksheet Math 124 Week 3 c This particular function f has an interval on which its derivative f r is constant What is this interval What does the derivative function look like there Estimate the slope of f r on that interval d On which interval or intervals is f x positive e On which interval or intervals is f r negative Again sketch a graph of the derivative on those intervals f Now use all your answers to the questions to sketch a graph of the derivative function f z on the coordinate plane below
Calculus
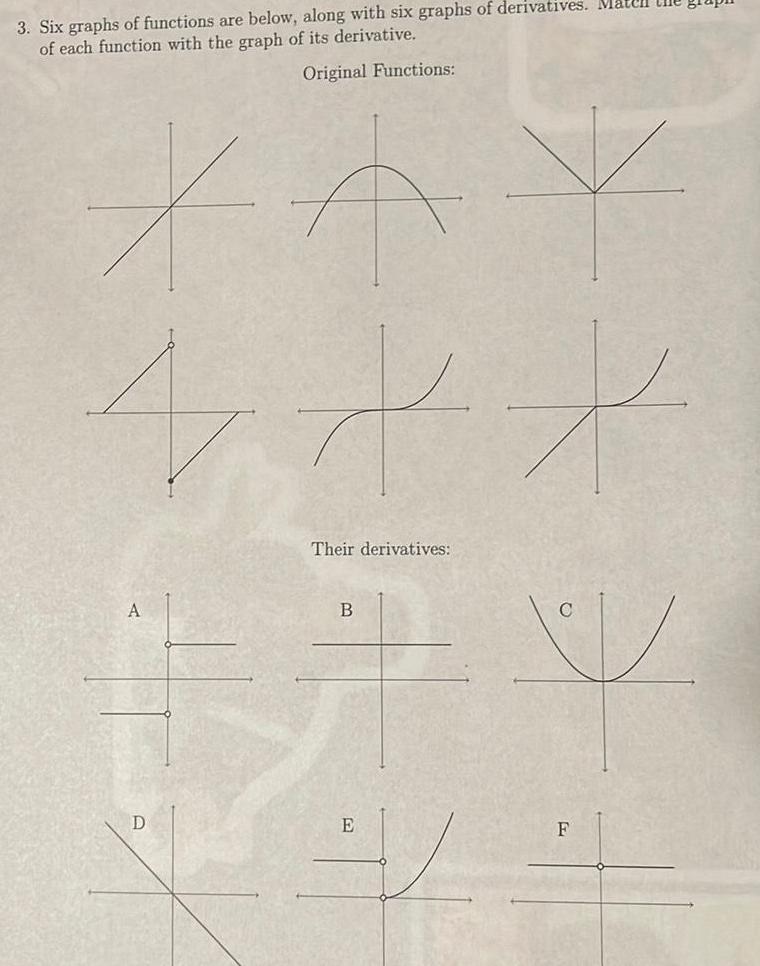
Limits & Continuity3 Six graphs of functions are below along with six graphs of derivatives Matell of each function with the graph of its derivative Original Functions X 4 A D 34 Their derivatives B E X W F
Calculus
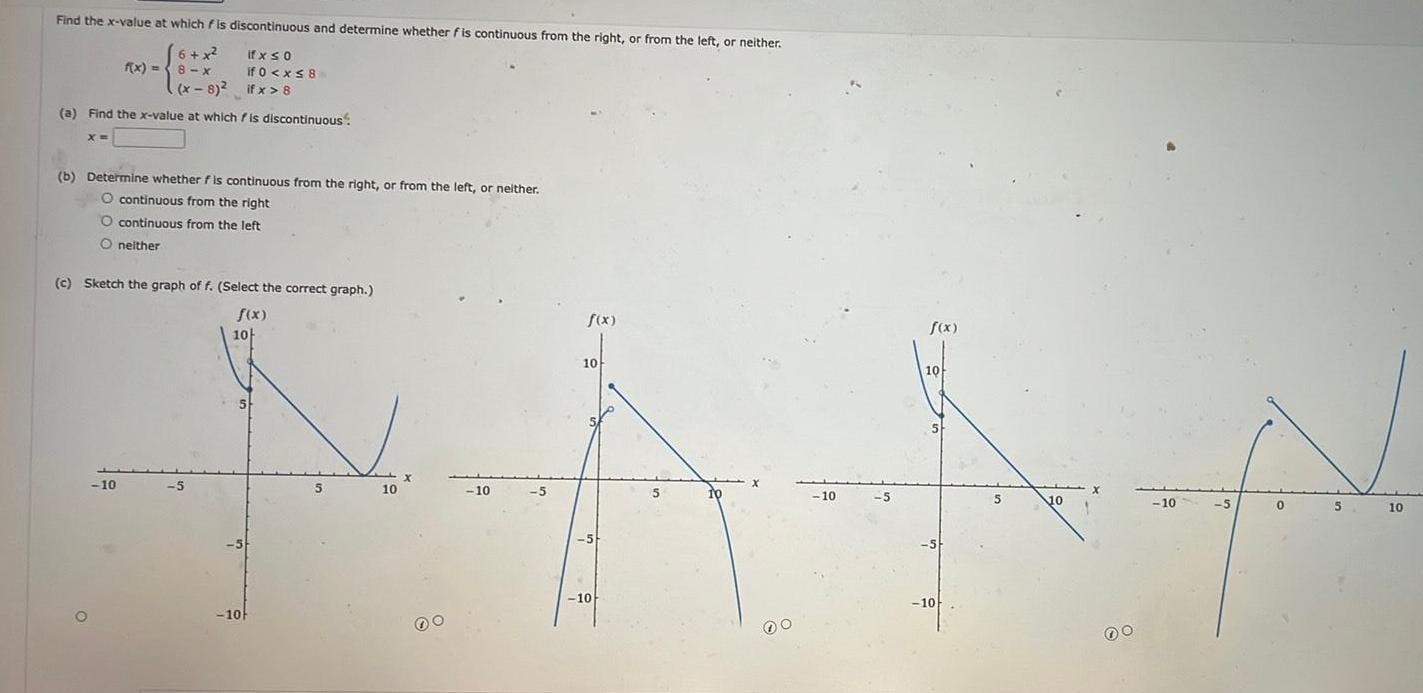
Limits & ContinuityFind the x value at which fis discontinuous and determine whether fis continuous from the right or from the left or neither ifx so 6 x 8 x x 8 if 0 x 8 if x 8 a Find the x value at which is discontinuous X f x 8 x b Determine whether f is continuous from the right or from the left or neither O continuous from the right O continuous from the left O neither c Sketch the graph of f Select the correct graph f x 10 10 5 10 5 10 f x f x 10 AAN 10 5 10 10 10 10 5 10 5 00 00 10 5 0 5 10

Calculus
Application of derivativesTo find the numbers for which f is discontinuous we look for x values for which the function is not defined or the left and right limits do not match Starting from the left and moving right the first x value for which f x is discontinuous is x At this point f x is not defined Therefore at this point f is which of the following O continuous from the right O continuous from the left O neither
Calculus
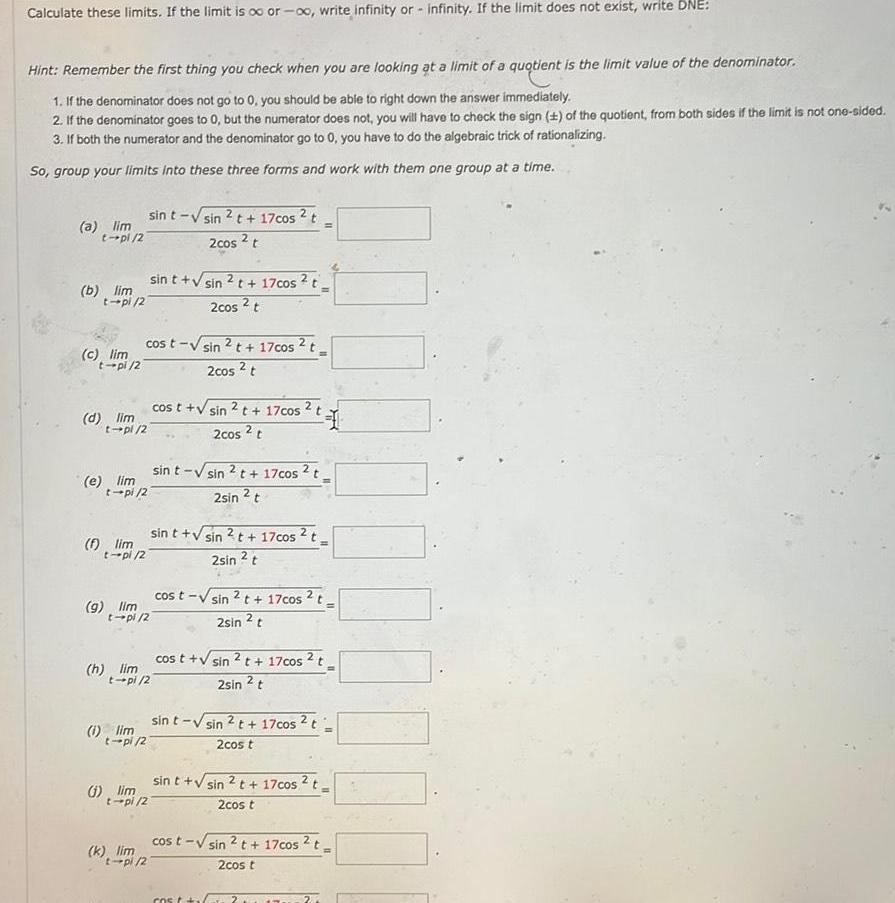
Limits & ContinuityCalculate these limits If the limit is o or oo write infinity or infinity If the limit does not exist write DNE Hint Remember the first thing you check when you are looking at a limit of a quotient is the limit value of the denominator 1 If the denominator does not go to 0 you should be able to right down the answer immediately 2 If the denominator goes to 0 but the numerator does not you will have to check the sign 1 of the quotient from both sides if the limit is not one sided 3 If both the numerator and the denominator go to 0 you have to do the algebraic trick of rationalizing So group your limits into these three forms and work with them one group at a time a lim t pl 2 b lim t pl 2 c lim t pi 2 d lim t pl 2 e lim f lim t pi 2 9 lim h lim sin t sin 2 t 17cos t 2cos 2 t cost sin t pl 27 t pl 2 1 lim t pi 2 sin t sin 2 t 17cos 2 t 2cos 2 t t pi 2 k lim t pl 2 1 lim t pi 2 2t 17cos t 2cos 2 t sin t sin 2t 17cos t 2sin t cos t sin 2 t 17cos 2 t 2cos 2 t 31 sin t sin 2 t 17cos t 2sin 2 t cos t sin 2 t 17cos 2 t 2sin t cost V sin 2 cos t 17cos 2 t 2sin 2 t sin t sin 2 t 17cos t 2cos t sin t sin 2 t 17cos 2 t 2cos t cost sin 2t 17cos 2 t 2cos t 700
Calculus
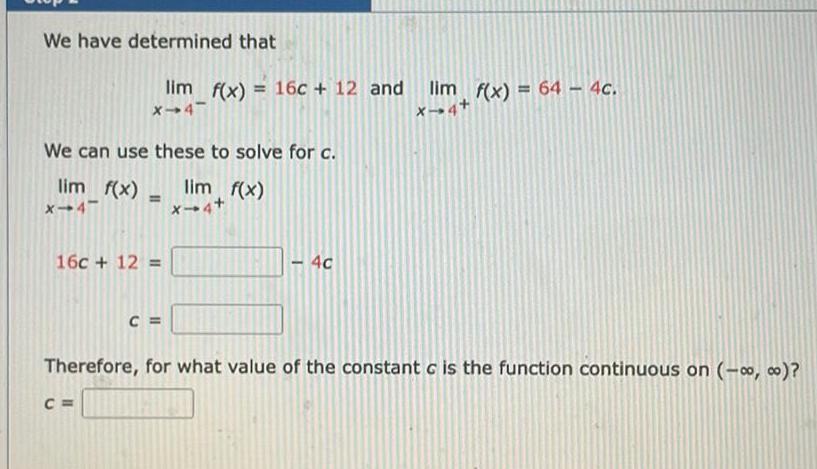
Application of derivativesWe have determined that lim f x 16c 12 and X 4 We can use these to solve for c lim f x x 4 16c 12 C C lim f x X 4 4c lim f x 64 4c X 4 Therefore for what value of the constant c is the function continuous on 0 o
Calculus
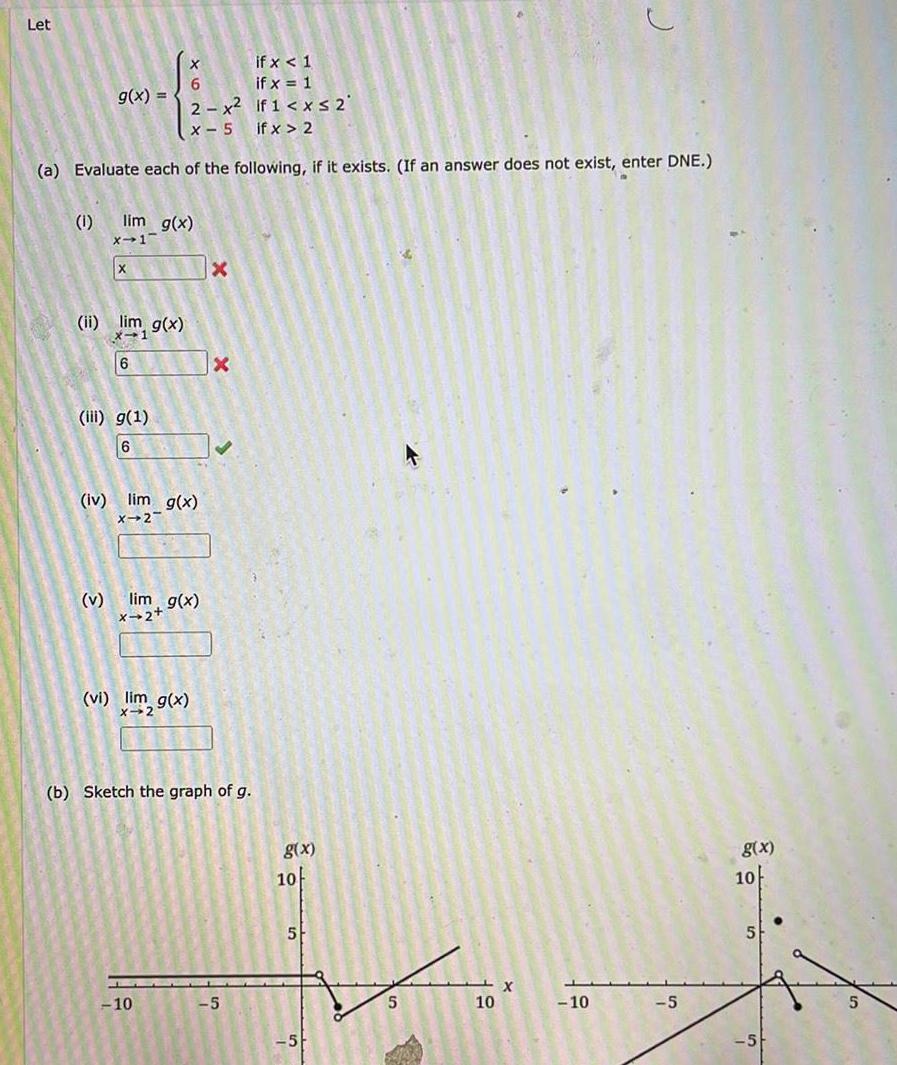
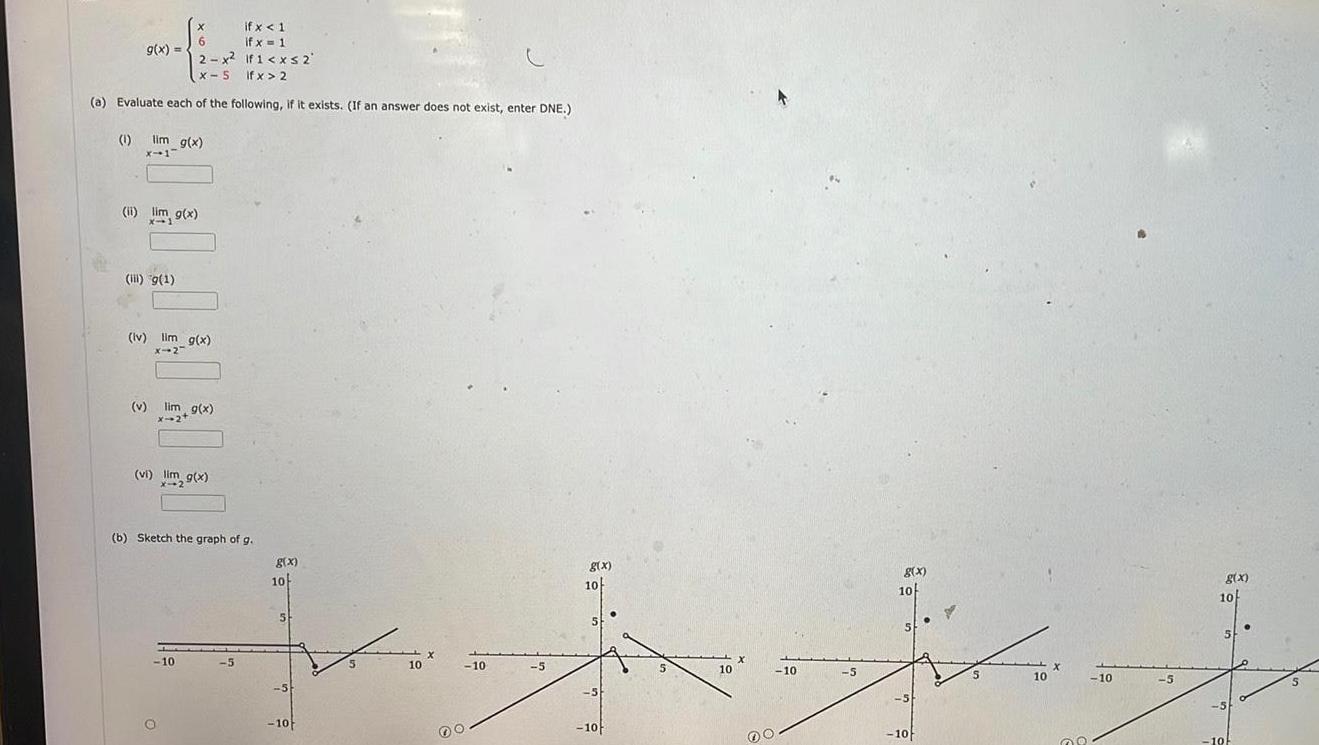
Application of derivativesLet if x 1 6 if x 1 2 x if 1 x 2 x 5 if x 2 a Evaluate each of the following if it exists If an answer does not exist enter DNE 1 g x lim g x x 1 v X ii lim g x x 1 6 iii g 1 6 iv lim g x X 2 lim g x x 2 vi lim g x X 10 Xx b Sketch the graph of g 5 g x 10 5 5 5 X 10 61 C 10 5 g x 10 5 5
Calculus
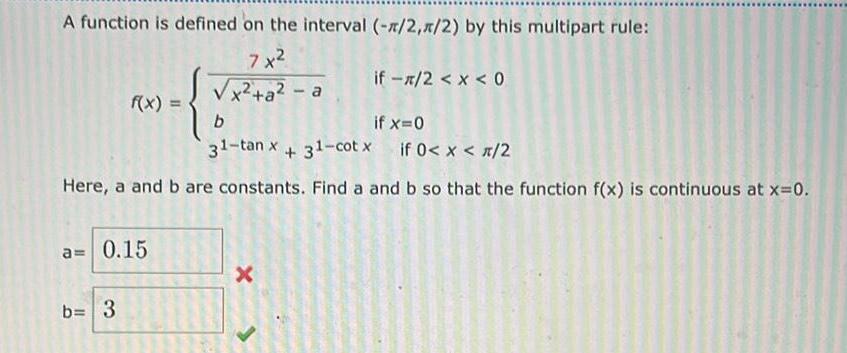
Limits & ContinuityA function is defined on the interval 2 1 2 by this multipart rule 7x x a a f x a 0 15 b 3 if x 0 31 tan x 31 cotx if 0 x 2 Here a and b are constants Find a and b so that the function f x is continuous at x 0 b if 2 x 0 X
Calculus
Application of derivativesLet f x cx if x 4 For what value of the constant c is the function f continuous on 0 Step 1 Recall that function is continuous at a number a if the following holds lim f x f a x10 We are given the following F x 2x Cx 3x If x 4 x cx if x 4 We note that for all values of the constant c the function f is continuous on both 4 and 4 The only case that we need to consider is when x 4 For the function f to be continuous on we need to ensure that there is not a discontinuity To do so we must determine the value of c such that the following holds lim f x lim f x X 44 x 4 Find the following limits lim f x lim cx 3x x 4 X 4 lim f x lim x cx x st x 4
Calculus
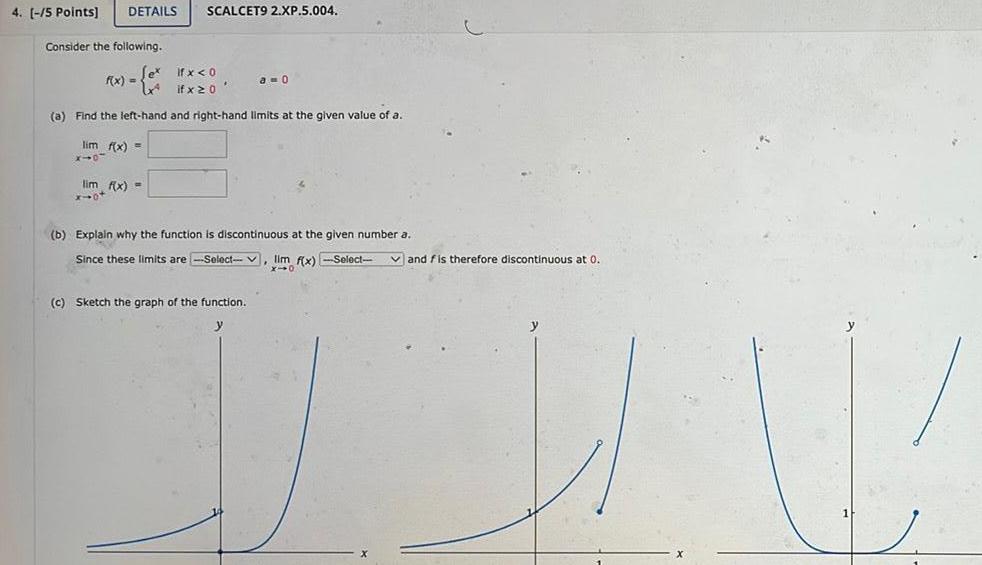
Limits & Continuity4 5 Points DETAILS SCALCET9 2 XP 5 004 Consider the following if x 0 if x 20 a Find the left hand and right hand limits at the given value of a lim f x X10 f x lim f x x ot a 0 b Explain why the function is discontinuous at the given number a Since these limits are Select lim f x Select c Sketch the graph of the function and fis therefore discontinuous at 0

Calculus
Application of derivativesA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t20 t is measured in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below I V t sin 2 A V t V 0 zt 2 t Sv x dx 0 b OC V t V 0 v t dt a V t 13 cos Find the volume function V assuming that V 0 14 L at 2 Type an exact answer b What is the breathingrate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs The tidal volume is liter s SOCCE t Sv x dx 0 OB V 0 V t b OD V 0 V t SV t dt a

Calculus
Definite IntegralsWhat is the difference between lim f x The limit as x approaches 3 and f 3 Z 3 B i US X x S EEE

Calculus
Definite IntegralsFor this question you should type which formula you should use simple compound annuity payout annuity loan You should also tell me which variable you will be solving for and you should type your final answer to two decimal places ALL OTHER WORK MUST BE ON PAPER YOU SEND TO ME so I can see you substituted into the equation properly and the steps you took to solve I need to know how much money will I need to have at retirement so I can withdraw 75 000 a year for 23 years from an account earning 4 compounded annually a How much do you need in your account at the beginning b How much total money will you pull out of the account c How much of that money is interest Formulas
Calculus
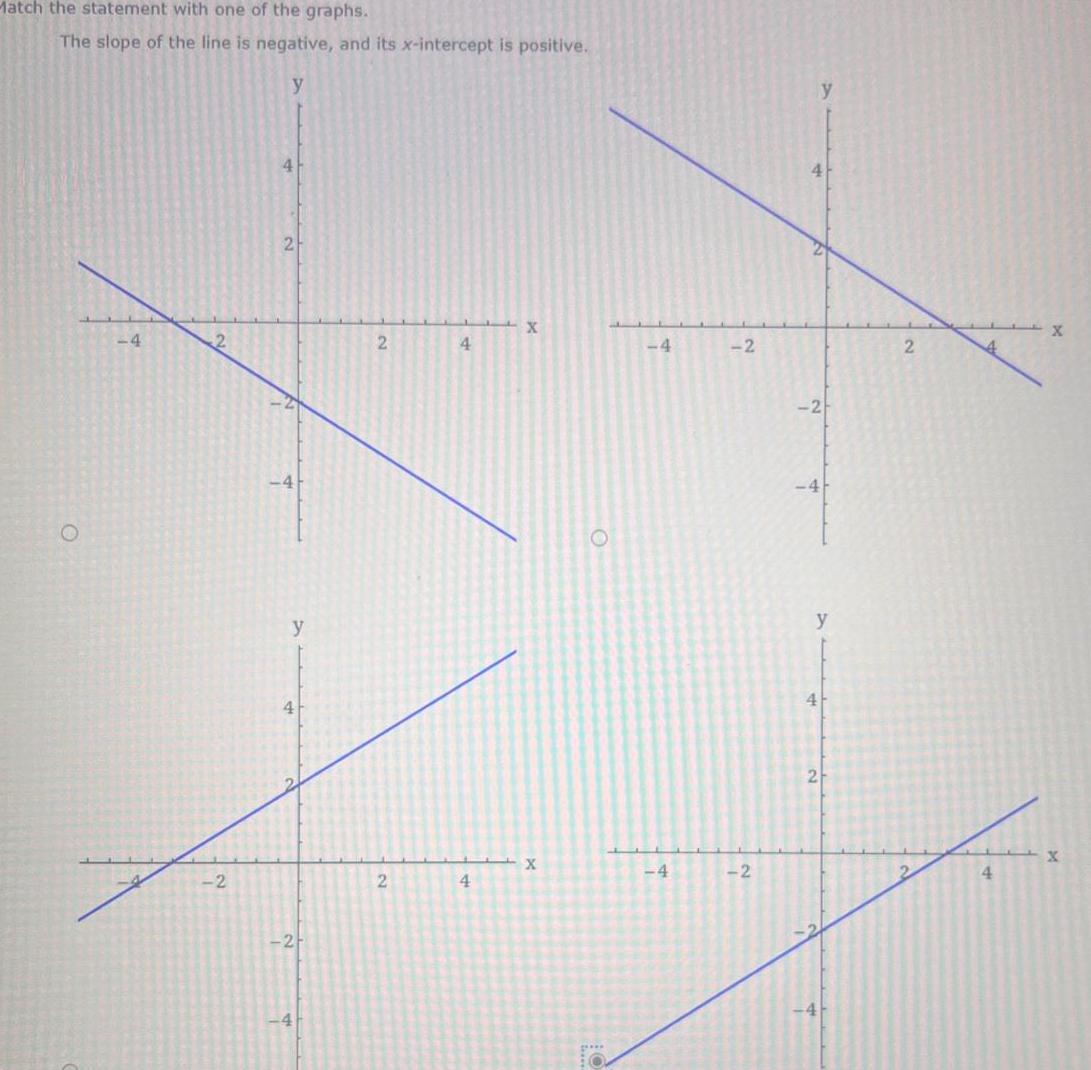
Limits & ContinuityMatch the statement with one of the graphs The slope of the line is negative and its x intercept is positive y 4 2 2 2 y 4 2 2 2 4 4 X X 4 4 2 2 4 y 2 y 4 2 2 4 X X

Calculus
Application of derivativesFor this question you should type which formula you should use simple compound annuity payout annuity loan You should also tell me which variable you will be solving for and you should type your final answer to two decimal places ALL OTHER WORK MUST BE ON PAPER YOU SEND TO ME so I can see you substituted into the equation properly and the steps you took to solve You deposit 2 500 in an account earning 3 25 interest compounded quarterly a How much will you have in 15 years b How much of that is interest Formulas
Calculus
Limits & Continuityif x 1 if x 1 2 x2 If1 xs 2 X 5 If x 2 a Evaluate each of the following if it exists If an answer does not exist enter DNE g x 1 lim g x x 1 ii lim g x X 1 ii g 1 lv lim g x x 2 v lim g x 124 X 2 vi lim g x b Sketch the graph of g 10 5 g x 10 5 5 10 fu 10 X 10 00 5 g x 10 5 5 10 5 10 X 00 10 5 g x 10 5 5 10 10 X 08 10 5 g x 10 10 5

Calculus
Limits & ContinuityEvaluate the limit if it exists If an answer does not exist enter DNE Hint Note the name of the question is double rationalize which you can see at the top right corner So you have rationalize the conjugate trick both the numerator and the denomina 12 x 2 24 x 4 lim x 8


Calculus
Differential equationsDetermine whether the statement is true or false lim x x245 5x 6 X 1 True False x 45X6 lim x 1 x 4x 5 lim x 4x 5 X 1
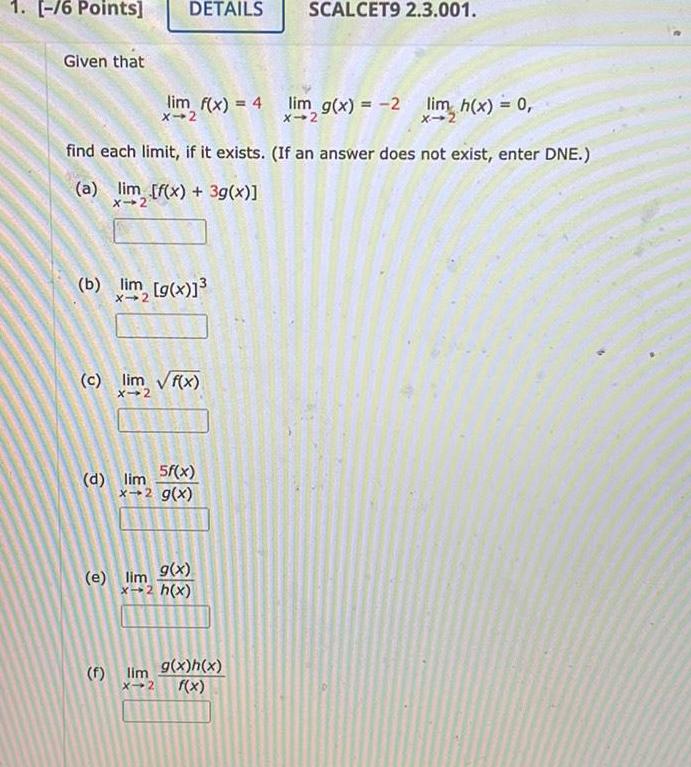
Calculus
Limits & Continuity1 6 Points Given that DETAILS lim f x 4 lim g x 2 lim h x 0 find each limit if it exists If an answer does not exist enter DNE a lim f x 3g x X 2 b lim g x c lim f x X 2 d lim 5f x x 2 g x e lim 9 x x 2 h x SCALCET9 2 3 001 f lim 9 x h x X 2 f x

Calculus
Definite IntegralsA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t 0 t is measured in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below V t sin 2 1 2 A V t V 0 v x dx 0 b OC V t V 0 v t dt V t 13 cos Find the volume function V assuming that V 0 14 L a at 2 Type an exact answer b What is the breathing rate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs The tidal volume is 7 3 2 liter s t OB V 0 V t t v x dx 0 b OD V 0 V t V t dt a

Calculus
Differentiation4 Each angle measure is given in radians Write the corresponding angle measure in degrees a 0 18 4 3 d 0 8 b 0 C 0 716

Calculus
Definite IntegralsConsider an object moving along a line with the following velocity and initial position v t 16 1 on 0 5 s 0 3 Determine the position function for t20 using both the antiderivative method and the Fundamental Theorem of Calculus Check for agreement between the two methods To determine the position function for t20 using the antiderivative method first determine how the velocity function and the position function are related Choose the correct answer below OA The position function is the absolute value of the antiderivative of the velocity function OB The position function is the derivative of the velocity function OC The velocity function is the antiderivative of the absolute value of the position function D The position function is the antiderivative of the velocity function Which equation below will correctly give the position function according to the Fundamental Theorem of Calculus b OA s t s 0 v t o Sv t dt C a t OC s 0 s t v x d v x dx 0 b fv t dt OB s t v t a OD s t s 0 t v x dx 0

Calculus
Differential equationsA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time 120 tis me in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is the tidal volume Complete parts a through c below V t T sin a Find the volume function V assuming that V 0 14 L Notice that V changes over time at a known rate V Which equation below correctly gives the volume function A V t V 0 V x dx Sv x d 0 OC V t V 0 at V t 13 cos at 2 b a Find the volume function V assuming that V 0 14 L t dt Type an exact answer COLLE b What is the breathing rate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs Sv x dx 0 OB V 0 V t b OD V 0 V t V t di fv t dt a

Calculus
Application of derivativesSet up a sum of two integrals that equals the area of the shaded region bounded by the graphs of the functions f and g on a c in the figure Assume the curves intersect at x b Choose the correct answer below b OB OA S x 9 C f x g x dx g x f x dx S g x f b b C f x 9 f x g x dx f x g x dx x S x a b b O C Sg x 1 x dx S x 9 b b g x dx BELLS y f x y g x
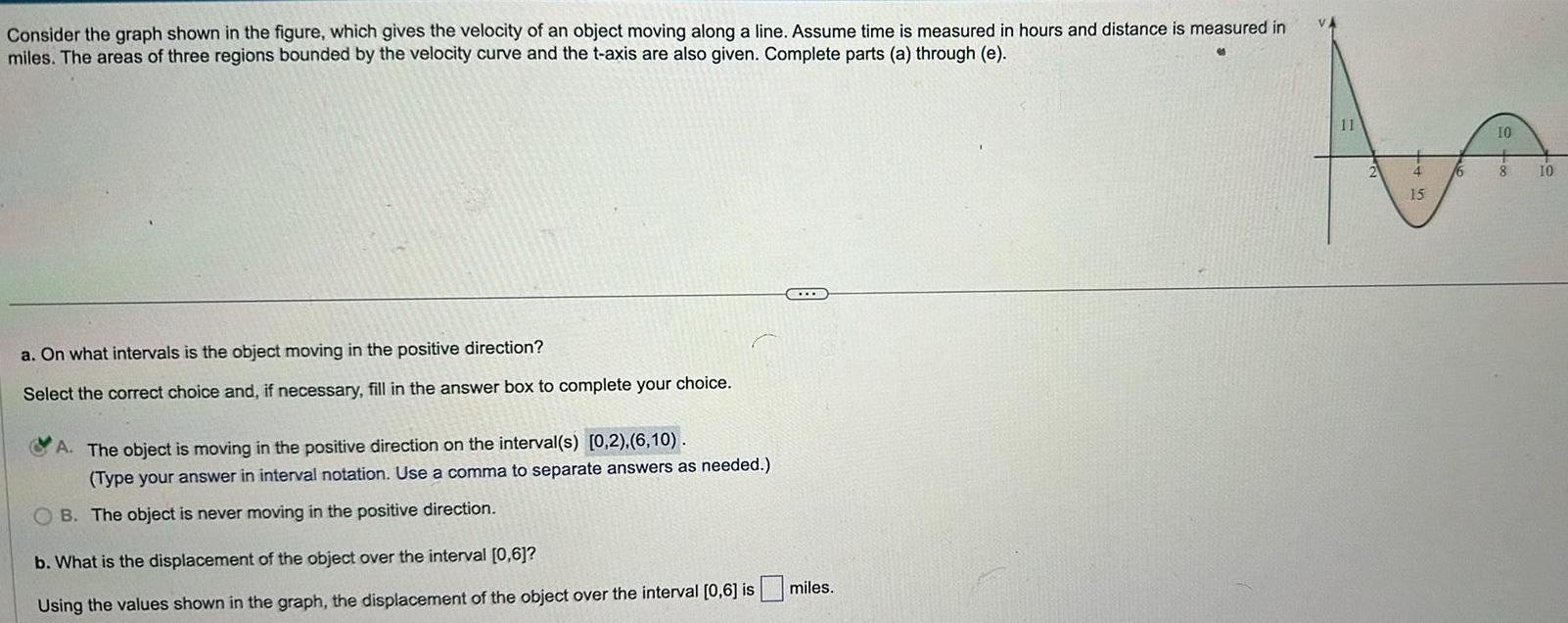
Calculus
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e a On what intervals is the object moving in the positive direction Select the correct choice and if necessary fill in the answer box to complete your choice A The object is moving in the positive direction on the interval s 0 2 6 10 Type your answer in interval notation Use a comma to separate answers as needed B The object is never moving in the positive direction STOR b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is miles 11 2 4 15 16 10 8 10
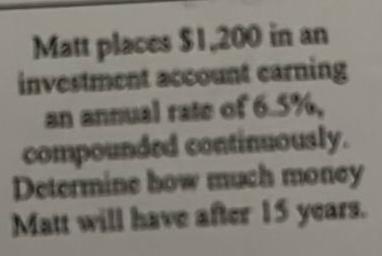
Calculus
Limits & ContinuityMatt places 1 200 in an investment account earning an annual rate of 6 5 compounded continuously Determine how much money Matt will have after 15 years
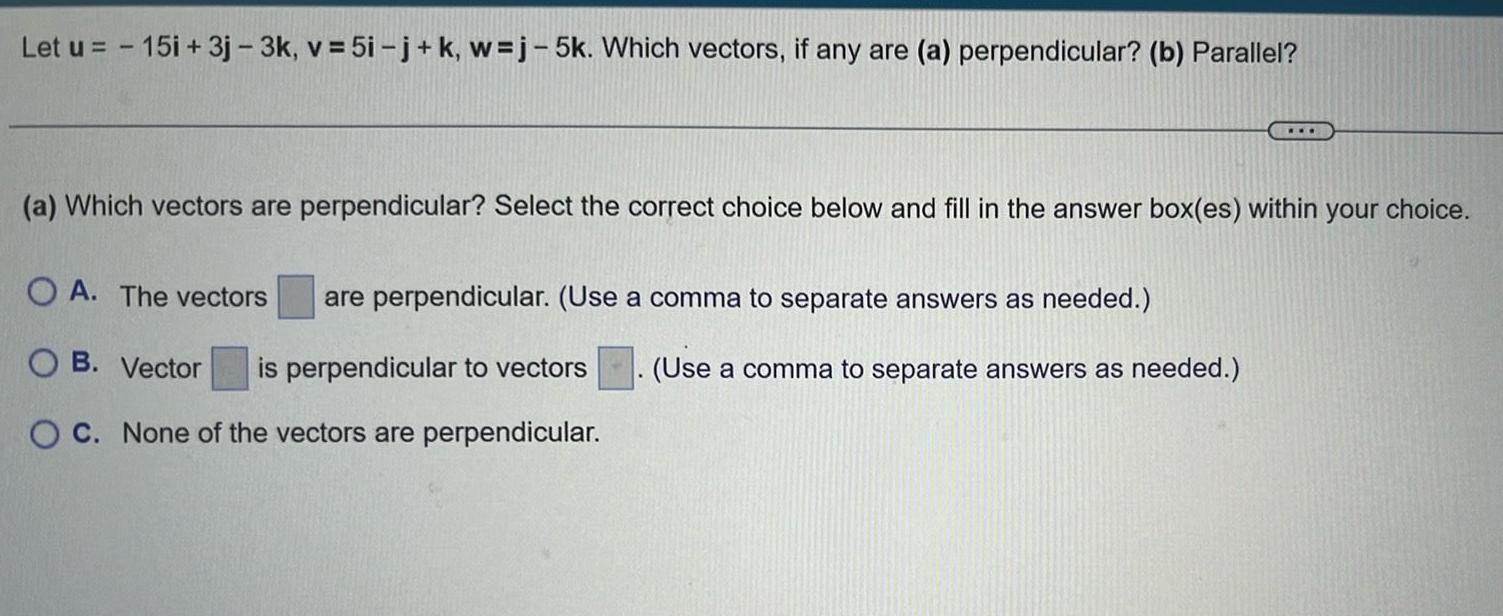
Calculus
Vector CalculusLet u 15i 3j 3k v 5i j k w j 5k Which vectors if any are a perpendicular b Parallel a Which vectors are perpendicular Select the correct choice below and fill in the answer box es within your choice OA The vectors OB Vector is perpendicular to vectors OC None of the vectors are perpendicular are perpendicular Use a comma to separate answers as needed Use a comma to separate answers as needed

Calculus
Vector Calculusrepresents due north What is the component form of the velocity of the airplane Round the final answer to one decimal place as needed WAP Find the component form of the velocity of the airplane assuming that the positive x axis represents due east and the positive y axis

Calculus
Vector CalculusSuppose that a box is being towed up an inclined plane as shown in the figure Find the force w needed to make the component of the force parallel to the inclined plane equal to 2 1 lb The force w is about lb Round to the nearest hundredth as needed W 33

Calculus
DifferentiationFind the length and direction when defined of u xv and vxu u 21 2j 3k v 3i 3k The length of uxvis 9 Type an exact answer using radicals as needed Select the correct choice below and if necessary fill in the answer boxes to complete your choice 1 3 Type exact answers using radicals as needed The direction of u xv is 2 3 i OB The direction of u xv is undefined j 2 3 The length of vx u is Type an exact answer using radicals as needed k

Calculus
DifferentiationFind the length and direction when defined of u xv and vxu u 2i 2j 3k v 3i 3k The length of u x v is Type an exact answer using radicals as needed
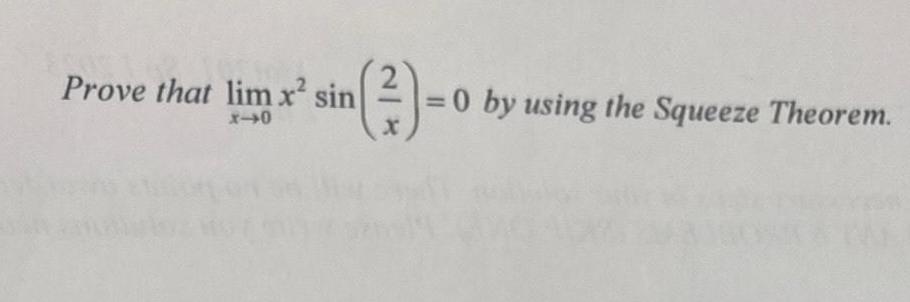
Calculus
Differentiation6 An angle in standard position has a measure of 5 8 radians In which quadrant is the terminal side of the angle

Calculus
Differential equations5 Each angle measure is given in degrees Write the corresponding angle measure in radians a 0 60 b 0 72 c 0 200 d 0 450
Calculus
Vector Calculuskr Consider an angle in standard position with a measure of radians for some integer constant k 6 Which of the following statements is true A If k is odd then the angle in degrees is a multiple of 60 B If k is odd then the angle in degrees cannot be a multiple of 45 C If k is even then the angle in degrees is a multiple of 60 D If k is even then the angle in degrees is a multiple of 90

Calculus
Vector Calculus8 Which of the following angles when graphed in standard position does NOT have a terminal side in the second quadrant A 200 B D 27T 5 8TT 11 4 100