Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Vector CalculusAn angle measure of x radians corresponds to an angle measure of 210 Find the value of x
Calculus
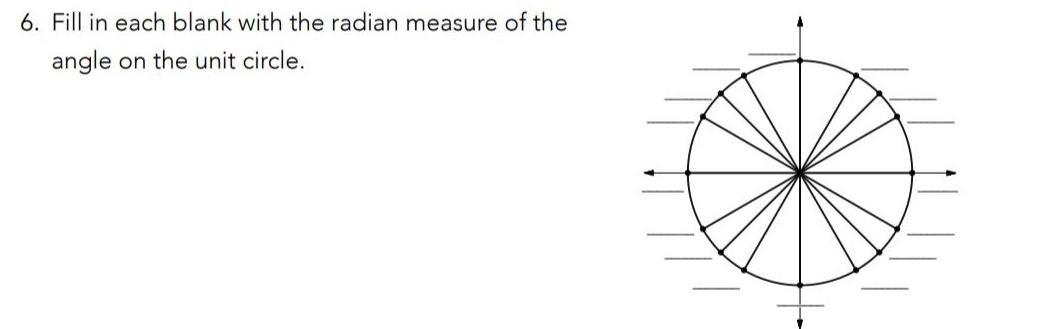
Indefinite Integration6 Fill in each blank with the radian measure of the angle on the unit circle
Calculus
Application of derivatives2 Consider a circle O with radius r How many arcs of length rare equal to the length of the following arcs a a semicircle of circle O b an arc that is three quarters of circle O

Calculus
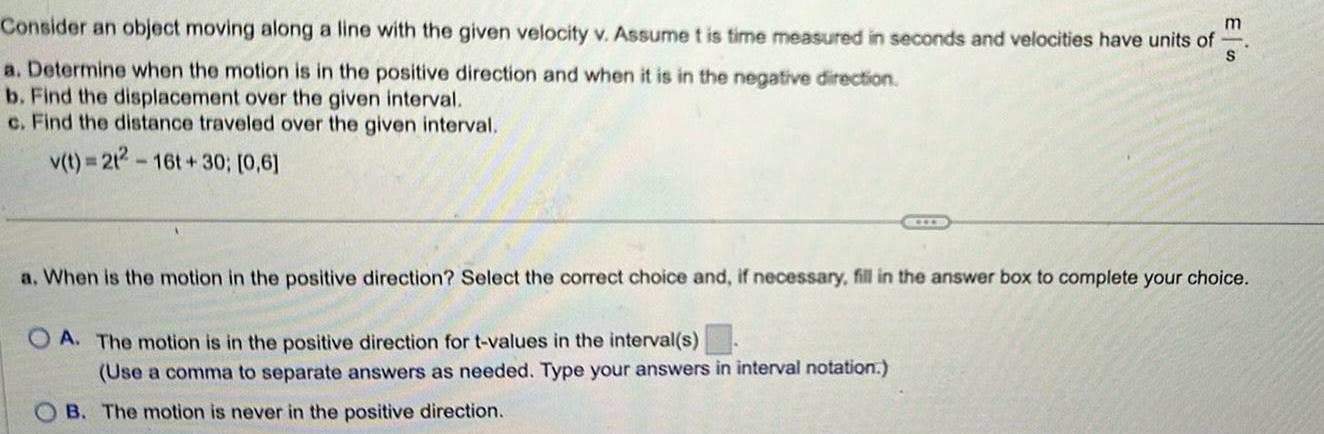
Definite IntegralsConsider an object moving along a line with the given velocity v Assume t is time measured in seconds and velocities have units of m S a Determine when the motion is in the positive direction and when it is in the negative direction b Find the displacement over the given interval c Find the distance traveled over the given interval v t 212 16t 30 0 6 a When is the motion in the positive direction Select the correct choice and if necessary fill in the answer box to complete your choice OA The motion is in the positive direction for t values in the interval s Use a comma to separate answers as needed Type your answers in interval notation OB The motion is never in the positive direction

Calculus
Vector Calculus3 At t 0 a train approaching a station begins decelerating from a speed of 160 mi hr according to the acceleration function a t 1280 1 4t 3 mi hr2 where t 0 How far does the train travel betwee t 0 and t 0 2 Between t 0 2 and t 0 5 Between t 0 and t 0 2 the train travels 49 78 mi Round to three decimal places as needed
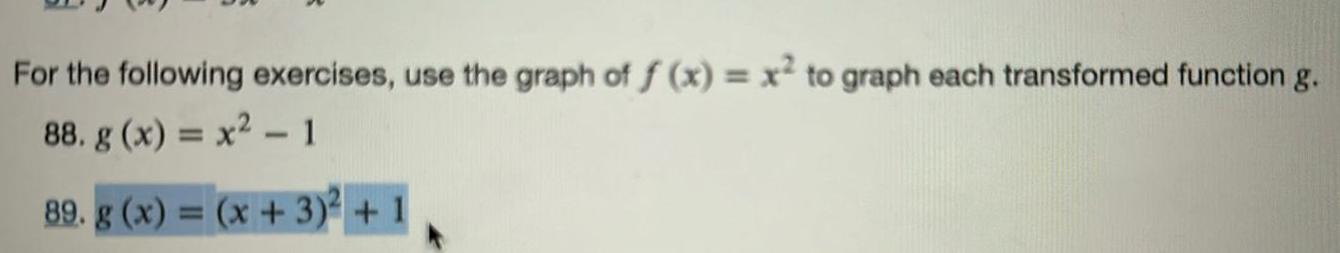
Calculus
Differential equationsFor the following exercises use the graph of f x x to graph each transformed function g 88 g x x 1 89 g x x 3 1

Calculus
Limits & Continuity66 1 4 and 1 0 For the following exercises write the equation of the line satisfying the given conditions in slope intercept form 67 Slope 6 passes through 1 3 68 Slope 3 passes through 3 2 69 Slope passes through 0 4 70 Slope x intercept 8 71 Passing through 2 1 and 2 1
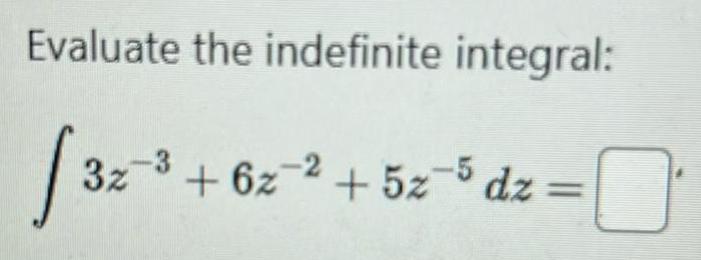

Calculus
Definite IntegralsFor the following exercises the position function of a ball dropped from the top of a 200 meter tall building is given by s t 200 4 9t where position s is measured in meters and time t is measured in seconds Round your answer to eight significant digits 16 T Compute the average velocity of the ball over the given time intervals a 4 99 5 b 5 5 01 c 4 999 5 d 5 5 001 17 Use the preceding exercise to guess the instantaneous velocity of the ball at t 5 sec
Calculus
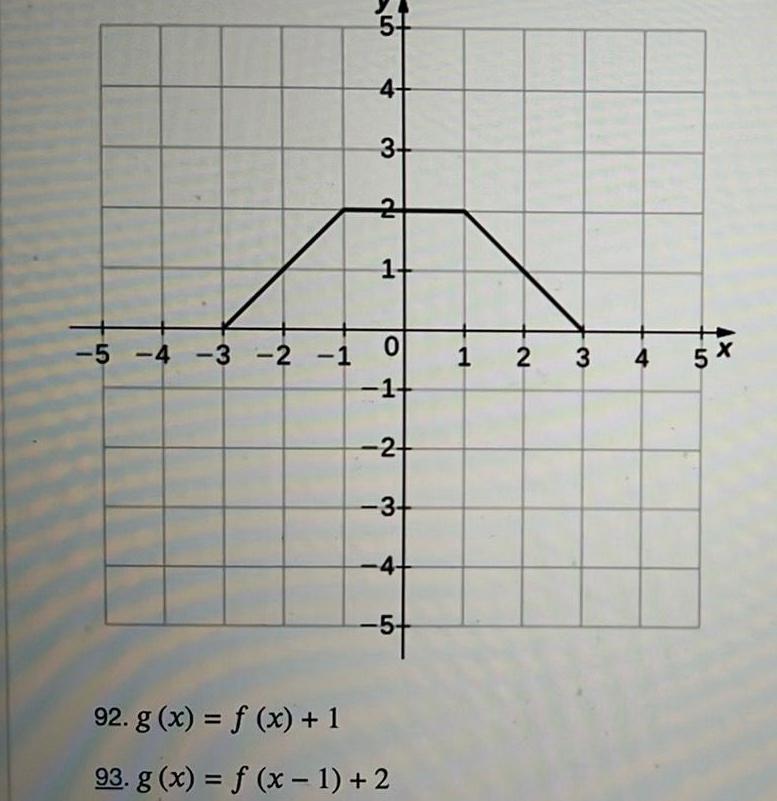
Application of derivatives5 4 3 2 1 5 4 3 2 1 0 14 2 3 4 5 92 g x f x 1 93 g x f x 1 2 1 2 3 4 5
Calculus
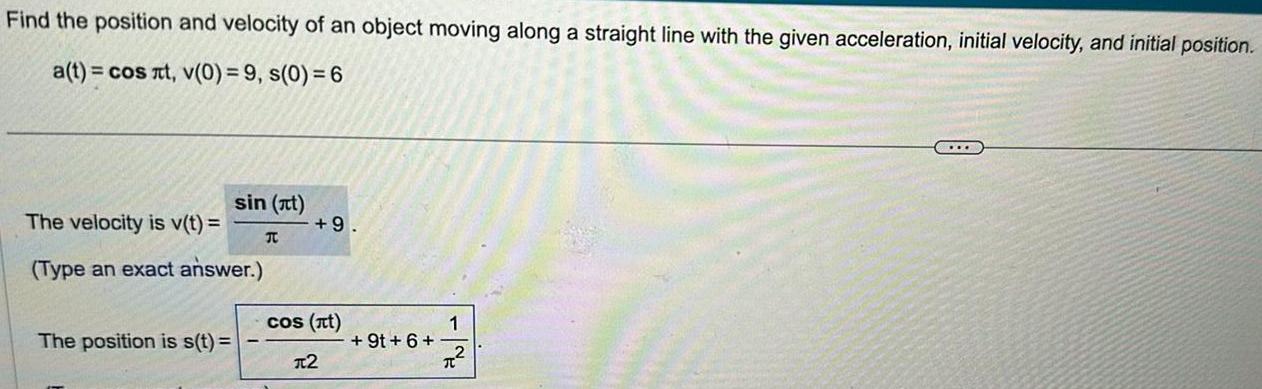
Differential equationsFind the position and velocity of an object moving along a straight line with the given acceleration initial velocity and initial position a t cos t v 0 9 s 0 6 sin it The velocity is v t Type an exact answer The position is s t T 9 cos t 2 9t 6 1 C

Calculus
Limits & ContinuityFor the following exercises for each of the piecewise defined functions a evaluate at the given values of the independent variable and b sketch the graph 4x 3 x 0 x 1 x 0 95 f x x 3 x 0 94 f x 96 h x 97 g x f 4 f 0 f 2 4x 3 x 0 x x 1 x 5 4 x 5 3 x 29 4 x 2 3 0 2 2 h 0 h h 5 g 0 g 4 g 2
Calculus
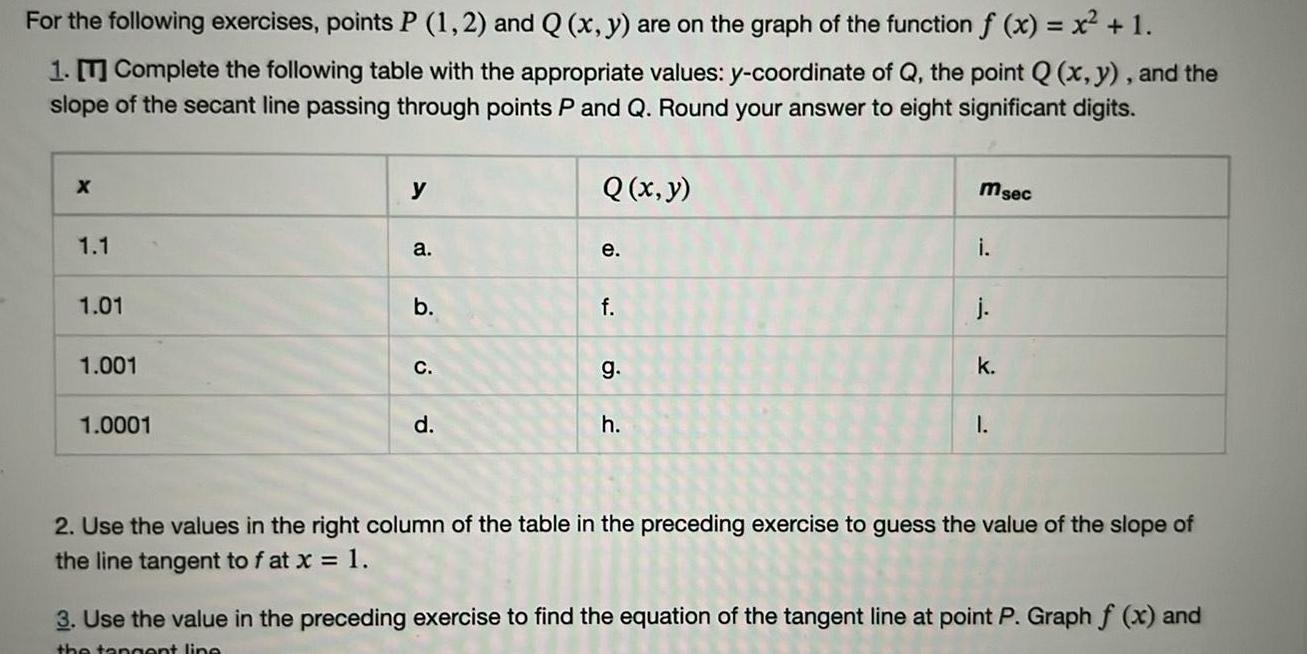
Application of derivativesFor the following exercises points P 1 2 and Q x y are on the graph of the function f x x 1 1 T Complete the following table with the appropriate values y coordinate of Q the point Q x y and the slope of the secant line passing through points P and Q Round your answer to eight significant digits X 1 1 1 01 1 001 1 0001 y a b C d Q x y e f g h Msec i j k I 2 Use the values in the right column of the table in the preceding exercise to guess the value of the slope of the line tangent to f at x 1 3 Use the value in the preceding exercise to find the equation of the tangent line at point P Graph f x and the tangent line

Calculus
Limits & ContinuityFind the position and velocity of an object moving along a straight line with the given acceleration initial velocity and initial positic a t cos at v 0 9 s 0 6 The velocity is v t Type an exact answer

Calculus
Indefinite IntegrationFind the position and velocity of an object moving along a straight line with the given acceleration initial velocity and initial position a t 64 v 0 50 and s 0 10 v t 64t 50 s t

Calculus
Limits & ContinuityThe total stopping distance T of a vehicle is shown below where T is in meters and x is the speed in kilometers per hour T 0 39x 0 006x Approximate the change and percent change in total stopping distance as speed changes from x 25 to x 28 kilometers per hour Round the percent change in total stopping distance to one decimal place dT x m X dT T m jaarna

Calculus
Limits & ContinuityFor the following exercises for each pair of functions find a f g x and b g f x Simplify the results Find the domain of each of the results 42 f x 3x g x x 5 43 f x x 4 g x 4x 1 44 f x 2x 4 g x x 2 45 f x x 7 g x x 3 46 f x x g x x 9 47 f x 2x18 x 48 f x x 11 g x x x 4

Calculus
Indefinite IntegrationFor the following exercises for each pair of functions find a f g x and b g f x Simplify the results Find the domain of each of the results 42 f x 3x g x x 5 43 f x x 4 g x 4x 1 44 f x 2x 4 g x x 2 45 f x x 7 g x x 3 46 f x x g x x 9 3 47 f x 2 8 x 2x 12 48 f x x 11 g x x x 4

Calculus
Indefinite Integration2 5 pts Prove 1 of the following identities for all permissible values of the variable Clearly YAMA AT indicate which identity the selected identity and the chosen side State any non permissible values A 1 sin x cos x cos x tan x tan x 1 B sinx cosx cos x sinx cosx secx csc x sinx 3 Solve the following equation for in the units specified Give the general form and solve for the specified domain Give exact solutions State any non permissible values 2 sin 0 tan 0 cos 0 1 0 F 3
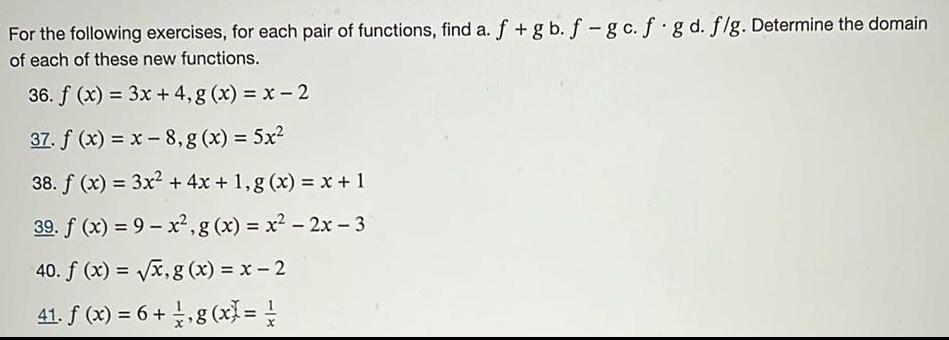
Calculus
Application of derivativesFor the following exercises for each pair of functions find a f gb f gc f g d f g Determine the domain of each of these new functions 36 f x 3x 4 g x x 2 37 f x x 8 g x 5x 38 f x 3x 4x 1 g x x 1 39 f x 9 x g x x 2x 3 40 f x x g x x 2 41 f x 6 g x

Calculus
Definite IntegralsEvaluate int 1 3 y d x where the values of y at regular intervals of are given as follows Table 13 3 begin tabular hline 1 2 3 4 5 6 7 8 91 hline x 1 0 1 25 1 50 1 75 2 00 2 25 2 50 2 75 3 00 hline y 2 45 2 80 3 44 4 20
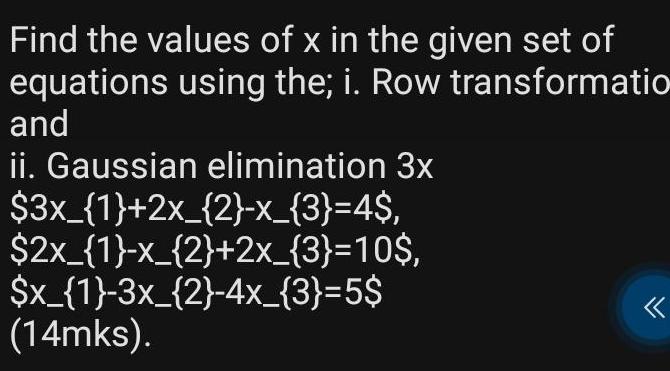
Calculus
Vector CalculusFind the values of x in the given set of equations using the i Row transformatio and ii Gaussian elimination 3x 3x 1 2x 2 x 3 4 2x 1 x 2 2x 3 10 x 1 3x 2 4x 3 5 14mks

Calculus
Application of derivativesThe velocity of a fast automobile on a straight highway is given by the function shown where t is measured in seconds and v has units of m s a Graph the velocity function for Osts 100 When is the velocity a maximum When is the velocity zero b What is the distance traveled by the automobile in the first 25 s c What is the distance traveled by the automobile in the first 75 s d What is the position of the automobile whent 90 OA AV 50 50 00 OB Av On 50 50 100 G OA At the specific time s t Use a comma to separate answers as needed OC 50 When is the velocity a maximum Select the correct choice and fill in the answer box to complete your choice 50 100 OA At the specific time s t Use a comma to separate answers as needed B At all values of t in the interval s 20 55 Type your answer in interval notation Use a comma to separate answers as needed When is the velocity zero Select the correct choice and fill in the answer box to complete your choice 21 v t 40 unur oft in the interval s Type your answer in interval notation Use a comma to separate answers as needed if 0 t 20 if 20 t 55 150 2t t255 D 50 50

Calculus
Limits & Continuitya Dylan teint un meuble en bois Il a besoin de 12 ml de teinture pour recouvrir 100 cm On s int resse la relation entre la superficie teindre et la quantit de teinture n cessaire b Pour l anniversaire de Liam sa m re a achet un g teau de 525 g qu elle veut partager de fa on gale entre tous les invit s On s int resse la relation entre le nombre d invit s et la quantit de g teau par personne
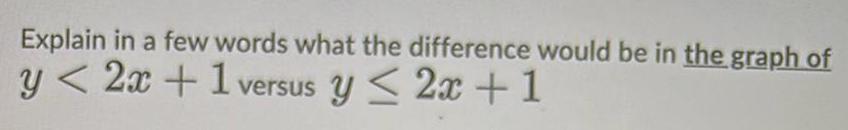
Calculus
Limits & ContinuityExplain in a few words what the difference would be in the graph of y 2x 1 versus y 2x 1

Calculus
Vector CalculusGiven the system of inequalities x 2y 10 3x 4y 0 x 0 V 0 A GRAPH THE SYSTEM ON A SHEET OF PAPER be sure to shade the appropriate region 15 points B List all of the vertices 10 points C Is the graph bounded or unbounded 10 pointe

Calculus
Differential equationsA rancher raises goats and llamas on her 500 acre ranch Each goat needs 3 acres of land and requires 100 of veterinary care per year and each llama requires 5 acres of land and requires 120 of veterinary care per year The rancher can afford no more than 11 700 for veterinary care this year If the expected profit is 60 for each goat and 100 for each llama how many type of each animal should she raise to obtain the maximum profit SET UP BUT DO NOT SOLVE BE SURE TO PUT YOUR MAXIMIZE OR MINIMIZE EQUATION ALSO
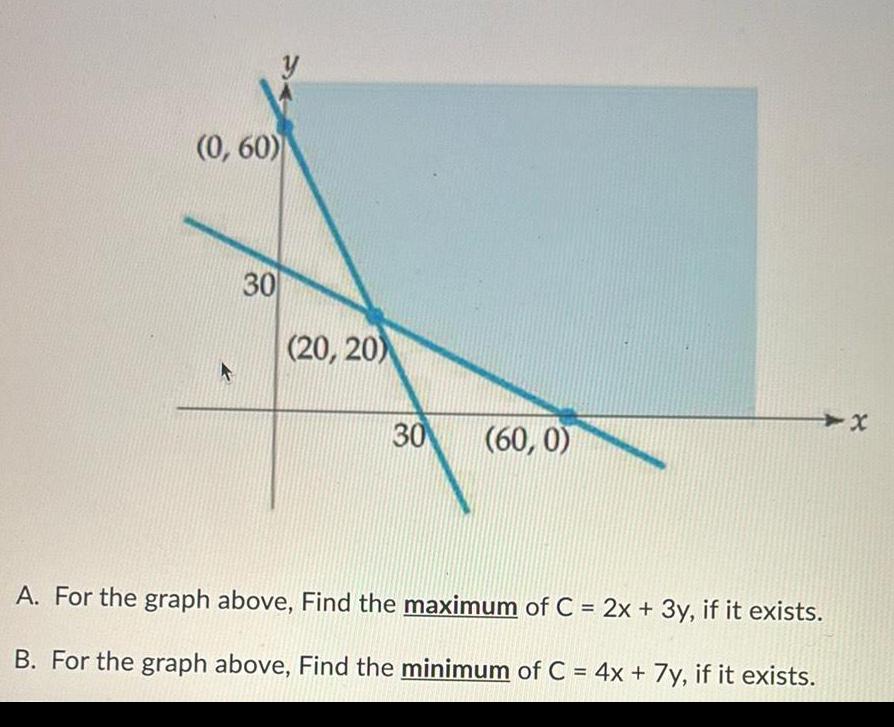
Calculus
Application of derivatives0 60 k 30 20 20 30 60 0 A For the graph above Find the maximum of C 2x 3y if it exists B For the graph above Find the minimum of C 4x 7y if it exists

Calculus
Application of derivativest Starting with an initial value of P 0 50 the population of a prairie dog community grows at a rate of P t 40 in units of prairie dogs month for 0 t 200 5 a What is the population 11 months later b Find the population P t for Ost 200
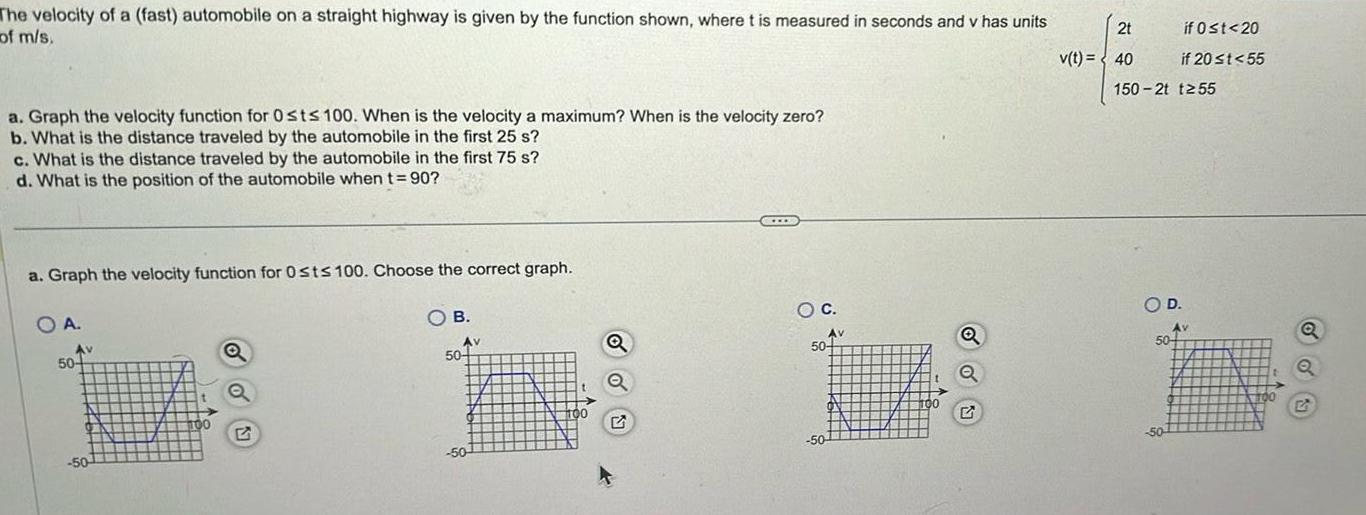
Calculus
Application of derivativesThe velocity of a fast automobile on a straight highway is given by the function shown where t is measured in seconds and v has units of m s a Graph the velocity function for Osts 100 When is the velocity a maximum When is the velocity zero b What is the distance traveled by the automobile in the first 25 s c What is the distance traveled by the automobile in the first 75 s d What is the position of the automobile when t 90 a Graph the velocity function for Osts 100 Choose the correct graph O B OA Av 50 50 Q Av 50 50 100 Q O C Av 50 50 00 Q Q 2t v t 40 150 2t t255 if 0 t 20 if 20 t 55 O D 50 50 Av TOO Q
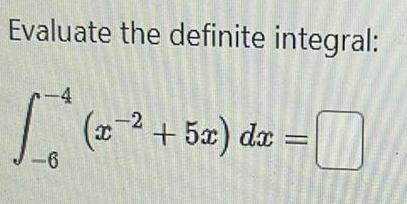
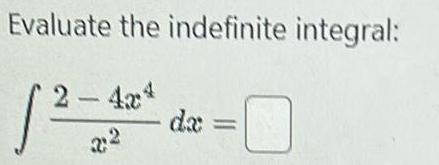


Calculus
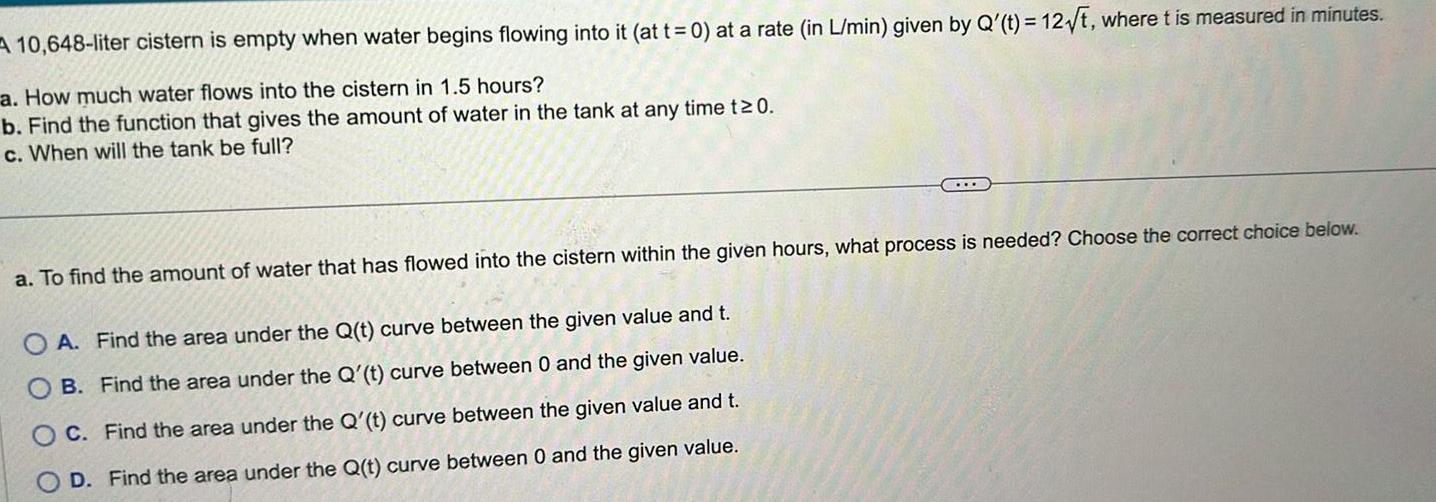
Application of derivatives10 648 liter cistern is empty when water begins flowing into it at t 0 at a rate in L min given by Q t 12 t where t is measured in minutes a How much water flows into the cistern in 1 5 hours b Find the function that gives the amount of water in the tank at any time t 0 c When will the tank be full a To find the amount of water that has flowed into the cistern within the given hours what process is needed Choose the correct choice below OA Find the area under the Q t curve between the given value and t B Find the area under the Q t curve between 0 and the given value C Find the area under the Q t curve between the given value and t D Find the area under the Q t curve between 0 and the given value


Calculus
Definite IntegralsUse the Evaluation Theorem to decide if the definite integral exists and either evaluate the integral or enter DNE if it does not exist 1 6 6 x x dx

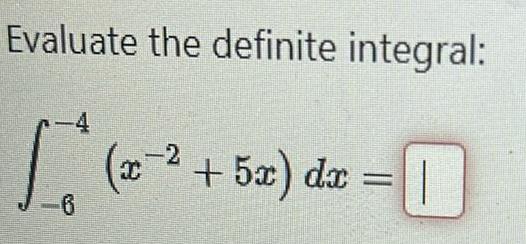

Calculus
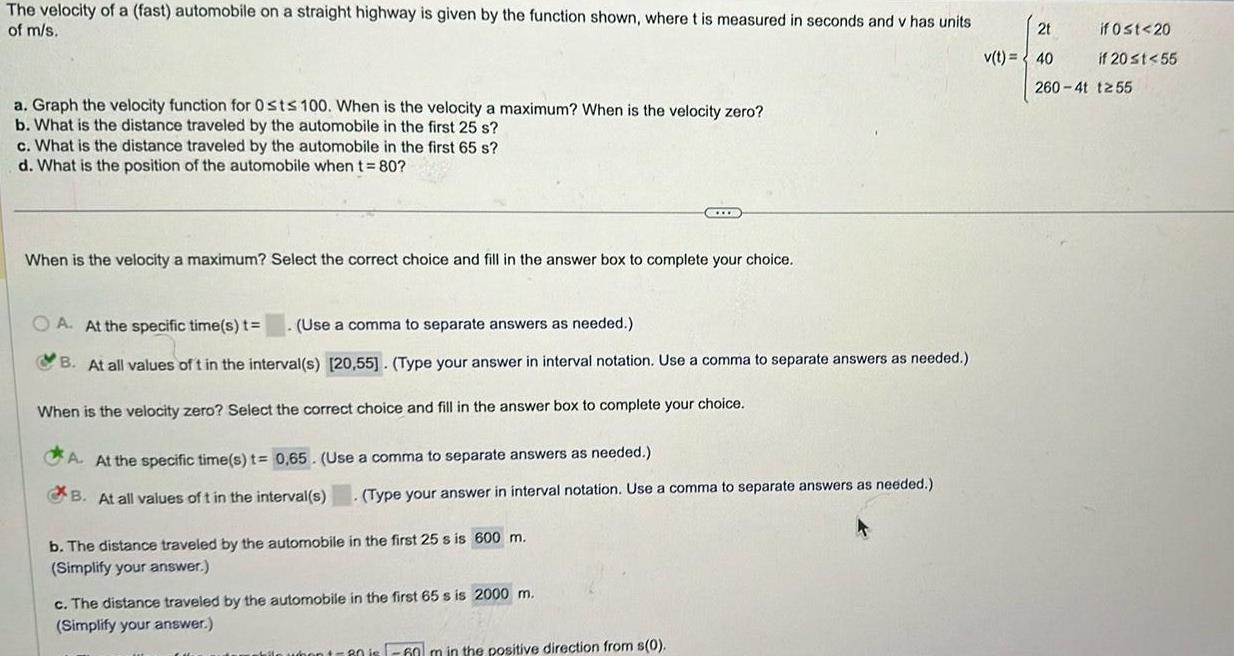
Definite IntegralsThe velocity of a fast automobile on a straight highway is given by the function shown where t is measured in seconds and v has units of m s a Graph the velocity function for Osts 100 When is the velocity a maximum When is the velocity zero b What is the distance traveled by the automobile in the first 25 s c What is the distance traveled by the automobile in the first 65 s d What is the position of the automobile when t 80 When is the velocity a maximum Select the correct choice and fill in the answer box to complete your choice A At the specific time s t Use a comma to separate answers as needed B At all values of t in the interval s 20 55 Type your answer in interval notation Use a comma to separate answers as needed When is the velocity zero Select the correct choice and fill in the answer box to complete your choice CELCB A At the specific time s t 0 65 Use a comma to separate answers as needed B At all values of t in the interval s Type your answer in interval notation Use a comma to separate answers as needed b The distance traveled by the automobile in the first 25 s is 600 m Simplify your answer c The distance traveled by the automobile in the first 65 s is 2000 m Simplify your answer 60 m in the positive direction from s 0 2t v t 40 if 0 t 20 if 20 t 55 260 4t 1255
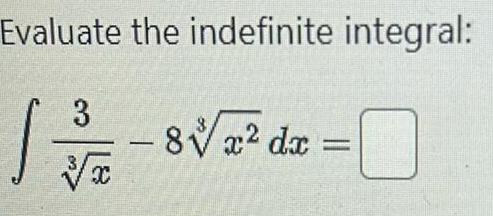

Calculus
Application of derivativesA population of cattle is increasing at a rate of 600 80t per year where t is measured in years By how much does the population increase between the 6 th and the 9 th years Total Increase
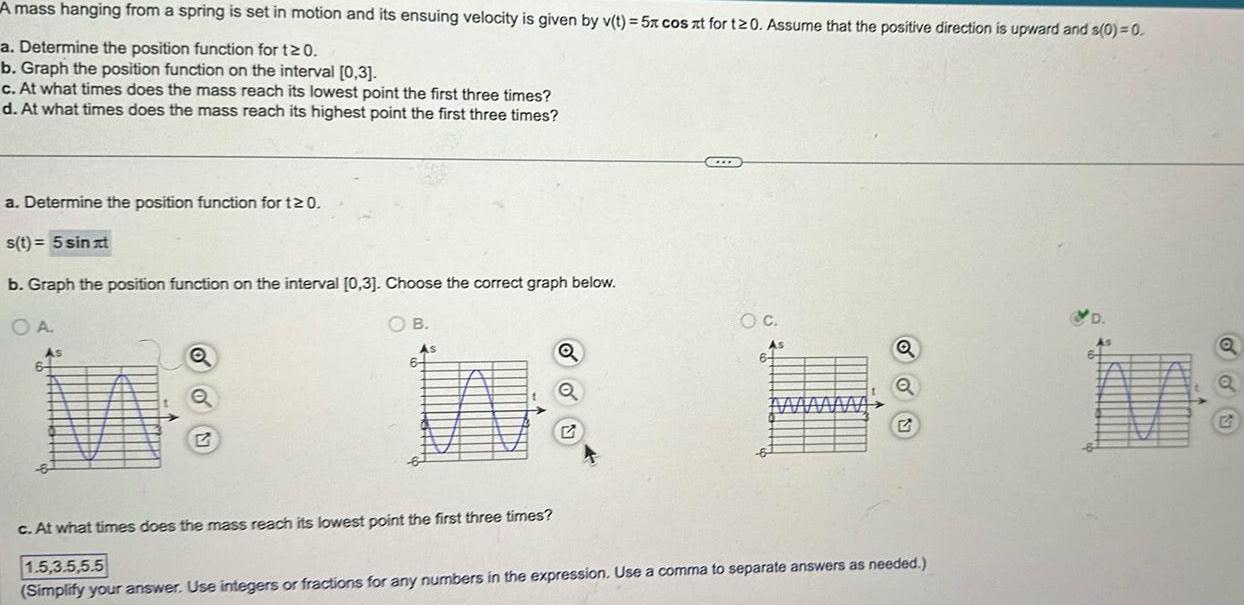
Calculus
Application of derivativesA mass hanging from a spring is set in motion and its ensuing velocity is given by v t 5x cos xt for t20 Assume that the positive direction is upward and s 0 0 a Determine the position function for t20 b Graph the position function on the interval 0 3 c At what times does the mass reach its lowest point the first three times d At what times does the mass reach its highest point the first three times a Determine the position function for 120 s t 5 sinat b Graph the position function on the interval 0 3 Choose the correct graph below OA As 6 Q B As 6 Q C O C As MAMA Q Q c At what times does the mass reach its lowest point the first three times 1 5 3 5 5 5 Simplify your answer Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed D in Q

Calculus
Definite IntegralsA mass hanging from a spring is set in motion and its ensuing velocity is given by v t 5x cos t for t 0 Assume that the positive direction is upward and s 0 C a Determine the position function for t 0 b Graph the position function on the interval 0 3 c At what times does the mass reach its lowest point the first three times d At what times does the mass reach its highest point the first three times

Calculus
Application of derivativesPower and energy are often used interchangeably but they are quite different Energy is measured in units of joules J or Calories Cal where 1 Cal 4184 J On the other hand power is the rate at which energy is used and is measured in watts W 1 W 1 J s Other useful units of power are kilowatts kW and megawatts 1 MW 106 W If energy is used at a rate of 1 kW for 1 hr the total amount of energy used is 1 kilowatt hour kWh which is 3 6x 106 J Suppose the power function of a large city over a 24 hr period is given by P t E t 255 170 sin t 12 where P is measured in MW and t 0 corresponds to 6 00 p m see accompanying figure Complete parts a through d below Click the icon to view the graph of P t E t 255 170 sin t 12 C a How much energy is consumed by this city in a typical 24 hr period Express the answer in MWh and in J The energy consumed in a typical 24 hour period in MWh is 6120 MWh Simplify your answer 13 The energy consumed in a typical 24 hour period in J is 2 2032 10 J Simplify your answer Use scientific notation b Burning 1 kg of coal produces about 450 kWh of energy How many kg of coal are required to meet the energy needs of the city for 1 day For 1 yr The amount of coal needed in a day is kg

Calculus
Definite IntegralsA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t20 tis measured in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below V t H sin 2 a Find the volume function V assuming that V 0 14 L Notice that V changes over time at a known rate V Which equation below correctly gives the volume function t OA V t V 0 V x dx Sv x dx 0 b OC V t V 0 v t dt a OB V 0 V t Sv x dx 0 b OD V 0 V t v t dt

Calculus
Application of derivativesPower and energy are often used interchangeably but they are quite different Energy is measured in units of joules J or Calories Cal where 1 Cal 4184 J On the other hand power is the rate at which energy is used and is measured in watts W 1 W 1 J s Other useful units of power are kilowatts kW and megawatts 1 MW 106 W If energy is used at a rate of 1 kW for 1 hr the total amount of energy used is 1 kilowatt hour kWh which is 3 6 x 106 J Suppose the power function of a large city over a 24 hr period is given by P t E t 255 170 sin t 12 where P is measured in MW and t 0 corresponds to 6 00 p m see accompanying figure Complete parts a through d below Click the icon to view the graph of P t E t 255 170 sin t 12 a How much energy is consumed by this city in a typical 24 hr period Express the answer in MWh and in J The energy consumed in a typical 24 hour period in MWh is MWh Simplify your answer