Indefinite Integration Questions and Answers

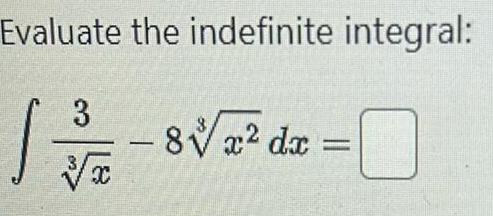

Calculus
Indefinite IntegrationFind the rational function s asymptotic x intercepts and holes Also sketch the graph of the rational function Then list the domain and range using interval notation Hint x 4 is a difference of two squares a b a b a b f x 3x 6x x 4 7

Calculus
Indefinite IntegrationFind the extremals for f y dx subject to the condition Sydx 3 y 0 1 y 1

Calculus
Indefinite IntegrationUse the given graphs of the function f left in blue and g right in red to find the following limits 1 lim f x g x help limits 2 lim f x g x 3 lim f x g x 2 0 f x z 0 g x 4 lim 5 lim 24 1 3 f x 1 0 qz 3 3

Calculus
Indefinite IntegrationEvaluate the integral 0x 81 sec 0 Ox 9 tan 0 x 9 sin 0 Ox 81 tan 0 Ox 9 sec 0 A Which trig substitution is correct for this integral O x 81 sin 0 282 1 cot 0 81 x dx B Which integral do you obtain after substituting for and simplifying Note to enter type the word theta 1134 sin de C What is the value of the above integral in terms of 0 D What is the value of the original integral in terms of x 1 1 x sin 2 sin x 1 2 4 C C










Calculus
Indefinite IntegrationProblem 30 1 point If f t 7 1 sin t 6 cos t and f 0 5 find f A 128 D 131 C 130 B 129 E 132

Calculus
Indefinite IntegrationIsy 19x a solution of the differential equation dx Explain BOCCOD The function y 19x a solution of the differential equation because when it is substituted into the differential equation side of the equation is equal to and the right side of the equation is equal to Simplify your answers

Calculus
Indefinite IntegrationFind the integral by whatever means are necessary either substitution or tables Remember to use absolute values where appropriate Use C for the constant of integration 1 25 x X dx 25 x In 25 1 5 25 x 5 CX

Calculus
Indefinite IntegrationFind the integral Hint Separate the integral into two integrals using the fact that the numerator is a sum or difference and find the two integrals by two different formulas Remember to use absolute values where appropriate Use C for the constant of integration 1 x 9 x 0 dx

Calculus
Indefinite IntegrationFind the integral by whatever means are necessary either substitution or tables Remember to use absolute values where appropriate Use C for the constant of integration 1 25 X dx X

Calculus
Indefinite IntegrationFind the indefinite integral Use C for the constant of integration Remember to use absolute values where appropriate e av x dx X

Calculus
Indefinite IntegrationFind the indefinite integral Use C for the constant of integration Remember to use absolute values where appropriate 45x 45x2 3x1 30e x dx

Calculus
Indefinite IntegrationDecember 15 2023 1 Integrate the following expressions a S 5x x 12 dx b S 5x 4x dx odnalgus oils gaivlover vd basera x 2x 2 A ball is rolling down a slope with an acceleration noget up J21 up J2ift ori sins veri 01 10802 Tir 1080251 3w elxs t a 4 2t where t is the time in s Find the bal f time if v 5 m s when t 0 babnued noigeted to abiono s ruod





Calculus
Indefinite Integration72 sin 2x 3 dx A cos 2x 3 C B cos 2x 3 C C cos 2x 3 D cos 2x 3 C 1 E cos 2x 3 C

Calculus
Indefinite Integration10 If y is implicitly defined by 4 cos x sin y 1 Then y A 1 4 1 1 sin x cos y bb C 1 4 tan x tan y D E tan r tan u B tan x tan y edmuntadt 50 sin y cos x

Calculus
Indefinite IntegrationYou go to the doctor and he gives you 17 milligrams of radioactive dye After 12 minutes 8 milligrams of dye remain in your system To leave the doctor s office you must pass through a radiation detector without sounding the alarm If the detector will sound the alarm if more than 2 milligrams of the dye are in your system how long will your visit to the doctor take assuming you were given the dye as soon as you arrived Give your answer to the nearest minute You will spend minutes at the doctor s office


Calculus
Indefinite IntegrationCalculate the indicated Riemann sum S4 for the function f x 34 4x Partition 0 12 into four subintervals of equal length and for each subinterval X 1X let c 2xx 1 xx 3 SA Simplify your answer SKELB





Calculus
Indefinite IntegrationFind the integral by using the integral table on the inside back cover Remember to use absolute values where appropriate Use C for the constant of integration 1 Z 25 2 dz

Calculus
Indefinite IntegrationFind the integral by using the integral table on the inside back cover Remember to use absolute values where appropriate Use C for the constant of integration x 36 dx

Calculus
Indefinite IntegrationFind the integral by using the integral table on the inside back cover Hint Use formula 15 with a 4 Use C for the constant of integration Remember to use absolute values where appropriate 1 x 16 dx

Calculus
Indefinite IntegrationFind the integral by using the integral table on the inside back cover Use C for the constant of integration Remember to us absolute values where appropriate x 1 x 9 dx


Calculus
Indefinite IntegrationConsider the function f t 5 sec t 4t Let F t be the antiderivative of f t with F 0 0 32 Then F 2 5 tan 2 OF

Calculus
Indefinite IntegrationUse Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function tanz S 6t t dt

Calculus
Indefinite IntegrationUse Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function 5 7 1 t 7 g x Question Help dt Video Message instructor



Calculus
Indefinite Integration2 Find I cos 0 sin 0 de 10 9 19 slingbaon do pilog off mot sa om my moldog nivellot si to lis od anoitourten evinson 1 1 tl dusze eld amplas haditios I tomusob eids gningiz va ogbolT ala orozite of qlod obivorq ton bib S bus ou widton hib bus avdellve od ni vjes


Calculus
Indefinite IntegrationUse a graphing calculator to find where the curves intersect and to find the area between the curves y ex y 3x 5x a The left point of intersection is Type integers or decimals rounded to the nearest thousandth as needed Type an ordered pair

Calculus
Indefinite IntegrationMonthly sales of a particular personal computer are expected to decline at a rate of S t 5te lt computers per month where t is time in months and S t is the number of computers sold each month The company plans to stop manufacturing this computer when monthly sales reach 900 computers If monthly sales now t 0 are 2 000 computers find S t How long to the nearest month will the company continue to manufacture the computer S t