Indefinite Integration Questions and Answers

An individual needs a daily supplement of at least 385 units of vitamin C and 240 of vitamin E and agrees to obtain this supplement by eating two foods I and II Each ounce of food 1 contains 70 units of vitamin C and 15 units of vitamin E while each ounce of food II contains 35 units of vitamin C and also 30 units of vitamin E The total supplement of these two foods must be at most 30 ounces Unfortunately food I contains 31 units of cholesterol per ounce and food II contains 25 units of cholesterol per ounce Find the appropriate amounts of the two food supplements so that cholesterol is minimized Find the minimum amount of cholesterol amount of food I oz amount of food II 02 minimum cholesterol units

the complex number in trigonometric form where r is exact and 0 0 2 Select the correct choice below and if necessary fill in the answer boxes to complete your choice Simplify your answer Type an integer or a simplified fraction Type any angle measures in radians OA 7 sin i cos OB 7 cos C 7 OD 7 cos sin M i sin i sin ww i cos

Find s t where s t represents the position function v t represents the velocity function and a t represents the acceleration function a t 301 6 with v 0 5 and s 0 8

10The mouse is a particularly useful model for studying human disease because mice and humans are 100 genetically a identical all mice are in essence clones mice do not feel pain and discomfort d mice and humans are the only species whose genomes have been sequenced b C e approximately 90 of human disease associated genes are present in the mouse genome

Consider the function f t 4 sec t 2t Let F t be the antiderivative of f t with F 0 0 Then F 5 4 tan 2 2 6

Consider the function f t 6 sec t 7t Let F t be the antiderivative of f t with F 0 0 Then F 2 6 tan 2 21 X

Find the producers surplus at a price level of p 58 for the price supply equation below p S x 5 0 1x 0 0003x The producers surplus is Round to the nearest intogor pooded

O x is the price in dollars per unit that consumers are willing to pay for x units of an item and S x is the price in dollars per unit that producers are willing to accept for x units Find a the equilibrium point b the consumer surplus at the equilibrium point and c the producer surplus at the equilibrium point D x x 9 S x x 4x 15 a What are the coordinates of the equilibrium point 3 36 Type an ordered pair b What is the consumer surplus at the equilibrium point Round to the nearest cent as needed

Evaluate the following indefinite integral J 3 3t 3 dt

The marginal revenue in thousands of dollars from the sale of x gadgets is given by the following function The revenue from 120 gadgets is 10 854 2 1 3 33 MR x 4x x 29 000 a Find the revenue function b What is the revenue from selling 250 gadgets c How many gadgets must be sold for a revenue of at least 50 000 a R x Simplify your answer Round to the nearest integer as needed b The revenue from selling 250 gadgets is Type a whole number c To generate a revenue of at least 50 000 approximately Type a whole number gadgets must be sold

PART 1 For each multiple choice problem circle only one answer There is no partial credit for multiple choice problems 1 5 points Which of the following is a critical point of the function f x ln x 8x fx In x 8x A x 1 16 B 16 x 1 4 D x 4 E f x has no critical points 2 5 points A function f t has a local minimum at t 2 and a local maximum at t 4 Assuming t 2 and t 4 are critical points found by setting f t 0 and solving for t which of the following must be true Af 2 is positive and f 4 is positive B f 2 is positive and f 4 is negative C f 2 is negative and f 4 is negative D f 2 is negative and f 4 is positive t 2 210 max t 9 9 0 4 4 20 242 0 3 5 points Below is table of values for the second derivative of a smooth continuous function g x If x 3 and x 1 are the only candidates for where the original function g x may have an inflection point what can we conclude X 4 g x 2 3 0 1 2 0 4 0 20 A g x has an inflection point at both x 3 and x 1 B g x has an inflection point at x 3 but not at x 1 C g x has an inflection point at x 1 but not at x 3 D g x has no inflection points

3 Stem cells are a b C d e unspecialized specialized unable to divide always pluripotent only found in embryos

b mit Stolpirtia 1 Use the graph of g x shown to the right to answer the following questions A g 2 B lim g x C lim g x D g 3 y g x E List the values of x when g x is discontinuous 10 points

6 Find the anti derivative sin 2 cos x dx

Suppose the rate of growth of bacteria in a Petri dish is given by q t 3 where t is given in hours and q t is given in thousands of bacteria per hour If a culture starts with 8000 bacteria find a function Q t that gives the number of bacteria in the Petri dish at any time t How many bacteria are in the dish after 2 hours You should round your answer to the nearest whole number Do not include any commas in your final answer if applicable Provide your answer below

TABLE OF INDEFINITE INTEGRALS f cf x dx c f f x dx fkdx kx C Xn 1 fxndx C n 1 n 1 fex dx ex C sin x dx cos x C sec x dx tan x C sec x tan x dx sec x tan x dx sec x C S 1 x 1 dx tan x C sinh x dx cosh x C 18 f x g x dx f f x dx f g x dx dx In x C faxdx ax In a cos x dx sin x C fcsc x dx cot x C csc csc x cot x dx C x cot x dx csc x C CSC dx sin x C 1 x cosh x dx sinh x C sin 2x dx

TABLE OF INDEFINITE INTEGRALS f cf x dx cf f x dx kdx kx C Xn 1 fxndx C n 1 n 1 fe dx e C S sec x dx tan x C S sec x tan x dx sec x C 1 S x 1 sinh x dx cosh x C sin x dx cos x C dx tan x C f x g x dx f f x dx f g x dx d dx n x C ax fa dx C In a f cos x dx cos x dx sin x C fcsc x dx cot x C CSC x cot x dx csc x C csc x cot x dx 1 S v x f cosh x dx sinh x C dx sin x C 6 x 3 x dx W x3 2

6 W x 1 dx x 4x x 1 a x 1 b x 4x C z4 4x 7 Find the area under the parabola y x 1 from x 2 to x 2

9 A particle moves along a line so that its velocity at time t is v t measured in meters per second Find the distance traveled during the time period 0 t 2 a 1 m b 0 m c 1 m d 2 m e 3 m

a 1 m 10 Which integral or the sum of integrals represents the area betw the following two curves y 6x 2x 20x and y 2x 4x a 6x 24x dx f 6x 24x dx b 2 6x 24x dx c 2 6x 24x dx d f 6x 24x dx f 6r 24x dx e 6x 24x dx br

4 Evaluate the indefinite integral S 4x 3 e 3x 7 dx a e 4x 3 C b e x 3x 7 C c 4x 3 e x 3x 7 C d e x 3x 7

2 Evaluate the indefinite integral f sin 5x 3 3x dx a 5 cos 5x 3 x C b cos 5x 3 x C c cos 5x 3 x C d sin 5x 3 x C e 5 cot 5x 3 x C torral

5 Evaluate the indefinite integral f 2x sin x 1 dx a cos x 1 C b 2x cos x 1 C c cos x 1 C d none of the above

Question Find the price demand equation for a particular brand of toothpaste at a supermarket chain when the demand is 36 tubes per week at 1 65 per tube given that the marginal price demand function p x for x number of tubes per week is given as p x 0 02e 0 04x If the supermarket chain sells 70 tubes per week what price should be set Round to the nearest cent Provide your answer below

Evaluate the indefinite integral given below e 20 Provide your answer below S e 2 csc 2x 2 csc 2x cot 2x csc 2x dx wwwww 2 csc 2x cot 2x csc 2x dx

Evaluate the indefinite integral given below S sin x 3 sin x sin x 4 sin x cos x dx Provide your answer below f sin x 3 sin x sin x 4 sin x cos x dx 4

Evaluate the indefinite integral given below Provide your answer below 8 36x sec 3x 2x tan 3x 2x dx 8 36x sec 3x 2x tan 3x 2x dx

Consider the function f x 12 Graph the exponential function by hand 0 5 4 Identity any asymptotes 300 250 200 150 100 300 250 200 150 100k 50

Find f f t 4 cost sec t 2 t 2 f 3 3

Find f Use C for the constant of the first antiderivative and D for the constant of the second antiderivative f x 25 6

Find f Use C for the constant of the first antiderivative and D for the constant of the second antiderivative f x 24x 15x 8x f x

1 Given a function of g x on 2 6 and g x 0 on 2 1 g x dx 10 g x 0 on 1 4 g x dx 4 g x 20 on 4 61 g x dx 6 estimate the following integrals 3 points each L g x dx D S Ig x dx A B 6 6 g x dx C lg x g x dx Ef g x dx E

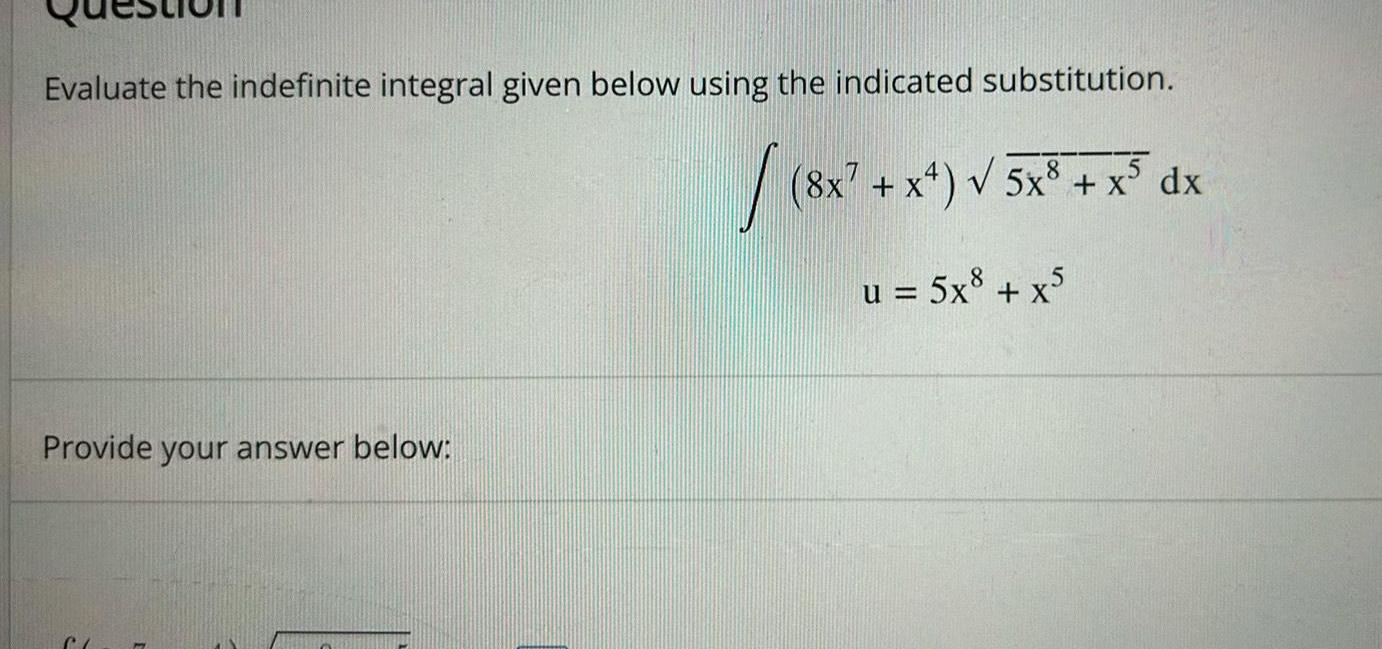
Evaluate the indefinite integral given below using the indicated substitution 8x x 5x x dx u 5x8 x5 Provide your answer below CL

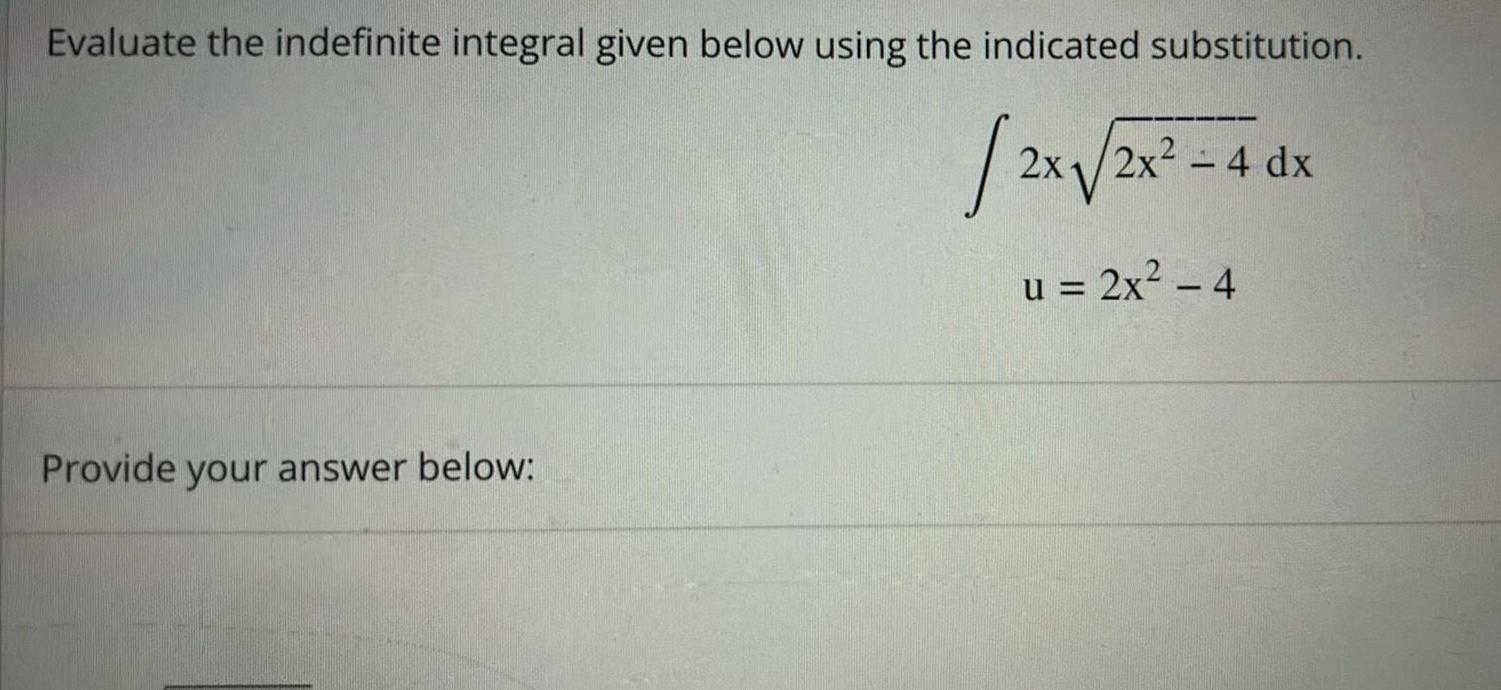
Evaluate the indefinite integral given below using the indicated substitution 2x 2x Provide your answer below 2x 4 dx u 2x 4

The questions in Level 1 are introductory problems The hints contain links to videos covering this content A Question 1 1 point Retake question Which of the following Type 1 Improper Integrals CONVERGE Select all that apply Ste 1 2 da dx 2 X Of 5 1 da of To 27 1 3 of a x dx da x sin x dx

Use a graphing utility to find the point of intersection if any of the graphs of the functions Round your result to three decimal places Enter NONE in any unused answer blanks x y y 110e0 01x y 13 500 x

Question 5 20 points 5 Find the moment of inertia in terms of its mass of a right circular cone of radius r and height h with respect to its axis h Axis

The weekly marginal revenue from the sale of x pairs of tennis shoes is given by the equation below where R x is revenue in dollar 300 x 1 R x 36 0 03x R 0 0 Find the revenue function Find the revenue from the sale of 1 000 pairs of shoes Find the revenue function R x R x Use integers or decimals for any numbers in the expression Find the revenue from the sale of 1 000 pairs of shoes The revenue the sale of 1 000 pairs of shoes is Round to the nearest cent as needed

The marginal average cost of producing x digital sports watches is given by the function C x where C x is the average cost in dollars c x 1 700 2 C 100 27 Find the average cost function and the cost function What are the fixed costs The average cost function is C x The cost function is C x The fixed costs are

The weekly marginal revenue from the sale of x pairs of tennis shoes is given by the equation below where R x is revenue in dollar 400 x 1 Find the revenue function Find the revenue from the sale of 1 000 pairs of shoes R x 30 0 02x R 0 0 Find the revenue function R x R x Use integers or decimals for any numbers in the expression

If tan 0 and sin 0 0 then find a sin 0 b cos 0 c sec 0 d csc 0 e cot 0 FI PI A A

A company determines that its marginal revenue per day is given by R t where R t is the total accumulated revenue in dollars on the fth day The company s marginal cost per day is given by C t where C t is the total accumulated cost in dollars on the fth day R t 130e R 0 0 C t 130 0 6t C 0 0 a Find the total profit P T from t 0 to t 10 the first 10 days P T R T C T R t C t dt The total profit is Round to the nearest cent as needed b Find the average daily profit for the first 10 days The average daily profit is Round to the nearest cent as needed

A company determines that its marginal revenue per day is given by R t where R t is the total accumulated revenue in dollars on the th day The company s marginal cost per day is given by C where C t is the total accumulated cost in dollars on the fth day R t 130e R 0 0 C t 130 0 6t C 0 0 a Find the total profit P T from t 0 to t 10 the first 10 days STIR P T R T C T R t C t dt The total profit is Round to the nearest cent as needed b Find the average daily profit for the first 10 days The average daily profit is Round to the nearest cent as needed GUL

Find the area between the curve and the x axis over the indicated interval y 16 x 4 4 The grounder the sun is Simplify your onewor

Problem 4 By making an appropriate substitution which of the following integrals is equal to SFR Problem 4 dx x x 9 5 2 8 A 37 sin 8 G Select de B 37 sin e cos 8 38 sin 8 de H de c f cos 8 37 sinf 8 de cos 0 37 sin 0 de D 38 sin 6 de E S de F cos 0 37 sin 8 cos 8 38 sin 8 S

Problem 2 By making an appropriate substitution which of the following integrals is equal to tan x sec 0 x dx Problem 2 A u 1 u du B x 1 u du C us 1 u 6 du D u 1 u du E u 1 u du F u 1 u 4 du G u 1 u 5 du H u 1 u du hs Select

A company models its income in thousands of dollars using the conti f t 20e 0 0251 12 where t is measured in months Which of the following denotes the correct formula to find the total income derived in the second year Select the correct answer below 24 O TI 20e 0 0251 1 2 dt 12 TI 2 20e 0 025r 2 dr 20e 0 025t dt O TI 36 O TI 2 20e 0 025z 2 dt O

y 3 M al JS Secti al ah Sketch the region enclosed by the given curves Decide whether to integrate with respect to x or y Draw a typical approximating rectangle y ex y x 1 x 1 x 1 y 3 5 2 0 webassign net y 3 y MacBook Air

2 1 1 M W Sketch the region enclosed by the given curves Decide whether to integrate with respect to x or y Draw a typical approximating rectangle 2x y 8 x y 4 4 al JS Secti 2 1 al WebAssign Plot ah 1 2

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin Foci 7 0 major axis of length 18