Indefinite Integration Questions and Answers

Calculus
Indefinite IntegrationWhat is the pressure on a horizontal surface with an area of 3 m that is 3 m underwater Use 1000 kg m for the density of water and 9 8 m s for the acceleration due to gravity OOO Points 0 of 1 30 3 1 100 What is the correct relationship to use to find the pressure on the horizontal surface OA pressure pgAh where p is the density of water g is the acceleration due to gravity A is the surface area of the water and h is the depth of the water B pressure pAh where p is the density of water A is the surface area of the water and h is the depth of the water OC pressure pgA where p is the density of water g is the acceleration due to gravity and A is the surface area of the water D pressure pgh where p is the density of water g is the acceleration due to gravity and h is the depth of the water C Sav

Calculus
Indefinite IntegrationFind the volume of the solid bounded by the surface z f x y and the xy plane Z 52 1 x2 2 y 2 V Type an exact answer using as needed 1 Z 52 1 x y 2

Calculus
Indefinite Integrationscuba diver 60 ft below the ocean surface inhales 90 0 mL of ompressed air from a scuba tank at an initial pressure of 3 50 tm and temperature of 9 C Part A What is the final pressure of air in atmo spheres in the lungs when the gas expands to 190 0 mL at a body temperature of 37 C and the amount of gas remai constant P VAEO atm
Calculus
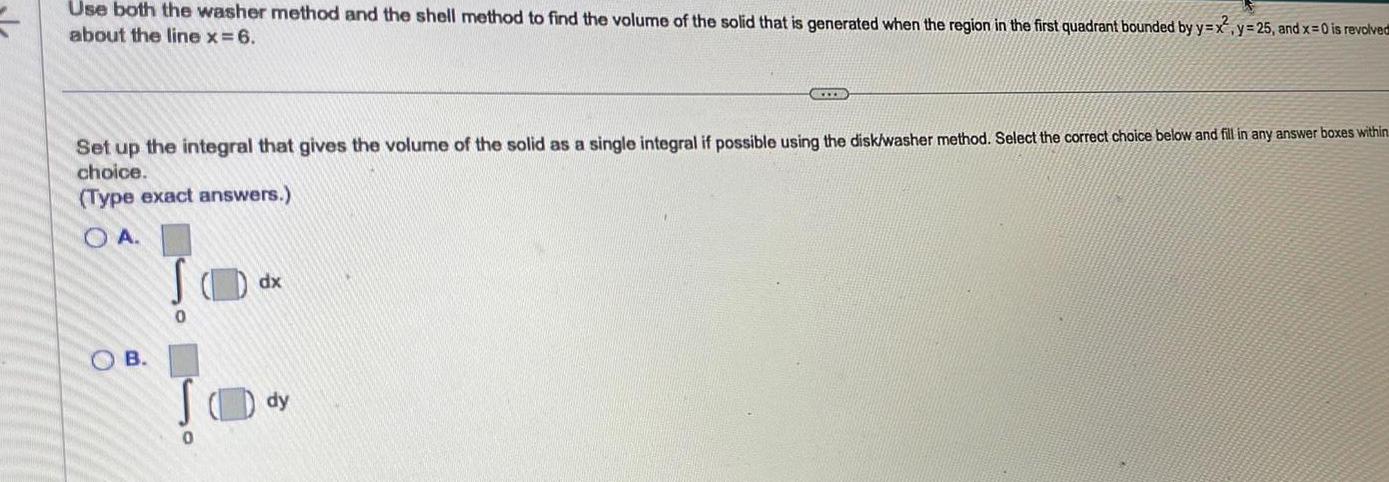
Indefinite IntegrationUse both the washer method and the shell method to find the volume of the solid that is generated when the region in the first quadrant bounded by y x about the line x 6 O Set up the integral that gives the volume of the solid as a single integral if possible using the disk washer method Select the correct choice below and fill in any answer boxes within choice Type exact answers OA B 0 0 dx www dy y 25 and x 0 is revolved
Calculus
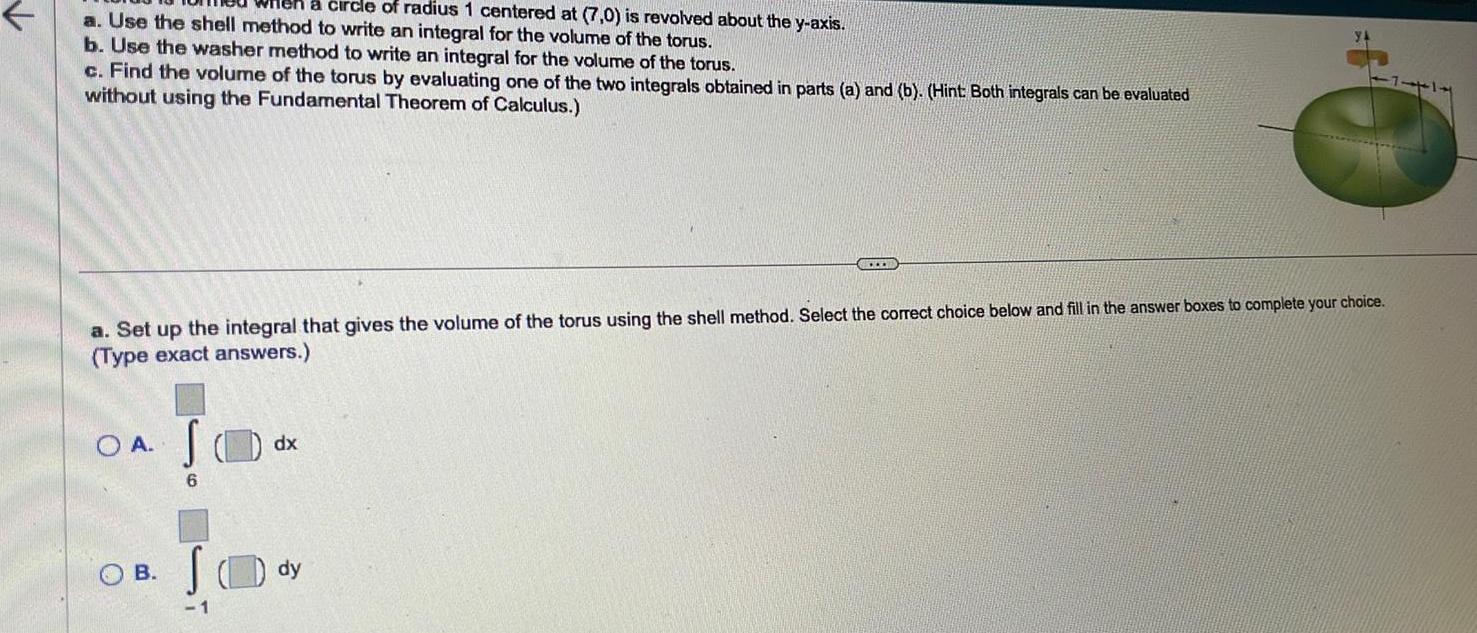
Indefinite Integrationa circle of radius 1 centered at 7 0 is revolved about the y axis a Use the shell method to write an integral for the volume of the torus b Use the washer method to write an integral for the volume of the torus c Find the volume of the torus by evaluating one of the two integrals obtained in parts a and b Hint Both integrals can be evaluated without using the Fundamental Theorem of Calculus a Set up the integral that gives the volume of the torus using the shell method Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers O A B S 6 1 dx dy

Calculus
Indefinite Integrationmine whether the following statements are true and give an explanation or counterexample a When using the shell method the axis of the cylindrical shells is parallel to the axis of revolution b If a region is revolved about the y axis then the shell method must be used c If a region is revolved about the x axis then in principle it is possible to use the disk washer method and integrate with respect to x or the shell method and integrate with respect to y a Choose the correct answer below www OA False The shell method produces shells that are always perpendicular to the axis of revolution OB True The shell method always produces shells parallel to the y axis O C True The rotation of the function about the axis creates a cylindrical shape parallel to the axis O D False The rotation of the function about the axis creates a disk shape perpendicular to the axis O O
Calculus
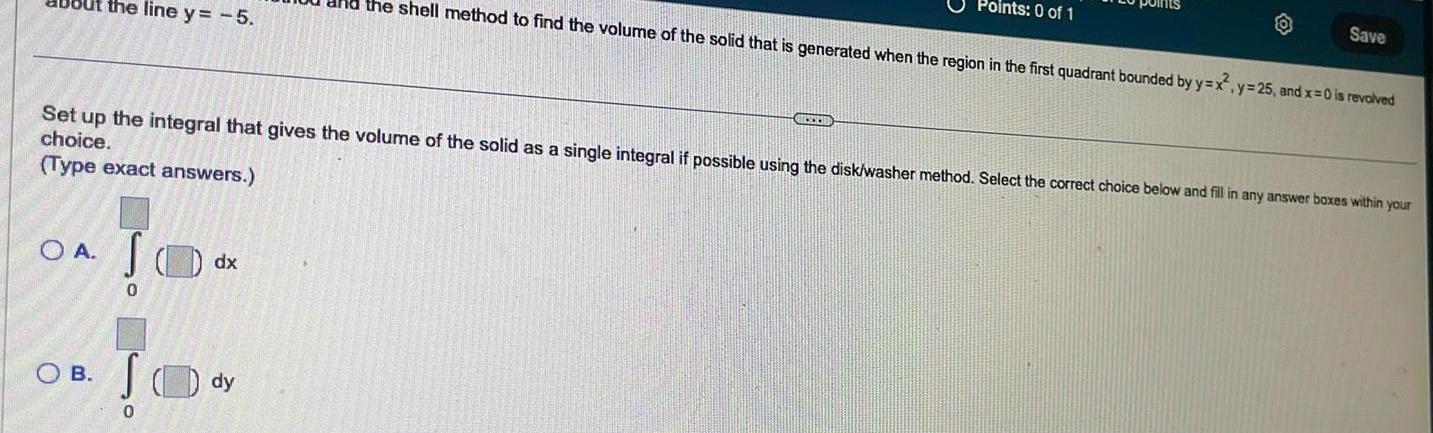
Indefinite Integrationthe line y 5 SOA S 0 OB 0 Set up the integral that gives the volume of the solid as a single integral if possible using the disk washer method Select the correct choice below and fill in any answer boxes within your choice Type exact answers dx the shell method to find the volume of the solid that is generated when the region in the first quadrant bounded by y x dy Points 0 of 1 GUCCHE Save y 25 and x 0 is revolved
Calculus
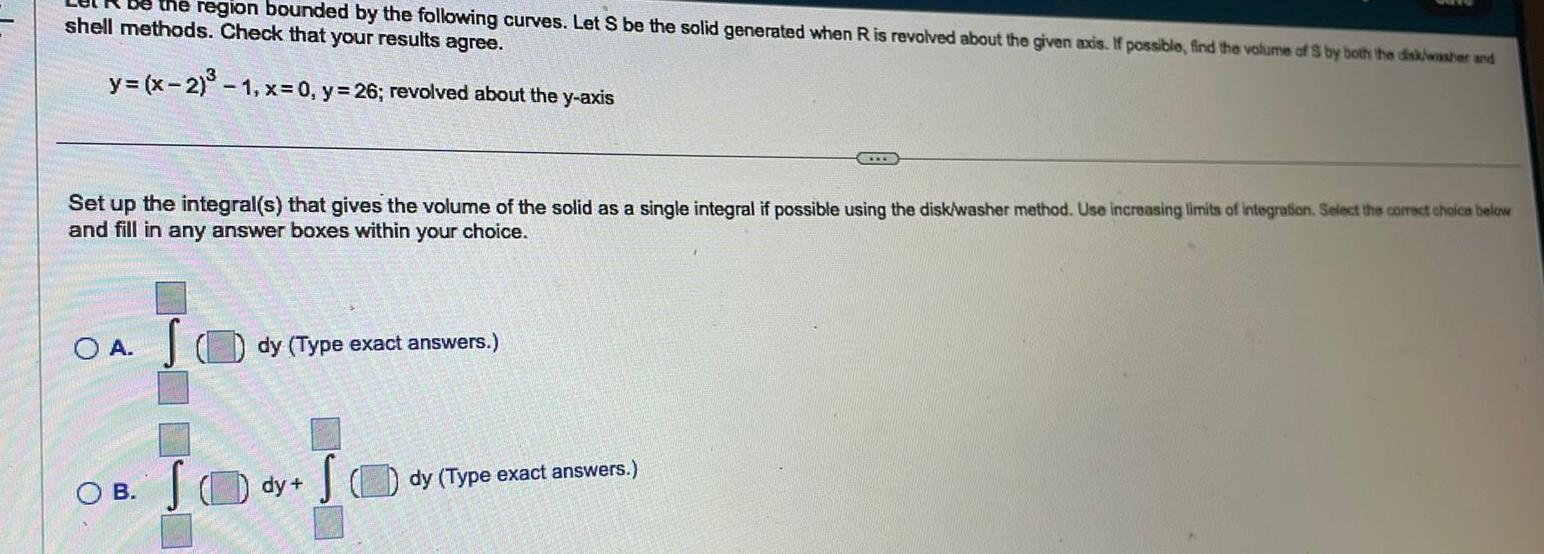
Indefinite Integrationbe the region bounded by the following curves Let S be the solid generated when R is revolved about the given axis If possible find the volume of S by both the disk washer and shell methods Check that your results agree y x 2 1 x 0 y 26 revolved about the y axis Set up the integral s that gives the volume of the solid as a single integral if possible using the disk washer method Use increasing limits of integration Select the correct choice below and fill in any answer boxes within your choice OA S OB dy Type exact answers S SO dy dy Type exact answers
Calculus
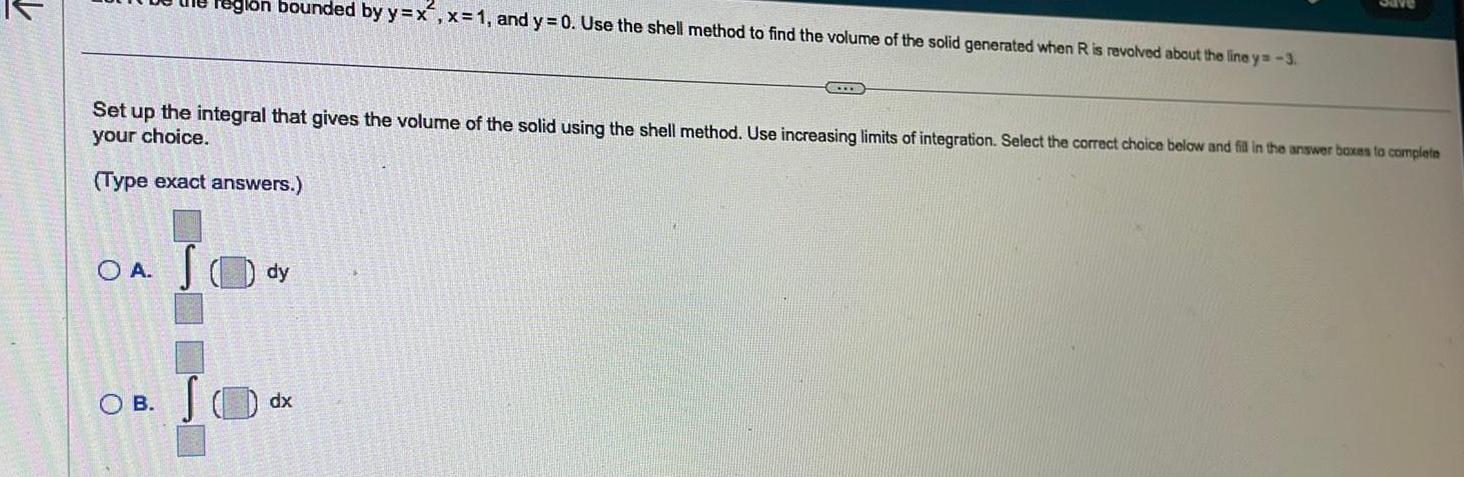
Indefinite Integrationregio bounded by y x x 1 and y 0 Use the shell method to find the volume of the solid generated when R is revolved about the line y 3 Set up the integral that gives the volume of the solid using the shell method Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers OB OA S dy dx
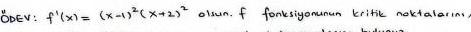
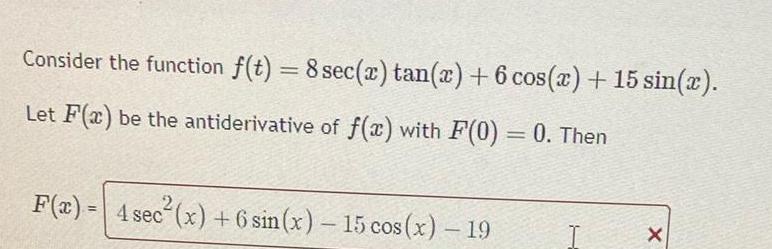
Calculus
Indefinite IntegrationConsider the function f t 8 sec x tan x 6 cos x 15 sin x Let F x be the antiderivative of f x with F 0 0 Then F x 4 sec x 6 sin x 15 cos x 19 X
Calculus
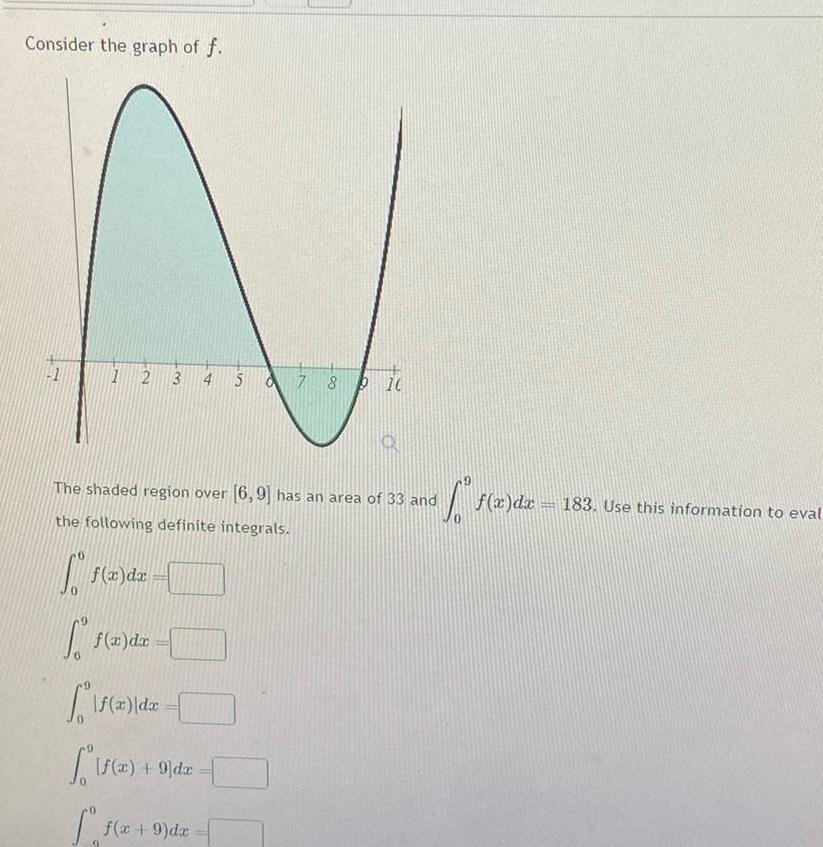
Indefinite IntegrationConsider the graph of f N 1 2 3 4 5 6 7 8 P10 The shaded region over 6 9 has an area of 33 and the following definite integrals 0 f x dx f x dx f x dx If a f x 9 dx f x 9 dx 9 f x dz 183 Use this information to eval

Calculus
Indefinite IntegrationThe portion of the graph Distance is measured in W 3360 651 y tan x between x 0 and x 1 is rotated around the y axis to form a container The container is filled with water Use n 6 subintervals and Simpson s rule to approximate the work required to pump all of the water out over the side of the container Give your a meters the density of water is 1000 kg m and use 9 8 m s for g
Calculus
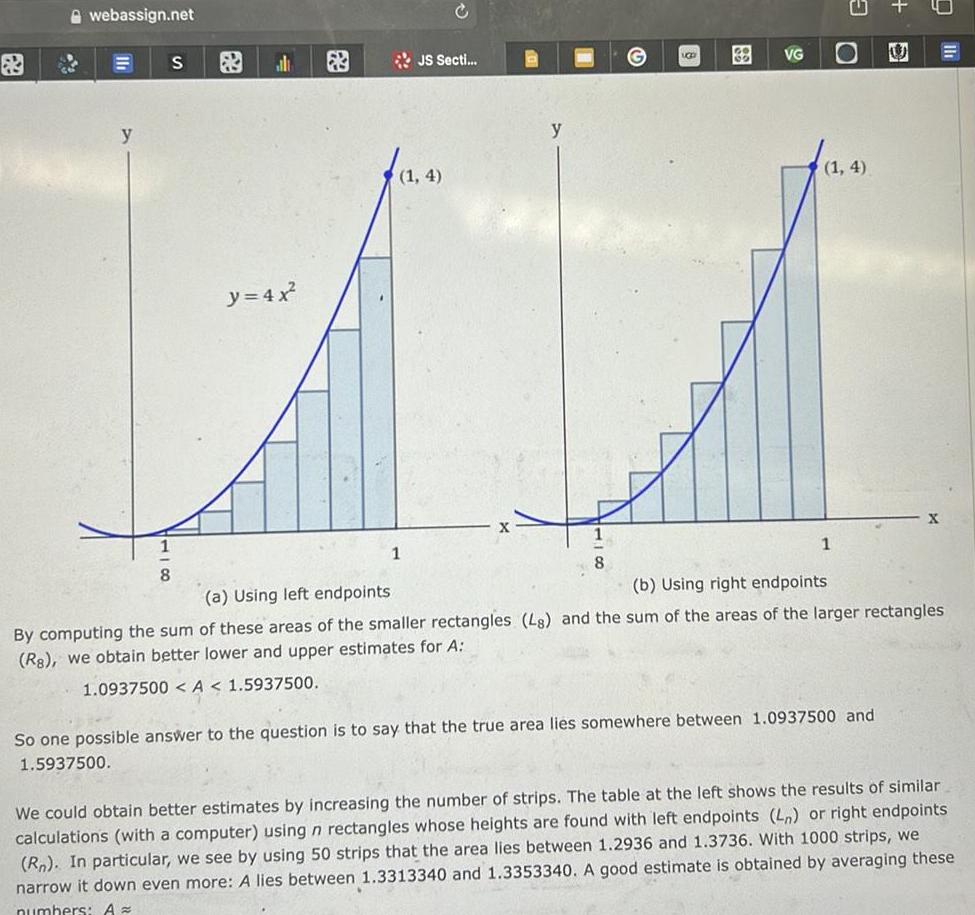
Indefinite Integrationwebassign net y S 1 8 al y 4x JS Secti 1 4 1 y 8 UGD VG 1 4 1 U So one possible answer to the question is to say that the true area lies somewhere between 1 0937500 and 1 5937500 X a Using left endpoints b Using right endpoints By computing the sum of these areas of the smaller rectangles Ls and the sum of the areas of the larger rectangles Rs we obtain better lower and upper estimates for A 1 0937500 A 1 5937500 We could obtain better estimates by increasing the number of strips The table at the left shows the results of similar calculations with a computer using n rectangles whose heights are found with left endpoints L or right endpoints Rn In particular we see by using 50 strips that the area lies between 1 2936 and 1 3736 With 1000 strips we narrow it down even more A lies between 1 3313340 and 1 3353340 A good estimate is obtained by averaging these numbers A
Calculus
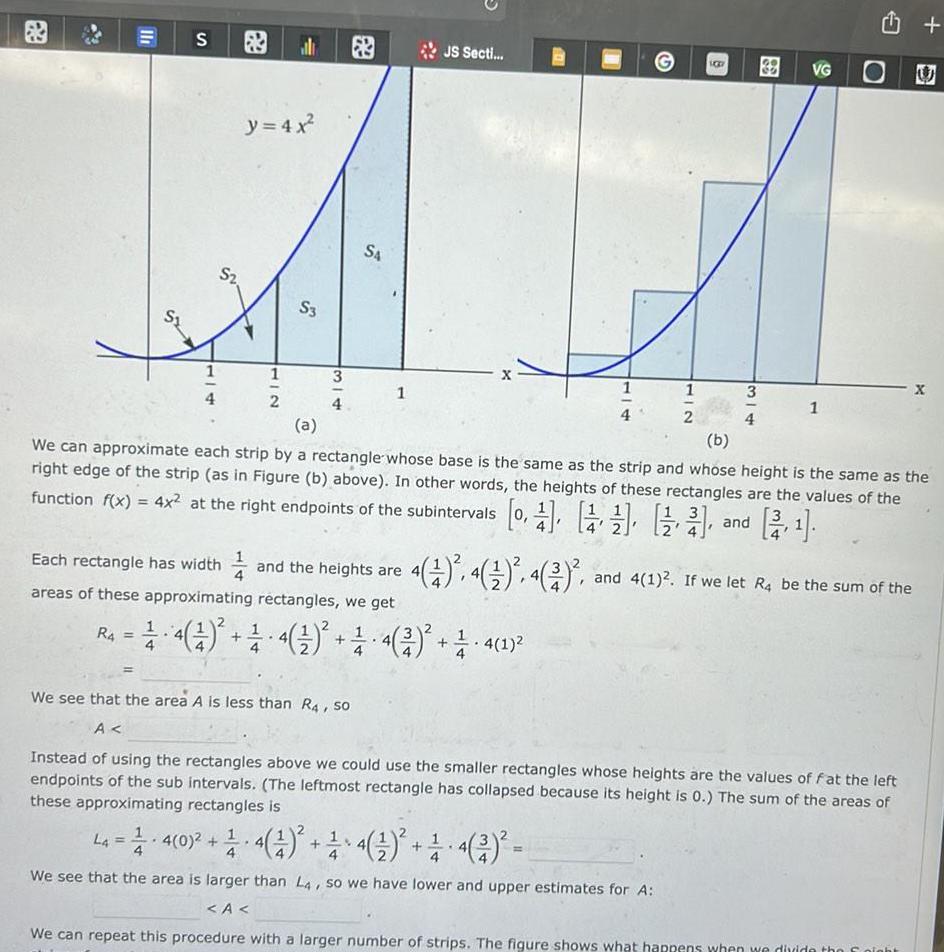
Indefinite Integration11 S R4 1 4 S y 4x 2 HIC al 2 S3 3 4 S4 1 Each rectangle has width and the heights are areas of these approximating rectangles we get JS Secti 201 2 4 4 4 4 2 1 4 1 BB 38 3 VG 1 a b We can approximate each strip by a rectangle whose base is the same as the strip and whose height is the same as the right edge of the strip as in Figure b above In other words the heights of these rectangles are the values of the function f x 4x at the right endpoints of the subintervals 0 and 4 1 4 4 2 and 4 1 If we let R4 be the sum of the We see that the area A is less than R4 so A Instead of using the rectangles above we could use the smaller rectangles whose heights are the values of fat the left endpoints of the sub intervals The leftmost rectangle has collapsed because its height is 0 The sum of the areas of these approximating rectangles is U La 4 0 4 1 4 4 We see that the area is larger than L4 so we have lower and upper estimates for A A We can repeat this procedure with a larger number of strips The figure shows what happens when we divide the night X
Calculus
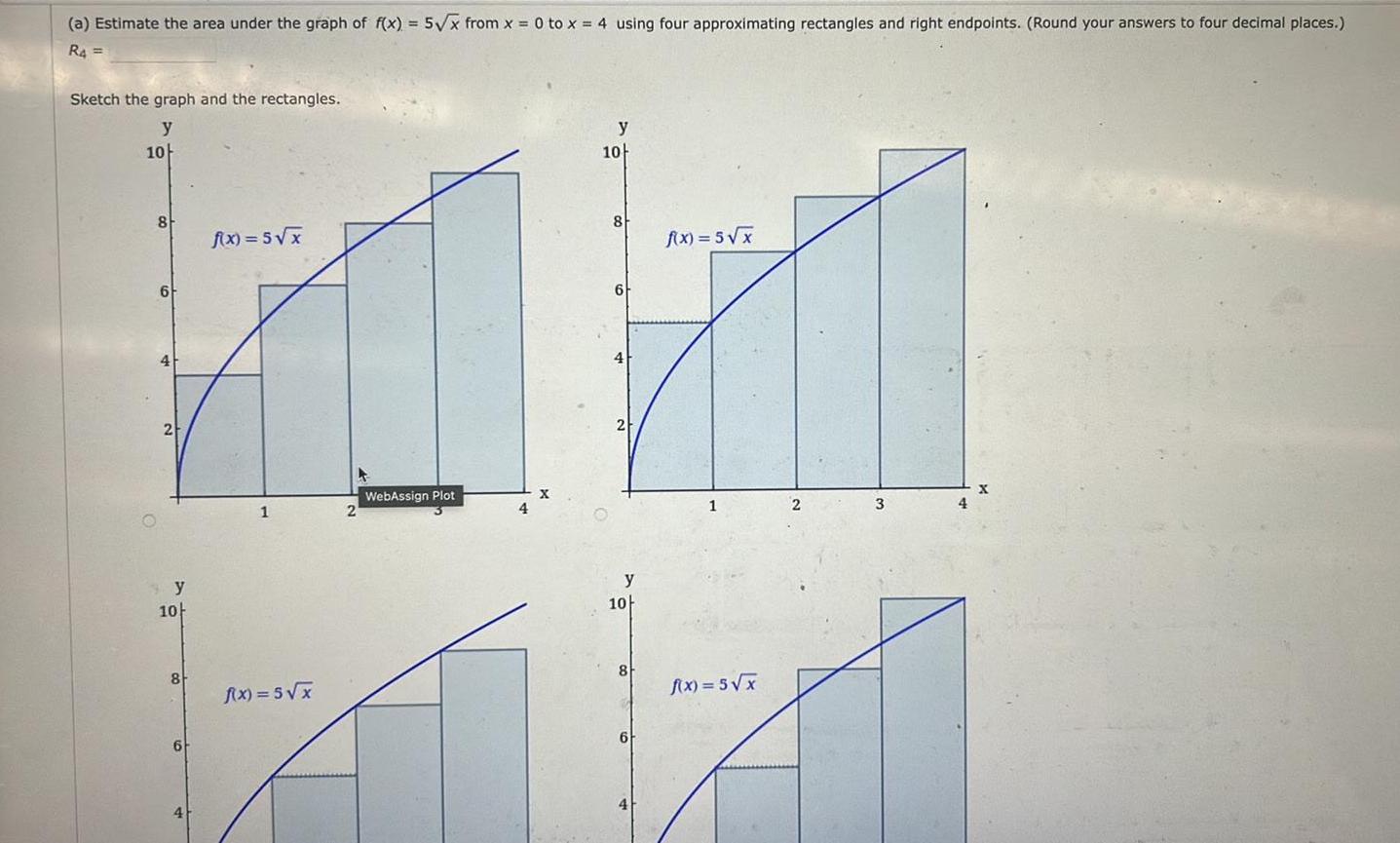
Indefinite Integrationa Estimate the area under the graph of f x 5 x from x 0 to x 4 using four approximating rectangles and right endpoints Round your answers to four decimal places R4 Sketch the graph and the rectangles y 10 8 6 2 y 10 8 6 4 f x 5 x 1 f x 5 x WebAssign Plot 4 y 10 8 2 f x 5 x 1 2 3 y 10 8 f x 5 x At 6 X

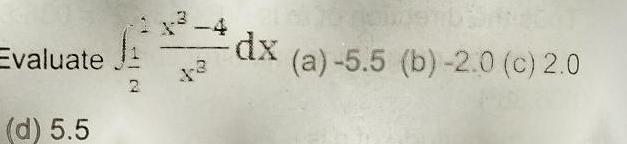
Calculus
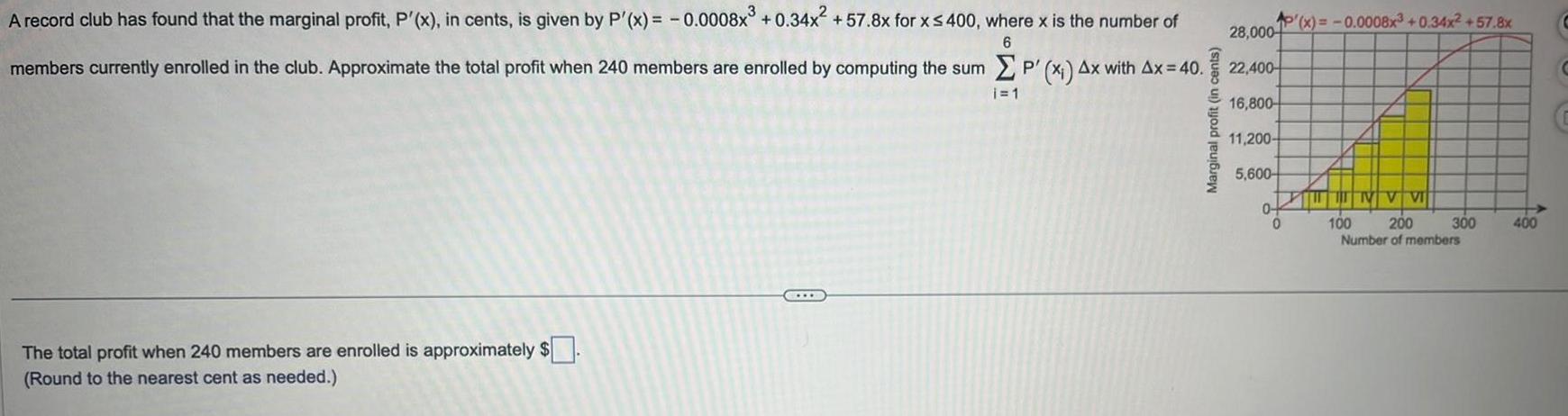
Indefinite Integration6 A record club has found that the marginal profit P x in cents is given by P x 0 0008x 0 34x 57 8x for x 400 where x is the number of members currently enrolled in the club Approximate the total profit when 240 members are enrolled by computing the sum P x Ax with Ax 40 i 1 The total profit when 240 members are enrolled is approximately Round to the nearest cent as needed Marginal profit in cents 28 000 22 400 16 800 11 200 5 600 0 P x 0 0008x 0 34x 57 8x 0 NV VI 100 200 Number of members 300 400

Calculus
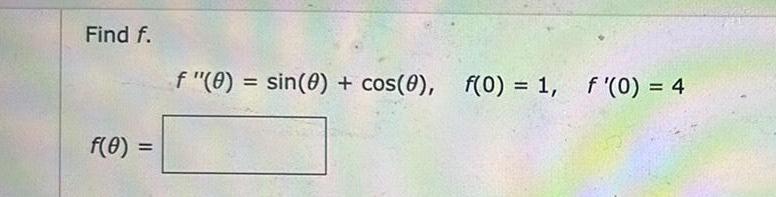
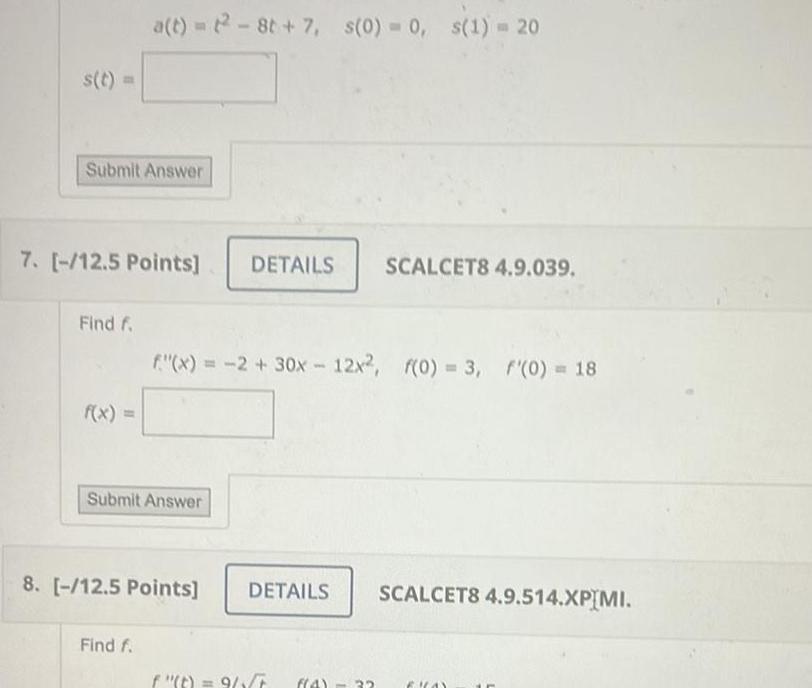
Indefinite Integrations t Submit Answer 7 12 5 Points Find f a t 2 8t 7 s 0 0 s 1 20 f x Submit Answer Find f f x 2 30x12x2 f 0 3 f 0 18 8 12 5 Points DETAILS SCALCET8 4 9 039 DETAILS SCALCET8 4 9 514 XPIMI f t 9 4 32 1 A

Calculus
Indefinite IntegrationA note card company has found that the marginal cost per card of producing x note cards is given by the function below where C x is the marginal cost in cents per card Find the total cost of producing 790 cards disregarding any fixed costs C x 0 06x 78 for x 1000 The total cost is cents
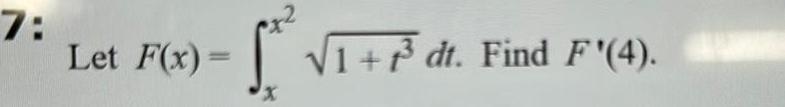

Calculus
Indefinite IntegrationVerify the identity Simplify your answers completely 9 csc x 9 cot x sec x 9 csc x sec x sin x 1 sin x 9 cot x
Calculus
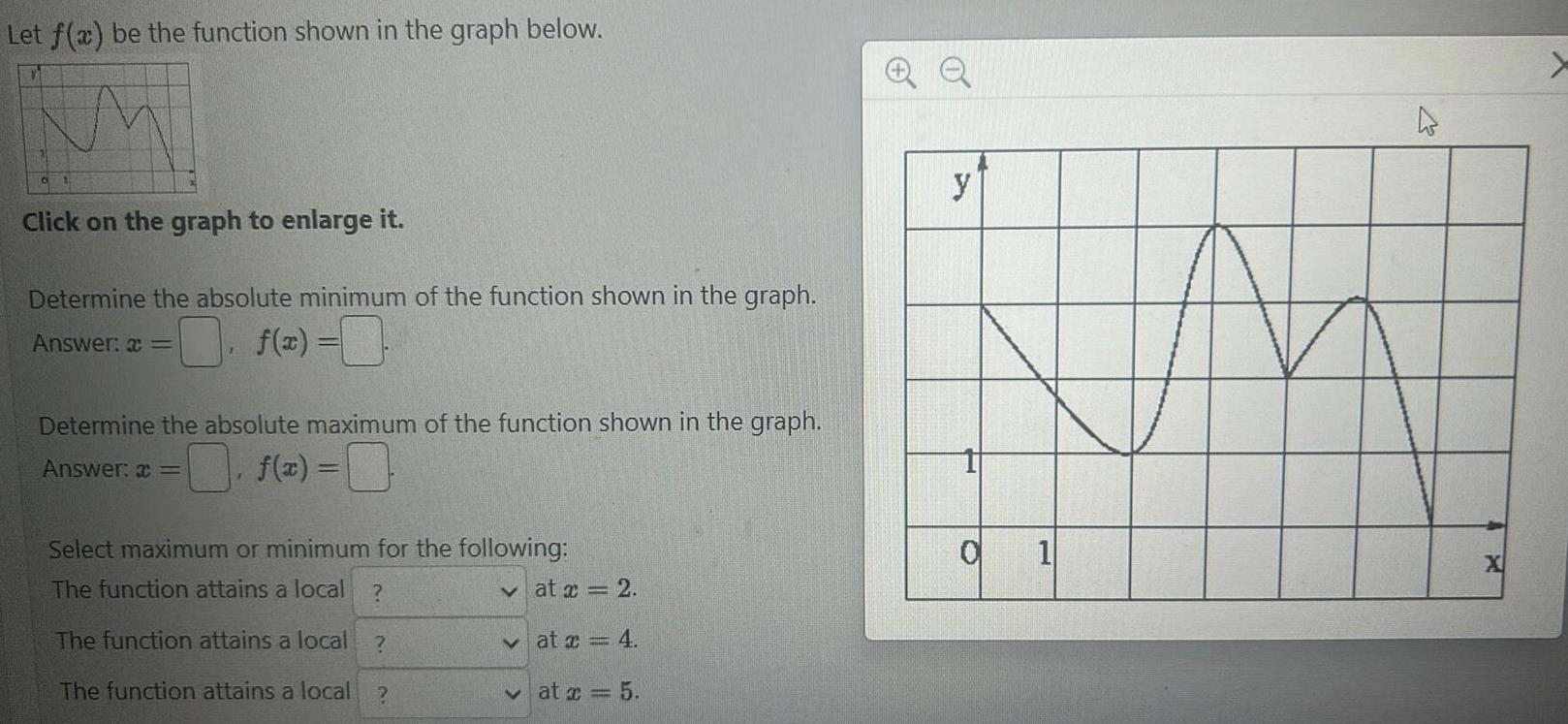
Indefinite IntegrationLet f x be the function shown in the graph below 6 Click on the graph to enlarge it Determine the absolute minimum of the function shown in the graph Answer f x Determine the absolute maximum of the function shown in the graph Answer f x 0 F Select maximum or minimum for the following The function attains a local The function attains a local The function attains a local at x 2 at x 4 at x 5 QQ y O 1 h X
Calculus
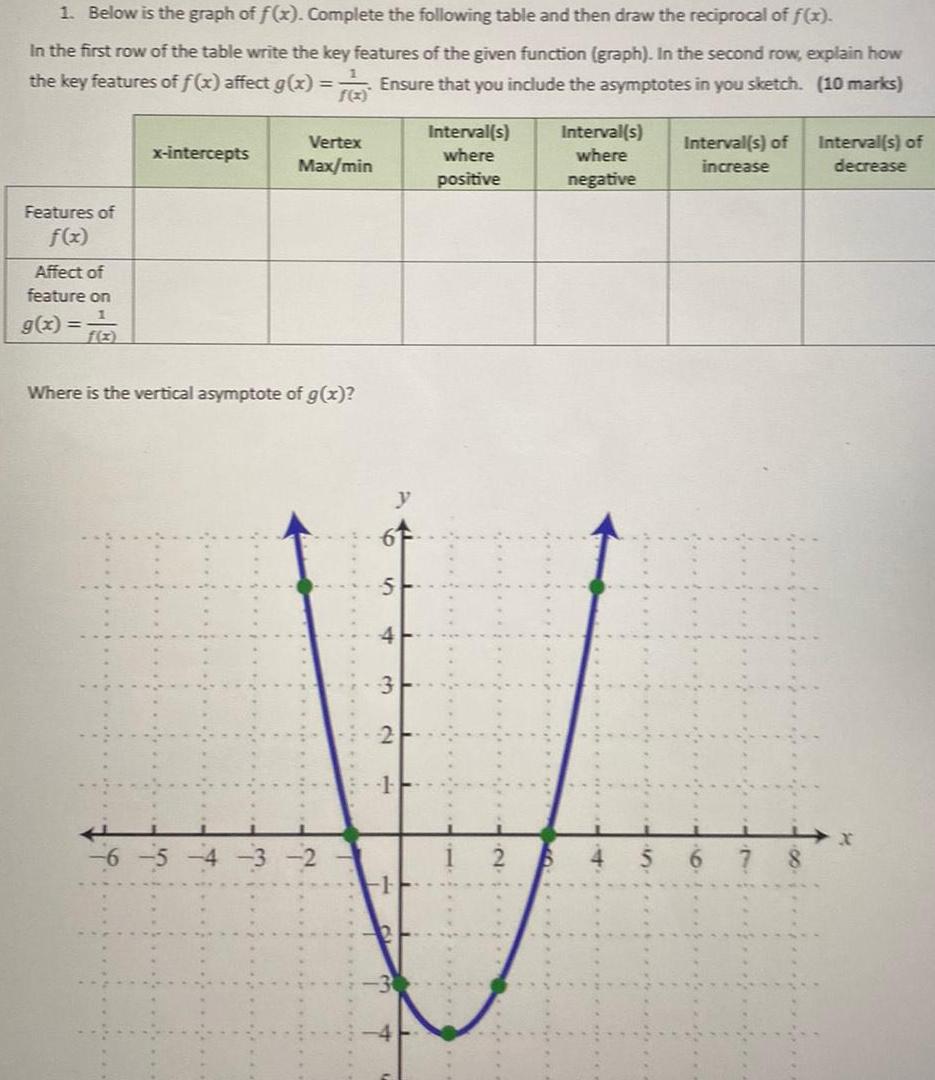
Indefinite Integration1 Below is the graph of f x Complete the following table and then draw the reciprocal of f x In the first row of the table write the key features of the given function graph In the second row explain how the key features of f x affect g x Ensure that you include the asymptotes in you sketch 10 marks Features of f x Affect of feature on 1 g x x intercepts Vertex Max min Where is the vertical asymptote of g x S d 1 Interval s where positive Interval s where negative Interval s of increase Interval s of decrease
Calculus
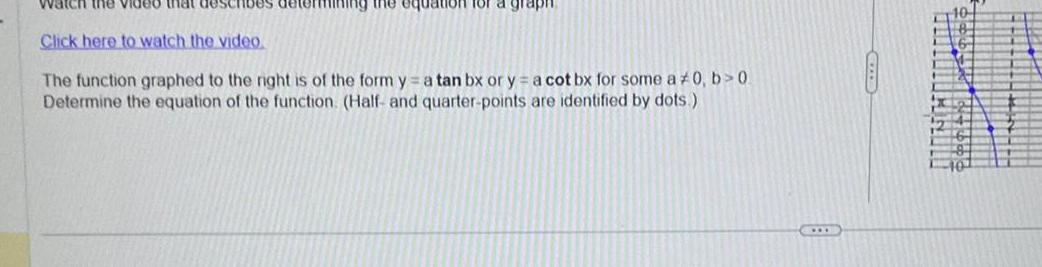
Indefinite IntegrationWatch the video that describes determining the equation for graph Click here to watch the video The function graphed to the right is of the form ya tan bx or y a cot bx for some a 0 b 0 Determine the equation of the function Half and quarter points are identified by dots
Calculus
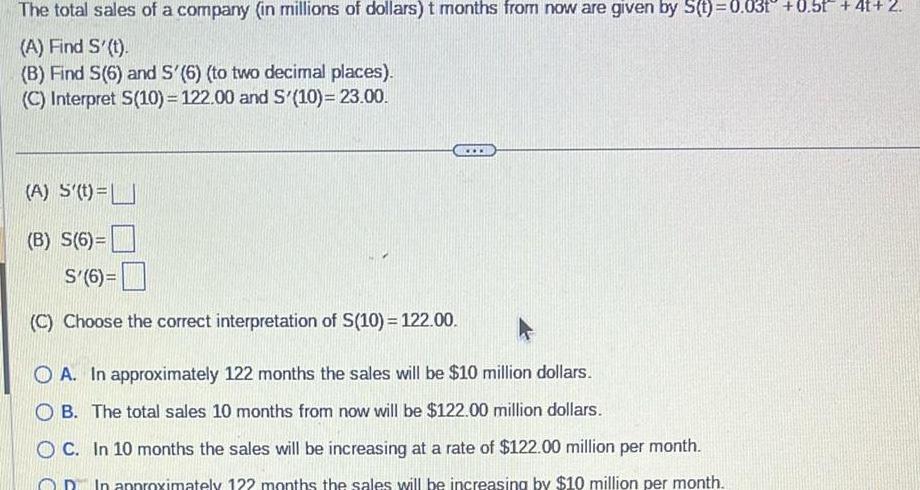
Indefinite IntegrationThe total sales of a company in millions of dollars t months from now are given by S t 0 031 0 5t 4t 2 A Find S t B Find S 6 and S 6 to two decimal places C Interpret S 10 122 00 and S 10 23 00 A S t B S 6 S 6 C Choose the correct interpretation of S 10 122 00 www OA In approximately 122 months the sales will be 10 million dollars OB The total sales 10 months from now will be 122 00 million dollars OC In 10 months the sales will be increasing at a rate of 122 00 million per month In approximately 122 months the sales will be increasing by 10 million per month

Calculus
Indefinite IntegrationThe total cost in dollars of producing x food processors is C x 2100 40x 0 2x A Find the exact cost of producing the 41st food processor B Use the marginal cost to approximate the cost of producing the 41st food processor A The exact cost of producing the 41st food processor is B Using the marginal cost the approximate cost of producing the 41st food processor is

Calculus
Indefinite IntegrationRefer to functions m and n Find the function m intervals as an integer or a simplified fraction m x x 8 n x x 7 Part 0 2 Part 1 of 2 n x and write the domain in interval notation Write any numb
Calculus
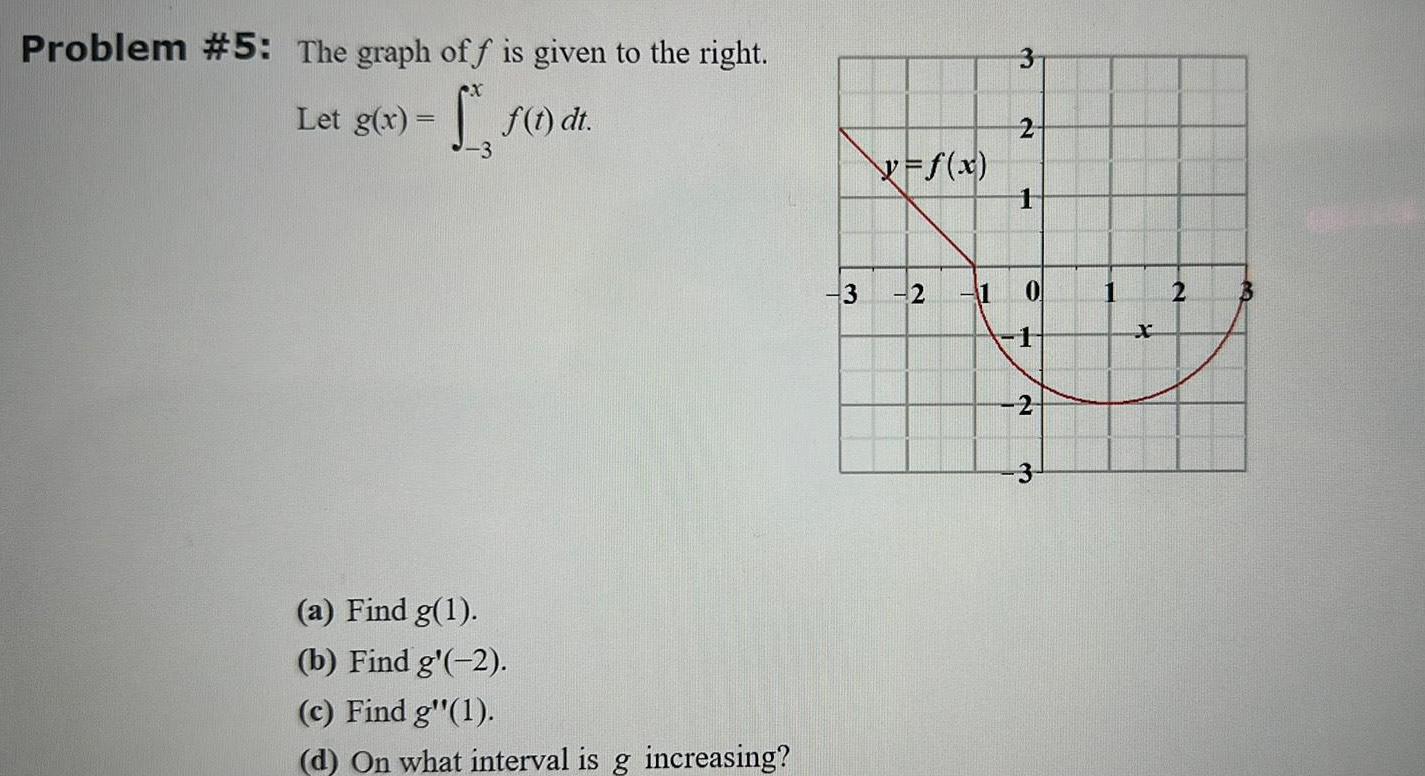
Indefinite IntegrationProblem 5 The graph off is given to the right Let g x f 1 di 3 a Find g 1 b Find g 2 c Find gr 1 d On what interval is g increasing 3 X f x 2 3 2 1 1 0 1 2 3 1 2 3
Calculus
Indefinite IntegrationProblem 4 Evaluate the following integrals by interpreting them in terms of areas a 5 1x 51 dx 7 49 x dx
Calculus
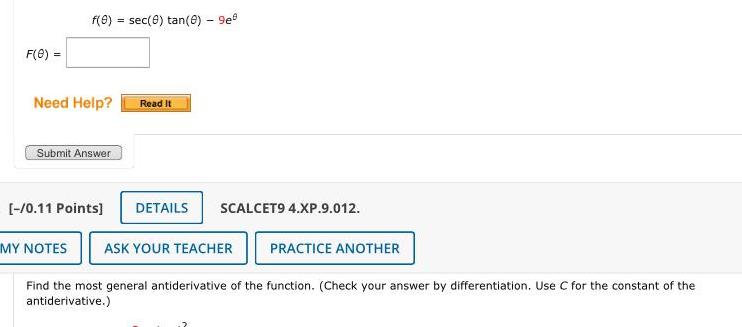
Indefinite IntegrationF 0 f 0 sec 0 tan 8 9e Need Help Submit Answer 0 11 Points Read It DETAILS SCALCET9 4 XP 9 012 MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the most general antiderivative of the function Check your answer by differentiation Use C for the constant of the antiderivative
Calculus
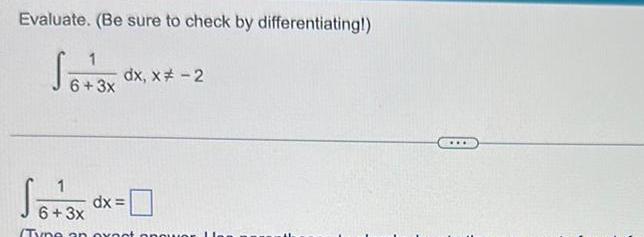
Indefinite IntegrationEvaluate Be sure to check by differentiating 1 6 3x dx dx x 2 6 3x dx Tyne an exo opou



Calculus
Indefinite IntegrationEvaluate Be sure to check by differentiating In x 29 X In x 29 dx x 0 dx X Type an exact answer Use parenthopon to

Calculus
Indefinite IntegrationFiling status single Gross income 75 000 Adjustments 7000 Deductions 11 500 mortgage interest 4100 property taxes 2000 charitable contributions Tax credit none Click the icon to view the 2021 marginal tax rates he income tax owed is SLITE

Calculus
Indefinite IntegrationFind an equation of the slant asymptote Do not sketch the curve 3x4 x x x x 3 y y X Enhanced Feedback Please try again keeping in mind that if lim X 8 f x mx b 0 or lim X 18 f x mx b 0 then th

Calculus
Indefinite IntegrationLet p 21 x and C x 746 2x where x is the number of garden hoses that can be sold at a price of p per unit and C x is the total cost in dollars of producing x garden hoses A Express the revenue function in terms of x B Graph the cost function and the revenue function in the same viewing window for 0 x 441 Use approximation techniques to find the break even points
Calculus
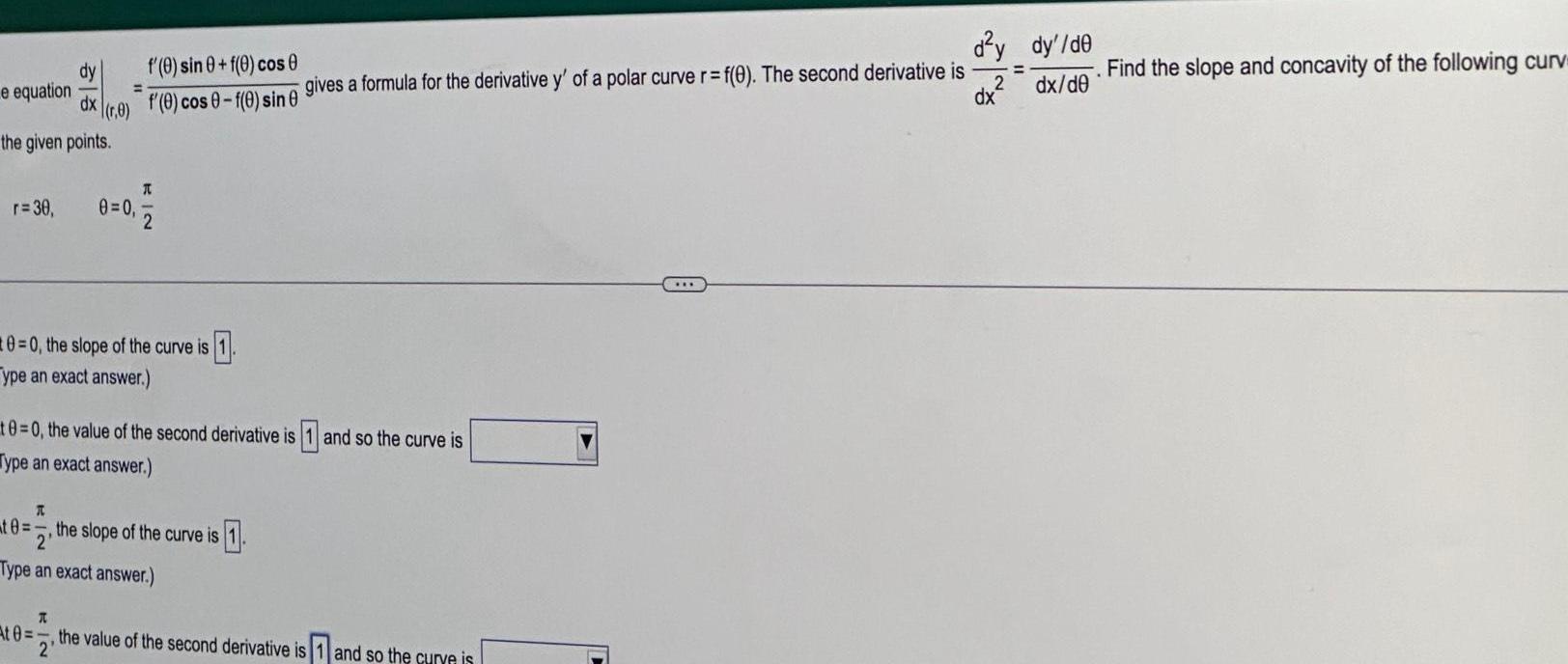
Indefinite Integrationdy dx the given points e equation 0 r 30 0 0 At 0 f 0 sin 0 f 0 cos f 0 cos 0 f 0 sin 0 A T 0 0 the slope of the curve is 1 ype an exact answer 2 10 0 the value of the second derivative is and so the curve is Type an exact answer A te the slope of the curve is 1 2 Type an exact answer gives a formula for the derivative y of a polar curve r f 0 The second derivative is the value of the second derivative is 1 and so the curve is 2 d y dy de 2 dx de dx Find the slope and concavity of the following curv

Calculus
Indefinite IntegrationThe amount of money SB in a bank account earning interest at a continuous rate r depends on the amount deposited P and the OB OB t r and time t it has been in the bank where B Pert Find OB OP OB t OB represents the change in the t amount of money in the bank JB r OB r OB OP and interpret each in financial terms OB OP Pret Ptert represents the change in the amount of money in the bank X represents the change in the as one unit of time passes by as the interest rate changes Choose one
Calculus
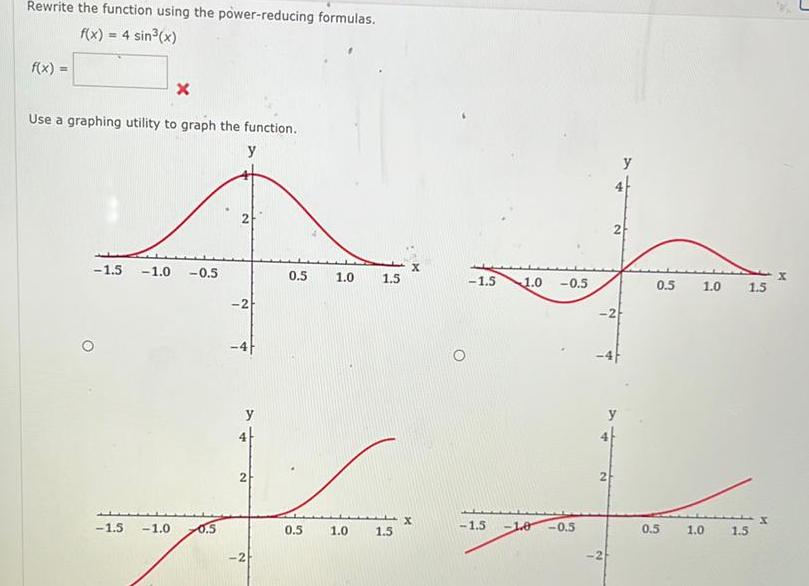
Indefinite IntegrationRewrite the function using the power reducing formulas f x 4 sin x f x X Use a graphing utility to graph the function y 1 5 1 0 0 5 2 1 5 1 0 0 5 0 5 1 0 1 5 y 2 d 0 5 2 1 0 1 5 X 1 5 1 0 1 5 0 5 1 0 0 5 y 2 y 2 0 5 0 5 1 0 1 0 1 5 1 5 X M J
Calculus
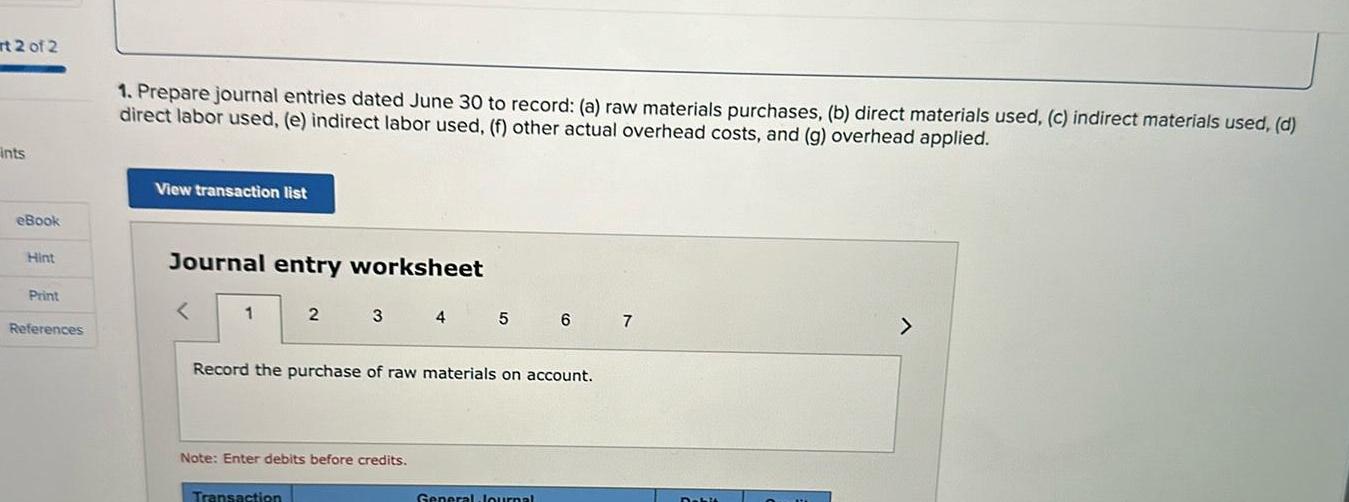
Indefinite Integrationrt 2 of 2 Ints eBook Hint Print References 1 Prepare journal entries dated June 30 to record a raw materials purchases b direct materials used c indirect materials used d direct labor used e indirect labor used f other actual overhead costs and g overhead applied View transaction list Journal entry worksheet 1 2 3 Transaction Note Enter debits before credits 4 5 Record the purchase of raw materials on account 6 General Journal 7

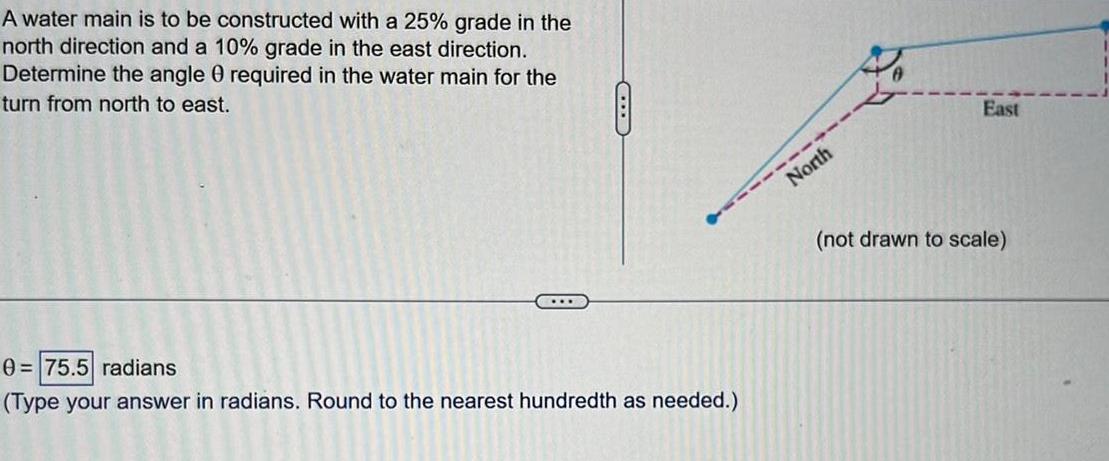
Calculus
Indefinite IntegrationA water main is to be constructed with a 25 grade in the north direction and a 10 grade in the east direction Determine the angle 0 required in the water main for the turn from north to east D 0 75 5 radians Type your answer in radians Round to the nearest hundredth as needed North East not drawn to scale
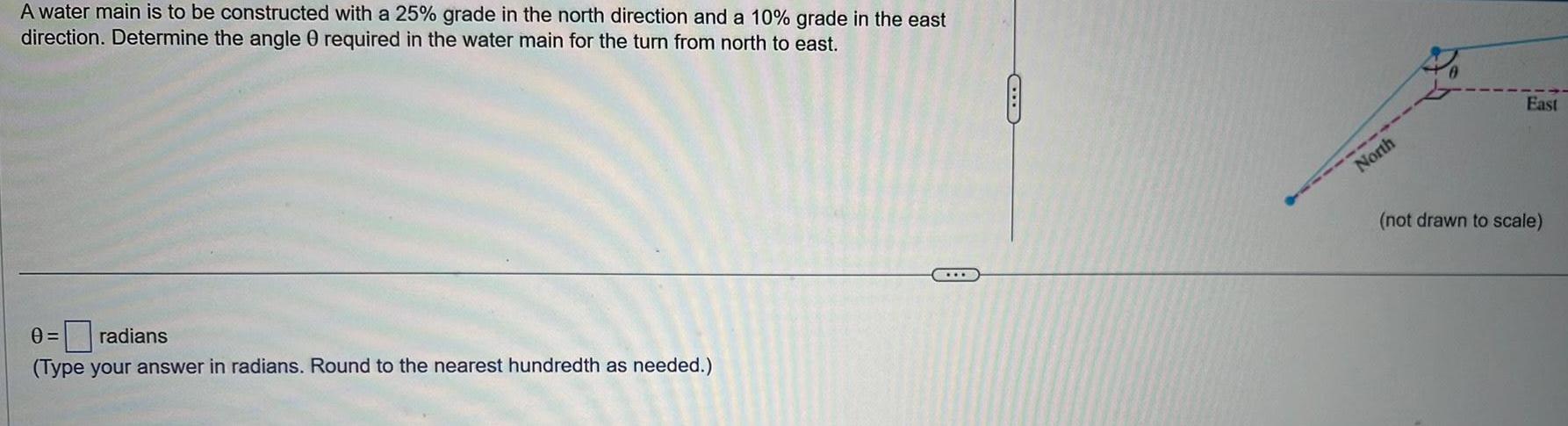
Calculus
Indefinite IntegrationA water main is to be constructed with a 25 grade in the north direction and a 10 grade in the east direction Determine the angle 0 required in the water main for the turn from north to east 0 radians Type your answer in radians Round to the nearest hundredth as needed CLB North East not drawn to scale
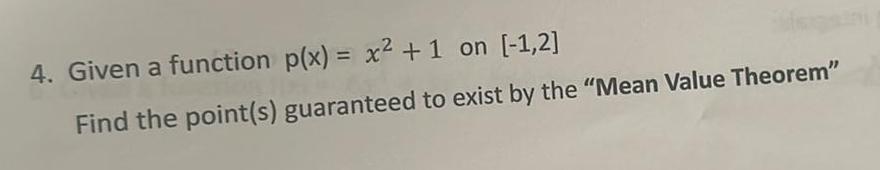
Calculus
Indefinite Integration4 Given a function p x x 1 on 1 2 Find the point s guaranteed to exist by the Mean Value Theorem