Vector Calculus Questions and Answers
Calculus
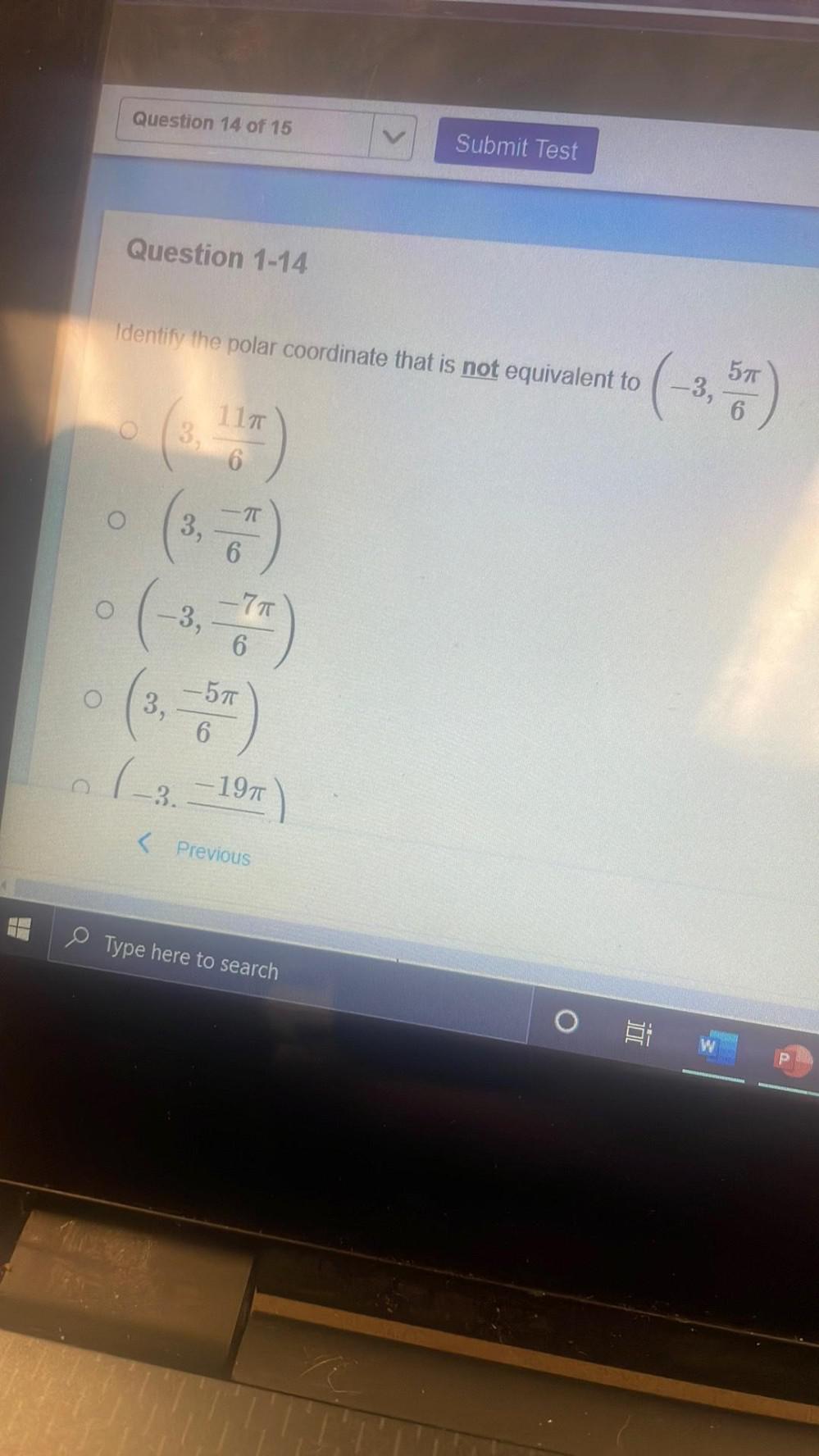
Vector CalculusIdentify the polar coordinate that is not equivalent to(-3,5π/6)
a. (3,11π/6)
b. (3 ,-π/6)
c. (-3,-7π/6)
d. (3,-5π/6)
Calculus
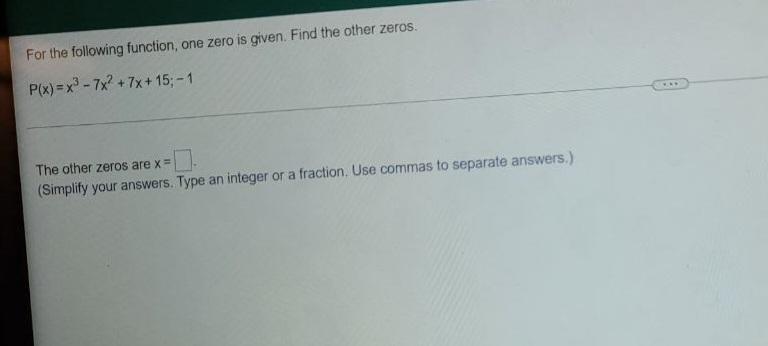
Vector CalculusFor the following function, one zero is given. Find the other zeros.
P(x)=x³-7x² +7x+15; -1
The other zeros are x =
(Simplify your answers. Type an integer or a fraction. Use commas to separate answers.)

Calculus
Vector CalculusDetermine the period of the following function.
y = 3 sin 2(x + 90°) - 1
a) 180°
c) 720°
b) 360°
d) 1080°


Calculus
Vector CalculusExpress the following expression in the form of a + bi: (14+ 5i) - ((2 - 3i) + (4 - 8i)).
5+4i
8+16i
4-2i
4+5i

Calculus
Vector CalculusThe distance between 3(2+ 4i) and 2(1 + 2i) is
4√3 units
2√7 units
3√5 units
4√5 units

Calculus
Vector CalculusDetermine the area of the region bounded between the two curves y = x³ and y = x² - 2x from x = -1 to x = 1. Use a graphing software or calculator to see a picture of the situation. Note that the upper and lower function will change along the interval!

Calculus
Vector CalculusFind a unit vector that has the same direction as the given vector.
-3i + 2j - k
![Vector b [Xb, Yb, Zb] has a magnitude of 6 and the same direction as the vector [2, 3, -1]. The value of Yb is:
a) 1.60
b) 3.20
c) 3.74
d) 4.81](https://media.kunduz.com/media/sug-question/raw/83532730-1658666189.1874952.jpeg?w=256)
Calculus
Vector CalculusVector b [Xb, Yb, Zb] has a magnitude of 6 and the same direction as the vector [2, 3, -1]. The value of Yb is:
a) 1.60
b) 3.20
c) 3.74
d) 4.81

Calculus
Vector CalculusThe scalar equation of the plane passes through (-1, 3, -2), (-1, 2, -1) and (4, 1, -2) is:
2x - 5y + 5z + 3 = 0
2x - 5y5z + 3 = 0
none of the options listed
2x + 5y +5z -3 = 0
Calculus
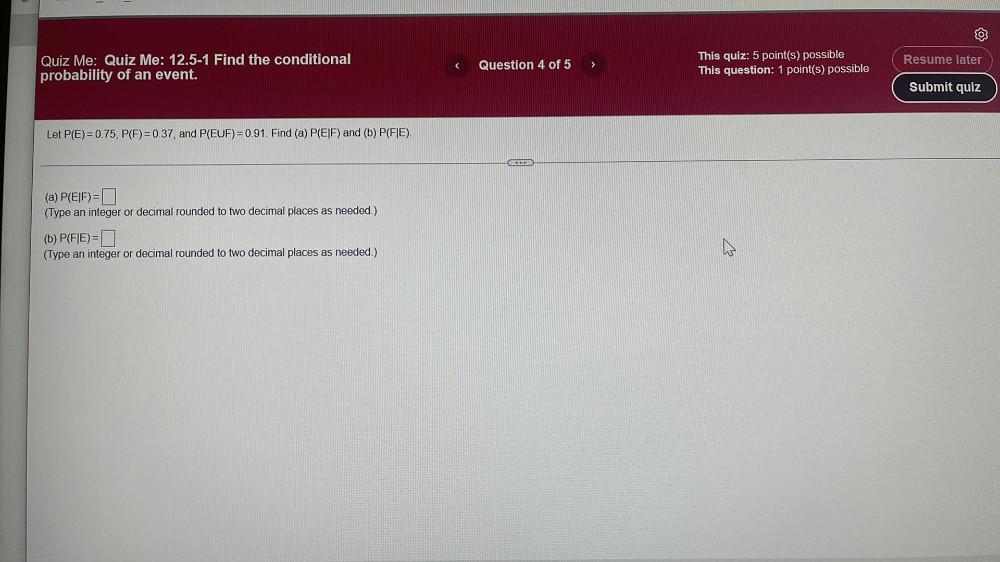
Vector CalculusLet P(E)=0.75, P(F) = 0.37, and P(EUF) = 0.91. Find (a) P(EIF) and (b) P(FIE).
(a) P(EIF) =
(Type an integer or decimal rounded to two decimal places as needed.)
(b) P(FIE)=
(Type an integer or decimal rounded to two decimal places as needed.)

Calculus
Vector CalculusSolve using elementary row operations:
x - y - 3z = -14
x + y + z = 4
-x + y + z = 6

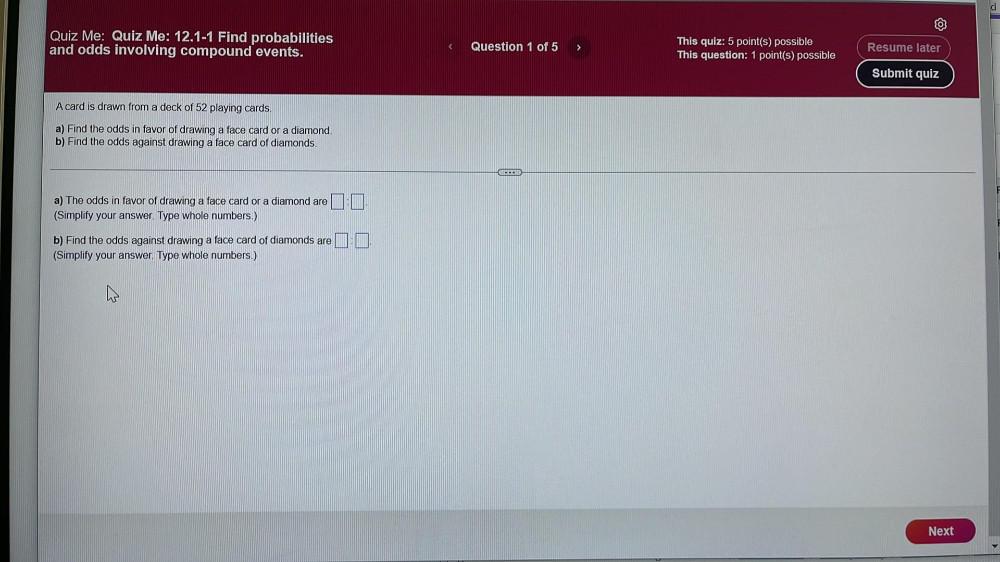
Calculus
Vector CalculusA card is drawn from a deck of 52 playing cards.
a) Find the odds in favor of drawing a face card or a diamond.
b) Find the odds against drawing a face card of diamonds.
a) The odds in favor of drawing a face card or a diamond are
(Simplify your answer. Type whole numbers.)
b) Find the odds against drawing a face card of diamonds are:
(Simplify your answer. Type whole numbers.)
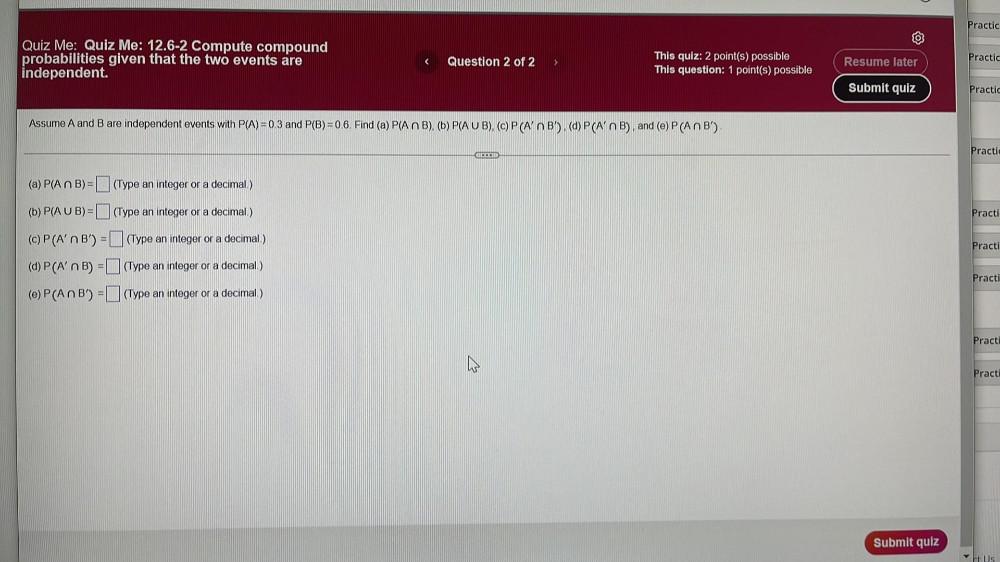
Calculus
Vector CalculusAssume A and B are independent events with P(A) = 0.3 and P(B) = 0.6. Find (a) P(An B), (b) P(A U B), (c) P (An B'), (d) P (A'n B), and (e) P (An B').
(a) P(A ⋂ B)=
(Type an integer or a decimal.)
(b) P(A U B)=
(Type an integer or a decimal.)
(c) P (A' ⋂ B') =
(Type an integer or a decimal.)
(d) P (A' ⋂ B) =
(Type an integer or a decimal.)
(e) P (A ⋂ B') =
(Type an integer or a decimal.)
![Which of the following vectors is coplanar to [1, 1, 1] and [1, 2, 3]?
a) [1, 4, 8]
b) [7, 5, 3]
c) [4, 2, -2]
d) (5, 7, 6]](https://media.kunduz.com/media/sug-question/raw/83532622-1658665802.4061432.jpeg?w=256)
Calculus
Vector CalculusWhich of the following vectors is coplanar to [1, 1, 1] and [1, 2, 3]?
a) [1, 4, 8]
b) [7, 5, 3]
c) [4, 2, -2]
d) (5, 7, 6]

![A baseball player's batting average is 0.337, which can be interpreted as the probability that he got a hit each time at bat. Thus, the probability that he did not get a hit is 1-0.337=0.663. Assume that the occurrence of a hit in any given at-bat has no effect on the probability of a hit in other at-bats. In one game, the player had 4 at-bats. What is the probability that he had 3 hits?
What expression can be used to calculate the probability?
A. [7 4] (0.337)⁴ (0.663)⁴
B. [4 3] (0.337)⁴ (0.663)¹
C. [4 3] (0.337+0.663)³
D. [4 3] (0.337)³ (0.663)¹
The probability that the player had 3 hits in 4 at-bats is
(Round to three decimal places as needed.)](https://media.kunduz.com/media/sug-question/raw/83650979-1658665767.007221.jpeg?w=256)
Calculus
Vector CalculusA baseball player's batting average is 0.337, which can be interpreted as the probability that he got a hit each time at bat. Thus, the probability that he did not get a hit is 1-0.337=0.663. Assume that the occurrence of a hit in any given at-bat has no effect on the probability of a hit in other at-bats. In one game, the player had 4 at-bats. What is the probability that he had 3 hits?
What expression can be used to calculate the probability?
A. [7 4] (0.337)⁴ (0.663)⁴
B. [4 3] (0.337)⁴ (0.663)¹
C. [4 3] (0.337+0.663)³
D. [4 3] (0.337)³ (0.663)¹
The probability that the player had 3 hits in 4 at-bats is
(Round to three decimal places as needed.)

Calculus
Vector CalculusFind the acute angle between the lines. Round your answer to the nearest degree.
5x - y = 4, 8x + y = 7

Calculus
Vector CalculusUse vectors to calculate the area of the parallelogram formed by the points A(-1, 1, -1), B(2, -1, 3) and C(5, 3, 4).
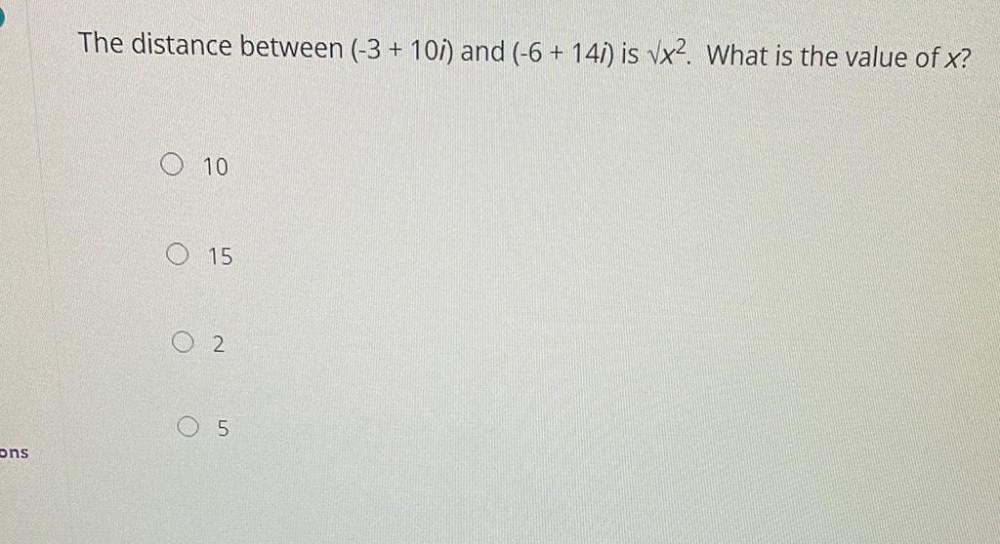
Calculus
Vector CalculusThe distance between (-3 + 10i) and (-6 + 14i) is √x². What is the value of x?
10
15
2
5

Calculus
Vector CalculusFind the intersection of the following planes by letting z = t.
5x - 4y + z- 1 = 0
x - z + 3 = 0

Calculus
Vector CalculusWhich of the following is not an equation for the line passing through the points P(1,4,-3) and Q(3,2,1)?
a. r = (1,4,-3) + s(2,-2,4), s∈R
b. x-3/2 = y-2/-2 = z+1/4
c. x = -t+3, y=t+2, z=-2t+1, t∈R
d. r = (3,2,1)+s(1,-1,2), s∈R
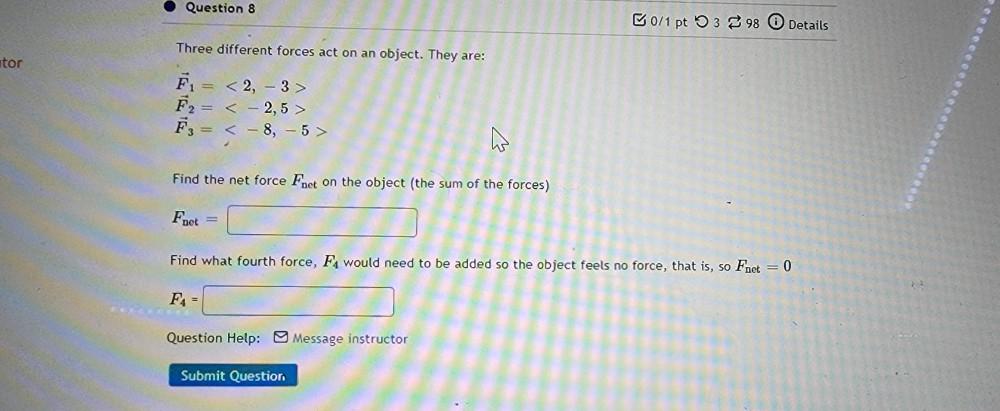
Calculus
Vector CalculusThree different forces act on an object. They are:
F₁ = <2, -3>
F₂ = <-2, 5>
F₃ = <-8, -5>
Find the net force Fnet on the object (the sum of the forces)
Fnet =
Find what fourth force, F₄ would need to be added so the object feels no force, that is, so Fnet = 0
F₄=
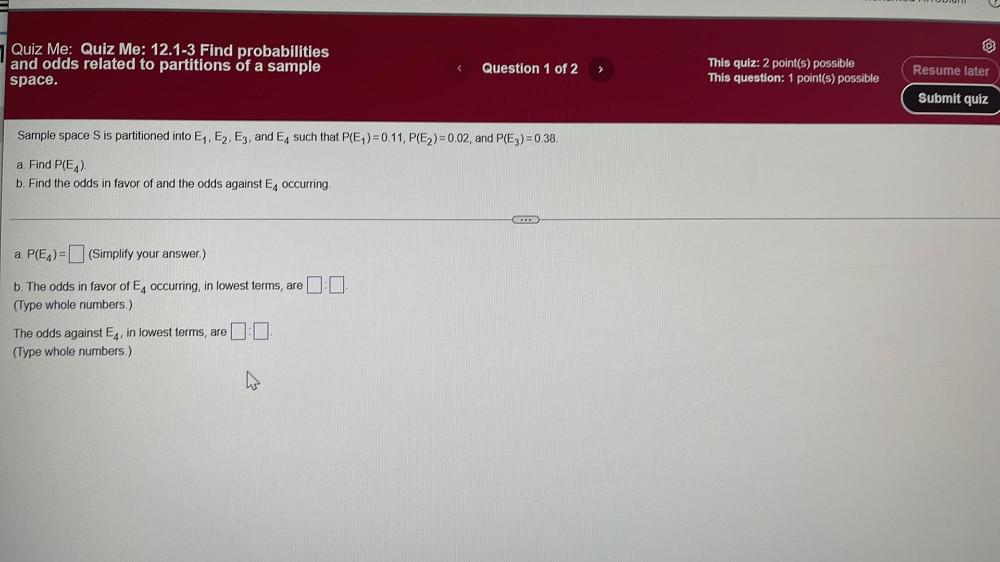
Calculus
Vector CalculusSample space S is partitioned into E₁, E₂, E₃, and E₄ such that P(E₁)=0.11, P(E₂)=0.02, and P(E₃) = 0.38.
a. Find P(E₄).
b. Find the odds in favor of and the odds against E₄ occurring.
a. P(E₄)= (Simplify your answer.)
b. The odds in favor of E₄ occurring, in lowest terms, are
(Type whole numbers.)
The odds against E₄, in lowest terms, are:
(Type whole numbers.)
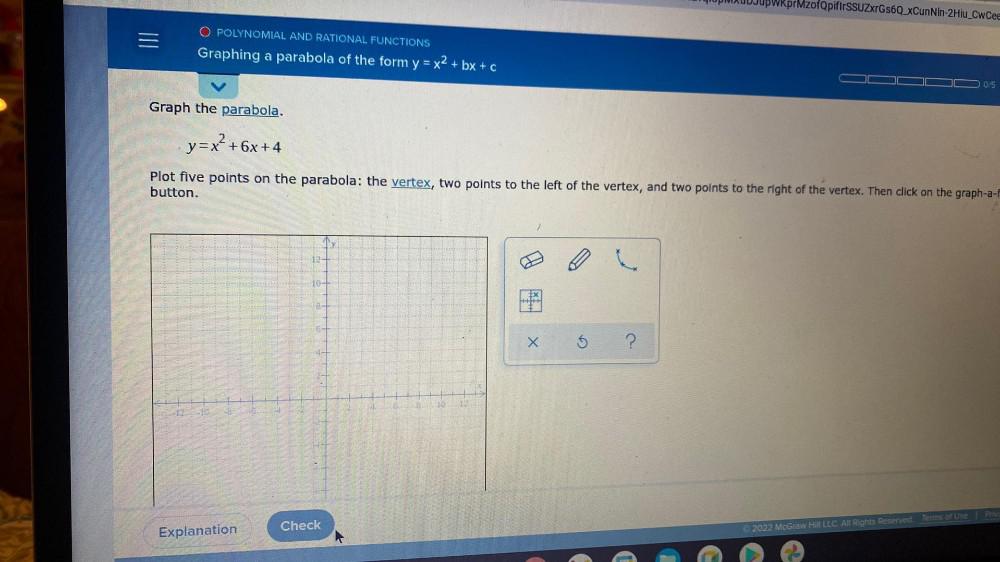
Calculus
Vector CalculusGraph the parabola.
y=x² +6x+4
Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-b button.

Calculus
Vector CalculusDetermine whether the given information results in one triangle, two triangles, or no triangle at all. Solve the triangle(s) that results. Round any side length to two decimal places and any angles to one decimal place.
a = 17, c = 34, A = 30°
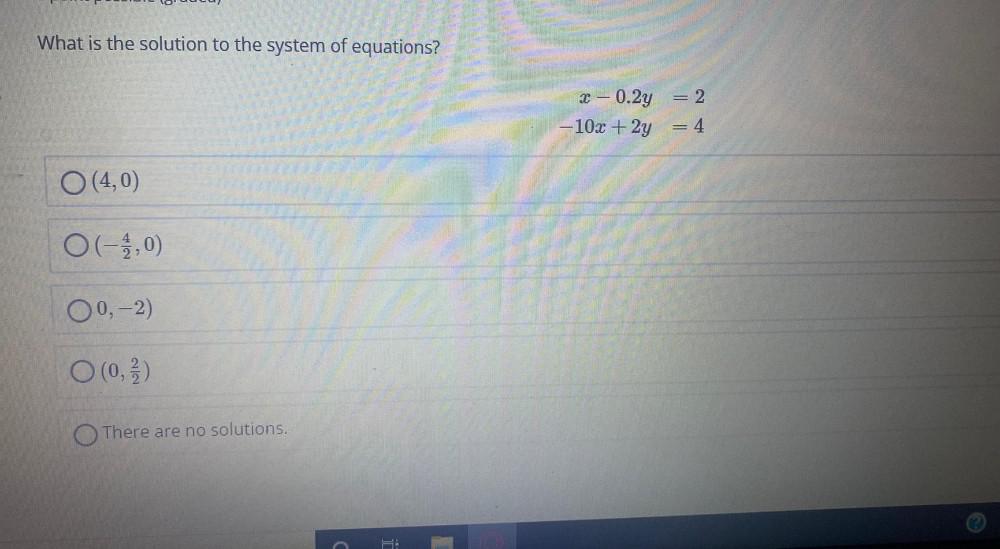
Calculus
Vector CalculusWhat is the solution to the system of equations?
x - 0.2y = 2
-10x + 2y = 4
(4,0)
(-4/2,0)
(0,-2)
(0, 2/2)
There are no solutions.
![Given the vector field F(x, y) = (y³, -x³) and the counterclockwise oriented unit circle
C: {
x = сosπt
y = sinπt, compute ∫F. dr.
t = [0,2]](https://media.kunduz.com/media/sug-question/raw/83962957-1658664647.5371466.jpeg?w=256)
Calculus
Vector CalculusGiven the vector field F(x, y) = (y³, -x³) and the counterclockwise oriented unit circle
C: {
x = сosπt
y = sinπt, compute ∫F. dr.
t = [0,2]
![4. (28 points) Given the vector field F(x, y) = (ye^xcos e^x, sin e^x), the clockwise oriented part of the
x=t
parabola C₁ : y = -t^2 + 5t-6, the line segment C₂ from (3,0) to (2,0):
t ∈ [2,3]
a) Sketch C₁ and C₂](https://media.kunduz.com/media/sug-question/raw/83965328-1658664638.6687186.jpeg?w=256)
Calculus
Vector Calculus4. (28 points) Given the vector field F(x, y) = (ye^xcos e^x, sin e^x), the clockwise oriented part of the
x=t
parabola C₁ : y = -t^2 + 5t-6, the line segment C₂ from (3,0) to (2,0):
t ∈ [2,3]
a) Sketch C₁ and C₂

Calculus
Vector CalculusJames and Abeer took a backpacking trip together. On the first day, they hiked 9 miles to a campsite. The next day, they took a different route back that was 4 miles longer than the route they took on the first day. How many miles did they hike all together?
22 miles
18 miles
13 miles
5 miles

Calculus
Vector CalculusResolve the following vectors into components:
(a) The vector i in 2-space of length 5 pointing up at an angle of 3/4 measured from the positive x-axis.
(b) The vector u in 3-space of length 3 lying in the ya-plane pointing upward at an angle of /4 measured from the positive y-axis.
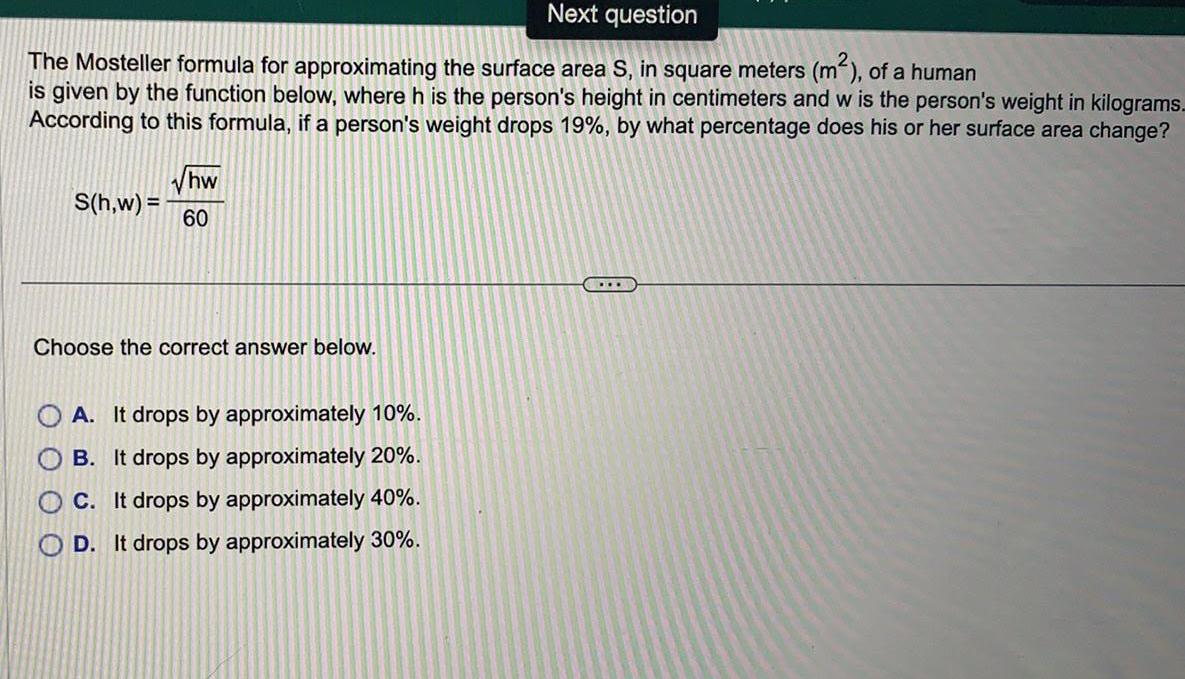
Calculus
Vector CalculusThe Mosteller formula for approximating the surface area S, in square meters (m²), of a human
is given by the function below, where h is the person's height in centimeters and w is the person's weight in kilograms.
According to this formula, if a person's weight drops 19%, by what percentage does his or her surface area change?
S(h,w) =hw/60
Choose the correct answer below.
A. It drops by approximately 10%.
B. It drops by approximately 20%.
C. It drops by approximately 40%.
D. It drops by approximately 30%.
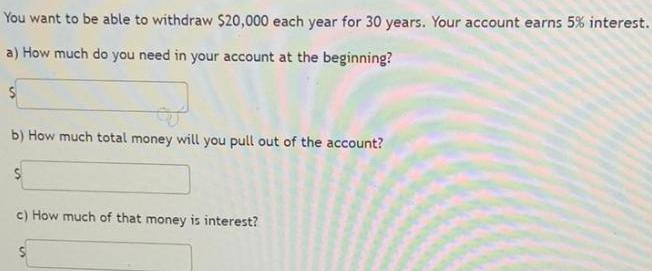
Calculus
Vector CalculusYou want to be able to withdraw $20,000 each year for 30 years. Your account earns 5% interest.
a) How much do you need in your account at the beginning?
b) How much total money will you pull out of the account?
c) How much of that money is interest?

Calculus
Vector CalculusA 30-ft tree casts a shadow horizontally along the ground. A girl standing at the tip of the shadow is looking at a bird nesting at the top of the tree at an angle of 70°. The girl then walks away from the tip of the shadow some distance and looks up at the nest at an angle of 55°. How many feet did the girl walk from the tip of the shadow to her new location? Assume that you can neglect the height of the girl.
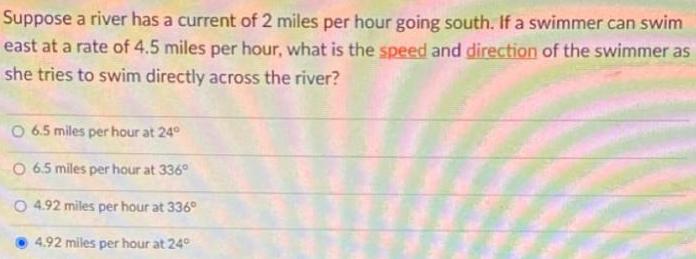
Calculus
Vector CalculusSuppose a river has a current of 2 miles per hour going south. If a swimmer can swim
east at a rate of 4.5 miles per hour, what is the speed and direction of the swimmer as
she tries to swim directly across the river?
6.5 miles per hour at 24°
6.5 miles per hour at 336°
4.92 miles per hour at 336°
4.92 miles per hour at 24°
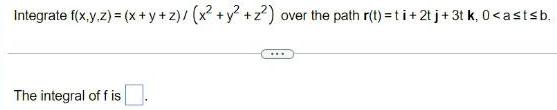
Calculus
Vector CalculusIntegrate f(x,y,z) = (x+y+z)/(x² + y² +z²) over the path r(t)=ti + 2t j + 3t k, 0<a≤t≤b.
The integral of f is

Calculus
Vector CalculusThe graph of f(x)= 3x³+1/8x3 will behave like which function for large values of |x|?
y= 3/8
y= 3x/8
y=3/8x
y=3/8 x3
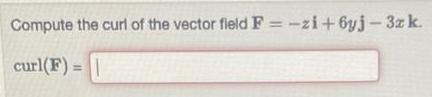
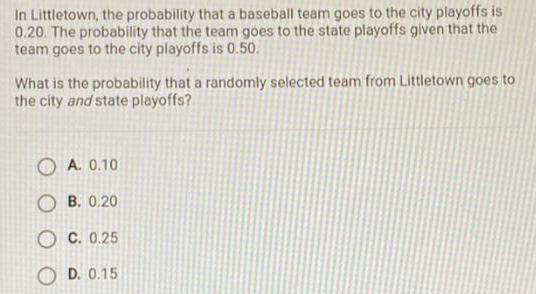
Calculus
Vector CalculusIn Littletown, the probability that a baseball team goes to the city playoffs is 0.20. The probability that the team goes to the state playoffs given that the team goes to the city playoffs is 0.50.
What is the probability that a randomly selected team from Littletown goes to the city and state playoffs?
A. 0.10
B. 0.20
C. 0.25
D. 0.15
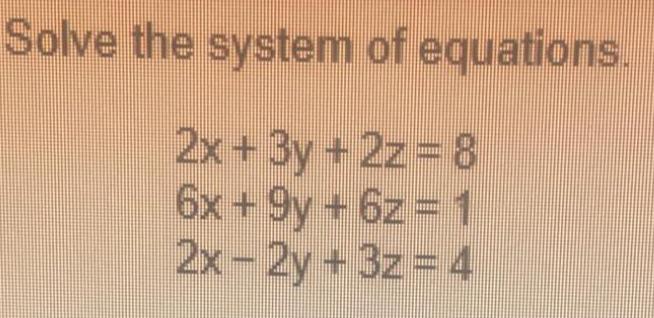

Calculus
Vector CalculusGiven the region R enclosed by y² = x² and x² + (y + 5)² = 10.
a) Sketch the region R.
b) Set up the double integral that represents the area of the region in two different ways.
c) Evaluate the area of the region
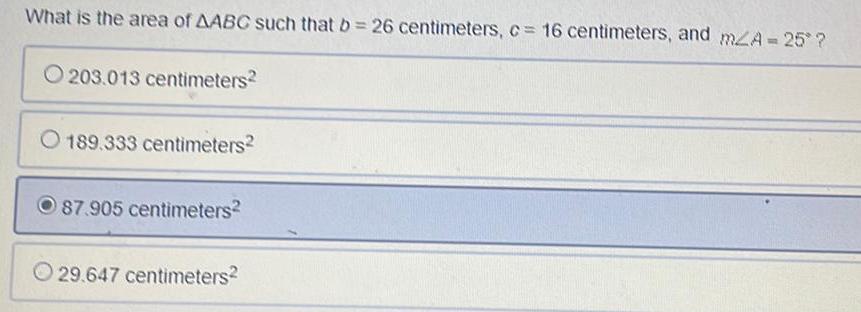
Calculus
Vector CalculusWhat is the area of ΔABC such that b = 26 centimeters, c = 16 centimeters, and m∠A = 25°?
203.013 centimeters²
189.333 centimeters²
87.905 centimeters²
29.647 centimeters²

Calculus
Vector CalculusModular cassettes are often used in long-term care settings for all of the following, except:
A. to simplify record keeping
B. to minimize waste
C. to decrease chances of medication errors
D. to decrease the workload of the pharmacist

Calculus
Vector CalculusGiven that the transformation C: R² → R² is the composite of counterclockwise rotation R about the point (-1,3) by 270° followed by a projection P onto the y-axis, use homogeneous coordinates to find C

Calculus
Vector CalculusThe produce manager at a market orders 50 lb of tomatoes, 10 lb of zucchini, and 20 lb of onions from a local farmer one week.
a) Write a 1x3 matrix A that represents the amount of each item ordered.
b) The following week, the produce manager increases his order by 10%. Find a matrix B that represents this order.
c) Find A+B and tell what the entries represent.
a) Write the entries in the order in which they are given in the problem statement.
A=
b) Write the entries in the order in which they are given in the problem statement.
B=
c) A+B=
What do the entries of A+B represent?
A. The entries represent the total produce orders for the two weeks.
B. The entries represent the projected produce orders for the third week.
C. The entries represent the change in produce orders between the two weeks.
D. The entries represent the maximum weekly produce orders for the two weeks.
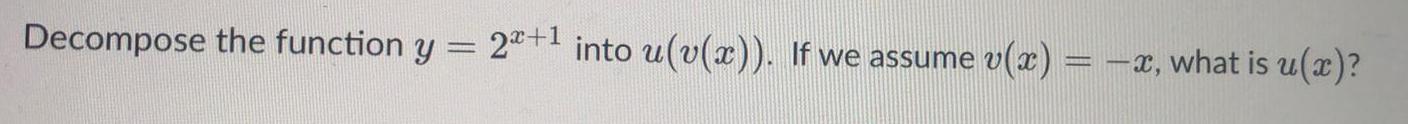
Calculus
Vector CalculusDecompose the function y = 2+¹ into u(v(x)). If we assume v(x) = -x, what is u(x)?

Calculus
Vector CalculusPlot the point whose cylindrical coordinates are given. Then find the rectangular coordinates of the point.
(a) (4, π/2, 3)
(x, y, z) = ( )
(b) (4, -π/4, -3)
(x,y,z) = ( )

Calculus
Vector CalculusWrite the equations in cylindrical coordinates.
(a) 3x² - 9x + 3y² + z² = 7
(b) z = 6x² - 6y²