Functions Questions and Answers

Math - Others
FunctionsProblem 1. A function f is given, and the indicated transformations are applied to its graph.
• Write an equation for the final transformed graph.
• Graph the function after the transformation
1. f(x) = x², stretch vertically by a factor of 2, shifted down 2 units and shift 3 units to the
right.
2. f(x)=√x, reflect over x- axis, stretch horizontally by a factor of 4, and shift up 2 units.
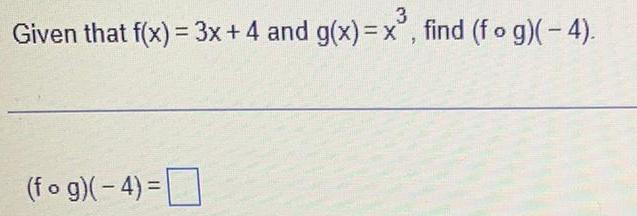
Math - Others
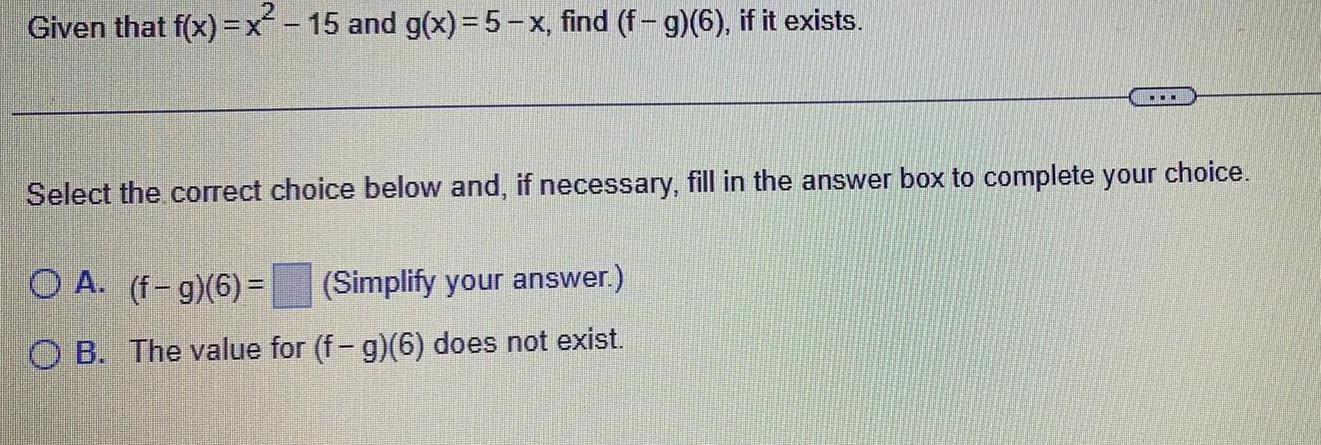
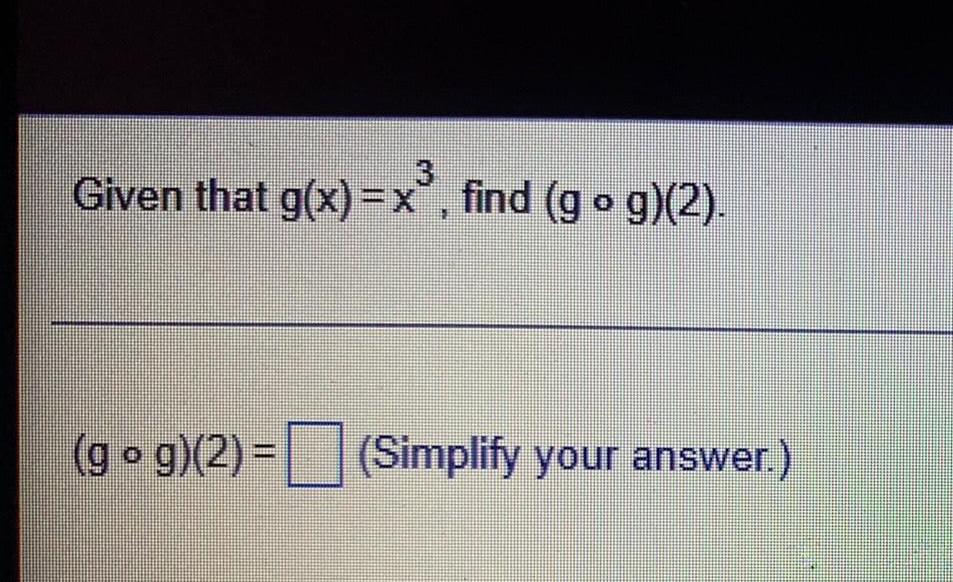
FunctionsGiven that f(x)=x²-15 and g(x)=5-x, find (f - g)(6), if it exists.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. (f-g)(6)=___ (Simplify your answer.)
B. The value for (f- g)(6) does not exist.
Math - Others
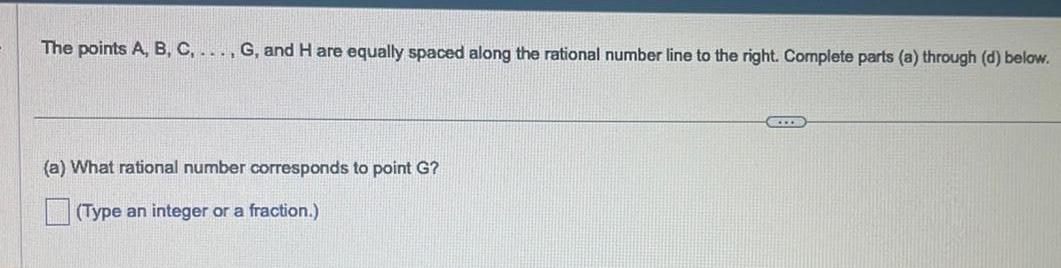
FunctionsThe points A, B, C, ..., G, and H are equally spaced along the rational number line to the right. Complete parts (a) through (d) below.
(a) What rational number corresponds to point G?
(Type an integer or a fraction.)
Math - Others
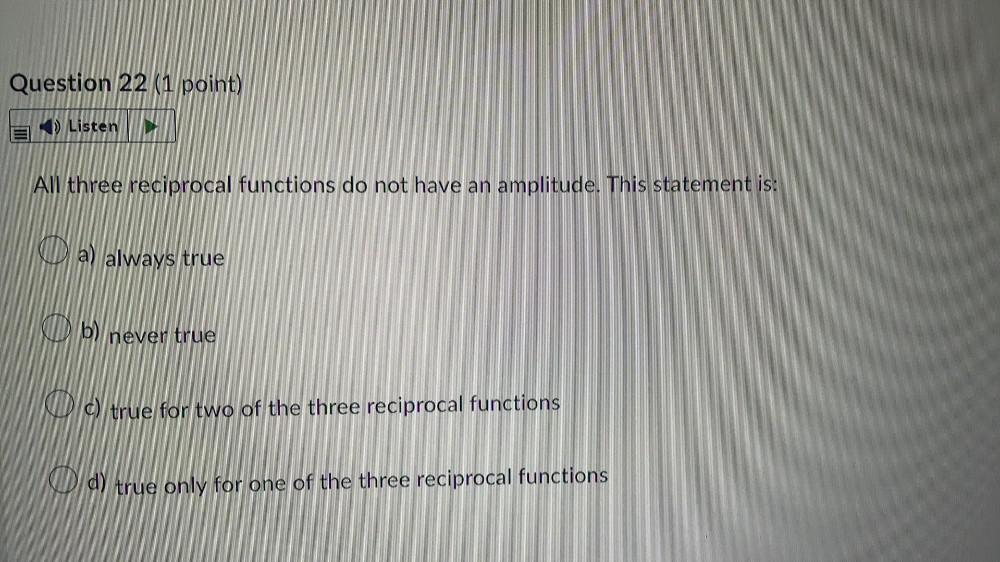
FunctionsAll three reciprocal functions do not have an amplitude. This statement is:
a) always true
b) never true
c) true for two of the three reciprocal functions
d) true only for one of the three reciprocal functions

Math - Others
FunctionsThe range for the function f(x) = -3 sin x is:
a)Range: {y|-2 ≤ y ≤ 3, y ∈ R}
b)Range:{y|0 ≤ y ≤ 3, y ∈ R}
c)Range: {y|2 ≤ y ≤ 3, y ∈ R}
d)Range: {yl-3 ≤ y ≤ 3, y ∈ R}
![(3) Identify the domain and range of the relation, and determine whether the relation is a function {(-7, -12), (-3, -5), (1, 16), (8, 18)}
(A) Domain: {-7, -3, 1, 8); Range: {-12, -5, 16, 18); Not a function
(B) Domain: {-12, -5, 16, 18); Range: {-7, -3, 1, 8); Not a function
(C) Domain: {-12, -5, 16, 18}; Range: {-7, -3, 1, 8); Function
(D) Domain: {-7, -3, 1, 8); Range: {-12, -5, 16, 18); Function
(4) Find the indicated function and write its domain in interval notation.
p( x) = x² + 2x, q(x) = √(1-x), (q/p)(x) = ?
(A) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, ∞)
(B) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0] U (0, 1]
(C) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, 1]
(D) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, ∞)](https://media.kunduz.com/media/sug-question/raw/82397408-1659196767.3630311.jpeg?w=256)
Math - Others
Functions(3) Identify the domain and range of the relation, and determine whether the relation is a function {(-7, -12), (-3, -5), (1, 16), (8, 18)}
(A) Domain: {-7, -3, 1, 8); Range: {-12, -5, 16, 18); Not a function
(B) Domain: {-12, -5, 16, 18); Range: {-7, -3, 1, 8); Not a function
(C) Domain: {-12, -5, 16, 18}; Range: {-7, -3, 1, 8); Function
(D) Domain: {-7, -3, 1, 8); Range: {-12, -5, 16, 18); Function
(4) Find the indicated function and write its domain in interval notation.
p( x) = x² + 2x, q(x) = √(1-x), (q/p)(x) = ?
(A) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, ∞)
(B) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0] U (0, 1]
(C) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, 1]
(D) (q/p)x = √(1-x)/(x² + 2x); (-∞, -2) U (-2, 0) U (0, ∞)

Math - Others
Functions2. Using the Lagrangian method without slack variables find the minima of:
f(x,y)=4x²-5xy+3y² +8x+7y-8.
listing all the KKT conditions applicable to this problem. The linear constraints are given below, one of which is inactive.
g1: y+0.84x-6 ≥0;
g2: y+1.6x-720;
g3: y-1.7x+5≤0;

Math - Others
FunctionsDetermine the interval(s) where the graph of the
function is decreasing.
(-1,-3)
(-3,-1)
(-∞,00)
(-3,-2)
(-3, -1), (-2, -3)
Math - Others
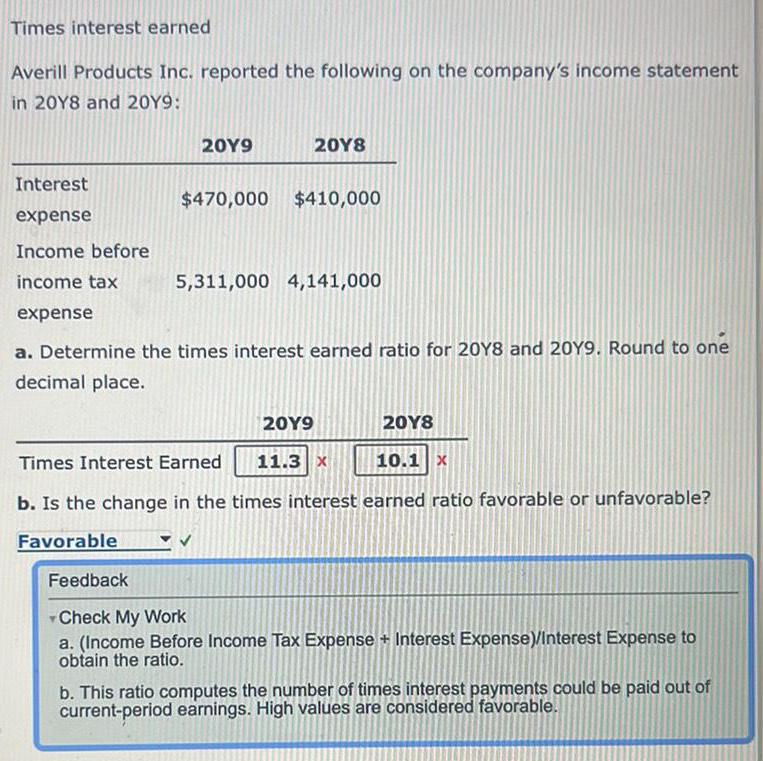
FunctionsTimes interest earned
Averill Products Inc. reported the following on the company's income statement
in 20Y8 and 20Y9:
Interest
expense
Income before
income tax
expense
20Y9
20Y8
$470,000 $410,000
5,311,000 4,141,000
a. Determine the times interest earned ratio for 20Y8 and 20Y9. Round to one
decimal place.
20Y9
20Y8
Times Interest Earned 11.3 x
10.1 x
b. Is the change in the times interest earned ratio favorable or unfavorable?
Favorable
Feedback
Check My Work
a. (Income Before Income Tax Expense + Interest Expense)/Interest Expense to
obtain the ratio.
b. This ratio computes the number of times interest payments could be paid out of
current-period earnings. High values are considered favorable.

Math - Others
FunctionsThe function f(x) = x+8/x-4
is one-to-one. For the function,
a. Find an equation for f-1(x), the inverse function.
b. Verify that your equation is correct by showing that f(f-¹(x)) = x and f-¹ (f(x)) = x.
Math - Others
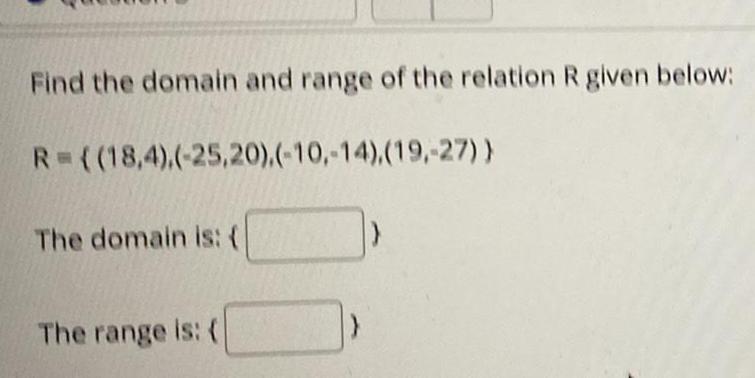
FunctionsFind the domain and range of the relation R given below:
R=((18,4),(-25,20),(-10,-14),(19,-27))
The domain is: {
The range is: (

Math - Others
Functions8. The equation of an exponential function is given as f(x) = -2(4)^3x-15 +6.
a) State the base function and describe the transformations that were applied to the
function f(x) = ab^x to obtain this function. Transformations must be written in
the correct order.
b) Write the domain and range of the function

Math - Others
FunctionsA function is given by the equation f(x) = 2(x - 1)² +3. Answer the following
questions. Show all your work/calculations!
a) Determine the value of f (4).
b) Determine the value of x when f (x) = 3.
c) Determine the inverse equation of this function.
d) Write the domain and range of the inverse function.

Math - Others
Functions(a) A consultant wants to ask workers at a factory about the workers' job satisfaction. Which of the following best describes a stratified sample of workers?
The consultant forms groups of 30 workers based on the lengths of time the workers have worked at the factory. Then, he randomly chooses 3 groups and selects all of the workers in these groups.
The consultant forms 5 groups of workers based on the workers' shifts. Then, he selects 18 workers at random from each group.
The consultant assigns each worker a different number. Using a random number table, he draws 90 of those numbers at random. Then, the consultant selects the workers assigned to the drawn numbers. Every set of 90 workers is equally likely to be drawn using the random number table.
(b) A manager at a bus company wants to survey employees about the new uniforms. Which of the following best describes a systematic sample of employees?
The manager takes a list of the employees and selects every 3rd employee until 78 employees are selected,
The manager asks for volunteers and selects every volunteer until 78 employees are selected. She selects the volunteers because these employees are easily accessible.
The manager forms 6 groups of employees based on the departments the employees are in. Then, she selects 13 employees at random from each group.
(c) A host on a cruise ship wants to collect data on the time passengers spend at various activities on board. Which of the following best describes a random sample of passengers?
The host forms groups of 8 passengers based on the passengers' ages. Then, he randomly chooses 7 groups and selects all of the passengers in these groups.
The host assigns each passenger a different number. Using a random number table, he draws 56 of those numbers at random. Then, he selects the passengers assigned to the drawn numbers. Every set of 56 passengers is equally likely to be drawn using the random number table.
The host takes a list of the passengers and selects every 7th passenger until 56 passengers are selected.
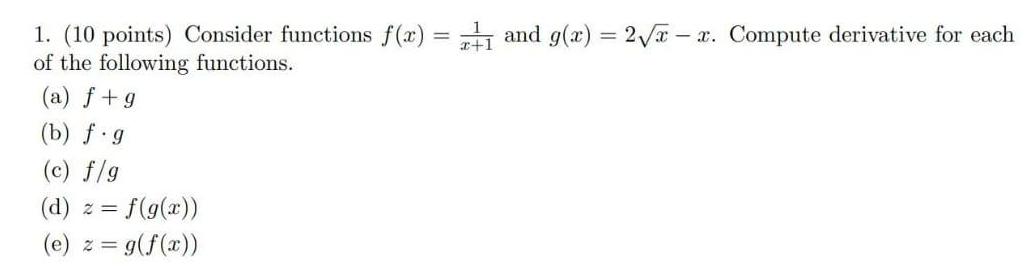
Math - Others
Functions1.Consider functions f(x) = 1/x+1 and g(x) = 2√x-x. Compute derivative for each of the following functions.
(a) f+g
(b) f.g
(c) f/g
(d) z = f(g(x))
(e) z = g(f(x))

Math - Others
Functions(a) A city manager wants to poll residents about a park renovation. Which of the following best describes a cluster sample of residents?
The city manager forms groups of 12 residents based on the streets the residents live on. Then, she selects all of the residents in 5 randomly chosen groups.
The city manager uses a computer program to draw 60 residents at random and selects these residents. Every set of 60 residents is equally likely to be drawn by the computer program.
The first 60 residents who walk into city hall one day are easily accessible. So, the city manager selects these residents.
(b) A manager at a bus company wants to survey employees about the new uniforms. Which of the following best describes a systematic sample of employees?
The manager forms groups of 8 employees based on the departments the employees are in. Then, she selects all of the employees in 7 randomly chosen groups.
The manager forms 7 groups of employees based on the departments the employees are in. Then, she selects 8 employees at random from each group.
The manager takes a list of the employees and selects every 7th employee until 56 employees are selected.
(c) A consultant wants to ask workers at a factory about the workers' job satisfaction. Which of the following best describes a convenience sample of workers?
All of the workers on the second floor of the factory building are easily accessible. So, the consultant selects the first 72 workers from the second floor to arrive at work on a particular day.
The consultant takes a list of the workers and selects every 3rd worker until 72 workers are selected.
The consultant assigns each worker a different number. Using a random number table, he draws 72 of those numbers at random. Then, the consultant selects the workers assigned to the drawn numbers. Every set of 72 workers is equally likely to be drawn using the random number table.

Math - Others
FunctionsAccording to lecture, which of these is a function of political parties? provide a certain ideology
recruiting candidates and running elections
policy formulation and promotion (governing)
unity/linkage/accountability
All of the above are functions of political parties
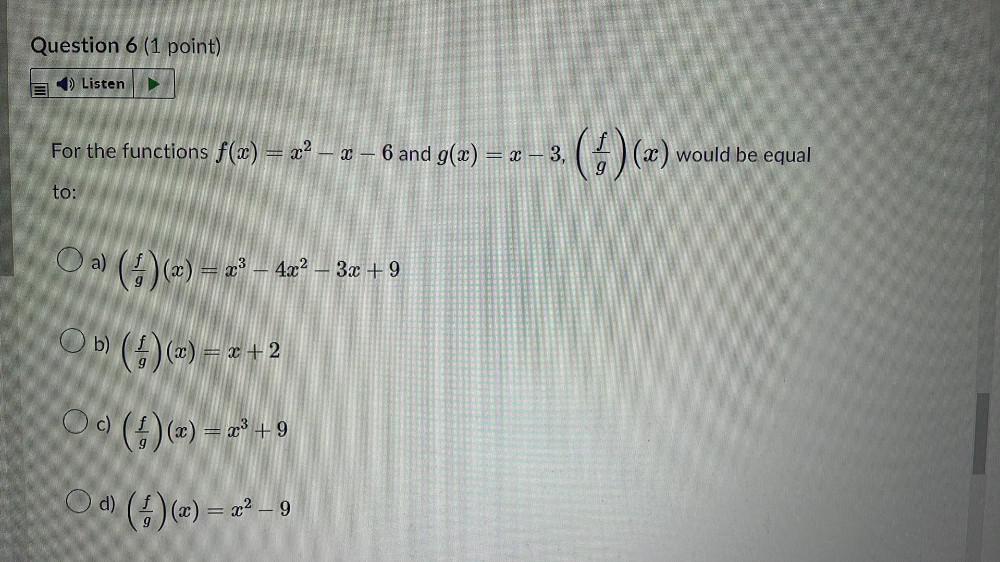
Math - Others
FunctionsFor the functions f(x) = x² - x - 6 and g(x) = x − 3,(f/g)(x) would be equal to:
a) (f/g) (x) = x³ − 4x² − 3x +9
b) (f/g) (x) = x + 2
c) (f/g) (x) = x³ + 9
d) (f/g) (x)=x²-9

Math - Others
FunctionsFor the functions f(x) = 3x - 5 and g(x) = x + 1, find (fog)(x):
a) (fog)(x) = x + 1
b) (fog)(x) = 3x - 5
c) (fog)(x) = 3x - 4
d) (fog)(x) = 3x - 2

Math - Others
FunctionsWhat type of reflection symmetry does the graph of f(x) = cosx display?
a) reflection in the line y = x
b) reflection in the y-axis
c) reflection in the x-axis
d) reflection through the origin

Math - Others
Functions(f/g) (x) and (g/f) (x) are the same function. This statement is:
a) true for most functions f(x) and g(x)
b) false for most functions f(x) and g(x)
c) always true
d) always false
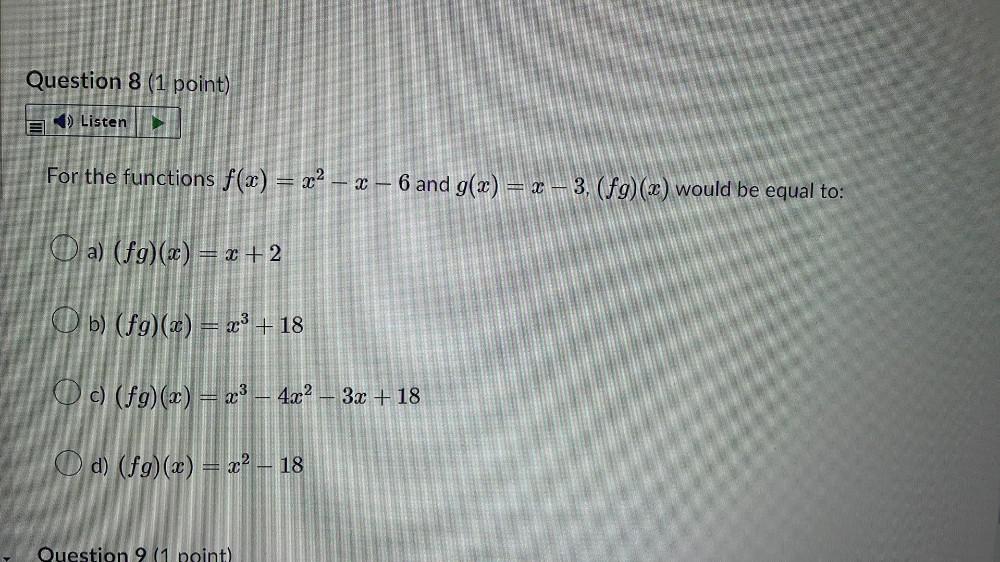
Math - Others
FunctionsFor the functions f(x) = x² - x - 6 and g(x) = x - 3, (fg)(x) would be equal to:
a) (fg)(x) = x + 2
b) (fg)(x) = x³ + 18
c) (fg)(x) = x³ − 4x² − 3x + 18
d) (fg)(x) = x² – 18
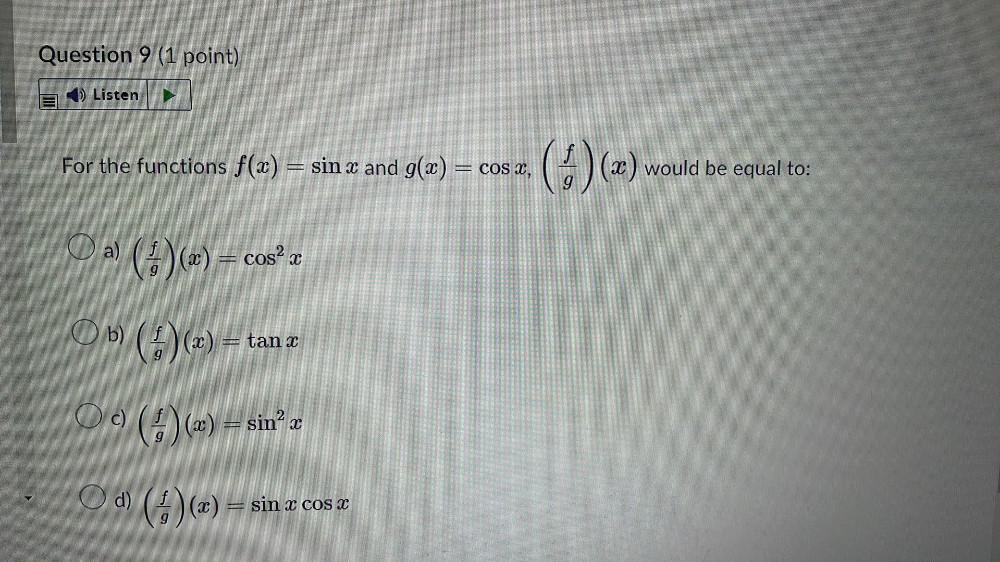
Math - Others
FunctionsFor the functions f(x) = sin x and g(x) = cos x,
A) (f/g)(x) = cos²x
B) (f/g)(x) = tan x
C) (f/g)(x) = sin² x
D) (f/g)(x) = sin x cos x
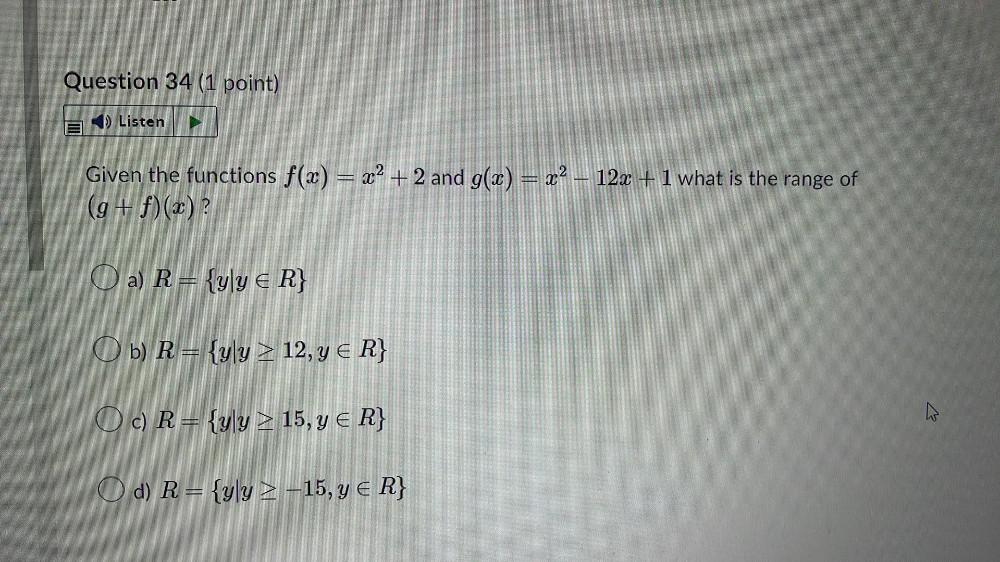
Math - Others
FunctionsGiven the functions f(x) = x² + 2 and g(x) = x² − 12x + 1 what is the range of (g + f)(x) ?
a) R = {y \ y ∈ R}
b) R = {y \ y ≥ 12, y ∈ R}
c) R = {y \ y ≥ 15, y ∈ R}
d) R = {y \ y ≥ -15, y ∈ R}
Math - Others
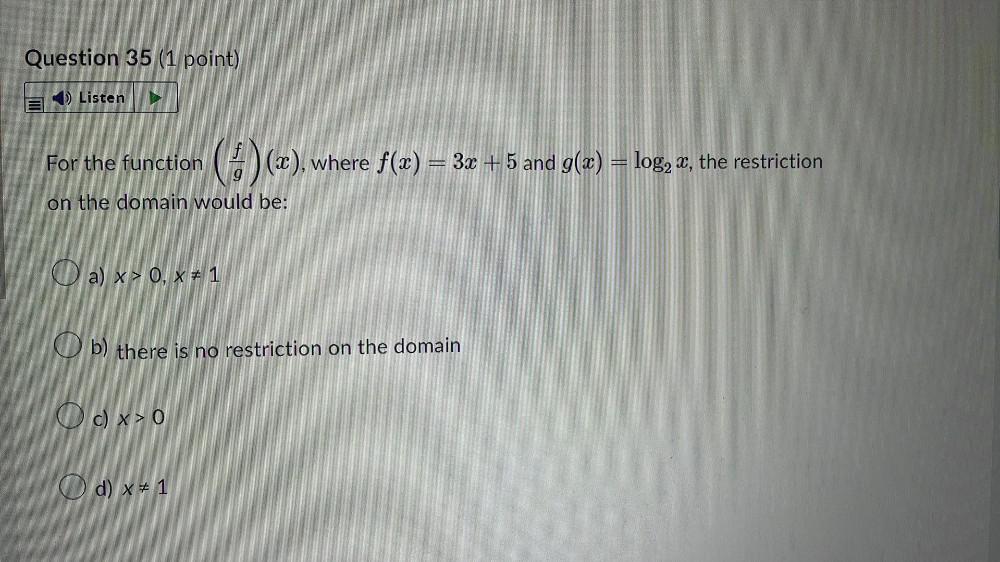
FunctionsFor the function (f/g)(x), where ƒ(x) = 3x + 5 and g(x) = log₂x the restriction on the domain would be:
a) x > 0, x ≠ 1
b) there is no restriction on the domain
c) x > 0
d) x ≠ 1

Math - Others
FunctionsIf r(t(x)) = t(x) then r(p) = p. Assuming that t(x) is not the zero function and p ∈ Range(t(x)).
a) This statement is always true.
b) This statement is sometimes true.
c) This statement is never true.

Math - Others
FunctionsThe sum of two linear functions is:
a) may be a linear or horizontal line.
b) always a horizontal line
c) always linear function.
d) always vertical line
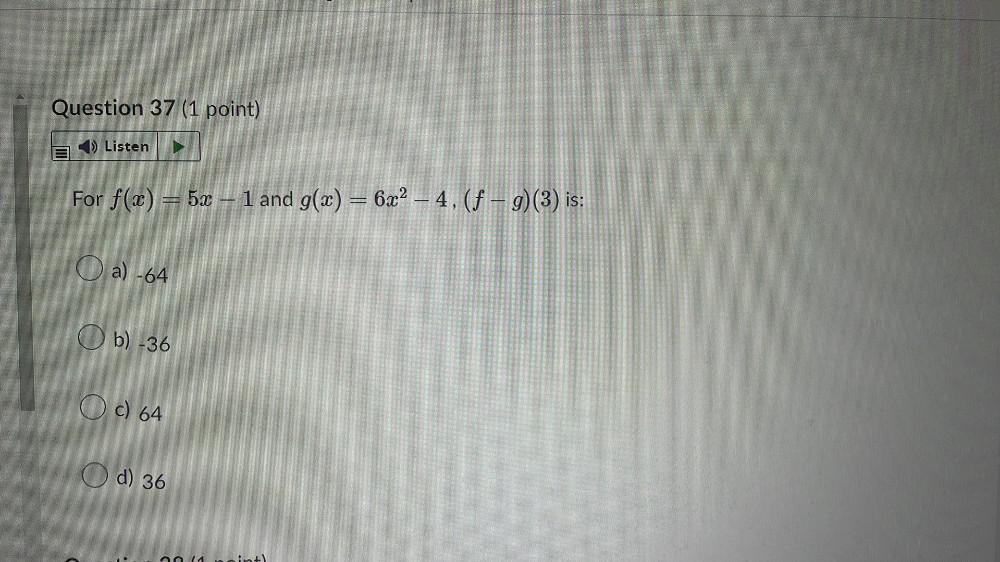

Math - Others
FunctionsFor two functions, f(x) and g(x)
g(f(x)) = f(g(x))
a) This statement is always true.
b) This statement is sometimes true.
c) This statement is never true.

Math - Others
FunctionsFor f(x) = x² + 2x − 2, what value of g(x) gives (ƒ – g)(3) = 11?
a)-11
b) -2
c) 11
d) 2
Math - Others
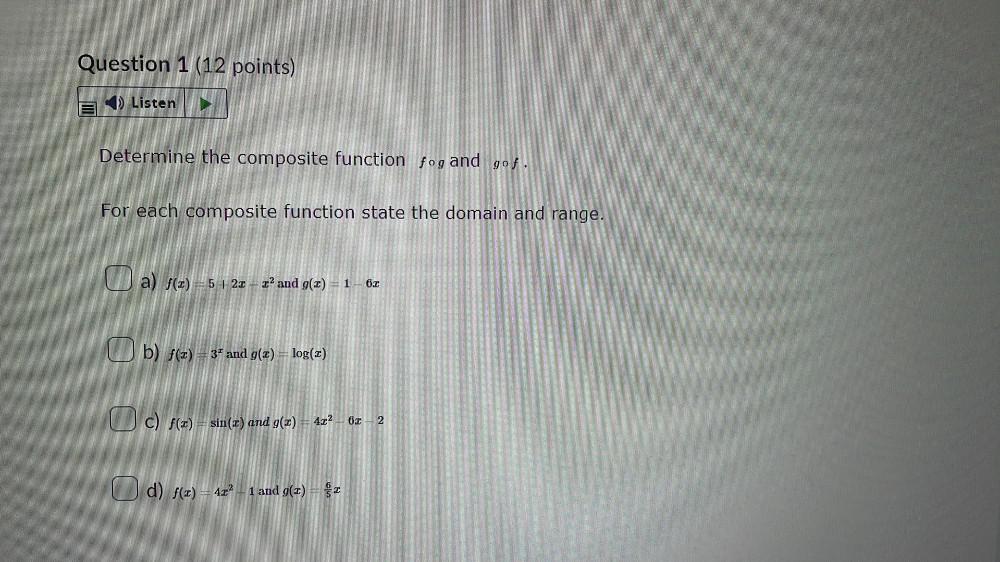
FunctionsDetermine the composite function fog and gof.
For each composite function state the domain and range.
a) f(z)-5-1-2x - z² and g(z) 1-6z
b) f(z) 3 and g(z) = log(z)
c) f(x) = sin(z) and g(x) 4x²- 6x- 2
d) f(z) - 42²-1 and g(z) = z

Math - Others
Functions(ƒ + g)(x) and (g + f)(x) are the same function. This statement is:
a) true for most functions f(x) and g(x)
b) false for most functions f(x) and g(x)
c) always true
d) always false
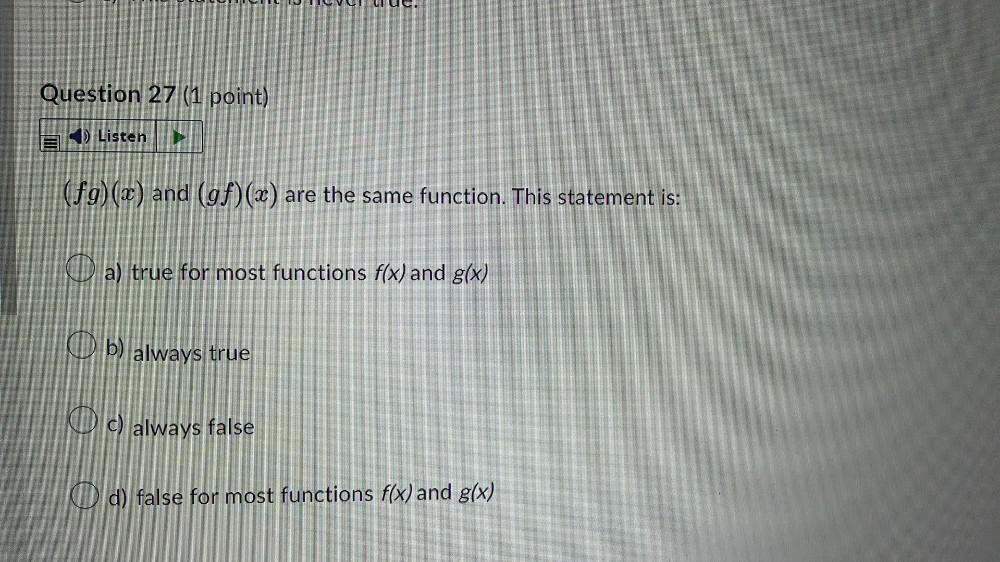
Math - Others
Functions(f g)(x) and (g f)(x) are the same function. This statement is:
a) true for most functions f(x) and g(x).
b) always true.
c) always false.
d) false for most functions f(x) and g(x).
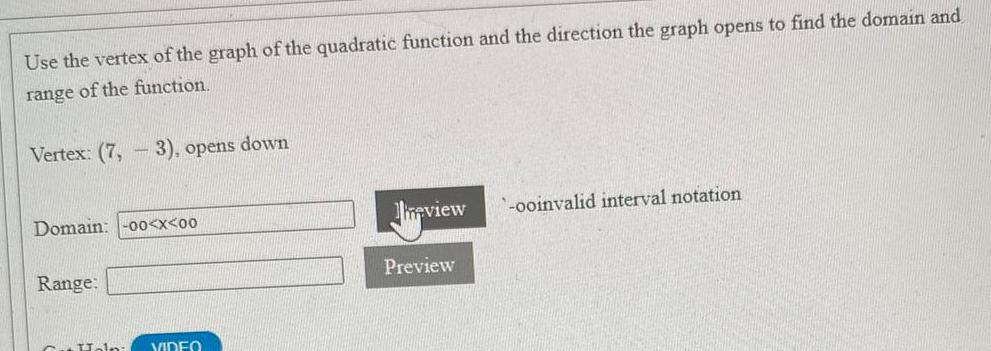
Math - Others
FunctionsUse the vertex of the graph of the quadratic function and the direction the graph opens to find the domain and range of the function.
Vertex: (7,3), opens down
Domain:
Range:

Math - Others
FunctionsSuppose that f is a function given as f(x)=x³ + bx² + cx Find the exact values of b and c if we know that the line y =4x-4 is a tangent line to the graph of f at x = - 1.
b=
c=
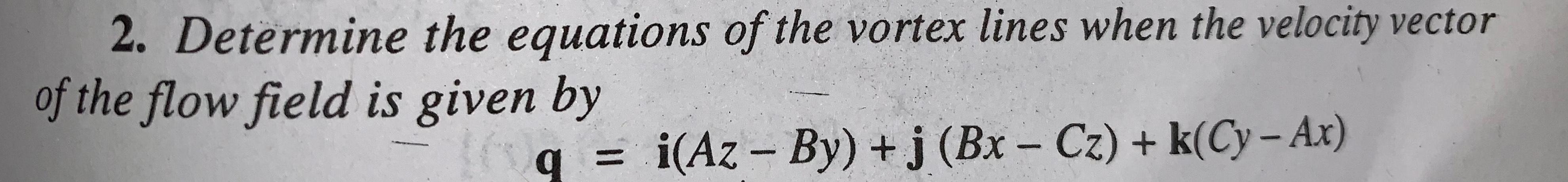
Math - Others
Functions2. Determine the equations of the vortex lines when the velocity vector
of the flow field is given by
i(Az - By) + j (Bx - Cz) + k(Cy-Ax)

Math - Others
FunctionsPopulation Growth in Clark County A certain county in Nevada is one of the fastest-growing metropolitan areas in the United States. The population of this county from 1 approximated by the function
P(t) = 43,059t³ - 86,394t2 + 234,633t + 273,288
(0 ≤ t ≤ 4)
where t is measured in decades, with t= 0 corresponding to the beginning of 1970.
(a) Was the population of the county always increasing or decreasing over the time period in question. Hint: Show that P'(t) > 0 for all t in the interval (0, 4).
increasing
decreasing
varies
(b) Find when the population is increasing or decreasing at the slowest pace. Hint: Find the inflection point of P in the interval (0, 4). (Round you answer to two decimal place
t=

Math - Others
FunctionsLet f(x) be a function such that f(2) = 1 and f 0 (2) 3. (a) Use linear approximation to estimate the value of f(2.5), using x0 = 2 (b) If x0 = 2 is an estimate to a root of f(x), use one iteration of Newton's Method to find a new estimate to a root of f(x).
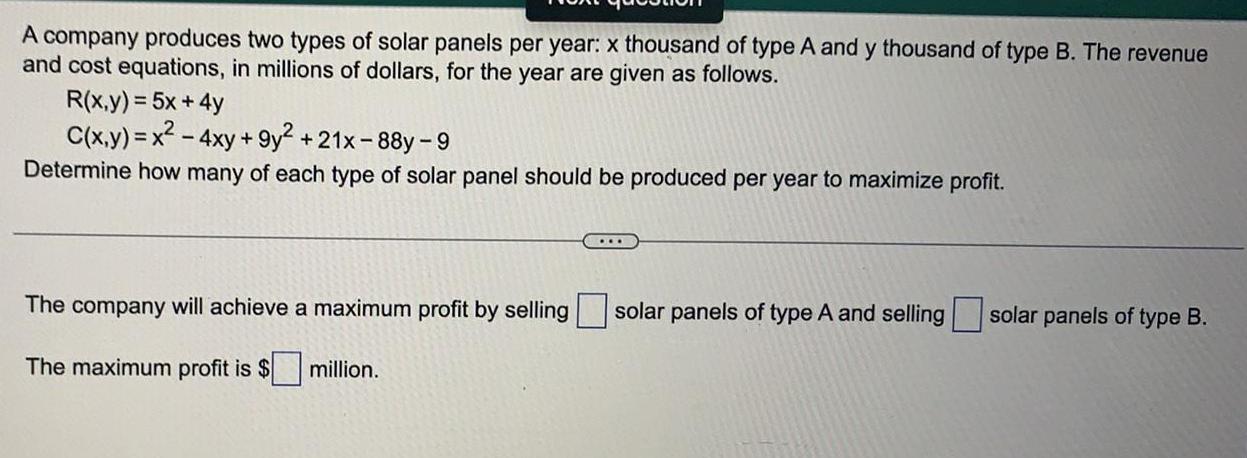
Math - Others
FunctionsA company produces two types of solar panels per year: x thousand of type A and y thousand of type B. The revenue and cost equations, in millions of dollars, for the year are given as follows.
R(x,y) = 5x + 4y
C(x,y)=x² - 4xy +9y² +21x-88y-9
Determine how many of each type of solar panel should be produced per year to maximize profit.
The company will achieve a maximum profit by selling ... solar panels of type A and selling ... solar panels of type B.
The maximum profit is $ million.


Math - Others
FunctionsSuppose Cineplex at Masonville Place can sell out a 300-seat theatre when tickets are sold for $24. For each $3 increase, 15 less tickets will be sold. Use a quadratic relation to determine the necessary ticket price to earn maximum revenue.

Math - Others
FunctionsA rectangular lot is bordered on one side by a stream and on the other three sides by 600 m of fencing.
Determine the dimensions of the lot if its area is a maximum.
Show your work
Math - Others
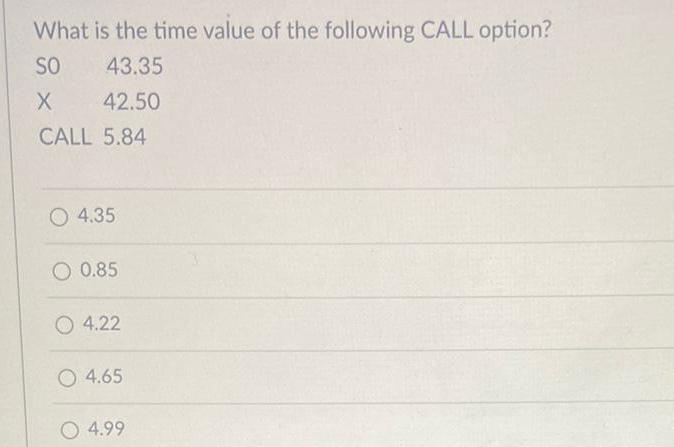
FunctionsWhat is the time value of the following CALL option? S 43.35 X 42.50 CALL 5.84 4.35 0.85 4.22 4.65 4.99
Math - Others
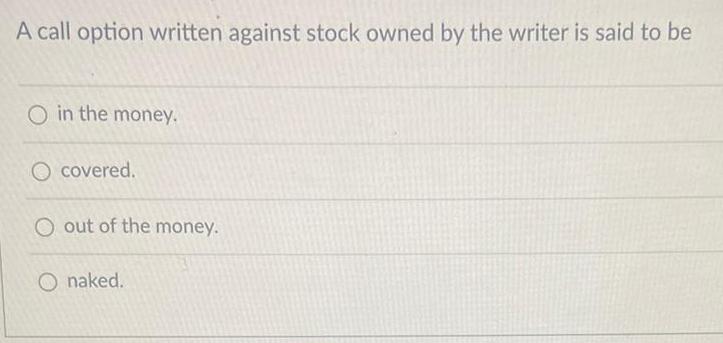
FunctionsA call option written against stock owned by the writer is said to be in the money. covered. out of the money. naked.

Math - Others
FunctionsIn a gambling game, a woman is paid $4 if she draws a five, a three, or a nine and $5 if she draws a ten, a six, or a two from an ordinary deck of 52 playing cards. If she draws any other card, she loses. How much should she pay to play if the game is fair? If the game is fair, the woman should play S to play. (Type an integer or a decimal. Round to the nearest cent as needed.)
Math - Others
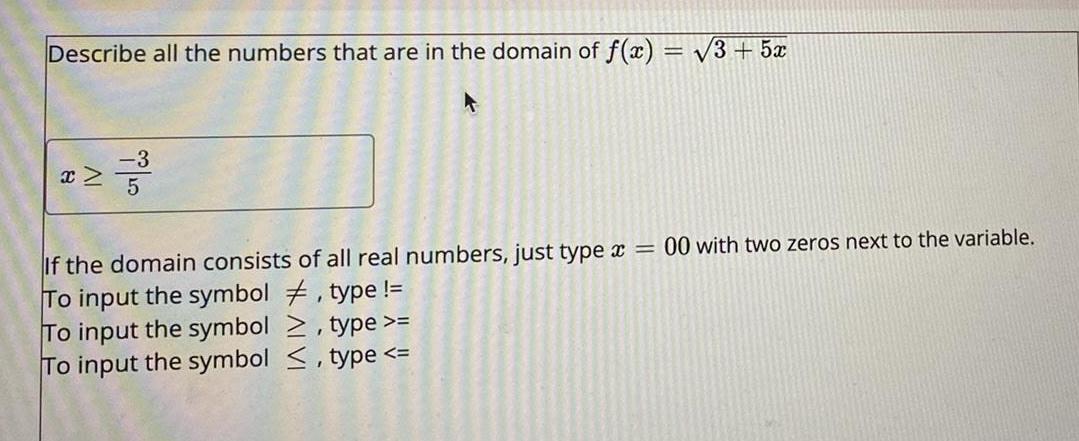
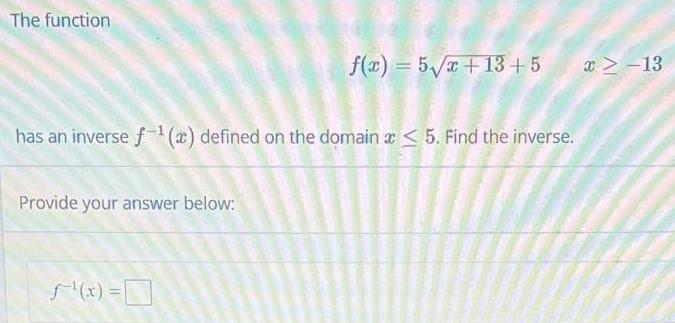
FunctionsThe function has an inverse f¹(a) defined on the domain x < 5. Find the inverse. Provide your answer below: f(x) = 5√√x+13+5 f'(x) = x>-13
Math - Others
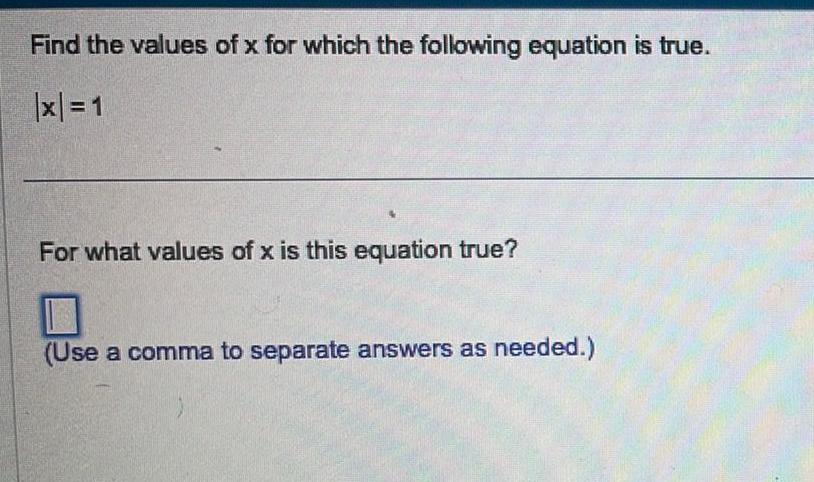
FunctionsFind the values of x for which the following equation is true. |x| = 1 For what values of x is this equation true? (Use a comma to separate answers as needed.)