Simple harmonic motion Questions and Answers

Physics
Simple harmonic motionCalculate the time period of a uniform metre stick if it is suspended from 20 cm mark Ans 1 52 sec Calculate the distance of centre of oscillation from the centre in the bove question Ins 0 27 metre
Physics
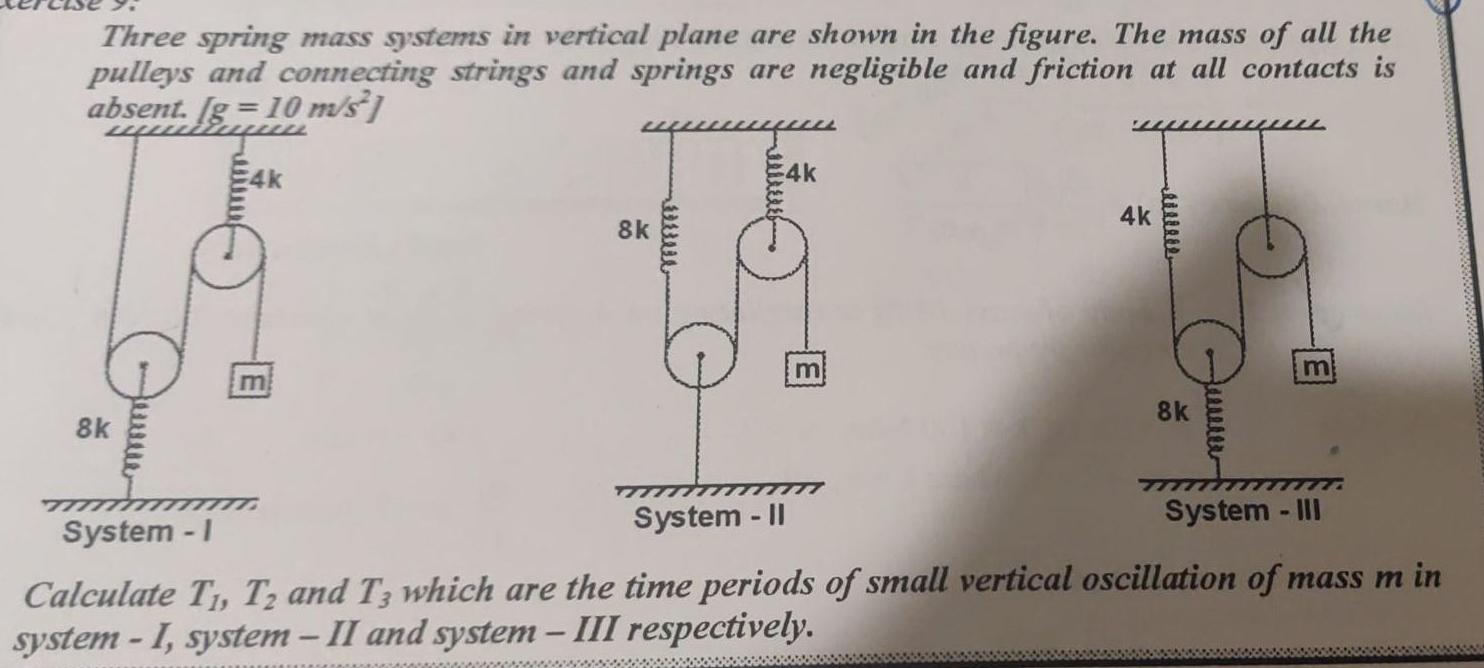
Simple harmonic motionThree spring mass systems in vertical plane are shown in the figure The mass of all the pulleys and connecting strings and springs are negligible and friction at all contacts is absent g 10 m s 8k 4k 8k www E4k m 4k e 8k m System I System II System III Calculate T T and T3 which are the time periods of small vertical oscillation of mass m in system I system II and system III respectively

Physics
Simple harmonic motionA particle performs S H M with time period T The time taken by the particle to move from half the amplitude to the maximum displacement is A 4 vest 2 Acoswt A 2 A coswt wt A Two pendulums begin to swing simultaneously During first fifteen oscillations of the first B D TIITIK t g L 57

Physics
Simple harmonic motion20 P3 CBSE PH EL SHM 76 A particle of mass m executing SHM makes foscillation per second The difference of its ki energy when at the centre and when at a distance x from the centre is A x x m B 27 f x m D f x m
Physics
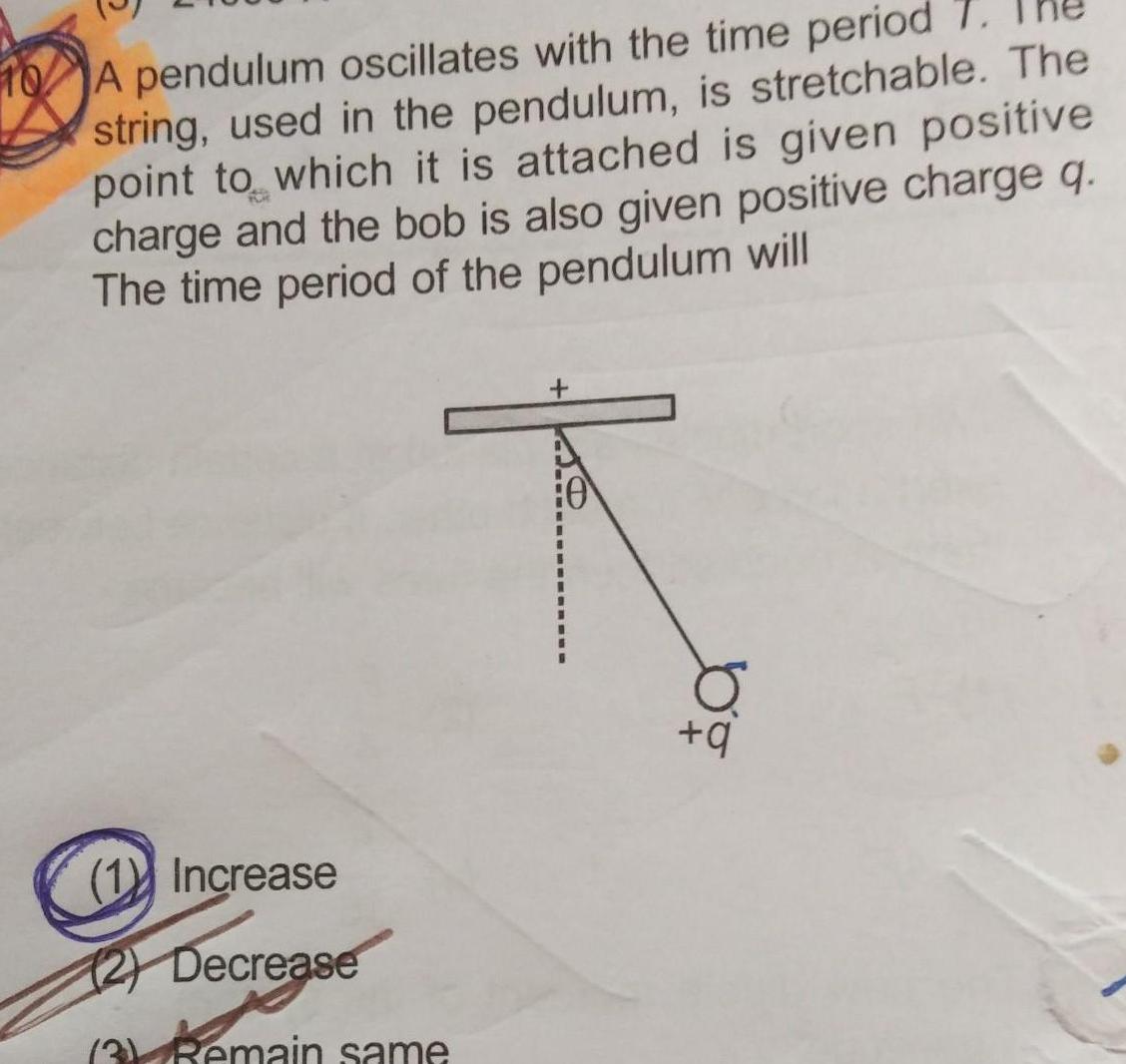
Simple harmonic motionA pendulum oscillates with the time period string used in the pendulum is stretchable The point to which it is attached is given positive charge and the bob is also given positive charge q The time period of the pendulum will 1 Increase 2 Decrease 3 Remain same 9
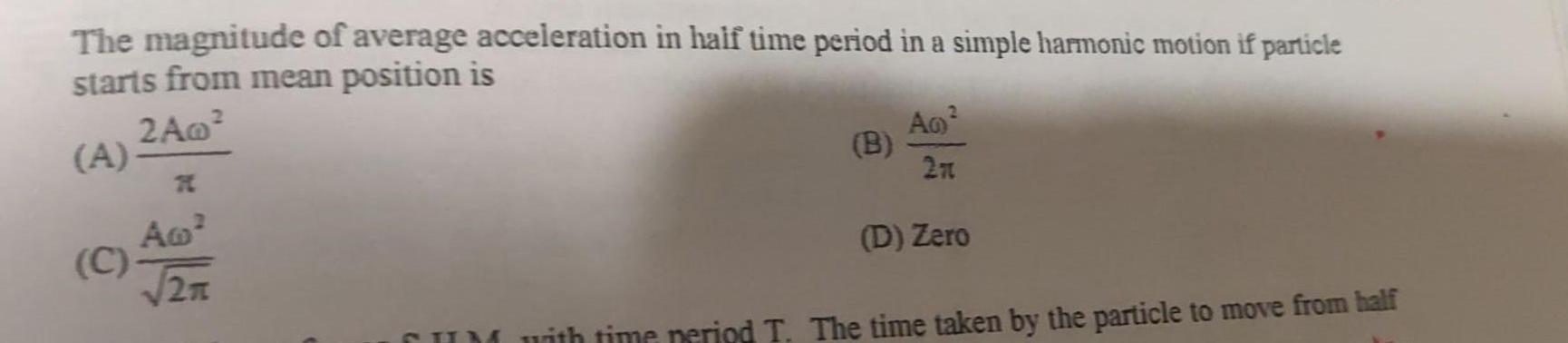
Physics
Simple harmonic motionThe magnitude of average acceleration in half time period in a simple harmonic motion if particle starts from mean position is 2A0 A A C T2TT B 2 A0 27 D Zero CUM with time period T The time taken by the particle to move from half
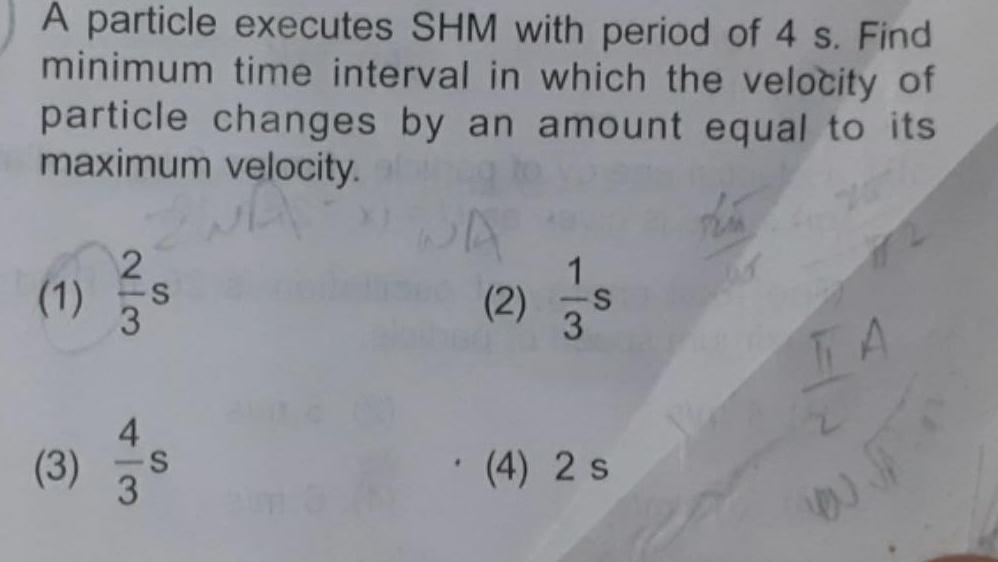
Physics
Simple harmonic motionA particle executes SHM with period of 4 s Find minimum time interval in which the velocity of particle changes by an amount equal to its maximum velocity 1 2 3 S 3 S 3 WA 2 1 3 4 2 s TA 4

Physics
Simple harmonic motion17 Bob is released from A from a small angular deflection 0 after which it collides elastically with wall l T 2 A Then its time period is given by 2T STY ZT 3 T 2 2 1 1 2 Y l 28 TOIN 3 5T 6 4 T

Physics
Simple harmonic motionlustration 21 A spring has a load of 1 0 kg attached to its one end A weight of 6 kg extends the spring by 24 cm This 6 0 kg wt is removed and the block is allowed to execute harmonic vibration with the 0 1 kg load Calculate its time period Given g 9 8 m s tion Since 6 kg wt extends the spring by 24 cm i e 0 24 m 6 9 8 force constant k 245 N m 0 24 T 27 m k 2 1 245 0 4 sec k mg extended
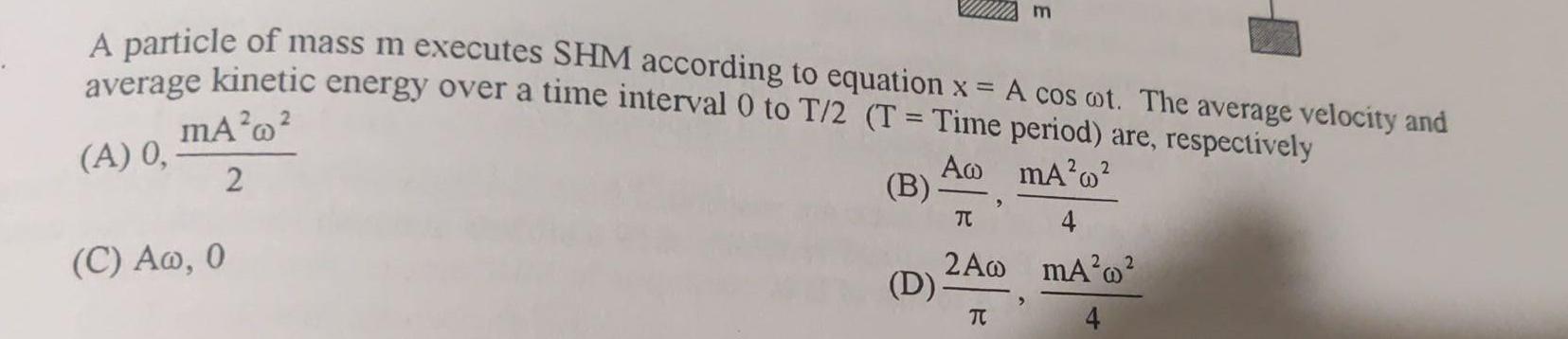
Physics
Simple harmonic motionA particle of mass m executes SHM according to equation x A cos ot The average velocity and average kinetic energy over a time interval 0 to T 2 T Time period are respectively mA A 0 A mA w 2 2 B C Aw 0 D TC m TC 2A0 mA 2 4

Physics
Simple harmonic motionD projectile motion Which of the following quantities are always positive in a simple harmonic motion AF B V T C a F D F 7 a w r F m dx
Physics
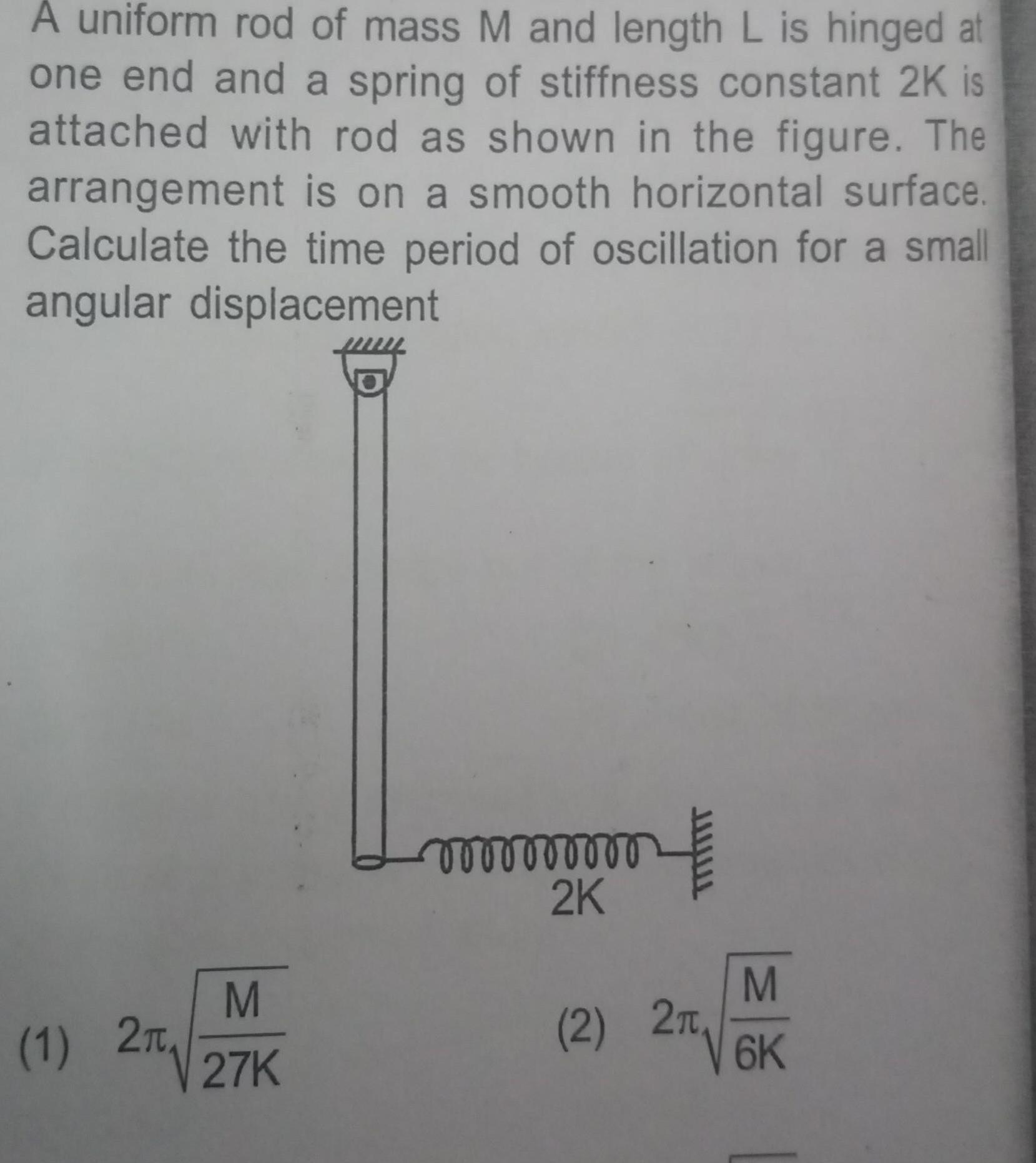
Simple harmonic motionA uniform rod of mass M and length L is hinged at one end and a spring of stiffness constant 2K is attached with rod as shown in the figure The arrangement is on a smooth horizontal surface Calculate the time period of oscillation for a small angular displacement 1 2T M 27K vooooooooo 2K M 2 26K
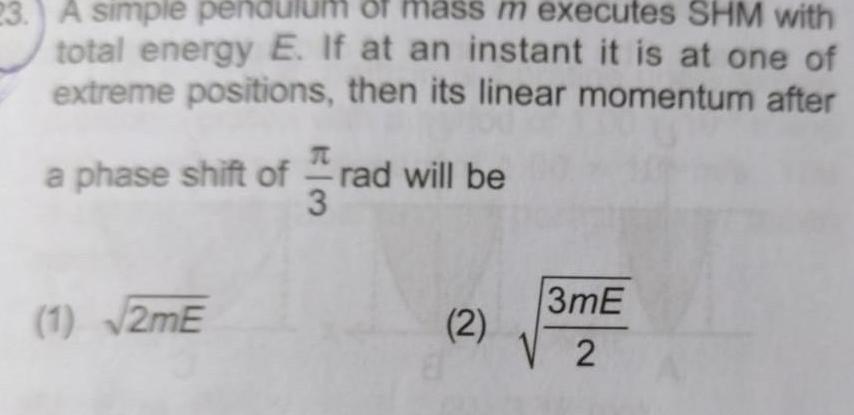
Physics
Simple harmonic motion23 A simple pendulum of mass m executes SHM with total energy E If at an instant it is at one of extreme positions then its linear momentum after a phase shift of rad will be 3 1 2mE 2 3mE 2
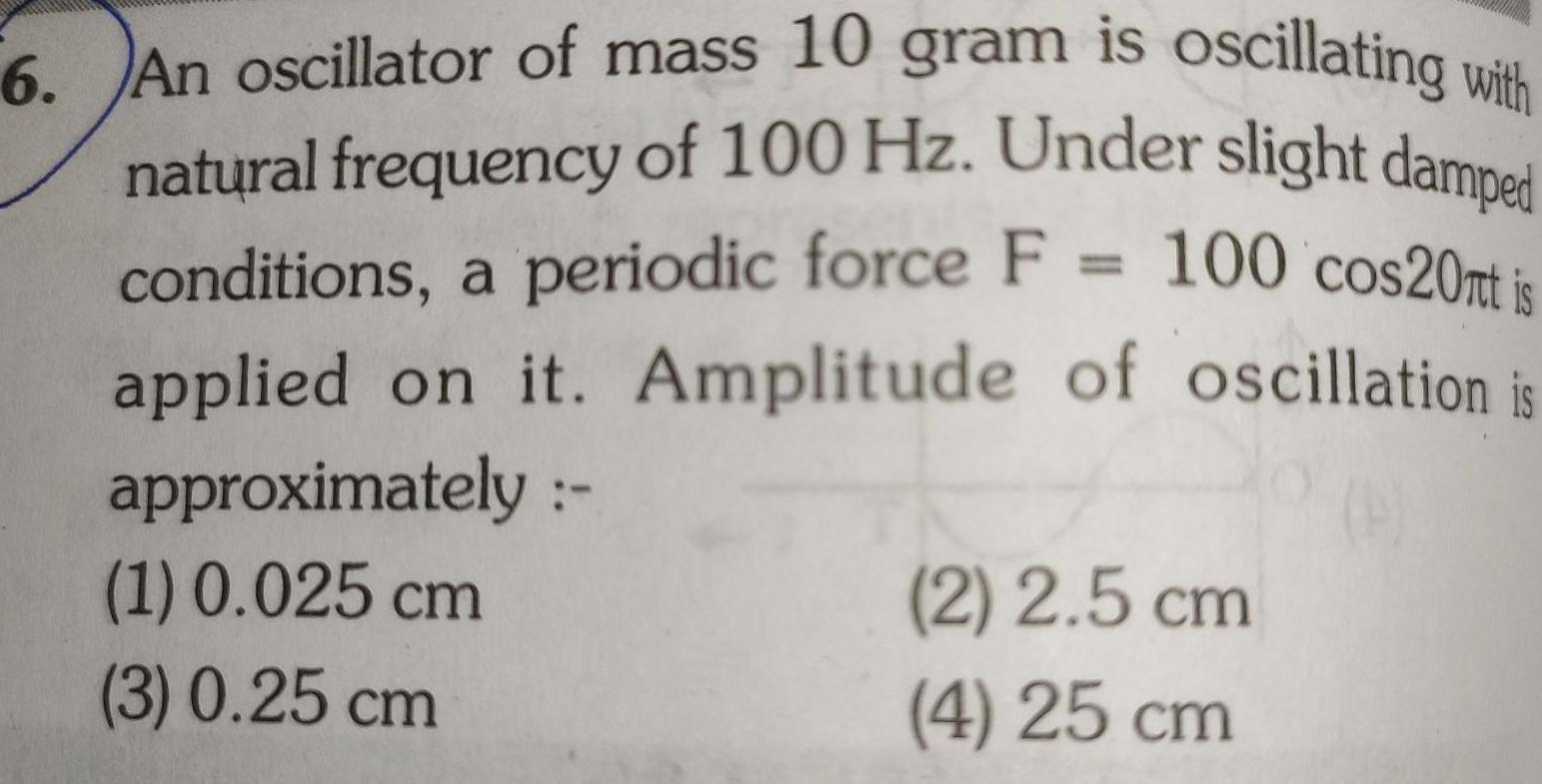
Physics
Simple harmonic motion6 An oscillator of mass 10 gram is oscillating with natural frequency of 100 Hz Under slight damped conditions a periodic force F 100 cos20nt is applied on it Amplitude of oscillation is approximately 1 0 025 cm 3 0 25 cm 2 2 5 cm 4 25 cm

Physics
Simple harmonic motionProblem 1 42 A body executing SHM with time period T and amplitude A When it is at A 4 from equilibrium position moving towards right It receives an impulse which doubles 2 its velocity without changing direction Find the a velocity after the blow b amplitude after the impulse and n taken by the block to reach the right extreme position

Physics
Simple harmonic motionD Two particles are executing simple harmonic motion of the same amplitude A and frequency w along the x axis Their mean position is separated by distance Xo Xo A If the maximum separation between them is X A the phase difference between their motion is AIEEE 2011
Physics
Simple harmonic motion134 A partilce is sub motions given by y 10 sin oot y 5 sin wt r The maximum speed of the particle is 1 10 5 w 2 10 5 w 3 5w 4 15w 5 A particle is subjected to two SHMs X A sin t sin t monic and X A sin ot

Physics
Simple harmonic motionA simple pendulum is made of a bob which is a hollow sphere containing mercury suspended by means of a wire If mercury is drained off continuously the period of the pendulum will A remain unchanged C decrease B first increase then decrease D become erratic T

Physics
Simple harmonic motion5 ation is zero 3 The energy changes from one form to another 4 The velocity at the mean position is zero In S H M which one of the following quantities has constant ratio with acceleration 1 Time 2 Displacement

Physics
Simple harmonic motionBob of simple pendulum of length I is made of iron The pendulum is oscillating over a horizontal coil carrying direct current If the time period of the pendulum s T then 1 T 2 g and damping is smaller than in air alone 2 T 2T 3 T 2T Vg and damping is larger than in air alone and damping is smaller than in air alone g 4 T 2 and damping is larger than in air alone gere 43 2013 g S

Physics
Simple harmonic motionThe angular frequency of the damped oscillator is given by k r m 4m where k is the spring is 8 the constant m is the mass of the oscillator and r is the damping constant If the ratio mk change in time period compared to the undamped oscillator is approximately as follows 1 increases by 1 2 decreases by 1 3 decreases by 8 4 increases by 8 2014 of magnitude of various elastic modulii is
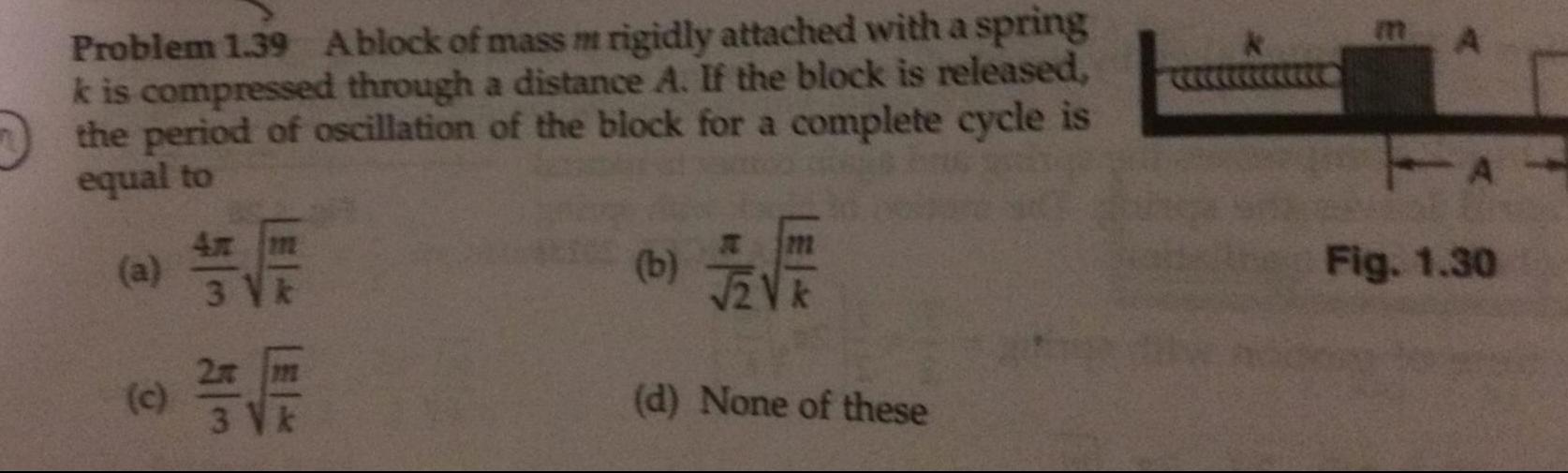
Physics
Simple harmonic motionProblem 1 39 Ablock of mass m rigidly attached with a spring k is compressed through a distance A If the block is released the period of oscillation of the block for a complete cycle is equal to a c 4x m 3 V k 2x m 3 V k b 12V d None of these A A Fig 1 30
Physics
Simple harmonic motionc 10 cm d 16 cm 22 A particle of mass m is executing oscillations about ust the origin on the x axis with amplitude A Its potential energy is given as U x axt where a is a positive constant The x coordinate of mass where potential energy is one third the kinetic energy of particle is c 1 12 a A b 2 d A 3

Physics
Simple harmonic motionTwo identical blocks P and Q have mass m each They are attached to two identical springs initially unstretched Now the left spring along with P is compressed by and the right 2 A spring along with Q is compressed by A Both the blocks are released simultaneously They collide perfectly inelastically The time period of both the blocks oscillating independently on there respective springs is T The time period of oscillation of combined mass is A T C T B 2 T T 2 D 2 00000000 PQ

Physics
Simple harmonic motionA particle at the end of a spring executes simple harmonic motion with a period t while the corresponding period for another spring is t2 If the period of oscillation with the two springs in series is t then 2004 1 T t t 1 3 T t t 2 T 1 1 4 T t t 2
Physics
Simple harmonic motion3 67 The elongation of spring is 1 cm and its potential energy is U If the spring is elongated by 3cm then potential energy will be 1 3U 2 U 3 9U 4 bla
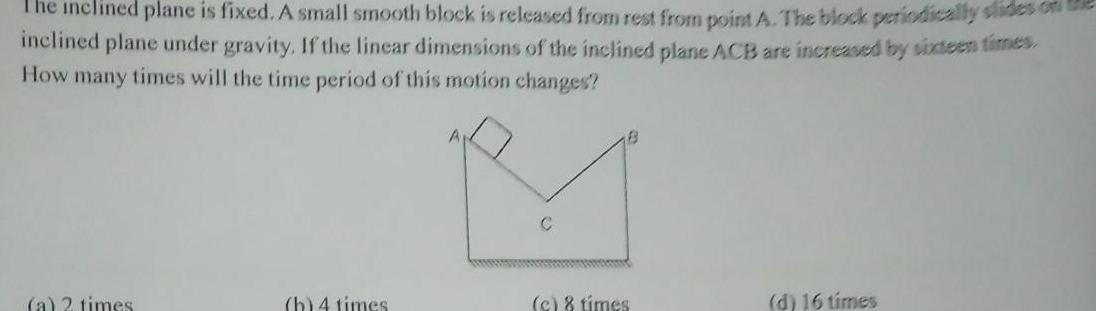
Physics
Simple harmonic motionThe inclined plane is fixed A small smooth block is released from rest from point A The block periodically slides of inclined plane under gravity If the linear dimensions of the inclined plane ACB are increased by sixteen times How many times will the time period of this motion changes a 2 times h 4 times C c 8 times d 16 times

Physics
Simple harmonic motionPre Medic cal 20 In an angular SHM angular amplitude of oscillation is rad and time period is 0 4 sec then calculate T its angular velocity at angular displacement 1 2 rad 1 34 3 rad sec 3 22 3 rad sec 2 42 7 rad sec In 4 50 3 rad sec 24

Physics
Simple harmonic motionnatural length The block of mass m is given a velocity vo towards the vertical support at t 0 The coefficient of friction between the block and the surface is given by ax where a is a positive constant and x is the position of the block from its starting position The block comes to rest for the first time at x which is 000000 a Vo m k amg Vo Fig 8 251 l b Vo m k
Physics
Simple harmonic motionA simple pendulum performs simple harmonic motion about x O with an amplitude a and time period T The speed of the pendulum a x a 2 will be 1 3 2 a 3 OF 3 Ta P 4 2 3 a m
Physics
Simple harmonic motionA point performs simple harmonic oscillation of period T and the equation of motion is given by x a sin wt 6 After the elapse of what fraction of the time period the velocity of the point will be equal to half of its maximum velocity 1 T 3 2 T 12 3 T 8 4 T 6

Physics
Simple harmonic motionProblem 1 Two identical particles each of mass m are interconnected by a light spring of stiffness k the time period for small oscillation is equal to 1 2 m k 100000 2 4 m F k 2m

Physics
Simple harmonic motionA uniform disc of mass M and radius R is hinged at its lowest point and placed in gravity free space It is attached with two identical springs in natural length and an unstreched string of cross sectional area A length L and Young s modulus Y The time period of angular oscillation of small amplitude of the disc is 3ML A 2n V10KL 8AY 3M C T 17AX 2R KXR B 2n l A KR Leno kehi 3M V10k D T 3M 40k 3ML 8AY k www AP Hun 0 m x R

Physics
Simple harmonic motion3 A particle executes linear simple harmonic motion with an amplitude of 3 cm When the particle is at 2 cm from the mean position the magnitude of its velocity is equal to that of its acceleration Then its time period in seconds is 1 5 2 2 4 5 3 2 3 vo 1949 4 5 TC

Physics
Simple harmonic motionAllM 1 A body of mass 600 gm is attached to a spring of spring constant k 100 N m and it is performing damped oscillations If damping constant is 0 2 and driving force is F F cos ot where F 20 N Find the amplitude of oscillation at resonance 0 2 0 57 m 4 0 98 m 1 4 1 m 3 7 7 m

Physics
Simple harmonic motionk m k When mass m oscillates with spring of spring constant k its frequency is 3Hz and with spring of spring constant k its frequency is 6Hz Then frequency of oscillations when mass is connected with springs as shown in figure is 1 6 7 2 4 5 3 9 4 3

Physics
Simple harmonic motion11 Two particles are oscillating along two close parallel straight lines side by side with the same frequency and amplitudes They pass each other moving in opposite directions when their displacement is half E of the amplitude The phase difference is 1 26 2 0 3 2 301 4 T RENK M 2000ot

Physics
Simple harmonic motionThe period of a particle is 8s At t 0 it is at the mean position The ratio of distance covered by the particle in first second and second second will be 1 3 2 1 2 1 2 1 2 1 2 4 2 1

Physics
Simple harmonic motion19R A neutral pendulum osciliates in an uniform electric field as shown in figure If a positive charge is given to the pendulum then its time period 11 11 1 will increase 3 will remain constant 2 will decrease 4 will first increase then decrease

Physics
Simple harmonic motion68 A particle of mass m and charge Q is placed in an electric field E which varies with time as E E sin ot It will undergo simple harmonic motion of amplitude 2 thoshor QE 0 xbo A 2 le B QE 0 2 mu bold owtQE ed sby C me 0 Vmw bria ertloc D motramsosiqeib QET AT mo
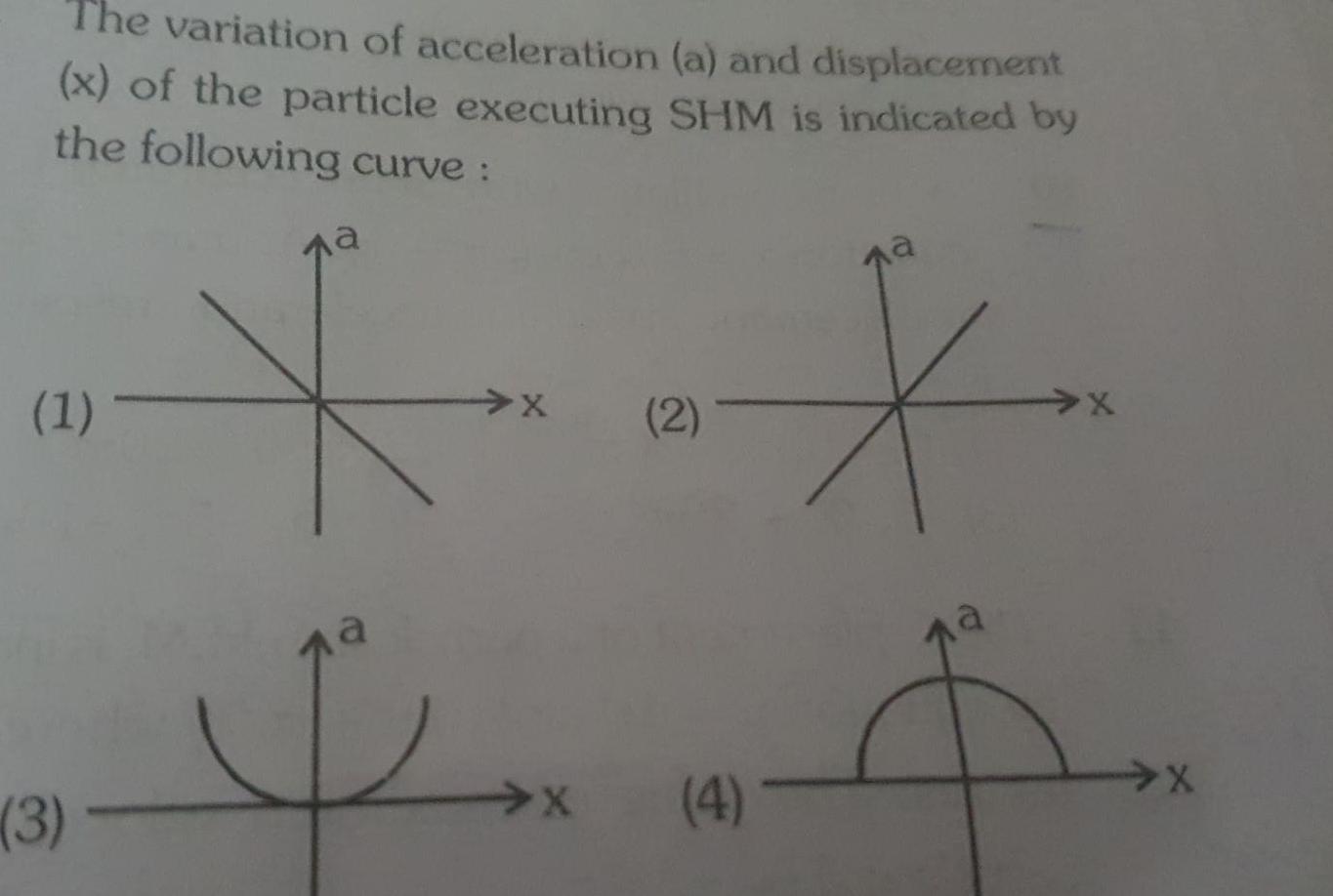
Physics
Simple harmonic motionThe variation of acceleration a and displacement x of the particle executing SHM is indicated by the following curve 1 3 na X 2 X LA X 4 X

Physics
Simple harmonic motionProblem 15 A simple pendulum has a time period T in vaccum Its time period when it is completely immersed in a liquid of density one eight of the density of material of the bob is 1 3 T 3 T 2 4 8 8 T

Physics
Simple harmonic motionA small block A of mass m is placed symmetrically over rectangular block B of mass 2 m and having dimensions shown in figure Block B is placed over frictionless horizontal surface Mass A is connected to extended walls of block B by springs of spring constant k 2mg b Now block A is made to perform SHM freely over block B If block B does not topple during subsequent motion then choose correct options A Torque due to contact force from ground about centre of mass of block will be 5 mgx B Maximum amplitude of oscillations of block A for no toppling of block B is 3b 10 b V6g D Block B will topple for amplitudes less than b 5 C Period of oscillation of blocks will be 2 B AT X

Physics
Simple harmonic motion7 A body of mass 600 gm is attached to a spring of spring constant k 100 N m and it is performing damped oscillations If damping constant is 0 2 and driving force is F 1 F cos ot where F 20 N Find the amplitude of oscillation at resonance 0 1 4 1 m 2 0 57 m 3 7 7 m 4 0 98 m
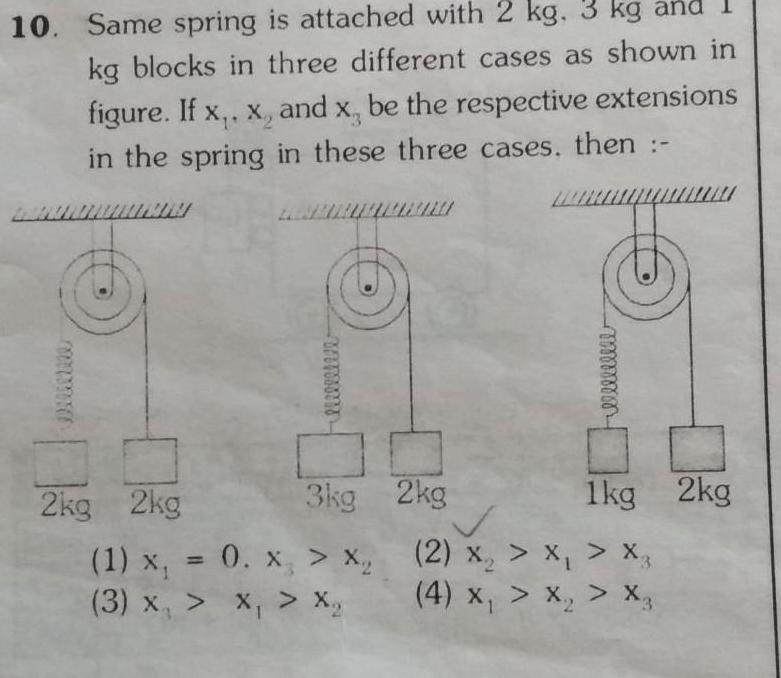
Physics
Simple harmonic motion10 Same spring is attached with 2 kg 3 kg and kg blocks in three different cases as shown in figure If x x and x be the respective extensions in the spring in these three cases then www lilllleee 2kg 2kg 3kg 1 x 0 x X 3 x X Xq Felllllllll 2kg 1kg 2kg 2 x x Xz x X 4 X X X3

Physics
Simple harmonic motionConsider the system shown below If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM P di q m
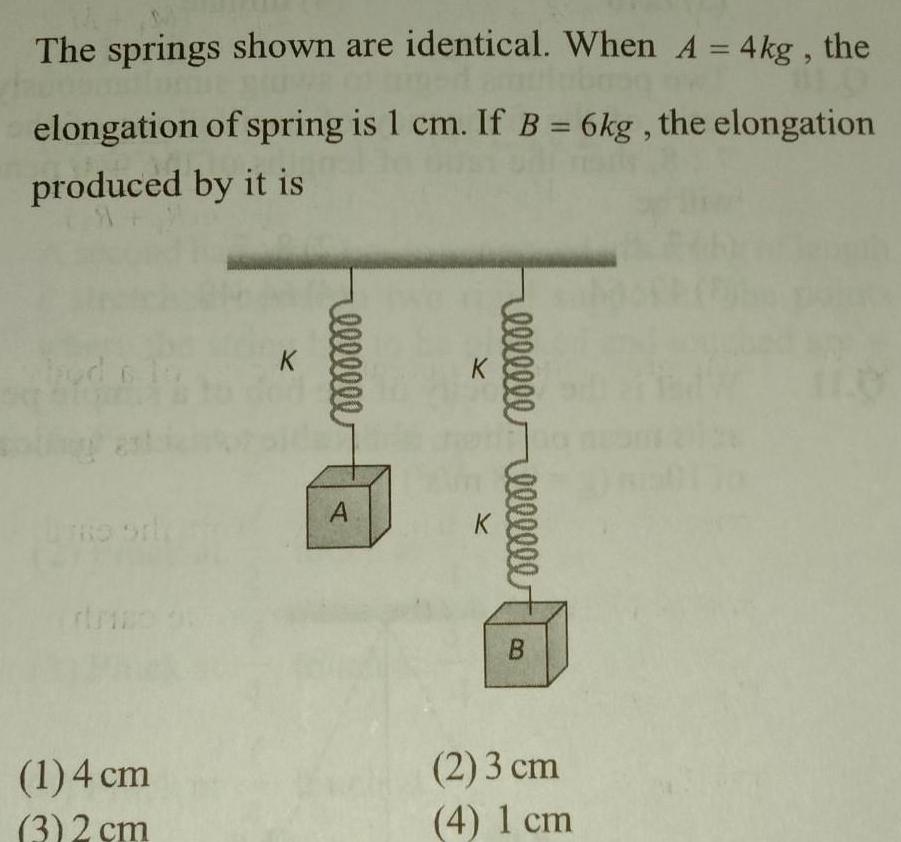
Physics
Simple harmonic motionThe springs shown are identical When A 4kg the elongation of spring is 1 cm If B 6kg the elongation produced by it is TRO 1 4 cm 3 2 cm rellllle A K K elllllllllllll B 2 3 cm 4 1 cm
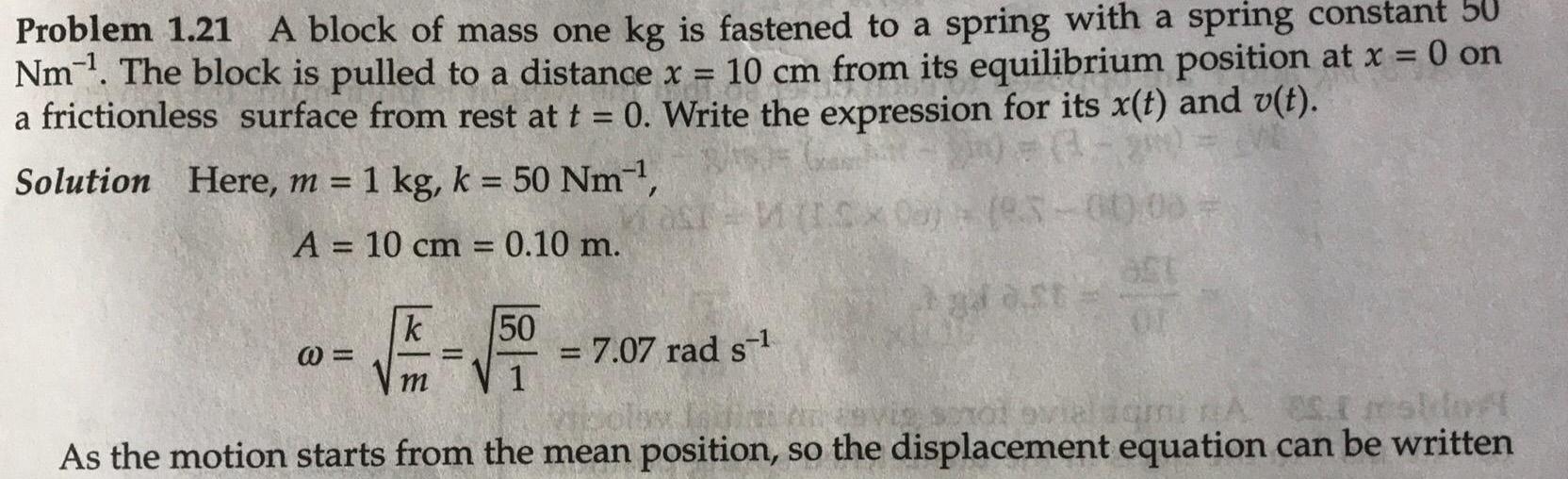
Physics
Simple harmonic motionProblem 1 21 A block of mass one kg is fastened to a spring with a spring constant 50 Nm The block is pulled to a distance x 10 cm from its equilibrium position at x 0 on a frictionless surface from rest at t 0 Write the expression for its x t and v t Solution Here m 1 kg k 50 Nm A 10 cm 0 10 m k E 1500 m MasT M ICX00 93 00 00 7 07 rad s 65 1 mshin As the motion starts from the mean position so the displacement equation can be written

Physics
Simple harmonic motionTwo SHM s with same amplitude and time period when acting together in perpendicular directions with a phase difference of r 2 give rise to a straight motion c circular motion b elliptical motion d none of these 1997
Physics
Simple harmonic motion3 Maximum 4 Maximum velocity A body oscillates with SHM according to the equation x 5 0 cos 2 t n At time t 2 s its displacement speed and acceleration respectively is 1 0 10 20 3 5 0 20 2 5 0 20 4 5 5m 10 The displacement of a particle in SHM is indicated 4