Simple harmonic motion Questions and Answers
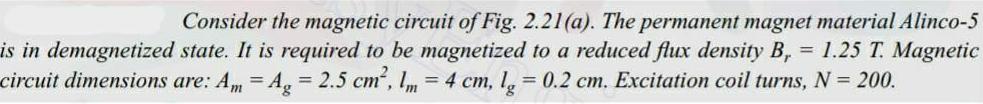
Physics
Simple harmonic motionConsider the magnetic circuit of Fig 2 21 a The permanent magnet material Alinco 5 is in demagnetized state It is required to be magnetized to a reduced flux density B 1 25 T Magnetic circuit dimensions are Am Ag 2 5 cm 1m 4 cm lg 0 2 cm Excitation coil turns N 200

Physics
Simple harmonic motionAn object of mass 0 2 kg is hung from a spring whose spring constant is 80 N m The object is subject to a resistive force given by bu where v is its velocity in meters per second a Set up the differential equation of motion for free oscillations of the system b If the damped frequency is 3 2 of the undamped frequency what is the value of the constant b
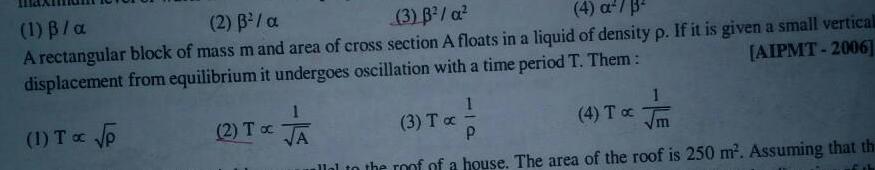
Physics
Simple harmonic motion1 B a 2 3 a 3 B a 4 a 3 A rectangular block of mass m and area of cross section A floats in a liquid of density p If it is given a small verticall displacement from equilibrium it undergoes oscillation with a time period T Them AIPMT 2006 1 T p 2 To A 1 3 Tx 4 To P allal to the roof of a house The area of the roof is 250 m Assuming that th

Physics
Simple harmonic motionA particle is doing SHM with a time period of 0 80 sec and amplitude of 10 cm At t 0 it is 5 0 cm to the left of equilibrium and moving to the left Then at t 2 0 sec Its position is 5 0 cm to the right of equilibrium It is moving towards right Its position is 5 0 cm to the left of equilibrium
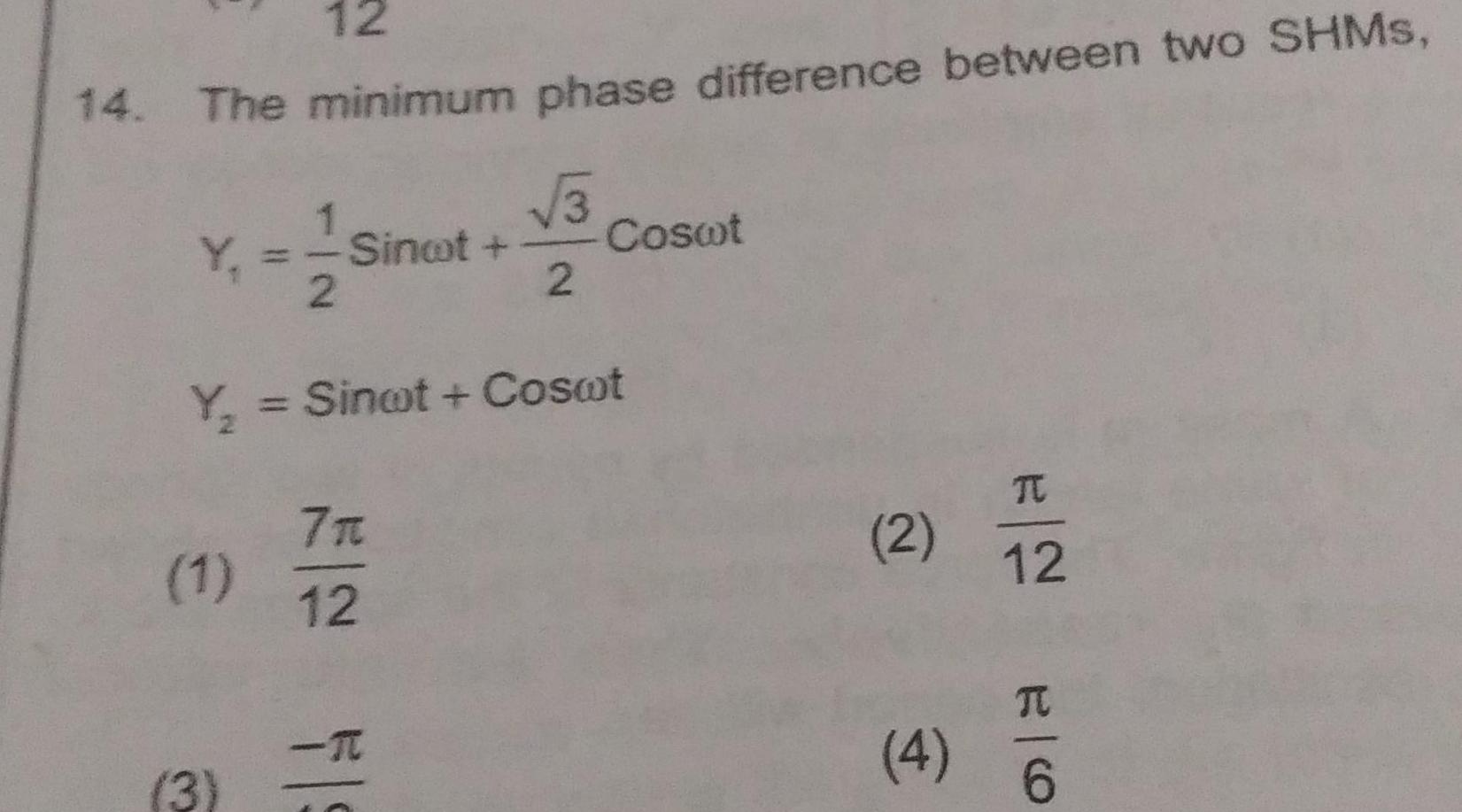
Physics
Simple harmonic motion12 14 The minimum phase difference between two SHMS 1 Y Sinot 2 1 Y Sinot Coswt 3 E FS 7 3 2 12 Coswt 2 4 TC 12 E O TU 6

Physics
Simple harmonic motionOscillations 121 0 A particle is executing SHM with time period T Starting from mean position time taken by it to 5 complete oscillations is 1 3 T 12 5T 12 2 4 7T 12

Physics
Simple harmonic motion3 12 cm s 4 8 cm s When a wave travels in a medium the particle 42 displacement is given by y asin 2x bt cx where a b and c are constants The maximum particle velocity will be twice the wave velocity if 1 c 3 b ac 2 a 4 b ac 3 12 cm s 2 y a sin 2x bt cx a fe a bac C n din n an yu m afa fazen Me 1 c 4 8 cm s 3 b ac 2 na 4 b ac

Physics
Simple harmonic motionThe displacement of two identical particle executing SHM are represented by equ 8 sin 10t 6 and x 5 sin wt For what value of w energy of both the particle is same a 4 units b 8 units d 20 units c 16 units A CO

Physics
Simple harmonic motion97 A cylindrical piston of mass M slides smoothly inside a long cylinder a certain mass of gas The cylinder is kept with its axis horizontal closed at one end enclosing the piston is disturbed from its equilibrium position it oscillates simple harmonically The period of oscillation will be h P 98 Gas A a T 2 c T 2 M Mh PA M PAh PHYSICSKOT 2 MA Ph d T 2n MPhA A hollow sphere is filled with water through the small hole in it It is then hung by a long thread
Physics
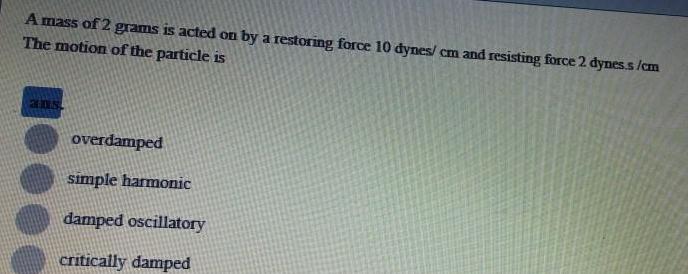
Simple harmonic motionA mass of 2 grams is acted on by a restoring force 10 dynes cm and resisting force 2 dynes s cm The motion of the particle is 205 overdamped simple harmonic damped oscillatory critically damped

Physics
Simple harmonic motionTwo particles are in SHM with same amplitude A and same angular frequency o At time t 0 on A A at x and other is at x Both are moving in same direction 2 2 A Phase difference between the two particle is B Phase difference between the two particle is C They will collide after time t D They will collide after time t NET 200

Physics
Simple harmonic motionA particle under the action of a SHM has a period of 3 s and under the effect of another it has a period 4 s What will be its period under the combined action of both the SHM s in the same direction a 7 s c 2 4 s b 5 s d 0 4 s

Physics
Simple harmonic motionIn damped oscillations the amplitude after 50 oscillations is 0 8 ao where ao is the initial amplitude then the amplitude after 150 oscillations is Question Type Single Correct Type 1 0 512 ao 2 0 280 aa

Physics
Simple harmonic motionA particle of mass 1 kg executing simple harmonic motion of period 20 s crosses the mean position at t 0 with velocity cm s A the maximum acceleration of the particle is 10 cm s B when it is 4 cm from the mean position its velocity is 67 10 cm s C the kinetic energy of the particle when its displacement is 5 cm from the mean position is D its velocity at displacement 6 cm from the mean position is 87 10 cm s 3 8x106 J

Physics
Simple harmonic motionConsider a damped harmonic oscillator whose mass m 0 05 kg k 5 0 N m and damping constant b With initial conditions xo 0 01 m p 0 A 0 1m and vo 0 m s Evaluate each case of damped oscillator and write the corresponding equation of motion of damped harmonic oscillator a Critically damped oscillator with b 1 0 b Underdamped oscillator with b 10 c Overdamped oscillator with b 5 0

Physics
Simple harmonic motionA particle of mass 0 2 kg oscillates according to the law x 0 08 cos 20 t T 4 where x is in metre and t is in second The instantaneous force acting on it is Select one a 315 5 cos 20nt n 4 b 1 26 1 sin40 t c 5 02 sin 20nt 4 d 63 1 cos 20ru TL 4 LEGE b

Physics
Simple harmonic motionIn a forced vibration of a particle of mass m restoring force per unit displacement s and the damping force per unit velocity Rm The amplitude resonant frequency of oscillation is Select one a 1 21 s 2m R2 4m b 1 2T s m R 4m c 1 2 s m R 4m d 1 2m s m R2 2m
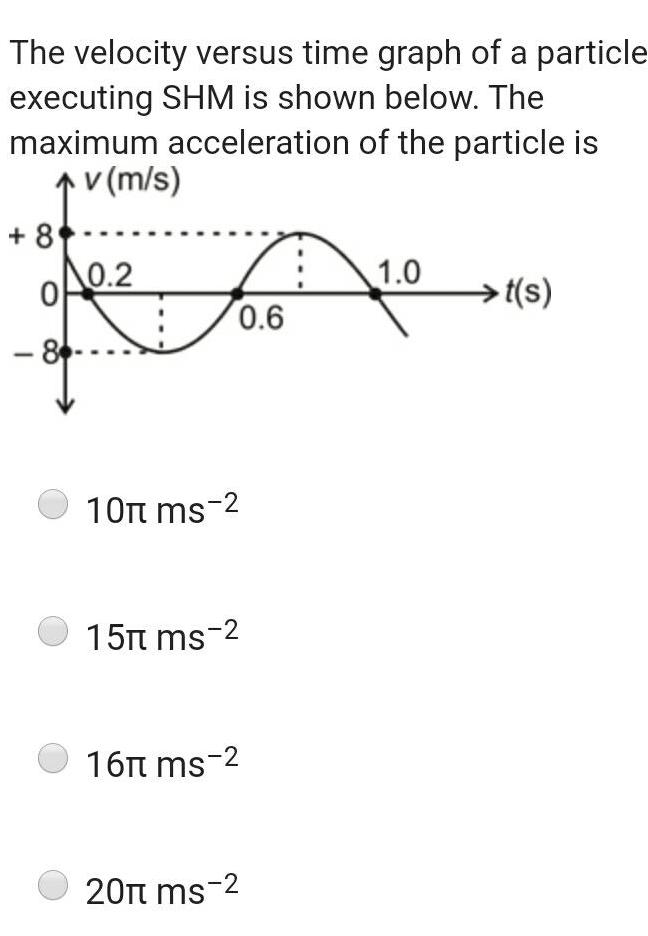
Physics
Simple harmonic motionThe velocity versus time graph of a particle executing SHM is shown below The maximum acceleration of the particle is v m s 8 0 86 0 2 7 foo 0 6 10 ms 2 15 ms 2 16 ms 2 20 ms 2 1 0 t s

Physics
Simple harmonic motionA mass of 2 kg is suspended by a light spring of stiffness constant 20 Nm11 The energy associated with the vertical oscillation of the system is observed to decay 1 e of its initial value in 50 s Assuming the damping force proportional to the velocity the damping force constant is Select one a 0 2 Nsm 1 b 0 004 Nsm c 0 002 Nsm 1 d 0 04 Nsm 1

Physics
Simple harmonic motionA solid ball of mass m is made to fall from a height H on a pan suspended through a spring of spring constant K as shown in figure If the ball does not rebound and the pan is massless then amplitude of oscillation is ABA A mg K mg C K 2HK mg 1 2 B D mg k mg K 1 2HK mg 1 1 1 2 2HK mg 1 2 fmmx

Physics
Simple harmonic motionAn oscillator consists of a block attached to spring k 400 N m At some time t the position measured from the system s equilibrium location velocity and acceleration of the block are x 0 100m v 15 0 m s and a 90 m s The amplitude of the motion and the mass of the block are 1 0 2 m 0 84 kg 3 0 4 m 0 54 kg 2 0 3 m 0 76 kg 4 0 5 m 0 44 kg

Physics
Simple harmonic motionwo simple harmonic motions are represented by the equations y 0 1 sin 100nt F 3 and Y 0 1 cos100nt The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is 1 2 3 3 3 4

Physics
Simple harmonic motionres A particle execute S H M with frequency f Find frequency with A particle of mass 10g is placed in potential field given by V 50x2 100 erg g What will be frequenc of oscillation of particle

Physics
Simple harmonic motionA particle describes SHM in a straight line about O OP If the time period of the motion is T then its kinetic energy at P be half of its peak value at O if the time taken by the particle to travel from O to P is 4 T 12 1 T T 2 T 3 2 2

Physics
Simple harmonic motionA particle executing linear SHM Its time period is equal to the smallest time interval in which particle acquires a particular velocity v the magnitude of v may be Vmax B Vmax C A Zero 2 D Vmax 2

Physics
Simple harmonic motion5 The function sin t represents a a periodic but not simple harmonic motion with a peria TC 0 b a periodic but not simple harmonic motion with a peria 2 c a simple harmonic motion with a period d a simple harmonic motion with a period 3 2

Physics
Simple harmonic motionTwo bodies performing have same amplitude and frequency Their phases at a certain instant are as shown in the figure The phase difference between them is x A 10 0 5 A A x

Physics
Simple harmonic motionThe period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which XL then find X moves without friction down on inclined plane of inclination a 60 is given by g I I T Scr 2000 1 35

Physics
Simple harmonic motion6 Extreme position to half of the amplitude A particle undergoes simple harmonic motion having time period T Find the time taken to complete 318 oscillation TC The displacement of a particle executing simple harmonic motion is given by y 10sin 6t 3 Here
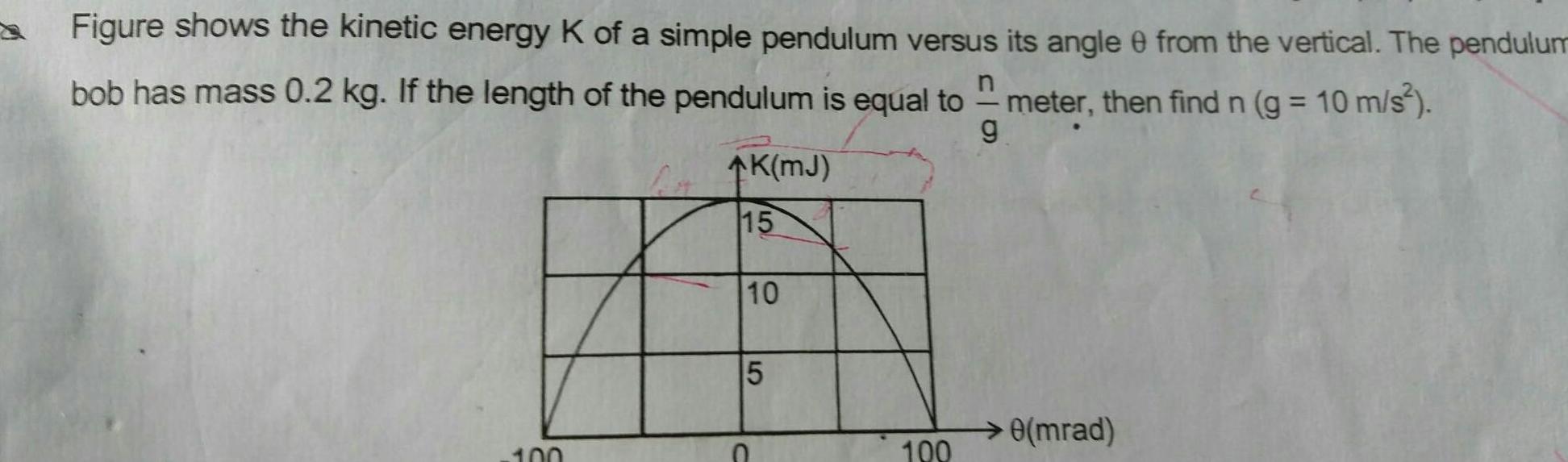
Physics
Simple harmonic motionFigure shows the kinetic energy K of a simple pendulum versus its angle 0 from the vertical The pendulum bob has mass 0 2 kg If the length of the pendulum is equal to g meter then find n g 10 m s 100 K MJ 15 10 5 100 0 mrad

Physics
Simple harmonic motion19 Two particles executing SHM of same frequency meet at x A 2 while moving in opposite directions Phase difference between the particles is It 1 3 51 2 4 2 3
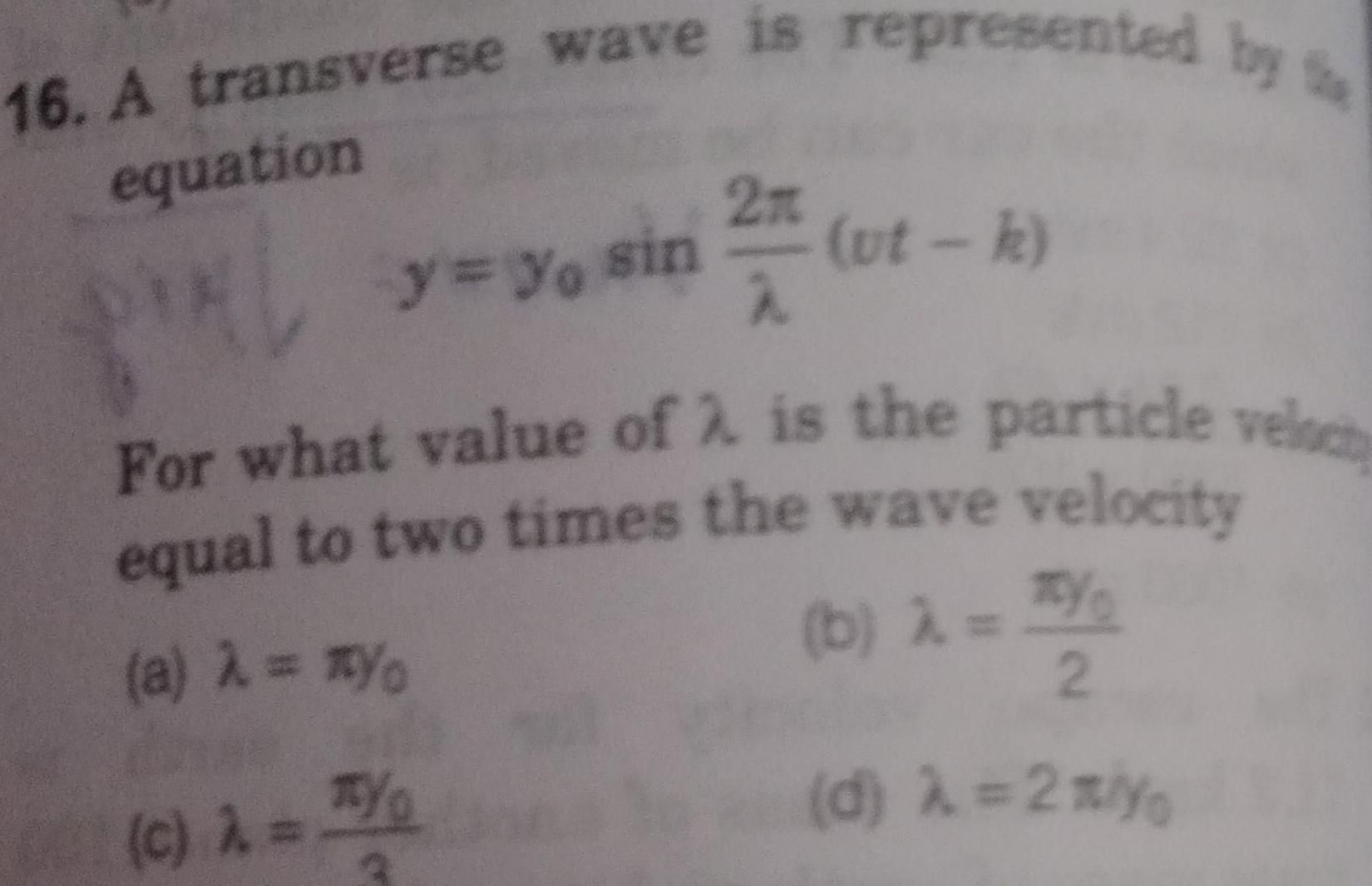
Physics
Simple harmonic motion16 A transverse wave is represented by equation y yo sin 32 74 ut k For what value of 2 is the particle veloc equal to two times the wave velocity a Yo b c TY 2 d 2 yo

Physics
Simple harmonic motionST 3 4 12 12 21 A particle is executing S H M between x A The time taken to go from 0 to is T and to go from to A is T then 1 T T T 2 T T T 2T

Physics
Simple harmonic motionQuestion 20 A A damped oscillator has a frequency that is 0 8 times its undamped frequency By what factor is the amplitude of the oscillator decreased during each oscillation B el 2x M M 4 00 1 5x N M 1 00 Correct Answer

Physics
Simple harmonic motion15 In the adjacent figure if the incline plane is smooth and the springs are identical then the period of oscilla of this body is 1 2n 3 2 M 2k M ksine 2 4 2 2M Msin 10

Physics
Simple harmonic motion1 point A frictionless spring with a 8 kg mass can be held stretched 1 2 meters beyond its natural length by a force of 100 newtons Find the position of the mass after t seconds if the mass experiences a retarding force equal to twice its velocity and it starts at a velocity of 2 m s meters
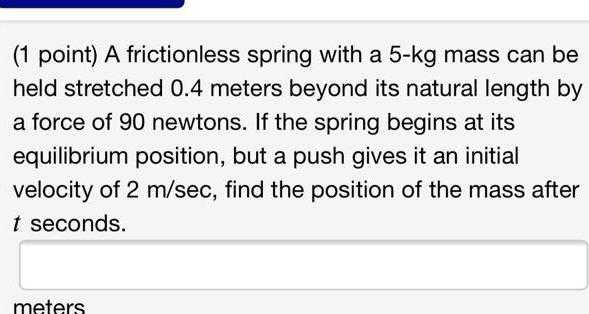
Physics
Simple harmonic motion1 point A frictionless spring with a 5 kg mass can be held stretched 0 4 meters beyond its natural length by a force of 90 newtons If the spring begins at its equilibrium position but a push gives it an initial velocity of 2 m sec find the position of the mass after t seconds meters

Physics
Simple harmonic motion6 The equation of simple harmonic motion may not be expressed as each term has its usual 14 meaning 1 x Asin et o 2 x Acos oof o 3 xasin cof bcos cof 4 x Asin oot o Bsin 2 0 Aakash Educational Services Pvt Ltd Regd Office Aakash Towe

Physics
Simple harmonic motionA particle of mass 200 g executes SHM The restoring force is provided by spring of spring constant 80 N m What is magnitude of acceleration when mass is 2 cm away from equilibrium position 4ms 2 6ms 8ms 2 10 ms

Physics
Simple harmonic motion13 A second pendulum is moved to moon where acceleration due to gravity is times that of the Earth the le of the Seconds pendulum on Moon would be 1 6 times 2 12 times 3 times 12 times

Physics
Simple harmonic motion3 PA PB Which of the following statements is true about stationary waves 1 All particle except particles at node execute SHM 2 All particles except particles at node come to their mean positions at the same time 3 All particles at antinodes have same velocity at mean position 4 All of these

Physics
Simple harmonic motionTwo masses m and m are suspended together by a massless spring of constant K as shown in figure When the masses are in equilibrium m is removed without disturbing the system Find the angular frequency and amplitude of oscillation of m2
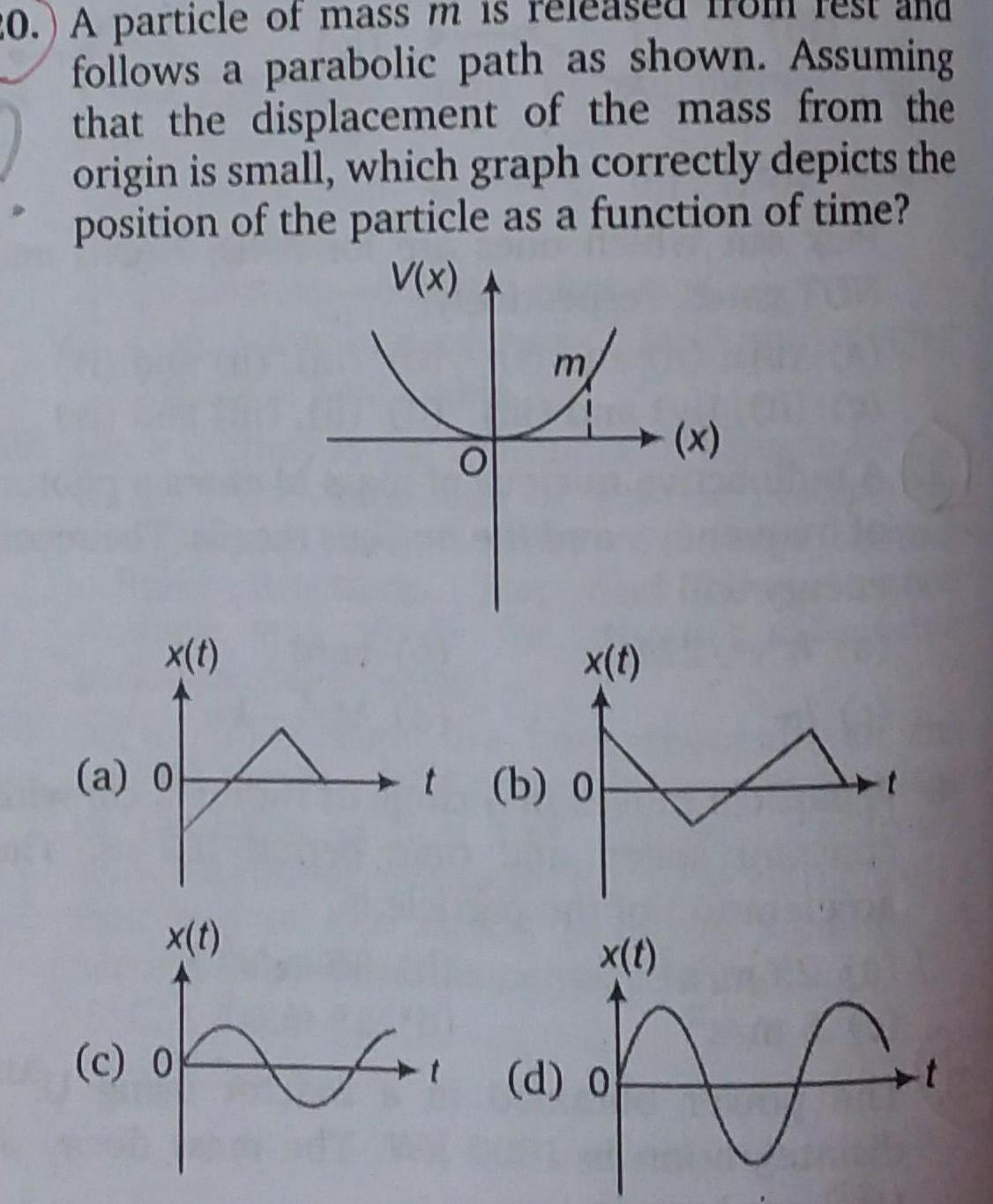
Physics
Simple harmonic motion20 A particle of mass m is released follows a parabolic path as shown Assuming that the displacement of the mass from the origin is small which graph correctly depicts the position of the particle as a function of time V x x t a o x t c 0 O x t b o x x t d o for t

Physics
Simple harmonic motionA uniform rod of mass m and length I is suspended through a light wire of length and torsional constant k as shown in figure The time periods of the system for small oscillations in the vertical plane about point of suspension is find the value of
Physics
Simple harmonic motion20 A body of mass m is attached to the lower end of a spring an whose upper end is fixed The spring has negligible mass supe When the mass m is slightly pulled down and released it oscillates with a time period of 3 s When the mass m is increased by 1 kg the time period of oscillations becomes 5 s The value of m in kg is 3 a 4 b 4 3 c 16 9 9 Lun 22 16
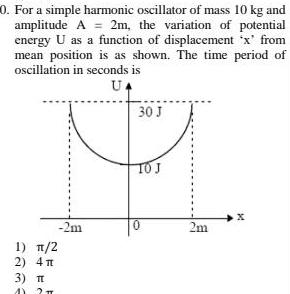
Physics
Simple harmonic motion0 For a simple harmonic oscillator of mass 10 kg and amplitude A 2m the variation of potential energy U as a function of displacement x from mean position is as shown The time period of oscillation in seconds is UA 1 2 2 4 3 T AY 2 T 2m 30 J TO J 0 2m X
Physics
Simple harmonic motionA mass of 1 kg attached to the bottom of spring has a certain frequency of vibration The following mass kg has to be added to it in order to reduce the frequency by half Answer DESELECT
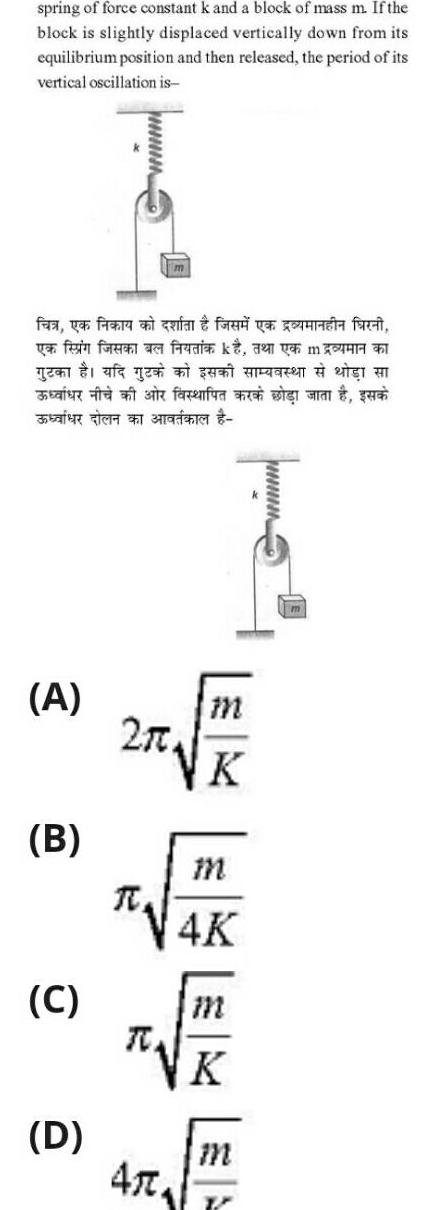
Physics
Simple harmonic motionspring of force constant k and a block of mass m If the block is slightly displaced vertically down from its equilibrium position and then released the period of its vertical oscillation is fea ya fiera an quan fad ya una farci yen fein foren a gen af g a A B C D facenfura a visi m 2 0 K R 47 m 4K K m

Physics
Simple harmonic motion13 The phase of a particle in SHM at time t is 1 6 The following inference is drawn from this 1 The particle is at x a 2 and moving in X direction 2 The particle is at x a 2 and moving in X direction 3 The particle is at x a 2 and moving in X direction 4 The particle is at x a 2 and moving in X direction

Physics
Simple harmonic motion5 The differential equation that describes the behavior of a spring mass apparatus is called the a governing equation b equation of motion c complementary function d steady state solution 6 Simple harmonic motion is also called a free undamped motion b pure resonant motion c forced motion d a and c 7 The period of the equation of motion given by x t 6 sin 4nt is a TT S b 2 s 1 c 47 d 0 5 s S 71 LJ