Simple harmonic motion Questions and Answers
Physics
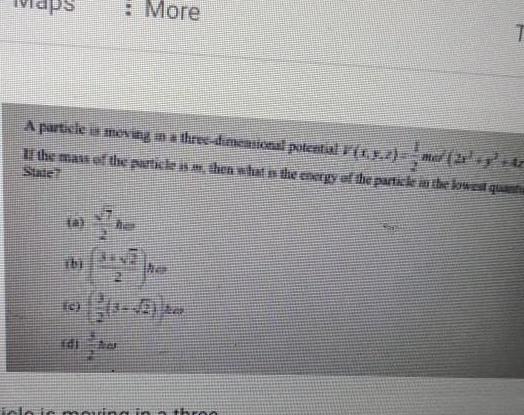
Simple harmonic motionaps A particle is moving in a three dimensional potential F 1 5 2 nd the mass of the particle is then what is the energy of the particle in the lowed quan ibi More c LAVE the inlois moving in a thr
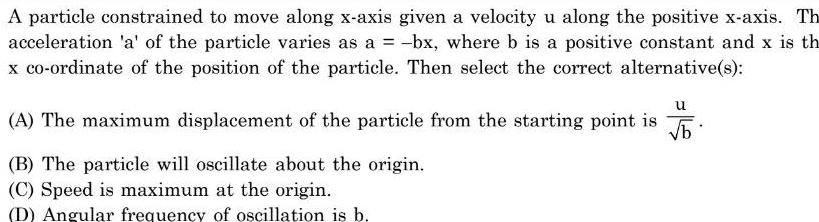
Physics
Simple harmonic motionA particle constrained to move along x axis given a velocity u along the positive x axis Th acceleration a of the particle varies as a bx where b is a positive constant and x is th x co ordinate of the position of the particle Then select the correct alternative s u A The maximum displacement of the particle from the starting point is b B The particle will oscillate about the origin C Speed is maximum at the origin D Angular frequency of oscillation is b

Physics
Simple harmonic motionThe bob of a simple pendulum of length L is released at time t 0 from a position of small angular displacement Its linear displacement at time t is given by 1 X a sin 2 x t 2 X a cos 2 x xt 3 X a sin x t 4 X a cos x t

Physics
Simple harmonic motionThe figure shows the circular motion of a particle which is at the topmost point on the y axis at t 0 The radius of the circle is B and the sense of revolution is clockwise The time period is indicated in the figure The simple harmonic motion of the x projection of the radius vector of the rotating particle P is B O 1 x t Bsin 2 30 T 30 s X
Physics
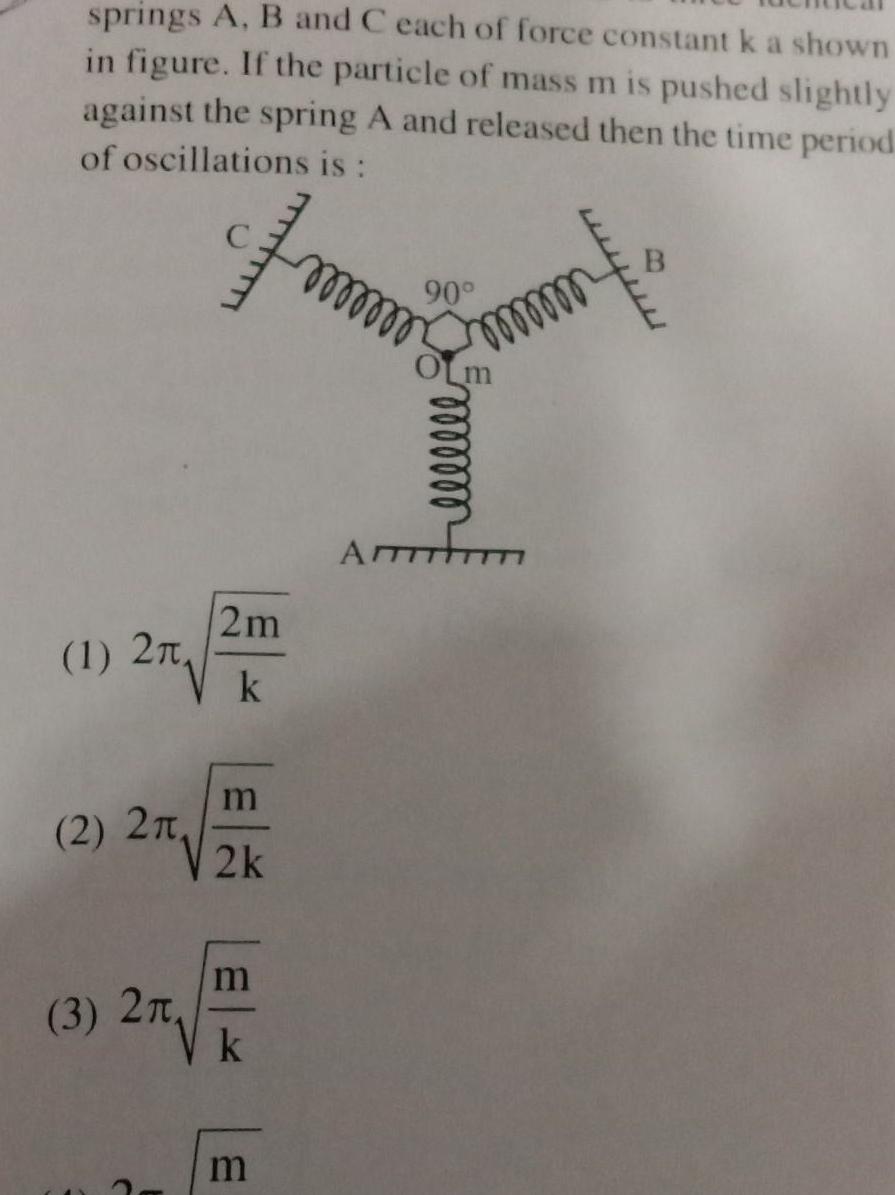
Simple harmonic motionsprings A B and C each of force constant k a shown in figure If the particle of mass m is pushed slightly against the spring A and released then the time period of oscillations is 1 2T 2 2 m 2 2k 3 2 2m k F m k m oooooo 90 OLM ATTT mm B

Physics
Simple harmonic motionThe bob of a simple pendulum is released at time t 0 from a position of sm angular displacement Its linear displacement is 1 length of simple pendulu and g acceleration due to gravity A amplitude of S H M A A sin B A cos C A t t A COS cos

Physics
Simple harmonic motionThe amplitude of a particle executing SHM is 36 made three fourth keeping its time period constant Its total energy will be E 0 1 1 20 2 3 E sua a 1 2 3 2 E dan faed Refendat

Physics
Simple harmonic motionA body attached to a spring oscillates in horizontal plane with frequency n Its total energy is E If the velocity in the mean position is v then the spring constant is A B C D n v2 4 n v2 8 n V 2 n v2

Physics
Simple harmonic motionIn the differential equation of linear simple harmonic motion w x 0 the term w represents A restoring force per unit mass per unit displacement B dax dt restoring force per unit displacement C restoring force per unit mass D acceleration per unit mass ner unit displacement

Physics
Simple harmonic motionA body executing S H M covers a b in successive seconds starting from one end If its amplitude is A and angular frequency is w then cos o cos o b a 2a a b a b Amplitude A 2a 3a b a Amplitude A
Physics
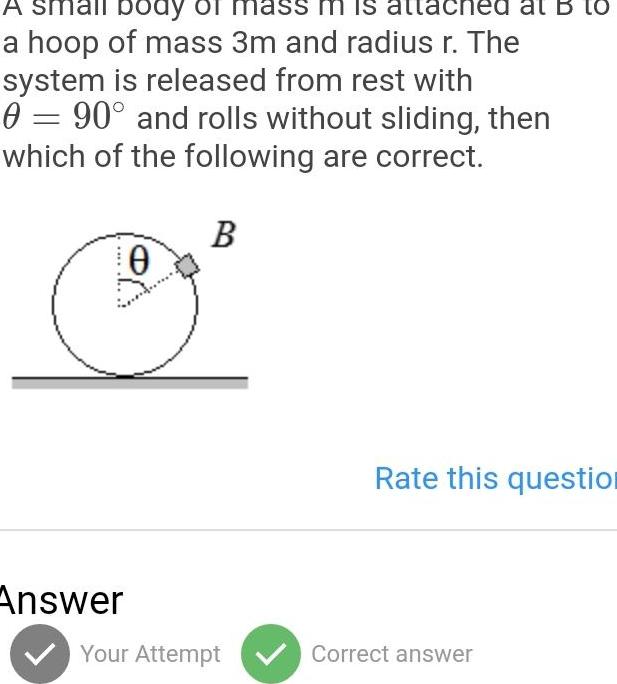
Simple harmonic motionA small boay lass m a hoop of mass 3m and radius r The system is released from rest with 0 90 and rolls without sliding then which of the following are correct B 10 Answer Your Attempt at B to Rate this question Correct answer

Physics
Simple harmonic motionHeight of a Wave As a wave passes by an offshore piling the height of the water is modeled by the function h t 4 cos t where h t is the height in feet above mean sea level at time t seconds a Find the period of the wave State the period in terms of the units of measure for the variable
Physics
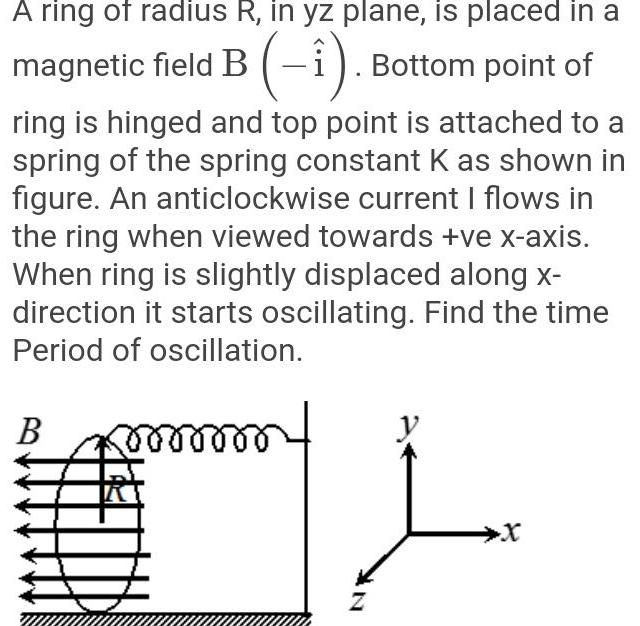
Simple harmonic motionA ring of radius R in yz plane is placed in a magnetic field B i Bottom point of ring is hinged and top point is attached to a spring of the spring constant K as shown in figure An anticlockwise current I flows in the ring when viewed towards ve x axis When ring is slightly displaced along x direction it starts oscillating Find the time Period of oscillation B mmmml my Z y
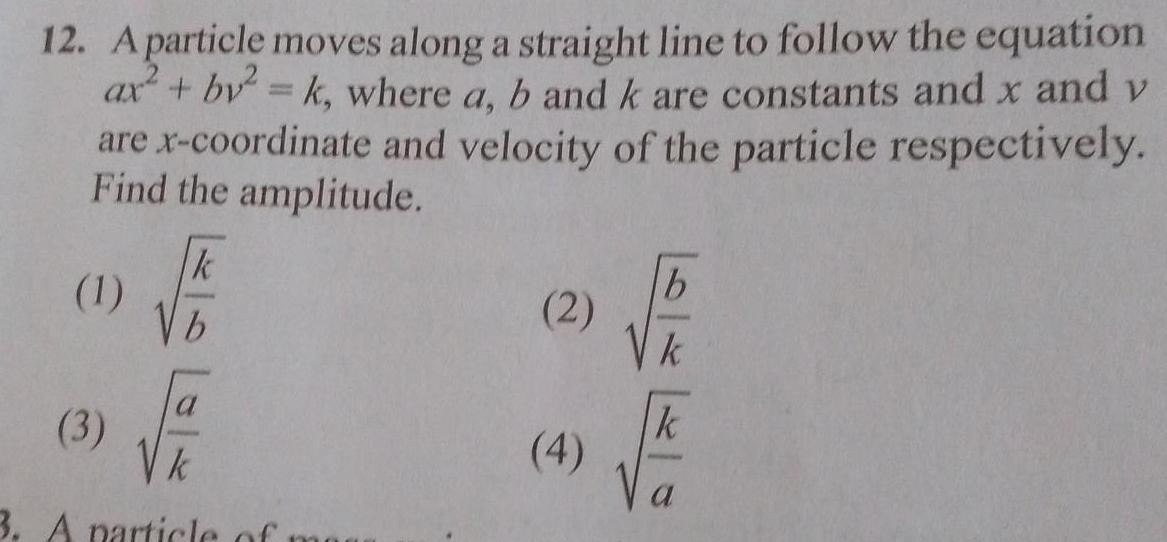
Physics
Simple harmonic motion12 A particle moves along a straight line to follow the equation ax by k where a b and k are constants and x and v are x coordinate and velocity of the particle respectively Find the amplitude 1 3 k V b k 3 A particle of mar 2 4

Physics
Simple harmonic motionA 175 g mass on a smooth surface is attached to a horizontal spring with a spring constant 8 N m 1 The mass is set to oscillate by pulling it 10 cm from its equilibrium position and released Calculate i the period of the oscillation ii the maximum speed of the mass iii the total energy of the system Answer T 0 93 s Answer Vmax 0 68 m s Answer E 0 04 J

Physics
Simple harmonic motionTwo points are located at a distance of 10 m and 15 m from the source of oscillation The period of oscillation is 0 05 s and the velocity of the wave is 300 m s What is the phase difference between the oscillations of two points AIPMT 2008 1 H 3 3 3 T 4 6 10000
Physics
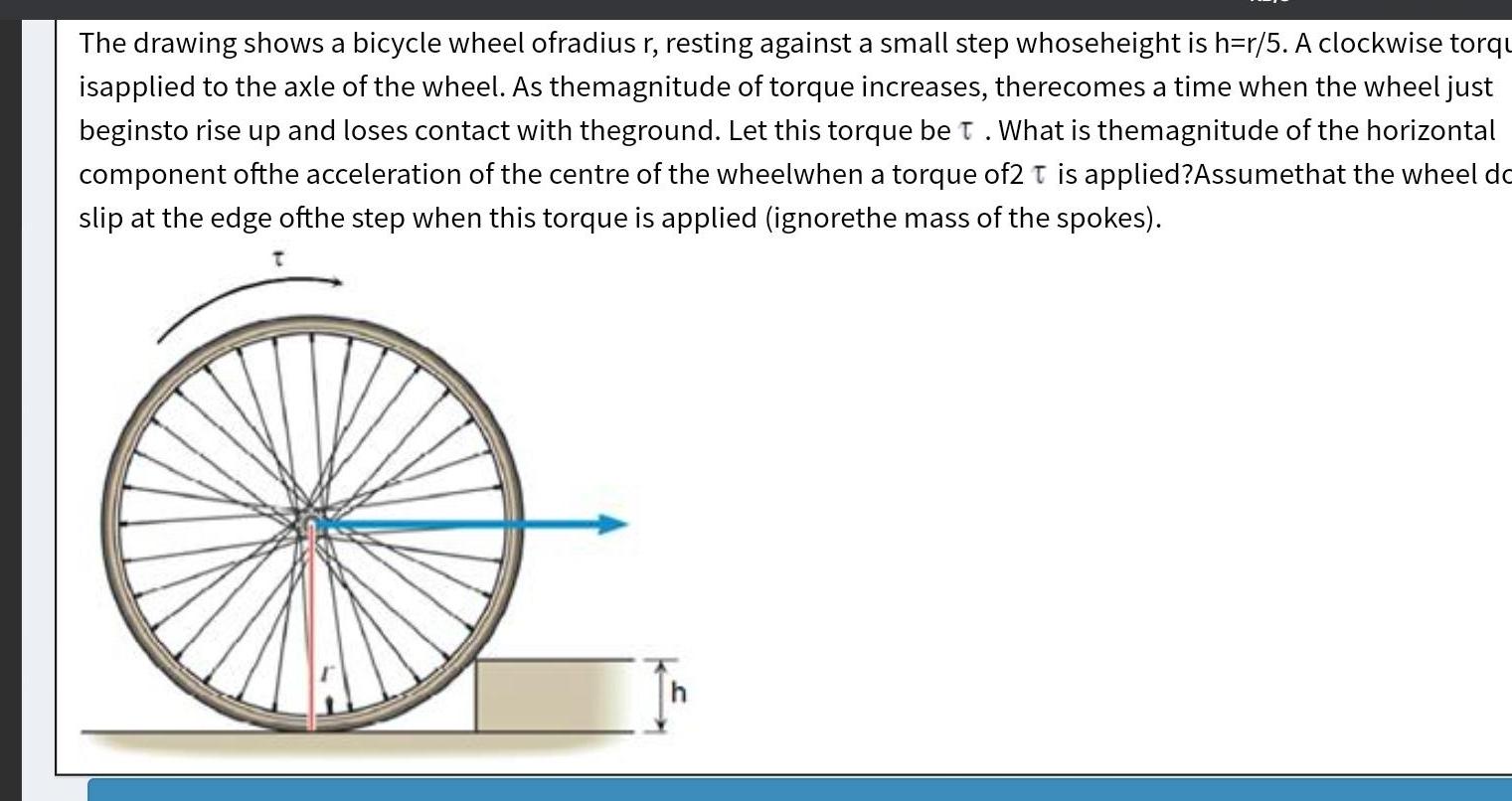
Simple harmonic motionThe drawing shows a bicycle wheel ofradius r resting against a small step whoseheight is h r 5 A clockwise torqu isapplied to the axle of the wheel As themagnitude of torque increases therecomes a time when the wheel just beginsto rise up and loses contact with theground Let this torque be T What is themagnitude of the horizontal component ofthe acceleration of the centre of the wheelwhen a torque of2 T is applied Assumethat the wheel do slip at the edge ofthe step when this torque is applied ignorethe mass of the spokes

Physics
Simple harmonic motionA child swings sitting and standing inside swing as shown in figure then period of oscillations have the relation KCET Engg Med 2000 AIEEE 2002 DPMT 2004 MP PMT 2009 b T Sitting T Standing d 2 T Sitting T Standing a T Sitting T Standing c T Sitting T Standing

Physics
Simple harmonic motion12 A body is performing simple harmonic motion along y axis with a frequency 20Hz and path length 40cm When it passes the mean position along ve y direction stop clock is started a How long it will take to reach the extreme top position b What will be the amplitude of motion c What is its displacement after 1 8 th of the time period d Find the magnitude of maximum velocity and maximum acceleration

Physics
Simple harmonic motionA 1 kg block is executing SHM of amplitude 0 1 m in vertical plane under restoring force of spring constant 100 N m A block of mass 24 kg at rest collides inelastically with the oscillating block of 1 kg and stick to it at the instant it passes through the mean position Find out the frequency of oscillation in sec 1 of the combined mass 1 3 TIE NI 2 2 SIR 5 4 Data insufficient

Physics
Simple harmonic motionThe constituent waves of a stationary wave have amplitude frequency and velocity as 8 cm 25 Hz and 150 cm s respectively What is the amplitude of the stationary wave at x 2 cm 2mv v y 2a sinkx y 16 sin Hint 2mv V TX

Physics
Simple harmonic motionTwo blocks of mass 5 kg and 1 kg connected by a spring are placed on a frictionless horizontal plane The massless spring is of natural length 2 m The spring is compressed by half of spring s natural length The system is now released from rest The spring constant is 100 N m 1kg eeeeee5kg Velocity of the 5 kg block when spring reaches its natural length is 10 5 m s 3 10 A 3 m s A The time period of S H M executed by the 5 kg block is 56 T 6 C 5 55 K A A 516 Time period of S H M executed by the 1 kg block is B S S B B T 6 5 10 C 2 m s 3 S S C 554 S TV5 S D 30 m s 55 D S D 5 5 F 56 S

Physics
Simple harmonic motionThe fundamental frequency of an organ pipe filled with air is 500Hz what will be its fundamental frequency when air is replaced by hydrogen at the same temperature density of air is 1 2kg m and hydrogen is 0 089kg m a 1850 Hz b 1840 Hz c 1830 Hz d 1860 Hz

Physics
Simple harmonic motionTwo circular rings each of radius a are joined together such that their planes are perpendicular to each other as shown in the figure The resistance of each half part of the ring is indicated A very small loop of mass m and radius r carrying current lo is placed in the plane of the paper at the common centre of each ring The loop can freely rotate about any of its diametric axes If the loop is slightly displaced find the time period of its oscillations m 192 192 192 202 E 2V

Physics
Simple harmonic motion112 A 2 0 kg block is attached to the end of a spring with a spring constant of 350 N m and forced to oscillate by an applied force F 15 N sin wat where wa 35 rad s The damping constant is b 15 kg s At t 0 the block is at rest with the spring at its rest length a Use numerical integration to plot the displacement of the block for the first 1 0 s Use the motion near the end of the 1 0 s interval to estimate the ampli tude period and angular frequency Repeat the calculation for b k m and c w 20 rad s wd

Physics
Simple harmonic motion1 A mass of 3 kg is attached to the free end of a spring as shown in the figure For this spring a force of 6 N causes a displacement of 0 03 m If the mass is pulled aside by a distance of 0 06 m and released then donac a Compute the force constant of the spring
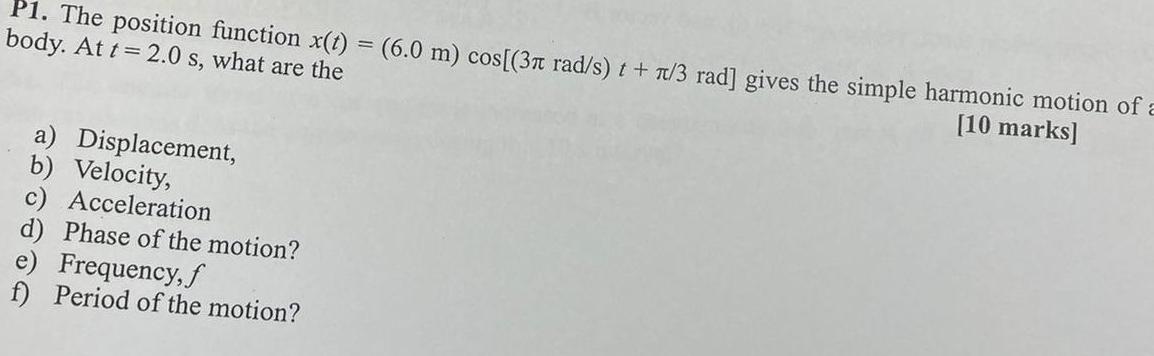
Physics
Simple harmonic motionP1 The position function x t 6 0 m cos 3 rad s t 7 3 rad gives the simple harmonic motion of a body At t 2 0 s what are the 10 marks a Displacement b Velocity c Acceleration d Phase of the motion e Frequency f f Period of the motion
Physics
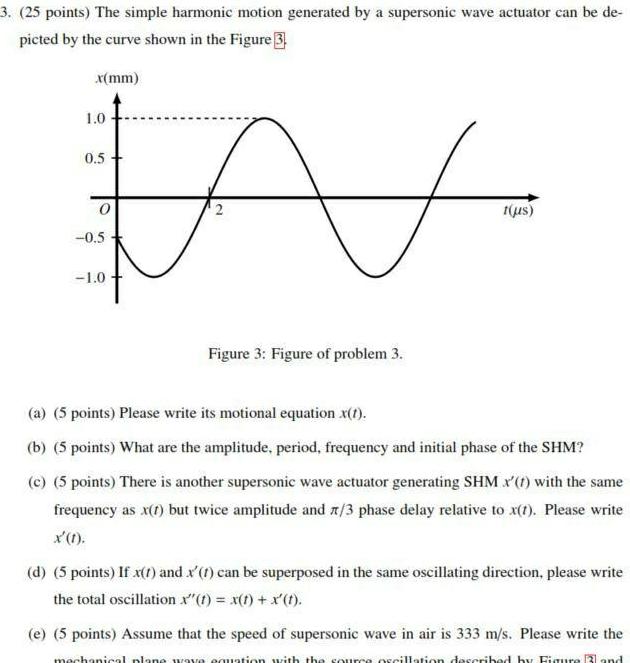
Simple harmonic motion3 25 points The simple harmonic motion generated by a supersonic wave actuator can be de picted by the curve shown in the Figure 3 x mm N 1 0 0 5 0 0 5 1 0 Figure 3 Figure of problem 3 1 us a 5 points Please write its motional equation x t b 5 points What are the amplitude period frequency and initial phase of the SHM c 5 points There is another supersonic wave actuator generating SHM x 1 with the same frequency as x 1 but twice amplitude and 3 phase delay relative to x t Please write x 1 d 5 points If x 1 and x 1 can be superposed in the same oscillating direction please write the total oscillation x t x t x t e 5 points Assume that the speed of supersonic wave in air is 333 m s Please write the mechanical plane wave equation with the source oscillation described by Figure and

Physics
Simple harmonic motionA 0 3 kg mass is attached to a spring with spring constant 30 N m along a horizontal frictionless surface The object oscillates in simple harmonic motion and has a speed of 2 m s at the equilibrium position What is the amplitude of vibration 1 56 m 0 50 m 3 57 m O 0 20 m

Physics
Simple harmonic motion103 For a simple pendulum find the angular amplitude m at which the restoring torque required for simple harmonic motion deviates from the actual restoring torque by 1 0 See Trigonometric Expansions in Appendix E
Physics
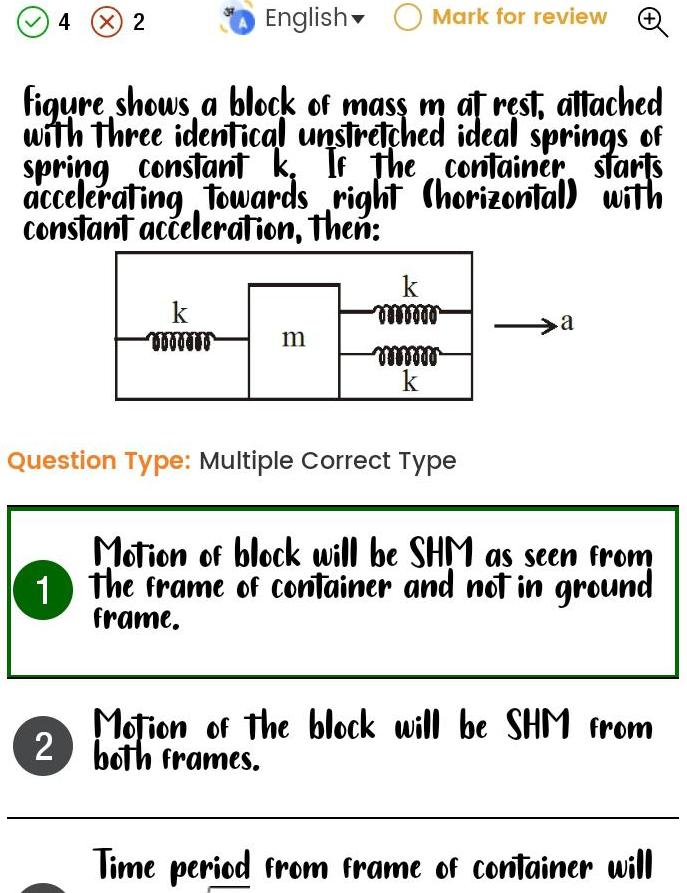
Simple harmonic motionEnglish Mark for review figure shows a block of mass m at rest attached with three identical unstretched ideal springs of spring constant k If the container accelerating towards right horizontal with constant acceleration then starts 4 X 2 k www m k mwww mmmmm k Question Type Multiple Correct Type a Motion of block will be SHM as seen from 1 The frame of container and not in ground frame Motion of the block will be SHM from 2 both frames Time period from frame of container will

Physics
Simple harmonic motionThe block of mass M in the figure is connected to a left spring k k The right spring k 2k is fixed to the other wall such that its free end is 6 cm away from block In this situation entire system is in equilibrium Now block is displaced to left by 6 2 cm and released Determine the time period of oscillatory motion of the block k mmmmmmmm m 2k mmmmmmmm my

Physics
Simple harmonic motionA uniform sphere of mass 1 4 kg and radius 0 045 m is suspended from its surface by a wire of a torsional constant 55 Nm The wire is twisted and let free to oscillate How long does it take to make one complete revolution ICM 2MR 5
Physics
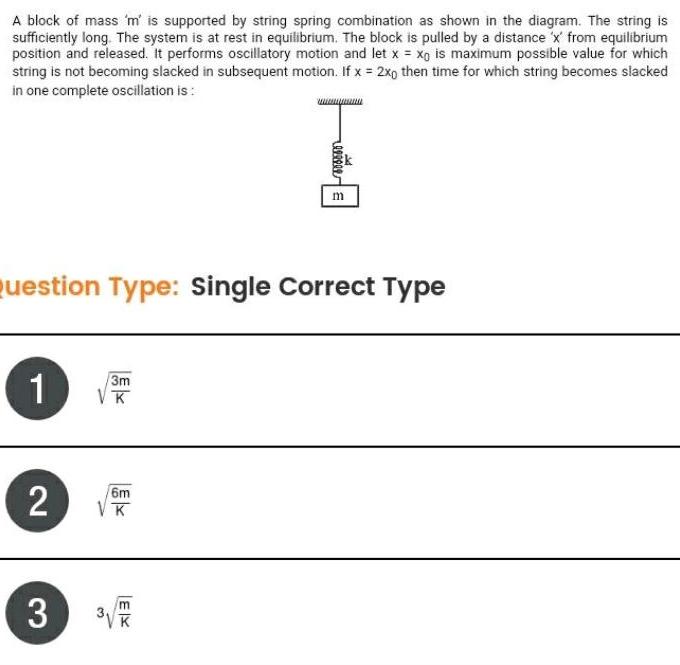
Simple harmonic motionA block of mass m is supported by string spring combination as shown in the diagram The string is sufficiently long The system is at rest in equilibrium The block is pulled by a distance x from equilibrium position and released It performs oscillatory motion and let x xg is maximum possible value for which string is not becoming slacked in subsequent motion If x 2x0 then time for which string becomes slacked in one complete oscillation is Question Type Single Correct Type 1 2 3 3m VK 6m K EX m 3 K

Physics
Simple harmonic motionA 1 000 m long simple pendulum is situated near the earth s surface where 9 800 see Figure 2 Determine the period and frequency of the simple pendulum assuming it oscillates with small amplitude or at small angles Figure 2 0 L 1 000 m

Physics
Simple harmonic motionThe total mechanical energy of a harmonic oscillato of amplitude 0 01m and force constant 2 x 10 N m is 160 J Then A The minimum potential energy is zero B The maximum potential energy is 100J C The minimum potential energy is 60 J D The maximum potential energy is 60 J

Physics
Simple harmonic motionThe displacement of a particle executing SHM is given by Y 5 sin 3t 7 3 m and t is in seconds The initial displacement and maximum velocity of the particle are respectively A 2 5 3 m and 15m sec B 15 m and 15 3m sec c 15 3 m and 30m sec D 20 3 m and 30m sec

Physics
Simple harmonic motionD When beats are produced by two progressive waves of nearly the same frequency which one of the following is correct a The particles vibrate simple harmonically with the frequency equal to the difference in the component frequencies b The amplitude of vibration at any point changes simple harmonically with a frequency equal to the difference in the frequencies of the two waves c The frequency of beats depends upon the position where the observer is d The frequency of beats changes as the time progresses
Physics
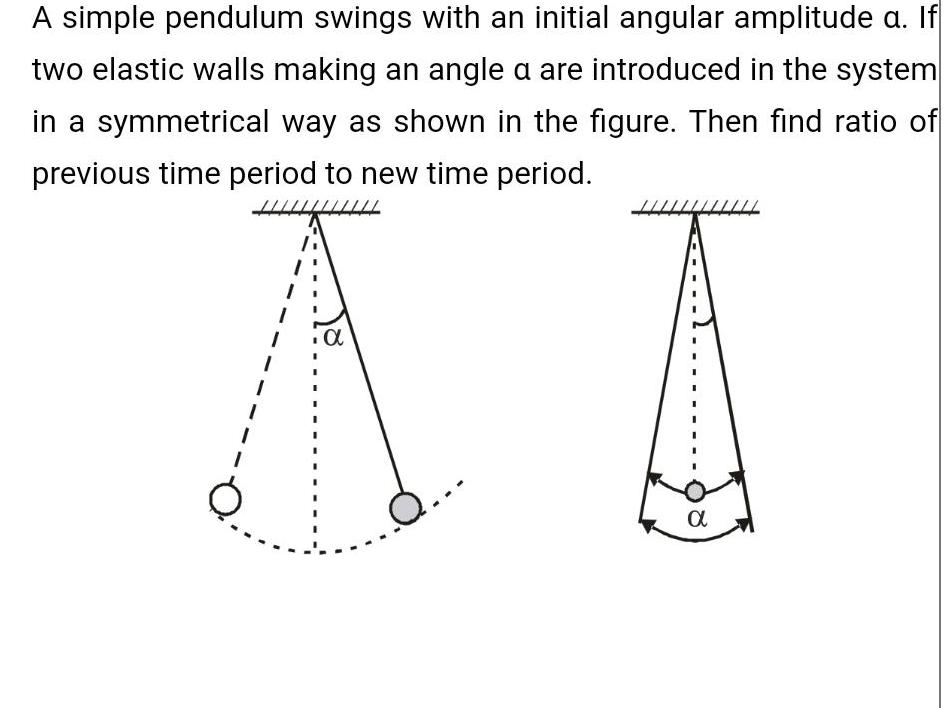
Simple harmonic motionA simple pendulum swings with an initial angular amplitude a If two elastic walls making an angle a are introduced in the system in a symmetrical way as shown in the figure Then find ratio of previous time period to new time period 4 A A
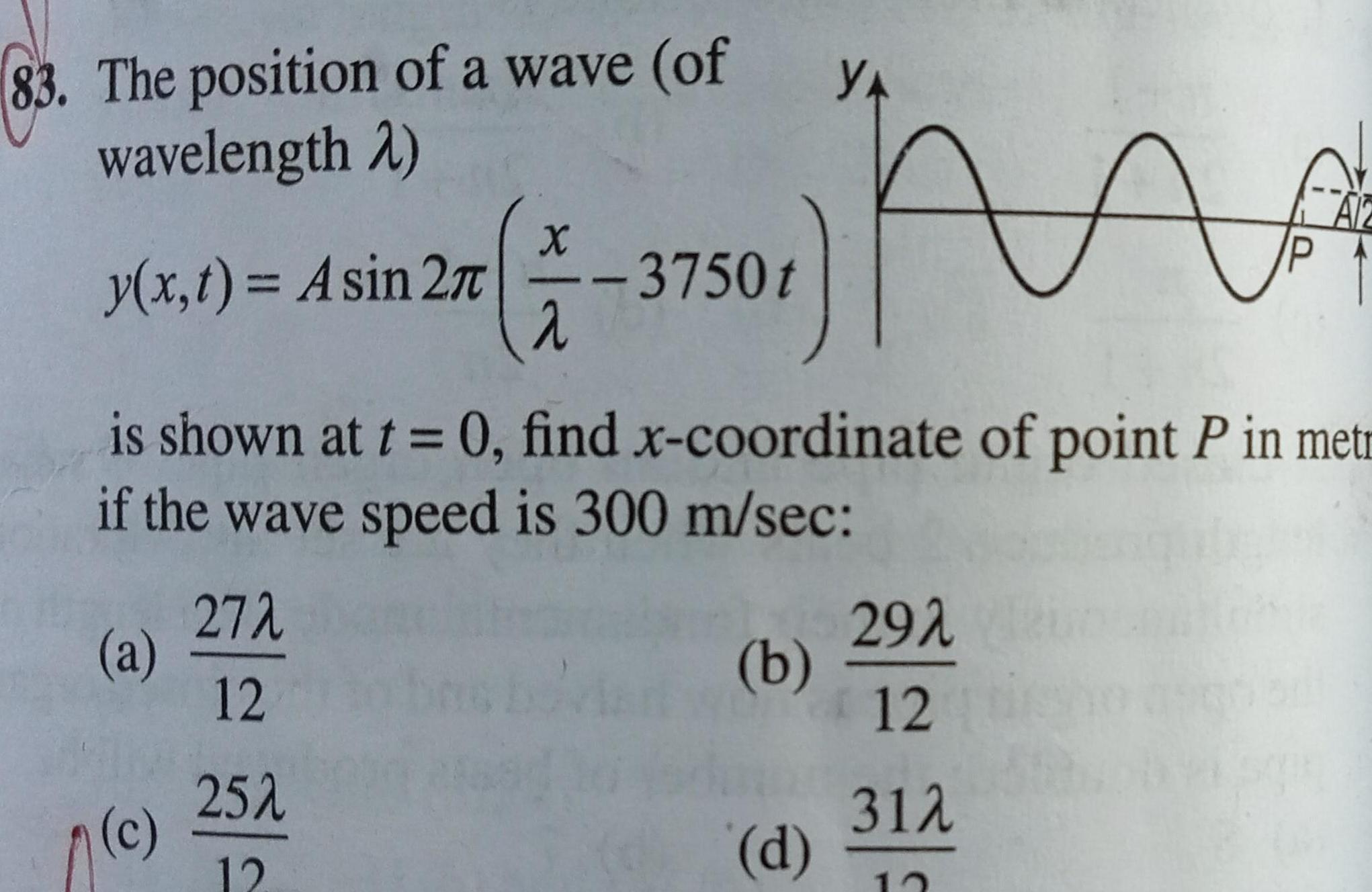
Physics
Simple harmonic motion83 The position of a wave of wavelength 2 A is shown at t 0 find x coordinate of point P in metr if the wave speed is 300 m sec y x t Asin 27 a c 27 12 25A 12 X 7 3750t b YA d 29 12 31 12
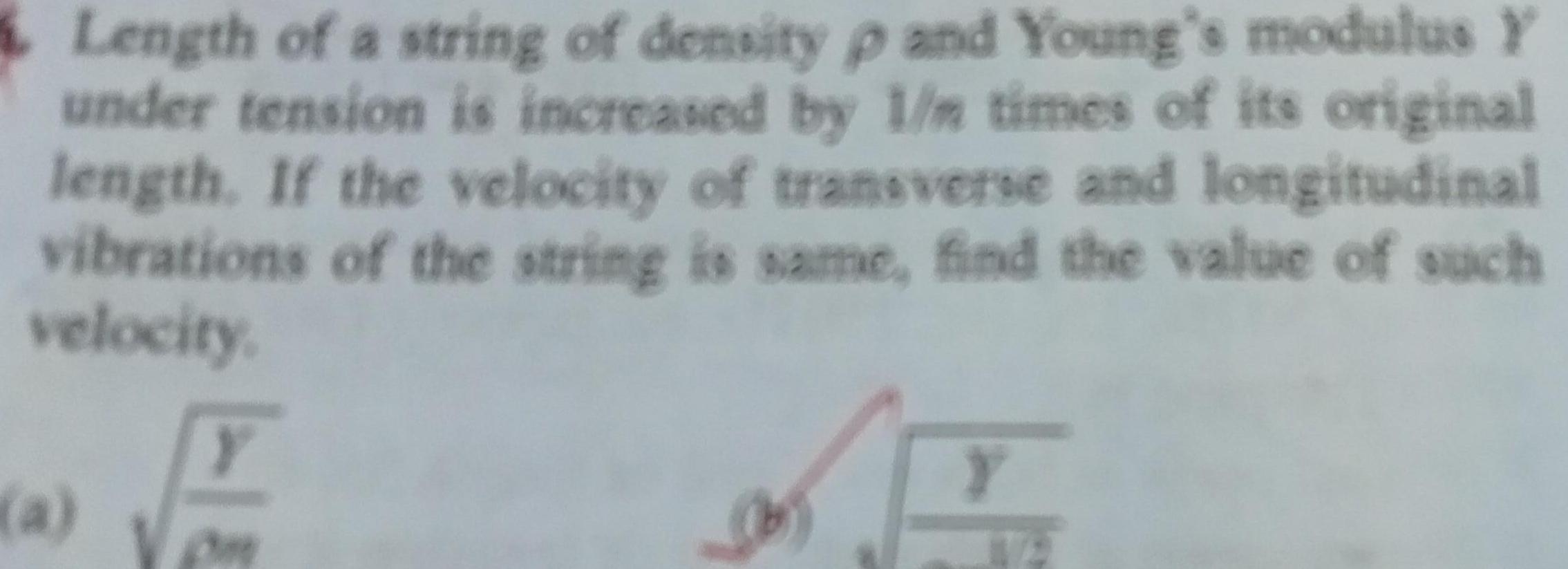
Physics
Simple harmonic motionLength of a string of density p and Young s modulus Y under tension is increased by 1 m times of its original length If the velocity of transverse and longitudinal vibrations of the string is same find the value of such velocity a Y 45 Y
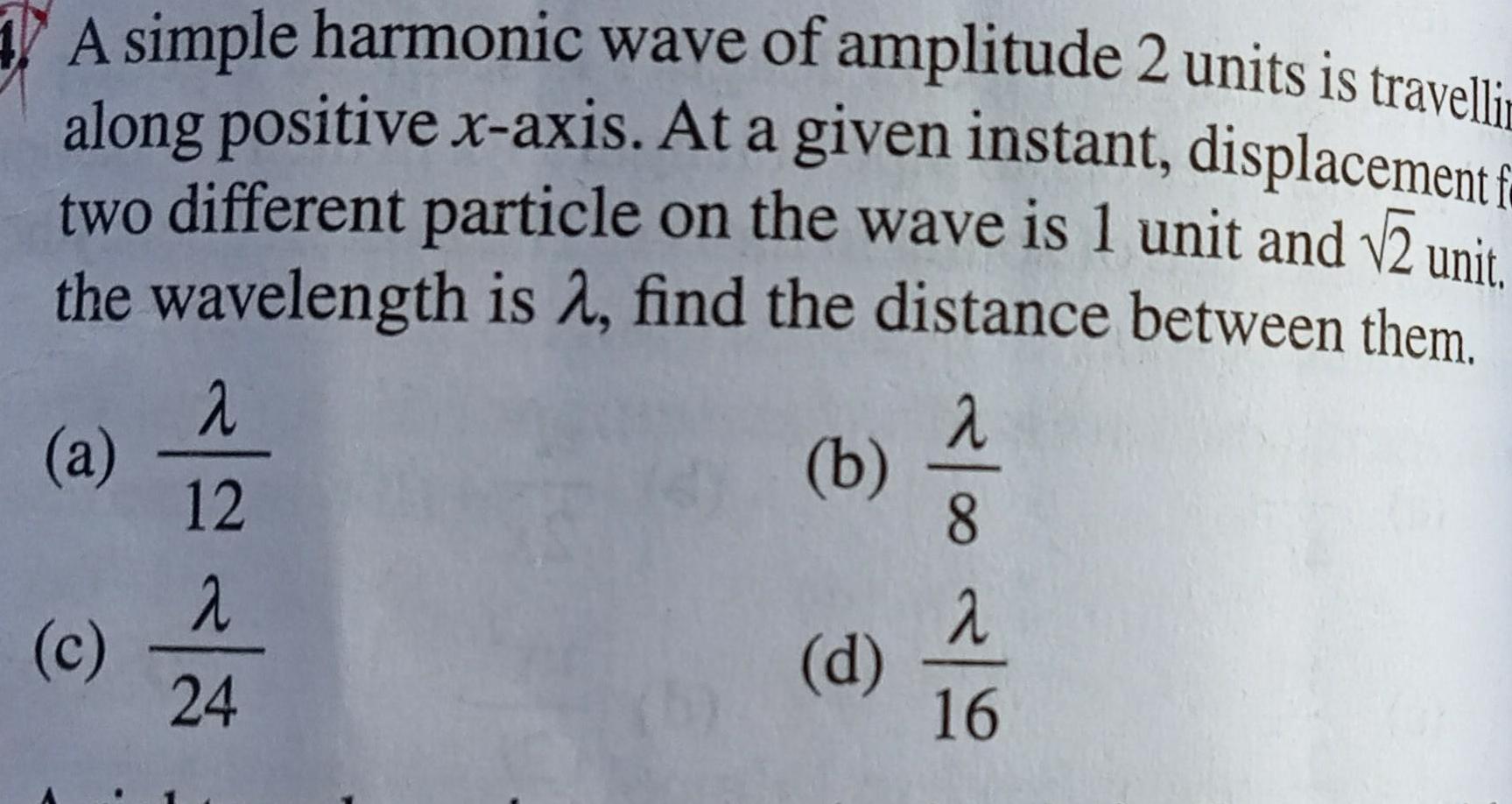
Physics
Simple harmonic motionA simple harmonic wave of amplitude 2 units is travelli along positive x axis At a given instant displacement f two different particle on the wave is 1 unit and 2 unit the wavelength is find the distance between them a c 2 12 2 24 b d 8 2 16
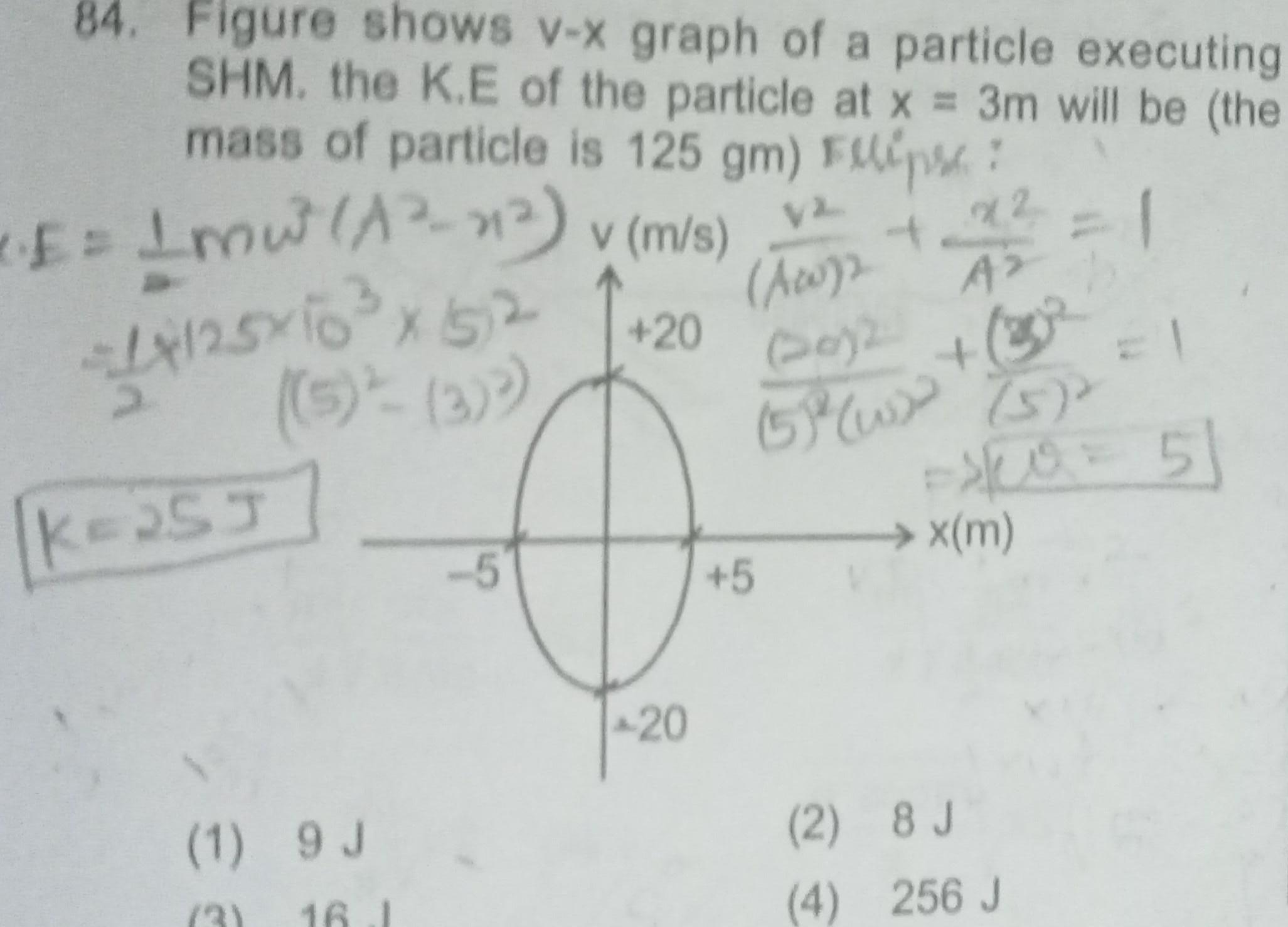
Physics
Simple harmonic motion84 Figure shows v x graph of a particle executing SHM the K E of the particle at x 3m will be the mass of particle is 125 gm Flipse E 1 mw A x v m s 4X125 10 x152 5 3 Y 4 22 A b 20 K 25J 1 9 J 3 16 5 20 VL Awys Day 2 5w 32 5 x m 2 8 J 4 256 J 1 5

Physics
Simple harmonic motionA uniform disc of radius R is to be suspended through a small hole made in the disc The minimum possible time period of the disc for small oscillation will be 1 2n 3 2 R g R 2 2 4 2 2R g 2R a

Physics
Simple harmonic motionis attac led to one end of a mass less spring of force constant K lying on a frictionless horizontal plane The particle starts moving horizontally from its equilibrium position at time t 0 with an initial velocity up When the speed of particle is 0 5u it collides elastically with a rigid wall After this collision Vmax Uo A 1 the instant of time at which the particle passes through the equilibrium position for 1st time is t 2 m 3 VK 2 the instant of time at which the particle passes through the equilibrium position for 1st time is T m 3 VK t 3 the instant of time at which the particle passes through the equilibrium position for 1st time is m 6 VK t 4 the instant of time at which the particle passes through the equilibrium position for 1st time is
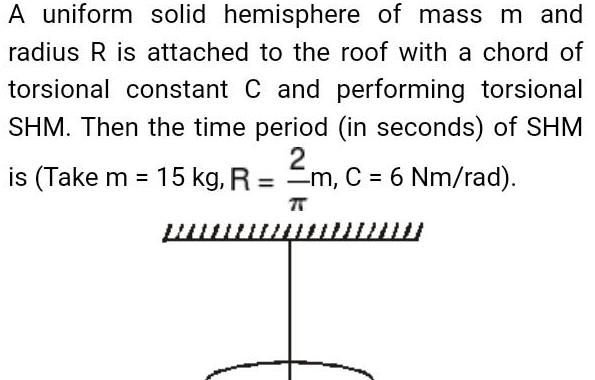
Physics
Simple harmonic motionA uniform solid hemisphere of mass m and radius R is attached to the roof with a chord of torsional constant C and performing torsional SHM Then the time period in seconds of SHM 2 is Take m 15 kg R m C 6 Nm rad wwww

Physics
Simple harmonic motionA wooden block performs simple harmonic motion on a frictionless surface with frequency Vo The block carries a charge Q on its surface If now a uniform electric field E is switched on as shown the simple harmonic motion of the block will be Q ooooooo 1 Of the same frequency and with shifted mean position 2 Of the same frequency and with same mean position 3 Of changed frequency and with shifted mean position 4 Of changed frequency and with same mean

Physics
Simple harmonic motionA uniform rod of length L is suspended by an end and is made to undergo small oscillations The length of the simple pendulum having the time period equal to that of rod is 1 L3 3 L 2 4 2L 3 4L 3
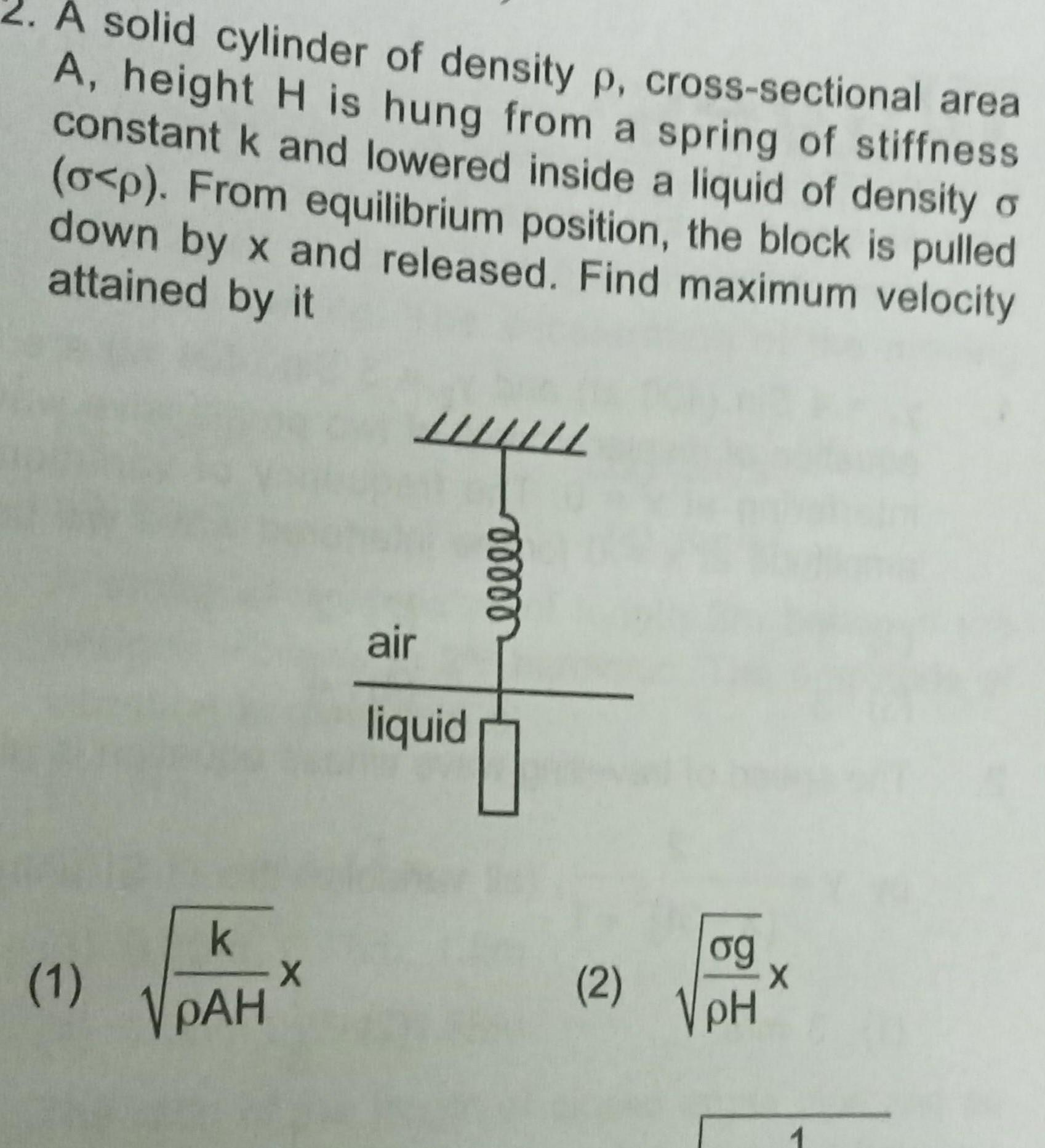
Physics
Simple harmonic motionA solid cylinder of density p cross sectional area A height H is hung from a spring of stiffness constant k and lowered inside a liquid of density o o p From equilibrium position the block is pulled down by x and released Find maximum velocity attained by it 1 k PAH X air liquid moooo 2 og pH 1
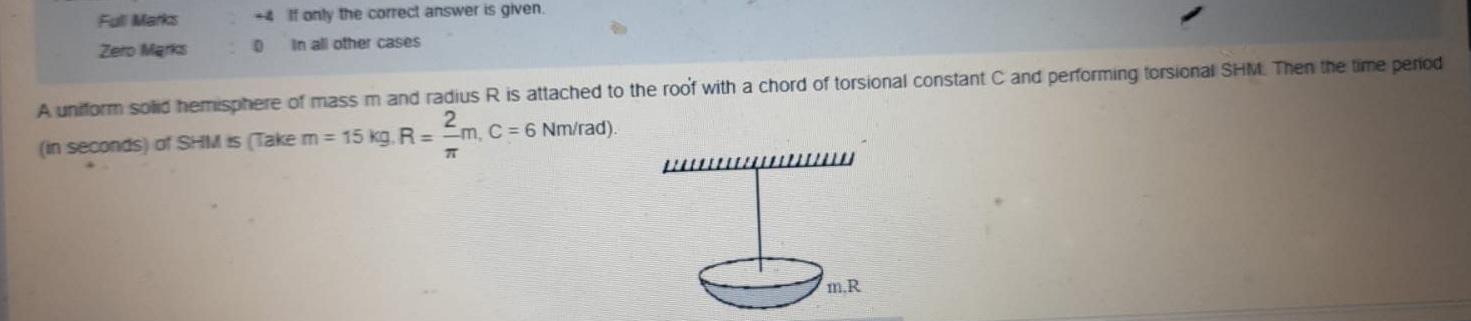
Physics
Simple harmonic motionFull Marks Zero Marks If only the correct answer is given 0 In all other cases A uniform solid hemisphere of mass m and radius R is attached to the roof with a chord of torsional constant C and performing torsional SHM Then the time period in seconds of SHM is Take m 15 kg R 2 m C 6 Nm rad T wwwwwwww m R