Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 25 30 and f 25 6 Then estimate the number of computers sold if the price is set at 2525 pe computer What does f 25 30 imply OA When the price per computer is 2500 for every 100 price increase the sales increase by 30 000 computers OB When the price per computer is 3000 for every 100 price increase the sales increase by 25 000 computers OC 30 000 computers are sold when the price is set at 250 OD 30 000 computers are sold when the price is set at 2500
Calculus
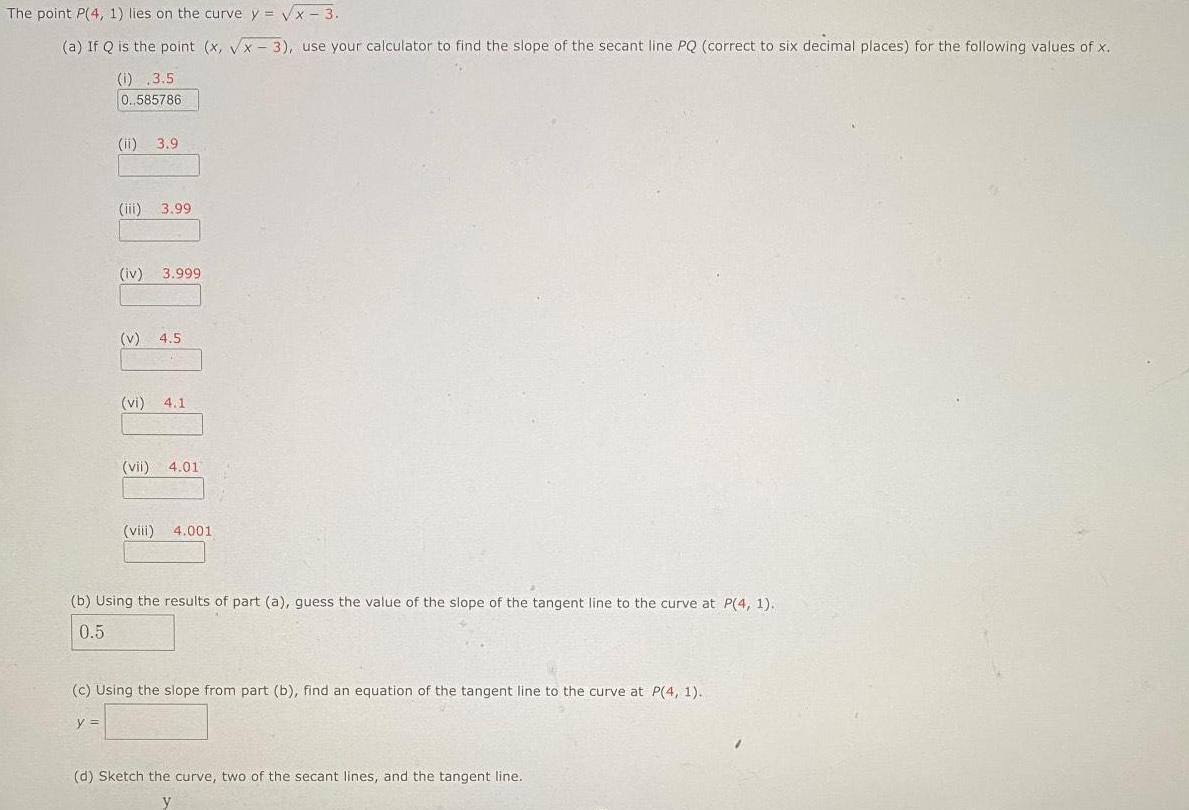
Vector CalculusThe point P 4 1 lies on the curve y x 3 a If Q is the point x x 3 use your calculator to find the slope of the secant line PQ correct to six decimal places for the following values of x 1 3 5 0 585786 ii 3 9 iii 3 99 iv 3 999 v 4 5 vi 4 1 vii 4 01 viii 4 001 b Using the results of part a guess the value of the slope of the tangent line to the curve at P 4 1 0 5 c Using the slope from part b find an equation of the tangent line to the curve at P 4 1 y d Sketch the curve two of the secant lines and the tangent line

Calculus
Application of derivativesLet f t be the temperature of a cup of coffee t minutes after it has been poured Interpret f 5 180 and f 5 8 Estimate the temperature of the coffee after 5 minutes and 12 seconds that is after 5 2 minutes What does f 5 180 imply OA 5 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 180 degrees per minute OB 180 minutes after the coffee has been poured the temperature of the cup of coffee is 5 degrees OC 5 minutes after the coffee has been poured the temperature of the cup of coffee is 180 degrees OD 180 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 5 degrees per minute

Calculus
Application of derivativesAy 500 500 000 500 000 500 000 00 0 0 2 4 6 8 10 12 14 16 18 Years after 1980 e blue curve shows national health expenditures in billions of dollars The red curve shows its ivative C National health expenditures in billions of dollars from 1980 to 1997 are given by the function f t in the graph to the left a How much money was being spent at the beginning of 1982 billion

Calculus
Vector Calculusecologist wishes to find the height of a redwood tree that is on the other side of a creek as shown in Figure 14 From point A he finds the angle of elevation to the top of the tree is 10 7 He then walks 24 8 feet at a right angle from point A and finds angle B is 86 6 What is the height of the tree FIGURE 14 24 8 B

Calculus
Differentiation15 Angle of Depression From a plane 3 000 feet in the air the angle of depression to the beginning of the runway is 3 50 What is the horizontal distance between the plane and runway That is if the plane flew at the same altitude how far would it be to the runway Give your answer to the nearest tenth of a mile 5 280 feet 1 mile
Calculus
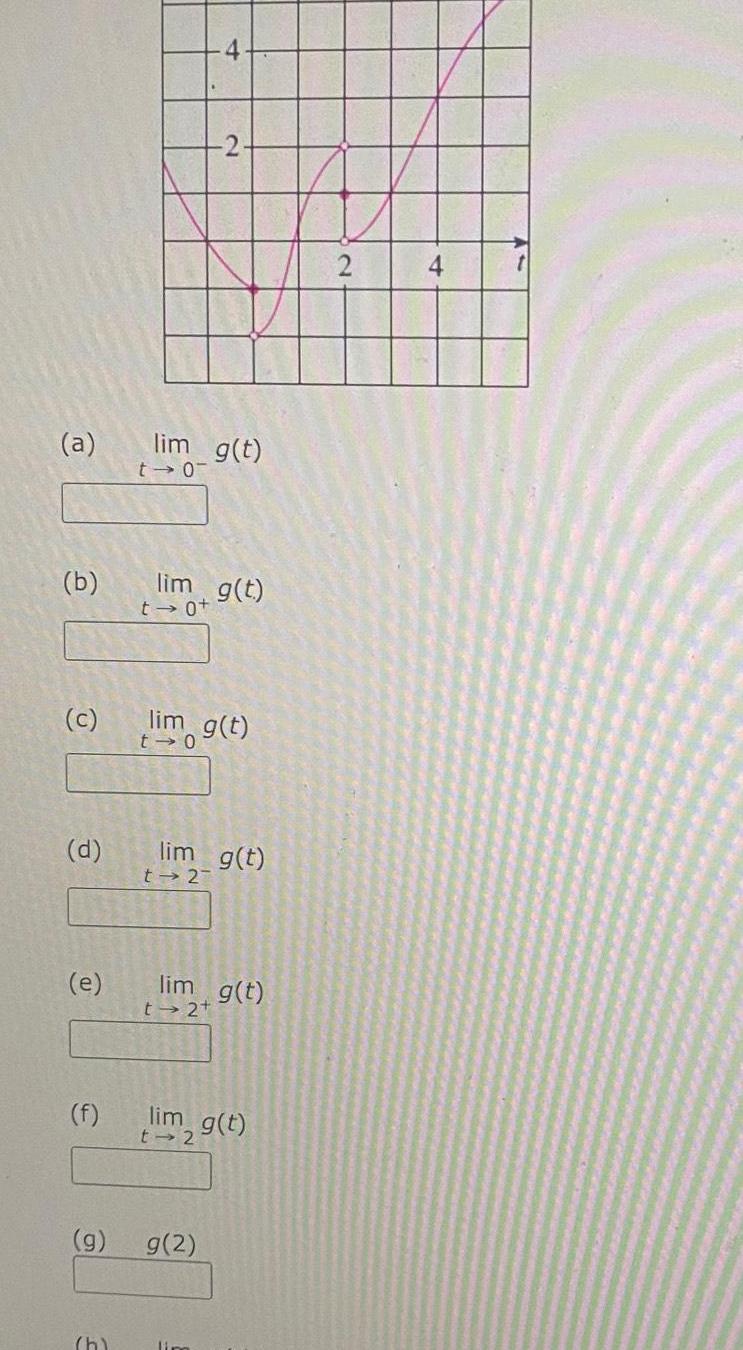
Limits & Continuitya b c d e f g h lim g t t 0 lim g t t 0 lim g t 2 lim g t t 2 lim g t t 2t lim g t t 2 g 2 lim 2 4 t
Calculus
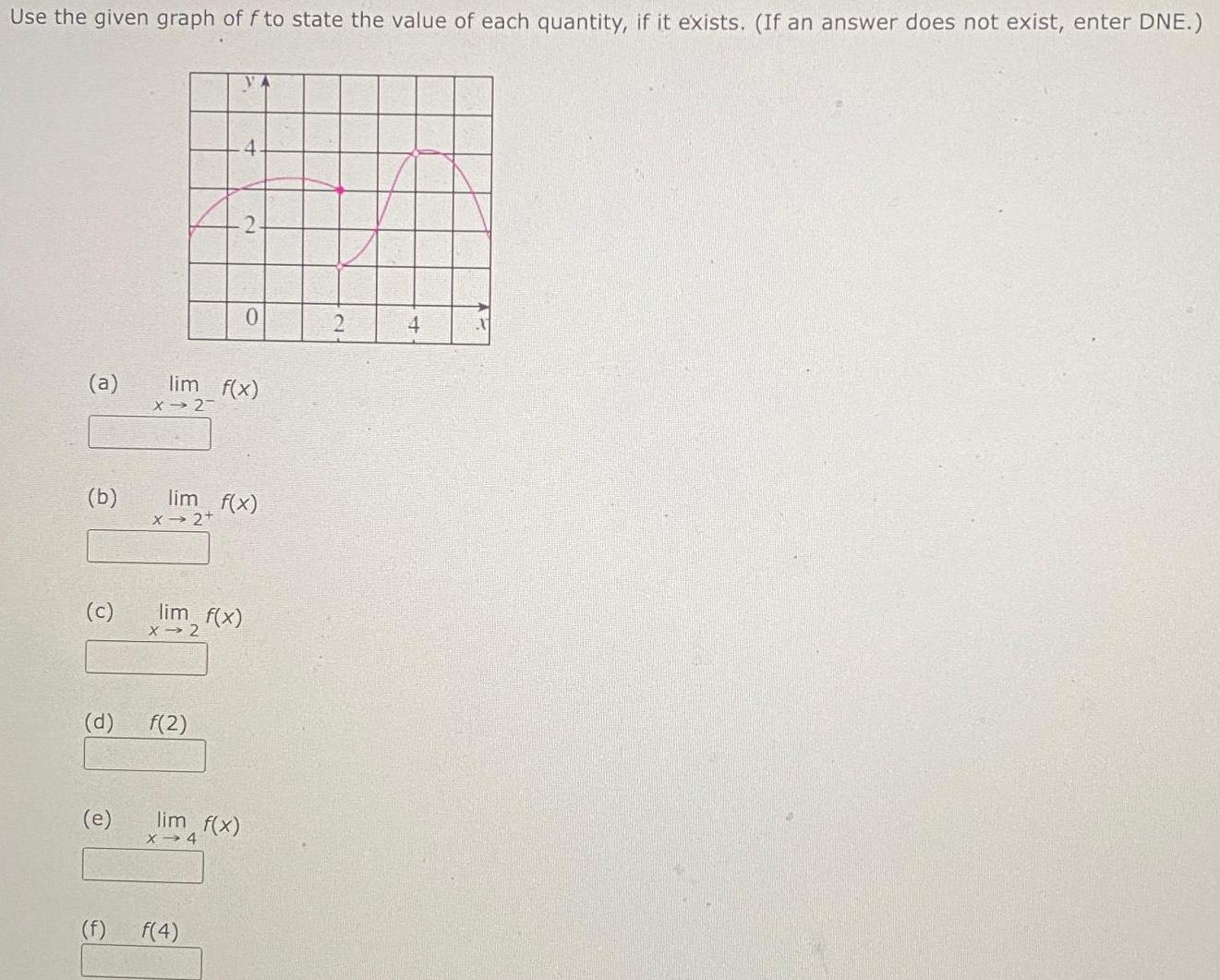
Limits & ContinuityUse the given graph of f to state the value of each quantity if it exists If an answer does not exist enter DNE a b c d e f X 2 lim f x lim f x X 2 lim f x X 2 f 2 lim f x 4 X 4 2 f 4 0 4
Calculus
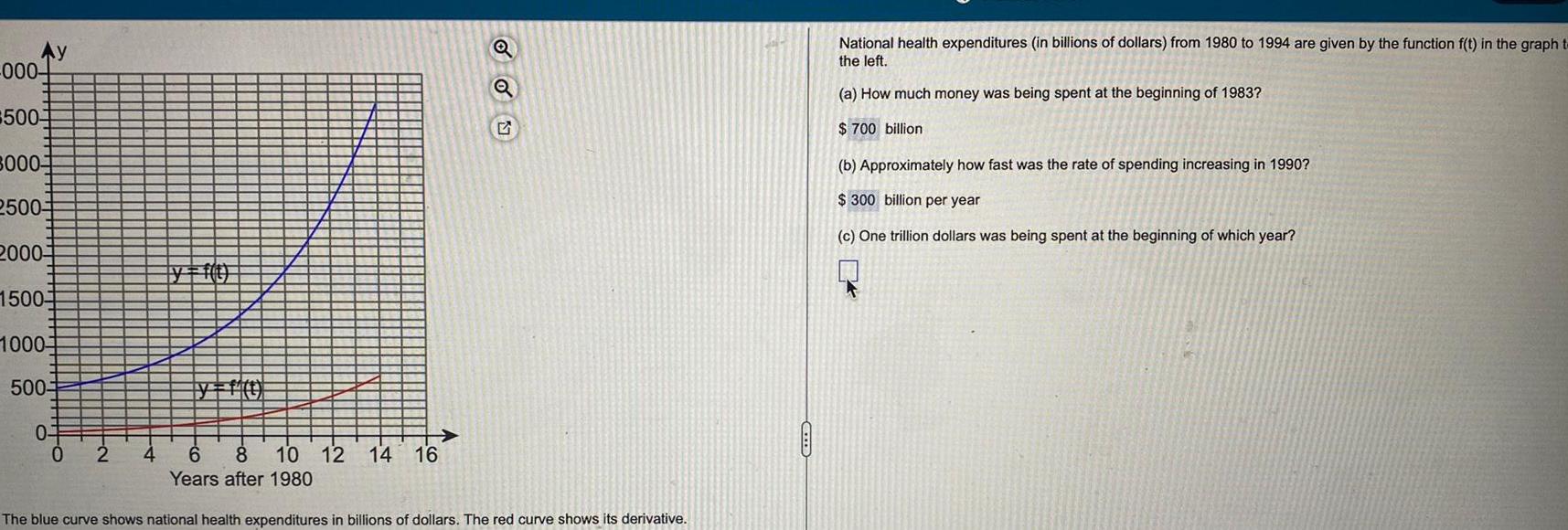
Application of derivativesAy 000 500 3000 2500 2000 1500 1000 500 0 0 2 6 8 10 12 14 16 Years after 1980 The blue curve shows national health expenditures in billions of dollars The red curve shows its derivative Q 4 National health expenditures in billions of dollars from 1980 to 1994 are given by the function f t in the graph to the left a How much money was being spent at the beginning of 1983 700 billion b Approximately how fast was the rate of spending increasing in 1990 300 billion per year c One trillion dollars was being spent at the beginning of which year

Calculus
Application of derivativesLet f t be the temperature of a cup of coffee t minutes after it has been poured Interpret f 5 190 and f 5 8 Estimate the temperature of the coffee after 5 minutes and 36 seconds that is after 5 6 minutes What does f 5 190 imply EXOD OA 190 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 5 degrees per minute OB 190 minutes after the coffee has been poured the temperature of the cup of coffee is 5 degrees C 5 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 190 degrees per minute OD 5 minutes after the coffee has been poured the temperature of the cup of coffee is 190 degrees

Calculus
Definite IntegralsSolve each of the following problems In each case be sure to make a diagram of the situation with all the given information labeled 1 Isosceles Triangle The two equal sides of an isosceles triangle are each 42 centimeters If the base measures 30 centimeters find the height and the measure of the two equal angles Round your answer to the nearest tenth 2 Equilateral Triangle An equilateral triangle one with all sides the same length has an altitude of 4 3 inches Find the length of the sides 3 Length of an Escalator How long should an escalator be if it is to make an angle of 33 with the floor and carry people a vertical distance of 21 feet between floors Round to the nearest tenth 4 Height of a Hill A road up a hill makes an angle of 5 with the horizontal If the road from the bottom of the hill to the top of the hill is 2 5 miles long how high is the hill 5 Circus Tent A rope from the top of a circus tent pole is 72 5 feet long and is anchored to the ground 43 2 feet from the bottom of the pole What angle does the rope make with the pole Give your answer to the nearest tenth of a degree
Calculus
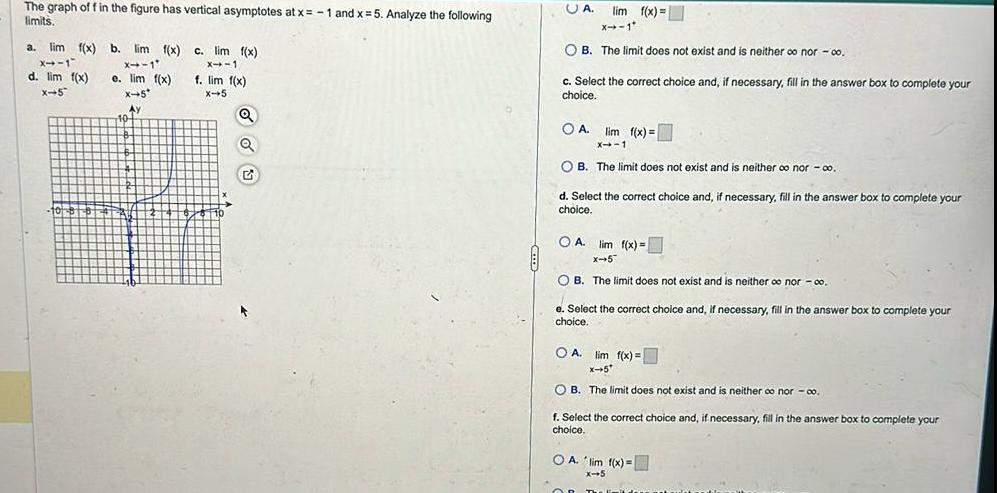
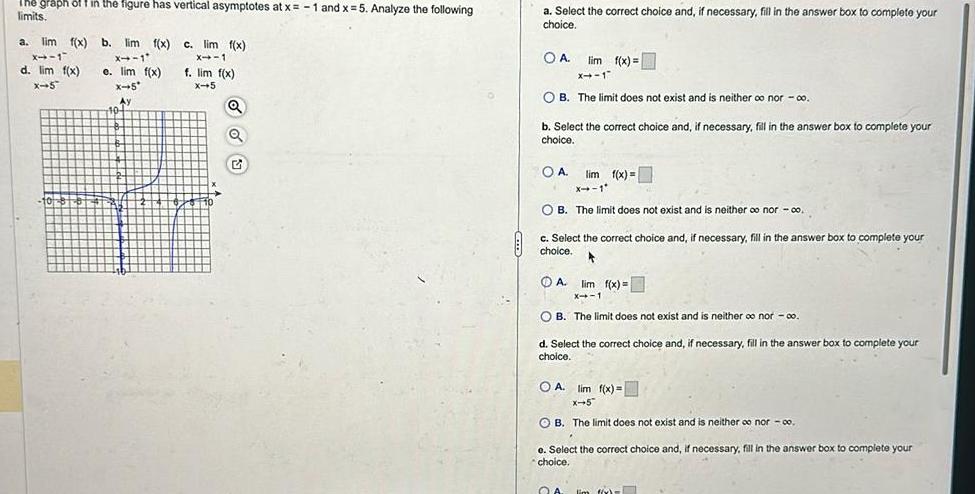
Limits & ContinuityThe graph of f in the figure has vertical asymptotes at x 1 and x 5 Analyze the following limits a lim f x b lim f x X 1 X 1 e lim f x d lim f x X 5 X 5 Ay 10 c lim f x X 1 f lim f x X 5 Q Q G UA lim f x X 1 OB The limit does not exist and is neither oo nor 00 c Select the correct choice and if necessary fill in the answer box to complete your choice lim f x X 1 OB The limit does not exist and is neither oo nor co O A d Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x X 5 OB The limit does not exist and is neither o nor 00 e Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x x 5 OB The limit does not exist and is neither co nor co f Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x x 5 OR

Calculus
DifferentiationCalculate the derivative of the following function dy dx 1 y 5x 4 11 5 3 5x 1
Calculus
Limits & Continuity3 Explain why sec is always greater than or equal to 1 or less than or equal to 1

Calculus
DifferentiationUse a calculator to find the trigonometric value tan 37 tan 37 Type an integer or decimal rounded to four decimal places as needed

Calculus
Limits & Continuitynd exact values of the six trigonometric functions by hand for the following angle Do not use a T 4 e exact values of the six trigonometric functions for the given angle are below sin 4 T COS tan T CSC sec cot T 4 T 4 I II Simplify your answer including any radicals Use integers or fractions for any numbers in the expression
Calculus
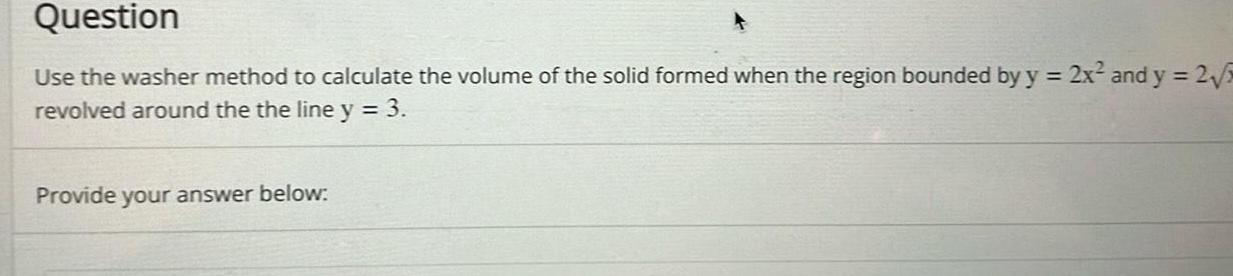
Definite IntegralsQuestion Use the washer method to calculate the volume of the solid formed when the region bounded by y 2x and y 2 5 revolved around the the line y 3 Provide your answer below

Calculus
Application of derivatives4 Evaluate a CSC b cos c tan 315 5TT 3 e sec 37 f fi cot 7 3 d 5TT 6 5 sin
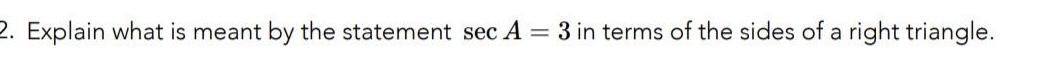
Calculus
Application of derivatives2 Explain what is meant by the statement sec A 3 in terms of the sides of a right triangle
Calculus
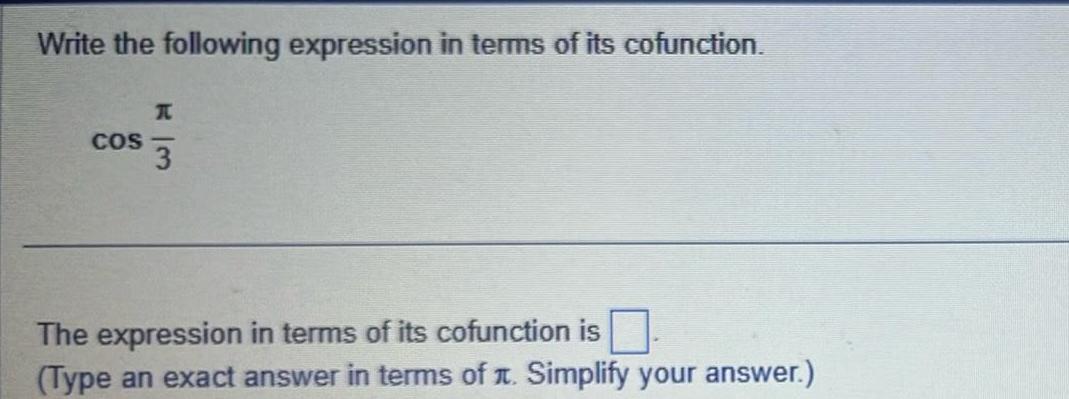
DifferentiationWrite the following expression in terms of its cofunction K COS 3 The expression in terms of its cofunction is Type an exact answer in terms of Simplify your answer


Calculus
Application of derivativesComplete the table with exact trigonometric function values Do not use a calculator 0 225 sin 0 2 2 sin 0 2 COS COS tan 0 1 tan 0 cot 0 1 cot 0 sec sec CSC 2 CSC 0 1 225 2 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression
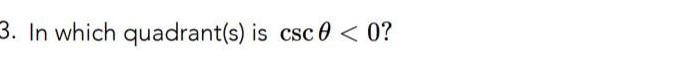

Calculus
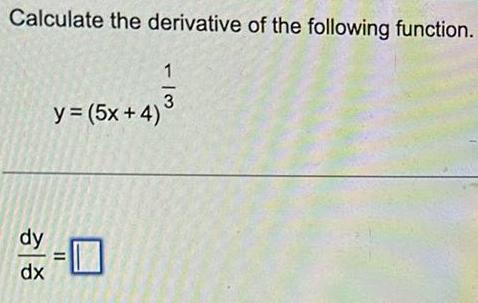
Limits & Continuity1 cot 0 sin 0 1 Which of the following shows the key steps in establishing the identity OA 1 cot20 sin 0 sin 0 cot 0 sin 0 sin 0 cos 0 1 OB sin 0 O C O D 1 cot20 sin 0 csc 0 sin 0 sin 20 1 cot 0 sin 0 cos 0 sec cos 0 0 1 ec 0 1 cot20 sin 0 tan 0 sin 0 sin 20 S 1 cot 0 sin 0 1 cos 20 sin 20 cos 0 1 2 sin 0 in 0 sin 0 1

Calculus
Vector CalculusConsider the position function s t 7 sin 3t that describes a block bouncing vertically on a spring Complete the following table with the appropriate average velocities Then make a conjecture about the value of the instantaneous velocity at t 2 Time Interval Average Velocity T 2 Time Interval Complete the following table 2 T 2 2 T T 2 2 0 1 0 1 Average Velocity Round to five decimal places as needed T T 2 2 EIN EN 2 2 T The value of the instantaneous velocity at t Round to the nearest integer as needed 2 is 0 01 0 01 T B EN 2 2 T 2 2 0 001 0 001 T 2 2 KIN T T 2 2 0 0001 0 0001

Calculus
Application of derivativesFind exact values or expressions for the six trigonometric functions of angle A Do not use a calculator sin A cos A tan A Tuno csc A sec A cot A gore or simplified fractions A 45 53 28

Calculus
Application of derivativesLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 18 60 and f 18 4 Then estimate the number of computers sold if the price is set at 1850 per computer What does f 18 60 imply OA 60 000 computers are sold when the price is set at 180 B When the price per computer is 6000 for every 100 price increase the sales increase by 18 000 computers OC When the price per computer is 1800 for every 100 price increase the sales increase by 60 000 computers O D 60 000 computers are sold when the price is set at 1800
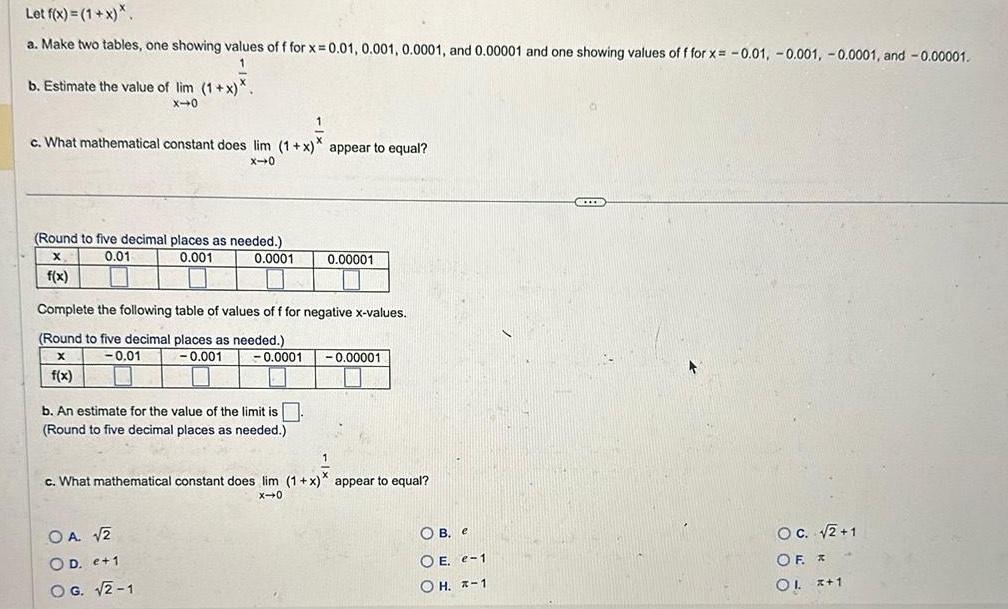
Calculus
Application of derivativesLet f x 1 x a Make two tables one showing values of f for x 0 01 0 001 0 0001 and 0 00001 and one showing values of f for x 0 01 0 001 0 0001 and 0 00001 1 b Estimate the value of lim 1 x X 0 1 c What mathematical constant does lim 1 x appear to equal x 0 Round to five decimal places as needed X 0 01 0 001 0 0001 f x Complete the following table of values of f for negative x values Round to five decimal places as needed X 0 01 0 001 0 0001 f x b An estimate for the value of the limit is Round to five decimal places as needed 0 00001 OA 2 OD e 1 OG 2 1 0 00001 1 c What mathematical constant does lim 1 x appear to equal X 0 OB e OE e 1 OH 1 II OC 2 1 OF OL x 1
Calculus
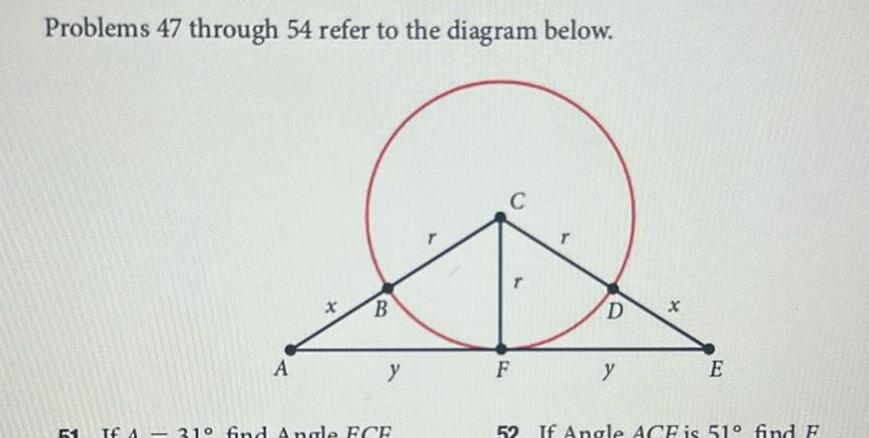
Application of derivativesProblems 47 through 54 refer to the diagram below Y A B y TE A 31 find Angle FCE C F T D y X E 52 If Angle ACE is 51 find F
Calculus
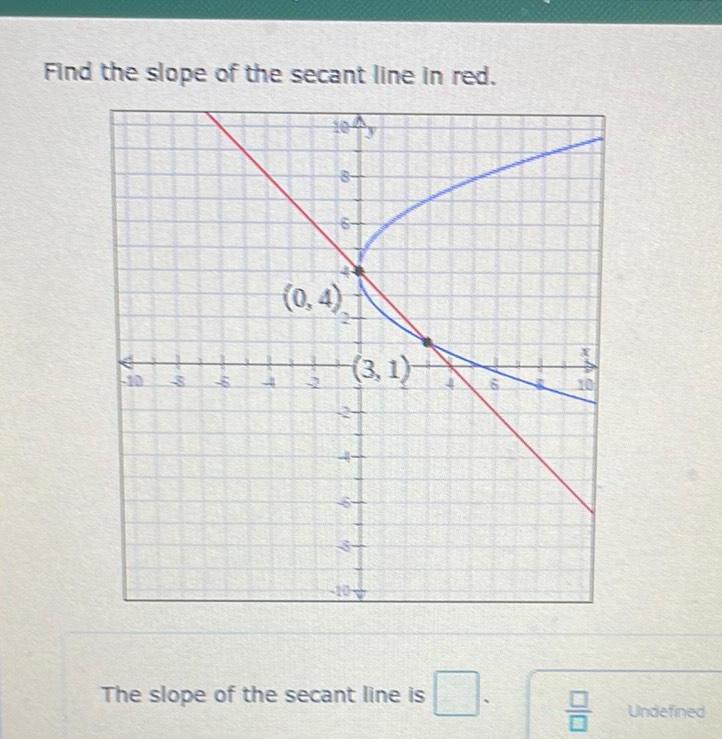
Limits & ContinuityFind the slope of the secant line in red 510 to br p 09 ind 10 0 4 3 1 The slope of the secant line is 00 Undefined

Calculus
Application of derivativesUse the graph of g in the figure to evaluate the function or analyze the limit a g 1 b lim g x c lim g x X 1 X 1 e g 3 f lim g x h g 4 k lim g x X 4 d lim g x X 1 g lim g x x 3 j lim g x x 4 X 3 i lim g x X 4 a Select the correct answer below and if necessary fill in the answer box within your choice A g 1 Type an integer or a decimal OB The value g 1 does not exist because g is not defined at x 1 b Select the correct answer below and if necessary fill in the answer box within your choice OA lim g x X 1 OB The limit does not exist because g is not defined for all x sufficiently close to 1 with x 1 c Select the correct answer below and if necessary fill in the answer box within your choice Type an integer or a decimal F OA lim g x Type an integer or a decimal X 1 OB The limit does not exist because g is not defined for all x sufficiently close to 1 with x 1 AY 3 0 yag
Calculus
Limits & ContinuityAssume lim f x 10 lim g x 8 and lim h x 6 Compute the following limit and state the limit laws used to justify the computations X 9 X 9 X 9 f x lim x 99 x h x f x x 99 x h x Simplify your answer State the limit law s used to justify the computation Select all that apply lim A Difference B Quotient C Root D Sum E Power F Product G Constant Multiple D
Calculus
Application of derivativesThe graph off in the figure has vertical asymptotes at x 1 and x 5 Analyze the following limits a lim f x b lim f x x 1 X 1 e lim f x d lim f x x 5 X 5 Ay 10 c lim f x X 1 f lim f x X 5 Q Q a Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x x 1 OB The limit does not exist and is neither co nor co b Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x X 1 OB The limit does not exist and is neither oo nor co c Select the correct choice and if necessary fill in the answer box to complete your choice 4 A lim f x X 1 OB The limit does not exist and is neither oo nor co d Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x X 5 OB The limit does not exist and is neither co nor 00 e Select the correct choice and if necessary fill in the answer box to complete your choice QA lim f x

Calculus
DifferentiationA sequence is an infinite ordered list of numbers that is often defined by a function For example the sequence 2 4 6 8 is specified by the function f n 2n where n 1 2 3 The limit of such a sequence is lim f n provided the limit exists All the nx limit laws for limits at infinity may be applied to limits of sequences Find the limit of the following sequence or state that the limit does not exist 1 4 1 16 5 12 16 17 2 19 4 7 which is defined by f n n 15 for n 1 2 3 Select the correct choice below and if necessary fill in the answer box to complete your choice OA The limit of the sequence is B The limit does not exist and is neither o nor 00

Calculus
Application of derivativesrmine a value of the g x x 3x 3x if x 1 ax 4 if x 1 ant a for wh X 1 g x exists and state the value of the limi possible Select the correct choice below and if necessary fill in the answer boxes to complete your choice OA The limit exists for a With that value for a lim g x X 1 OB There is no value of a for which lim g x exists X 1

Calculus
Limits & Continuity1 cos 3x Hint What to do with that 1 cos 3x Maybe use conjugates Or maybe x if you rearrange one of the half angle formulas from Week 1 you get 2 sin 0 1 cos 20 could that help Actually either of these ideas will work so choose one d lim 20

Calculus
Application of derivativesDetermine the value of the constant a for which the function f x is continuous at 4 x 6x 8 X 4 a if x 4 if x 4 The function f x is continuous at 4 when a Type an integer or a fraction O
Calculus
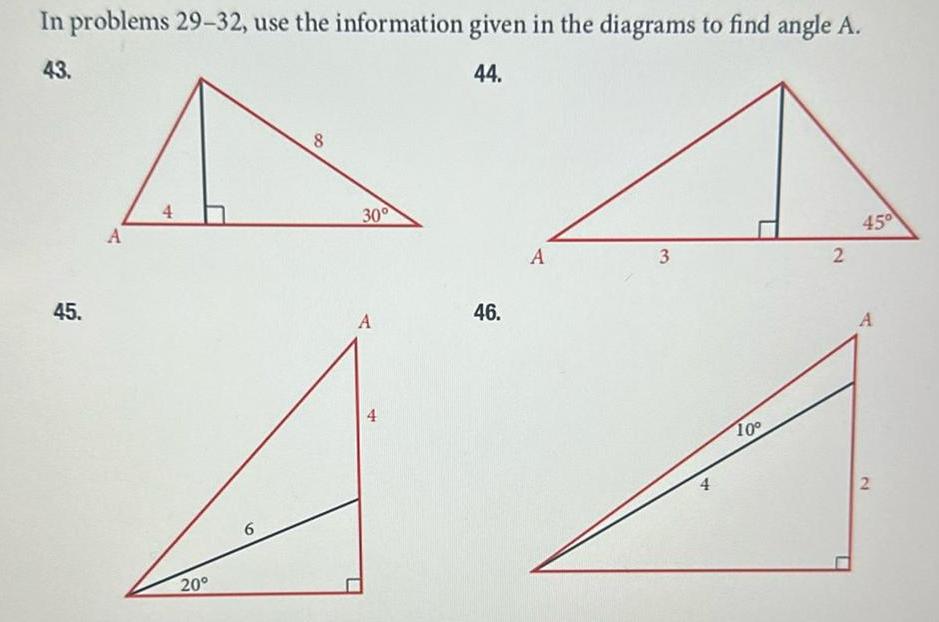
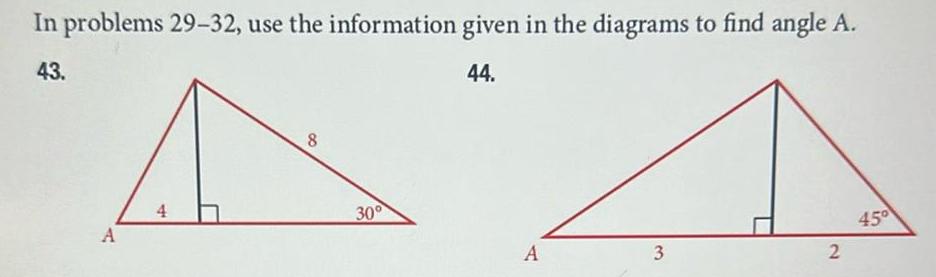
Limits & ContinuityIn problems 29 32 use the information given in the diagrams to find angle A 43 44 45 A 4 20 6 8 30 A 4 46 A 3 10 2 45 A 2
Calculus
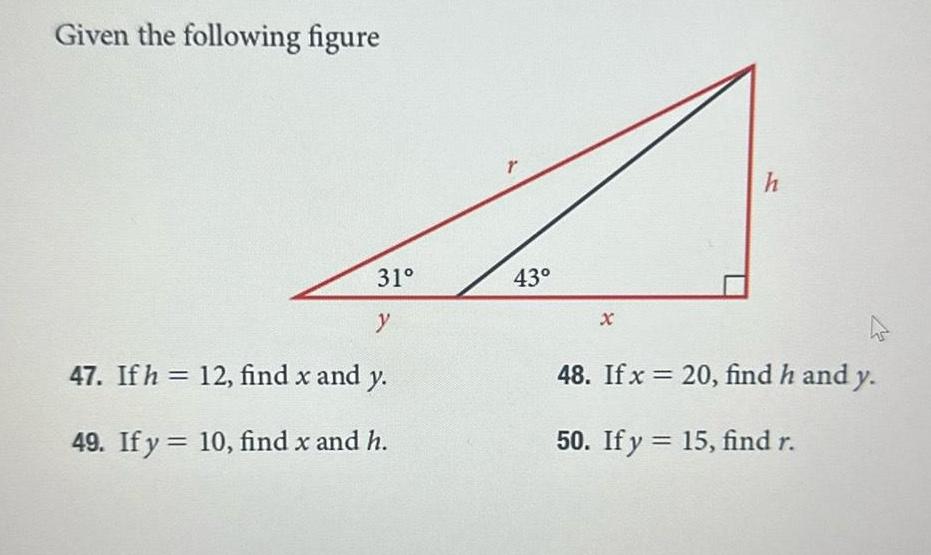
DifferentiationGiven the following figure 31 y 47 If h 12 find x and y 49 If y 10 find x and h r 43 h 48 If x 20 find h and y 50 If y 15 find r
Calculus
Application of derivativesIn problems 29 32 use the information given in the diagrams to find angle A 43 44 A 4 8 30 A 3 2 45
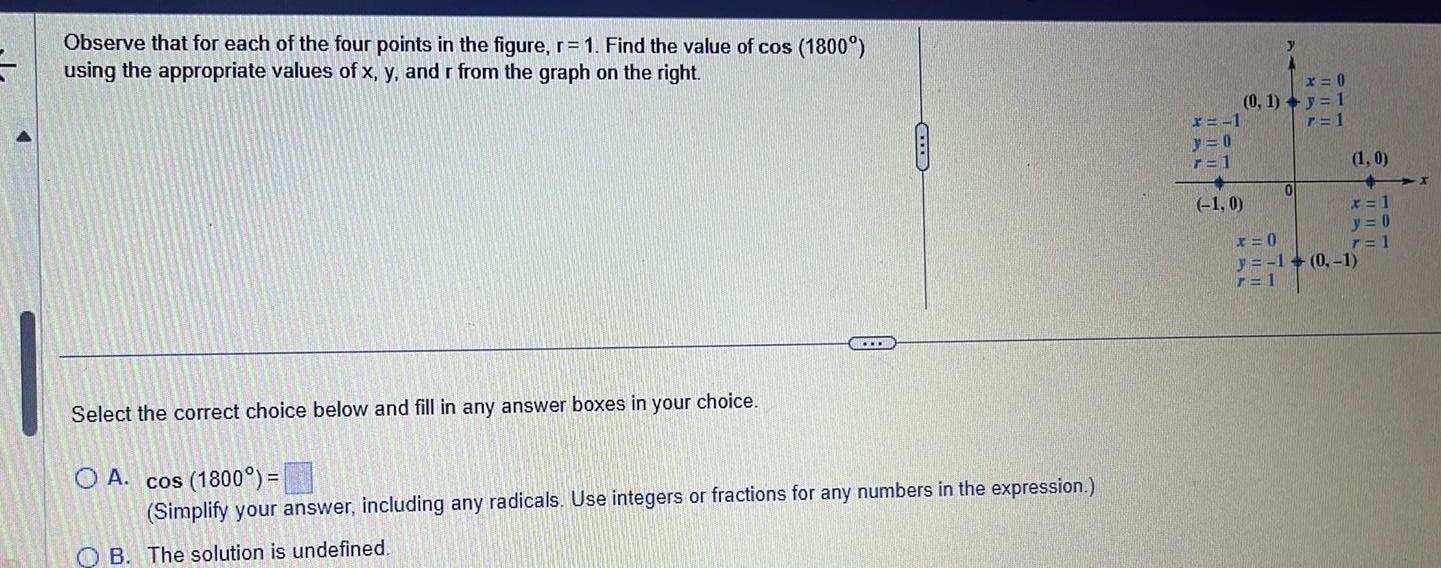
Calculus
Application of derivativesObserve that for each of the four points in the figure r 1 Find the value of cos 1800 using the appropriate values of x y and r from the graph on the right www Select the correct choice below and fill in any answer boxes in your choice O A cos 1800 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression B The solution is undefined y x 0 0 1 y 1 7 1 x 1 y 0 r 1 1 0 0 1 0 x 1 y 0 r 1 x 0 y 1 0 1 r 1

Calculus
Vector CalculusUse the appropriate reciprocal identity to find the value of sin 0 given that csc 0 13 Rationalize denominators when applicable sin 0 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression Rationalize all denominators
Calculus
Application of derivativesse the appropriate reciprocal identity to find the value of tan 0 given that cot 0 2 5 0 Type an integer or a decimal


Calculus
Differentiationuate the trigonometric function at the quadrantal angle or state that the expression is undefine 90 at is the value of csc 90 A 1 3 The answer is undefined C 1

Calculus
Vector Calculusan 0 3 ot 0 Simplify your answer including any radicals Use integers or fractions for any numbers in the
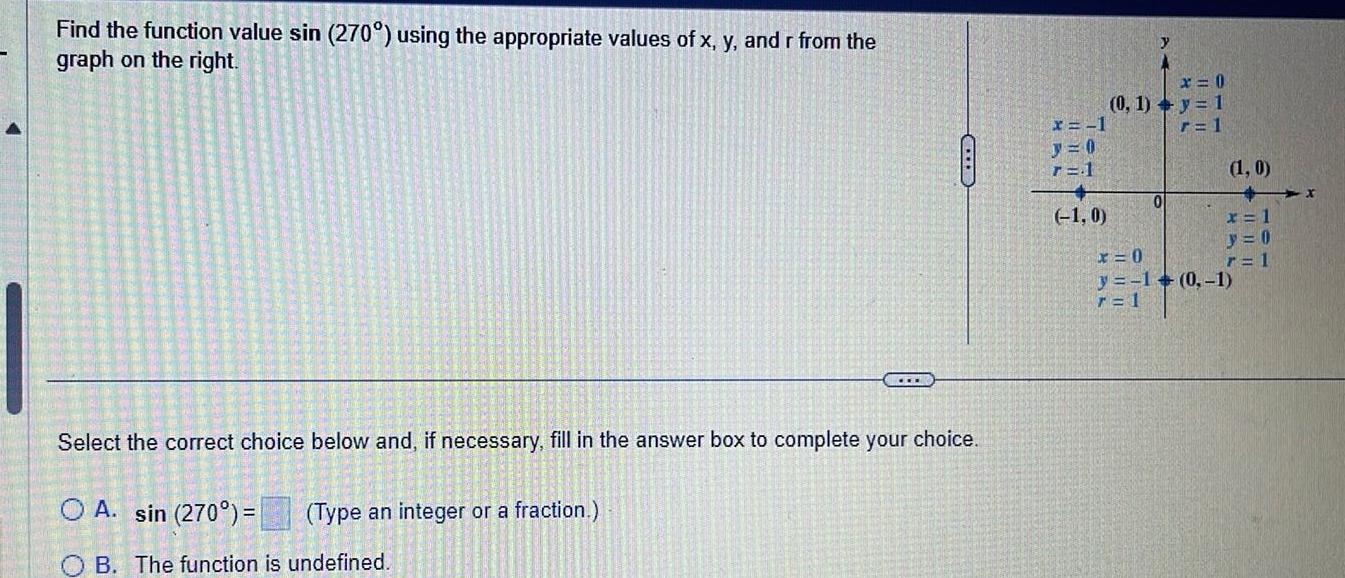
Calculus
Application of derivativesFind the function value sin 270 using the appropriate values of x y and r from the graph on the right Select the correct choice below and if necessary fill in the answer box to complete your choice O A sin 270 Type an integer or a fraction CEL B The function is undefined x 1 r 1 1 0 y x 0 0 1 y 1 r 1 0 1 0 x x 1 y 0 r 1 x 0 y 1 0 1 7 1

Calculus
Differential equationsthe appropriate reciprocal identity to find the exact value of sec 0 for the given valu 6 9 9 95 0 an integer or a fraction