Center of mass and momentum Questions and Answers
Physics
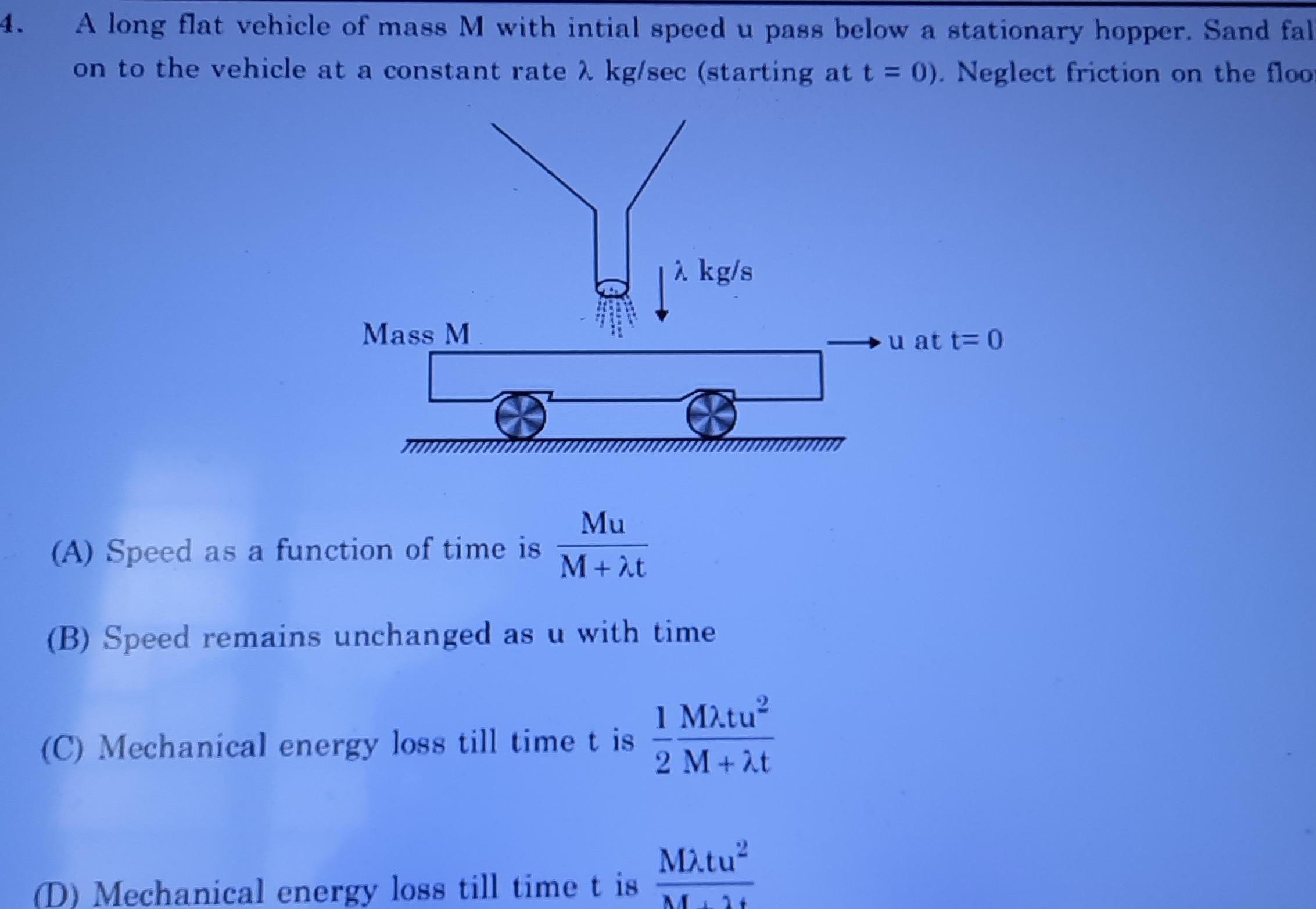
Center of mass and momentum4 A long flat vehicle of mass M with intial speed u pass below a stationary hopper Sand fal on to the vehicle at a constant rate kg sec starting at t 0 Neglect friction on the floor Mass M Mu M t B Speed remains unchanged as u with time A Speed as a function of time is C Mechanical energy loss till time t is kg s D Mechanical energy loss till time t is 1 Matu 2 M t Matu M 2 u at t 0

Physics
Center of mass and momentumTwo blocks of masses 2m and 3m are connected by a ligh string of length 2L Both blocks can slide freely along a horizontal bar A block of mass m is attached to the mid point of the string Initially the string is straight and all three blocks are held at rest as shown Then the blocks are released simultane ously Find the speeds of blocks 2m and 3m immediately before they collide The acceleration due to gravity is g 2m 3m

Physics
Center of mass and momentumChoose the correct alternative a For general rotational motion angular momentum L and angular velocity w need not to be parallel b For a rotational motion about a fixed axis angular momentum L and angular velocity w are always parallel c For a general translational motion linear momentum P and velocity v are always parallel d For general translational motion acceleration a and velocity are always parallel 1 a b 2 b d 3 ac
Physics
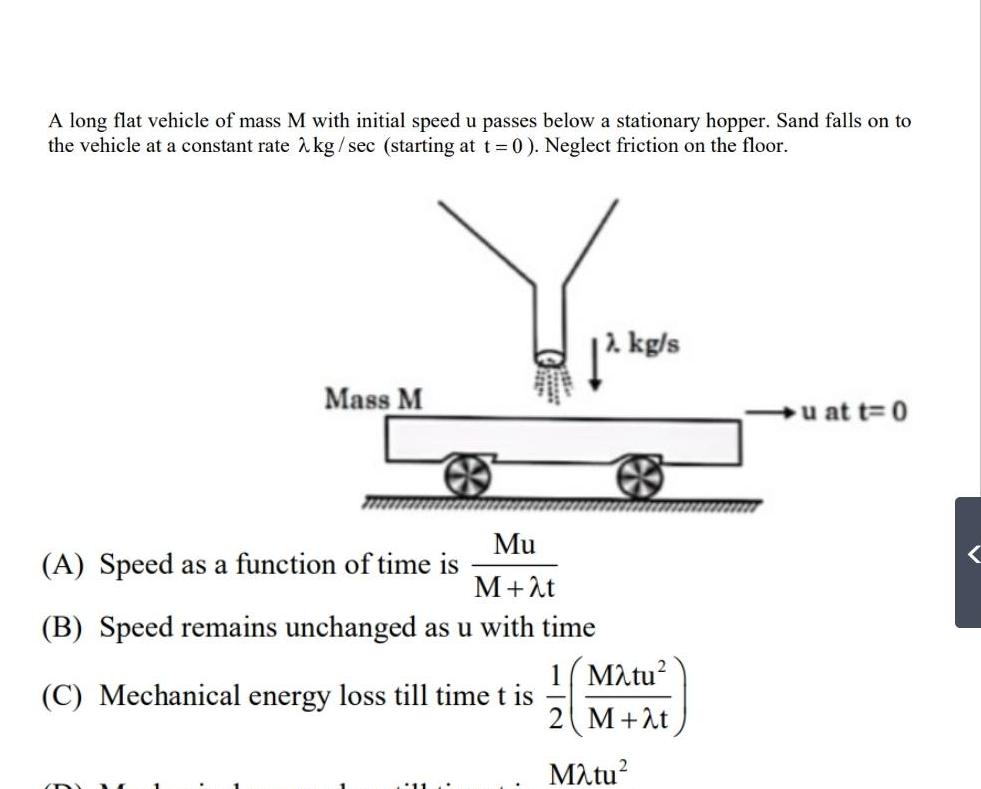
Center of mass and momentumA long flat vehicle of mass M with initial speed u passes below a stationary hopper Sand falls on to the vehicle at a constant rate kg sec starting at t 0 Neglect friction on the floor Mass M Mu M t B Speed remains unchanged as u with time C Mechanical energy loss till time t is A Speed as a function of time is kg s 1 Matu M t M tu u at t 0
Physics
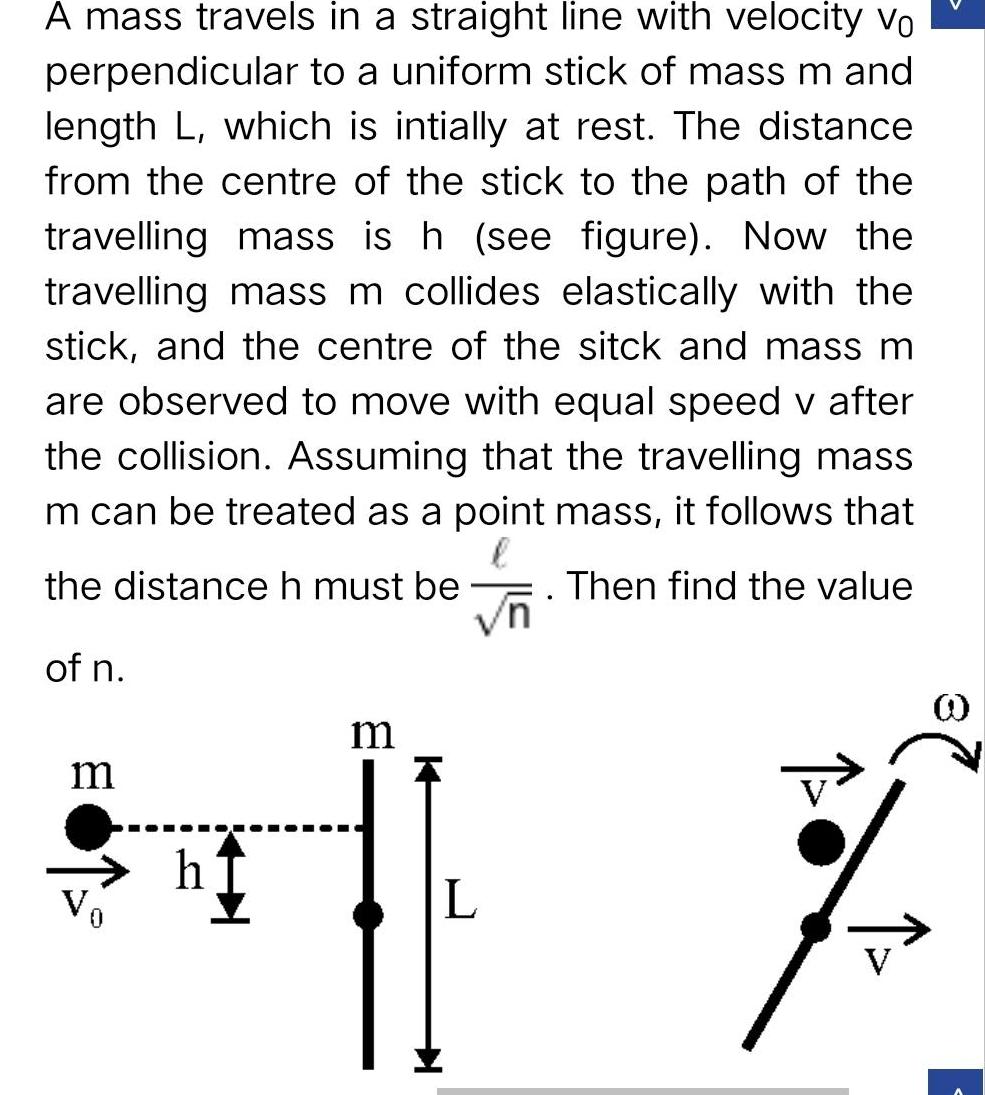
Center of mass and momentumA mass travels in a straight line with velocity vo perpendicular to a uniform stick of mass m and length L which is intially at rest The distance from the centre of the stick to the path of the travelling mass is h see figure Now the travelling mass m collides elastically with the stick and the centre of the sitck and mass m are observed to move with equal speed v after the collision Assuming that the travelling mass m can be treated as a point mass it follows that the distance h must be Then find the value vn of n m h m L

Physics
Center of mass and momentumA block of mass m moving with a velocity vo collides with a stationary block of mass M at the end of whic a spring of stiffiness k is attached as shown Choose the correct alternatives s m Smooth 000000 M The velocity of the center of mass is V The initial kinetic energy of the system in the centre of mass frame is The maximum compression in the spring is vol mM 1 m Mk mM 4 M m v
Physics
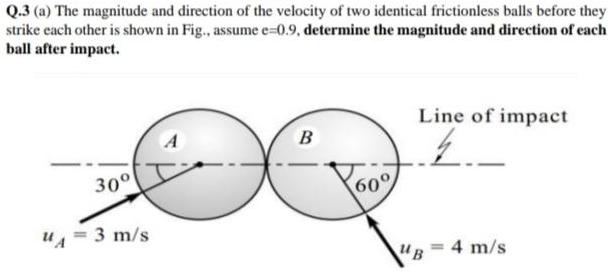
Center of mass and momentumQ 3 a The magnitude and direction of the velocity of two identical frictionless balls before they strike each other is shown in Fig assume e 0 9 determine the magnitude and direction of each ball after impact 30 UA 3 m s A B 60 Line of impact 2 UB 4 m s

Physics
Center of mass and momentumCase 1 Carts A starts from rest on a hill at a height h above the ground It rolls down and collides head on with cart B which is initially at rest on the ground The two carts stick together Case 2 Carts A and B are at rest on opposite hills at heights 1 2h above the ground They roll down collide head on with each other on the ground and stick together h na nd and stick togetics case 1 B A 1 2h case 2 B 1 h Which of the following statements is true about the about two cart system just after the carts collide in these two cases Surface is frictionless a the total kinetic energy of the system is the same in both cases b the total momentum of the system in non zero in case 1 while it is zero in case 2 c the total momentum of the system is the same in both cases d the total momentum of the system is greater in case 2 than in case 1
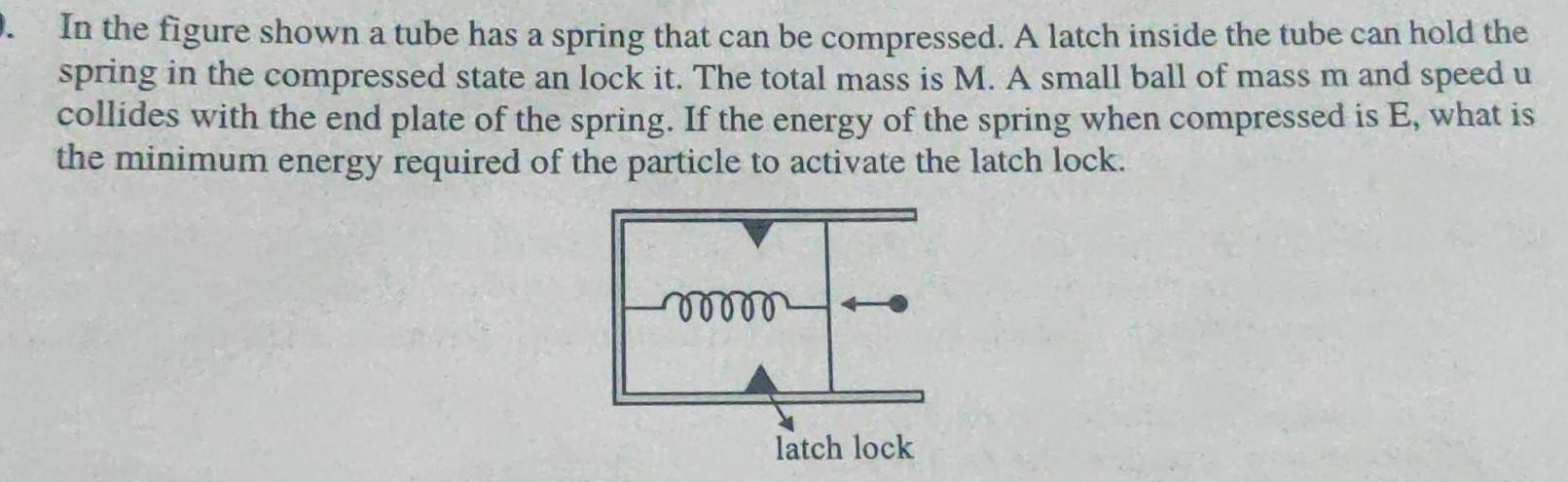
Physics
Center of mass and momentumIn the figure shown a tube has a spring that can be compressed A latch inside the tube can hold the spring in the compressed state an lock it The total mass is M A small ball of mass m and speed u collides with the end plate of the spring If the energy of the spring when compressed is E what is the minimum energy required of the particle to activate the latch lock voooo latch lock

Physics
Center of mass and momentumpendulum with bob of mass 4 kg and length 1 m initially held at an angle 600 with the vertical The bob of the pendulum hits a block of mass 5 kg initially at rest at its position lowest The block after comes to rest moving a distance 0 8 Find the coefficient of friction between block and table and coefficient of restitution 1m 4kg
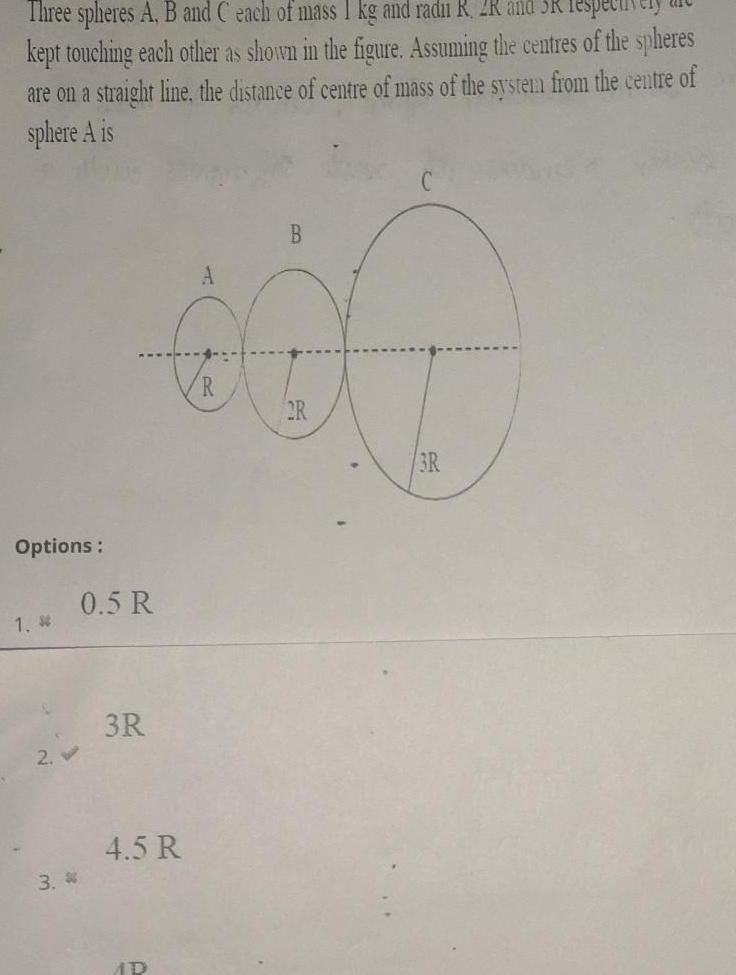
Physics
Center of mass and momentumThree spheres A B and C each of mass I kg and radu R 2K and kept touching each other as shown in the figure Assuming the centres of the spheres are on a straight line the distance of centre of mass of the system from the centre of sphere A is Options 1 S 3 0 5 R 3R 4 5 R AD A R B R 3R

Physics
Center of mass and momentumThe figure shows two rods BC and OA hinged from B and O respectively Rod BC has a groove in which point A of rod OA can slide smoothly At a given instant the rod BC has an angular velocity wo The speed of end A of the rod OA at this instant will be

Physics
Center of mass and momentumfrom the beginning Determine the minimum speed v of its mass centre at the bottom so that it rolls completely around the loop of radius R r without leaving the track in between Sphere R 1

Physics
Center of mass and momentumstitution e is 1 3 IN 13 2 lew In English height of 50 m and rebounds several times from ground If total distance covered by the ball is 100 m the value of coefficient

Physics
Center of mass and momentumA hollow cylinder closed at both ends of length L and mass m is attached with a spring of force constant K An equal mass with negligible radius is kept inside the cylinder Initially the spring is stretched by a distance L Find out the time period of the resultant motion If all collisions are assumed elastic There is no friction anywhere Initially mass is touching the left side of the cylinder wa ya utud a Aic Kys Ga YG ADA TU La czy ma 1 fef of ze uz c s adu as 2 T N L eeeeeeeeeeeeeeeee K 2 x 1 m 2 x 2 m K m 2 x 1 K Correct Answer

Physics
Center of mass and momentumQ 8 A 4 pole induction motor is working on 50Hz ac supply and the value of slip is 0 04 at no load and 0 03 at full load Then calculate following a Synchronous speed 5 Rotor speed at no load E Rotor speed at full load
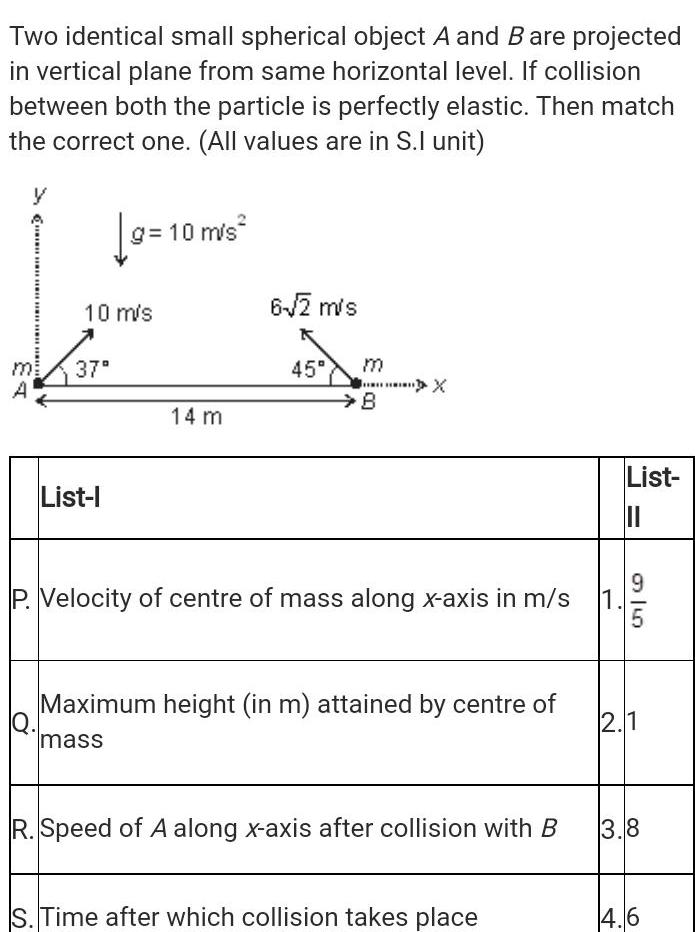
Physics
Center of mass and momentumTwo identical small spherical object A and B are projected in vertical plane from same horizontal level If collision between both the particle is perfectly elastic Then match the correct one All values are in S l unit y Q m A Q 10 m s 37 g 10 m s List l 14 m 6 2 m s 45 B X P Velocity of centre of mass along x axis in m s Maximum height in m attained by centre of mass R Speed of A along x axis after collision with B S Time after which collision takes place 1 List II 9 5 2 1 3 8 4 6

Physics
Center of mass and momentum10 Assertion Two particles moving in the same direction do not lose all their energy in completely inelastic collision Reason Principle of conservation of momentum holds true for all kinds of collisions AIIMS a Both Assertion and Reason are correct and Reason is the correct explanation of Assertion b Both Assertion and Reason are correct but Reason is not the correct explanation of Assertion c Assertion is correct but Reason is incorrect d Assertion is incorrect but Reason is correct
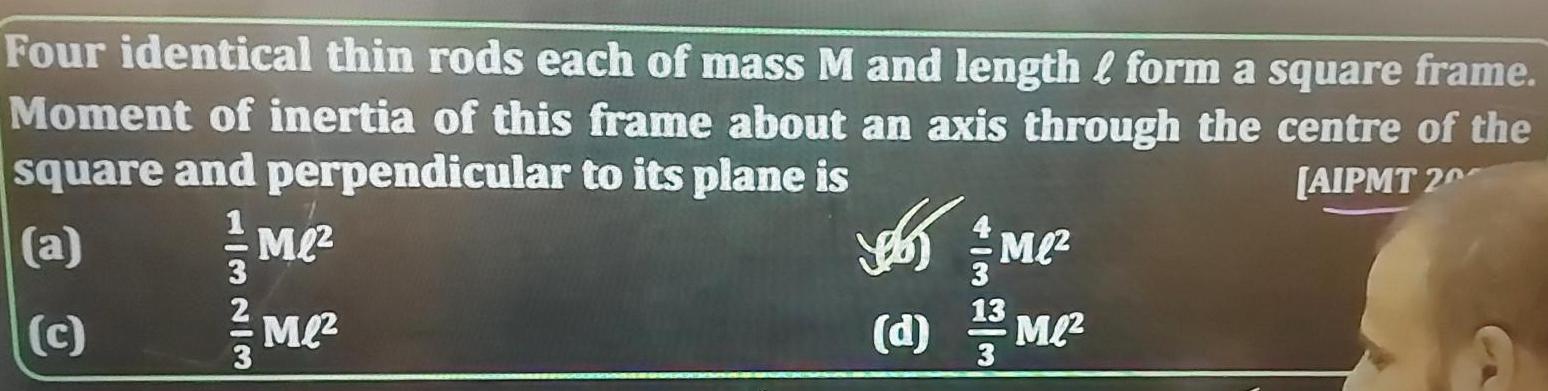
Physics
Center of mass and momentumFour identical thin rods each of mass M and length form a square frame Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is AIPMT 20 a c 113213 Me Me Jobs Me d 1 32 M

Physics
Center of mass and momentum3 Two smooth spheres A and B of masses 4 kg and 8 kg move with velocities 9 m s and 3 m s in opposite directions If A rebounds with velocity 1 m s then 1 The velocity of sphere B after the impact 2 m s 1 2 The coefficient of impact e 4 3 The loss of kinetic energy 180 J 4 None of these

Physics
Center of mass and momentumA uniform semicircular wire of mass M 1 2 kg and radius R 1m is free to rotate about a fixed horizontal axis coinciding with the diameter passing through open ends First the wire is taken asid such that its plane becomes horizontal and then it is released from rest Choose the correct option s when vertical component of velocity of the centre of mass is maximum take g 10 m s n 10 A Angular displacement of wire is cot 2 B Vertical component of force exerted by the axis on the wire is 5 2 N C Vertical component of force exerted by the axis on the wire is 10 2 N D Horizontal component of the force exerted by the axis on the wire is 8N
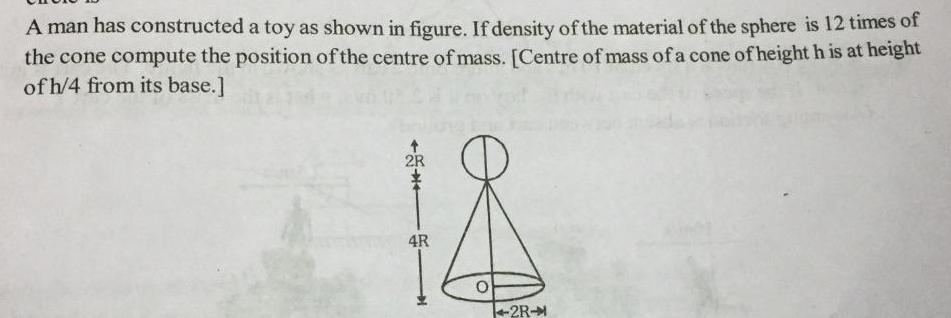
Physics
Center of mass and momentumA man has constructed a toy as shown in figure If density of the material of the sphere is 12 times of the cone compute the position of the centre of mass Centre of mass of a cone of height h is at height of h 4 from its base 2R 18 4R O 2R

Physics
Center of mass and momentumA thin circular disc lying in the xy plane has a surface mass density o given by 1 0 11 1 1 0 if rsR if r R where r is the distance from its center Its moment of inertia about the z axis passing through its center is a b R c 0 R d 2no R

Physics
Center of mass and momentum56 Three resistances P Q R each of 2 92 and a unknown resistance S form the four arms of Wheatstone bridge circuit When a resistance 62 is connected in parallel to S the bridge get balanced What is the value of S AIPMT Prelims 2007 14
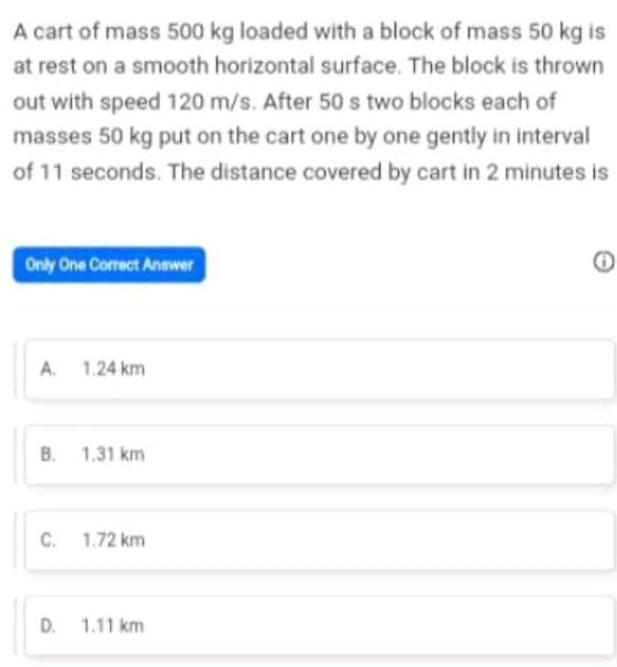
Physics
Center of mass and momentumA cart of mass 500 kg loaded with a block of mass 50 kg is at rest on a smooth horizontal surface The block is thrown out with speed 120 m s After 50 s two blocks each of masses 50 kg put on the cart one by one gently in interval of 11 seconds The distance covered by cart in 2 minutes is Only One Correct Answer A 1 24 km B 1 31 km C 1 72 km D 1 11 km

Physics
Center of mass and momentum1 4 C A ball is projected with velocity vo gh at an angle q to the horizontal towards a vertical smooth wall distant d from the point of projection After collision the ball returns to the point of projection The coefficient of restitution is 1 3 d hsin 0 d d hsin 20 d 2 4 d 2hsin 0 d d sin 20 2d

Physics
Center of mass and momentumb A toy car of mass 1 kg moves westwards with a speed of 2 m s It collides head on with a toy train The toy train has a mass of 1 5 kg and is moving at a speed of 1 5 m s eastwards The toy car then rebounds at 2 05 m s Calculate the final velocity of the toy train

Physics
Center of mass and momentumc 25 Three girls Shivangi Radhika and Saili sat or one side of see saw at distances of 1m 1 2m and 1 5m from the fulcrum that is situated at the center of the see saw The masses of the thre girls were 30kg 40kg and 50kg respectively Where should Rakesh sit on the other side a seesaw so as to balance it Given the mass a Rakesh is 80kg b 1 5m d 1 75m a 2m c 1 91m PE 4 DIAGRAM BASED MCQ 14
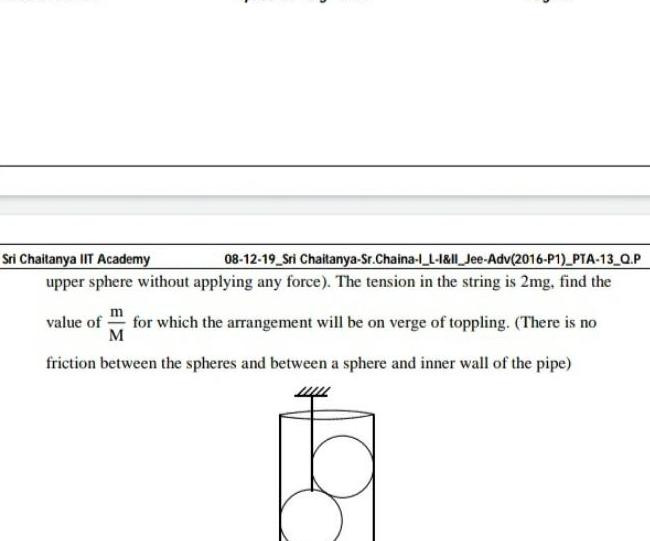
Physics
Center of mass and momentumSri Chaitanya IIT Academy 08 12 19 Sri Chaitanya Sr Chaina 1 L 1 1l Jee Adv 2016 P1 PTA 13 Q P upper sphere without applying any force The tension in the string is 2mg find the value of for which the arrangement will be on verge of toppling There is no M friction between the spheres and between a sphere and inner wall of the pipe ba
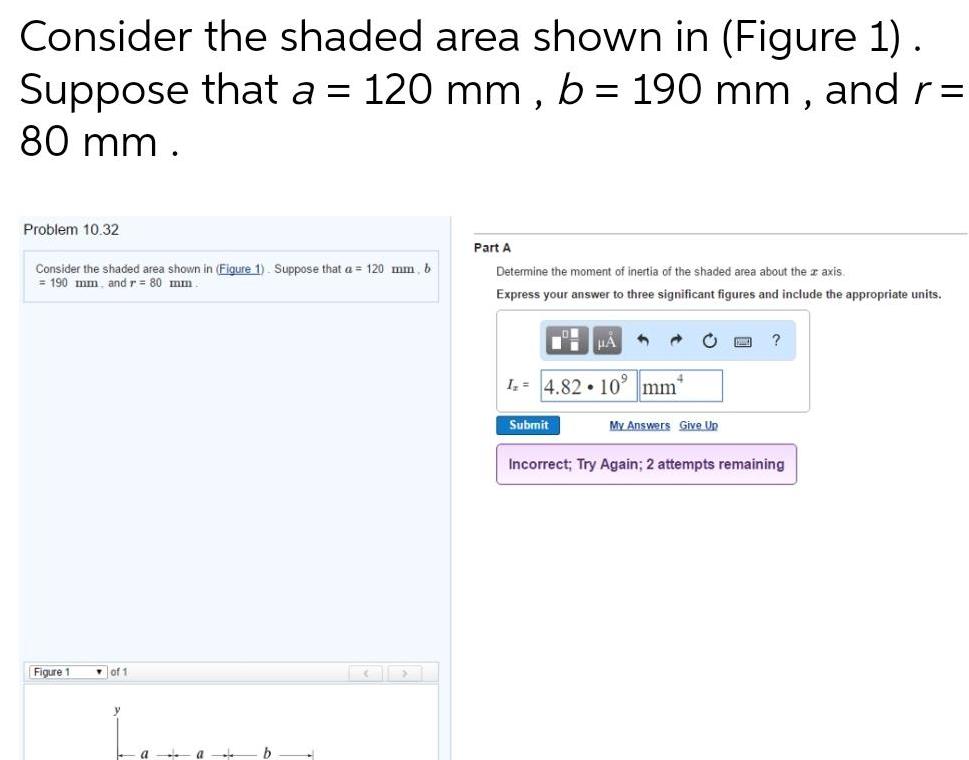
Physics
Center of mass and momentumConsider the shaded area shown in Figure 1 Suppose that a 120 mm b 190 mm and r 80 mm Problem 10 32 Consider the shaded area shown in Figure 1 Suppose that a 120 mm b 190 mm and r 80 mm Figure 1 of 1 a b Part A Determine the moment of inertia of the shaded area about the axis Express your answer to three significant figures and include the appropriate units HA I 4 82 10 Submit mm My Answers Give Up Incorrect Try Again 2 attempts remaining

Physics
Center of mass and momentum1 SECTION A For the vertices given arrangement of masses on the and at mid point of side of an equilater triangle of side d as shown the height of cent of mass of system from base of triangle is M M V 2M 340 COS 60 1 Cos 30 1 M

Physics
Center of mass and momentumTwo particles having masses m and m are placed at a separation r between them Let m2 be displaced away from m by a distance x By what distance m should be displaced in order to keep the position of centre of mass unchanged Let the masses be placed on x axis with centre of mass at origin

Physics
Center of mass and momentum6 A solid cube of edge a is melted and moulded in eight identical small solid cubes and are placed on one other on a straight line with the edge of bottom cube on the same horizontal plane on which big cube was placed then the vertical shift in centre of mass is 1 3a 2 2 2a 3 5a 2 4 3a

Physics
Center of mass and momentumel ball of mass 15 0 g is fired from the small canon onto a wooden plank on that is placed horizontal to the ground The wooden plank slides to the dista m after collision with ball Find the velocity of the ball before impact with the idering the value of coefficient of friction as 0 5 a 178 25 m s b 185 37 m s c 225 35 m s d 201 54 m s
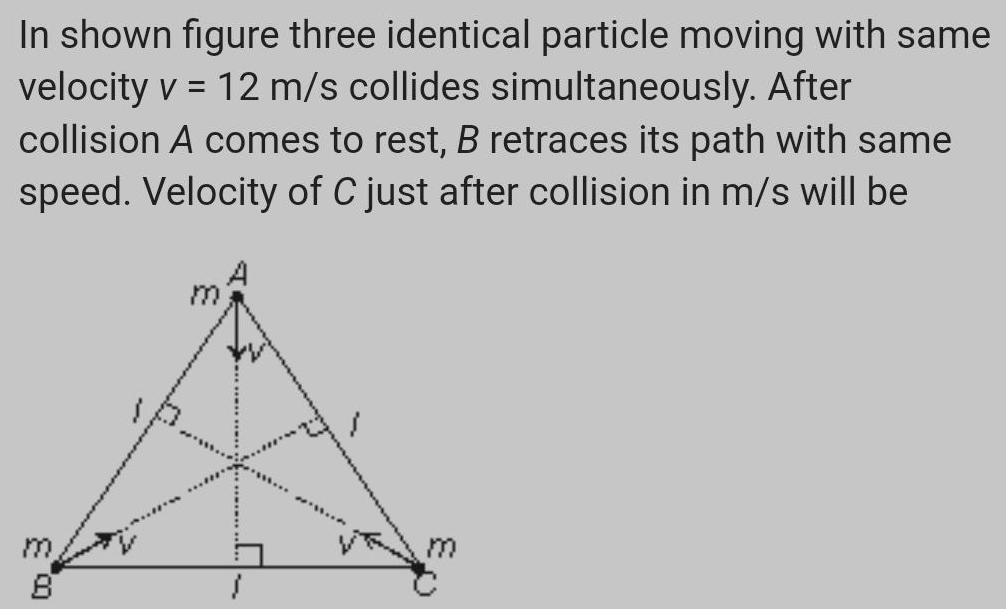
Physics
Center of mass and momentumIn shown figure three identical particle moving with same velocity v 12 m s collides simultaneously After collision A comes to rest B retraces its path with same speed Velocity of C just after collision in m s will be ED 8 m

Physics
Center of mass and momentum21 22 A thin rod of mass m and length L lies on a frictionless horizontal surface and is hinged at one of its ends such that it can rotate freely about a vertical axis passing through the hinge A particle of same mass m hits the rod at the extreme end as shown with velocity vo and does not stick with rod and come to rest immediately such that the rod rotates with a constant angular velocity w after the collision 1 Then angular velocity just after collision is equal to 3v0 L A 2v0 5L A B 2 Magnitude of hinge reaction just after the collision is 7mv 5mv 2L 2L B C C 5vo 7L 9mv 2L D D 5vo 9L 9mv 4L N s m
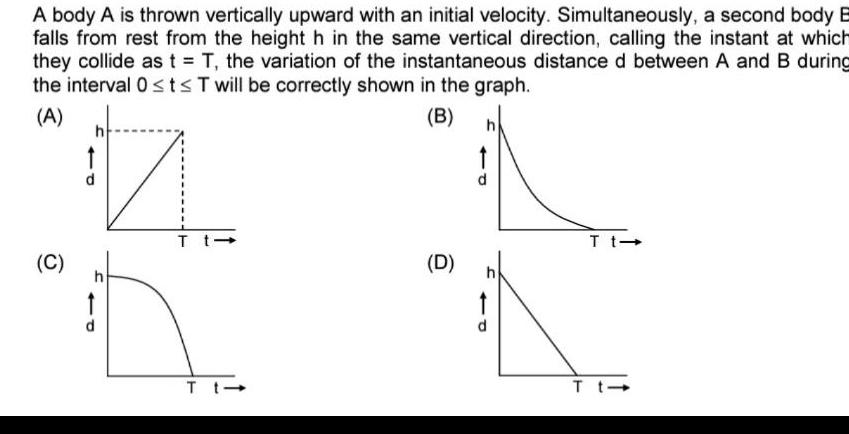
Physics
Center of mass and momentumA body A is thrown vertically upward with an initial velocity Simultaneously a second body B falls from rest from the height h in the same vertical direction calling the instant at which they collide as t T the variation of the instantaneous distance d between A and B during the interval 0 t T will be correctly shown in the graph A B C S T t T t D T t T t

Physics
Center of mass and momentumA rubber ball of mass 1 kg hits the surface at an angle of 30 with surface and rebounds at angle of 60 with surface without change in speed If the speed of ball is 1 m s then impulse imparted by surface to ball is 30 60
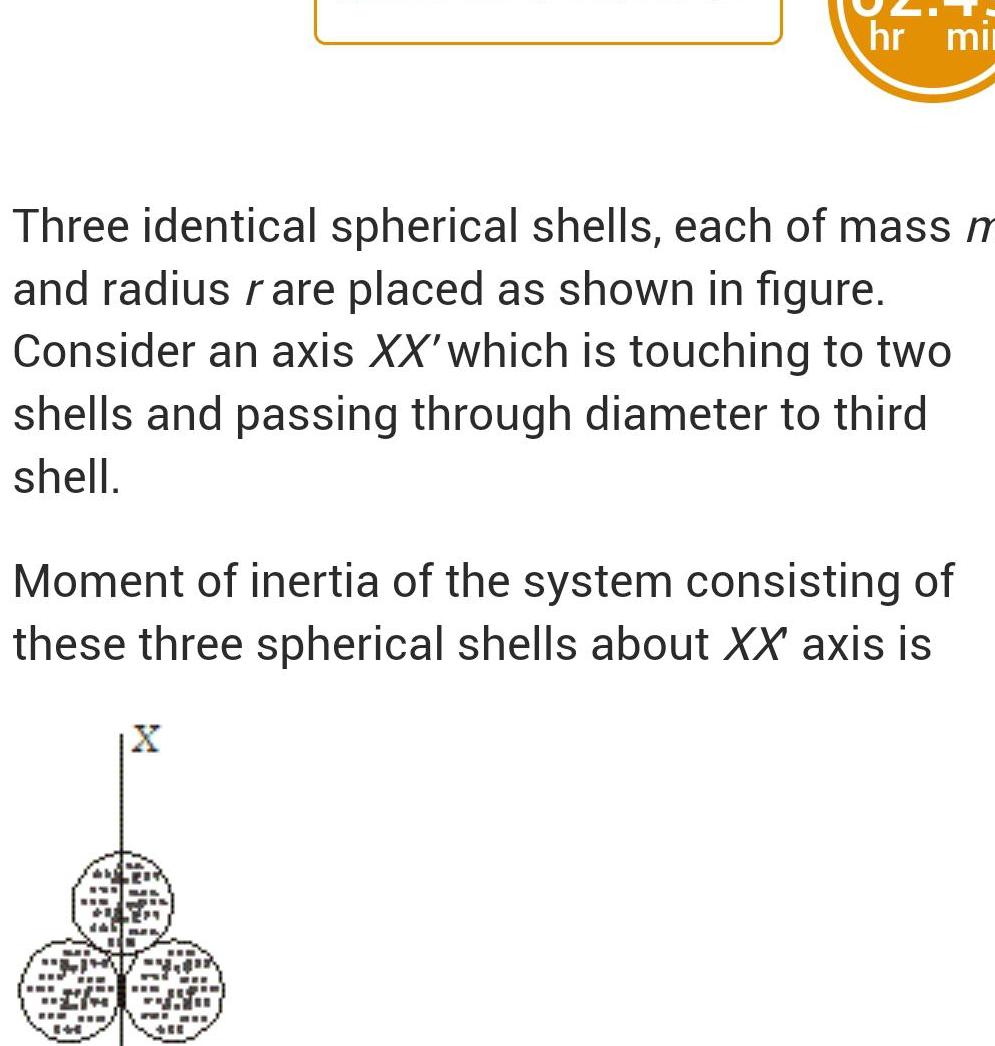
Physics
Center of mass and momentumhr mir Three identical spherical shells each of mass m and radius rare placed as shown in figure Consider an axis XX which is touching to two shells and passing through diameter to third shell Moment of inertia of the system consisting of these three spherical shells about XX axis is

Physics
Center of mass and momentumFrom a uniform disk of radius a an isosceles right angled triangle with hypotenuse as the diameter of this disk is removed The distance of the centre of mass of the remaining portion from the centre of the disk comes out a N x 1 Find N

Physics
Center of mass and momentumA 9 900 g bullet is fired into a stationary block of wood having mass m 4 990 kg The bullet imbeds into the block The speed of the bullet plus wood combination immediately after the collision is 0 6080 m s What was the original speed of the bullet Express your answer with four significant figures x Note that after the collision the bullet is imbedded in the block so that both are moving with the velocity 0 608 m s Check the number of significant figures m s More Information Need Help Read It Watch f
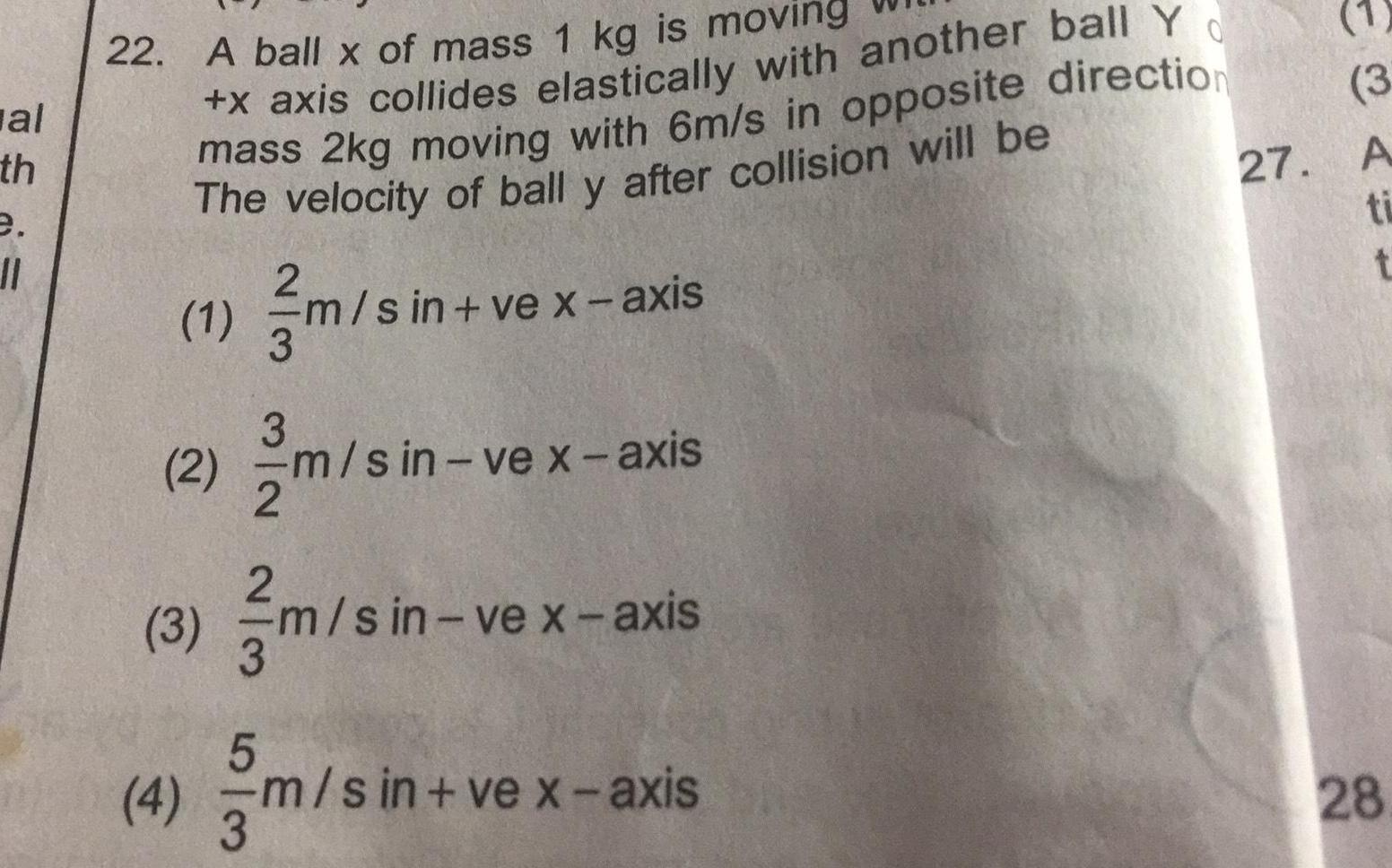
Physics
Center of mass and momentumal th e 11 22 A ball x of mass 1 kg is moving x axis collides elastically with another ball Y mass 2kg moving with 6m s in opposite direction The velocity of ball y after collision will be 1 2 3 2 m s in ve x axis W N N w 3 3 5 2 m sin vex axis m s in m sin vex axis 4 m sin ve x axis 3 27 1 3 A ti t 28

Physics
Center of mass and momentum33 If the linear density of the rod of length L varies as A Bx where x is distance from one end then its centre of mass is given by af fart La 1 XCM 3 XCM L 2A BL 3 3A 2BL L 3A 2BL 3 A Bx 2 XCM 4 XCM xuch for g i 34ch G8TH L 3A 2BL 3 2A BL L 2A 3BL 3
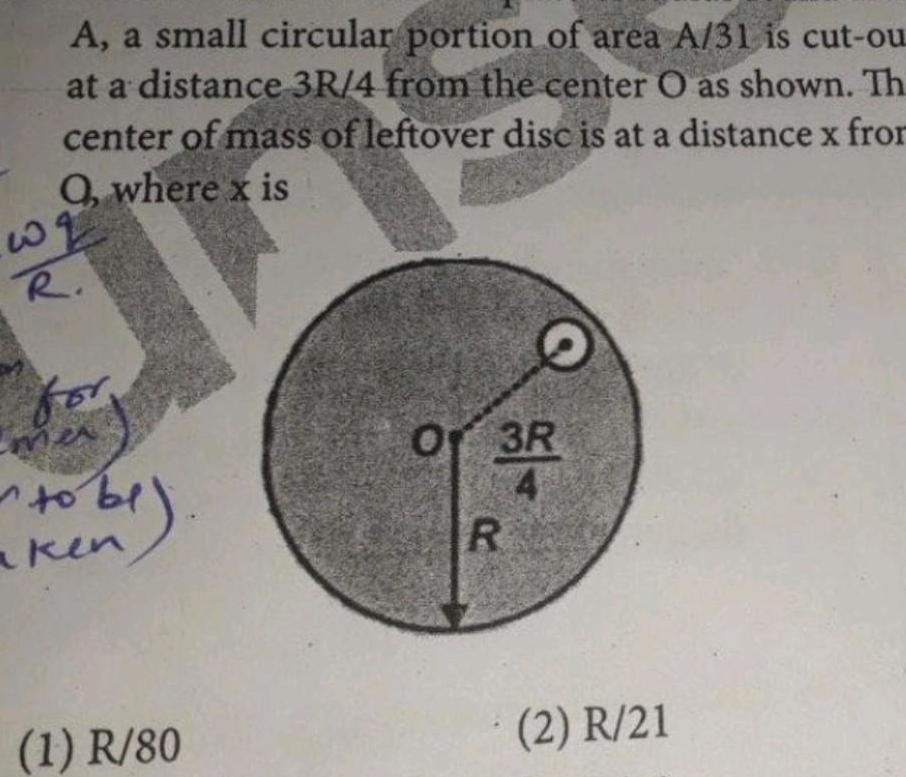
Physics
Center of mass and momentumw A a small circular portion of area A 31 is cut ou at a distance 3R 4 from the center O as shown Th center of mass of leftover disc is at a distance x from Q where x is R fo mer to be aken 1 R 80 21 Of 3R R 2 R 21
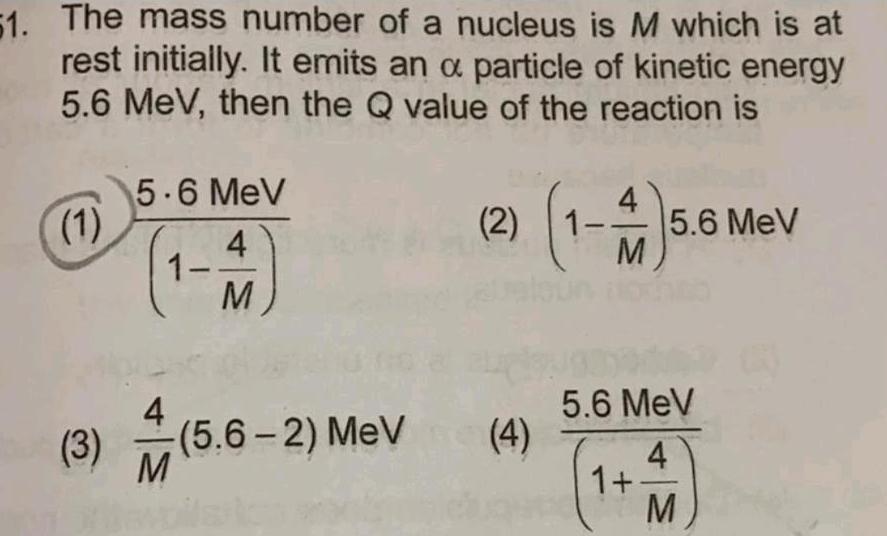
Physics
Center of mass and momentum51 The mass number of a nucleus is M which is at rest initially It emits an a particle of kinetic energy 5 6 MeV then the Q value of the reaction is 1 5 6 MeV 4 M 1 3 A 1 5 6 2 MeV M 2 1 4 4 M 5 6 MeV 5 6 MeV 4 M 1

Physics
Center of mass and momentumThe surface mass density mass per unit area of a semi circular disc of radius R varies as ax where is a constant vector along positive x axis and is position vector with respect to origin It is kept on smooth horizontal surface with flat surface in contact with surface Now force F is applied in such a way that it moves translationally without any rotation The value of h is k R 16 then find value of k

Physics
Center of mass and momentumVo D A particle of mass m moving with a velocity 1 1 collides elastically with another particle of mass 2 m which is at rest initially Here vo is a constant Which of the following statement is true 1 The direction along which centre of mass moves before collision is 1 2 2 The speed of particle of mass m before collision in centre of mass frame is 2 vo 3 After collision the speed of particle of mass 2 m in the 2 centre of mass frame is 3 Vo 4 Speed of particle of mass 2 m before collision in the centre of mass frame is 2 vo
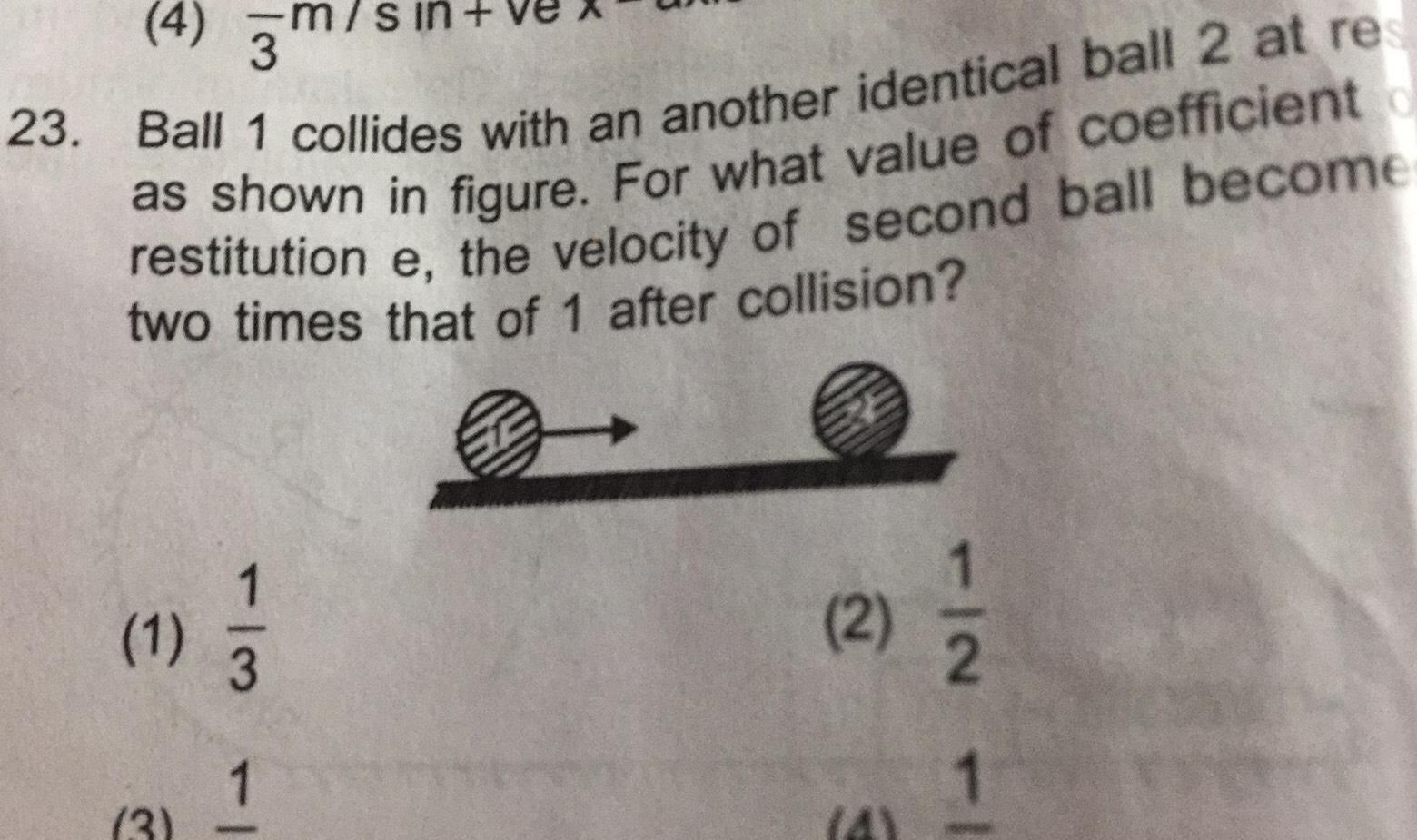
Physics
Center of mass and momentum4 3 m s 23 Ball 1 collides with an another identical ball 2 at res as shown in figure For what value of coefficient restitution e the velocity of second ball become two times that of 1 after collision 1 3 1 3 1 2 E TIN TI

Physics
Center of mass and momentumA bullet of mass mis shot through a wooden block of mass M suspended on a massless rod of length The centre of gravity of the block rises a distance y Find the speed of the bullet as it emerges from the block if the initial speed of the bullet is u M A u 2gy M C u 2gy m B u M m M D u m gy

Physics
Center of mass and momentumBody A of mass 2 kg collides with the another body B at rest initially The collision is perfectly elastic After collision body A continues to move in its original direction with the speed one fourth of its original speed Calculate the mass of body B A 2 kg B 1 6 kg D 0 8 kg C 1 2 kg