Heights and Distances Questions and Answers

Math
Heights and DistancesAn engineer designs a 70-foot cellular telephone tower. Find the angle of elevation to the top of the tower at a point on level ground 55 feet from its base.

Math
Heights and DistancesA plane takes off and travels at an angle of 25° north of east at 105 mph for 2 hours. It then adjusts its path to head 60° west of north and travels in that direction for an hour at a speed of 95 mph. Approximately how far away is the plane from its starting point?
130 miles
190 miles
174 miles
182 miles

Math
Heights and DistancesA balloon flying at 3000 feet above the ocean measures the angles of depression of each end of an island directly in front of the balloon to be 75.8º and
15.6°. What is the length of the island to the nearest tenth of a foot?
The length of the island is
feet.

Math
Heights and DistancesAU.S. Coast Guard Response Boat leaves Charleston, South Carolina at 1:00 p.m. heading due
east at an average speed of 34 knots (nautical miles per hour). At 6:00 p.m., the boat changes
course to N 13° E. At 8:30 p.m. what is the boat's bearing and distance from Charleston, South
Carolina? Round all units to the nearest hundredth.
Bearing from Charleston, South Carolina: (Click For List)
Distance from Charleston, South Carolina:
nautical miles
0
(Click For List)

Math
Heights and DistancesFrom a lookout Tower A, a column of smoke is sighted due south. From a second lookout Tower B, 5 miles west of A, the smoke is observed with a bearing of S63 E. How far is the fire from Tower A?
distance from Tower A = miles (round to the nearest hundredth)
distance from Tower B = miles (round to the nearest hundredth)

Math
Heights and DistancesRachel walked 2.0 meters south. Then she made a right hand turn and walked 16.0
meters west. She turned right again and walked 24.0 meters north. Then she turned
left and walked 36.0 meters west. What is the magnitude of the overall
displacement?
O 50.2m
O53.7m
56.5m
62.9m

Math
Heights and DistancesA piece of cardboard is 2.6 times as long as it is wide. It is to be made into a box with an open top by cutting 3-inch squares from each comer and folding up the sides. Let x represent the width (in inches) of the original piece of cardboard. Answer the following questions.
a) Represent the length of the original piece of cardboard in terms of x.

Math
Heights and DistancesA hill on Oak Street has an angle of elevation of 11°. A hill on Broadway Street has a 21% grade. Which hill is steeper?

Math
Heights and DistancesYou are standing at the edge of a cliff. You look down with an angle of depression of 20 degrees and see a a dog at the bottom that is 130 feet away from where you're standing. What is the height of the cliff? Round your answer to the nearest tenth, and round only once.

Math
Heights and DistancesTrain A has a speed 15 miles per hour greater than that of train B. If train A travels 230 miles in the same times train B travels 200 miles, what are the speeds of the two trains?
Train A was traveling at miles an hour where train B was traveling at miles per hour.

Math
Heights and DistancesThe equation h(t) = -4.9t² + 25t expresses the approximate height, h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?
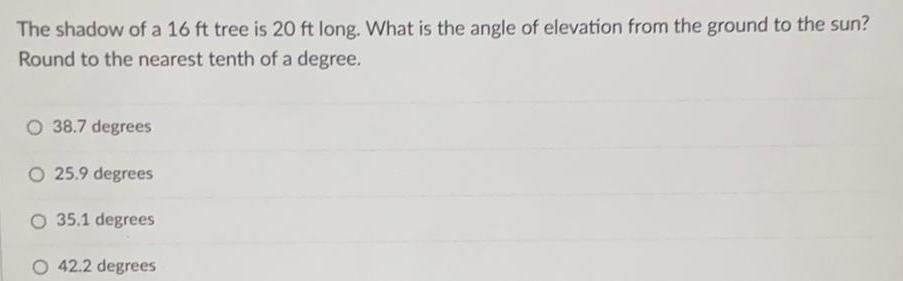
Math
Heights and DistancesThe shadow of a 16 ft tree is 20 ft long. What is the angle of elevation from the ground to the sun?
Round to the nearest tenth of a degree.
38.7 degrees
25.9 degrees
35.1 degrees
42.2 degrees

Math
Heights and DistancesA is due north of City B. Find the distance between City A (41°4' north latitude) and City B (24°52' north latitude).
ume that the radius of Earth is 3960 miles.
distance between City A and City B is
und to the nearest mile as needed.)
miles.

Math
Heights and DistancesTwo artillery bases are located at the points A and C represented in the figure. Each of the bases locates an enemy airplane at point B and measures the angles of elevation to the airplane. Given the elevation angles in the figure and the fact that the enemy airplane is 2,135 meters from the base at point C, how far apart, in meters, are the two bases? (Round your answer to the nearest tenth if necessary. Do not include any units.)

Math
Heights and DistancesThe radius of the base of a cone is decreasing at a rate of 2 centimeters per minute.
The height of the cone is fixed at 9 centimeters.
At a certain instant, the radius is 13 centimeters.
What is the rate of change of the volume of the cone at that instant (in cubic centimeters per minute)?

Math
Heights and DistancesThe height of a firework
launched straight up from the
ground is given by the equation
h(r) = -16² +1441, where is the
time in seconds. Find the average
rate of change in the height of the
firework from when it reaches its
maximum height until when it
reaches the ground.
A) -58 ft/sec
B) -72 ft/sec
C) -36 ft/sec
D) -64 ft/sec
E) 48 fl/sec
making a video
singing the ABCs
whistling
playing poker
bowling

Math
Heights and DistancesYou are designing a rectangular poster to contain 48 in² of printing with a 3-in margin at the top and bottom and a 1-in margin at each side. What overall dimensions will minimize the amount of paper used?
What is the vertical height of the poster that will minimize the amount of paper used?
h = in

Math
Heights and DistancesThe Gateway Arch in St. Louis, Missouri, is 630 feet tall. Suppose a
12-foot-tall pole that is near the Arch casts a 5-foot shadow. How long is the
Arch's shadow?

Math
Heights and DistancesLuis buys 16 bellflowers and 20 roses. He wants to plant an equal number of bellflowers and an equal number of roses in each of his flower boxes. What is the greatest number of flower boxes Luis can plant using all the bellflowers and roses? Show your work.

Math
Heights and DistancesStacy is mountain climbing with Janelle and has just climbed a 7-meter vertical rock face. Janelle is standing at the bottom of the cliff, looking up at Stacy. If Janelle is 10 meters away from Stacy, how far away from the cliff is Janelle standing? If necessary, round to the nearest tenth.

Math
Heights and DistancesA tree standing vertically on level ground casts a 103 foot long shadow. The angle of elevation from the end of the shadow to the top of the tree is 23.8°. Give the exact answer, do not use a calculator.
Again, remember, all trig functions in MOM are in radian mode. You'll have to convert 23.8° into radians. Don't use a calculator.

Math
Heights and DistancesA hot-air balloon is floating above a straight road. To calculate their height above the ground, the balloonists simultaneously measure the angle of depression to two consecutive mileposts on the road on the same side of the balloon.
The angles of depression are found to be 26° and 29º. How high (in feet) is the ballon?

Math
Heights and DistancesQuincy is about to ride a straight water slide. The length of the water slide itself is 17 meters. The splash pool at the end of the slide is 15 meters away from the base of the tower that leads up to the launching platform. How high is the launching platform?

Math
Heights and DistancesA 6 foot tall man walked due west, in the exact direction of the setting sun, at a rate of 1.5
ft/sec. At the moment just before he sees the sun disappear behind a building that is 150
feet high, at what rate is the length of his shadow changing?
6 ft/sec
-0.063 ft/sec
O-1.44 ft/sec
O 0.06 ft/sec

Math
Heights and DistancesFrom an angle of depression of 40°, John watches his friend approach his building
while standing on the rooftop. The rooftop is 16 m from the ground, and John's eye
level is at about 1.8 m from the rooftop. What is the distance, to the nearest tenth
of a meter, between John's friend and the building?
Math
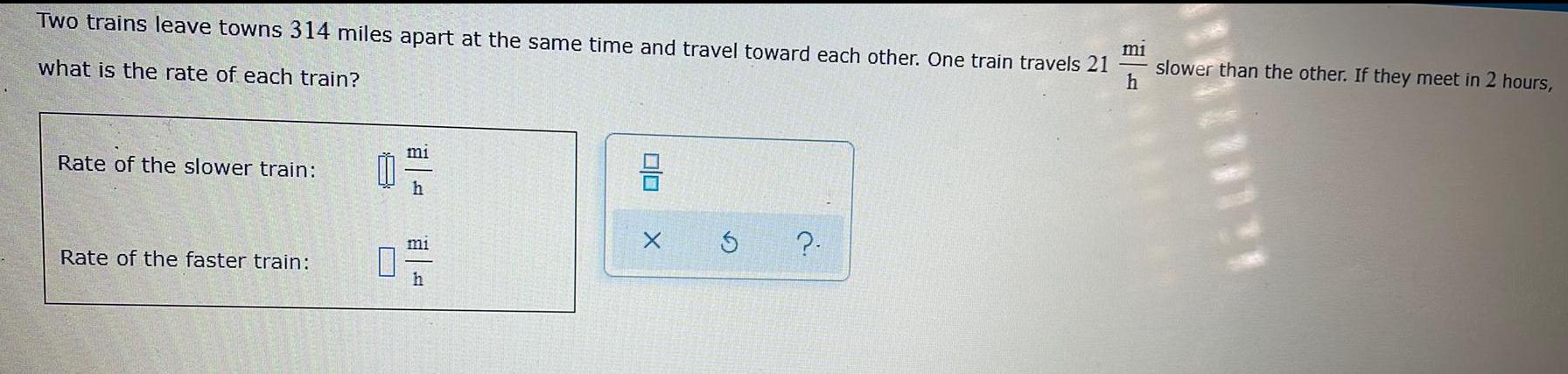
Heights and DistancesTwo trains leave towns 314 miles apart at the same time and travel toward each other. One train travels 21 mi/h slower than the other. If they meet in 2 hours,
what is the rate of each train?
Rate of the slower train: mi/h
Rate of the faster train: mi/h

Math
Heights and DistancesA baseball player running forward at 3 meters per second throws a ball with a velocity of 20 meters per second at an angle of 20° with the horizontal. What is the resultant speed and direction of the throw?

Math
Heights and DistancesSuperman must stop a 120-km/h train in 150 m to keep it from hitting a stalled car on the tracks. If the train's mass is 3.6 × 105 kg, how much force must he exert? Compare to the weight of the train (give as %). How much force does the train exert on Superman?

Math
Heights and DistancesWhile doing bicep curls, Tamara applies 155 Newtons of force to lift the dumbbell. Her forearm is 0.366 meters long and she begins the bicep curl with her elbow bent at a 15° angle below the horizontal, in the direction of the positive x-axis. Determine the magnitude of the torque about her elbow.161

Math
Heights and DistancesThe breadth of a street between two houses is 30 meters and the angle of the depression of the top of one, as observed from the top of the other which is 40 meters height is 30°. Find the height of the other house. From a light house the angle of depression of two ships on opposite sides of the lighthouse be 100 m. Find the distance between the ships the line joining them passes through the foot of the light house. An aeroplane when 2000 meters high passes vertically above another at an instant when the angle sof elevation at the same observing point are 63° and 45° respectively. How many meters in the one lower than the other.

Math
Heights and DistancesFrom a point 525 feet in horizontal distance from the foot of a vertical cliff, the angle of elevation for the top of the cliff is 360. How high is the cliff (to the nearest whole number)?
308 ft.
381 ft.
722 ft.

Math
Heights and DistancesAndrea has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same
distance to cool down. If she runs at a speed of 10 mph and walks back at a speed of 2 mph, how long should she plan to spend walking back?

Math
Heights and DistancesFrom his eye, which stands 1.61 meters above the ground, Jacob measures the angle
of elevation to the top of a prominent skyscraper to be 25°. If he is standing at a
horizontal distance of 281 meters from the base of the skyscraper, what is the height
of the skyscraper? Round your answer to the nearest tenth of a meter if necessary.

Math
Heights and DistancesQuestion 5(Multiple Choice Worth 2 points)
(04.03 MC)
A ball bounces to a height of 6.1 feet on the first bounce. Each subsequent bounce reaches a height that is 82% of the previous bounce. What is the height, in feet, of the fifth bounce?
Round your answer to the thousandths place.
5.002 ft
2.758 ft
2.262 ft
1.784 ft

Math
Heights and DistancesA boat is heading towards a lighthouse, where Jack is watching from a vertical
distance of 108 feet above the water. Jack measures an angle of depression to the
boat at point A to be 9º. At some later time, Jack takes another measurement and
finds the angle of depression to the boat (now at point B) to be 66°. Find the distance
from point A to point B. Round your answer to the nearest tenth of a foot if
necessary.

Math
Heights and DistancesTristin is attempting to dive
from an 8 foot diving board
into a tube that is located
12 feet from the base of the
diving board. What should be
his angle of depression to
ensure he hits the tube?
A) 30.5° sunglasses
B) 31.9° bow-ties
C) 32.2° gorilla costumes
D) 33.7°
tu-tus
E) 35.1°
snow suits

Math
Heights and DistancesTwo persons are to run a race, but one can run 11 meters per second, whereas the other can run 6 meters per second. If
the slower runner has a 55-meter head start, how long will it be before the faster runner catches the slower runner, if
they begin at the same time?

Math
Heights and DistancesFrom a hot-air balloon, Jace measures a 31° angle of depression to a landmark that's
331 feet away, measuring horizontally. What's the balloon's vertical distance above
the ground? Round your answer to the nearest hundredth of a foot if necessary.

Math
Heights and DistancesJosue leans a 26-foot ladder against a wall so that it forms an angle of 80° with the
ground. How high up the wall does the ladder reach? Round your answer to the
nearest hundredth of a foot if necessary.

Math
Heights and DistancesA man on the deck of a ship is 14 ft. above water level. He observes that the angle of
elevation of the top of a cliff is 40° and the angle of depression of the base is 20°. Find the
distance of the cliff from the ship and the height of the cliff if the base of the cliff is at sea
level.

Math
Heights and DistancesThe angle of elevation from aship to the top of a 42-meter lighthouse onthe shore measures 33°. How far is the shipfrom the shore? (Assume the horizontal line ofsight meets the bottom of the lighthouse.)

Math
Heights and DistancesGRIDDED RESPONSE To approach runway 17 ofthe Ponca City Municipal Airport in Oklahoma, the pilotmust begin a 3° descent starting from a height of 2714 ftabove sea level. The airport is 1007 ft above sea level. Tothe nearest tenth of a mile, how far from the runway isthe airplane at the start of this approach?

Math
Heights and DistancesA boat is heading towards a lighthouse, whosebeacon-light is 110 feet above the water. Theboat's crew measures the angle of elevation tothe beacon, 7°. What is the ship's horizontaldistance from the lighthouse (and the shore)?Round your answer to the nearest tenth of a footif necessary.

Math
Heights and DistancesThe family trip to Grandma's consisted of both a train ride and a car ride. The average speed of the train ride was 68 miles per hour, and the average speed of the car ride was 55 miles per hour. The entire trip lasted 7 hours.
Let x be the number of hours the train ride lasted. Write an expression for the total distance of the trip, in miles.