Ellipse Questions and Answers

Math
Ellipse4 An elliptical whispering gallery is 10 m long Anna and Francis find that if they each stand 4 m away from the ends of the gallery at its foci they can hear each other perfectly What is the width of the gallery

Math
EllipseIn a solar system two comets pass near the sun which is located at the origin Comet E is modeled by all measurements are in astronomical units Part A What are the vertices for the path of Comet E Show your work 4 points x 16 y 1 and Comet H is modeled by 400 144 Part B Which comet travels closer to the sun Give evidence to support your answer 5 points Part C What key feature does the sun represent for both comets Give evidence to support your answer 6 points x 13 y 25 144 1 where

Math
EllipseA tunnel is constructed with a semielliptical arch The width of the tunnel is 70 feet and the maximum height at the center of the tunnel is 20 feet What is the height of the tunnel 10 feet from the edge Round your answer to the hundredths place 19 17 feet 16 41 feet 014 01 feet 10 30 feet

Math
EllipseA one way road passes under an overpass in the shape of half an ellipse 20 ft high at the center and 20 ft wide Assuming a truck is 16 ft wide what is the tallest truck that can pass under the overpass The tallest truck that can pass under the overpass is ft tall
Math
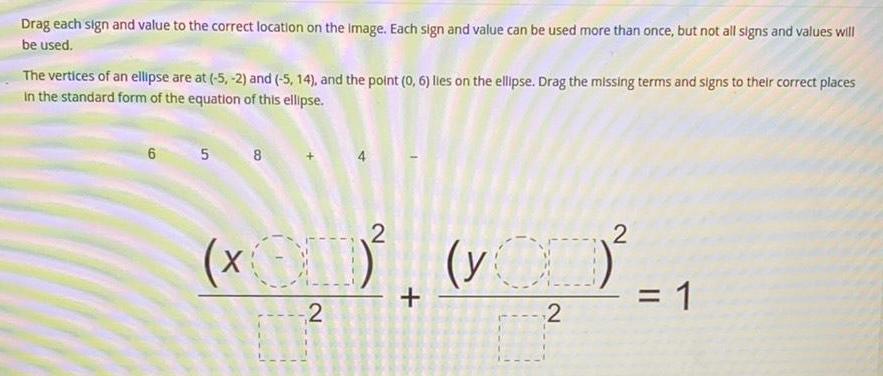
EllipseDrag each sign and value to the correct location on the image Each sign and value can be used more than once but not all signs and values will be used The vertices of an ellipse are at 5 2 and 5 14 and the point 0 6 lies on the ellipse Drag the missing terms and signs to their correct places in the standard form of the equation of this ellipse 6 5 8 2 OD 2 2 VOD 2 1
Math
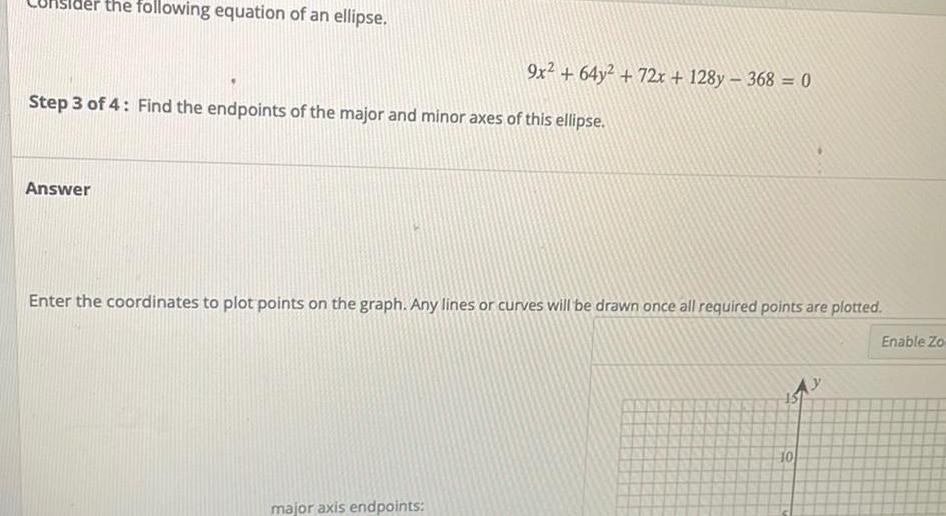
Ellipsethe following equation of an ellipse Answer Step 3 of 4 Find the endpoints of the major and minor axes of this ellipse 9x 64y 72x 128y 368 0 Enter the coordinates to plot points on the graph Any lines or curves will be drawn once all required points are plotted major axis endpoints Ay 15 10 Enable Zo
Math
EllipseFind the equation of the ellipse with the following properties. Express your answer in standard form.
Vertices at (-5, -2) and (-5, 12)
Minor axis of length 2
Math
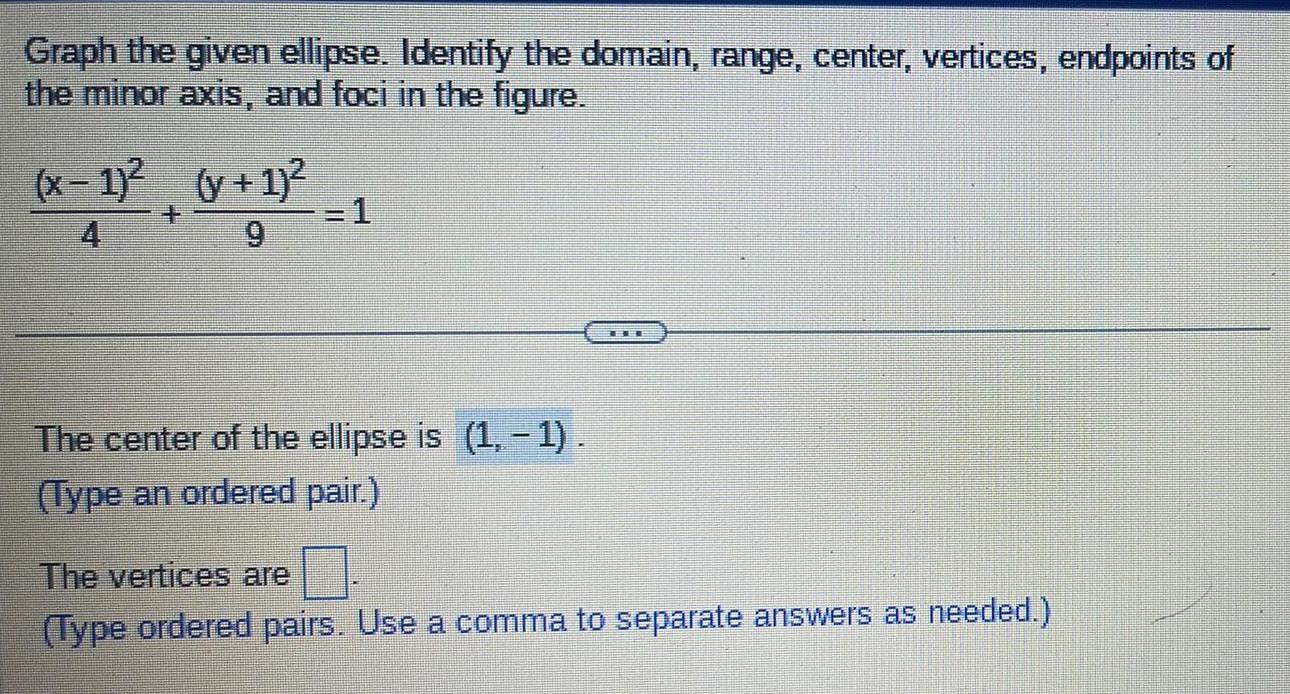
EllipseGraph the given ellipse. Identify the domain, range, center, vertices, endpoints of
the minor axis, and foci in the figure.
(x-1)²/4 + (y + 1)²/9 =1
The center of the ellipse is (1,-1).
(Type an ordered pair.)
The vertices are .
(Type ordered pairs. Use a comma to separate answers as needed.)

Math
EllipseConsider the following equation of an ellipse.
9x² + 49y² +90x+ 392y + 568 = 0
Step 1 of 4: Rewrite this equation in the standard form of an ellipse.
Answer
Math
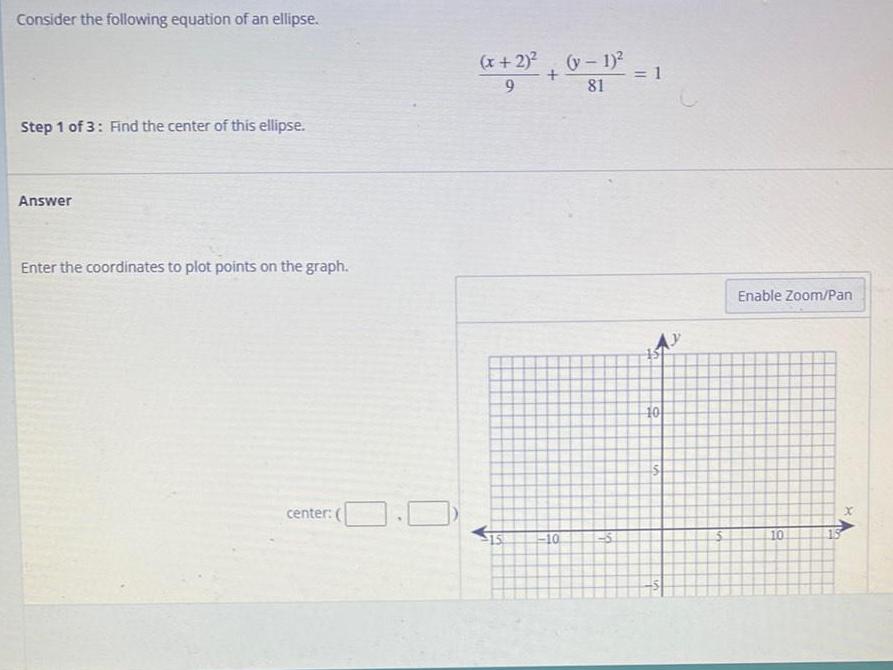
EllipseConsider the following equation of an ellipse. (x+2)^2 /9 + (y-1)^2 /81 =1
Find the center of this ellipse.
Answer
Enter the coordinates to plot points on the graph.
center:
Math
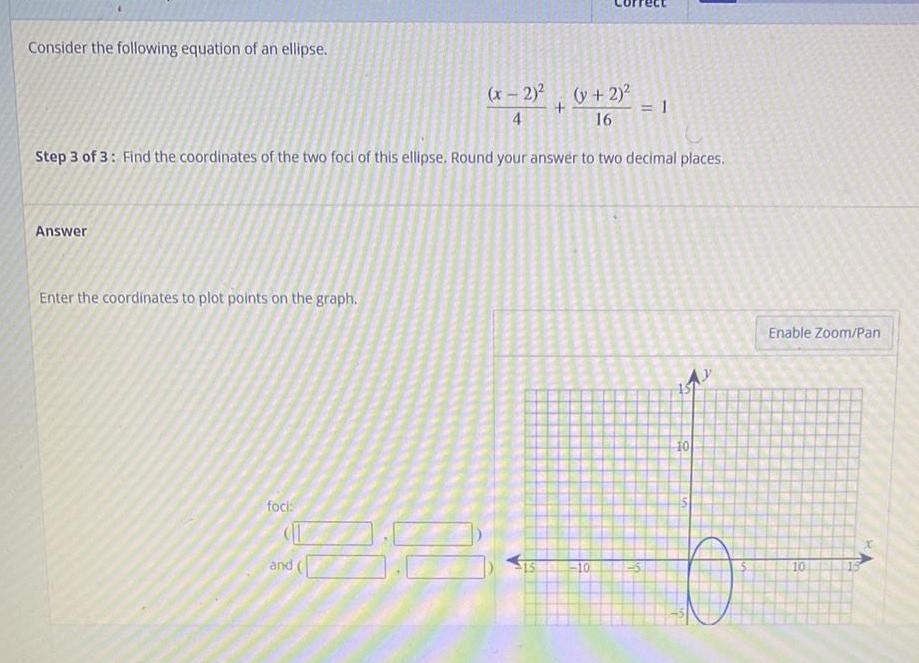
EllipseConsider the following equation of an ellipse.
(x - 2)²/4+(y + 2)² /16 =1
Step 3 of 3: Find the coordinates of the two foci of this ellipse. Round your answer to two decimal places
Enter the coordinates to plot points on the graph.
Math
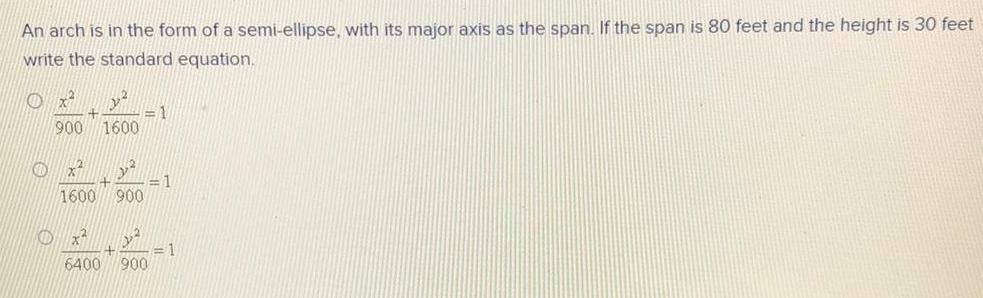
EllipseAn arch is in the form of a semi-ellipse, with its major axis as the span. If the span is 80 feet and the height is 30 feet
write the standard equation.
x²/900+ y²/1600=1
x²/1600+ y²/900=1
x²/6400+ y²/900=1

Math
EllipseFind an equation of an ellipse satisfying the given conditions.
Foci: (-4, 0) and (4, 0)
Length of major axis: 12

Algebra
EllipseFind the equation of the ellipse with the center (6,3), a focus at (3,3), and a vertex at (11,3).

Math
EllipseAn equation of an ellipse is given.
x2/25 + y²/16 = 1
25 16
(a) Find the vertices, foci, and eccentricity of the ellipse.
Math
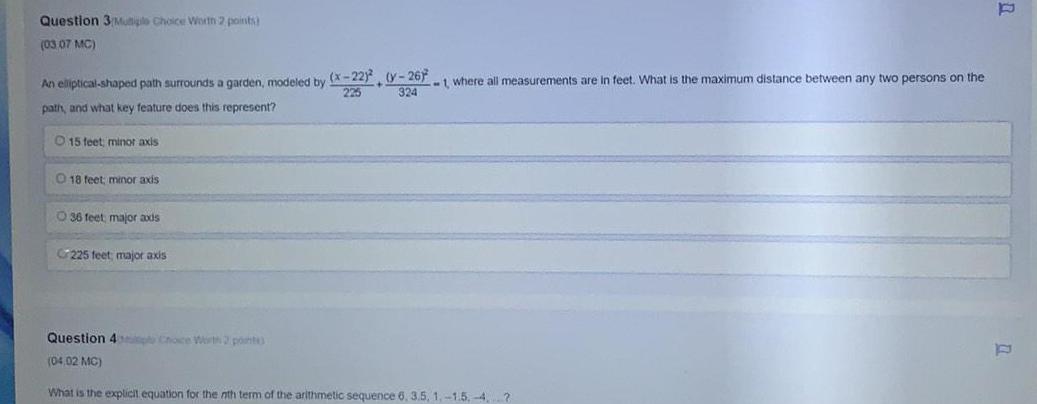
EllipseAn elliptical-shaped path surrounds a garden, modeled by (x-22)/225+ (y-26)²/324 =1, where all measurements are in feet. What is the maximum distance between any two persons on the path, and what key feature does this represent?
15 feet; minor axis
18 feet; minor axis
36 feet major axis
225 feet; major axis

Math
EllipseAn equation of an ellipse is given.
(a) Identify the center of the ellipse.
(b) Determine the value of a.
(c) Determine the value of b.
(d) Identify the vertices.
(e) Identify the endpoints of the minor axis.
(f) Identify the foci.
(g) Determine the length of the major axis.
(h) Determine the length of the minor axis.
(i) Graph the ellipse.
Express numbers in exact, simplest form.
9x^2 + 64y^2 = 576

Math
EllipseConsider the standard form of the equation x²/25 + y²/36 = 1
The value of a² is, so the y-intercepts are The graph passes through the ordered pairs which are the vertices.
The value of b² is, so the x-intercepts are The graph passes through the ordered pairs
The value of a² is, so the y-intercepts are The graph passes through the ordered pairs , which are the vertices.
The value of b² is, so the x-intercepts are The graph passes through the ordered pairs

Math
EllipseConsider the equation of the following (x+8)²/4 conic section: + (y + 6)² = 1. Use Desmos and scratch paper to determine the following characteristics of the conic section:
Name of Conic Section:
Center.
Foci:
Eccentricity:
Math
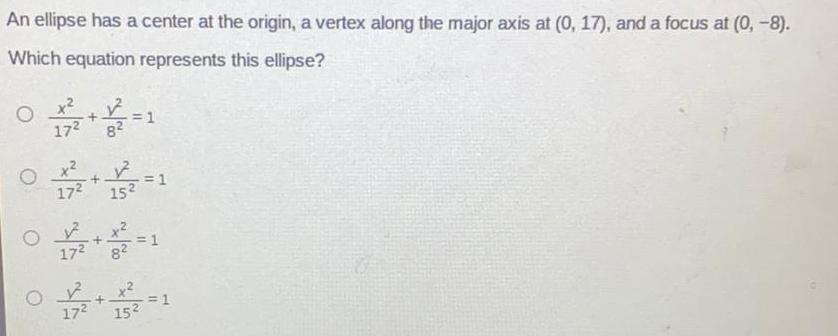
EllipseAn ellipse has a center at the origin, a vertex along the major axis at (0, 17), and a focus at (0, -8).
Which equation represents this ellipse?

Math
EllipseSemielliptical Arch Bridge An arch in the shape of the upper half of an ellipse is
used to support a bridge that is to span a river 12 meters wide. The center of the
arch is 5 meters above the center of the river (see the figure). Write an equation
for the ellipse in which the x-axis coincides with the water level and the y-axis
passes through the center of the arch.
Type the left side of the equation below.
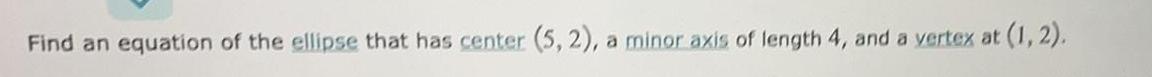
Math
EllipseFind an equation of the ellipse that has center (5, 2), a minor axis of length 4, and a vertex at (1,2).
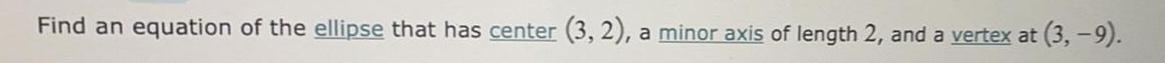
Math
EllipseFind an equation of the ellipse that has center (3, 2), a minor axis of length 2, and a vertex at (3,-9).
Math
EllipseFind an equation of the ellipse that has center (1,-4), a minor axis of length 4, and a vertex at (-2,-4).
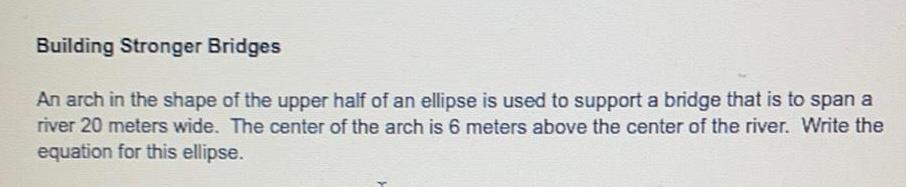
Math
EllipseAn arch in the shape of the upper half of an ellipse is used to support a bridge that is to span a river 20 meters wide. The center of the arch is 6 meters above the center of the river. Write the equation for this ellipse.

Math
EllipseConvince me that the equation of an ellipse that has foci at (2,0) and (-2,0) and a major axis length of 6 has an equation of x^2/9 + y^2/5 = 1

Math
EllipseWhich of the following could be the equation of an ellipse? (More than one answer may
be possible)
(x-4)² = 24 (y + 8)
(x-4)² + (y + 8)² = 1
(x-4)²/2 - (y + 8)² =1
(x-4)²/2+ (y + 8)²/16 =1
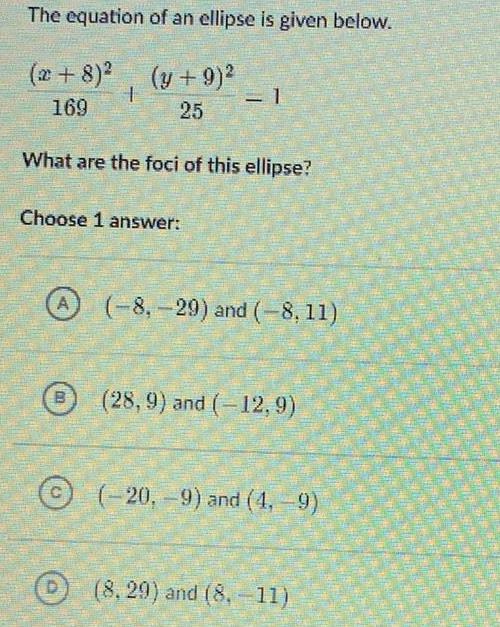
Math
EllipseThe equation of an ellipse is given below.
(x+8)²/169 + (y + 9)²/25 =1
What are the foci of this ellipse?
Choose 1 answer:
A(-8,-29) and (-8, 11)
(28,9) and (-12,9)
(-20, -9) and (4, 9)
(8.29) and (8, −11)
Math
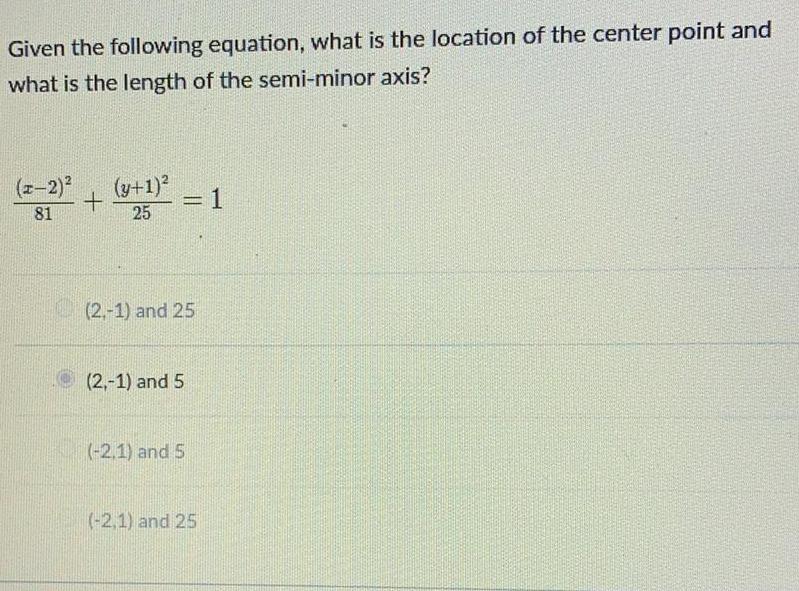
EllipseGiven the following equation, what is the location of the center point and what is the length of the semi-minor axis?
(x-2)²/81 + (y+1)²/25 =1
(2,-1) and 25
(2,-1) and 5
(-2,1) and 5
(-2,1) and 25

Math
EllipseComplete the sentence below.
For the ellipse x²/25 + y²/9 = 1, the value of a is , the value of b is , and the major axis is the -axis.
For the ellipse x²/25 + y²/9 = 1, the value of a is , the value of b is , and the major axis is the -axis.

Math
EllipseGiven the ellipse below, determine the coordinates of the two foci. Enter your answers as ordered pairs (x, y) and leave in radical form.
(x-1)2/36 + (y+2)2/16 = 1

Math
EllipseThe vertices of an ellipse are located at (1,4) and (9,4) and its co-vertices are located at (5, 7) and
(5, 1).
a. Find the center of the ellipse.

Math
EllipseAn elliptical whispering gallery is 10 m long. Anna and Francis find that if they each stand 4 m away from the ends of the gallery at its foci, they can hear each other perfectly. What is the width of the gallery?

Math
EllipseFill in the blanks below:
a. If an ellipse has a major axis length of 8, then its semi-major axis length is_
b. If an ellipse has a minor axis length of 6, then its semi-minor axis length is
c. If an ellipse has vertices at (0, 2) and (0, 2) then its major axis length is
semi-major axis length is
d. If an ellipse has co-vertices at (0, 1) and (0, 1) then its semi-minor axis length is
Is this ellipse a horizontal ellipse or a vertical ellipse?
e. If a vertical ellipse has a major axis length of 4, its vertices are at
f. If a horizontal ellipse has a semi-minor axis length of 3, its co-vertices are at

Math
EllipseTo determine the break-even point, or the number of units that must be sold so that no profit or loss occurs, an economist uses the formula Px = Cx + F, where P is the selling price per unit, x is the number of units that must be sold to break even, C is the cost to make each unit, and F is the fixed cost. A business analyst has determined that the selling price per unit for a laser printer is $1600. The cost to make one laser printer is $950, and the fixed cost is $211,250. Find the break-even point.
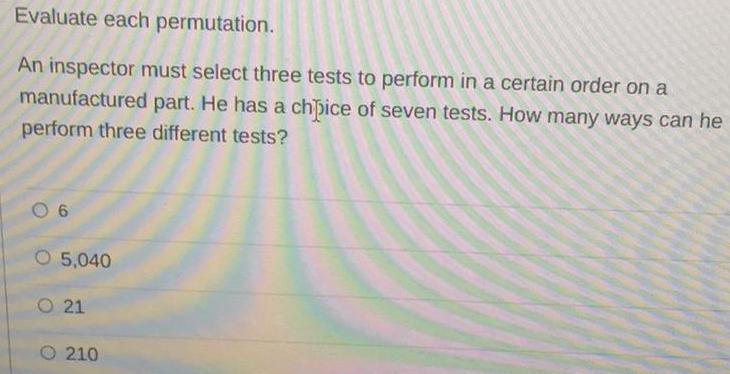
Math
EllipseAn inspector must select three tests to perform in a certain order on a manufactured part. He has a choice of seven tests. How many ways can he perform three different tests?
5,040
21
210

Math
EllipseThe plane x + y + 2z = 12 intersects the paraboloid z = x² + y² in an ellipse. Find the points on the ellipse that are nearest to and farthest from the origin.
nearest point (x, y, z) =
farthest point (x, y, z) =

Math
EllipseWrite the equation of the ellipse 36x² + 4y² - 360x + 32y + 820 = 0 in standard form
(x - h)²
p²
Where:
h =
k =
P =
q=
+
(y – k)²
-
q²
=
1
M

Math
EllipseBob's backyard is a rectangle 40 meters by 100 meters. He uses this backyard for an exercise area for his dog. He
drove two posts into the ground and fastened a rope to each post, passing the rope through the metal ring on his
dog's collar. When the dog pulls on the rope while running, its path is an ellipse. If the dog can just reach all four
sides of the rectangle, find the equation of the elliptical path.
What is the equation of the elliptical path?
(Type your answer in standard form.)
.....

Math
EllipseA system of equations is made up of an ellipse and a hyperbola.
Part A: Create the equation of an ellipse centered at the origin, with a horizontal major axis of 8 units and a minor axis of 6 units. Show your work. (3 points)
6
Part B: Create the equation of a hyperbola centered at the origin, with a horizontal transverse axis, vertex at (-7, 0), and asymptotes of y-t-x. Show your work. (4 points)
Part C: Determine the domain of each conic section and use it to explain why there is no solution to the system. (3 points)

Math
EllipseWhich of the following is the equation of the ellipse with a vertical major axis, center at (1, -3), a = 7, and b = 5?

Math
EllipseA moon's elliptical orbit around a planet is modeled by the equation 225x² + 900y2 = 202,500, where distance is measured in megameters (Mm). If the planet is the center of the orbit's path, what is the maximum distance between the planet and its moon?
45 Mm
30 Mm
26 Mm
15 Mm

Math
Ellipse(x+16)²²
400
In a solar system, two comets pass near the sun, which is located at the origin. Comet E is modeled by
all measurements are in astronomical units.
Part A: What are the vertices for the path of Comet E? Show your work. (4 points)
Part B: Which comet travels closer to the sun? Give evidence to support your answer. (5 points)
Part C: What key feature does the sun represent for both comets? Give evidence to support your answer. (6 points)
144
= 1 and Comet H is modeled by
(x-13)² ²
144
25
= 1, where

Math
EllipseComplete the square to determine whether the equation represents an ellipse, parabola, or hyperbola, showing all your work. If the graph is an ellipse, find the center, vertices, and length of the major axis. If it is a hyperbola, find the center, vertices, and asymptotes. If it is a parabola, find the vertex, focus, and directrix.
x² + 2y² + 40x + 20y + 434 = 0

Math
EllipseFind an equation for the ellipse. Graph the equation.
center at (0,0); focus at (0,20); vertex at (0, - 25)
Type the left side of the equation of the ellipse.

Math
EllipseFind an equation for the ellipse whose vertices are at (2, -9) and (2,3), and focus is at (2,2). Graph the equation.

Math
EllipseA tunnel is constructed with a semielliptical arch. The width of the tunnel is 70 feet, and the maximum height at the center of the tunnel is 20 feet. What is the height of the tunnel
10 feet from the edge? Round your answer to the hundredths place.
19.17 feet
16.41 feet
14.01 feet
10.30 feet

Math
EllipseGraph the ellipse. Identify the center, vertices, endpoints of the minor axis, and foci.
8x²=160-5y²
The center is ().
The vertices are
(Simplify your answer. Type an ordered pair. Type exact answers for each coordinate, us

Math
EllipseAn elliptical track has a major axis that is 80 yards long and a minor axis that is 72 yards long. Find an equation for the track if its center is (0, 0) and the major axis is the x-axis.

Math
EllipseLet S be the ellipsoid(x/4)² + ( y/3 ) ² + (z/2) ²= 1. Calculate the flux of F = zi over the portion of S where x, y, z ≤ 0 with upward-pointing normal. Hint: Parametrize S using a modified form of spherical coordinates (θ,ϕ).