Parabola Questions and Answers
Math
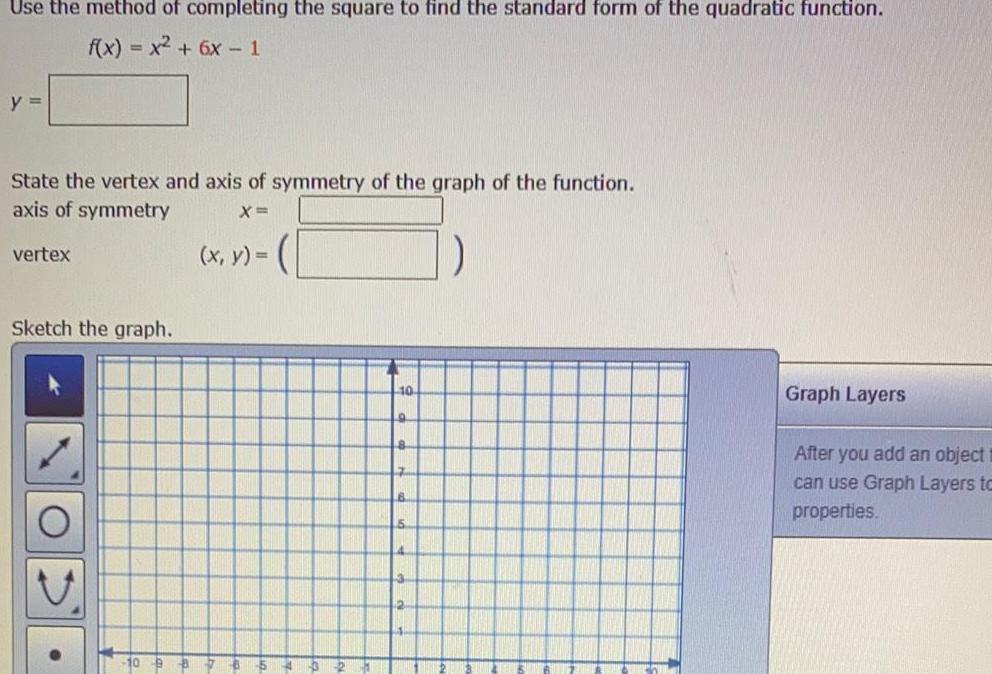
ParabolaUse the method of completing the square to find the standard form of the quadratic function f x x 6x 1 y State the vertex and axis of symmetry of the graph of the function axis of symmetry X vertex Sketch the graph O x y 10 9 8 Graph Layers After you add an object can use Graph Layers to properties

Math
ParabolaTodd hit a golf ball 250 yards The maximum height the golf ball reached was 35 yards Assume the path of the ball is parabolic Write an equation for the path of the ball OA B C D y y y y 5 49 x 125 35 7 3125 x 125 35 5 301 x 35 125 5 1849 x 35 125

Math
ParabolaConsider the parabola given by the equation: f(x) = 4x² – 10x-4
Find the following for this parabola:
A) The vertex:
B) The vertical intercept is the point
C) Find the coordinates of the two x intercepts of the parabola and write them as a list, separated by commas:

Math
ParabolaThe height y (in feet) of a ball thrown by a child is
y=-1/14 x² + 2x + 3
where is the horizontal distance in feet from the point at which the ball is thrown.
(a) How high is the ball when it leaves the child's hand? feet
(b) What is the maximum height of the ball? feet
(c) How far from the child does the ball strike the ground? feet

Math
ParabolaFind the reflection of the function y = x² over y-axis.
The reflection along the y-axis is (-x)².
The reflection along the y-axis is x³.
The reflection along the y-axis is -x².

Math
ParabolaDescribe the transformations to the parent function. Check all boxes
that apply.
f(x)=1/3(x - 2)²
Reflects across the x-axis (open down)
Stretched by a factor of 3 (Narrower)
Compressed by a factor of 3 (Wider)
shifts right 2
shifts left 2
shifts up 2
shifts down 2

Math
ParabolaFind the x-intercept(s) and the coordinates of the vertex for the parabola y=x²-4x-5. If there is more than one x-intercept, separate them with commas.

Math
ParabolaUse the information provided to write the vertex form equation of each parabola.
Vertex: (-7,-5), Focus: (-7,-41/8)
y = (x +9) ² - 7
y = 2(x - 5)² +7
y- 1/2(x-5)²-7
y = -2(x+7)² - 5
y = 1/2( x − 4 )² + 6

Math
ParabolaFarmer Jones, and his wife, Dr. Jones, decide to build a fence in their field, to keep the sheep safe. Since Dr. Jones is a mathematician, she suggests building fences described by y = 112² and y = x² + 4. Farmer Jones thinks this would be much harder than just building an enclosure with straight sides, but he wants to please his wife. What is the area of the enclosed region?
Math
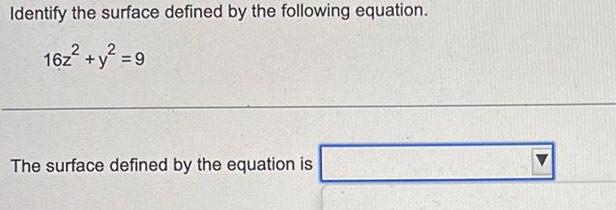
ParabolaIdentify the surface defined by the following equation.
16z² + y² = 9
The surface defined by the equation is _____

Math
ParabolaGiven the function g(x) = -(x-3)² - 2. Determine if the function has a maximum or
minimum and what are the coordinates of the vertex?
a. (-3, -2) minimum
b. (3,-2) maximum
c. (-3, -2) minimum
d. (3, 2) maximum

Math
ParabolaThe mirror in an automobile headlight has a parabolic cross-section with the light bulb at the focus. On a schematic, the equation of the parabola is given as x^2= 4y. if we want to construct the mirror so that the focus is located at (0,1.25), what is the equation of the parabola?
Math
ParabolaSketch the graph of the quadratic function and the axis of symmetry. State the vertex, and give the equation for the axis of symmetry.
h(x) = (x + 3)^2
Use the graphing tool to graph the function as a solid curve and the axis of symmetry as a dashed line.
Click to enlarge graph.
The vertex is ____.
(Type an ordered pair.)
The axis of symmetry is _______.
(Type an equation.)
Math
ParabolaAn arch is in the shape of a parabola. It has a span of 800 feet and a maximum height of 40 feet. Find the equation of the parabola (assuming the origin is halfway between the arch's feet).Determine the height of the arch 143 feet from the center.
Math
ParabolaConvert the equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola.
x² +10x-4y+5=0

Math
ParabolaFind the standard form of the equation of the parabola satisfying the given conditions.
Focus: (0,30); Directrix: y=-30
The equation of the parabola is
Math
ParabolaGive the domain and range of the quadratic function whose graph is described.
The vertex is (-8, -7) and the parabola opens down.
The domain off is. (Type your answer in interval notation.)
The range of the function is (Type your answer in interval notation.)
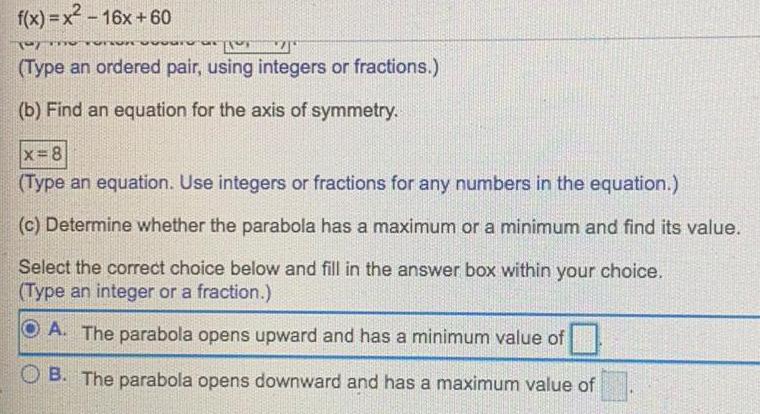
Math
Parabolaf(x)=x²-16x +60
(Type an ordered pair, using integers or fractions.)
(b) Find an equation for the axis of symmetry.
x=8
(Type an equation. Use integers or fractions for any numbers in the equation.)
(c) Determine whether the parabola has a maximum or a minimum and find its value.
Select the correct choice below and fill in the answer box within your choice.
(Type an integer or a fraction.)
A. The parabola opens upward and has a minimum value of
B. The parabola opens downward and has a maximum value of

Math
ParabolaWhich of the following describes the parabola with the equation y = 4x² - 12x + 9?
The axis of symmetry is x = -1.5 and the vertex is (-1.5, 36).
The axis of symmetry is x = 4 and the vertex is (4, -12).
The axis of symmetry is x = 0 and the vertex is (0, 9).
The axis of symmetry is x = 1.5 and the vertex is (1.5, 0).

Math
ParabolaFind the equation for the
following parabola.
Vertex (2, -1)
Focus (2, 3)
A. (x-2)² = (y+1)
B. (x-2)² =16(y+1)²
C. (x-2)² = 4(y+1)
D. (x-2)² 16(y+1)

Math
ParabolaFind the axis of symmetry for the parabola whose equation is given. Use the axis of symmetry to find a second point on the parabola whose y-coordinate is the same as the given point.
f(x) = 2(x+3)²-3; (-2,-1)
The axis of symmetry is
(Type an equation. Simplify your answer)
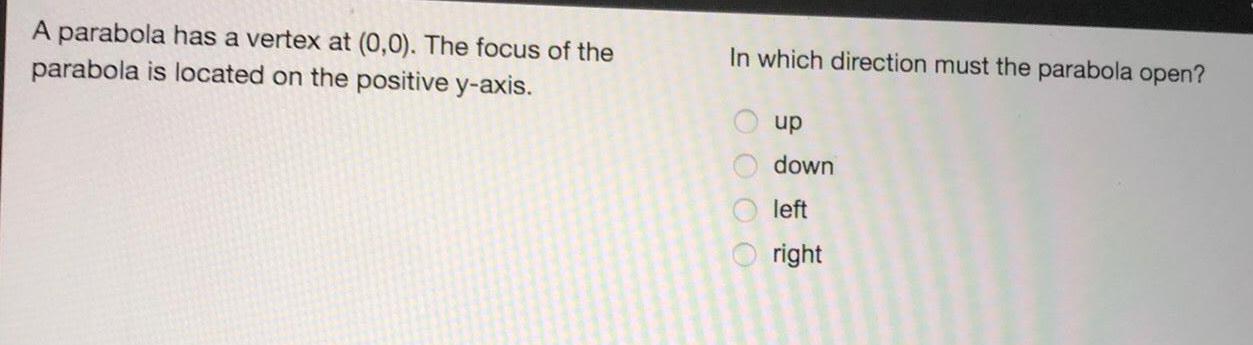
Math
ParabolaA parabola has a vertex at (0,0). The focus of the parabola is located on the positive y-axis. In which direction must the parabola open?
up
down
left
right

Math
ParabolaWhich equation represents the circle described?
The radius is 2 units.
The center is the same as the center of a circle whose equation is ²2+2-8x-6y + 24 = 0.
(x+4)2 + (y + 3)² = 2
(x-4)2+(y-3)²=2
(x-4)2+(y-3)² =2²
(x+42 + (y + 3)² = 2²
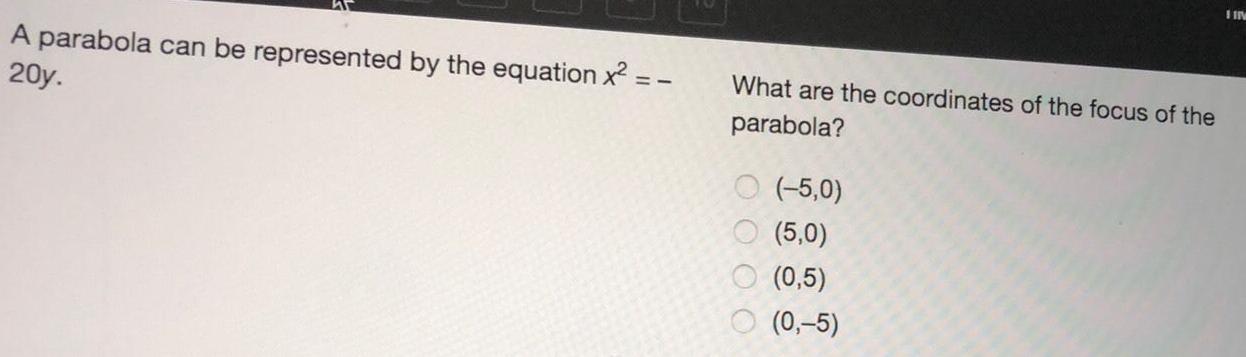
Math
ParabolaA parabola can be represented by the equation x² = - 20y.
What are the coordinates of the focus of the parabola?
(-5,0)
(5,0)
(0,5)
(0,-5)
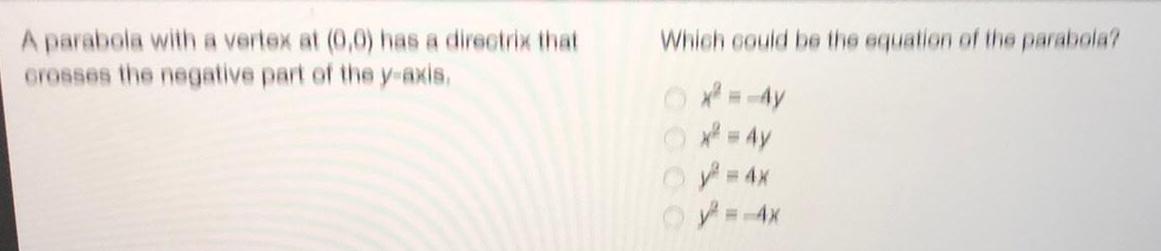
Math
ParabolaA parabola with a vertex at (0,0) has a directrix that crosses the negative part of the y-axis.
Which could be the equation of the parabola?
x^2 = -4y
x² = 4y
y² = 4x
y=-4x

Math
ParabolaFind the dimensions of a rectangle with a perimeter of 192 feet that has the maximum area. The side lengths are feet. (Use a comma to separate answers as needed.)
Math
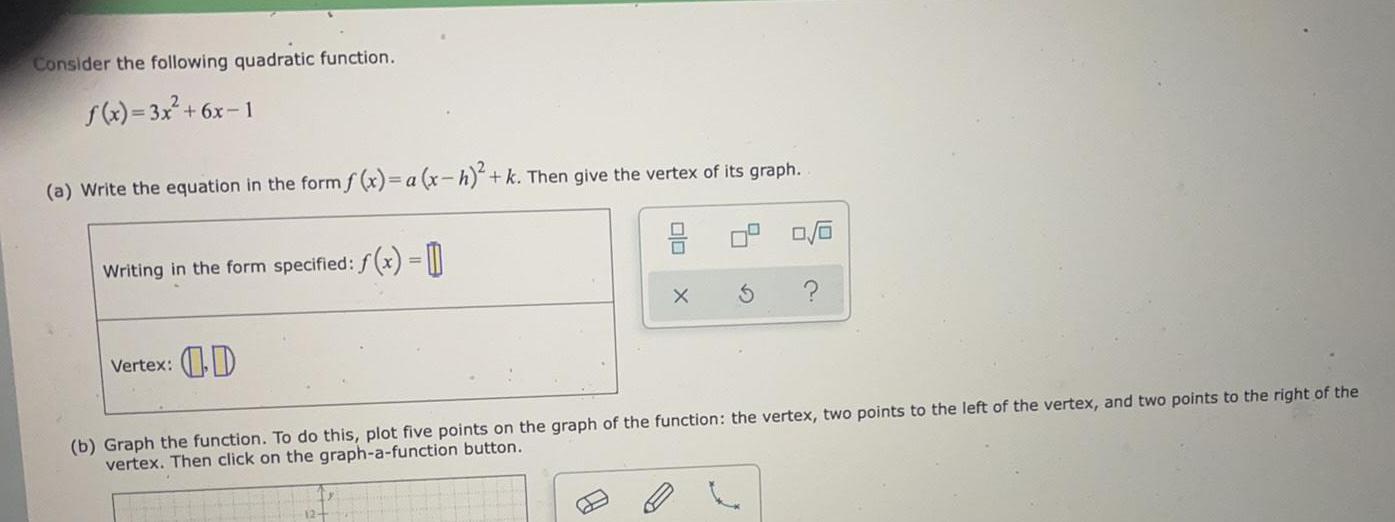
ParabolaConsider the following quadratic function.
f(x)= 3x² +6x-1
(a) Write the equation in the form f(x)= a (x-h)²+ k. Then give the vertex of its graph.
Writing in the form specified: f(x) =
Vertex:
(b) Graph the function. To do this, plot five points on the graph of the function: the vertex, two points to the left of the vertex, and two points to the right of the
vertex. Then click on the graph-a-function button.

Math
ParabolaA parabola can be drawn given a focus of (1, 2) and a directrix of x = -11. What
can be said about the parabola?
The parabola has a vertex at
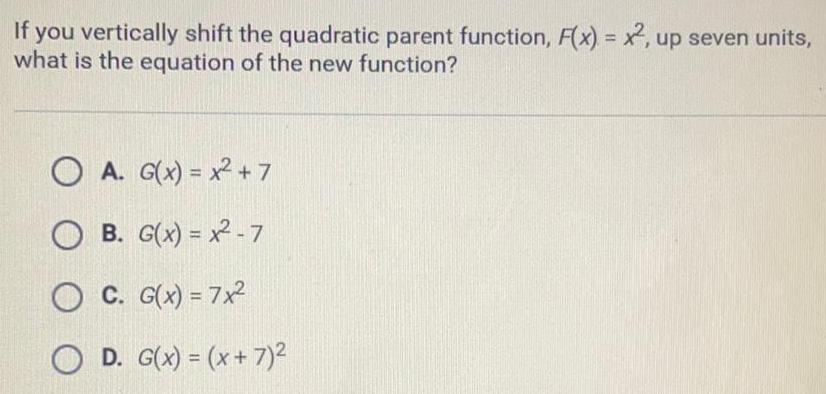
Math
ParabolaIf you vertically shift the quadratic parent function, F(x) = x2, up seven units,
what is the equation of the new function?
A. G(x) = x² +7
B. G(x)=x2-7
C. G(x) = 7x²
D. G(x) = (x + 7)²

Math
ParabolaIf you horizontally compress the quadratic parent function, F(x)=x2, by 7 units, what is the equation of the new function?
A. G(x) = (x+7)²
B. G(x) = 7x²
C. G(x) = (7x)²
D. G(x)=x²-7

Math
ParabolaGiven that a parabola has its vertex at (-2, 1). Which of the following can not be the function expression of the parabola?
f(x) = -(x + 2)²+1
f(x)=(x-2)²+1
f(x)=(x + 2)²+1
f(x)=3(x+2)²+1

Math
ParabolaA parabola has a vertex at (-1, -2) and opens down. Which of the following equations could represent the equation of this parabola in vertex form?
y=2(x+1)2-6
y=-2(x+1)²-6
y= 1/3 (x+1)²-6
y=-6(x+1)²-2

Math
Parabola1. Select the best choice for the definition of a parabola. *
A. The graph of a quadratic function that is a U-shaped curve.
B. Is defined by an ordered pair and is considered the minimum point or the maximum point.
C. A vertical line that passes through the vertex of the graph of a quadratic function.
D. A term that describes the x-intercept(s) of the graph of a quadratic function.
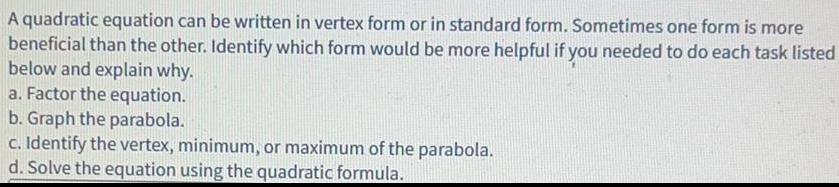
Math
ParabolaA quadratic equation can be written in vertex form or in standard form. Sometimes one form is more
beneficial than the other. Identify which form would be more helpful if you needed to do each task listed below and explain why.
a. Factor the equation.
b. Graph the parabola.
c. Identify the vertex, minimum, or maximum of the parabola.
d. Solve the equation using the quadratic formula.
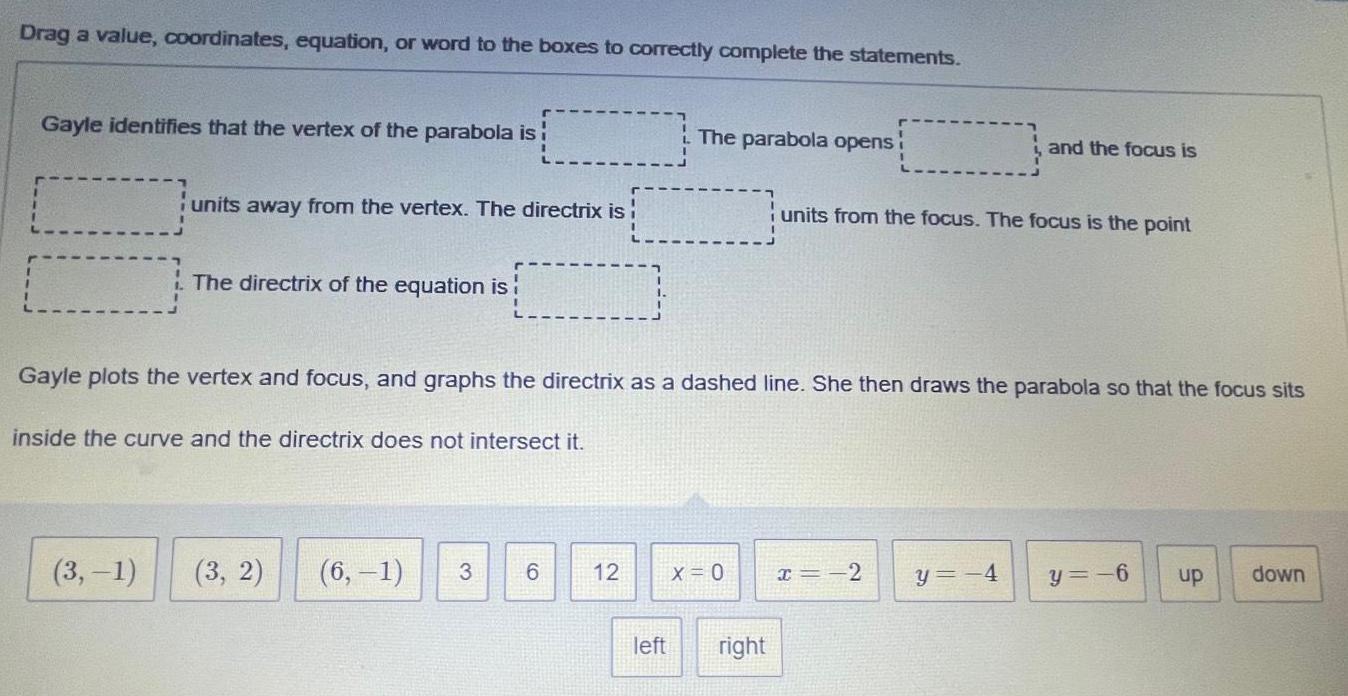
Math
ParabolaDrag a value, coordinates, equation, or word to the boxes to correctly complete the statements.
Gayle identifies that the vertex of the parabola is!
units away from the vertex. The directrix is
(3,-1)
The directrix of the equation is!
(3, 2)
Gayle plots the vertex and focus, and graphs the directrix as a dashed line. She then draws the parabola so that the focus sits
inside the curve and the directrix does not intersect it.

Math
ParabolaThe parabola y = x² +4 has two tangents which pass through the point (0, -4). One is tangent to the parabola at (A, A²+4) and the other at (-A, A² + 4). Find (the positive number) A.
Math
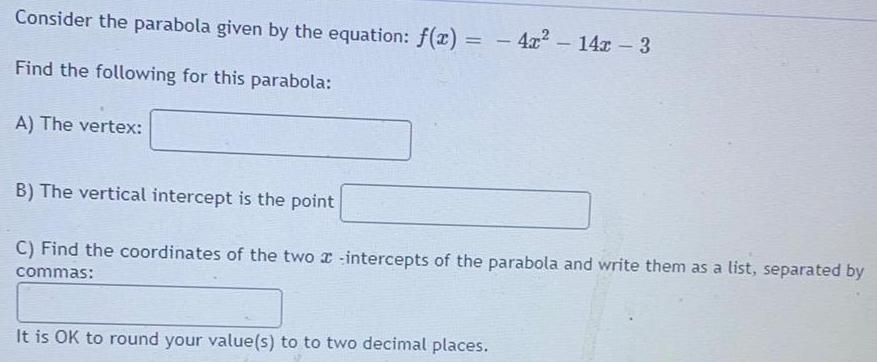
ParabolaConsider the parabola given by the equation: f(x) = - 4x² - 14x - 3
Find the following for this parabola:
A) The vertex:
B) The vertical intercept is the point
C) Find the coordinates of the two intercepts of the parabola and write them as a list, separated by
commas:
It is OK to round your value(s) to to two decimal places.
Math
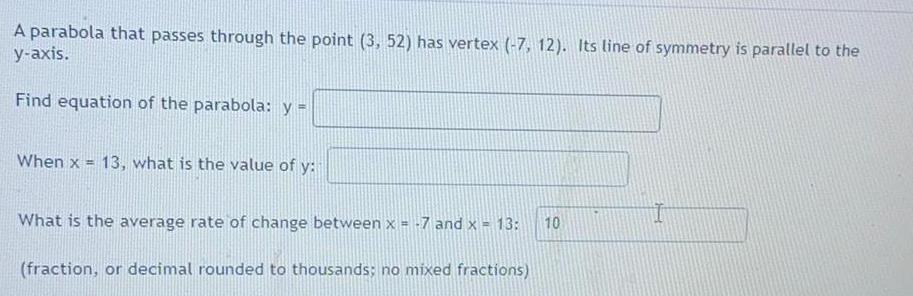
ParabolaA parabola that passes through the point (3, 52) has vertex (-7, 12). Its line of symmetry is parallel to the y-axis.
Find equation of the parabola: y =
When x = 13, what is the value of y:
What is the average rate of change between x = -7 and x = 13:
Math
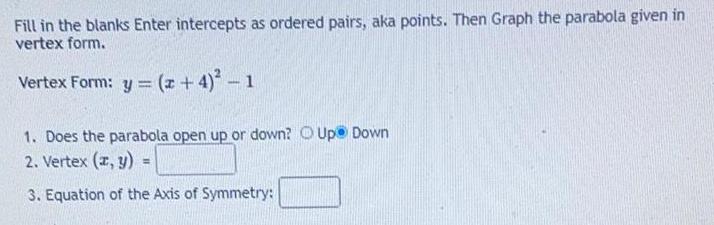
ParabolaFill in the blanks Enter intercepts as ordered pairs, aka points. Then Graph the parabola given in vertex form.
Vertex Form: y = (x + 4)² - 1
1. Does the parabola open up or down? Up Down
2. Vertex (x, y) =
3. Equation of the Axis of Symmetry:
Math
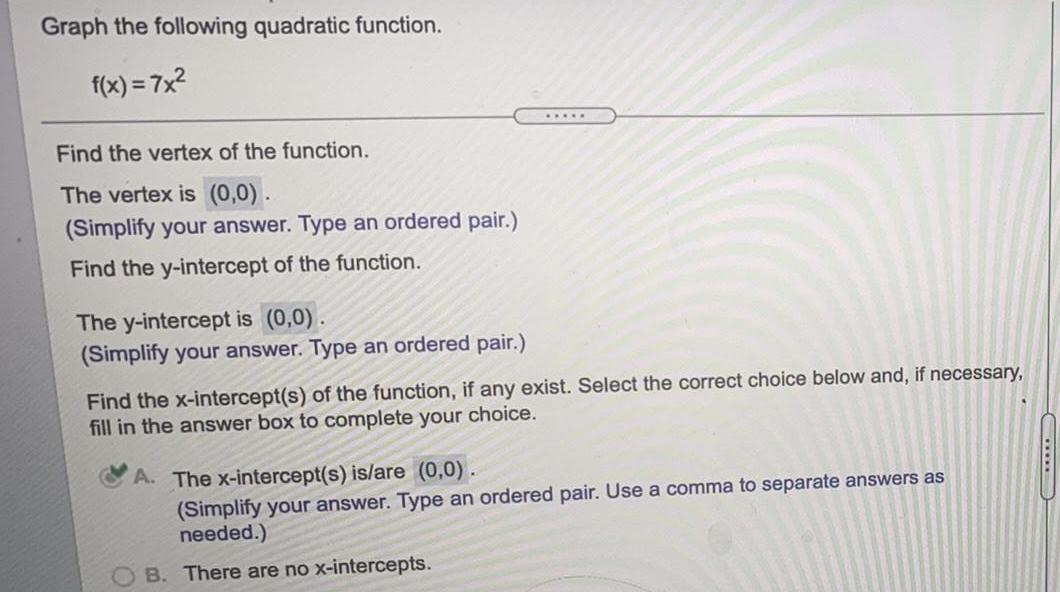
ParabolaGraph the following quadratic function.
f(x) = 7x²
Find the vertex of the function.
The vertex is (0,0).
(Simplify your answer. Type an ordered pair.)
Find the y-intercept of the function.
The y-intercept is (0,0).
(Simplify your answer. Type an ordered pair.)
Find the x-intercept(s) of the function, if any exist. Select the correct choice below and, if necessary,
fill in the answer box to complete your choice.
A. The x-intercept(s) is/are (0,0).
(Simplify your answer. Type an ordered pair. Use a comma to separate answers as
needed.)
B. There are no x-intercepts.
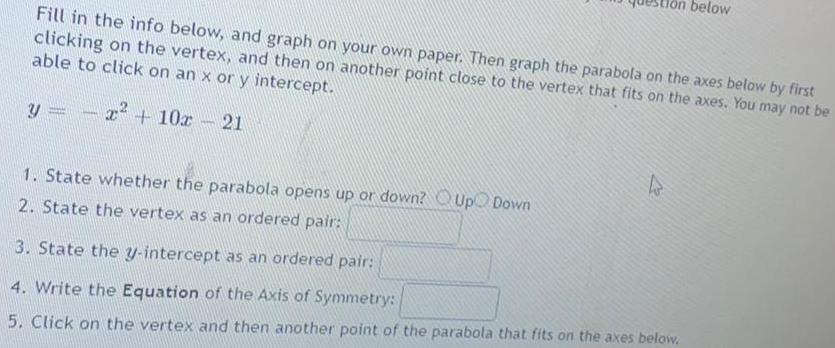
Math
ParabolaFill in the info below, and graph on your own paper. Then graph the parabola on the axes below by first
clicking on the vertex, and then on another point close to the vertex that fits on the axes. You may not be able to click on an x or y intercept.
y = -x² + 10x - 21
1. State whether the parabola opens up or down?
2. State the vertex as an ordered pair:
3. State the y-intercept as an ordered pair:
4. Write the Equation of the Axis of Symmetry:
5. Click on the vertex and then another point of the parabola that fits on the axes below.

Math
ParabolaFind the points of intersection of the graphs of the equations.
x² + y = 19
-4x + y = 14
(x, y)= (smaller x-value)
(x, y) = (larger x-value)

Math
ParabolaIf a parabola opens upward and has x-intercepts at (3, 0) and (-9, 0), what is the equation?
y=a(x+3)(x-9), a < 0
y = a(x-3)(x - 9), a < 0
y = a(x+3)(x-9), a>0
y = a(x-3)(x + 9), a > 0
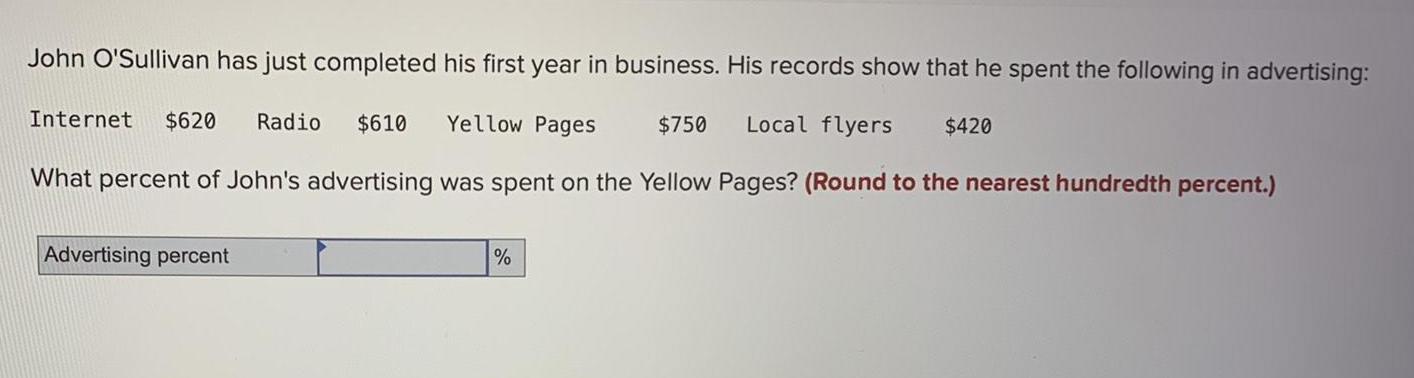
Math
ParabolaJohn O'Sullivan has just completed his first year in business. His records show that he spent the following in advertising:
Internet $620 Radio $610 Yellow Pages $750 Local flyers $420
What percent of John's advertising was spent on the Yellow Pages? (Round to the nearest hundredth percent.)

Math
ParabolaGraph the parabola (do not place any dots) then fill in the blanks about the vertex, any intercepts, the domain, and range. Enter intercepts as ordered pairs, aka points.
y = x² + 10x + 21
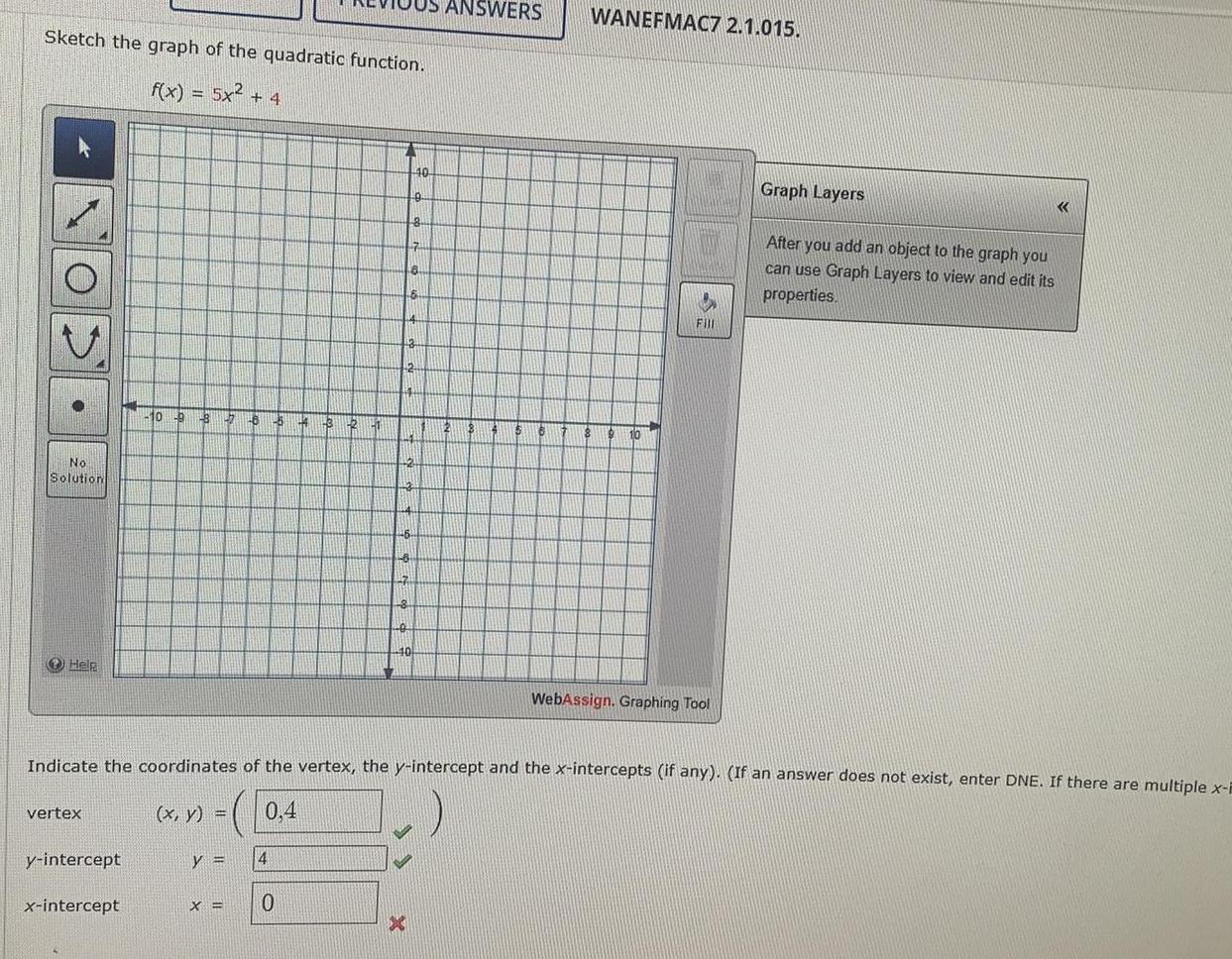
Math
ParabolaSketch the graph of the quadratic function.
f(x) = 5x² + 4
Indicate the coordinates of the vertex, the y-intercept and the x-intercepts (if any). (If an answer does not exist, enter DNE. If there are multiple x-
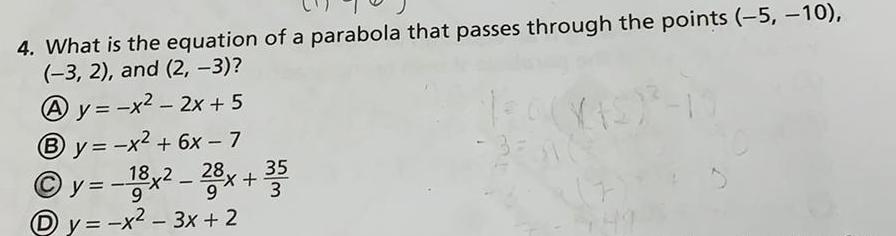
Math
Parabola4. What is the equation of a parabola that passes through the points (-5, -10),
(-3, 2), and (2, -3)?
Ay=-x² - 2x + 5
By=-x² + 6x - 7
Ⓒy=-18x²-28x +35
9
y = -x² - 3x + 2
(7)
5,49