Indefinite Integration Questions and Answers
Math
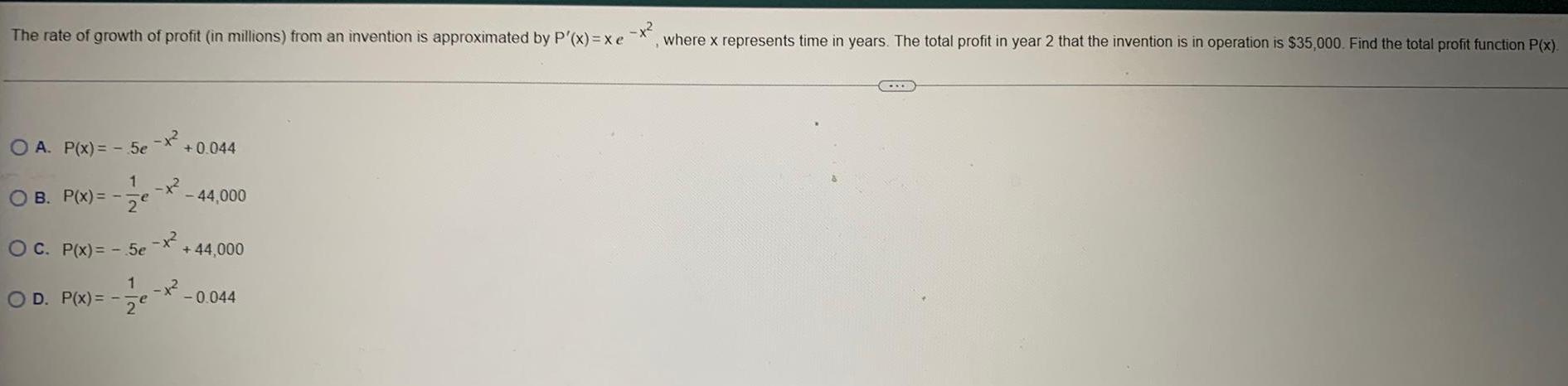
Indefinite IntegrationThe rate of growth of profit (in millions) from an invention is approximated by P'(x)=xe OA. P(x) = -5e 1 OB. P(x) = -- ze OC. P(x) = -5e OD. P(x)=-e -+² -x² 1² +0.044 - 44,000 + 44,000 -0.044 where x represents time in years. The total profit in year 2 that the invention is in operation is $35,000. Find the total profit function P(x).

Math
Indefinite IntegrationEvaluate the following integral using trigonometric substitution.
∫√64-x² dx
Be sure your written work includes your trigonometric substitution (for x, dx) and the conversion back to the original variable.
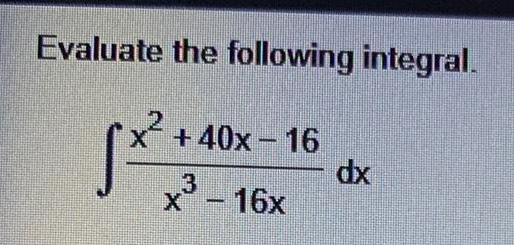
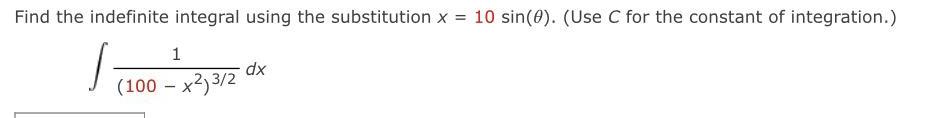
Math
Indefinite IntegrationFind the indefinite integral using the substitution x = 10 sin(θ). (Use C for the constant of integration.)
∫1/(100 - x²)3/2dx

Math
Indefinite IntegrationFind the indefinite integral. (Note: Solve by the simplest method-not all require integration by parts. Use C for the constant of integration.)
∫ xe4x dx

Math
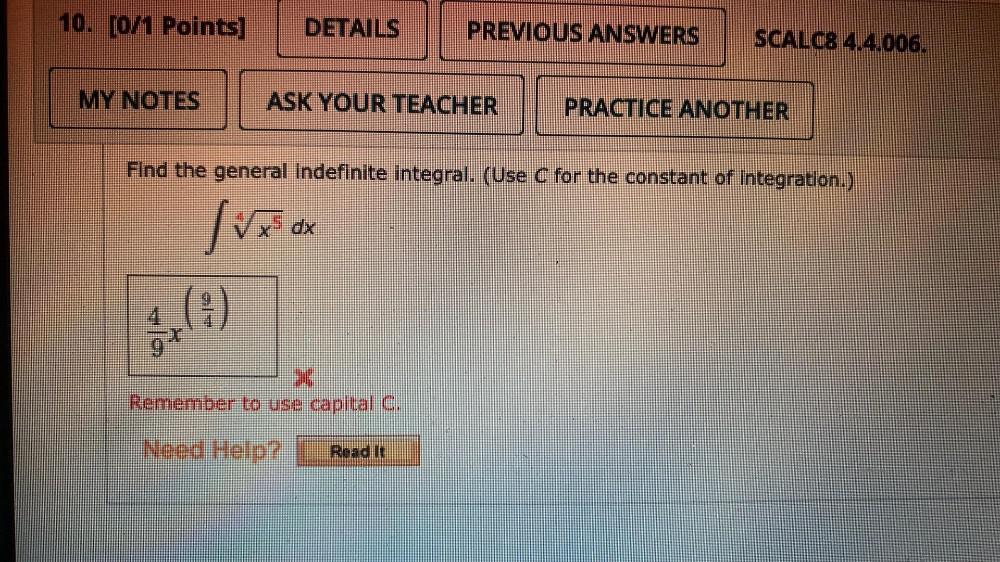
Indefinite IntegrationFind the general indefinite integral. (Use C for the constant Integration.)
∫(x^5)^1/4 dx

Math
Indefinite IntegrationFind the indefinite integral. (Use C for the constant of integration.)
∫eˣ√(1-e²ˣ) dx
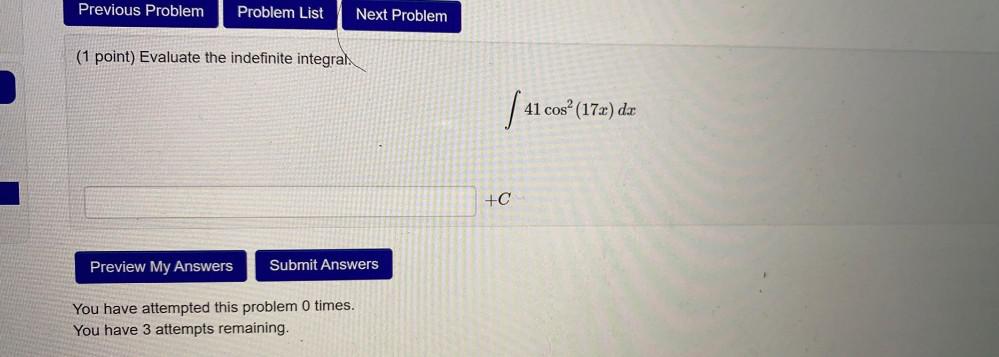

Math
Indefinite IntegrationEvaluate the integral using the fundamental theorem of calculus when appropriate (your answer should be exact. Make sure you use C if needed.):
f(x) = ∫(4x^2 –3x+4+3x-¹-x-^2) da

Math
Indefinite IntegrationA factory is discharging pollution into a lake at the rate of r(t) tons per year given below, where t is the number of years that the factory has been in operation. Find the total amount of pollution discharged during the first 9 years of operation. (Round your answer to two decimal places.)
r(t) = t/ t2 + 1

Math
Indefinite IntegrationFind the general solution of the differential equation. (Use C for the constant of integration.)
dy/dx = 9x² / √(7 + x³)
y =

Math
Indefinite IntegrationFind the indefinite integral and check the result by differentiation.
∫(7x² +1/(3x)² ) dx

Math
Indefinite IntegrationFind the particular solution that satisfies the differential equation and the initial condition.
f'(s) = 18s-8s³,
f(3) = 6
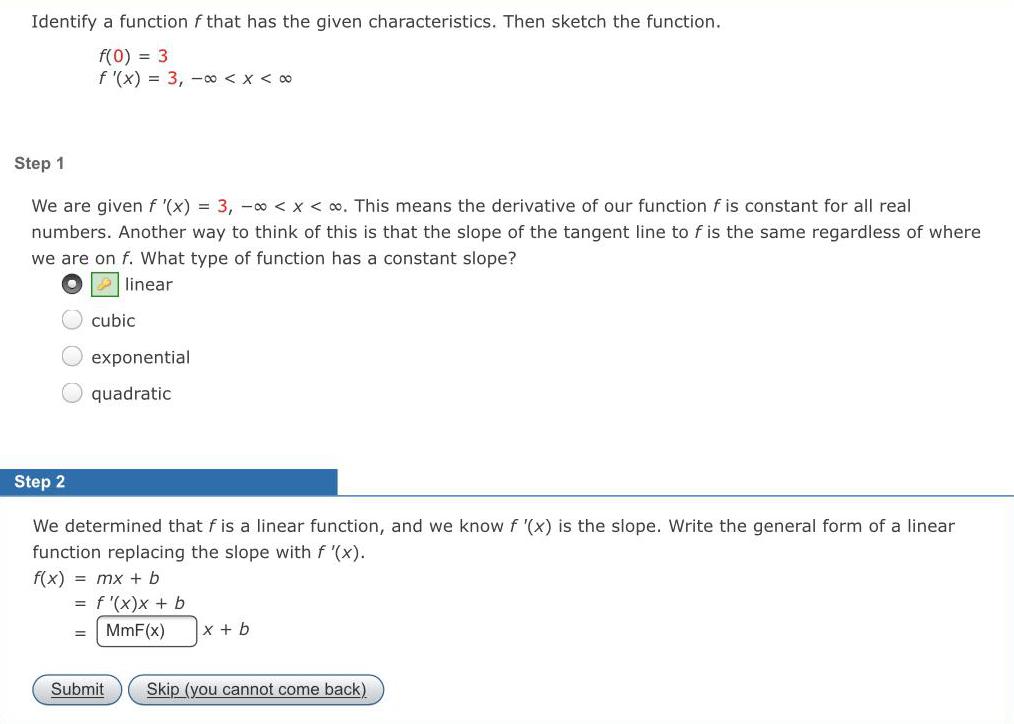
Math
Indefinite IntegrationIdentify a function f that has the given characteristics. Then sketch the function.
f(0) = 3
f'(x) = 3,00 < x < 00
Step 1
We are given f '(x) = 3, -∞0 < x < . This means the derivative of our function f is constant for all real
numbers. Another way to think of this is that the slope of the tangent line to f is the same regardless of where
we are on f. What type of function has a constant slope?
linear
cubic
exponential
quadratic
Step 2
We determined that f is a linear function, and we know f '(x) is the slope. Write the general form of a linear
function replacing the slope with f '(x).
f(x) = mx + b
=
= f'(x) x + b
MmF(x)
Submit
x + b
Skip (you cannot come back)

Math
Indefinite IntegrationFind the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative.)
7x² - 9x + 3
x²
F(x) =
f(x):
=
X>0
-3
-9 ln(x)=³ +7x+C
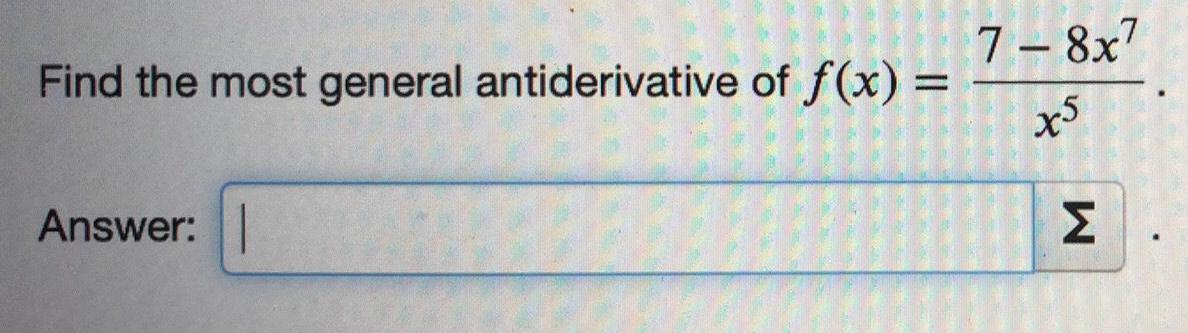

Math
Indefinite Integration5
A curve y = f(x) defined for values of x > 0 goes through the point (1, 0) and is such that the slope of its tangent line at (x, f(x)) is
x > 0.
x²
Find f(x).
f(x) =
Σ,x>0
-
10
x6
1
for

Math
Indefinite IntegrationAn object moves along a coordinate line with acceleration a(t) = (t + 2)³ units per second per second.
The initial velocity is 5 units per second.
The velocity function is v(t) =
The initial position is 7 units to the right of the origin.
The position function is s(t) =
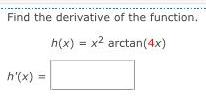
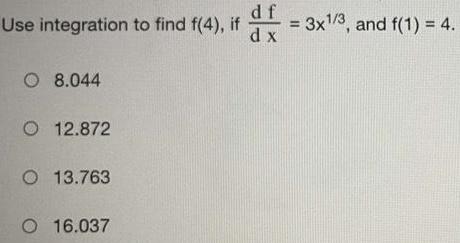
Math
Indefinite IntegrationUse integration to find f(4), if df/dx = 3x^1/3, and f(1)=4.
8.044
12.872
13.763
16.037


Math
Indefinite IntegrationYou wake up one morning, and find yourself wearing a toga and scarab ring. Always a logical person, you conclude that you must have become an Egyptian pharoah. You decide to honor yourself with a pyramid of your own design. You decide it should have height h = 4470 and a square base with side S = 1210 To impress your Egyptian subjects, find the volume of the pyramid using integration.
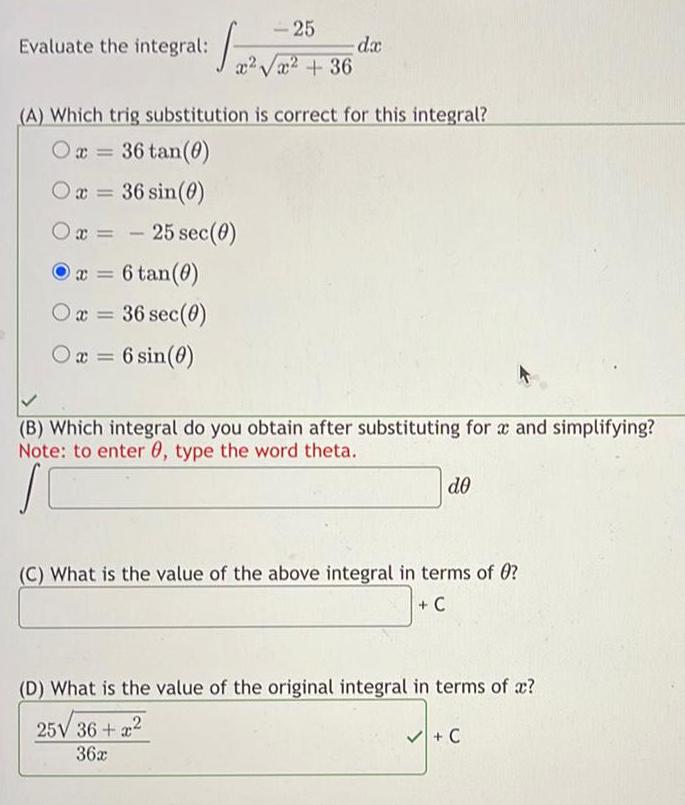
Math
Indefinite IntegrationEvaluate the integral:
∫ -25 / (x²√(x²+36) dx
(A) Which trig substitution is correct for this integral?
x= 36 tan(θ)
x= 36 sin(θ)
x= -25 sec (θ)
x = 6 tan(θ)
x = 36 sec (θ)
x = 6 sin(θ)
(B) Which integral do you obtain after substituting for x and simplifying?
(C) What is the value of the above integral in terms of θ?
(D) What is the value of the original integral in terms of x?

Math
Indefinite IntegrationFor any time t>0, the acceleration of a particle is given by a(t) = 1 +3/√t
A) The velocity at a general time t> 0 is v(t)=
B) Now suppose the particle has velocity v = -20 when t= 1. The velocity of the particle when t = 16 is
Enter an exact number. No decimal approximations.

Math
Indefinite IntegrationThe temperature at time t hours is T(t) = -0.3t² + 4t + 50 (for 0 ≤ t ≤ 12). Find the average temperature between time 0 and time 10.
![A certain vehicle can accelerate from a standing start to a speed of v(t) = -0.27t² + 12t feet per second after t seconds (for
0 ≤ t < 30).
(a)
Find a formula for the distance that it will travel from its starting point in the first t seconds. [Hint: Integrate velocity to find
distance, and then use the fact that distance is 0 at time t = 0.]
D(t) =
(b) Use the formula that you found in part (a) to find the distance (in ft) that the car will travel in the first 10 seconds. (Round
your answer to the nearest whole number.)
D(10) =
ft](https://media.kunduz.com/media/sug-question/raw/61091600-1657300971.627181.jpeg?w=256)
Math
Indefinite IntegrationA certain vehicle can accelerate from a standing start to a speed of v(t) = -0.27t² + 12t feet per second after t seconds (for
0 ≤ t < 30).
(a)
Find a formula for the distance that it will travel from its starting point in the first t seconds. [Hint: Integrate velocity to find
distance, and then use the fact that distance is 0 at time t = 0.]
D(t) =
(b) Use the formula that you found in part (a) to find the distance (in ft) that the car will travel in the first 10 seconds. (Round
your answer to the nearest whole number.)
D(10) =
ft

Math
Indefinite IntegrationLet f be the function with derivative defined by f '(x) = cos(x2) on the interval -2<x<2. How many points of inflection does the graph of f have on this interval?
1
2
3
4
1