Definite Integrals Questions and Answers

Math
Definite Integralset R be the region bounded by the following curves Use the shell method to find the volume of the solid generated when R is revolved about the x axis x x 0 and y 11 Set up the integral that gives the volume of the solid Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your Choice Type an exact answer OA Sody O B JO
Math
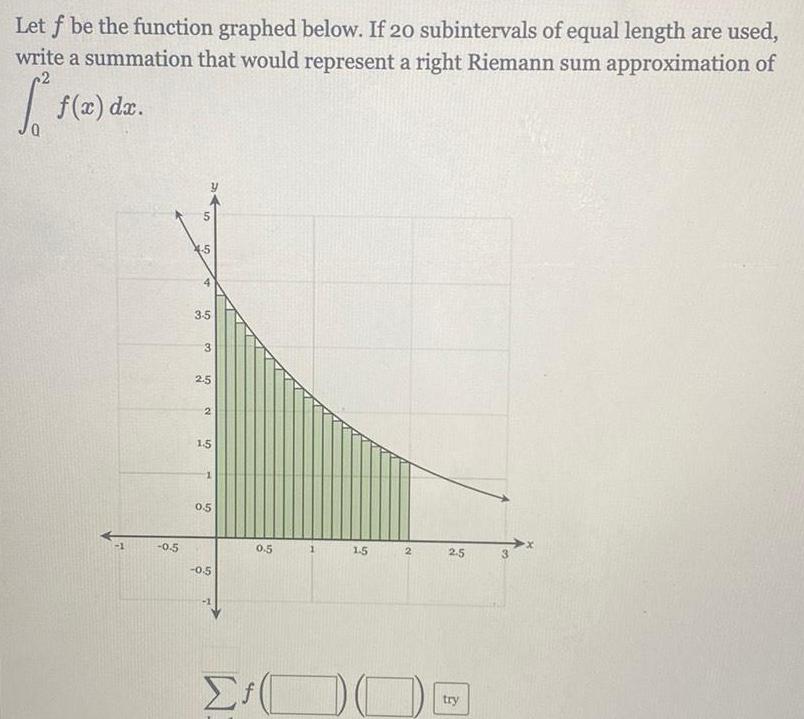
Definite IntegralsLet f be the function graphed below If 20 subintervals of equal length are used write a summation that would represent a right Riemann sum approximation of 2 f x dx 0 5 5 4 5 3 5 3 2 5 2 1 5 0 5 0 5 0 5 1 1 5 DO 2 2 5 try 3
Math
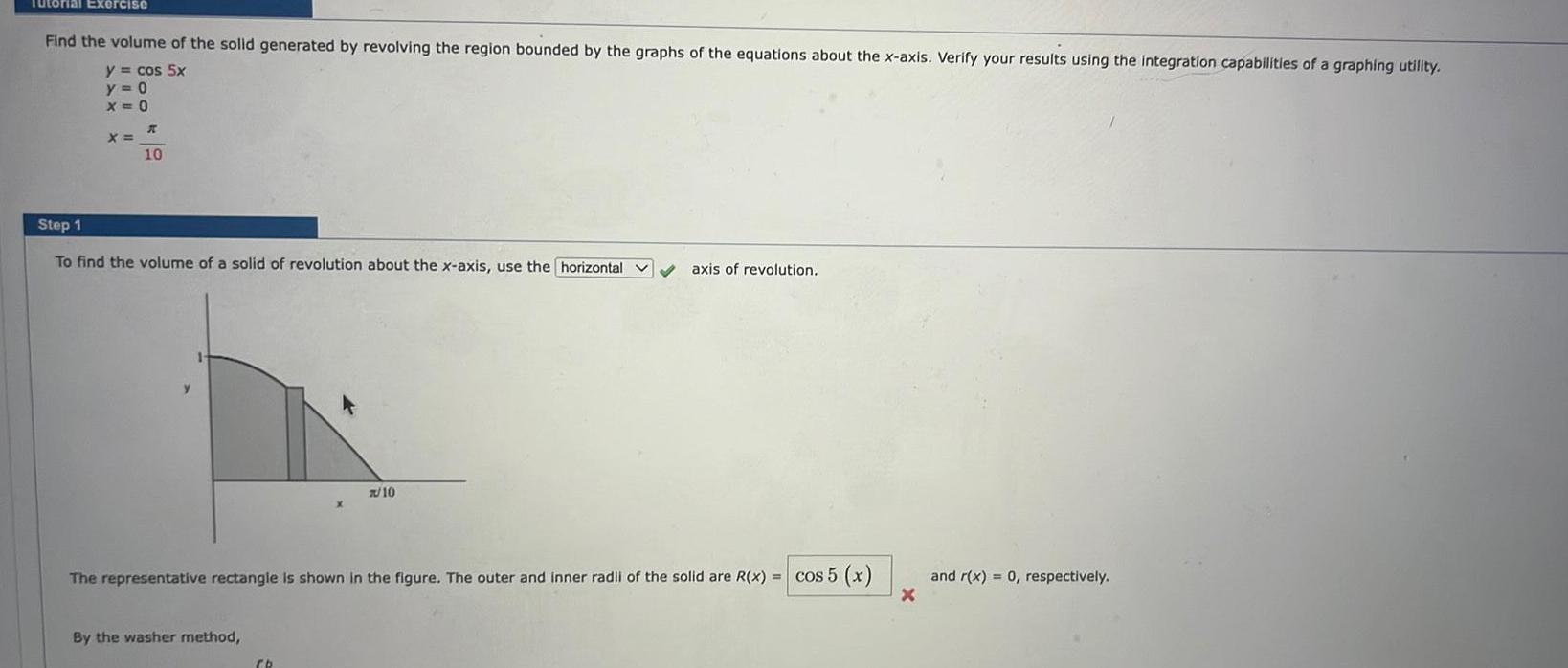
Definite IntegralsTutorial Exercise Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x axis Verify your results using the integration capabilities of a graphing utility y cos 5x y 0 X 0 X K 10 Step 1 To find the volume of a solid of revolution about the x axis use the horizontal By the washer method 7 10 The representative rectangle is shown in the figure The outer and inner radii of the solid are R x cos 5 x Cb axis of revolution X and r x 0 respectively
Math
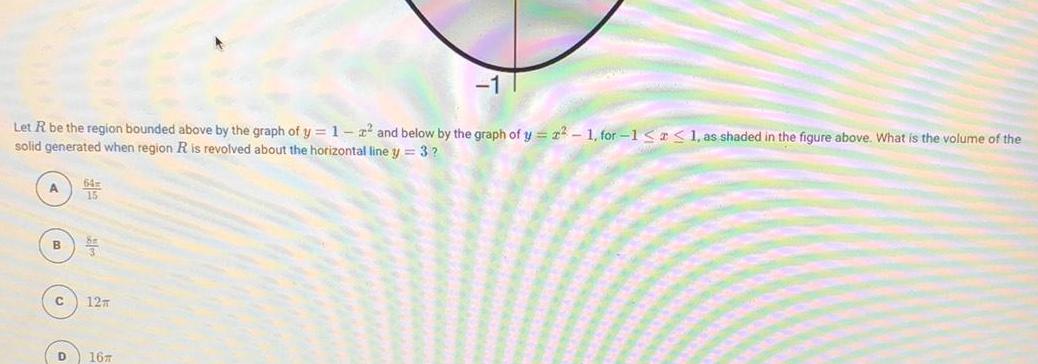
Definite IntegralsLet R be the region bounded above by the graph of y 1 2 and below by the graph of y 22 1 for 1 1 as shaded in the figure above What is the volume of the solid generated when region R is revolved about the horizontal line y 3 A 15 C 35 12m D 16

Math
Definite IntegralsUse the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about y = 8.
64y=x^3, y=0, x=8

Math
Definite IntegralsFind the volume generated by rotating the area bounded by the graph of the following set of equations around the y-axis.

Math
Definite IntegralsA particle is moving with acceleration given by a(t) = 6t-12 and an initial velocity of 9 m/s.
(a) Find the velocity of the particle at time t.
(b) Find the velocity of the particle after 3 seconds.
(c) When is the particle at rest?
(d) When is the particle moving in the positive direction?
(e) Find the total displacement of the particle during the first 8 seconds.
(f) Find the total distance travelled by the particle during the first 8 seconds.

Math
Definite IntegralsThe infectivity of a certain pathogen is quantified by measuring the area between two curves. The greater the area between the curves, the greater the infectivity of the disease and this quantification provides a means to compare infectivity among various different pathogens. As an example, consider the function f(t) = -0.5t(t + 1)(t - 21) which represents number of infected cells carrying a particular pathogen in the blood of a patient as a function of time t, where t is measured in days. Suppose a patient is considered contagious during the period from time t = 3 days to t = 18 days. Compute the infectivity of this particular disease during the contagious period by finding the area between the function f(t) and the line segment connecting the points (3,f(3)) and (18,f(18)). Include a graph of the area computed.
Algebra
Definite IntegralsRefer to the figure and find the volume generated by rotating the given region about the specified line.
Math
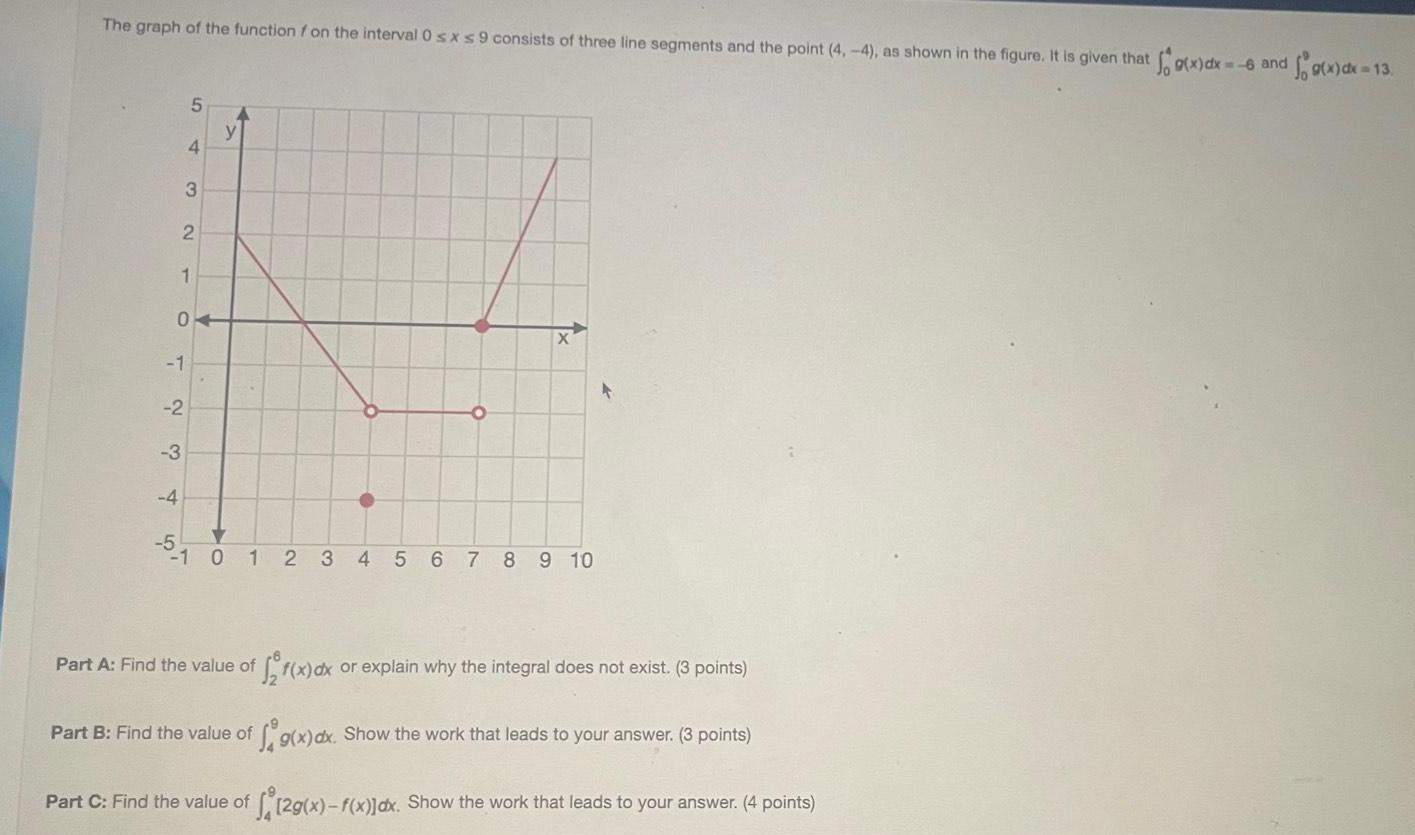
Definite IntegralsThe graph of the function f on the interval 0 s x s9 consists of three line segments and the point (4,-4), as shown in the figure. It is given that
Sog(x) dx =
Find the value of
Part B: Find the value of
Part C: Find the value of
f5₂f(x) dx or explain why the integral does not exist. (3 points) g(x) dx. Show the work that leads to your answer.

Math
Definite IntegralsA graph consists of the line y=5 for 1 sxs 5 and y=-1 for-3 sxs 1. Find the accumulation of change under the curve from x=-3 to x = 5 using geometric formule
-4 square units
4 square units
16 square units
24 square units
![Let x)=x², and compute the Riemann sum off over the interval [4, 51, choosing the representative points to be the midpoints of the subintervals and using the following number of subintervals
(n). (Round your answers to two decimal places.)
(a) two subintervals of equal length (n=2)
(b) five subintervals of equal length (n = 5)
(c) ten subintervals of equal length (n = 10)
(d) Can you guess at the area of the region under the graph of fon the interval [4, 5]?](https://media.kunduz.com/media/sug-question/raw/77311801-1660454184.3500469.jpeg?w=256)
Math
Definite IntegralsLet x)=x², and compute the Riemann sum off over the interval [4, 51, choosing the representative points to be the midpoints of the subintervals and using the following number of subintervals
(n). (Round your answers to two decimal places.)
(a) two subintervals of equal length (n=2)
(b) five subintervals of equal length (n = 5)
(c) ten subintervals of equal length (n = 10)
(d) Can you guess at the area of the region under the graph of fon the interval [4, 5]?

Math
Definite IntegralsHow long will it take the bar to reach 99° C? (Round your answer to one decimal place.)
sec
A small metal bar, whose initial temperature was 30° C, is dropped into a large container of boiling water. How long will it take the bar to reach 80° C if it is known that its
temperature increases 2° during the first second? (The boiling temperature for water is 100° C. Round your answer to one decimal place.)
sec

Math
Definite IntegralsThe curve y² = x, the line x = 2, and the x-axis form the sides of the bounded region. Find the volume of the solid generated by revolving about the x-axis.
A π/2
B π/4
C 2π
D π

Math
Definite IntegralsThe volume produced by revolving about the x-axis the region above the curve y= x³, below the
line y = 1 and between x = 0 and x = 1 is ...
A π/42
B π/7
C √2/2π
D 6π/7

Math
Definite IntegralsUse a double integral in polar coordinates to find the volume V of the solid bounded by the graphs of the equations.
z =√x² + y²
z = 0
x² + y²= 4

Math
Definite IntegralsSet up a triple integral for the volume of the solid. Do not evaluate the integral.
The solid in the first octant bounded by the coordinate planes and the plane z = 5 - x - y

Math
Definite IntegralsFor the regions bounded by y = 6cosx and y= 1/3x²-7
Part A: Find the limits of integration. (10 points)
Part B: Write an expression representing the total area. (10 points)
Part C: Solve for the total area. (10 points)

Math
Definite IntegralsFind the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis. Verify your results using the integration capabilities of a graphing utility.
y = cos 3x
y = 0
X = 0
X =π/6

Math
Definite IntegralsThe traffic flow rate (cars per hour) across an intersection is r(t) = 500 + 600t - 120t^2, where t is in hours, and t=0 is 6am. How many cars pass through the intersection between 6 am and 8 am?

Math
Definite IntegralsIf a cup of coffee has temperature 92°C in a room where the ambient air temperature is 21°C, then, according to Newton's Law of Cooling, the
temperature of the coffee after t minutes is T(t) = 21 + 71e^-t /45. What is the average temperature of the coffee during the first 32 minutes?
Math
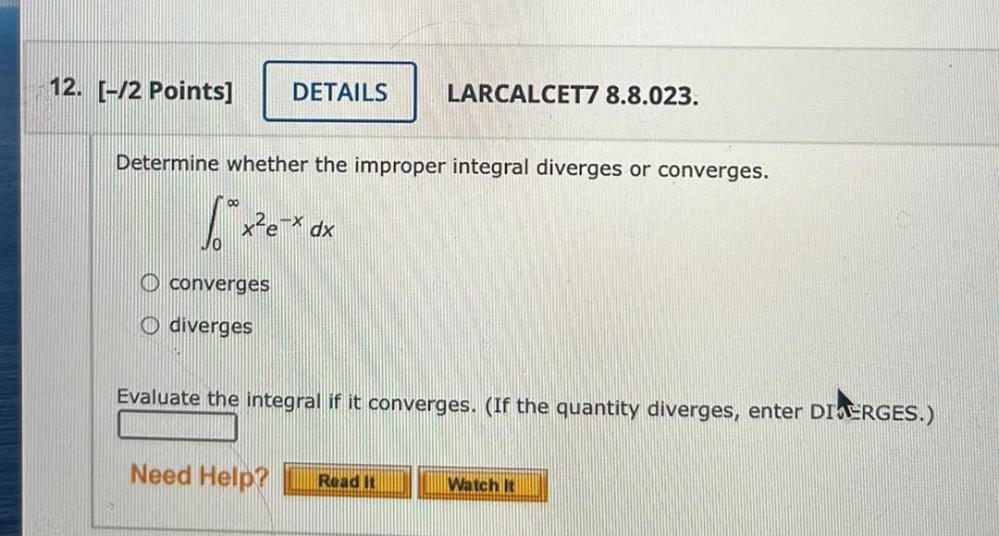
Definite IntegralsDetermine whether the improper integral diverges or converges.
∞
∫ x^2(e^-x)dx
0
a) converges
b) diverges
Evaluate the integral if it converges. (If the quantity diverges, enter DIVERGES.)
Math
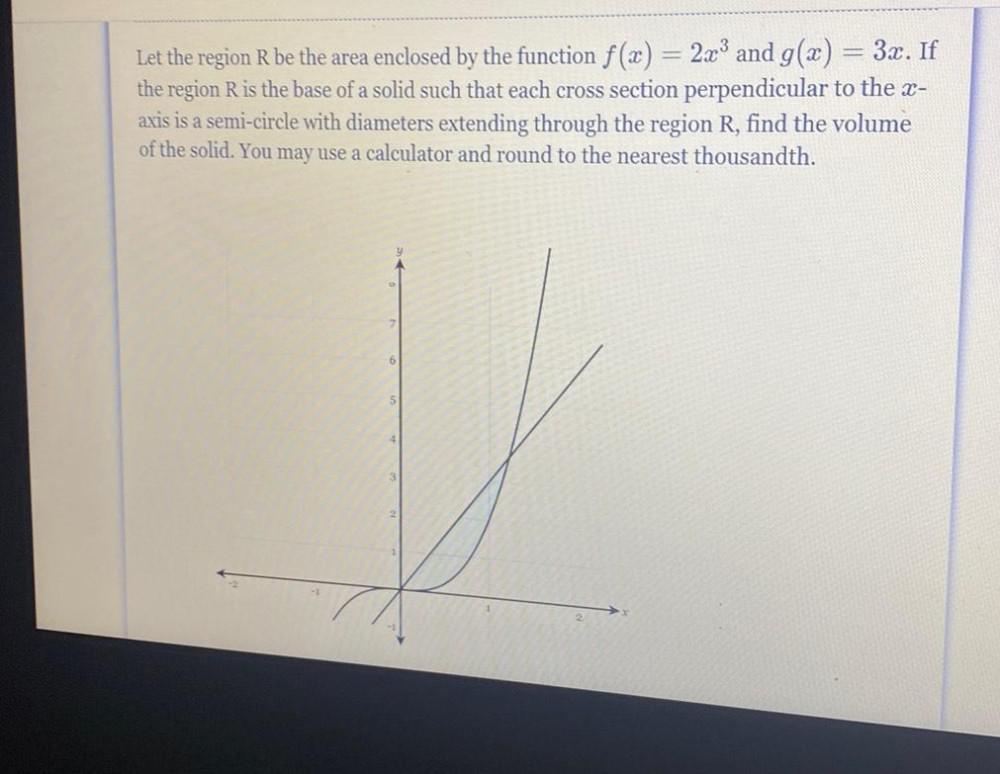
Definite IntegralsLet the region R be the area enclosed by the function f(x) = 2x³ and g(x) = 3x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is a semi-circle with diameters extending through the region R, find the volume of the solid.
Math
Definite IntegralsThe water level of a certain body of water is changing at a rate of W(t)=(3/4)cos(4-t/2) inches per hour, where t represents hours since 12 a.m.
A): Using correct units, explain the meaning of ∫w(t)dt in terms of the context of this problem.
B): Write the integral that represents the number of inches that the water level changes from 7 p.m. to midnight
C): Use your calculator to evaluate your integral from Part B. Explain the meaning of the answer in terms of the context. )
D): What is the average hourly number of inches that the water level changes for this lake in one day?

Math
Definite IntegralsEvaluate each integral using the definition of the definite integral with right endpoints (given in Theorem 4 of the book) and taking the limit.
(a) ∫₀³ (x² +2x-5)dx
(b) ∫₁⁵ x³ dx
Δx=b-a/n=
xi=a+iΔx=

Math
Definite IntegralsIn 1970 the population of the United States was 203 million. Ten years later, in 1980, the population of the United States was 226 million.
Write a function for the exponential growth of population in the U.S. using:
● t(0) = 203
● t(10) = 226
Write your answer in the space provided.

Math
Definite IntegralsA tank that is 8 feet deep, with a square bottom with sides 4 feet each, has
1 foot of water that weighs 62.3 lb/ft³ in it.
How much work, to the nearest whole unit (in ft-lb), will it take to pump the
water to the rim of the tank?
Math
Definite IntegralsA construction worker, 36 feet up on a scaffold, lifts a 4-lb rope hand over hand up to the scaffold to raise a cement block weighing 8 pounds off the ground. (Assume the rope is 36 feet long.) How much work (in ft-lb) is required to pull the rope and the block up to the scaffolder?
![Consider the function f(x) = − 1/2x²+2x+8.
What is the overestimate of the area under the curve of f using rectangular approximations on the interval [-2, 4] with three equal subintervals?
Note: Round to the nearest whole number.](https://media.kunduz.com/media/sug-question/raw/46494464-1658300780.1044607.jpeg?w=256)
Math
Definite IntegralsConsider the function f(x) = − 1/2x²+2x+8.
What is the overestimate of the area under the curve of f using rectangular approximations on the interval [-2, 4] with three equal subintervals?
Note: Round to the nearest whole number.

Math
Definite IntegralsA particle moves along a line so that its velocity at time t is v (t) = t² + 3t - 11 in meters per second.
Find the displacement of the particle (in meters) during the time period 0 ≤ t ≤7.

Math
Definite IntegralsIf a cup of coffee has temperature 93°C in a room where the ambient air temperature is 20°C, then, according to Newton's Law of Cooling, the temperature of the coffee after t minutes is T(t) = 20 + 73e-t/45. What is the average temperature of the coffee during the first 22 minutes?
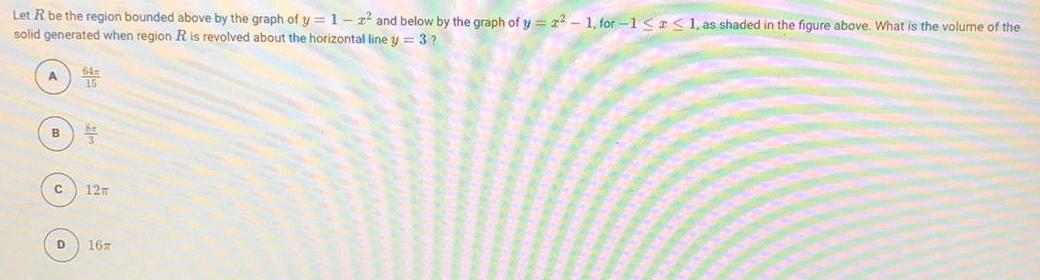
Math
Definite IntegralsLet R be the region bounded above by the graph of y = 1-² and below by the graph of y= 2²-1, for-1 ≤ ≤ 1, as shaded in the figure above. What is the volume of the solid generated when region R is revolved about the horizontal line y = 3?
A 64π/15
B 8π/3
C 12π
D 16π

Math
Definite IntegralsCREDIT CARDS IN CHINA The total number of credit cards issued in China from 2009 through 2012 grew at the rate of
r(t) = 153e0.21t (1 ≤1≤4)
million/year, where (t = 1) corresponds to 2009. What was the average growth in the number of credit cards issued in China for the period under consideration?

Math
Definite IntegralsCONCENTRATION OF A DRUG IN THE BLOODSTREAM The concen- tration of a certain drug in a patient's bloodstream thr after injection is
C (t) = = 0.2t / t² + 1 mg/cm³.
Determine the average concentration of the drug in the patient's bloodstream over the first 4 hr after the drug is injected.
Math
Definite Integrals-X Answer the following questions about the function whose derivative is f'(x) = (x+3) e ¯X.
a. What are the critical points of f?
b. On what open intervals is f increasing or decreasing?
c. At what points, if any, does f assume local maximum and minimum values?
a. Find the critical points, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The critical point(s) of f is/are x = (Simplify your answer. Use a comma to separate answers as needed.)
B. The function f has no critical points.

Math
Definite IntegralsAIR PURIFICATION To test air purifiers, engineers ran a purifier in a smoke-filled 10-ft X 20-ft room. While con- ducting a test for a certain brand of air purifier, they
determined that the amount of smoke in the room was decreasing at the rate of
R(t) = 0.00032t4 -0.01872t³ + 0.39481²
- 3.83t+ 17.63 (0 ≤t≤20)
percent of the (original) amount of the smoke per minute, t min after the start of the test. How much smoke was left in the room 5 min after the start of the test? 10 min after the start of the test?

Math
Definite IntegralsUsing rectangles each of whose height is given by the value of the function at the midpoint of the rectangle's base (the midpoint rule), estimate the area under the graph of the following function, using first two and then four rectangles.
f(x)= 5/x between x = 2 and x = 6
Using two rectangles, the estimate for the area under the curve is
(Round to three decimal places as needed.)
![Let Ln denote the left - endpoint sum u sing n subintervals and let Rn denote the corresponding right - endpoint sum. In the following exercises, compute the indicated left and right sums for the
given functions on the indicated interval. L4 for f(x) =1/x²+1 on [-2, 2]. Write your answer to two decimal places.](https://media.kunduz.com/media/sug-question/raw/59892907-1658209855.7992141.jpeg?w=256)
Math
Definite IntegralsLet Ln denote the left - endpoint sum u sing n subintervals and let Rn denote the corresponding right - endpoint sum. In the following exercises, compute the indicated left and right sums for the
given functions on the indicated interval. L4 for f(x) =1/x²+1 on [-2, 2]. Write your answer to two decimal places.

Math
Definite IntegralsThe marginal revenue function for Hedgemony, a bush planting service, is given by r(x) = 31 - 0.2x dollars per plant, when x bushes are planted. Find the change in revenue for the first 97 bushes planted. (Round your answer to the nearest cent.)

Math
Definite IntegralsWrite and evaluate the definite integral that represents the area of the surface generated by revolving the curve on the indicated
interval about the y-axis. (Round your answer to three decimal places.)
y = x²/2 +6₁
0≤x≤5

Math
Definite Integrals7. Set up, but do not simplify or evaluate, the integrals to find the volumes of the solids obtained by rotating the region bounded by the curves y = x and y = x² about the following lines. Use whichever method your prefer; clearly specify which method you use for each solid.
(a) The x-axis.
(b) The y-axis.
(c)y = 2

Math
Definite IntegralsSet up, but do not simplify or evaluate, the integrals to find the volumes of the solids obtained by rotating the region bounded by the curves y = x and y = x² about the following lines. Use whichever method your prefer; clearly specify which method you use for each solid.
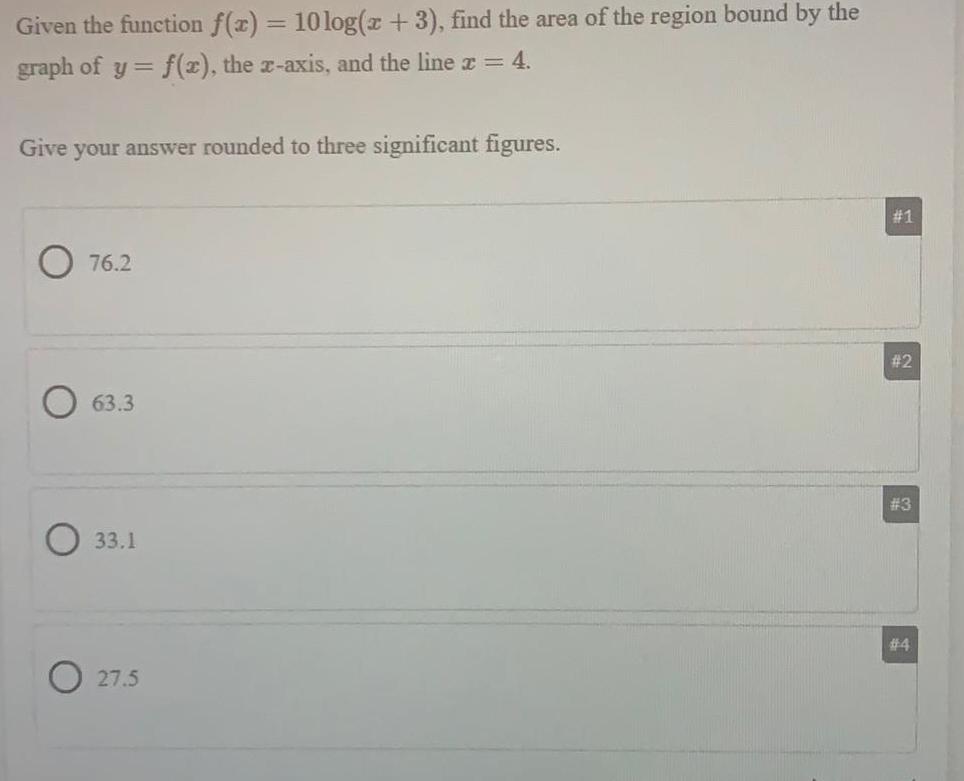
Math
Definite IntegralsGiven the function f(x) = 10log(x + 3), find the area of the region bound by the graph of y= = f(x), the x-axis, and the line x = 4. Give your answer rounded to three significant figures.
76.2
63.3
33.1
27.5
![What is the exact volume of a solid that is formed by rotating the area
between the functions f (x) = 4x + 2 and g(x) = 2x + 2
about the x-axis on the interval [0, 3]?
Note: Maintain fractions if applicable.](https://media.kunduz.com/media/sug-question/raw/53454558-1657919229.420172.jpeg?w=256)
Math
Definite IntegralsWhat is the exact volume of a solid that is formed by rotating the area
between the functions f (x) = 4x + 2 and g(x) = 2x + 2
about the x-axis on the interval [0, 3]?
Note: Maintain fractions if applicable.
![Use the cylindrical shell method to calculate the approximate volume
of the solid formed by rotating the graph of f (x) =−x² + 5x
about the y-axis on the interval [0, 5].
Note: Round to the nearest hundredth.](https://media.kunduz.com/media/sug-question/raw/53454577-1657916985.7862957.jpeg?w=256)
Math
Definite IntegralsUse the cylindrical shell method to calculate the approximate volume
of the solid formed by rotating the graph of f (x) =−x² + 5x
about the y-axis on the interval [0, 5].
Note: Round to the nearest hundredth.

Math
Definite IntegralsA satellite radio station is launching an advertising campaign in order to increase the number of
daily listeners. The station currently has 27000 daily listeners, and management experts the
numbers of the daily listeners, S(t), to grow at a rate of S'(t) = 60t1/2 listeners per day, where
t is the number of days since the campaign began. How long should the campaign last if the
station wants the number of daily listeners to grow to 41000?

Math
Definite Integrals2.) (3 pts) Let R be the region in the first quadrant bounded only by
the lines y = 0, z + y = 10 and the curve y = ï³. After sketching the
region, determine its type (either dydr or drdy, but not both). Use
this information to set up and calculate a double integral for the area of
R. As this problem asks for area, you will be integrating the function
(constant) 1 over R.

Math
Definite IntegralsAssume that sin(x) equals its Maclaurin series for all x.
Use the Maclaurin series for sin(4x²) to evaluate the
integral
0.65
sin(4x²) dx
Your answer will be an infinite series. Use the first two
terms to estimate its value.
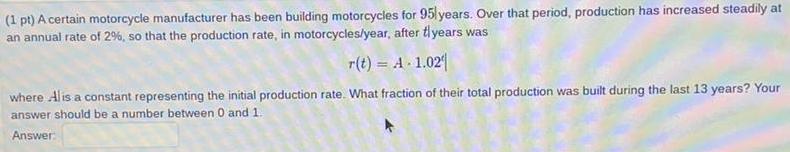
Math
Definite Integrals(1 pt) A certain motorcycle manufacturer has been building motorcycles for 95 years. Over that period, production has increased steadily at
an annual rate of 2%, so that the production rate, in motorcycles/year, after flyears was
r(t) = A - 1.02
where Alis a constant representing the initial production rate. What fraction of their total production was built during the last 13 years? Your
answer should be a number between 0 and 1.
Answer:

Math
Definite IntegralsThe graph of the velocity of a car accelerating from rest to a speed of 90 km/h over a period of 30 seconds is shown. Use this graph and a midpoint Riemann sum with six equal subintervals to estimate the distance traveled (in km) by the car during this time period.