Matrices & Determinants Questions and Answers

Math
Matrices & DeterminantsSome ecologists divided a female bird population into three categories juvenile up to 1 yr old subadult 1 to 2 yr old and adult over 2 yr old They concluded hat the change in the makeup of the bird population in successive years could be described by the matrix equation below The numbers in the column matrices give the numbers of females in the three age groups after n years and n 1 years n 1 Sn 1 an 1 0 0 31 0 0 0 0 72 0 95 0 0 20 In Sn an a Suppose there are currently 920 juveniles 280 subadults and 2800 adults Determine the total number of female birds for each of the next 5 years In the first year there will be female birds Do not round until the final answer Then round to the nearest whole number as needed
Math
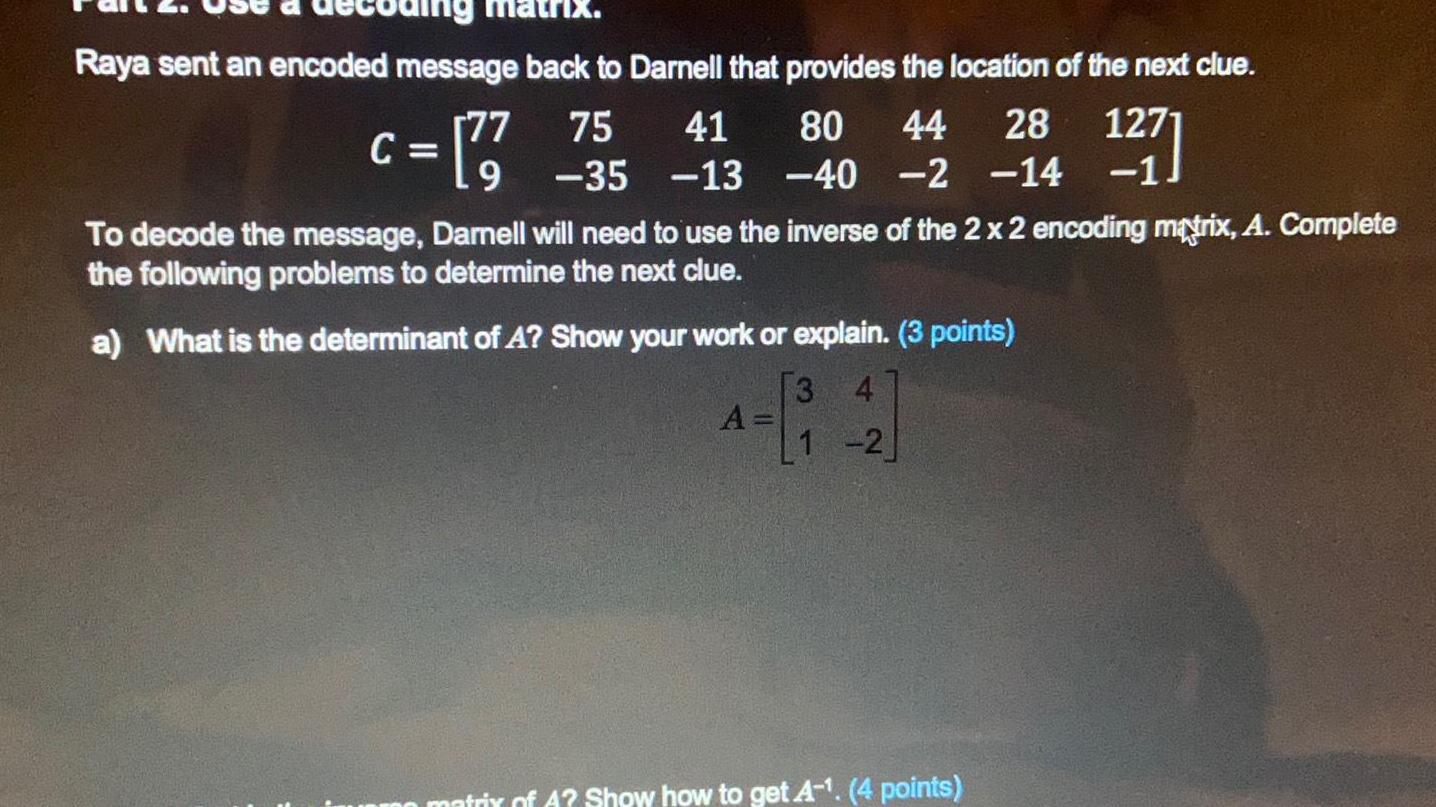
Matrices & DeterminantsRaya sent an encoded message back to Darnell that provides the location of the next clue 28 1271 41 80 44 C 77 755 13 240 2 14 1 To decode the message Darnell will need to use the inverse of the 2 x 2 encoding matrix A Complete the following problems to determine the next clue a What is the determinant of A Show your work or explain 3 points 3 4 1 2 A matrix of A Show how to get A 4 points
Math
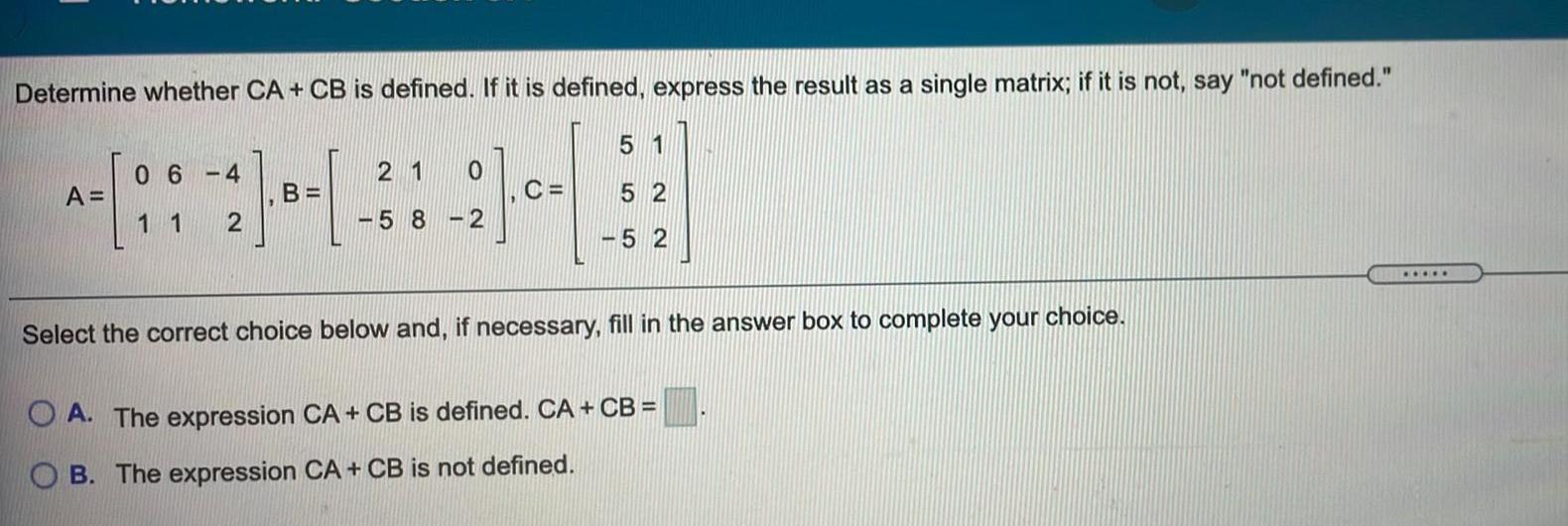
Matrices & DeterminantsDetermine whether CA CB is defined If it is defined express the result as a single matrix if it is not say not defined 44 B 2 A 06 4 11 5 1 C 52 52 21 58 2 21 0 Select the correct choice below and if necessary fill in the answer box to complete your choice A The expression CA CB is defined CA CB B The expression CA CB is not defined
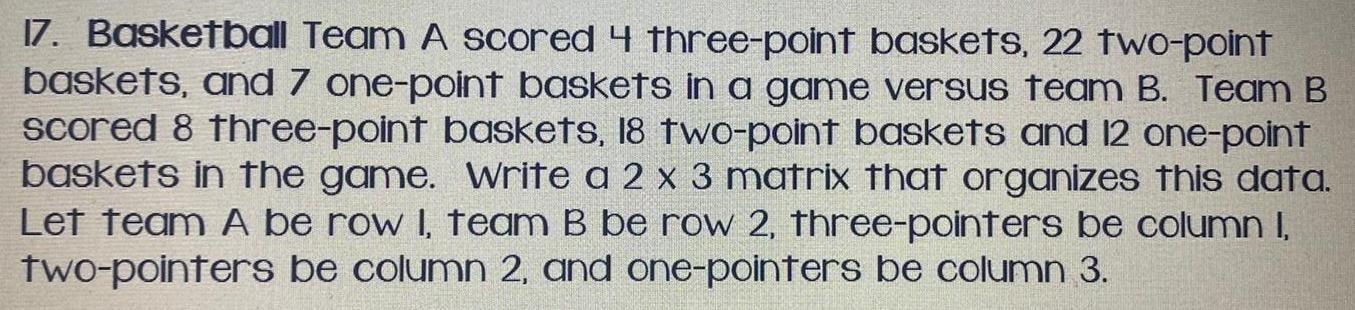
Math
Matrices & Determinants17. Basketball Team A scored 4 three-point baskets, 22 two-point baskets, and 7 one-point baskets in a game versus team B. Team B scored 8 three-point baskets, 18 two-point baskets and 12 one-point baskets in the game. Write a 2 x 3 matrix that organizes this data. Let team A be row I, team B be row 2, three-pointers be column I, two-pointers be column 2, and one-pointers be column 3.

Math
Matrices & DeterminantsDetermine the values of a for which the system has no solutions, exactly one solution, or infinitely many solutions.
x + 3y - 2z = 4
3x - y + 2z = 3
5x + 5y + (a²-11)z = a +8

Math
Matrices & DeterminantsFind the coordinate matrix of p relative to the standard basis for P3.
p = 17 + 118x + 3x²

Math
Matrices & DeterminantsConsider the following system of equations.
x+y+z=1
2x + 2y = 6
3x + 4y -z = 13
a) Write the system as an augmented matrix.
buse row operations to write the augmented matrix from part (a) in row echelon form. Show your
work, clearly label each row operation used.
c) Using your final matrix from part (b), solve for the values of x, y, and z for the solution to the system of
equations. Write your solution. If the system has no solution, write "inconsistent'".
Math
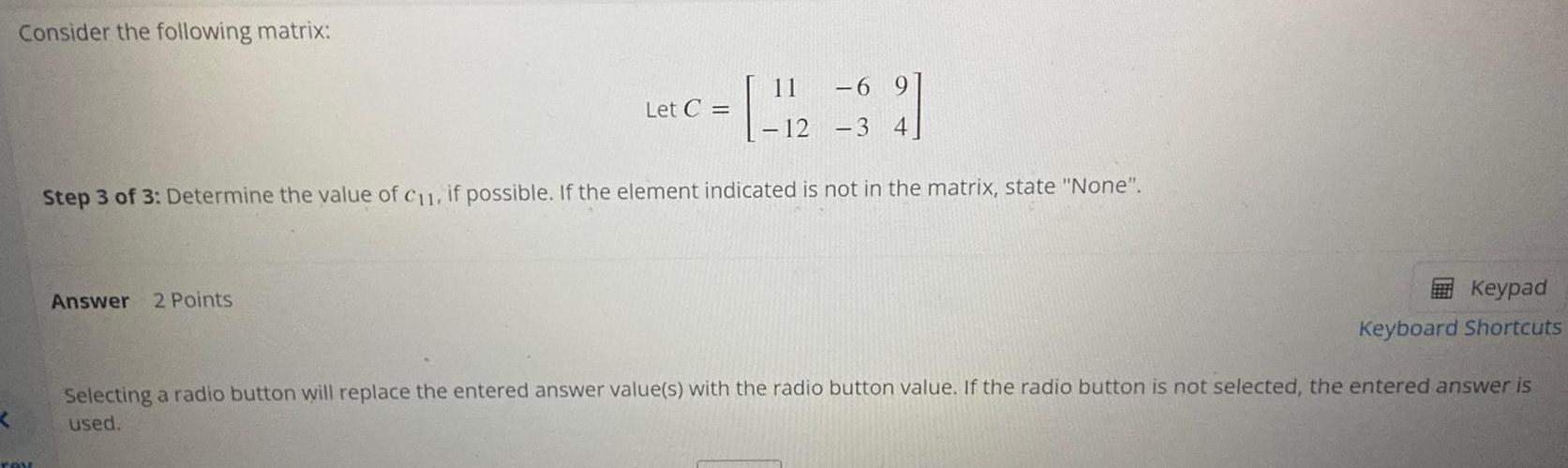
Matrices & DeterminantsConsider the following matrix:
Step 3 of 3: Determine the value of C11, if possible. If the element indicated is not in the matrix, state "None".
Math
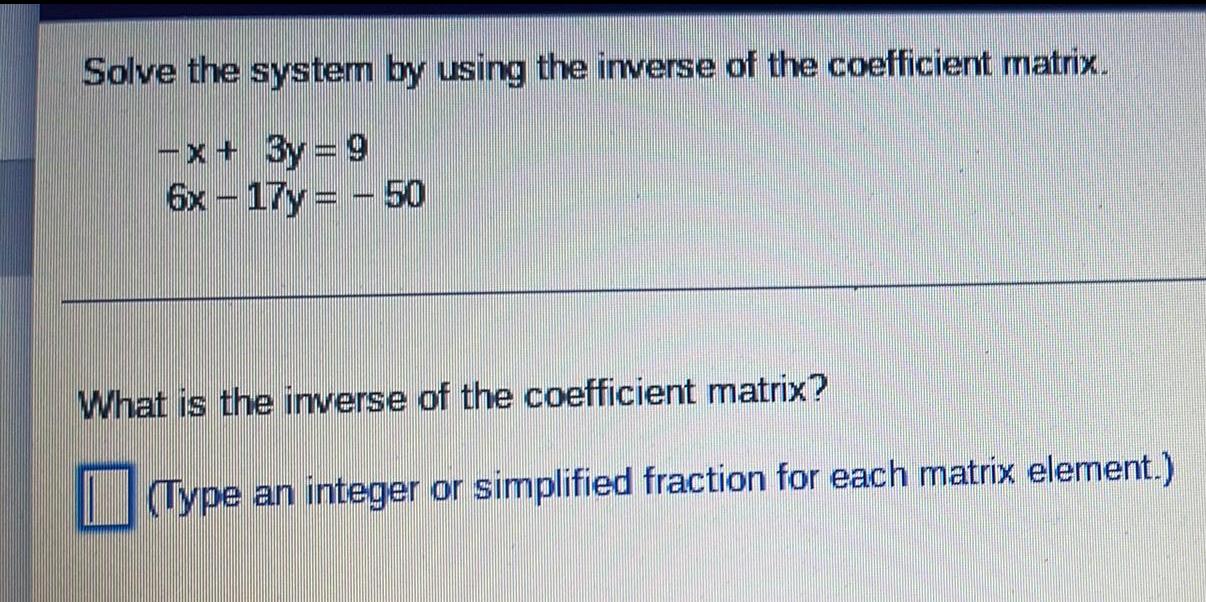
Matrices & DeterminantsSolve the system by using the inverse of the coefficient matrix.
-x+ 3y=9
6x-17y - 50
What is the inverse of the coefficient matrix?
(Type an integer or simplified fraction for each matrix element.)

Math
Matrices & DeterminantsSolve the 3 by 3 system of equations by using the matrix capabilities of your calculator to solve the system. For full credit you must write the augmented matrix you entered in your calculator, the matrix resulting from using the calculator function, and the solution as an ordered triple.
2x -y + 5z = -2
x+3y-z=6
4x + y + 3z = -2

Math
Matrices & DeterminantsWrite the augmented matrix of the system and use it to solve the system. If the system has an infinite number of solutions, express them in terms of the parameter z.
x-10y-35z=3
-5x+11y+58z=-15
x-2y-11x=3
x=________________
y=________________
z=________________

Math
Matrices & DeterminantsSolve the system using Cramer's Rule.
4x - 3y = -13
5x – 5y = -15
Find the determinant D (denominator).
D =
Find the determinant Dₓ associated with x.
Dₓ =
Find the determinant Dᵧ associated with y.
Dᵧ=
The solution is (x, y) =( , ).
Math
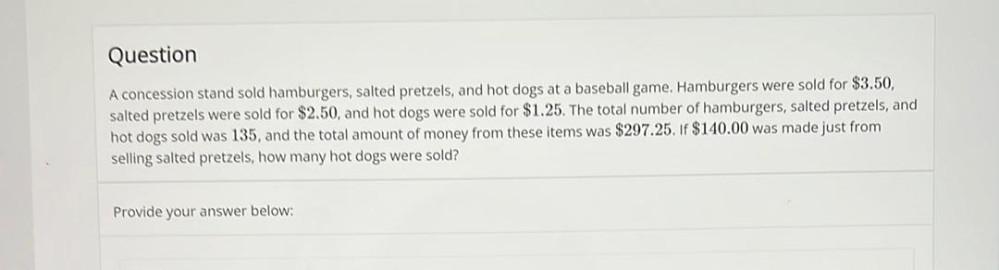
Matrices & DeterminantsA concession stand sold hamburgers, salted pretzels, and hot dogs at a baseball game. Hamburgers were sold for $3.50, salted pretzels were sold for $2.50, and hot dogs were sold for $1.25. The total number of hamburgers, salted pretzels, and hot dogs sold was 135, and the total amount of money from these items was $297.25. If $140.00 was made just from selling salted pretzels, how many hot dogs were sold?
Math
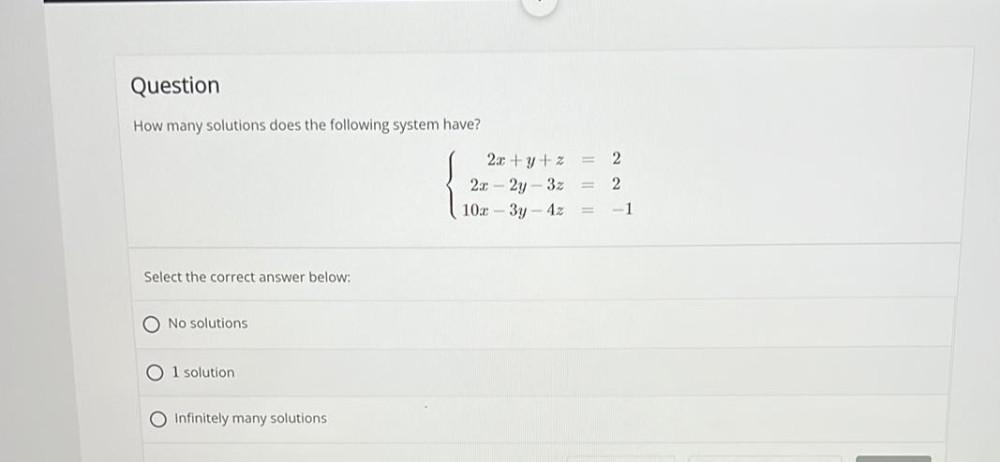
Matrices & DeterminantsHow many solutions does the following system have?
2x + y + z=2
2x - 2y - 3z=2
10x - 3y - 4z=-1
Select the correct answer below:
a) No solutions
b)l solution
c)Infinitely many solutions
Math
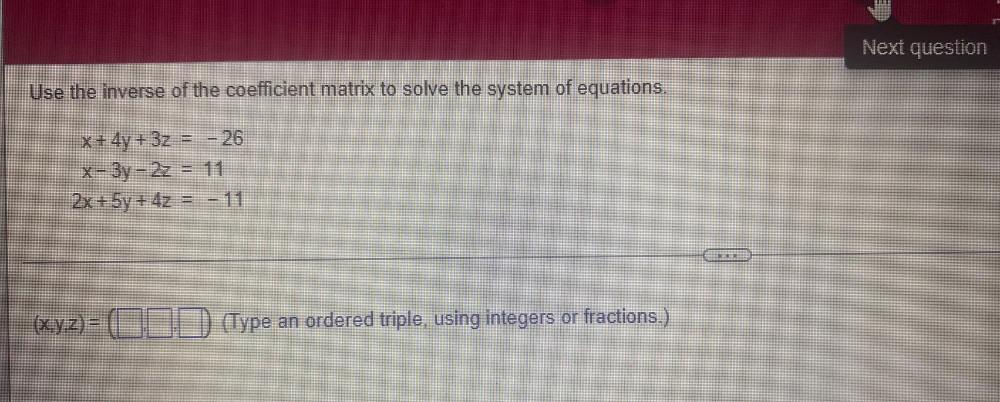
Matrices & DeterminantsUse the inverse of the coefficient matrix to solve the system of equations.
x + 4y + 3z = - 26
x - 3y - 2z = 11
2x + 5y + 4z = -11
(x,y,z)= (__,__,__)

Math
Matrices & DeterminantsUsing the information below to create the initial simplex matrix. Assume all variables are nonnegative.
Maximize f = 6x₁ +5x₂ + 7x₃ subject to
9x₁ + 7x₂ + 10x₃ ≤ 65
10x₁ + 3x₂ + 6x₃ ≤ 50
4x₁ + 10x₂ + 6x₃ ≤ 45
x₁ ≥0
x₂ ≥ 0
x₃ ≥ 0
![Consider a two sector economy with input-output matrix
A= [0.4 0.5]
[0.2 0.6]
(a) Are the sectors in the economy profitable? Give a reason for your answer.
(b) Is the economy productive? Give a reason for your answer.](https://media.kunduz.com/media/sug-question/raw/77460694-1658830183.086395.jpeg?w=256)
Math
Matrices & DeterminantsConsider a two sector economy with input-output matrix
A= [0.4 0.5]
[0.2 0.6]
(a) Are the sectors in the economy profitable? Give a reason for your answer.
(b) Is the economy productive? Give a reason for your answer.

Math
Matrices & DeterminantsA certain experiment produces the data (1, 1.7), (2, 2.6), (3, 3.2), (4, 3.6), and (5, 3.9). Describe the model that produces a least-squares fit of these points by a function of the form y = β1*x+ β2*x^2. Such a function might arise, for example, as the revenue from the sale of x units of a product, when the amount offered for sale affects the price to be set for the product. Answer parts (a) through (c) below.
a. Give the design matrix, the observation vector, and the unknown parameter vector. Choose the correct design matrix X below.
The observation vector is y =
Choose the correct form of the parameter vector β below.
b. Find the associated least-squares curve for the data.
c. If a machine learned the curve you found in (b), what output would it provide for an input of x = 6?
![Let the matrix below be the augmented matrix [A|B] of a linear system Ax = b. Write the most general solution (the sum of a particular one and the general solution of the homogeneous system) in parametric form. Write it in vector form. Give a basis of NulA.
0 2 0 0 2
0 0 1 0 3
0 0 0 1 2](https://media.kunduz.com/media/sug-question/raw/77898310-1658745324.8269083.jpeg?w=256)
Math
Matrices & DeterminantsLet the matrix below be the augmented matrix [A|B] of a linear system Ax = b. Write the most general solution (the sum of a particular one and the general solution of the homogeneous system) in parametric form. Write it in vector form. Give a basis of NulA.
0 2 0 0 2
0 0 1 0 3
0 0 0 1 2
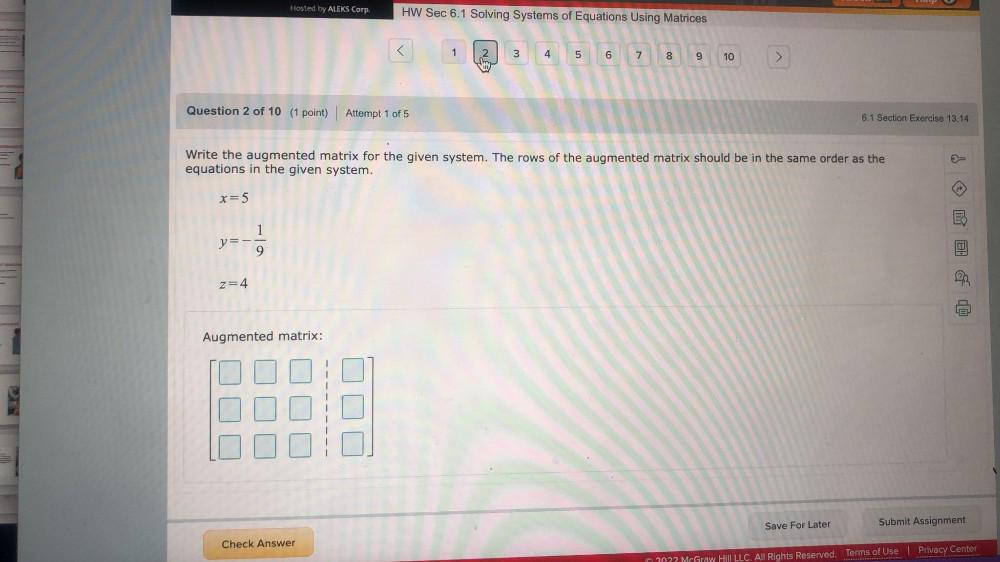
Math
Matrices & DeterminantsWrite the augmented matrix for the given system. The rows of the augmented matrix should be in the same order as the equations in the given system.
x=5
y= -(1/9)
z=4
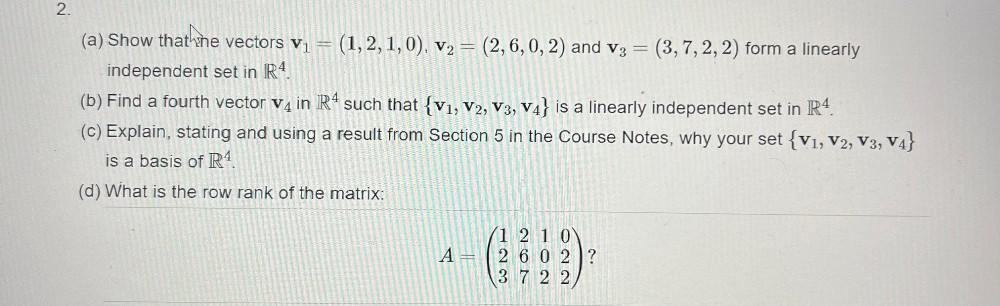
Math
Matrices & Determinants(a) Show that the vectors v1 = (1,2,1,0), v2 = (2,6,0,2) and v3 = (3,7,2,2) form a linearly independent set in R^4.
(b) Find a fourth vector v4 in R^4 such that {V1, V2, V3, V4} is a linearly independent set in R^4.
(c) Explain, stating and using a result from Section 5 in the Course Notes, why your set {v1, v2, v3, v4} is a basis of R4.
(d) What is the row rank of the matrix:
A= 1 2 1 0
2 6 0 2
3 7 2 2

Math
Matrices & DeterminantsUse Gaussian elimination to solve.
The Burkes pay their babysitter $5 per hour before 11 P.M. and $7.50 after 11 P.M. One evening they went out for 5 hr and paid the sitter $35.00. What time did they come home?
They came home at A.M.

Math
Matrices & DeterminantsUse a graphing utility that gives a matrix in a row-echelon form or a matrix in a reduced row-echelon form, if available, to solve the system of equations given to the right.
{3a-b+4c = 1
{2a-b+5c= -3
{a+2b-3c= 2

Math
Matrices & DeterminantsUse Cramer's rule to solve for y.
2x + 5y + 5z = -15
3x+4y-5z = 17
4x-3y-2z= -21
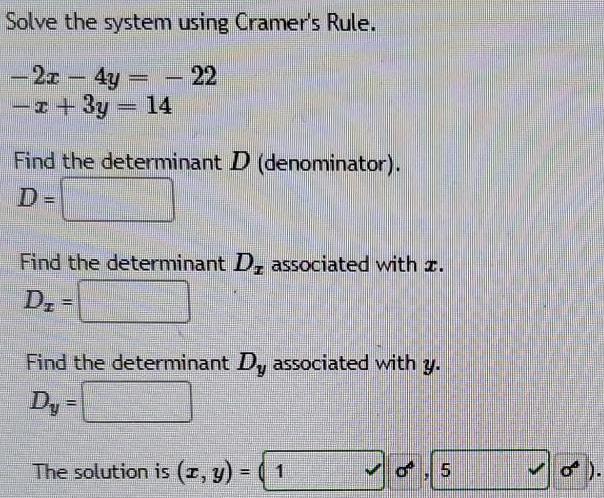
Math
Matrices & DeterminantsSolve the system using Cramer's Rule.
-2x - 4y = -22
-x+3y = 14
Find the determinant D (denominator).
D=
Find the determinant D, associated with z.
Dz
Find the determinant Dy associated with y.
Dy =
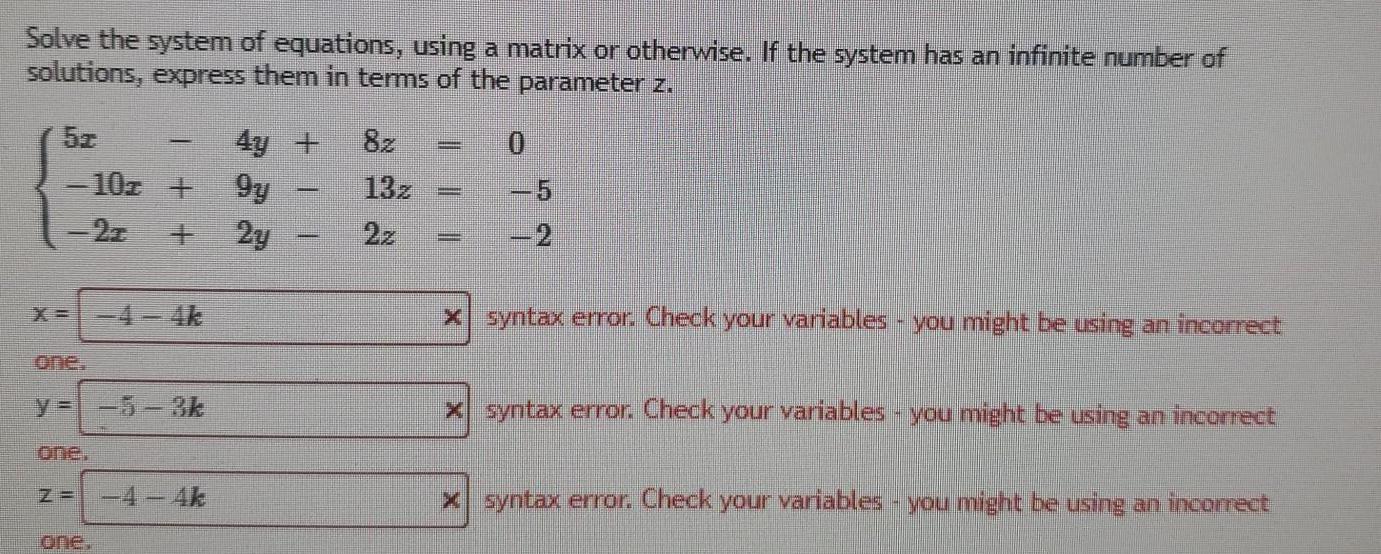
Math
Matrices & DeterminantsSolve the system of equations, using a matrix or otherwise. If the system has an infinite number of solutions, express them in terms of the parameter z.
{5x - 4y +8z = 0
{-10x +9y - 13z= -5
{-2x +2y -2z= -2
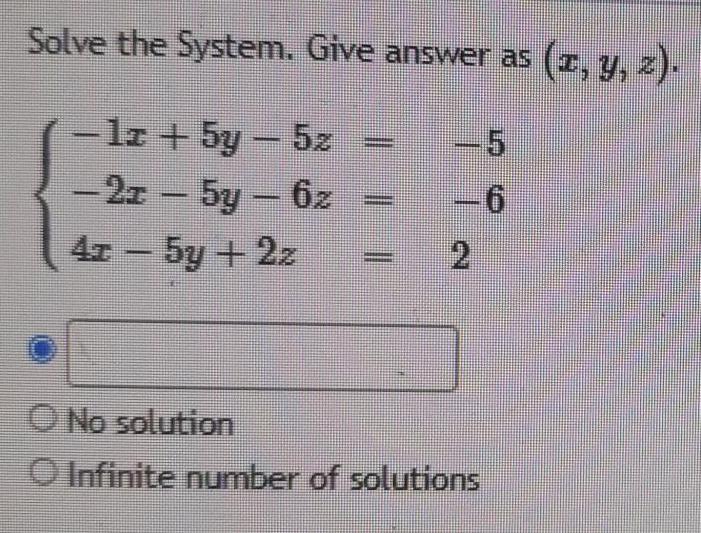
Math
Matrices & DeterminantsSolve the System. Give answer as (x, y, z).
{-1x+5y-5z= -5
{-2x-5y-6z=-6
{4x-5y+2z=2
No solution
Infinite number of solutions
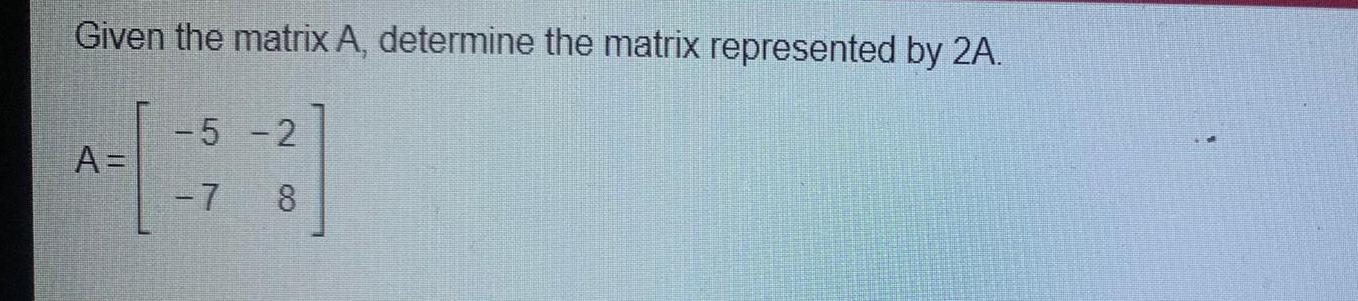
Math
Matrices & DeterminantsGiven the matrix A, determine the matrix represented by 2A.
A= -5 -2
-7 8

Math
Matrices & DeterminantsUse Cramer's rule to find the solution to the following system of linear equations.
5x-4y=-8
3x+y=3

Math
Matrices & DeterminantsUse Cramer's rule and the calculator provided to find the value of x that satisfies the system of linear equations.
-4x-4y+5z=-2
-4x+2y+ 5z = -5
5x-3y-2z=1
Note that the ALEKS graphing calculator can be used to make computations easier.

Math
Matrices & DeterminantsConsider the following system of linear equations.
4x-16y=-4
-4x+21y=-11
Solve the system by completing the steps below to produce a reduced row-echelon form. R, and R₂ denote the first and second rows, respectively. The arrow notation () means the expression/matrix on the left becomes the expression/matrix on the right once the row operations are performed
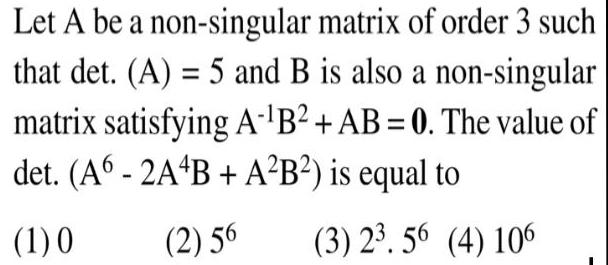
Math
Matrices & DeterminantsLet A be a non-singular matrix of order 3 such
that det. (A) = 5 and B is also a non-singular
matrix satisfying A-¹B²+ AB = 0. The value of
det. (A6- 2A4B + A²B²) is equal to
(1) 0
(2) 5^6
(3) 2^3.5^6
(4) 10^6
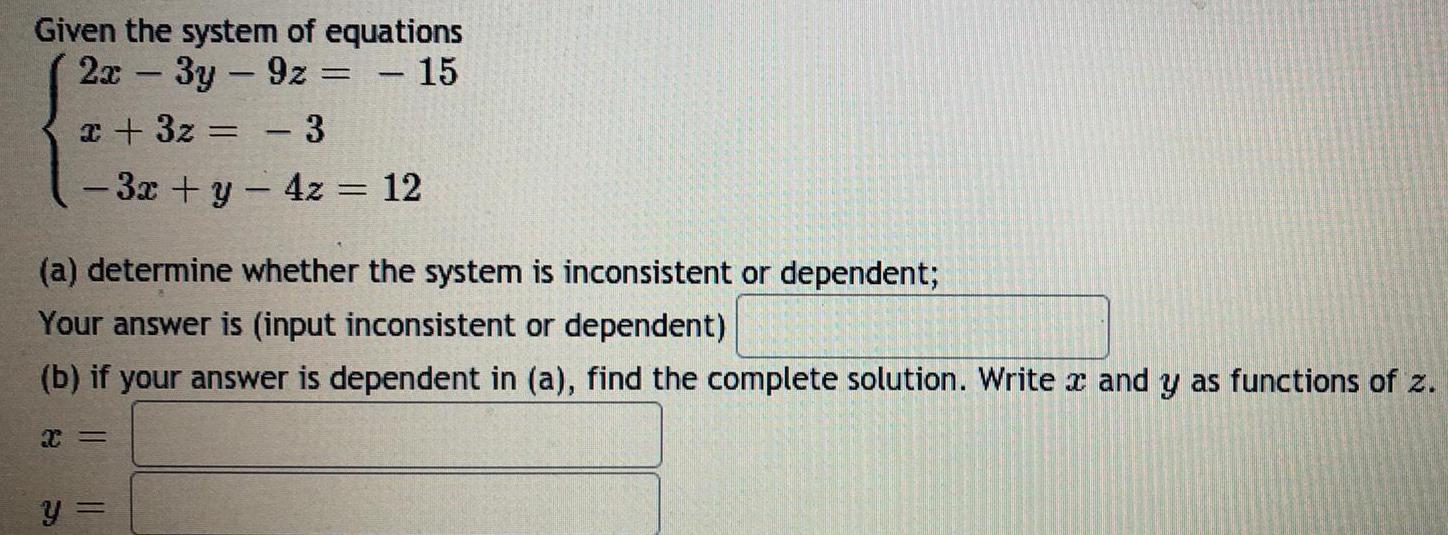
Math
Matrices & DeterminantsGiven the system of equations
2x - 3y - 9z = -15
x + 3z = -3
- 3x + y - 4z = 12
(a) determine whether the system is inconsistent or dependent;
Your answer is (input inconsistent or dependent)
(b) if your answer is dependent in (a), find the complete solution. Write and y as functions of z.
x =
y =
Math
Matrices & DeterminantsLet A be an n x n matrix. Suppose that there exists an invertible matrix P such that
P-¹AP = D, where D is a diagonal matrix. Consider the following statements.
(i) A² = P²D² (P-¹)²
(ii) A² = P-¹D²P
Which of the above statements is always true?
(a) (i) only (b) (ii) only (c) (i) and (ii) (d) neither
![Solve the following system of equations using Cramer's Rule if it is applicable. If Cramer's Rule is not applicable, say so.
X + y - z = 6
2x - y + 2z = -5
x + 2y - z = 9
Write the fractions using Cramer's Rule in the form of determinants. Do not evalate the determinants.
(Type an integer or simplified fraction for each matrix element.)
Select the correct choice below and fill in any answer boxes within your choice.
A. Cramer's Rule is applicable. The solution is x = 1, y = [3], and z = -2
(Simplify your answers. Type integers or simplified fractions.)
B. Cramer's Rule is not applicable.](https://media.kunduz.com/media/sug-question/raw/59898416-1658209442.1265583.jpeg?w=256)
Math
Matrices & DeterminantsSolve the following system of equations using Cramer's Rule if it is applicable. If Cramer's Rule is not applicable, say so.
X + y - z = 6
2x - y + 2z = -5
x + 2y - z = 9
Write the fractions using Cramer's Rule in the form of determinants. Do not evalate the determinants.
(Type an integer or simplified fraction for each matrix element.)
Select the correct choice below and fill in any answer boxes within your choice.
A. Cramer's Rule is applicable. The solution is x = 1, y = [3], and z = -2
(Simplify your answers. Type integers or simplified fractions.)
B. Cramer's Rule is not applicable.
Math
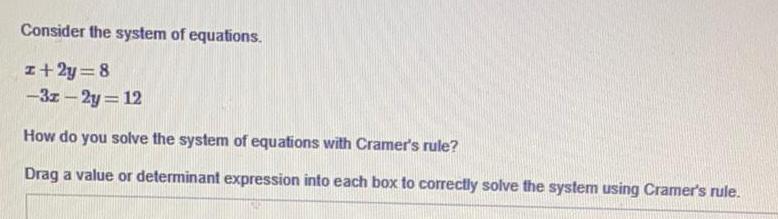
Matrices & DeterminantsConsider the system of equations.
x+2y=8
-3x-2y=12
How do you solve the system of equations with Cramer's rule?
Drag a value or determinant expression into each box to correctly solve the system using Cramer's rule.
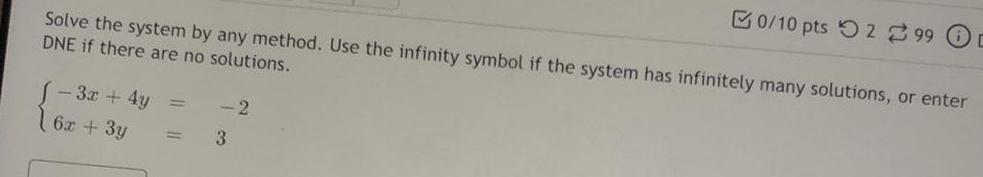
Math
Matrices & DeterminantsSolve the system by any method. Use the infinity symbol if the system has infinitely many solutions, or enter DNE if there are no solutions.
- 3x + 4y = -2
6x + 3y = 3
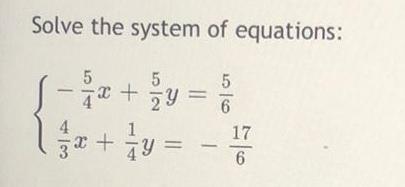
Math
Matrices & DeterminantsSolve the system of equations:
-5/4 x + 5/2 y = 5/6
4/3 x + 1/4 y = -17/6

Math
Matrices & DeterminantsSolve the system using addition/elimination method. If there is exactly one solution, write as an ordered pair. If not, choose one of the other options.
- 3x - 4y = 11
4x + 4y = - 12
No solution
Infinite number of solutions

Math
Matrices & Determinants2. Given the system below, do the following:
(x-2y+3z=0
2xy + 5z = 5
x + y + 4z = 7
a. Write the augmented matrix that represents this system below. Then enter this matrix into your calculator.
b. Use the rref function on your calculator to put the matrix in reduced row echelon form and write that result below.
c. Write the solution to this system as an ordered triple.

Math
Matrices & DeterminantsFind the inverse of the given matrix.
Select the correct choice below and, if necessary, fill in the answer box to co
A. A¹=
B. The matrix is not invertible.
![[SolveLancer Test] A, B and C are both N-order matrices, E is the identity matrix and satis-
fies ABC-E, then which of the following options is true: [SolveLancer Test]
(a) ACB = E
(b) BCA = E
(c) CBA = E
(d) BAC = E](https://media.kunduz.com/media/sug-question/raw/54470056-1658051973.1433823.jpeg?w=256)
Math
Matrices & Determinants[SolveLancer Test] A, B and C are both N-order matrices, E is the identity matrix and satis-
fies ABC-E, then which of the following options is true: [SolveLancer Test]
(a) ACB = E
(b) BCA = E
(c) CBA = E
(d) BAC = E
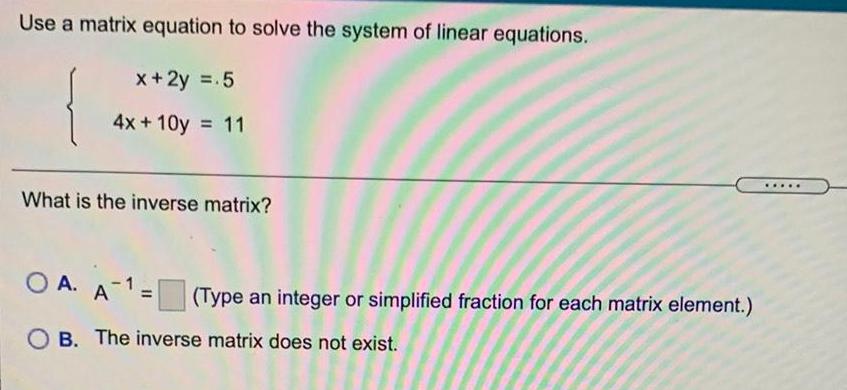
Math
Matrices & DeterminantsUse a matrix equation to solve the system of linear equations.
x + 2y =.5
4x+10y = 11
What is the inverse matrix?
A. A-1
B. The inverse matrix does not exist.
(Type an integer or simplified fraction for each matrix element.)

Math
Matrices & DeterminantsA square matrix A is said to be idempotent if A2 = A. Let A be an idempotent matrix. (a) Show that I - A is also idempotent.
(b) Show that if A is invertible, then A = I.
(c) Show that the only possible eigenvalues of A are 0 and 1. (Hint: Suppose x is an eigenvector with associated eigenvalue A and then multiply x on the left by A twice.)
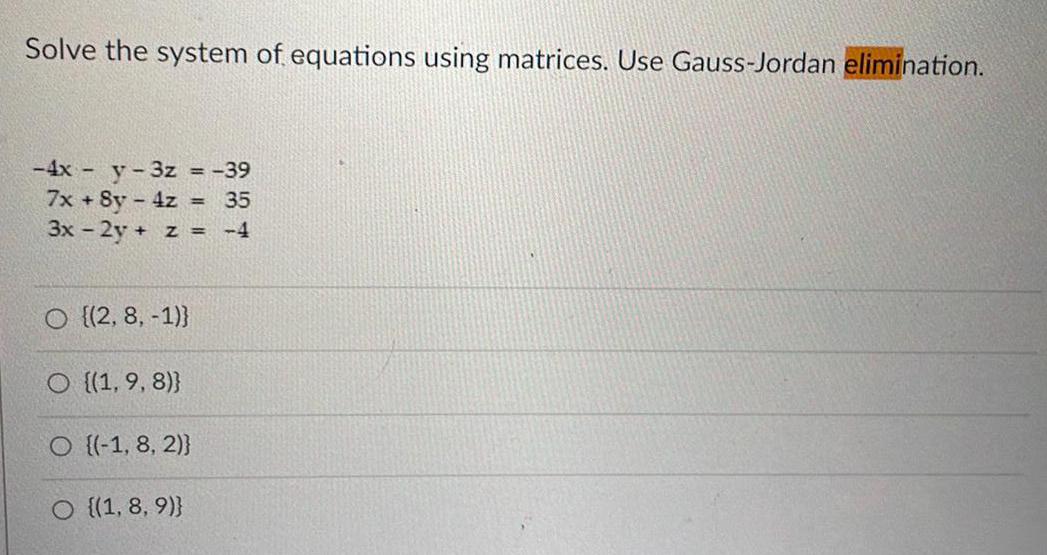
Math
Matrices & DeterminantsSolve the system of equations using matrices. Use Gauss-Jordan elimination.
-4x - y - 3z = -39
7x + 8y - 4z = 35
3x - 2y + z = -4
{(2, 8, -1)}
{(1,9, 8)}
{(-1, 8, 2)}
{(1, 8, 9)}

Math
Matrices & Determinants10.045
You invest in AAA-rated bonds, A-rated bonds, and B-rated bonds. The average yields are 4.5% on AAA bonds, 5% on A bonds, and 9% on B bonds. You invest twice as much in B bonds as in A bonds. Let x, y, and z
represent the amounts invested in AAA, A, and B bonds, respectively.
X +
y + z = (total investment)
0.045x+0.05y + 0.09z = (annual return)
2y-
Z = 0
MY NOTES
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond for the given total investment and annual return. (Round your answers to the nearest cent.)
Total Investment Annual Return
$12,700
$815
amount invested in AAA-bonds $
amount invested in A-bonds
$
amount invested in B-bonds
$
PRACTICE ANOTHER

Math
Matrices & DeterminantsA natural history museum borrows $2,000,000 at simple annual interest to purchase new exhibits. Some of the money is borrowed at 5%, some at 6.5%, and some at 7.5%. Use a system of linear equations to determine how much is borrowed at each rate given that the total annual interest is $129,750 and the amount borrowed at 6.5% is four times the amount borrowed at 7.5%. Solve the system of linear equations using matrices.

Math
Matrices & DeterminantsUse Cramer's rule to solve the system.
4x + 3y - z = 31
x - 3y + 2z = -5
4x + y + z = 29
O {(7, 6, 7)}
O {(4, -7, -6)}
O {(4, 7, 6)}
O {(5, 5, 6)}

Math
Matrices & DeterminantsDetermine whether the following inequality is true or false.
When graphing 2x − 8y ≥ 16, to determine which side of the line to shade, choose a test point on 2x - 8y = 16.
Choose the correct answer below.
False
True
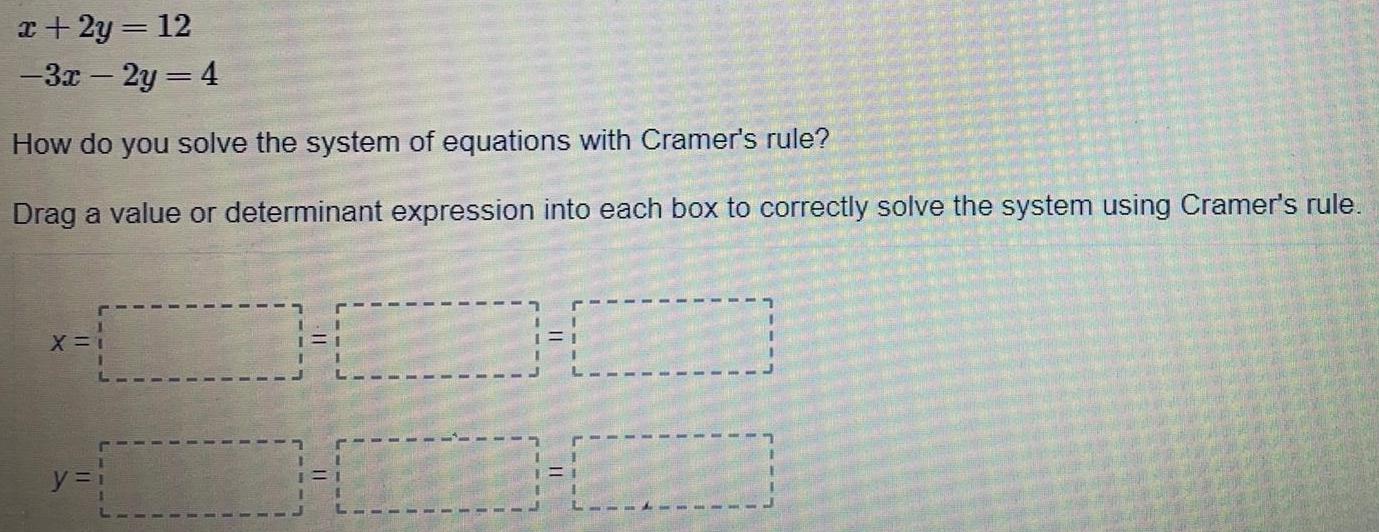
Math
Matrices & Determinantsx+2y=12
-3x - 2y = 4
How do you solve the system of equations with Cramer's rule?
Drag a value or determinant expression into each box to correctly solve the system using Cramer's rule.