Sequences & Series Questions and Answers

Math
Sequences & Seriesphotograph What is special about A They are consecutive terms in the Fibonacci sequence B The value of the 13th term of the pyramidal sequence is 21 C The value of the 13th term of the Fibonacci sequence is 21 D They are consecutive terms in the pyramidal sequence O

Math
Sequences & SeriesSEQUENCES b Describe the domain and the range of the sequence SEQUENCES Post Te

Math
Sequences & SeriesPenn stacks all of his snowballs in a square pyramid The number of snowballs P n in n layers of the square pyramid is given b P n P n 1 n Which could not be the number of snowballs Penn has OA 5 OB 14 O C 30 OD 25

Math
Sequences & SeriesThe first term in a sequence is 18 and each term after the first is 4 times the preceding term Which of the following recursive functions defines the sequence described above A B C D f 1 18 f n 4f n 1 n 1 f 1 18 f n 4 f n 1 n 1 1 18 f n 4f n 1 n 1 f 1 18 f n 4 f n 1 n 1
Math
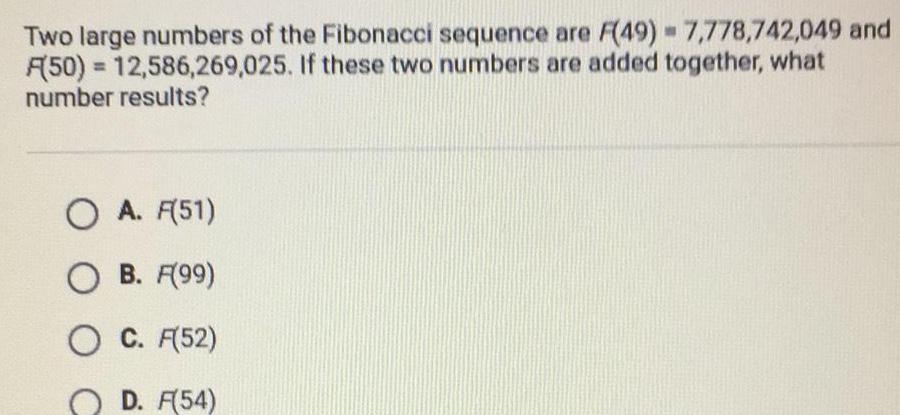
Sequences & SeriesTwo large numbers of the Fibonacci sequence are F 49 7 778 742 049 and A 50 12 586 269 025 If these two numbers are added together what number results O A F 51 O B F 99 O C F 52 OD F 54
Math
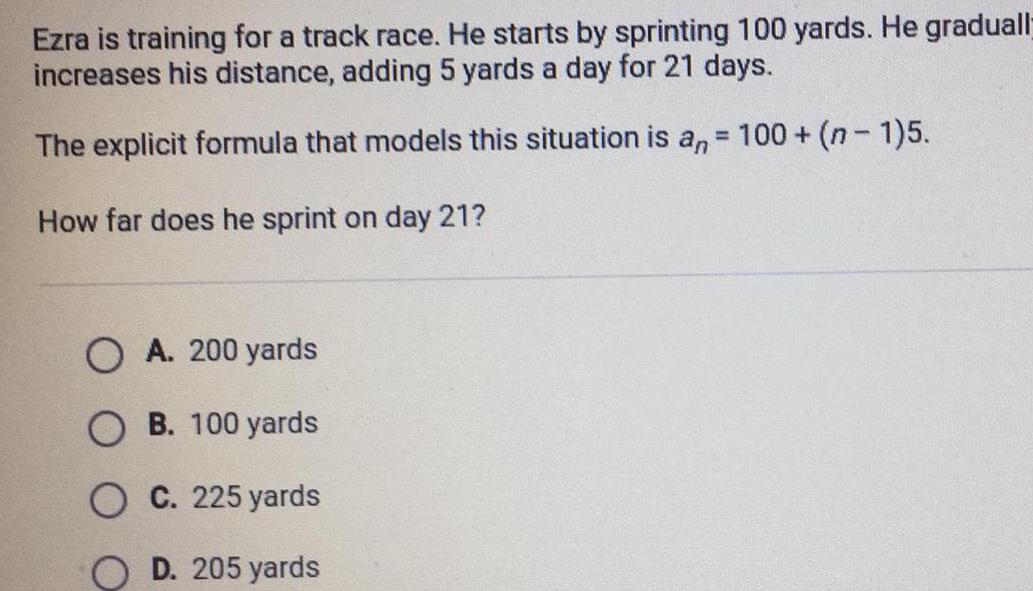
Sequences & SeriesEzra is training for a track race He starts by sprinting 100 yards He graduall increases his distance adding 5 yards a day for 21 days The explicit formula that models this situation is an 100 n 1 5 How far does he sprint on day 21 OA 200 yards OB 100 yards OC 225 yards D 205 yards

Math
Sequences & Seriesam and Drew decide to mow lawns during their summer break with different companies am gets a flat 15 00 every day plus 8 00 for every yard he mows Drew gets paid 5 00 daily plus 6 00 for each yard he mows When will they have mowed the same mber of yards and earned the same amount How much will they have earned

Math
Sequences & Series829 Exercises 10 16 write the first four of each sequence whose general term is given 1 a 3n 2 2 a 4n 1 3 An 3n 4 An 5 An 6 An 7 An 8 An 9 an 10 An 11 1 3 3 n 1 3 1 n 3 1 n n 4 2n n n 4 3n n n 5 1 1
Math
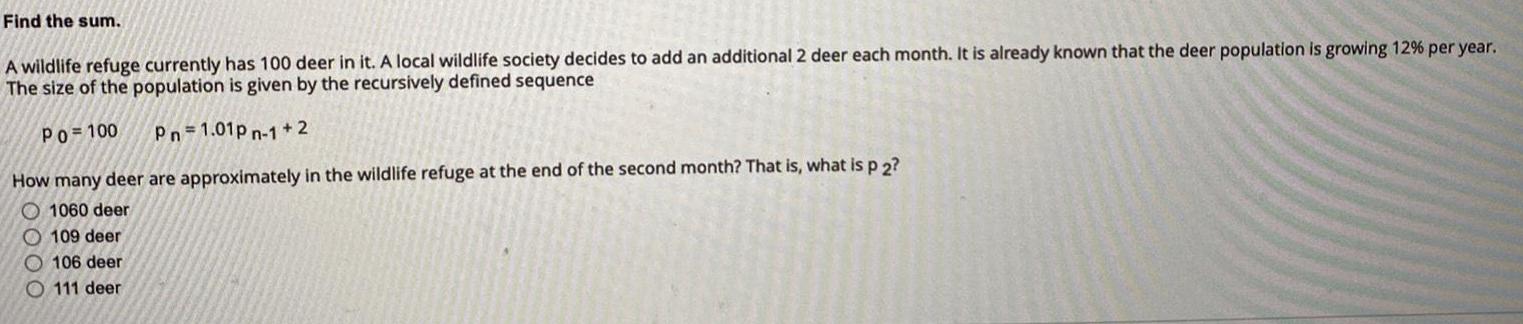
Sequences & SeriesFind the sum A wildlife refuge currently has 100 deer in it A local wildlife society decides to add an additional 2 deer each month It is already known that the deer population is growing 12 per year The size of the population is given by the recursively defined sequence Po 100 Pn 1 01pn 1 2 How many deer are approximately in the wildlife refuge at the end of the second month That is what is p 2 O1060 deer 109 deer 106 deer O111 deer

Math
Sequences & Series3 A grocery store worker has to collect all the shopping carts left out in the parking lot He collects 4 carts and measures the length of the 4 carts he is pushing to be 51 inches He collects another cart for a total of 5 carts and measures the length of the 5 carts to be 57 inches a He sees that there are a total of 21 carts in the parking lot How long will the line of 21 carts be

Math
Sequences & Series4a 2 marks Series Sequence Mia baked a very large apple pie that she cuts into slices to share with her friends The smallest slice is cut first The volume of each successive slice of pie forms a geometric sequence The second smallest slice has a volume of 30cm The fifth smallest slice has a volume of 240cm Find the common ratio of the sequence 4b 2 marks Find the volume of the smallest slice of pie 4c 2 marks The apple pie has a volume of 61425cm Find the total number of slices Mia can cut from this pie

Math
Sequences & Series2 Determine how many primes there are in the ranges 1 1000 1001 2000 and so on up to 9001 10000 Can you see why the Greeks might have wondered if they would run out Hint there are a number of websites that have lists of prime numbers Even easier use the Mathematica command Prime Pi k which gives the number of primes less than or equal to k

Math
Sequences & SeriesA retailer needs to purchase 10 printers The first printer costs 57 and each additional printer costs 3 less than the price of the previous printer up to 15 printers What is the total cost of 10 printers 552 90

Math
Sequences & SeriesDoes this show an arithmetic or geometric sequence Write the recursive for the pattern shown PODL Arithmetic or Geometric ecursive Formula f 1 f n
Math
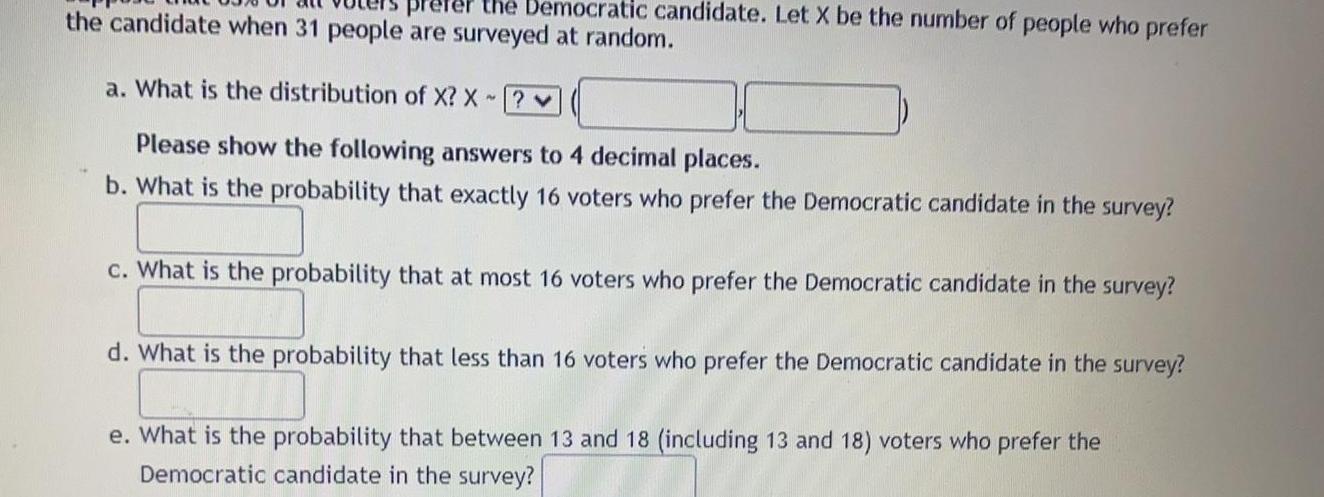
Sequences & Seriesthe Democratic candidate Let X be the number of people who prefer the candidate when 31 people are surveyed at random pre a What is the distribution of X X Please show the following answers to 4 decimal places b What is the probability that exactly 16 voters who prefer the Democratic candidate in the survey c What is the probability that at most 16 voters who prefer the Democratic candidate in the survey d What is the probability that less than 16 voters who prefer the Democratic candidate in the survey e What is the probability that between 13 and 18 including 13 and 18 voters who prefer the Democratic candidate in the survey

Math
Sequences & Seriesball is dropped from a height of 60 feet Each time it hits the ground It bounces two thirds of its evious height Find the total distance the ball has traveled before coming to rest 60 ft 40 ft 40 ft 26 7 ft 26 7 ft 17 8 ft 17 8 ft

Math
Sequences & SeriesGiven a2 6 and a5 384 of a geometric sequence what is the recursive equation for the nth term an 4 an 1 a 1 5 an 4 an 1 a 1 5 an 4 an 1 a 1 5 an 4 an 1 a 1 5
Math
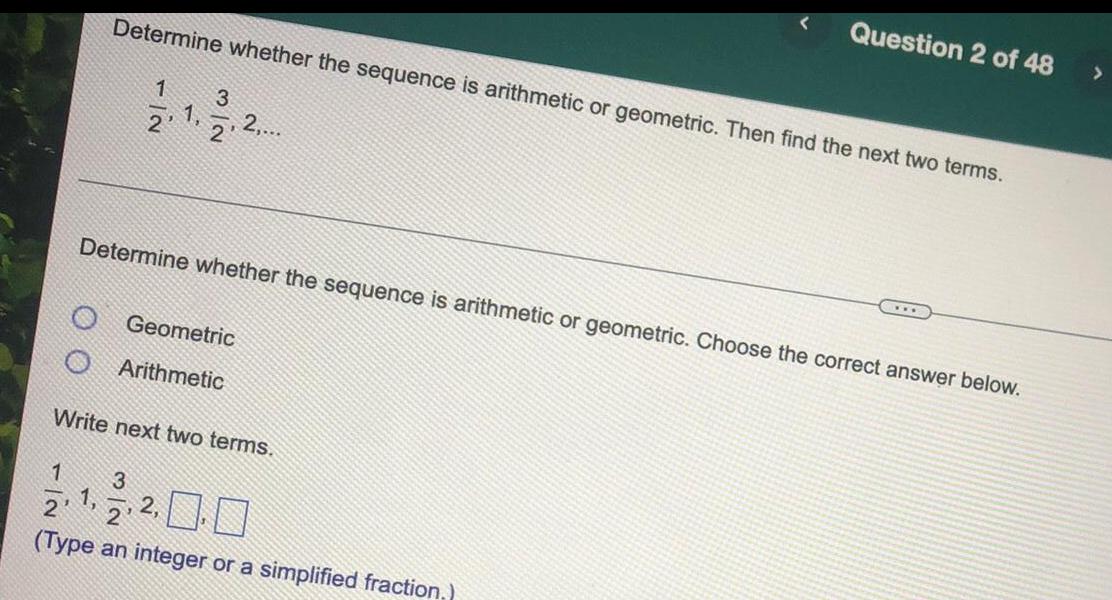
Sequences & SeriesDetermine whether the sequence is arithmetic or geometric. Then find the next two terms.
1/2, 1, 3/2, 2..
Determine whether the sequence is arithmetic or geometric. Choose the correct answer below.
Geometric
Arithmetic
2,..
Write next two terms.
1/2, 1, 3/2, 2..

Math
Sequences & SeriesFor each arithmetic series described below, write the series and calculate its sum. If it is not possible, explain why not.
a. You know that the first term is 18, the last term is 72, and the common difference is 4.5. What is the series? What is the sum?
b. You know that the series has nine terms and the last term is 18. What is the series? What is the sum?
c. You know that the third term of an 18-term series is 29 and the terms are increasing by 10. What is the series? What is the sum?

Math
Sequences & SeriesRosurvastatin/Crestor is a medicine used to decrease bad cholesterol and increase good cholesterol in the body. The half-life of Rosurvastatin is 1 day, which means that at the end of 1 day, half as much of the medication is left in your system. 1. If you take 60 mg of Rosurvastatin, how long do you think will it stay in your system?

Math
Sequences & SeriesFind a formula for the nº partial sum of the series series converges.
The formula for the n
A. The series converges. The series' sum is
B. The series diverges.
If the series converges, what is the series' sum? Select the correct choice below and fill in any answer boxes within your choice.

Math
Sequences & Series11. (a) Write the first 5 terms of a power series approximation for f(x) = e-x*² centered at
X = 0.
(b) Use the above power series approximation to find an approximation to S₁¹₁e-x² dx,
rounding to 3 decimal places. Show work needed to produce this approximation.
(c) Include a graph, shade the region corresponding to the integration and confirm your
answer above using the computer or calculator to evaluate the integral.

Math
Sequences & SeriesThe real number 0.9 can be written as an infinite series as shown below:
(a) Write the infinite series in sigma notation and use the formula for the sum of a
infinite geometric series to find the sum.
(b) Write the exact value of the infinite sum (not as a repeating decimal).

Math
Sequences & SeriesA bottle contains 95 milliliters of lemon extract solution. If. the extract contains 25 milliliters of alcohol, what is the volume percent (v/v) of the alcohol in the solution? Make sure to include a correct unit symbol with the answer choice.


Math
Sequences & SeriesDetermine whether the following statement is true or false, and explain why.
In a Markov chain, the outcome of an experiment depends only on the present state and not on any past states.
Is the statement true or false?
A. True.
B. False. In a Markov chain, the outcome of an experiment depends on past states found using transition matrice
C. False. In a Markov chain, the outcome of an experiment depends on past states found using probability vector
D. False. In a Markov chain, the outcome of an experiment depends on both past and present states.

Math
Sequences & SeriesWrite the first five terms of the sequence whose general term, an, is given as
an=-5n+ 8.
Math
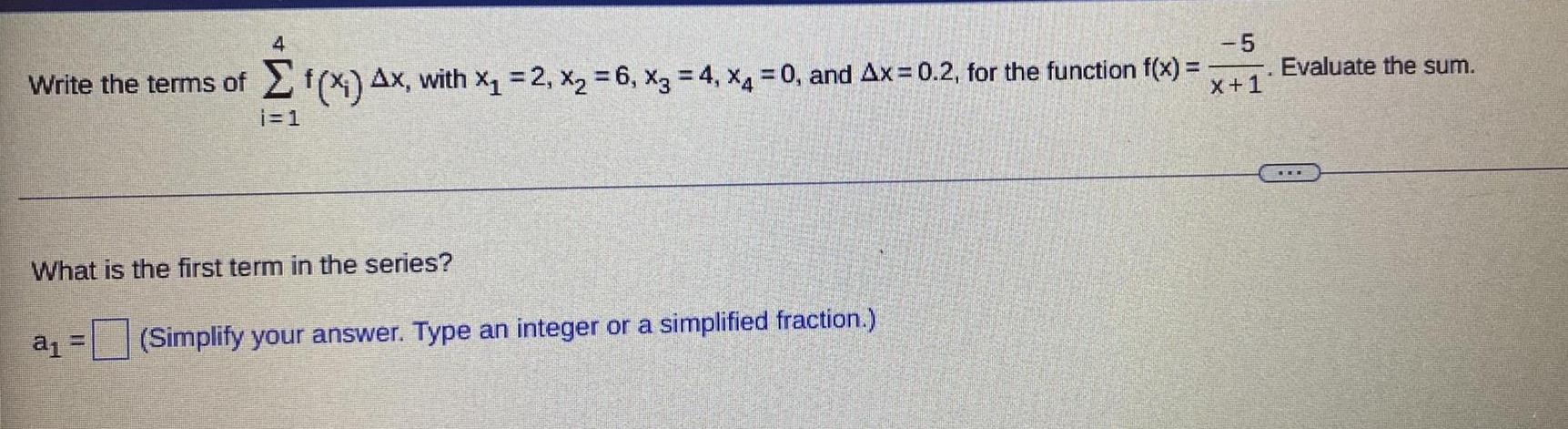
Sequences & SeriesWrite the terms of 4Σi=1 f(xi) Δx., with x₁ = 2, X₂ = 6, x3 = 4, x4 = 0, and Ax=0.2, for the function f(x) =-5/x+1
What is the first term in the series?
a₁ = (Simplify your answer. Type an integer or a simplified fraction.)
Evaluate the sum.
Math
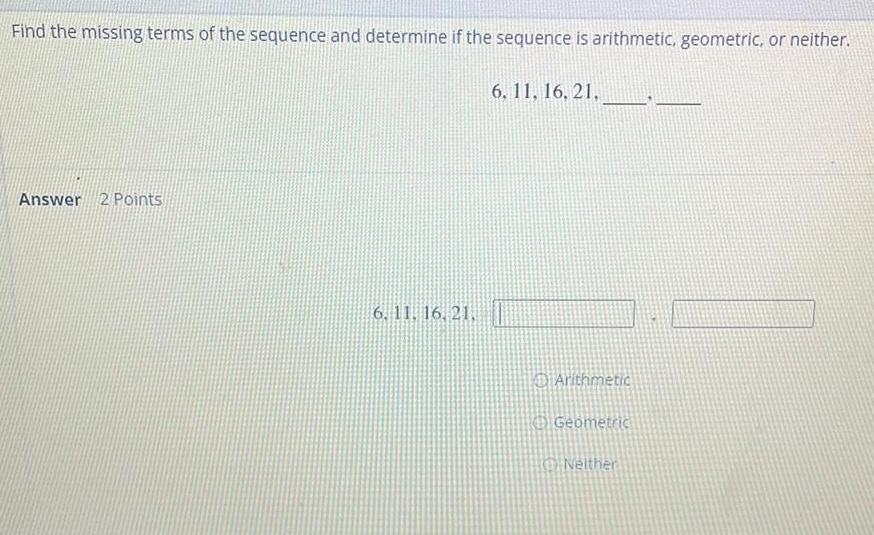
Sequences & SeriesFind the missing terms of the sequence and determine if the sequence is arithmetic, geometric, or neither.
6, 11, 16, 21,_______,______ .
Math
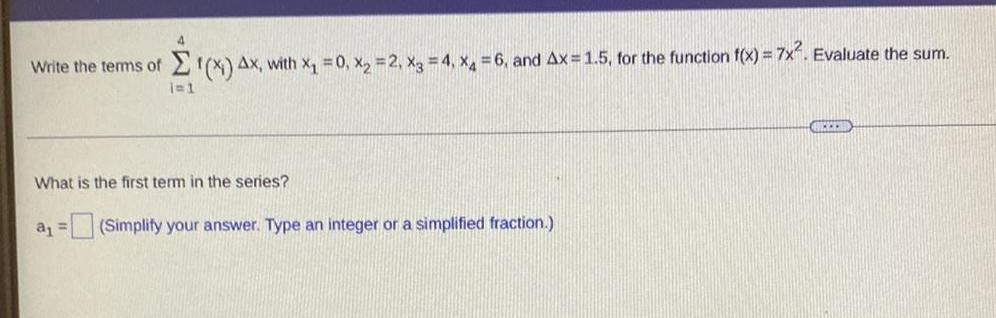
Sequences & SeriesWrite the terms of 4Σi=1 f(x1) Δx with x₁ = 0, x₂ = 2, x3 = 4, x4= 6, and Δx=1.5, for the function f(x) = 7x². Evaluate the sum.
What is the first term in the series?
a₁ = (Simplify your answer. Type an integer or a simplified fraction.)

Math
Sequences & SeriesA painting sold for $277 in 1978 and was sold again in 1990 for $485. Assume that the growth in the value V of the collector's item was exponential.
a) Find the value k of the exponential growth rate. Assume V₂ = 277.
k=_
(Round to the nearest thousandth.)
b) Find the exponential growth function in terms of t, where t is the number of years since 1978.
V(t)=_
c) Estimate the value of the painting in 2015.
$_
(Round to the nearest dollar.)
d) What is the doubling time for the value of the painting to the nearest tenth of a year?
_years
(Round to the nearest tenth.)
e) Find the amount of time after which the value of the painting will be $2173.
_years
(Round to the nearest tenth.)
![A manufacturer producing a new product, estimates the annual sales to be 9,200 units. Each year, 8% of the units that have been sold will become inoperative. So, 9,200 units will be in use after 1 year, [9,200+ 0.92(9,200)] units will be in use after 2 years, and so on. How many units will be in use after n years?](https://media.kunduz.com/media/sug-question/raw/61292401-1659979563.3720424.jpeg?w=256)
Math
Sequences & SeriesA manufacturer producing a new product, estimates the annual sales to be 9,200 units. Each year, 8% of the units that have been sold will become inoperative. So, 9,200 units will be in use after 1 year, [9,200+ 0.92(9,200)] units will be in use after 2 years, and so on. How many units will be in use after n years?
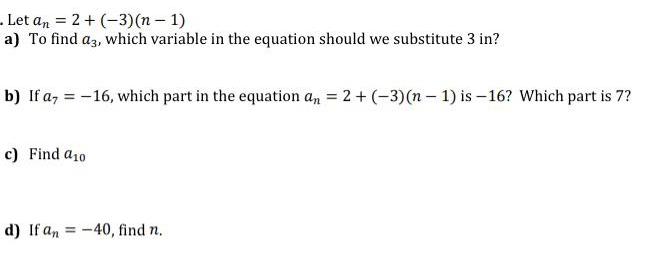
Math
Sequences & SeriesLet an 2 + (-3)(n-1)
a) To find a3, which variable in the equation should we substitute 3 in?
b) If a7 = -16, which part in the equation an = 2 + (-3)(n-1) is -16? Which part is 7?
c) Find a10
d) If an = -40, find n.
Math
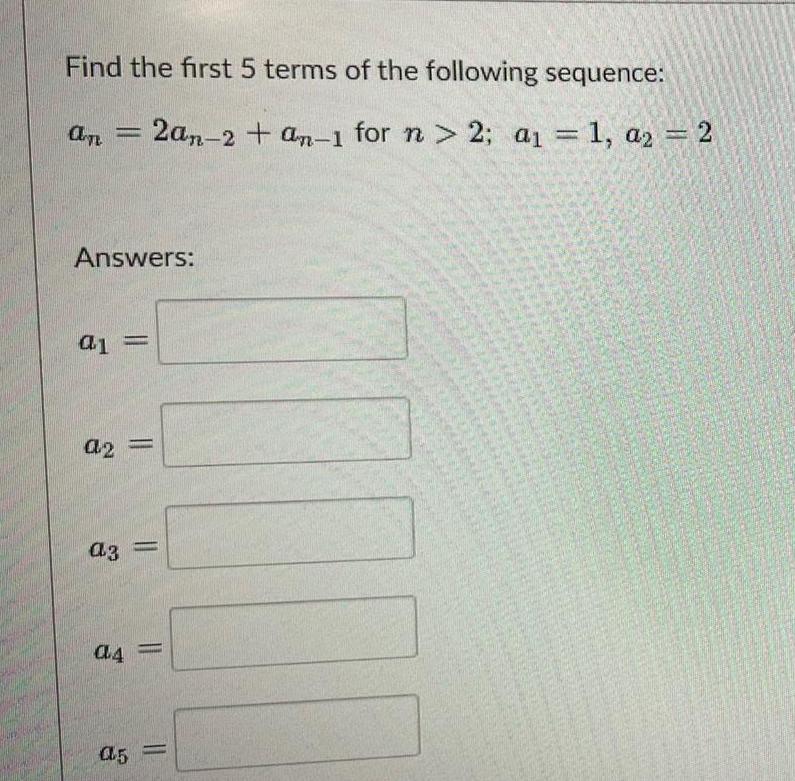
Sequences & SeriesFind the first 5 terms of the following sequence:
an = 2an-2+ an-1 for n > 2; a₁ = 1, a₂ = 2
Answers:
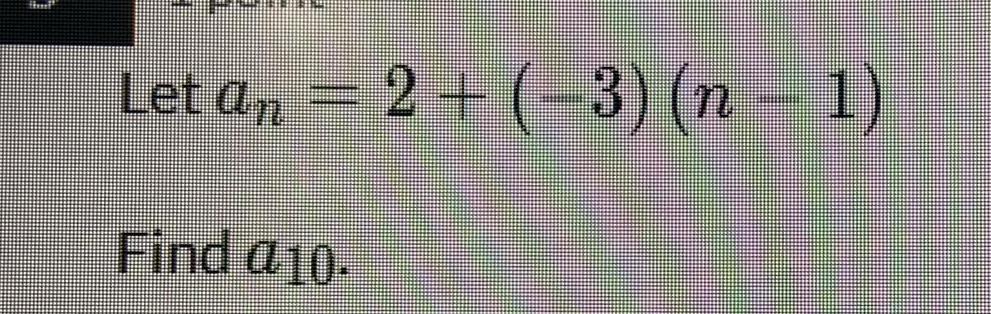

Math
Sequences & SeriesUse the notation for sequences to translate the following to mathematical equations.
"The nth term of the sequence is 78."
Use fx to type math equations or insert a image of your hand written equation.

Math
Sequences & SeriesDetermine whether the sequence is geometric, arithmetic, neither with a defined general term, or neither with an undefined term, in any case justify your answer.
3, 1, 4, 1, 5, 9, 2, 6, . . .
Math
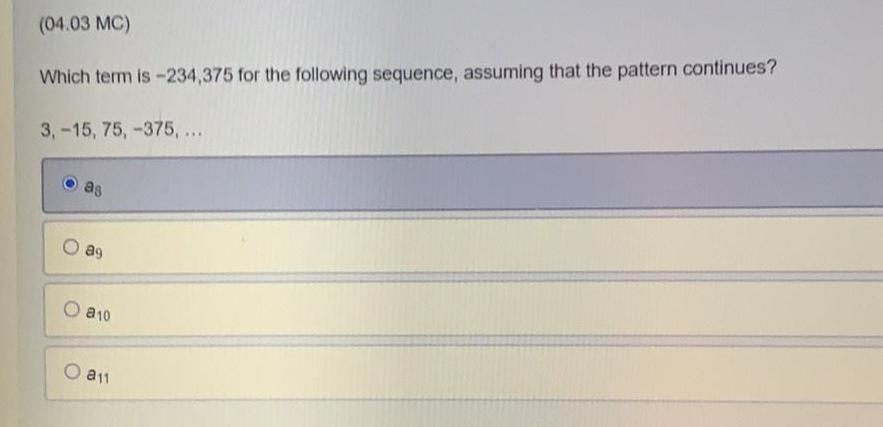
Sequences & SeriesWhich term is -234,375 for the following sequence, assuming that the pattern continues?
3, -15, 75, -375,...
a8
a9
a10
a11

Math
Sequences & SeriesSuppose a flu epidemic has broken out in all math 120 courses at your school. Assume a total of 12 people have the flu as of today and that each day the total number people who have the flu quadruples. Estimate numerically when the number of people will reach 3072. {your answer input will be number only)
Math
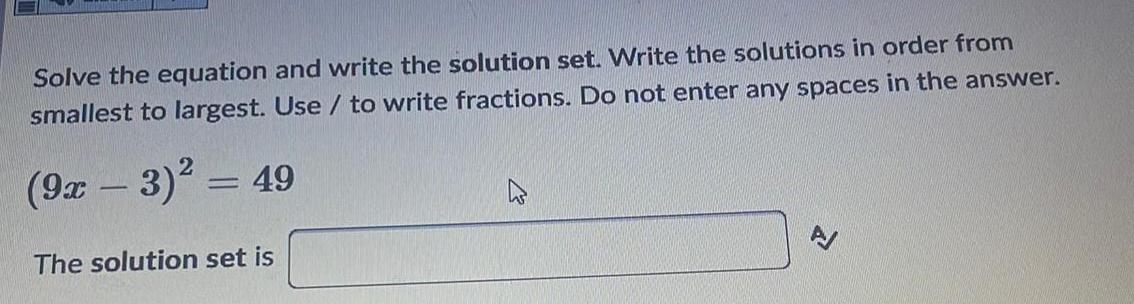
Sequences & SeriesSolve the equation and write the solution set. Write the solutions in order from
smallest to largest. Use / to write fractions. Do not enter any spaces in the answer.
(9x - 3)²=49
The solution set is
Math
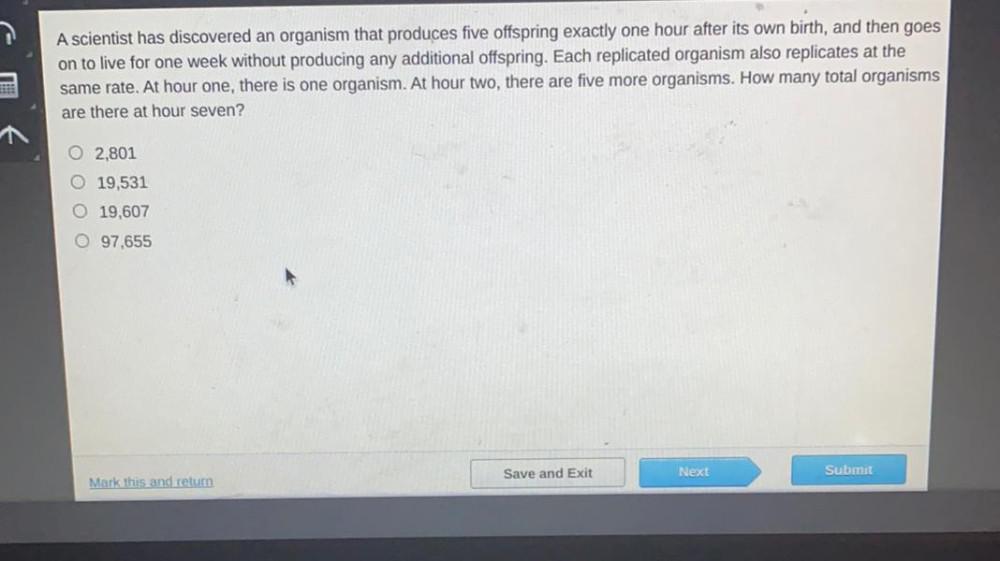
Sequences & SeriesA scientist has discovered an organism that produces five offspring exactly one hour after its own birth, and then goes on to live for one week without producing any additional offspring. Each replicated organism also replicates at the same rate. At hour one, there is one organism. At hour two, there are five more organisms. How many total organisms are there at hour seven?
(A) 2,801
(B) 19,531
(C) 19,607
(D) 97,655

Math
Sequences & SeriesZina spends 15 hours setting up her sewing machine and making one hat. The total amount of time spent making hats can be represented by the sequence below
1.5, 2.25, 30,3.75. . .
Which recursive formula can be used to determine the total amount of time spent making hats based on the total amount of time spent previously?
(1) f(n + 1) = f(n) + 1.5
(2) f(n + 1) = f(n) + 0.75
(3) f(n+ 1) = 1/2f(n)
(4) f(n + 1) = 3/2f(n)
Math
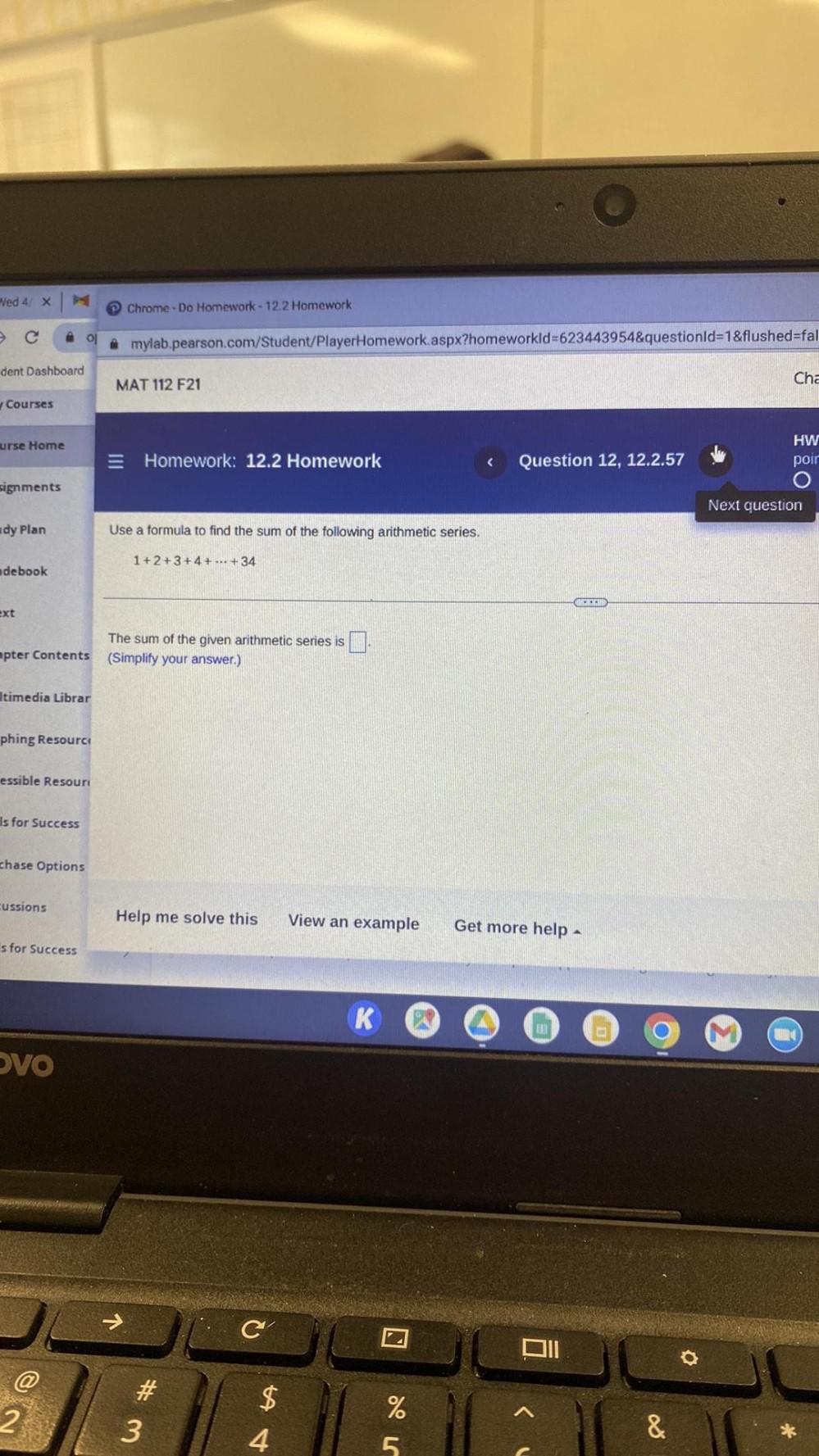
Sequences & SeriesUse a formula to find the sum of the following arithmetic series.
1+2+3+4+ ... +34
The sum of the given arithmetic series is
(Simplify your answer)
Math
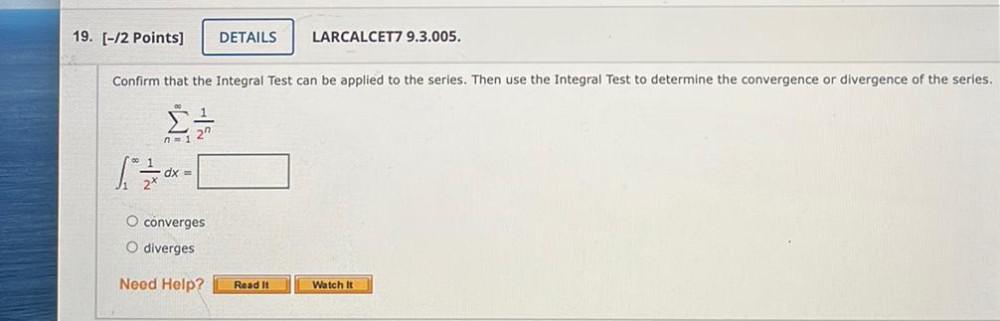
Sequences & SeriesConfirm that the Integral Test can be applied to the series. Then use the Integral Test to determine the convergence or divergence of the series.
∑ 1/2ⁿ
∫ 1/(2^x) dx= _____
converges
diverges
Math
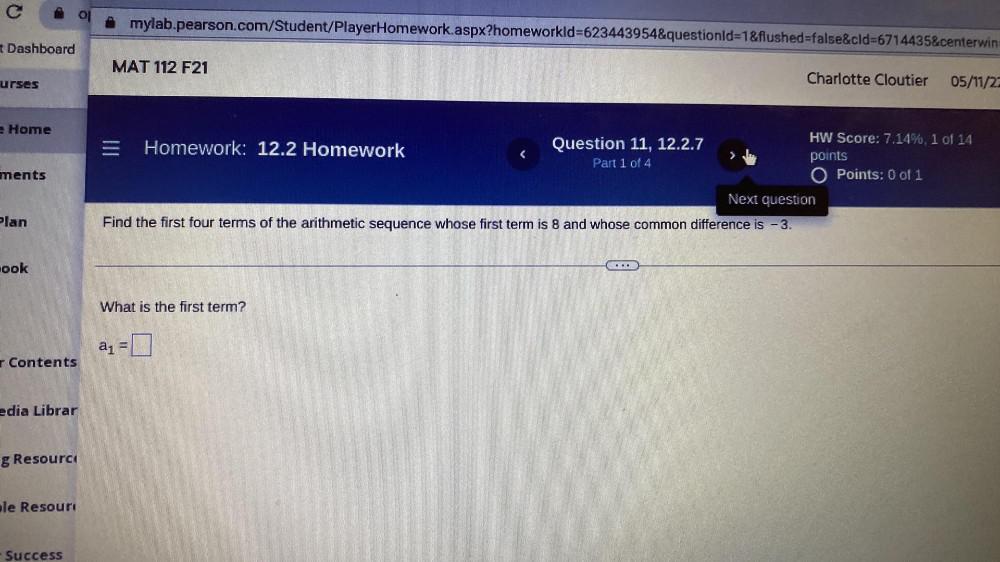
Sequences & SeriesFind the first four terms of the arithmetic sequence whose first term is 8 and whose common difference is -3.
What is the first term?
a₁ = ▢
Math
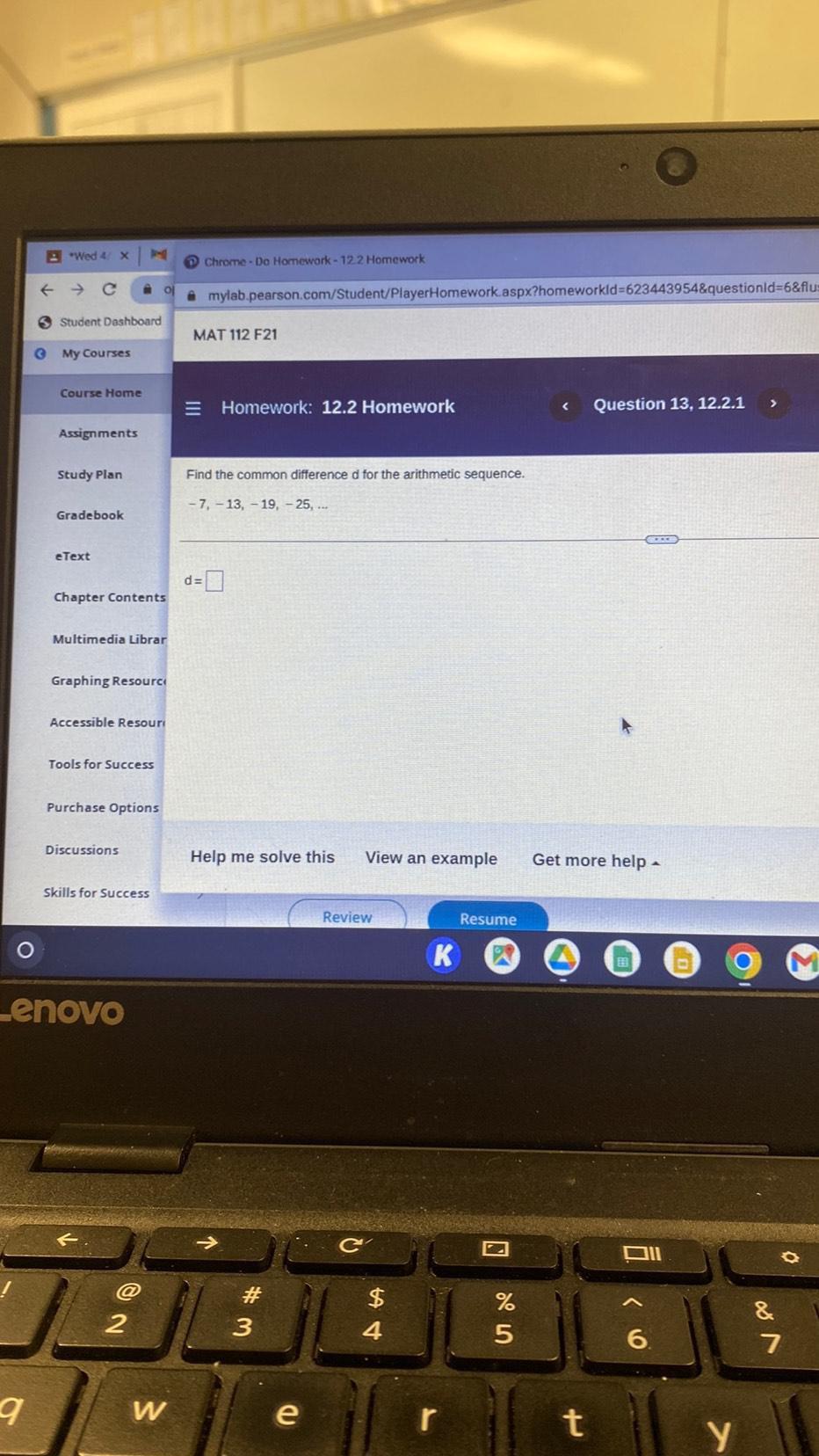
Sequences & SeriesFind the common difference d for the arithmetic sequence.
-7, -13, -19, -25,...
d = ▢
Math
Sequences & SeriesAn auditorium has 20 rows of seats. There are n = 24 seats in the first row, 25 seats in the second row, 26 seats in the third row, and so on (see figure). How many seats are there in all 20 rows? ______________ seats

Math
Sequences & SeriesConsider the series Σ1/n
(a) Does the sequence {an} = 1/n converge or diverge?
(b) Does this series converge or diverge?
(c) How many terms are required for the sum to exceed 50? Show work used to find this value.