Quadratic equations Questions and Answers

Math
Quadratic equationsA carpenter is creating two new templates for his designs One template will be in the shape of a right triangle where the longer leg is three inches more than three times the shorter leg The second template will be in the shape of a rectangle where one side length is one inch less than three times the length of the triangle s shorter leg and the other side length is one inch more than twice the width The carpenter needs the lengths of both diagonals to be the same Write a system of equations to represent this situation where yis the length of the diagonals and x is the shorter leg of the triangle Which statement describes the number and viability of the system s solutions O A OB The system has only one solution and it is viable because it results in a figure with only positive side lengths The system has only one solution but it is not viable because it it results in a figure with a negative side length OC The system has two solutions and both are viable because they result in figures with only positive side lengths OD The system has two solutions but only one is viable because the other results in a figure with negative side lengths

Math
Quadratic equationsThe value of a particular rookie baseball card was 2 00 when it was first printed Five years later when the player was at his peak the card wa valued at 25 00 Ten years after printing the card was valued at 8 00 Model the above scenario showing the value of the card y with respect to years since it was printed x Write the equation in standard form y ax bx c where a b and care real numbers rounded to the nearest tenth o 0 10 y Vo d X S 2 X 0 x 0 T a A B E 9 P P sin cos tan sin cos csc sec cot log log In tan 1 LANE U O

Math
Quadratic equations03 04 One factor of the function f x x 8x 17x 10 is x 5 Describe how to find the x intercepts and the y intercept of the graph of f x without using technology Show your work and include all intercepts in your answer

Math
Quadratic equationsMr Waller owns a company that manufactures decorative statues The revenue earned in thousands of dollars by the company each year over an eight year period is modeled by this quadratic function 3 22t2 40 63 11 17

Math
Quadratic equationsTry It Abigail has 30 00 to buy groceries She needs to buy some apples some bananas and 3 pounds of potatoes Fuji apples are 1 79 a pound bananas are 0 36 each and potatoes are 2 99 for a 3 lb bag If a represents the number of pounds of apples Abigail buys and b represents the number of bananas she buys which expression represents the amount of change she receives after her purchases 30 00 a b O 1 79a 0 36b 2 99 30 00 1 79a 0 36b 2 99 30 00 1 79a 0 36b 2 99

Math
Quadratic equationsSelect the correct answer from each drop down menu Determine the number and type of solutions for the following quadratic equations using the discriminant x2 Equation 6x 5 11 x2 241 50 L 4x 8x 10 0 15x2 2 7x 8x Number and Type of Solutions

Math
Quadratic equationsQuestion 9 of 46 Todd is attempting to predict how much money his furniture company will make based on the amount raw materials the company currently has at its disposal The average profit from the sale of 1 piece of furniture can be expressed as x 4 and the average number of pieces of furniture that can be made using the current supply of raw materials can be expressed as x 4 What polynomial function can Todd use to calculate the average profit F x x 8x 16 A B F x 4 C F x x 16 OD F x 16x 16
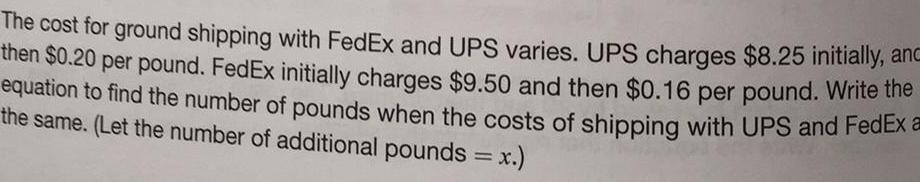
Math
Quadratic equationsThe cost for ground shipping with FedEx and UPS varies UPS charges 8 25 initially anc then 0 20 per pound FedEx initially charges 9 50 and then 0 16 per pound Write the equation to find the number of pounds when the costs of shipping with UPS and FedEx a the same Let the number of additional pounds x

Math
Quadratic equationsNeftali Moreno Miranda Solve by Trinomial Factor a 1 Nov 16 5 09 12 PM Watch help video Solve the quadratic by factoring 2x 9x13 8
Math
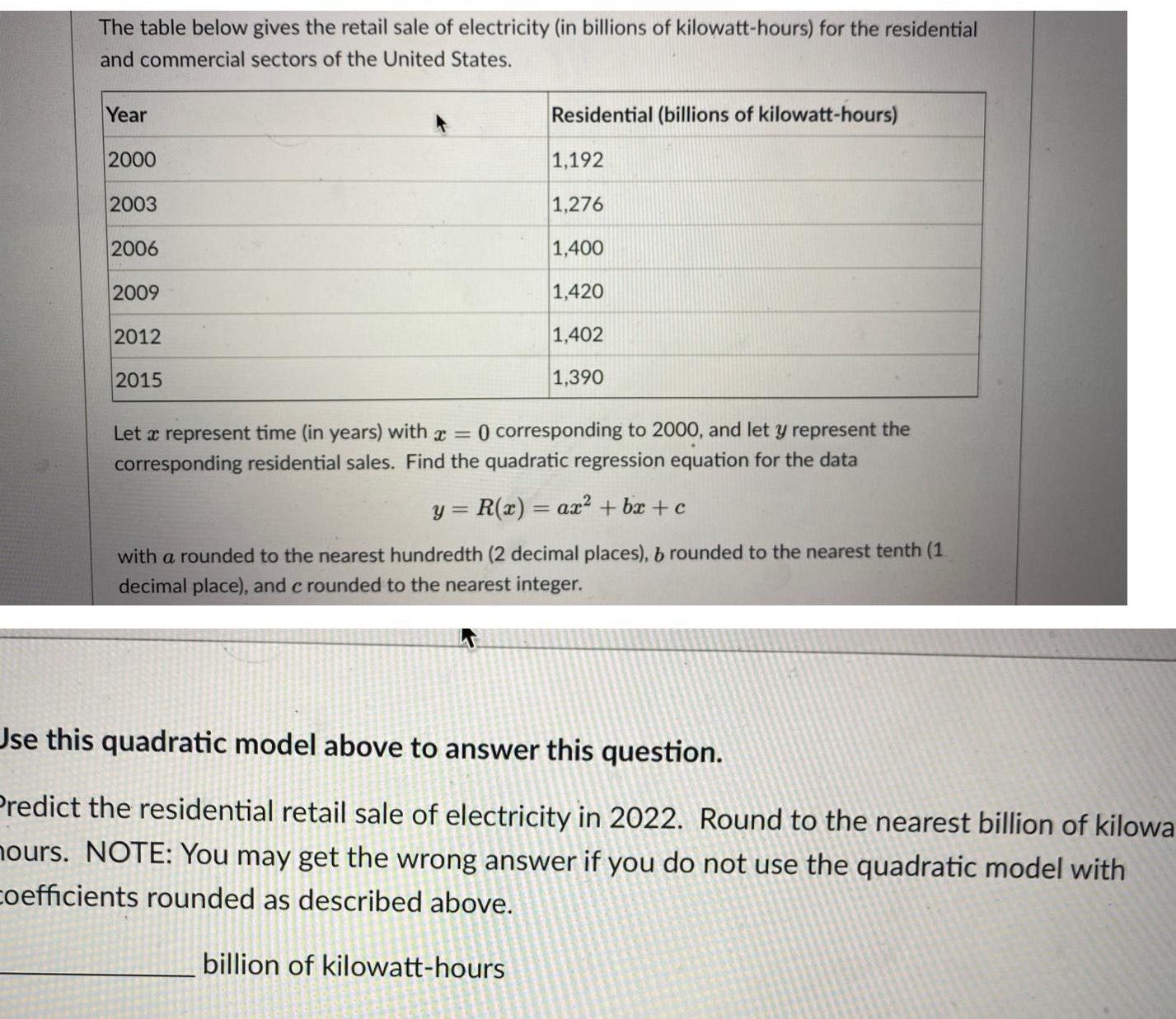
Quadratic equationsThe table below gives the retail sale of electricity in billions of kilowatt hours for the residential and commercial sectors of the United States Year 2000 2003 2006 2009 2012 2015 Residential billions of kilowatt hours 1 192 1 276 1 400 1 420 1 402 1 390 Let a represent time in years with 0 corresponding to 2000 and let y represent the corresponding residential sales Find the quadratic regression equation for the data y R x ax bx c with a rounded to the nearest hundredth 2 decimal places b rounded to the nearest tenth 1 decimal place and c rounded to the nearest integer Use this quadratic model above to answer this question Predict the residential retail sale of electricity in 2022 Round to the nearest billion of kilowa hours NOTE You may get the wrong answer if you do not use the quadratic model with coefficients rounded as described above billion of kilowatt hours
Math
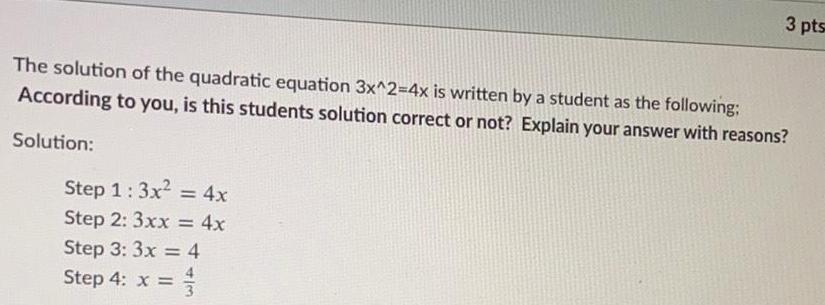
Quadratic equations3 pts The solution of the quadratic equation 3x 2 4x is written by a student as the following According to you is this students solution correct or not Explain your answer with reasons Solution Step 1 3x 4x Step 2 3xx 4x Step 3 3x 4 Step 4 x
Math
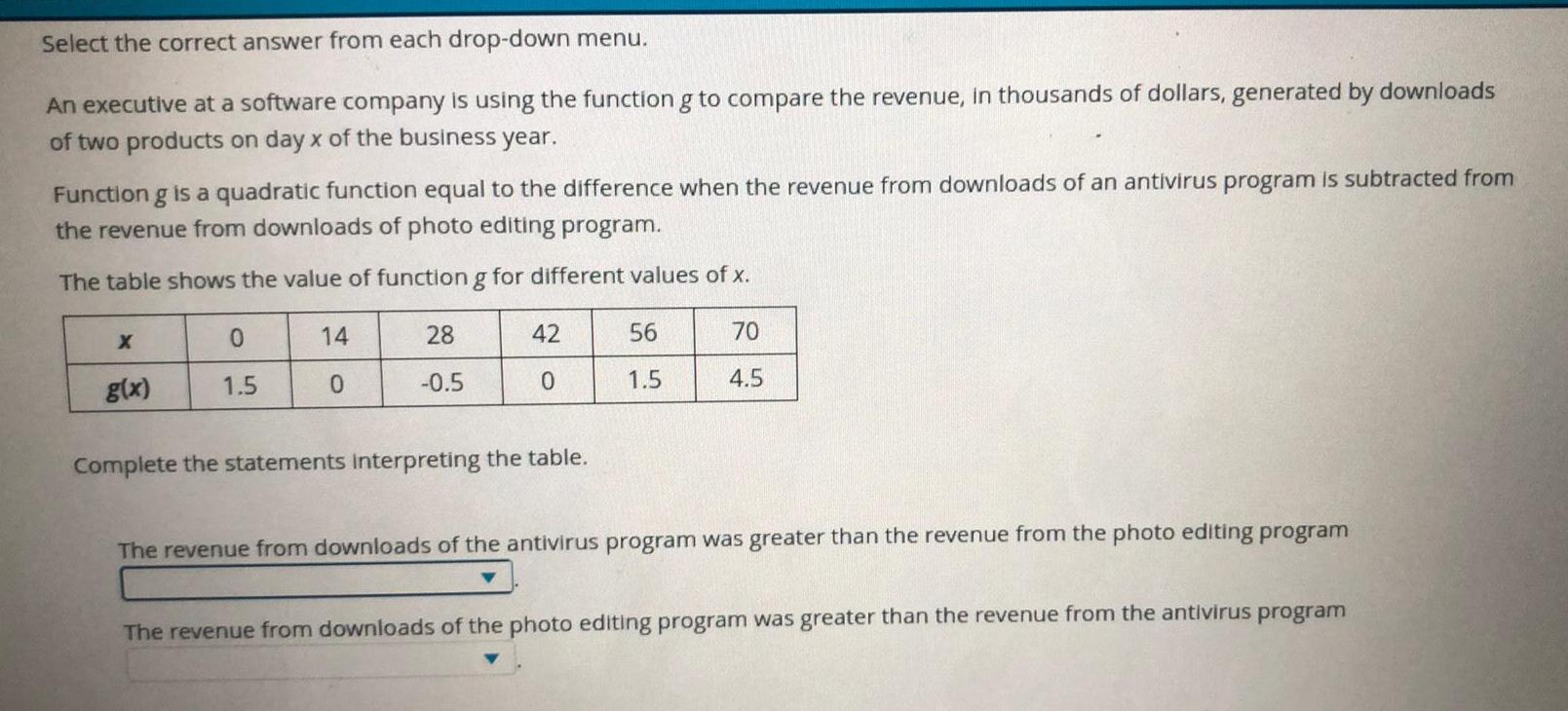
Quadratic equationsSelect the correct answer from each drop down menu An executive at a software company is using the function g to compare the revenue in thousands of dollars generated by downloads of two products on day x of the business year Function g is a quadratic function equal to the difference when the revenue from downloads of an antivirus program is subtracted from the revenue from downloads of photo editing program The table shows the value of function g for different values of x X g x 0 1 5 14 0 28 0 5 42 0 Complete the statements Interpreting the table 56 1 5 70 4 5 The revenue from downloads of the antivirus program was greater than the revenue from the photo editing program The revenue from downloads of the photo editing program was greater than the revenue from the antivirus program

Math
Quadratic equationsYou throw a baseball upward with an initial velocity of 56 feet per second. The height h (in feet) of the baseball relative to your glove is modeled by the position function h(t)= -16t2+56t where t is the time in seconds. How long does it take for the ball to reach your glove? (Round your answer to one decimal place.)

Math
Quadratic equationsYou are working with the following quadratic function: y = x² - 2x - 8
a) Write the quadratic in factored form: y=
b) Complete the square to write the quadratic in vertex form: y =
Identify the vertex of the parabola:
Remember that the vertex is a point!
Identify the y-intercept of the parabola:
Remember that the y-intercept is a point!
Identify the x-intercepts: and
Remember that the x-intercepts represent points on the graph!
Math
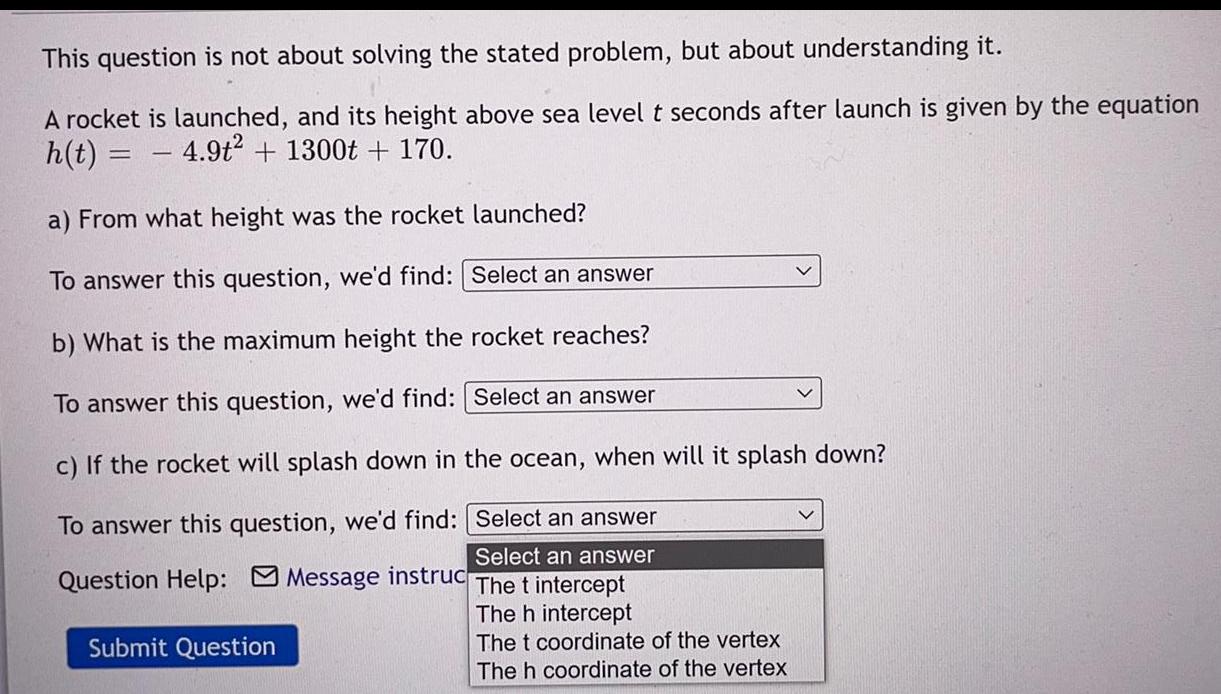
Quadratic equationsThis question is not about solving the stated problem, but about understanding it.
A rocket is launched, and its height above sea level t seconds after launch is given by the equation h(t) = 4.9t² + 1300t + 170.
a) From what height was the rocket launched?
b) What is the maximum height the rocket reaches?
c) If the rocket will splash down in the ocean, when will it splash down?
Math
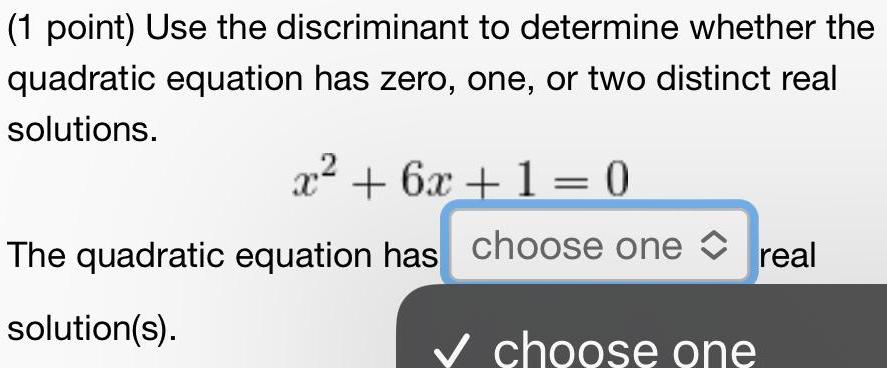
Quadratic equationsUse the discriminant to determine whether the quadratic equation has zero, one, or two distinct real solutions.
x² + 6x + 1 = 0
The quadratic equation has choose one real
solution(s).
Math
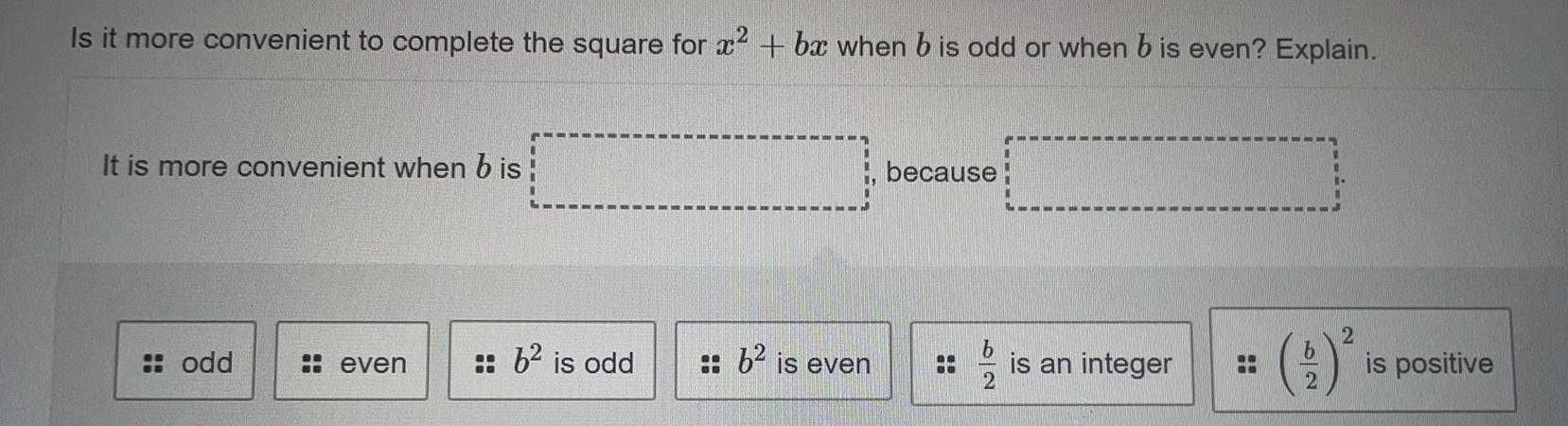
Quadratic equationsIs it more convenient to complete the square for x^2 + bx when bis odd or when b is even? Explain.

Math
Quadratic equationsSolve the following quadratic expressions by factoring. First write the expressions in completely factored form. Then write the real number solutions. [Hint: Remember to use proper notation when writing the real number solutions. For example: if the solutions are a = 1 and x = 4, write x 1,4

Math
Quadratic equationsA jazz group on tour has been drawing average crowds of 1000 people. It is projected that for every $1 increase in the $17 ticket price, the average attendance will decrease by 60. What equation could be used to solve this problem and at what ticket price will nightly receipts be $16,400?
A) (17+x)(1000-60x)=16400;
$20
B) (17x)(1000x-60)=16400;
$20
C) (17+x)(1000-60x)=16400;
$19
D) (17-x)(1000+60x)=16400;
Math
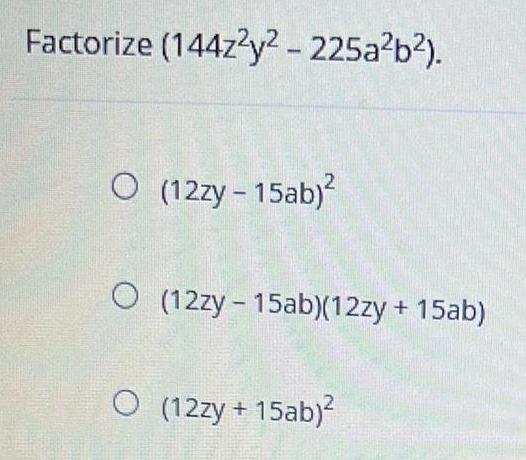
Quadratic equationsFactorize (144z2y² - 225a²b²).
(12zy - 15ab)²
(12zy-15ab)(12zy + 15ab)
(12zy + 15ab)²

Math
Quadratic equations3. Find the zeros of the quadratic function by graphing. Round to the nearest tenth if necessary.
f(x) = -2x² + 3x + 1
0.8,2.1) is a zero of the quadratic function because it is the peak of the parabola.
(-0.3,0) and (1.8,0) are zeros of the quadratic function because it is where the parabola crosses the x-axis.
(0.8,2.1) and (0,1) are zeros of the quadratic function because it is where the parabola crosses the x-axis...
(0.1) is a zero of the quadratic because it is where the parabola crosses the y-axis.
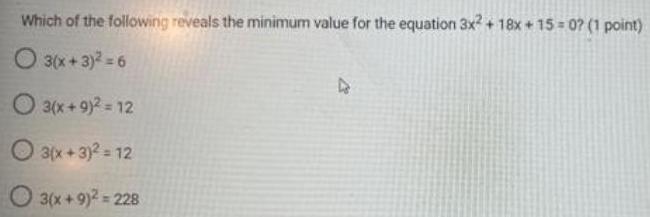
Math
Quadratic equationsWhich of the following reveals the minimum value for the equation 3x2 + 18x+15=0?
3(x+3)² = 6
3(x+9)² = 12
3(x+3)² = 12
3(x+9)² = 228

Math
Quadratic equationsConsider the parabola given by the equation:
y = 1x² + 14x - 33
Find the following for this parabola:
A) The vertex = (
B) The y intercept is the point (0,
C) Find the two values of a that correspond to the intercepts of the parabola and write them as a list, separated by commas:

Math
Quadratic equationsA person standing close to the edge on top of a 112-foot building throws a ball vertically upward. The quadratic function h(t)=16t² +96t+ 112 models the ball's height about the ground, h(t), in feet, t seconds after it was thrown.
a) What is the maximum height of the ball?
b) How many seconds does it take until the ball hits the ground?
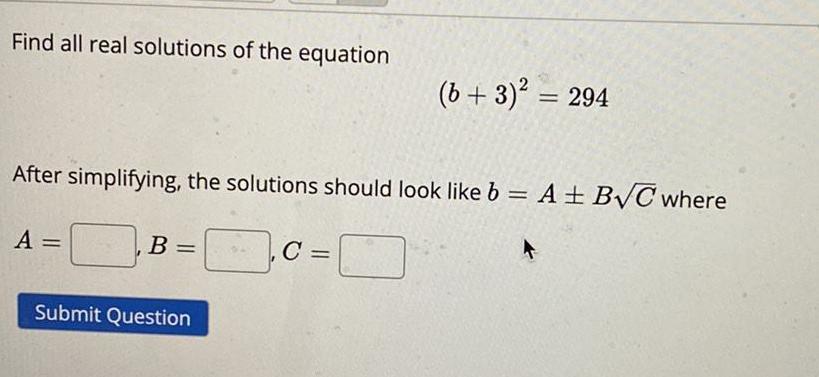
Math
Quadratic equationsFind all real solutions of the equation
(b + 3)² = 294
After simplifying, the solutions should look like b = A +- B√C where
A =
B =
C =
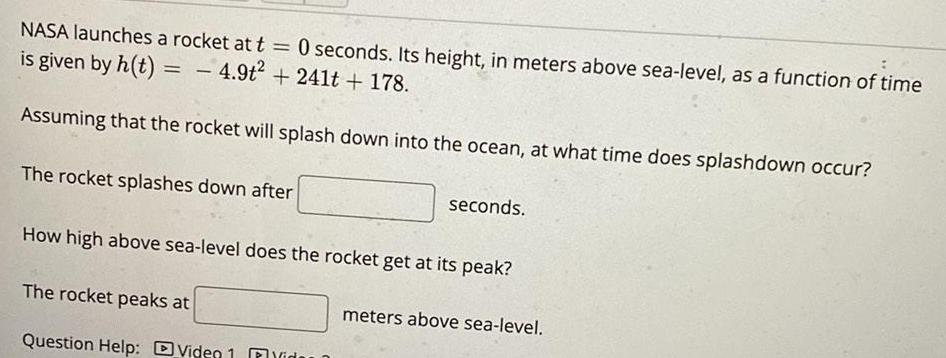
Math
Quadratic equationsNASA launches a rocket at t = 0 seconds. Its height, in meters above sea-level, as a function of time is given by h(t) = -4.9t² +241t+ 178. Assuming that the rocket will splash down into the ocean, at what time does splashdown occur? The rocket splashes down after seconds. How high above sea-level does the rocket get at its peak?

Math
Quadratic equationsAn object is thrown upward at a speed of 132 feet per second by a machine from a height of 17 feet
off the ground. The height of the object after t seconds can be found using the equation
s(t) = 16t² + vot + so, where is the initial velocity and so is the initial height. Give all
numerical answers to 2 decimal places.
(a) When will the object reach its maximum height?
(b) What is its maximum height?
(c) When will the object reach the ground?
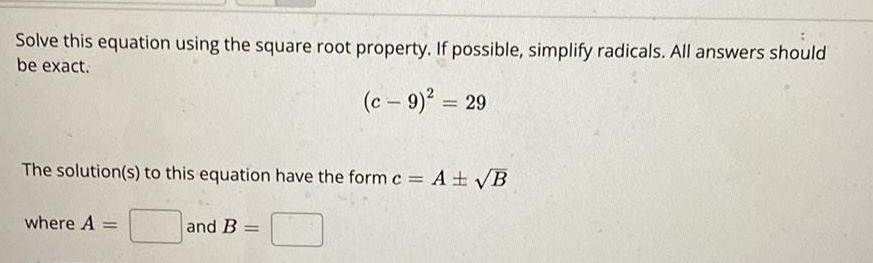
Math
Quadratic equationsSolve this equation using the square root property. If possible, simplify radicals. All answers should be exact.
(c - 9)² = 29
The solution(s) to this equation have the form c = A ± √B
Math
Quadratic equationsGraph f(x) = 2x² 24x70 below by first selecting the correct shape, clicking the vertex, then clicking an x-intercept.

Math
Quadratic equationsConsider the quadratic function f(x) = x² - 2x - 24.
Determine the following: (enter all numerical answers as integers, fractions, or decimals):
The smallest x-intercept is =
The largest x-intercept is x =
The y-intercept is y =
The vertex is =
The line of symmetry has the equation

Math
Quadratic equationsSolve for x.
x²+2x+1=0
If there is more than one solution, separate them with commas.
If there is no solution, click on "No solution."

Math
Quadratic equationsUse the discriminant b² 4ac to determine the number of solutions.
9x² - 6x +1=0
Remember:
If discriminant = negative --> no real solutions
If discriminant = zero --> 1 real solution
if discriminant = positive --> 2 real solutions
No real solutions
1 real solution
O2 real solutions
Math
Quadratic equationsSolve by completing the square.
-3f² + 18f = -33
Write your answers as integers, proper or improper fractions in simplest form, or decimal rounded to the nearest hundredth.
f = or f =

Math
Quadratic equationsSolve by completing the square.
h² + 4h = 29
Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.
h
or h=

Math
Quadratic equationsJohn owns a hot dog stand. He has found that his profit is given by the equation P= -x² + 60x + 71, where x is the number of hot dogs sold. How many hot dogs must he sell to earn the maximum profit?
20 hot dogs
31 hot dogs
41 hot dogs
30 hot dogs

Math
Quadratic equationsGiven f(x) = x² - 2x - 3
a. Evaluate f(-3).
b. Find the vertex of the parabola.
c. Determine the x- and y-intercepts. Write the intercepts as ordered pairs.
d. Sketch the graph. Label the vertex and intercepts.

Math
Quadratic equationsA farmer needs to enclose three sides of a plot with a fence (the fourth side is a river). The farmer has 35 feet of fence and wants the plot to have an area of 150 sq-feet. What should the dimensions of the plot be? (For the purpose of this problem, the width will be the smaller dimension (needing two sides); the length with be the longer dimension (needing one side). Additionally, the length should be as long as possible.)
length= feet
width= feet
Math
Quadratic equationsThere are two machines that produce aluminum cans. The newer machine can produce 5400 cans in 180 minutes. It takes the older machine 270 minutes to produce that many cans. If the two machines work together, how long will it take them to produce 5400 cans?
________minutes
Math
Quadratic equationsFind the formula, in standard form y = ar²+bx+c, for a quadratic that has roots at x = -9 and x = 5, and has leading coefficient of 1.
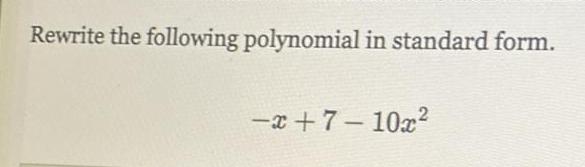


Math
Quadratic equationsThe sum of a number and its reciprocal is 17/4
The number is
Find the number.
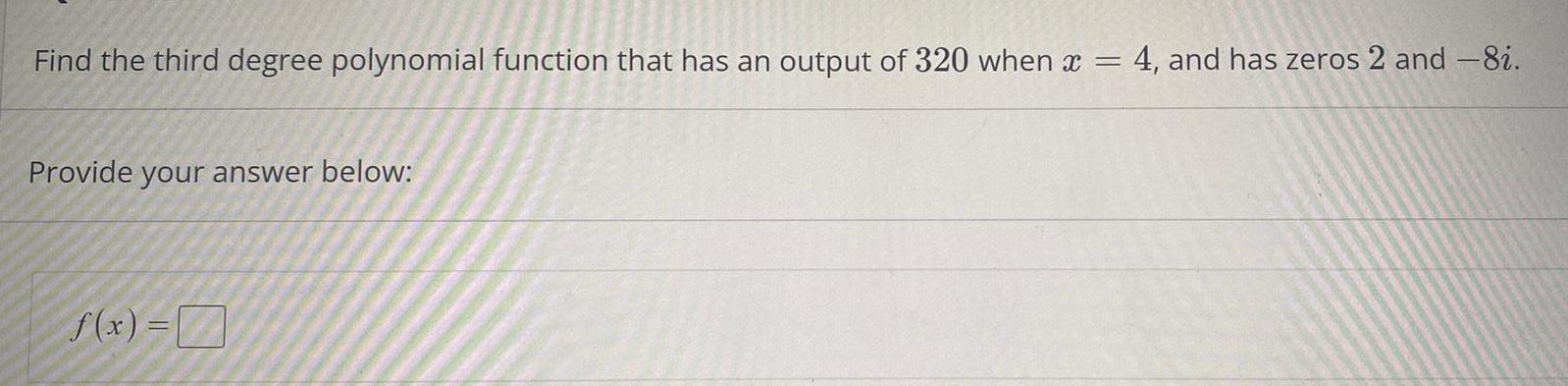
Math
Quadratic equationsFind the third degree polynomial function that has an output of 320 when x = = 4, and has zeros 2 and -8i. Provide your answer below:
f(x) = 7
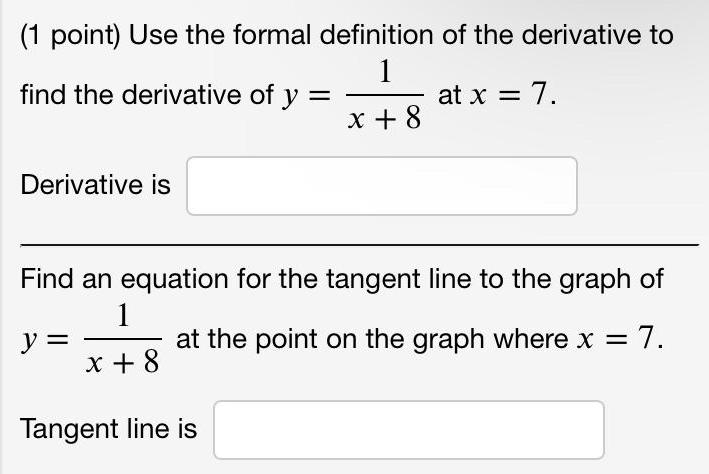
Math
Quadratic equationsUse the formal definition of the derivative to find the derivative of y= 1/x+8 at x= 7
Derivative is
Find an equation for the tangent line to the graph of y= 1/x+8
Tangent line is
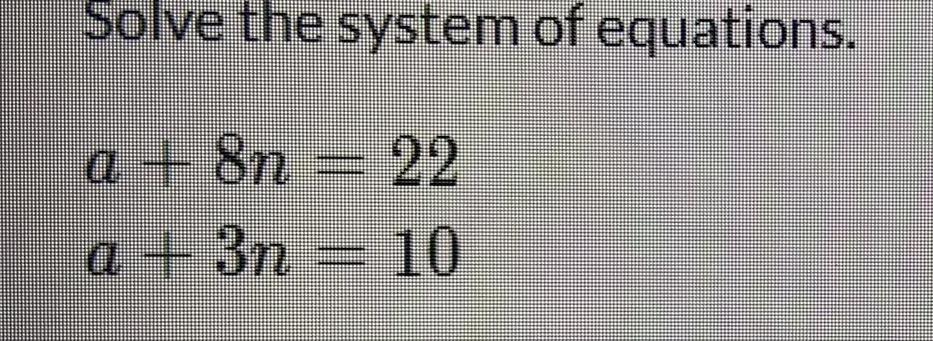

Math
Quadratic equations5. Jessica is building a model rocket for her physics class. After studying the flight path of her rocket, she has concluded that she wants her rocket to achieve a maximum height of 50 ft. The equation for her rocket is -3x² + 6x + 48. Will Jessica's rocket clear 50 ft?: (Hint Find the vertex of the equation to find the maximum height of the rocket)

Math
Quadratic equationsGiven the functiony = -2x² -5x - 4, give the number and type of solutions. Then use the quadratic formula to find the zeros. Show all work to receive full credit. Please upload a photo of your work.
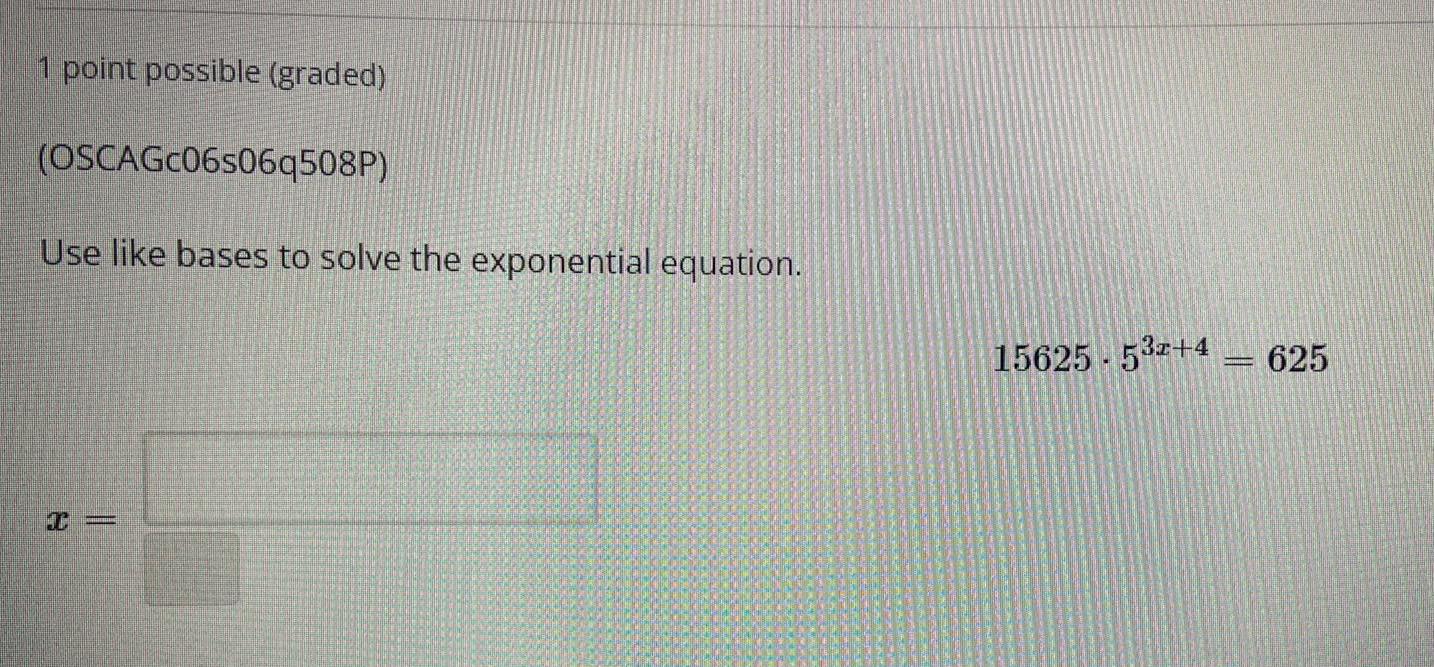

Math
Quadratic equationsFind the coordinates for the vertex of the following quadratic function algebraically.
Be prepared to show your algebraic work.
P(x) = -9x + x2
Enter the exact coordinates separately in each blank. (Do not round values.)
The vertex is (
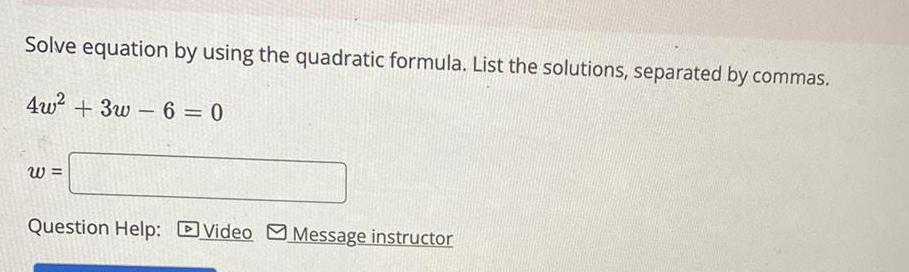
Math
Quadratic equationsSolve equation by using the quadratic formula. List the solutions, separated by commas.
4w²+3w6=0
W=