Hyperbola Questions and Answers
Math
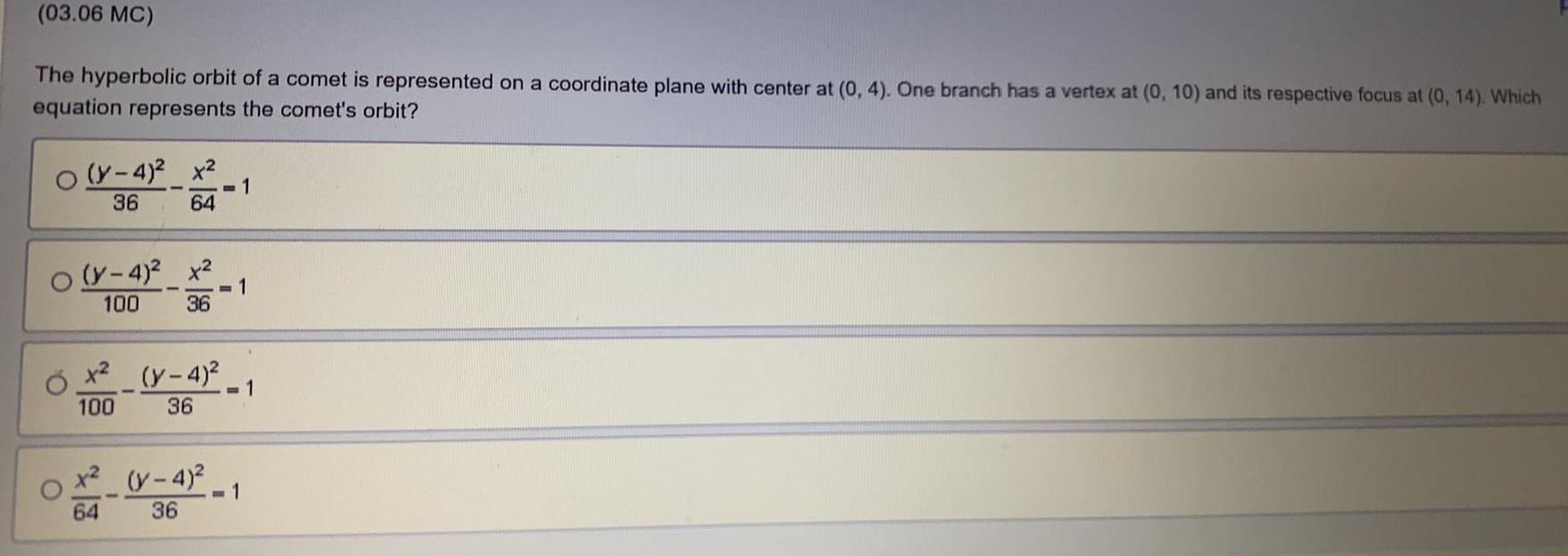
Hyperbola03 06 MC The hyperbolic orbit of a comet is represented on a coordinate plane with center at 0 4 One branch has a vertex at 0 10 and its respective focus at 0 14 Which equation represents the comet s orbit O O O y 4 x 36 y 4 x 100 36 64 52 1 64 1 x y 4 100 36 1 y 4 1 36
Math
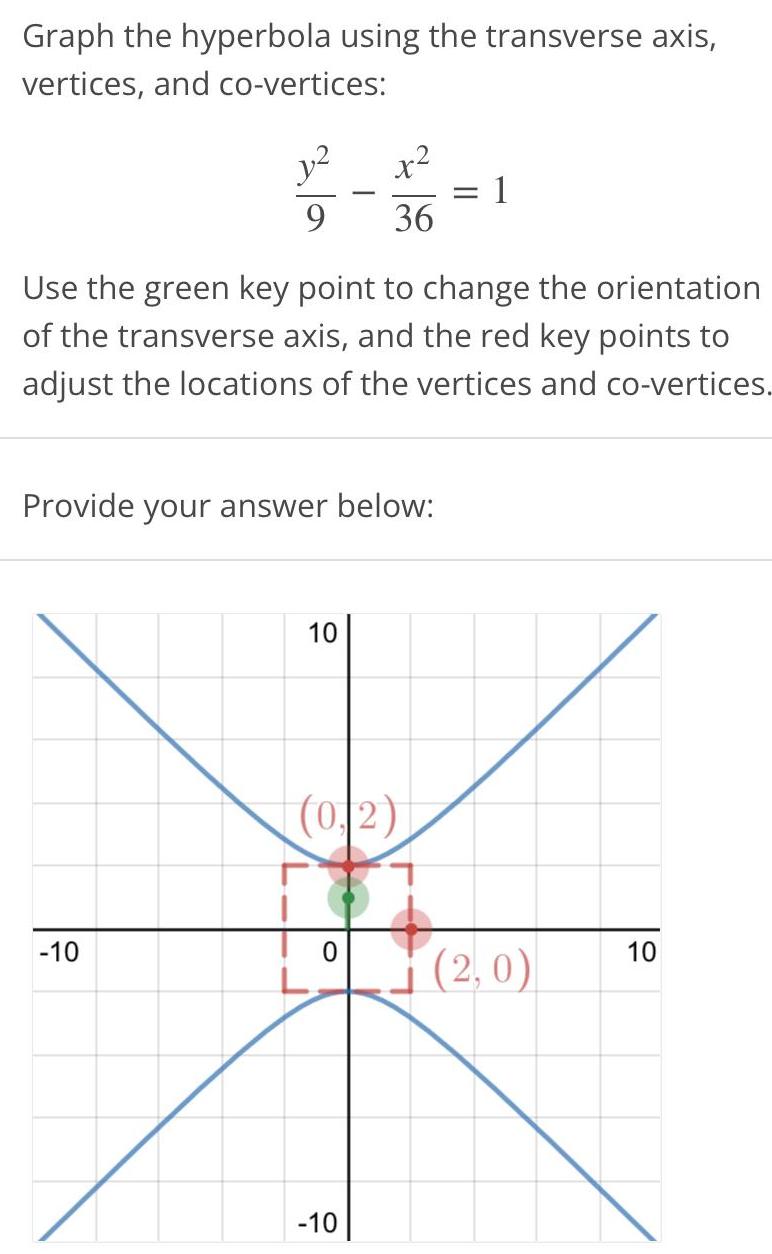
HyperbolaGraph the hyperbola using the transverse axis vertices and co vertices y x 22 12 1 9 36 Use the green key point to change the orientation of the transverse axis and the red key points to adjust the locations of the vertices and co vertices Provide your answer below 10 10 0 2 10 2 0 10

Math
HyperbolaA table lamp emits light in the shape of a hyperbola If the hyperbola is modeled by the equation 25x 144y 2 3 600 0 which of the following equations represents the boundaries of the light Oy 5 12 5 x and y 12 X Oy 12x and y 12x 5 5 5 Oy x and y x X 13 13

Math
HyperbolaFind the standard form of the equation of the hyperbola satisfying the given conditions.
x-intercepts ±6, foci at (-10,0) and (10,0)
Math
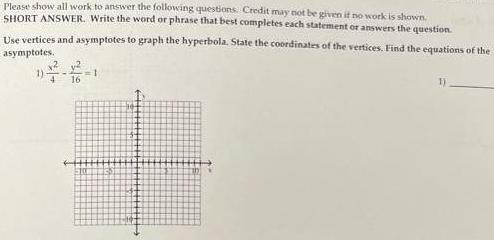
HyperbolaUse vertices and asymptotes to graph the hyperbola. State the coordinates of the vertices. Find the equations of the asymptotes.
1) (x^2/4)-(y^2/16)=1
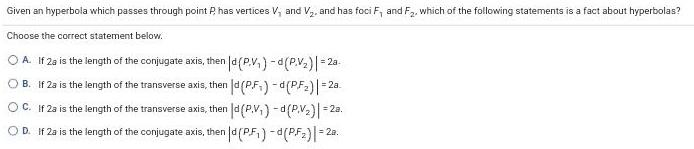
Math
HyperbolaGiven an hyperbola which passes through point P has vertices V, and V₂, and has foci F, and F₂, which of the following statements is a fact about hyperbolas?
Choose the correct statement below.
A. If 2a is the length of the conjugate axis, then |d (P,V₁)-d(P,V₂)|= 2a.
B. If 2a is the length of the transverse axis, then d (P,F₁)-d(P,F₂)|=2a.
C. If 2a is the length of the transverse axis, then |d (P,V₁)-d(P,V₂)|=2a.
D. If 2a is the length of the conjugate axis, then |d (P,F₁) -d (P,F₂)|=20.
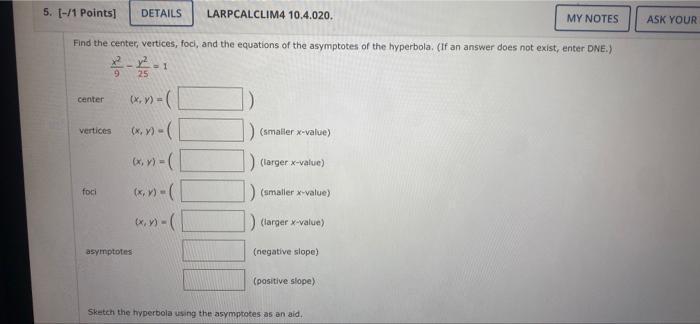
Math
HyperbolaFind the center, vertices, foci, and the equations of the asymptotes of the hyperbola. (If an answer does not exist, enter DNE.)
(x^2)/9 - (y)^2/25 =1
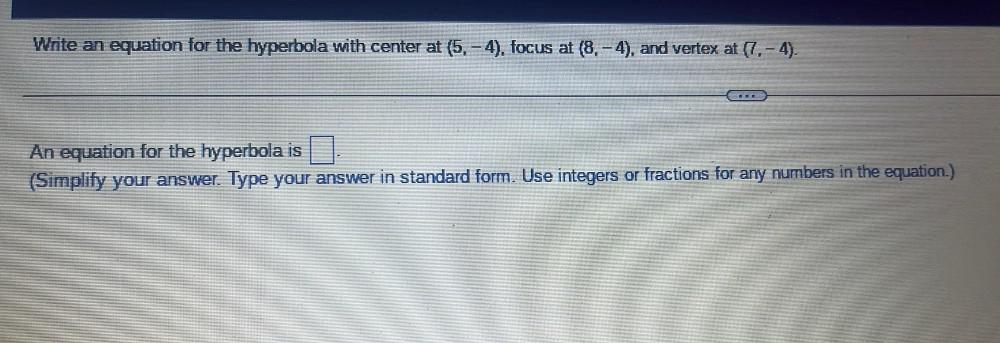
Math
HyperbolaWrite an equation for the hyperbola with center at (5, – 4), focus at (8, – 4), and vertex at (7, - 4).
An equation for the hyperbola is ____ .

Math
HyperbolaThe cross-section of a nuclear power plants cooling tower is in the shape of a hyperbola. Suppose the tower has a base diameter of 264 meters and the diameter at its narrowest point, 56 meters above the ground, is 88 meters. If the diameter at the top of the tower is 176 meters, how tall is the tower?

Math
HyperbolaThe cross-section of a nuclear power plant's cooling tower is in the shape of a hyperbola. Suppose the tower has a base diameter of 210 meters and the diameter at its narrowest point, 48 meters above the ground, is 70 meters. If the diameter at the top of the tower is 140 meters, how tall is the tower?
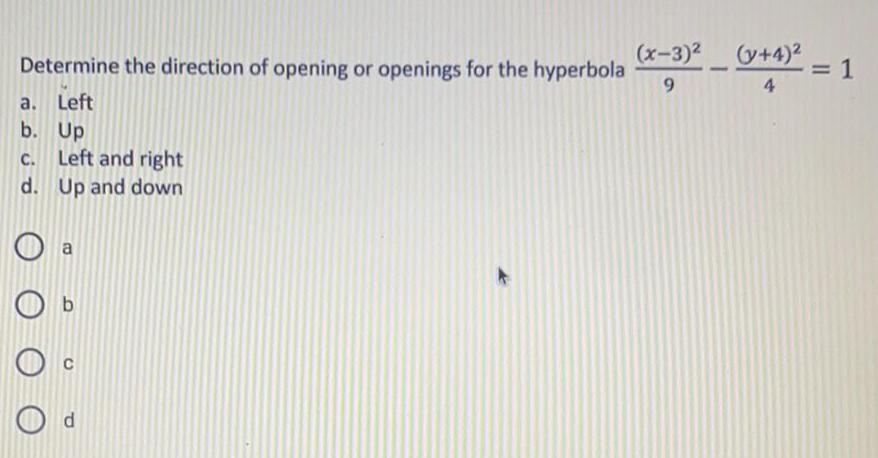
Math
HyperbolaDetermine the direction of opening or openings for the hyperbola (x-3)²/9 - (y+4)²/4 = 1
a. Left
b. Up
c. Left and right
d. Up and down
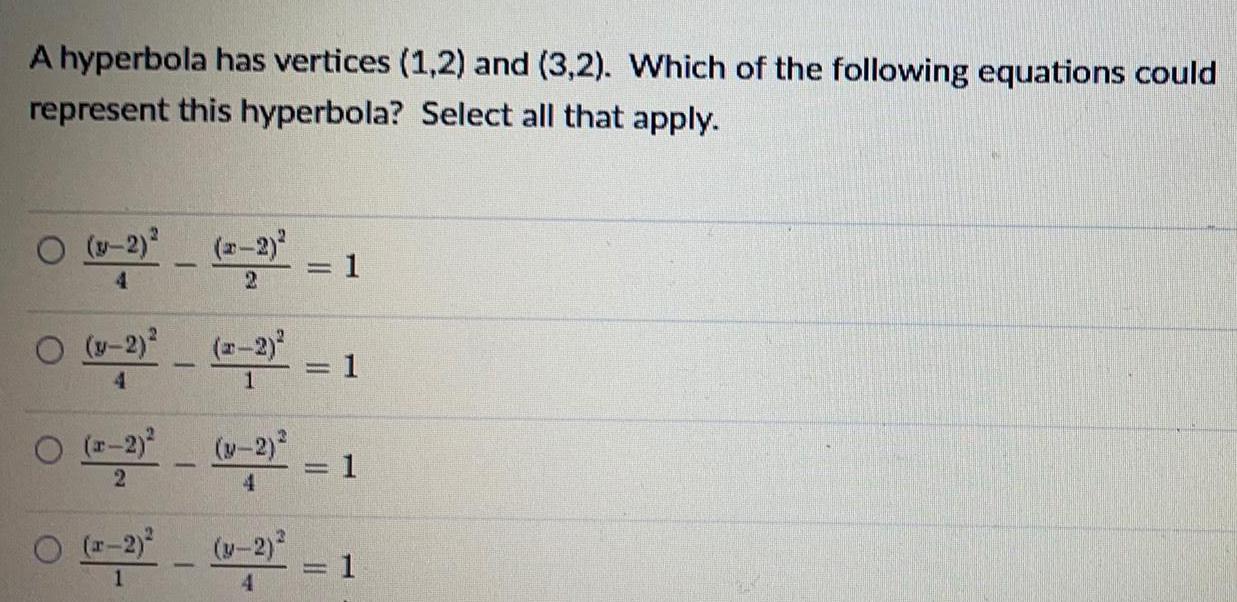
Math
HyperbolaA hyperbola has vertices (1,2) and (3,2). Which of the following equations could
represent this hyperbola? Select all that apply.

Math
Hyperbola7. Given the following information, write the standard form equation of each hyperbola and determine the equations for the asymptote lines of the hyperbola.
a. Vertices: (-5, 5), (-5, 3): Foci: (-5, 6), (-5, 4)
b. Vertices: (-10, 1), (-10, 17); Perimeter of Central Rectangle = 76

Math
HyperbolaConsider the equations below and complete the following:
Before completing any calculations, consider the equation and write down an educated guess
as to which type of conic section is represented. Explain briefly how you made your prediction.
Complete the square to rearrange each equation into standard form and identify the conic
section.
Compare the equation in standard form to the original version. Look closely at the coefficients of
each term (specifically which terms are positive or negative). Is there anything you notice that is
similar between the two equations? How can this help you to identify conic sections that are not
in standard form?
a. x² + y² + 6x - 4y - 15 = 0
b. 49x² + 196x + 4y² - 40y + 100 = 0
c. x² - y² - 2x - 8=0

Math
HyperbolaA telescope contains both a parabolic mirror and a hyperbolic mirror. They share focus F₁, which is 42 feet above the vertex of the parabola. The hyperbola's second focus F2 is 6 ft above the parabola's vertex. The vertex of the hyperbolic mirror is 3 ft below F₁. Find the equation of the hyperbola if the center is at the origin of a coordinate system and the foci are on the y-axis. Complete the equation.

Math
HyperbolaThe eccentricity of a hyperbola is defined as e = c/a. Find an equation of a hyperbola with vertices (1,-1) and (-5, -1) and e=5/3 The equation of the hyperbola is

Math
HyperbolaFind the vertices and asymptotes of x²/49-y²/9=1
List the coordinates of the vertices:
Write the equation of the asymptote with positive slope:
y=

Math
HyperbolaYour mission is to track incoming meteors to predict
whether or not they will strike Earth. Since Earth has a
circular cross section, you decide to set up a coordinate
system with its origin at Earth's center. The equation of
Earth's surface is x² + y² = 40.68, where x and
y are distances in thousands of kilometers.
You observe a meteor moving along a path from left to
240/289(y – 14)² – x² = 60
y ≤ 5.5. What conic section does the path of the meteor
travel?
The meteor's path is a(n)
What is the center of the conic section that describes the
path of the meteor?
Determine if the meteor will strike the earth and if it does
strike the earth at what point.
If the meteor doesn't strike the earth then enter NAN for
the coordinate.

Math
HyperbolaSketch a graph of each conic section from the Discuss below without using a graphing calculator. Show all of
your work. For ellipses, circles, and hyperbolas, clearly label the coordinates of the center, vertices, and
co-vertices on your graph. For parabolas, clearly label the coordinates of the vertex and focus and equation of
the directrix on your graph.
1. 2y² +12y=x²-14
Math
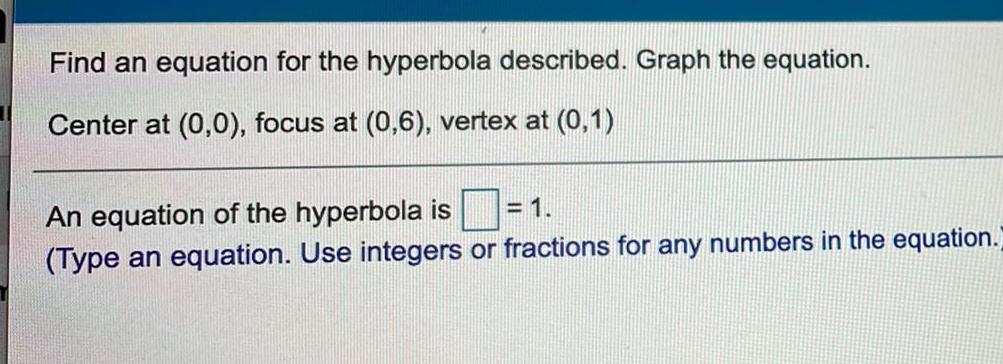
HyperbolaFind an equation for the hyperbola described. Graph the equation.
Center at (0,0), focus at (0,6), vertex at (0,1)
An equation of the hyperbola is
= 1.
(Type an equation. Use integers or fractions for any numbers in the equation.
Math
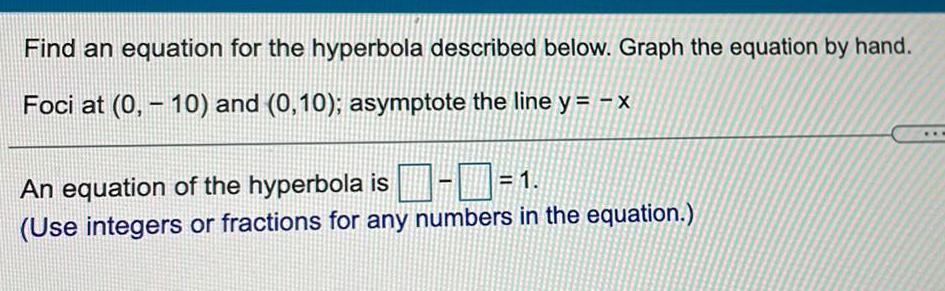
HyperbolaFind an equation for the hyperbola described below. Graph the equation by hand.
Foci at (0, 10) and (0,10); asymptote the line y = -x
An equation of the hyperbola is-= 1.
(Use integers or fractions for any numbers in the equation.)

Math
HyperbolaA table lamp emits light in the shape of a hyperbola. If the hyperbola is modeled by the equation 25x2 - 144y2 + 3,600 = 0, which of the following equations represents the
boundaries of the light?
5
y-x and y=--
3
y =
5
12
Oy-1x and y--12x
5
12
13
X
5
5
-x and y=-- X
13
13
y-x and y--13x
y=-
Math
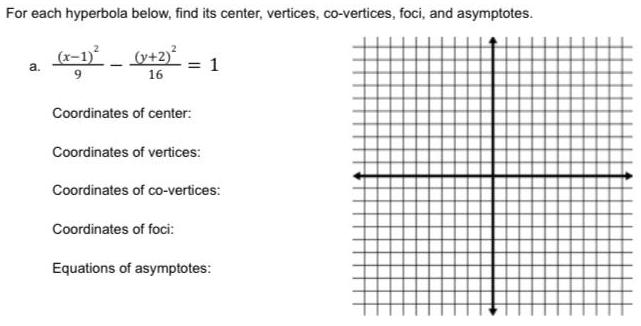
HyperbolaFor each hyperbola below, find its center, vertices, co-vertices, foci, and asymptotes.
a.(x−1)²/9 -(y+2)² /16= 1
Coordinates of center:
Coordinates of vertices:
Coordinates of co-vertices:
Coordinates of foci:
Equations of asymptotes:
Math
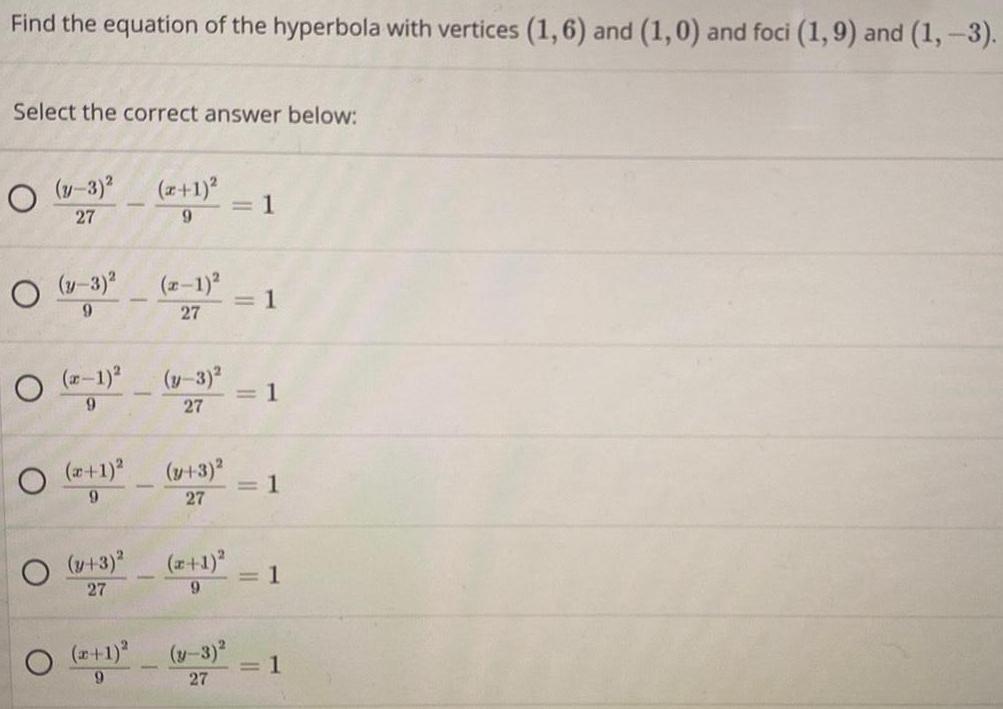
HyperbolaFind the equation of the hyperbola with vertices (1,6) and (1,0) and foci (1,9) and (1, -3).
Select the correct answer below:
(y-3)²/27 - (x+1)³/9 = 1
(y-3)²/9 -(x-1)²/27 = 1
(x-1)²/9 - (y-3)²/27 = 1
(x+1)²/9 - (y+3)²/27 = 1
(y+3)²/27 - (x+1)²/9 = 1
(x+1)²/9 - (y-3)²/27 = 1
Math
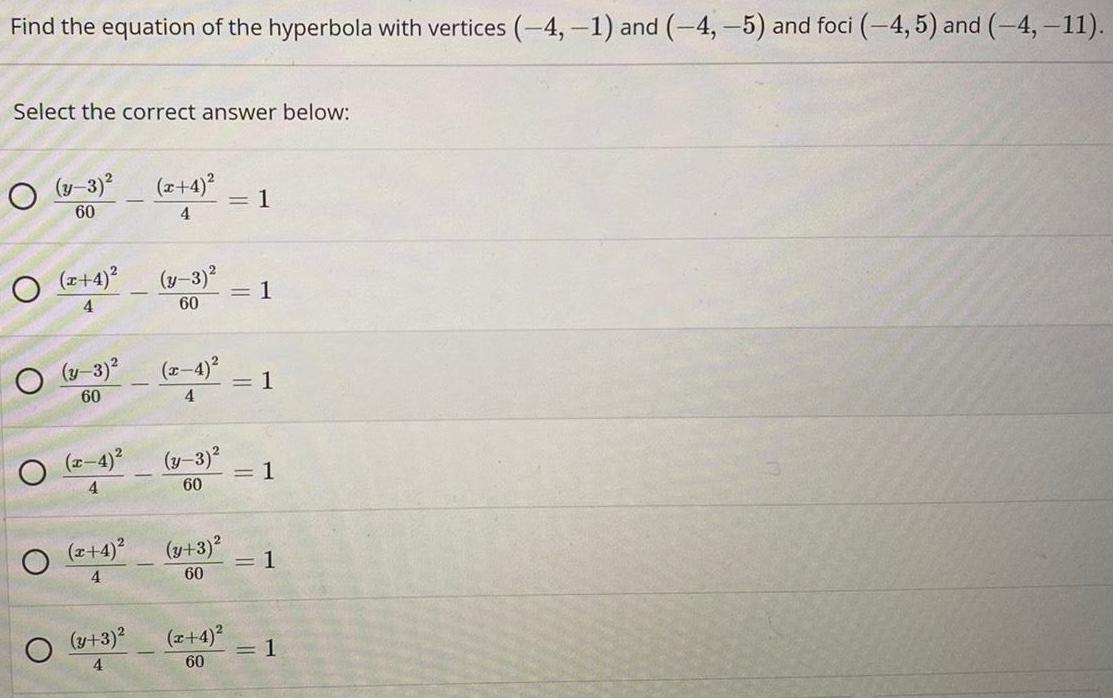
HyperbolaFind the equation of the hyperbola with vertices (-4,-1) and (-4,-5) and foci (-4,5) and (-4,-11).
Select the correct answer below:
O (3-3)²
60
(x+4)²
O (3-3)²
60
O(x-4)²
4
O(x+4)²
4
(y+3)²
4
(x+4)²
4
(y-3)²
60
4
(y-3)²
60
(y+3)²
60
(x+4)²
60
= 1
= 1
= 1
= 1
= 1
= 1

Math
HyperbolaWrite the following conic equation in standard form and use that equation to graph the conic. Identify any vertices, foci, major, minor or transverse axes or directrixes that apply.
4x²-25y² +50y-24 = 16x+85

Math
HyperbolaUse the information provided to write the standard form equation of the hyperbola. Show your work using either the equation editor or submit your work in the dropbox.
Vertices: (8, -1) and (-4,-1)
Endpoints of Conjugate Axis: (2, 2) and (2,-4)
Math
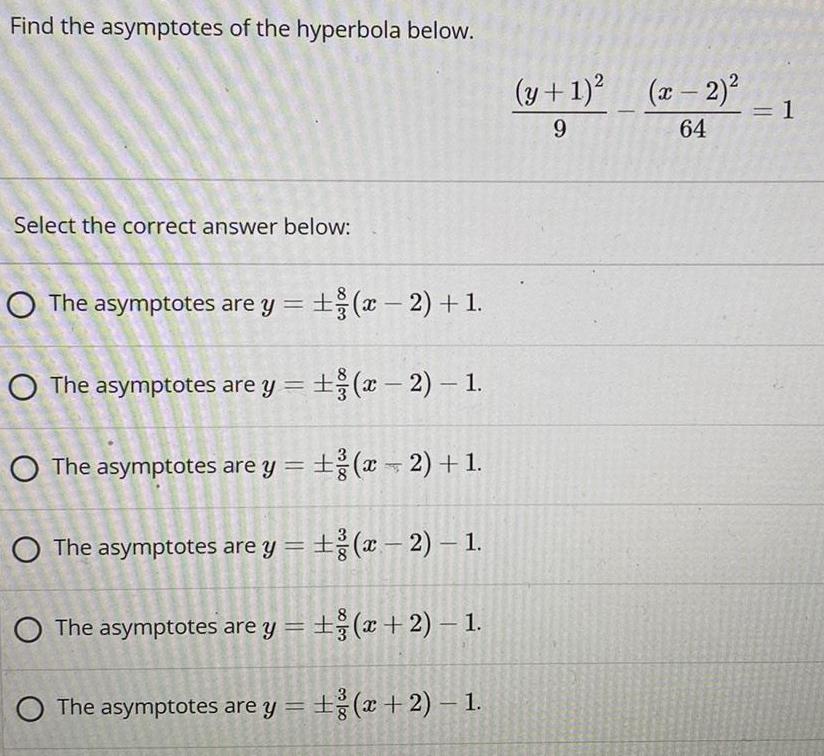
HyperbolaFind the asymptotes of the hyperbola below.
(y + 1)²/9 - (x - 2)² / 64 = 1
Select the correct answer below:
The asymptotes are y = ±8/3(x − 2) + 1.
The asymptotes are y = ±8/3(x − 2) - 1.
The asymptotes are y = ±3/8(x-2) + 1.
The asymptotes are y = ±3/8(x-2) – 1.
The asymptotes are y = ±8/3(x+2) – 1
The asymptotes are y = ±3/8(x+2) – 1
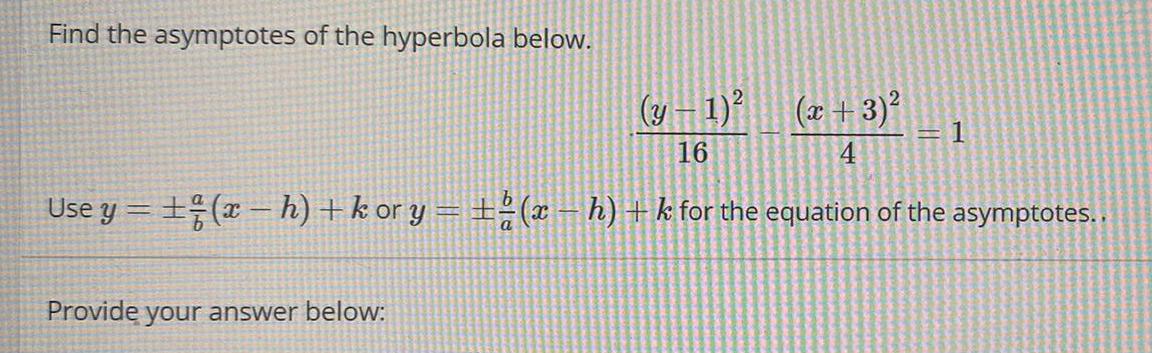
Math
HyperbolaFind the asymptotes of the hyperbola below.
Use y -
(y − 1)²/16- (x+3)²/4 = 1
±a/b(x − h) + k or y = ±2b/a(x − h) + k for the equation of the asymptotes..

Math
HyperbolaA vase can be modeled using x^2 / 5.5225 - (y-5)^2 / 42.25 = 1 and the x-axis, for 0 ≤ y ≤ 20, where the measurements are in inches. Using the graph, what is the distance across the base of the vase, and how does it relate to the hyperbola?
5.93 inches; distance between the x-intercepts
4.50 inches; length of the transverse axis
2.97 inches; distance between the intercepts
2.35 inches; length of the transverse axis

Math
HyperbolaA telescope contains both a parabolic mirror and a hyperbolic mirror. They share focus F₁, which is 42 feet above the vertex of the parabola. The hyperbola's second focus F2 is 8 ft above the parabola's vertex. The vertex of the hyperbolic mirror is 3 ft below F₁. Find the equation of the hyperbola if the center is at the origin of a coordinate system and the foci are on the y-axis.
Complete the equation.
1