Functions Questions and Answers

Math
Functions10 The function f t 1200 1 75 60t represents the change in a quantity over t minutes What does the constant 1 75 reveal about the rate of change of the quantity The function is exponentially are a rate of every

Math
FunctionsGiven the equation 2 x 5 2 solve for x and identify if it is an extraneous solution 2 points O a Ob OC x 6 solution is not extraneous x 6 solution is extraneous x 11 solution is not extraneous x 11 solution is extraneous
Math
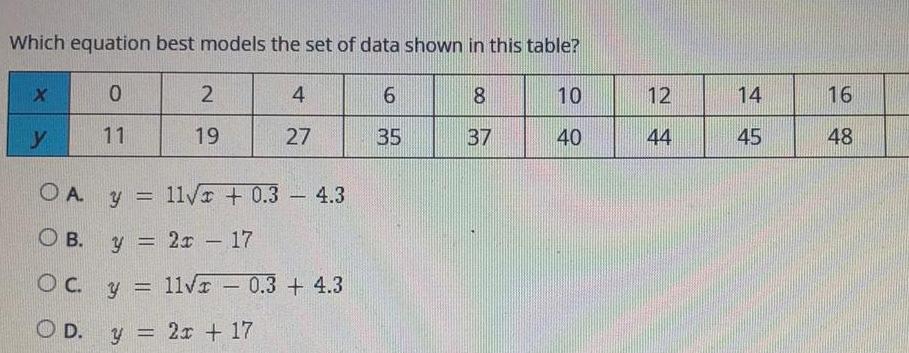
FunctionsWhich equation best models the set of data shown in this table y 0 11 2 19 OA OB y 2x 17 y 11 x 0 3 OC y OD 4 27 y 2x 17 11 x 0 3 4 3 4 3 6 35 8 37 10 40 12 44 14 45 16 48

Math
FunctionsPart 1 of 2 Use the remainder theorem to find the remainder when f x is divided by x 1 Then use the factor theorem to determine whether x 1 is a factor of f x f x 3x6 11x 8 The remainder is E
Math
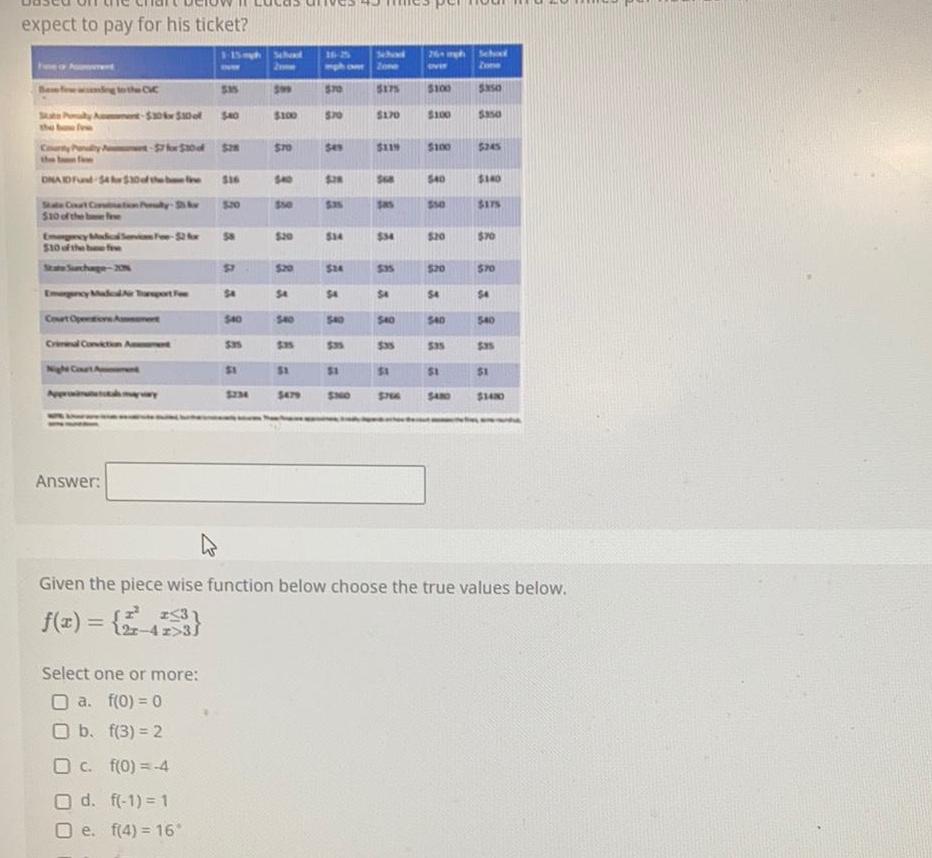
Functionsexpect to pay for his ticket Bew Party 30k 30of DNAID Fund 4 30 of the bene State Court Coban Puy Av 10 of the be wet 7 for 30 d Emergecy Modical Servics Free 52 fm 10 of the be fre mergency Made Tusport Fee Court Opention Amet Night Court A Criminal Conviction Amet Answer wy 15mph Schod Select one or more a f 0 0 O b f 3 2 O c f 0 4 O d f 1 1 O e f 4 16 535 40 516 58 ST 54 40 535 1 5234 599 100 70 40 550 520 54 5 35 1 5479 mph one 570 5 70 38 514 24 4 540 1 SNO 5175 170 5119 568 sas 34 535 4 540 535 1 766 26 mgh over 100 100 100 540 550 20 20 54 540 535 51 SAND Schad Zone 5350 350 245 140 175 70 570 4 540 35 1 143 Given the piece wise function below choose the true values below f x 2 121 4 z 3
Math
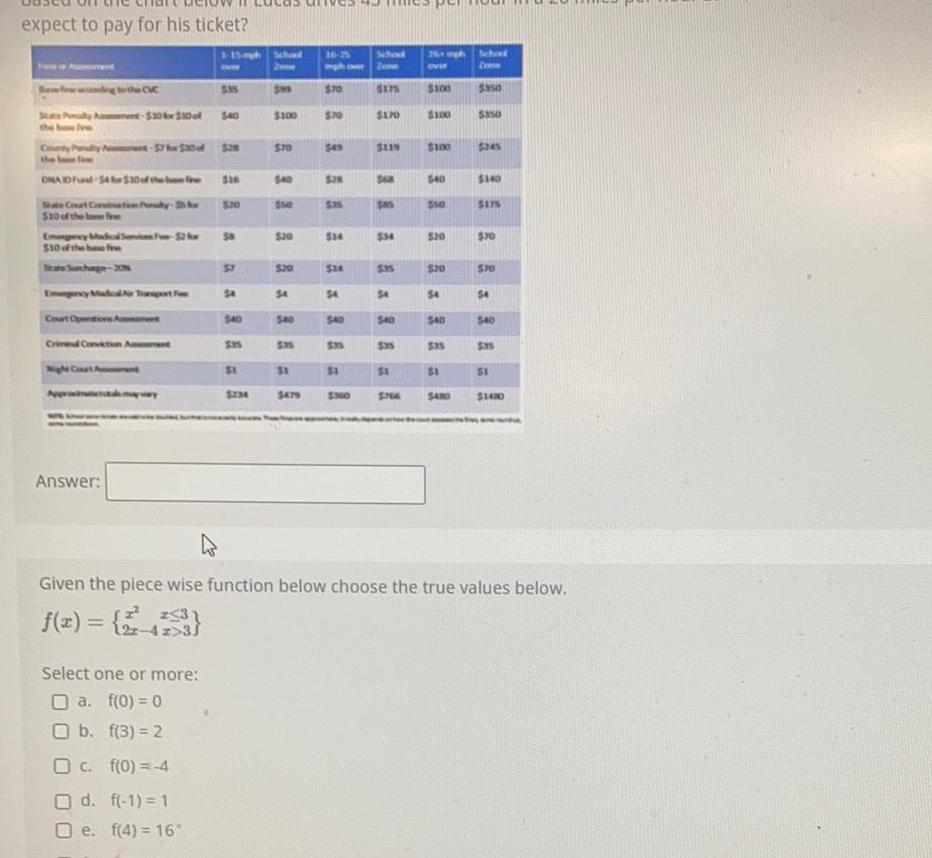
Functionsexpect to pay for his ticket Bew Party 30x530of DNAID Fund 4 30 of the bene State Court Cobain Pully Av 10 of the be wet 7 for 20 d Emergecy Modical Servics Free 52 fm 10 of the be fre mergency Made Tosport Fee Court Opetions Amet Night Court A Criminal Conviction Amet Answer wy 15mph Schod Select one or more a f 0 0 O b f 3 2 O c f 0 4 O d f 1 1 O e f 4 16 535 40 516 58 ST 54 40 535 1 5234 599 100 70 40 550 520 54 5 35 1 5479 mph one 570 5 70 38 514 24 4 540 1 SNO 5175 170 5119 568 sas 34 535 4 540 535 1 766 26 mgh over 100 100 100 540 550 20 20 54 540 535 51 SAND Schad Zone 5350 350 245 140 175 70 570 4 540 35 1 143 Given the piece wise function below choose the true values below f x 2 121 4 z 3
Math
FunctionsThe pany expression to represent the total number of rooms that Jake Lionel and Donald can paint together in one hour BIUX X Characters used 0 15000 15px A V E V Part F Find the nhor of rooms per hour that lake Linnel and Donald can paint working together if t is 6 hours
Math
Functionsat which jake Lionel the new rate is faster or slower and by how much BIUX X 15px Characters used 0 15000 paint part F with the rate at which jake Lionel and Wayne paint part C Determine whether AV A EEEEEE
Math
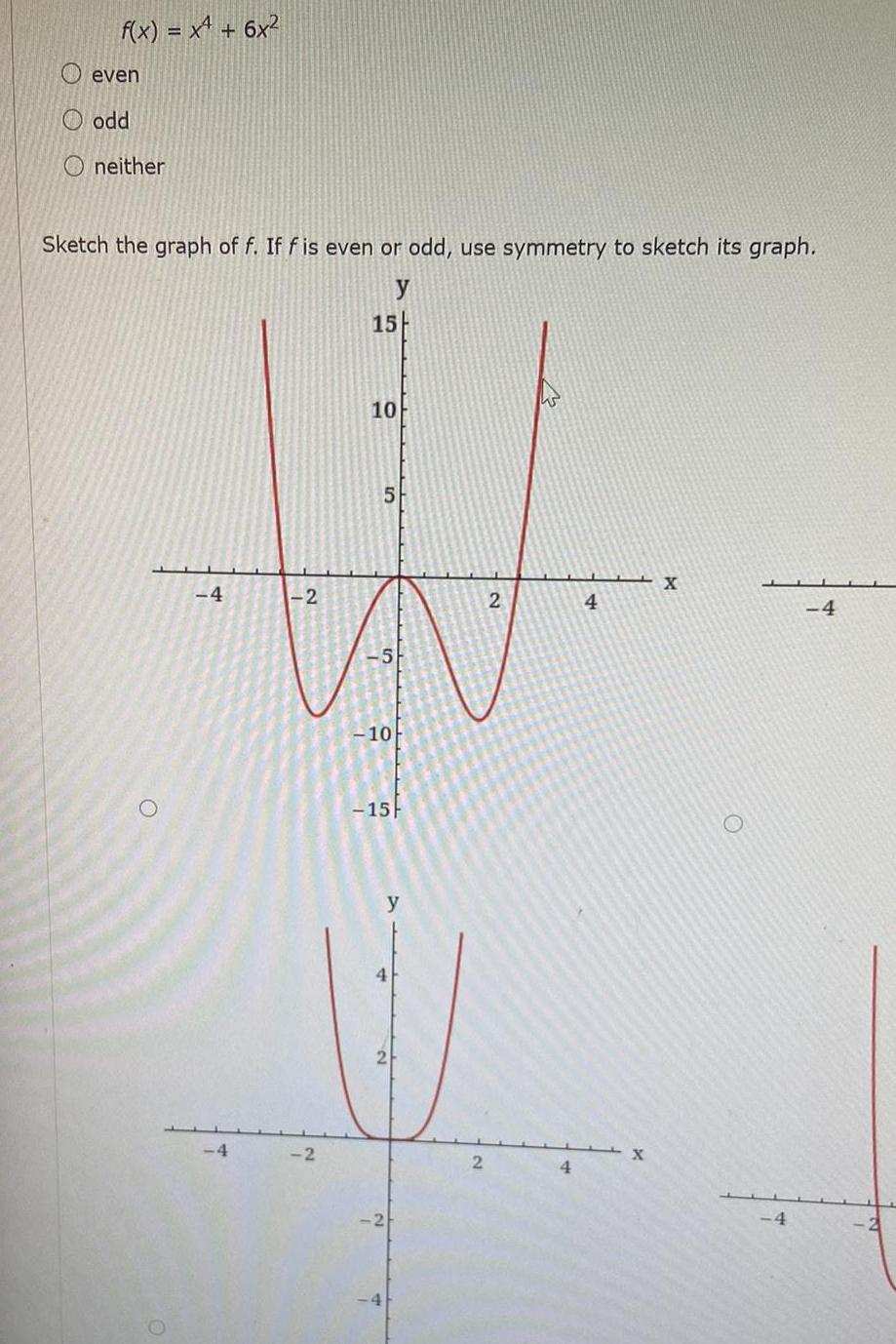
Functionsf x x 6x even O odd Oneither Sketch the graph of f If f is even or odd use symmetry to sketch its graph y 4 4 2 2 15 10 5 10 15 y 4 2 2 2 4 4 X X 4 4
Math
FunctionsApply Ana is bowling She pays 4 per game and 7 to rent shoes After three games each additional game is free Is the total cost to bowl a function of the number of games played Use a table or graph to help explain your answer

Math
FunctionsApplication 1 A rocket is tossed from a platform and follows a parabolic path through the air The height of the rocket in meters is given by h t 3t2 10t 8 where t is measured in seconds a How high is the rocket off the ground when it is thrown b For what times is the height of the rocket above 10m Round to 2 dec places 1 mark 3 marks
Math
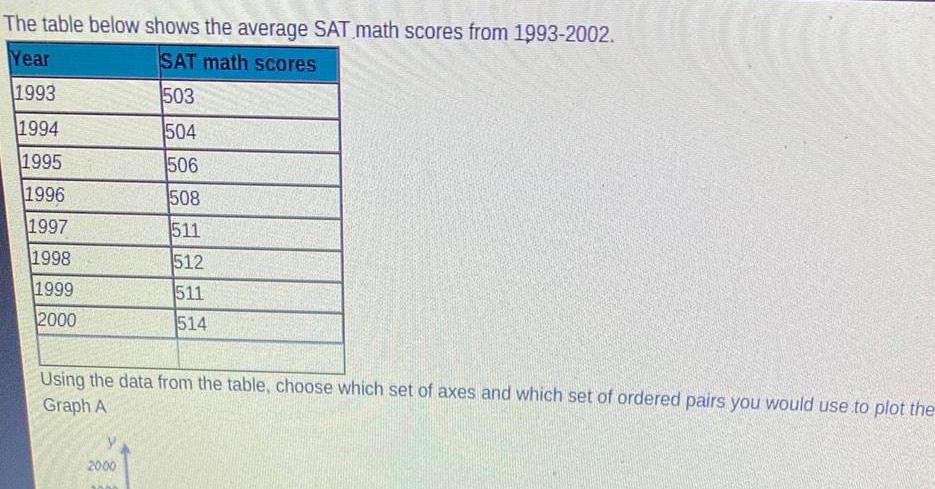
FunctionsThe table below shows the average SAT math scores from 1993 2002 Year SAT math scores 1993 503 1994 504 1995 506 1996 508 1997 511 1998 1999 2000 512 511 514 Using the data from the table choose which set of axes and which set of ordered pairs you would use to plot the Graph A 2000
Math
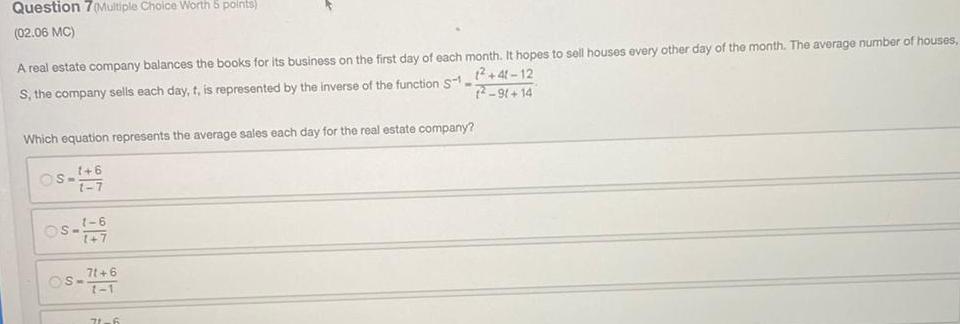
FunctionsQuestion 7 Multiple Choice Worth 5 points 02 06 MC A real estate company balances the books for its business on the first day of each month It hopes to sell houses every other day of the month The average number of houses 1 41 12 S the company sells each day t is represented by the inverse of the function S1 2 9 14 Which equation represents the average sales each day for the real estate company 1 6 1 7 S OS 1 6 1 7 S 71 6 1 1 71 6
Math
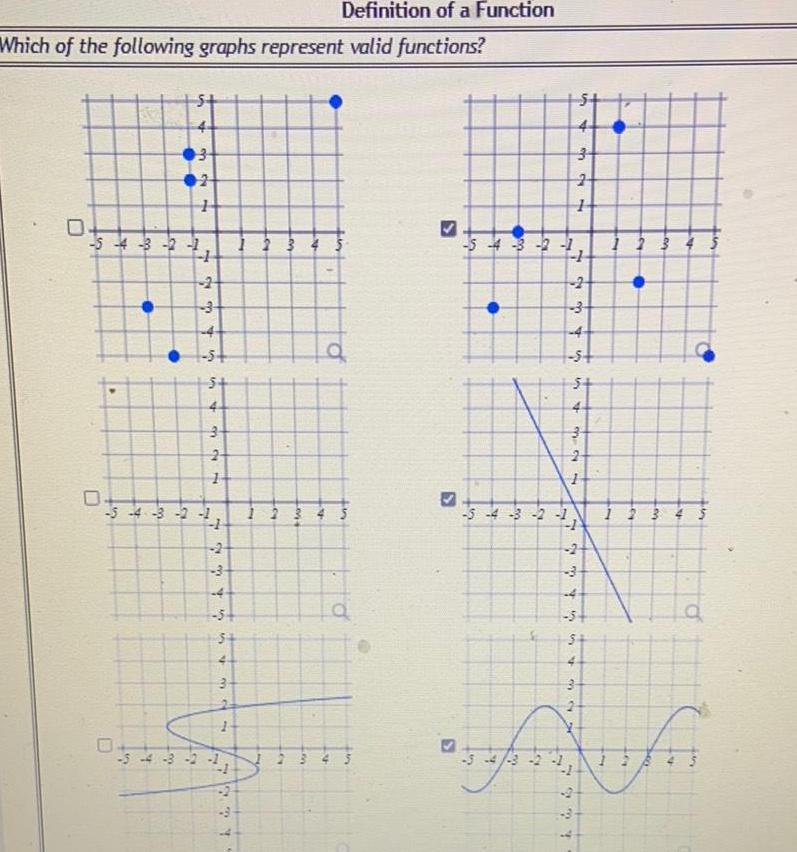
FunctionsWhich of the following graphs represent valid functions 0 5 4 3 2 1 0 4 3 2 5 4 3 H 4 1 2 3 4 5 5 34 32 1 5 4 3 2 1 12 2 3 75 5 t 3 32 PHA 04 1934 m MAX 23 y 4 Definition of a Function wy q P 5 4 3 2 1 5 4 3 2 f 1 1 3 1 ch 9 3 4 5 2 3 4 st 5 54 4 3 324 ST 2 34 3 2 3 1 2 3 1 2 3 1 A
Math
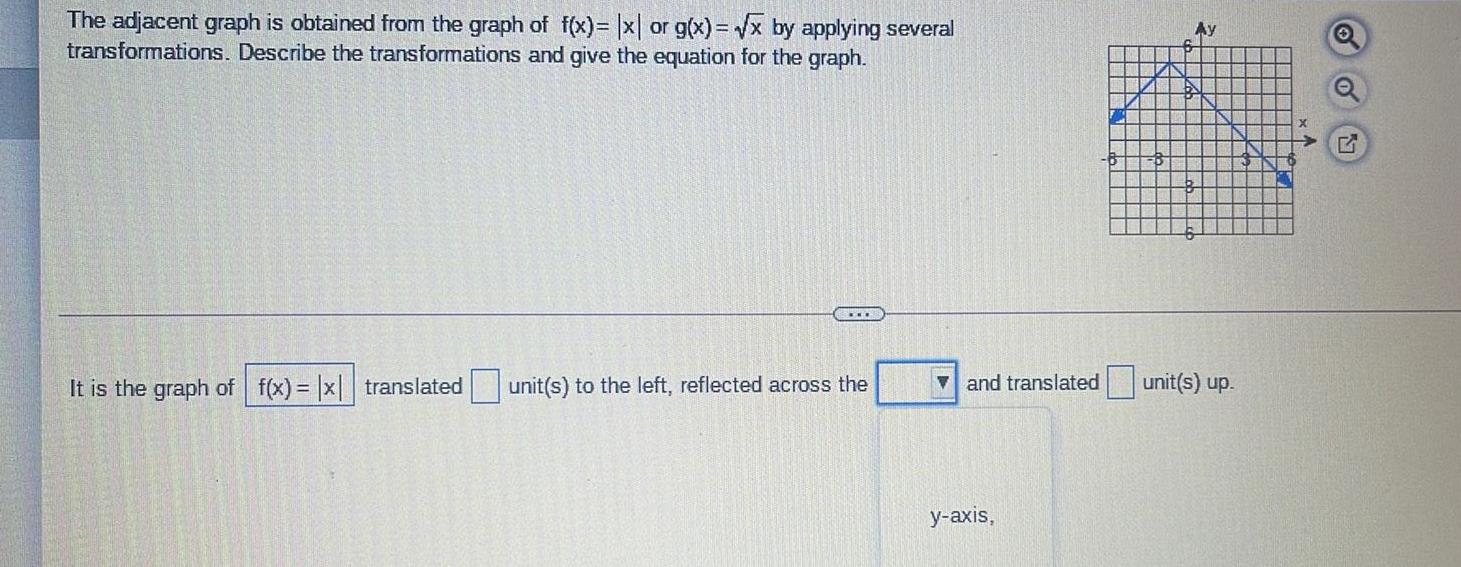
FunctionsThe adjacent graph is obtained from the graph of f x x or g x x by applying several transformations Describe the transformations and give the equation for the graph It is the graph of f x x translated unit s to the left reflected across the Sell Se 5 DPR 201 and translated y axis Ay unit s up 4 G
Math
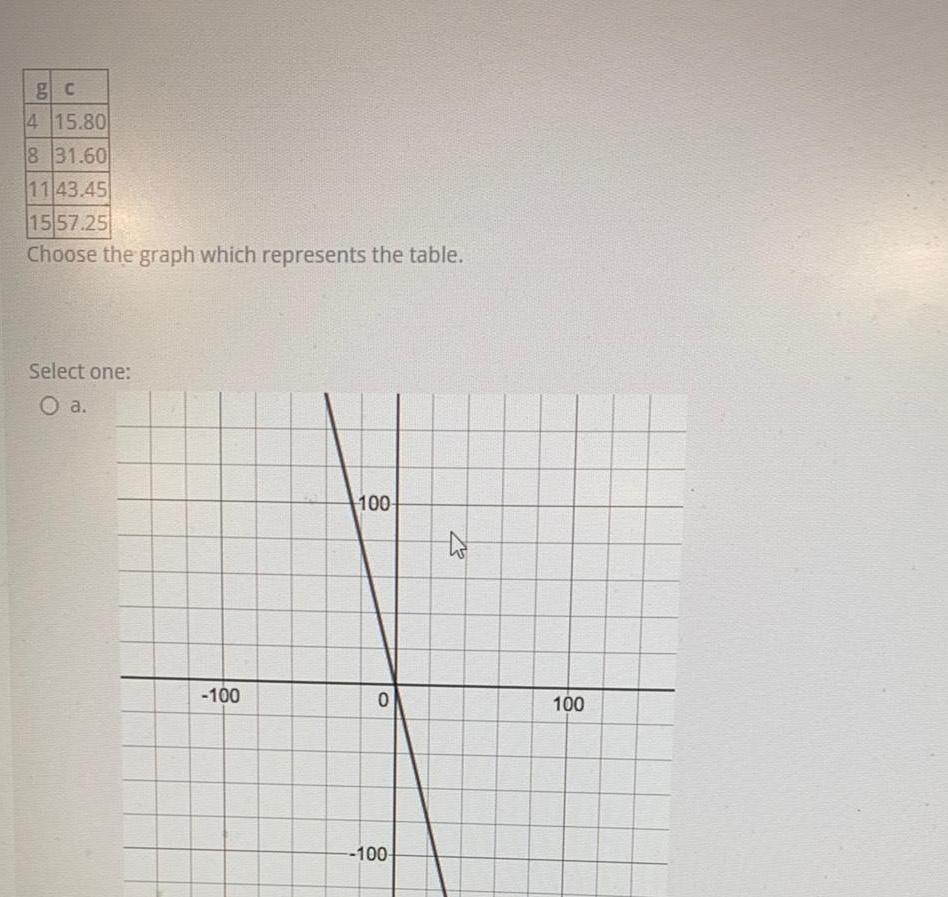
Functionsg c 4 15 80 8 31 60 1143 45 1557 25 Choose the graph which represents the table Select one O a 100 100 0 100 EZ 100
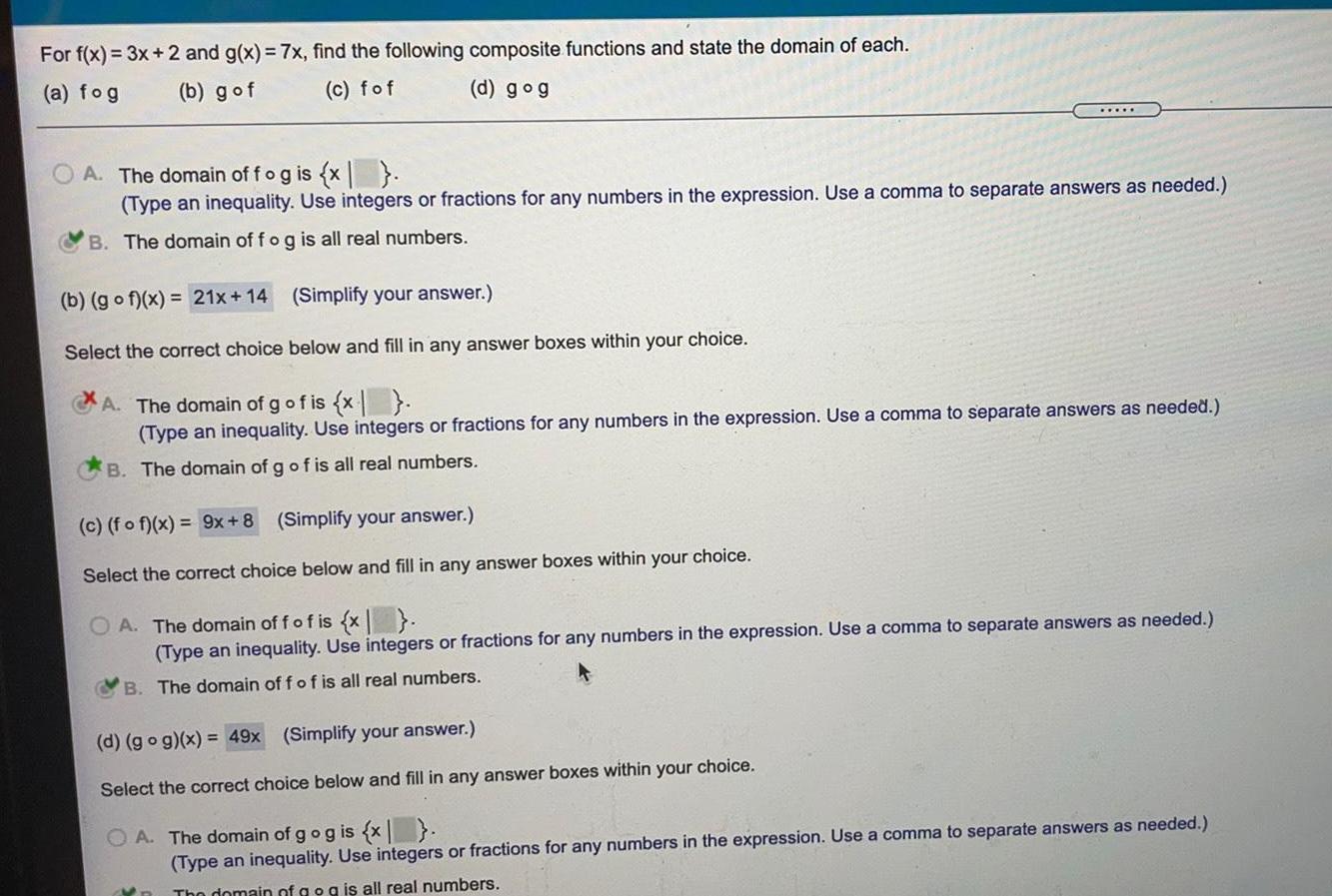
Math
FunctionsFor f x 3x 2 and g x 7x find the following composite functions and state the domain of each a fog b gof c fof d gog A The domain off og is x Type an inequality Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed B The domain of fog is all real numbers b gof x 21x 14 Simplify your answer Select the correct choice below and fill in any answer boxes within your choice A The domain of g of is x Type an inequality Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed B The domain of g of is all real numbers c fo f x 9x 8 Simplify your answer Select the correct choice below and fill in any answer boxes within your choice OA The domain off of is x Type an inequality Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed B The domain of f of is all real numbers d go g x 49x Simplify your answer Select the correct choice below and fill in any answer boxes within your choice OA The domain of g og is x Type an inequality Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed The domain of g og is all real numbers

Math
Functions7 120 1 30 18 The number of gallons of gasoline in a truck s tank at time t is given by the twice differentiable function S where t is measured in minutes and 0 t 240 which the number of gallons of oil in the tank is changing at time t 140 minutes 1 point Estimate the rat 0 30 90 180 240 t minutes S t gallons 16 15 12 7 2
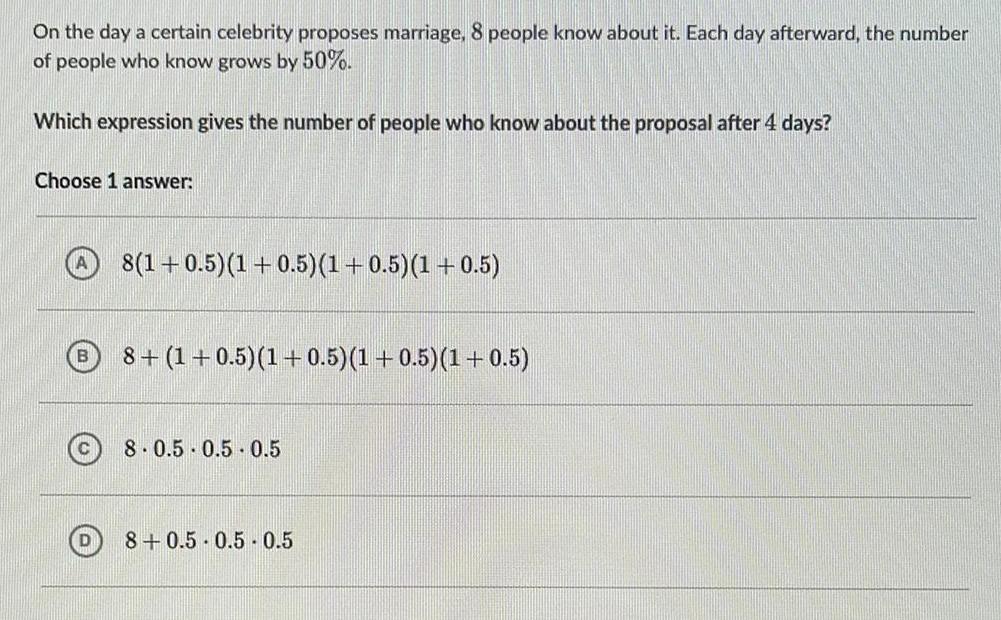
Math
FunctionsOn the day a certain celebrity proposes marriage 8 people know about it Each day afterward the number of people who know grows by 50 Which expression gives the number of people who know about the proposal after 4 days Choose 1 answer B 8 1 0 5 1 0 5 1 0 5 1 0 5 8 1 0 5 1 0 5 1 0 5 1 0 5 8 0 5 0 5 0 5 8 0 5 0 5 0 5

Math
Functions01 03 LC Consider the function f x x 12 Which of the following would be an appropriate horizontal and vertical scale of a viewing window on a graphing calculator for the function 1 point Xmin 12 Xmax 12 Ymin 10 Ymax 10 Xmin 10 Xmax 10 Ymin 12 Ymax 12 OXmin 5 Xmax 25 Ymin 5 Ymax 5 Xmin 5 Xmax 5 Ymin 5 Ymax 25
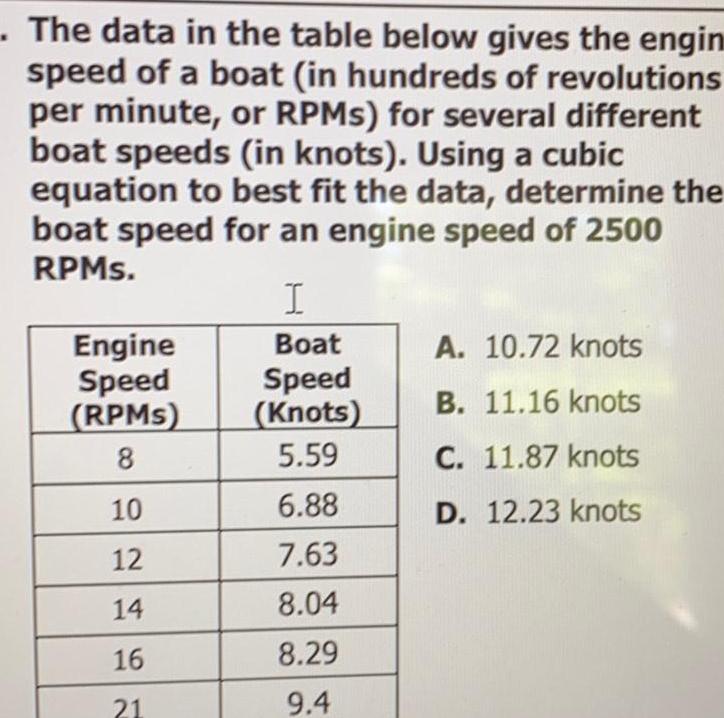
Math
FunctionsThe data in the table below gives the engin speed of a boat in hundreds of revolutions per minute or RPMs for several different boat speeds in knots Using a cubic equation to best fit the data determine the boat speed for an engine speed of 2500 RPMs Engine Speed RPMS 8 10 12 14 16 21 I Boat Speed Knots 5 59 6 88 7 63 8 04 8 29 9 4 A 10 72 knots B 11 16 knots C 11 87 knots D 12 23 knots
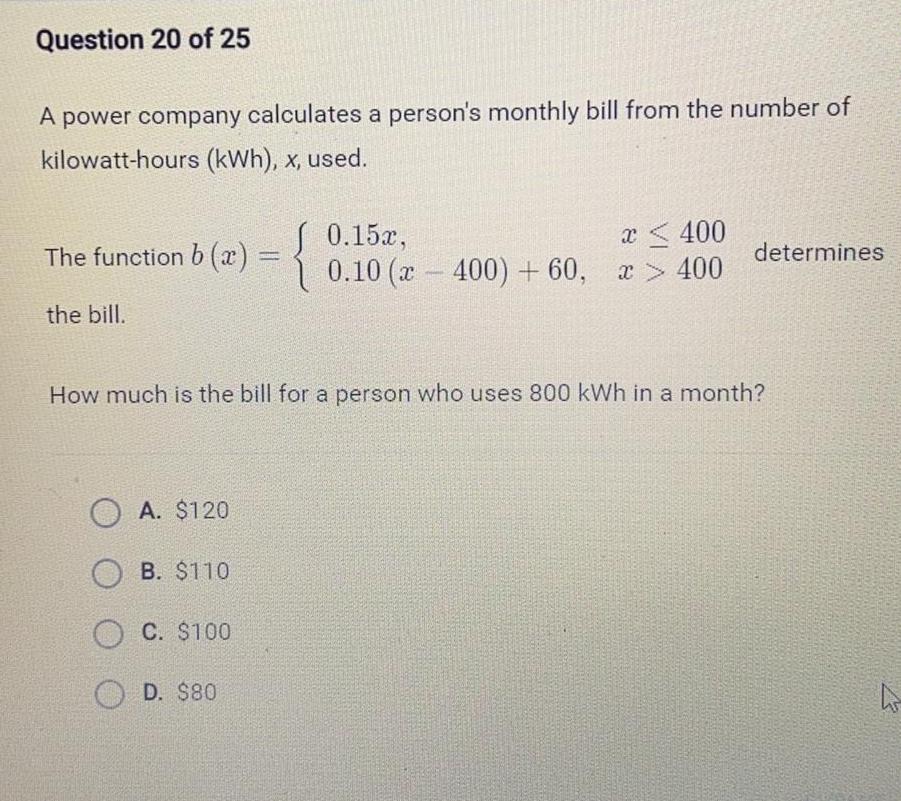
Math
FunctionsQuestion 20 of 25 A power company calculates a person s monthly bill from the number of kilowatt hours kWh x used The function b x the bill OA 120 OB 110 OC 100 0 15x 0 10 2 400 60 D 80 x 400 x 400 How much is the bill for a person who uses 800 kWh in a month determines h

Math
Functions3 The population of a town increased from 3500 in 2010 to 4100 in 2017 Let x 0 for year 2010 a 6 pts Build a model exponential function of the form P t Pekt for the population of this town Clearly show your algebraic work b 4 pts Use your answer from part a to predict the year when the town s population will reach 7000 Clearly show your algebraic work

Math
FunctionsThis table represents values of a cubic polynomial function X y 2 12 1 0 0 1 7 5 2 6 3 3 6 Based on the information in the table which sentence best describes the interval 2 1 The function is decreasing on the interval 2 1 The function is constant on the interval 2 1 The function is increasing on the interval 2 1 The function is both increasing and decreasing on the interval 2 1 O A O B O C OD

Math
FunctionsThe function V t 3500t 19000 where V is value and t is time in years can be used to find the valu a large copy machine during the first 5 years of use a What is the value of the copier after 2 years and 6 months After 2 years and 6 months the copier is worth b What is the salvage value of the copier if it is replaced after 5 years After 5 years the salvage value of the copier is c State the domain of this function d Sketch the graph of this function t
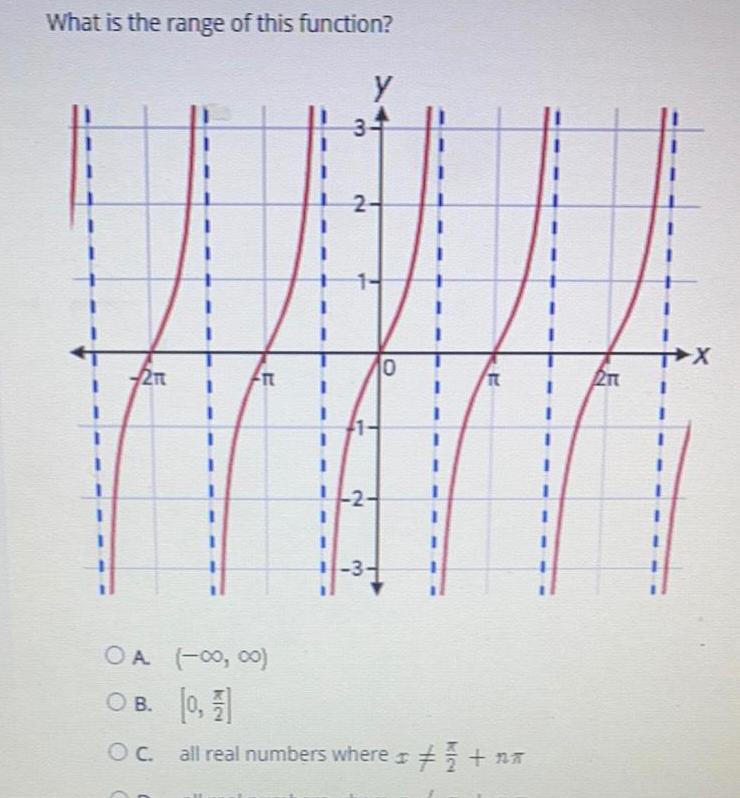
Math
FunctionsWhat is the range of this function 2 FIT 3 Y 2 10 T it OA 0 00 O B 0 1 OC all real numbers where na 211 X
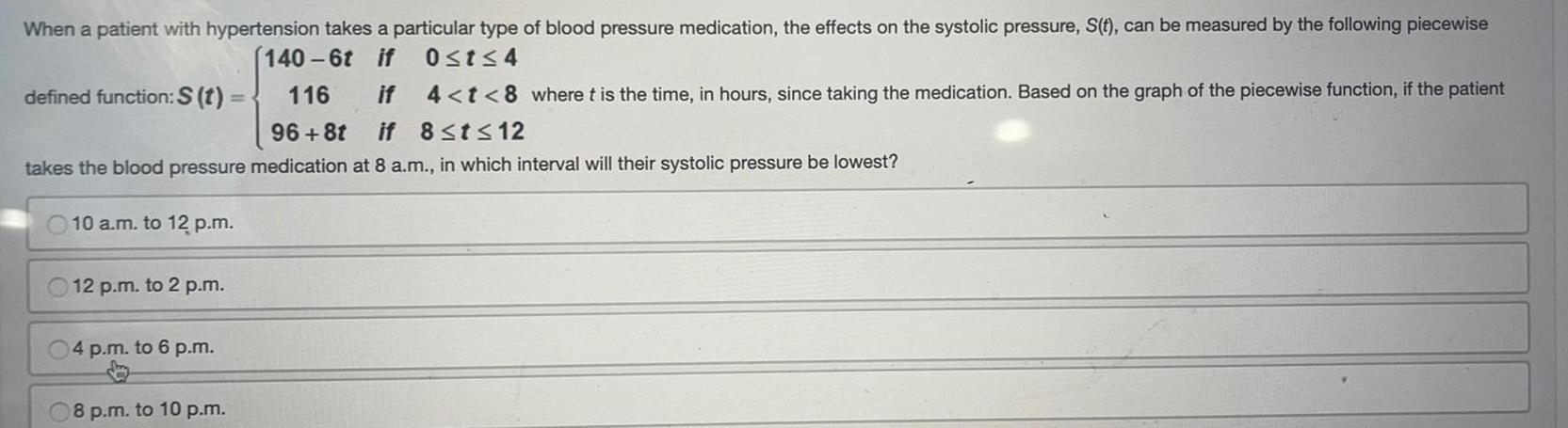
Math
FunctionsWhen a patient with hypertension takes a particular type of blood pressure medication the effects on the systolic pressure S t can be measured by the following piecewise 0 t 4 140 6t if 116 if 4 t 8 where t is the time in hours since taking the medication Based on the graph of the piecewise function if the patient 96 8t if 8 t 12 defined function S t takes the blood pressure medication at 8 a m in which interval will their systolic pressure be lowest 10 a m to 12 p m 12 p m to 2 p m 04 p m to 6 p m 08 p m to 10 p m

Math
FunctionsA piecewise function f x is defined by f x 3x 1 4 x 3x 4 x 7x 12 for x 3 for x 3 Part A Graph the piecewise function f x and determine the range 5 points Part B Determine the asymptotes of f x Show all necessary calculations 5 points Part C Describe the end behavior of f x 5 points

Math
FunctionsThe function P m 2m represents the number of points in a basketball game P as a function of the number of shots made m Given that the number of shots made is 40 find the number of points label required
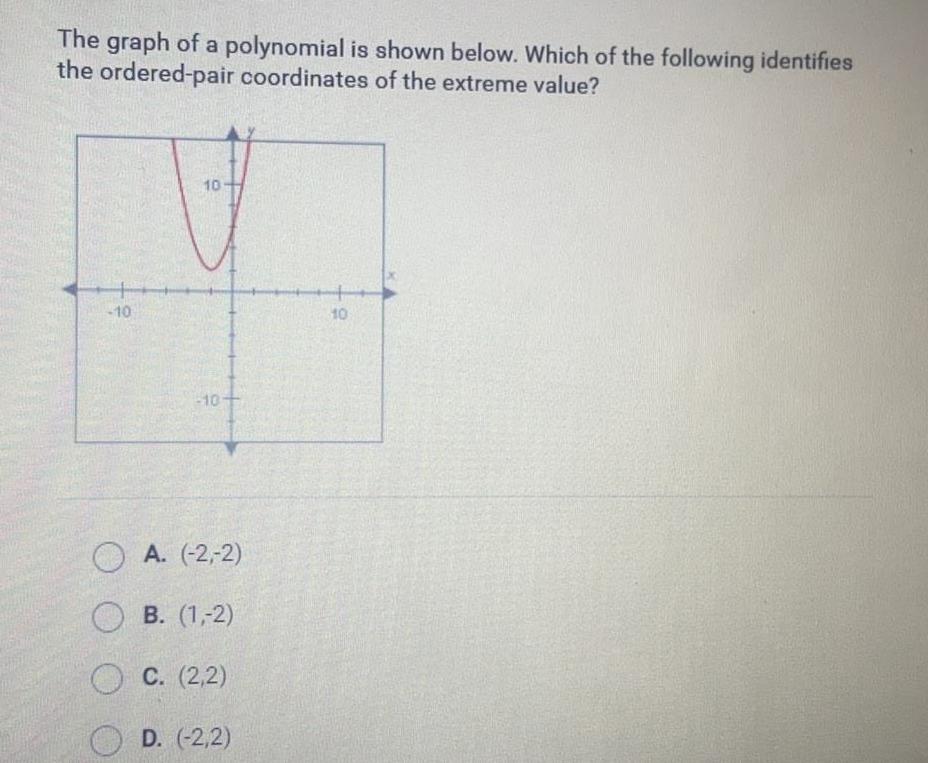
Math
FunctionsThe graph of a polynomial is shown below Which of the following identifies the ordered pair coordinates of the extreme value 10 10 10 A 2 2 B 1 2 C 2 2 D 2 2 10

Math
FunctionsLet D be the domain and let f be the possible function Determine if the relation is an example of a function D xl x is a person s social security number f x the person s name Yes One output results in one input Yes One input results in one output No At least one input results in two outputs No At least one output results in two inputs
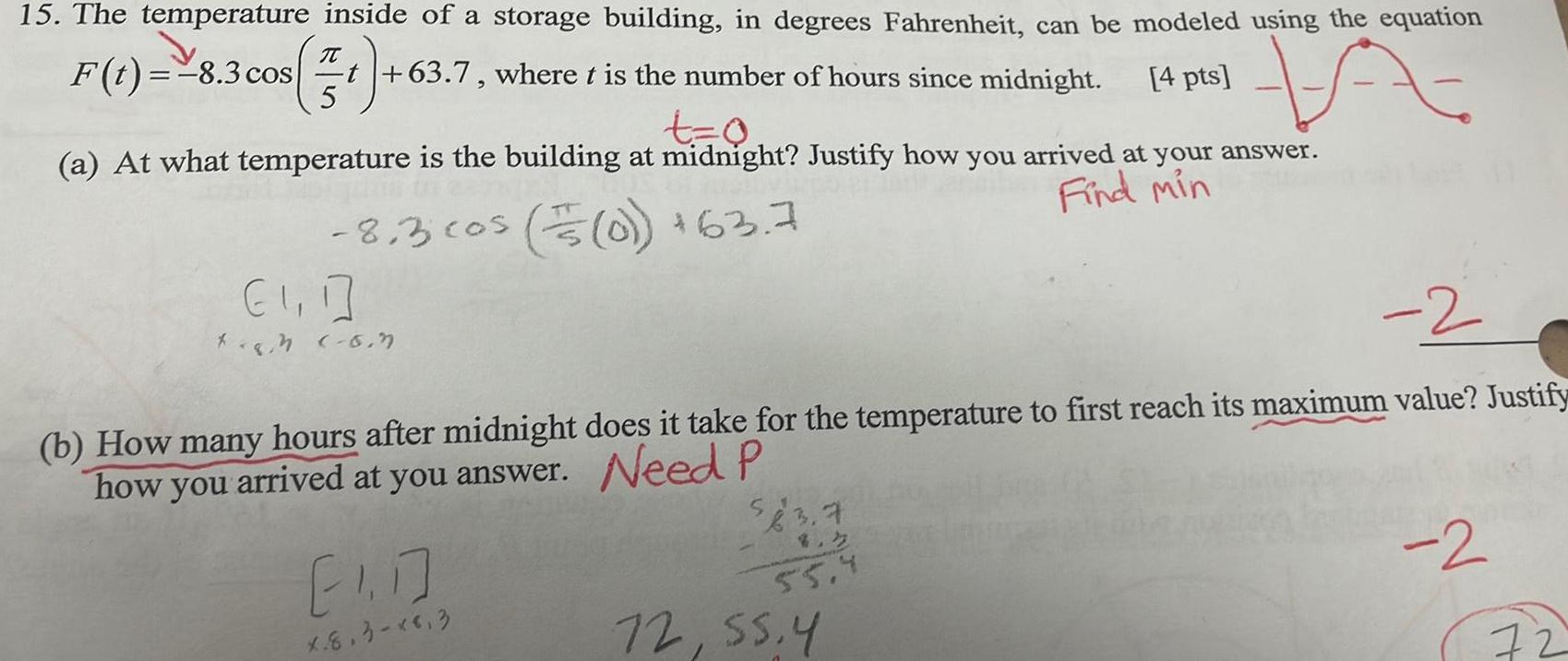
Math
Functions15 The temperature inside of a storage building in degrees Fahrenheit can be modeled using the equation 4 pts A F t 8 3 cos 57 t 63 7 where t is the number of hours since midnight t 0 a At what temperature is the building at midnight Justify how you arrived at your answer Find min 8 3 cos 0 63 7 1 1 tegn 6 7 2 b How many hours after midnight does it take for the temperature to first reach its maximum value Justify how you arrived at you answer Need P 1 7 X 8 3 8 3 55 4 72 55 4 2 72

Math
Functions1 The table shows the number of vis the Daisy Festival on certain days since May 1 Days Since May 1 Number of Visitors 0 215 3 520 6 725 9 865 12 955 15 1025 18 970 21 874 710 490 24 27 30 207 Which type of function would best model the data A linear B quadratic C exponential D piecewise function

Math
FunctionsThe number of views on an interesting video after it s uploaded is represented by the following table Which model for V t the number of views t days after its uploaded best fits the data Time days Views 0 10 4 452 8 889 12 1330 16 1770 20 2211 O V t 10 440t O O V t 10 x 11 3 t O V t 10 110t V t 10 x 45 2 t

Math
FunctionsConsider this absolute value function f x 1 8 How can function fbe written as a piecewise function O A O B O C O D f x f x f x f x 8 8 8 8 I 8 8 2 8 I 8 I 8 8 8 8 8 8 8
Math
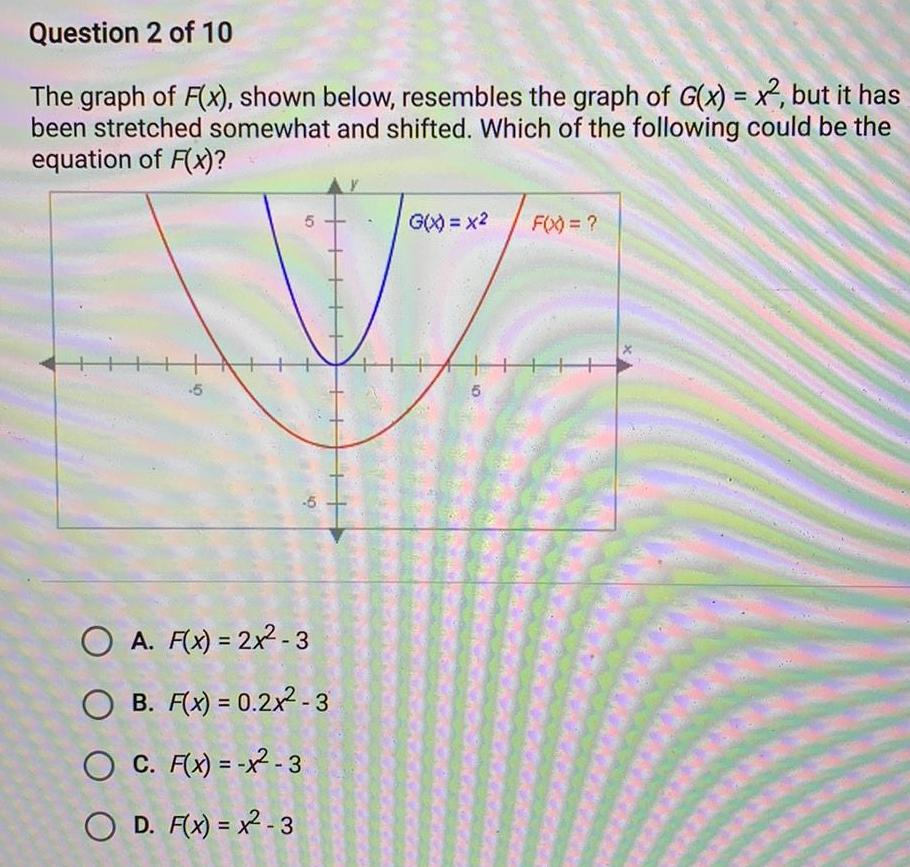
FunctionsQuestion 2 of 10 The graph of F x shown below resembles the graph of G x x but it has been stretched somewhat and shifted Which of the following could be the equation of F x 5 5 49 OA F x 2x2 3 OB F x 0 2x 3 O C F x x 3 OD F x x 3 G X x 5 F X

Math
FunctionsConsider these functions f x 3x3 2 g x Which statements if any are true about these functions 1 The function g x x for all real x II The function g x x for all real x III Functions fand g are inverse functions 3 OA I only OB II only OC I II and III

Math
FunctionsConsider function fand function g f 1 In 1 g 1 5 In I How does the graph of function g compare with the graph of function f O Unlike the graph of function f the graph of function g has a y intercept Unlike the graph of function f the graph of function g has a domain of x 5 The graph of function g is the graph of function fvertically stretched by a factor of 5 The graphs of both functions have a vertical asymptote of x 0 Unlike the graph of function f the graph of function g decreases as x increases
Math
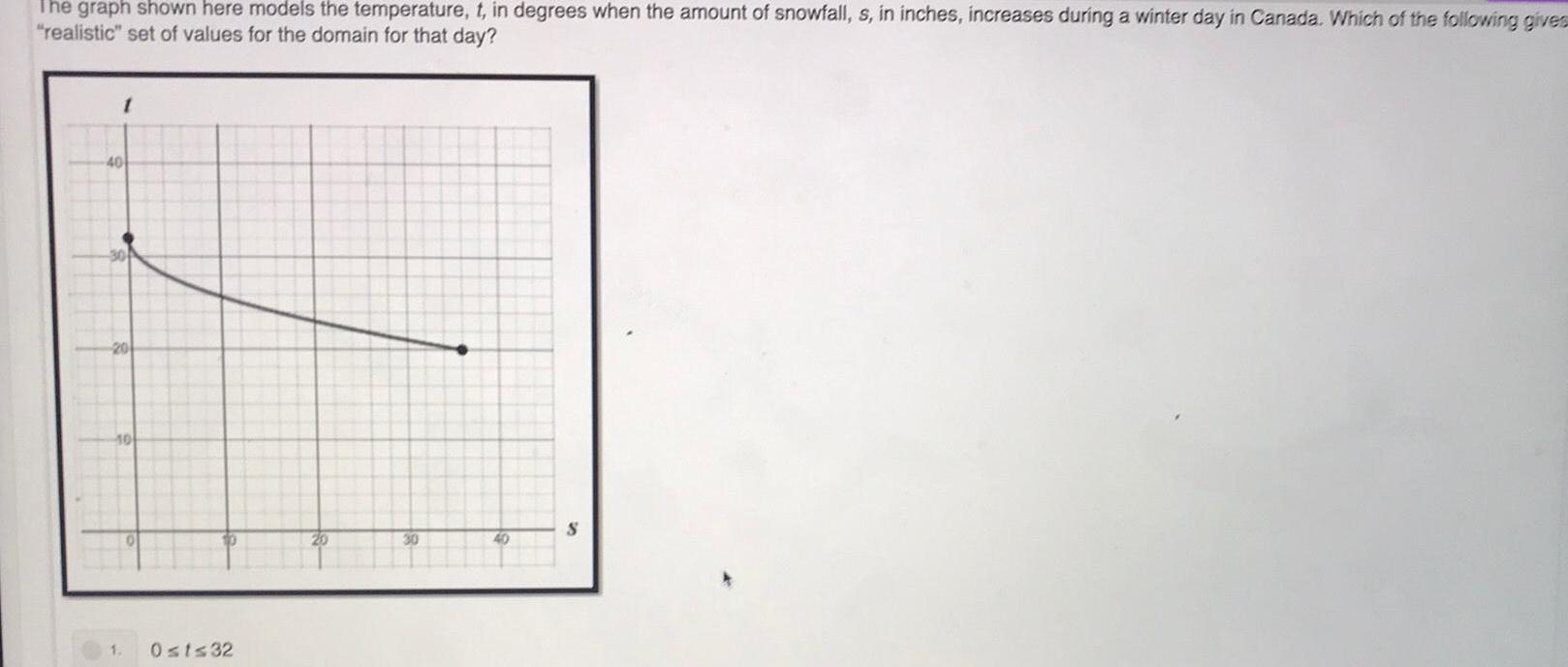
FunctionsThe graph shown here models the temperature t in degrees when the amount of snowfall s in inches increases during a winter day in Canada Which of the following gives realistic set of values for the domain for that day 1 40 20 10 1 O 10 0 t 32 20 30 40 S
Math
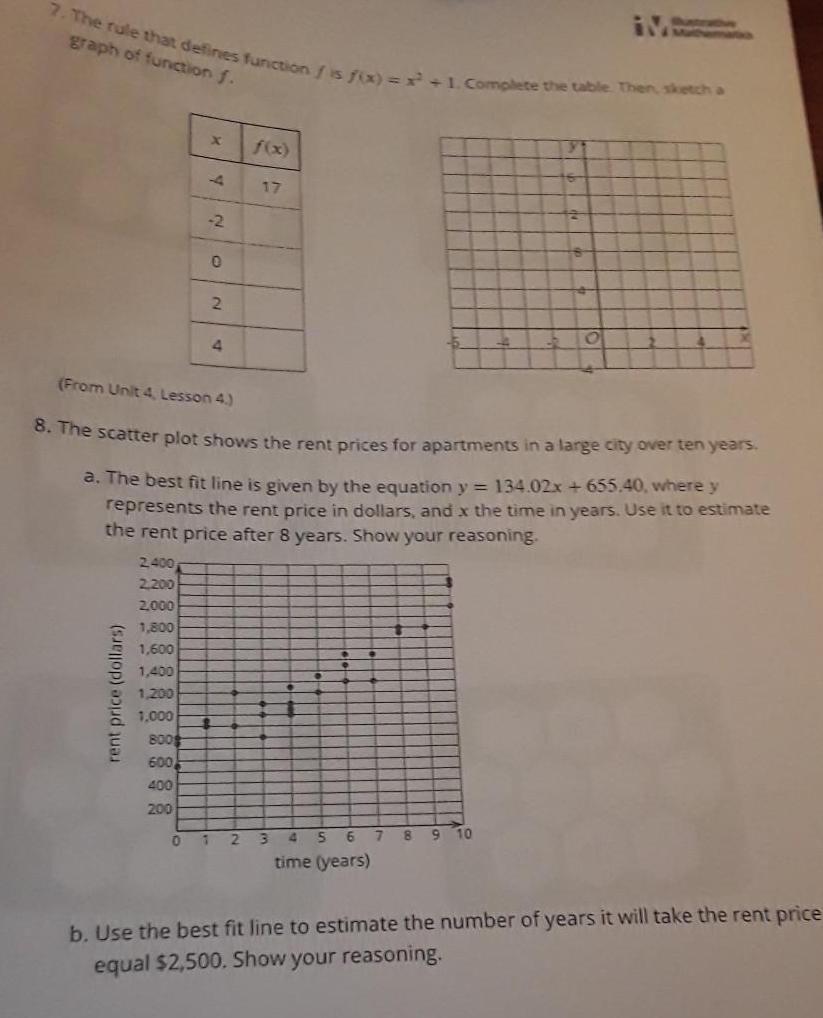
Functions7 The rule that defines function is fix x 1 Complete the table Then sketch a graph of function f rent price dollars x 2 400 2 200 2 000 1 800 1 600 1 400 1 200 1 000 800 600 400 200 2 0 0 2 From Unit 4 Lesson 4 8 The scatter plot shows the rent prices for apartments in a large city over ten years 4 a The best fit line is given by the equation y 134 02x 655 40 where y represents the rent price in dollars and x the time in years Use it to estimate the rent price after 8 years Show your reasoning 123 4 5 6 time years 7 O 10 9 8 b Use the best fit line to estimate the number of years it will take the rent price equal 2 500 Show your reasoning

Math
FunctionsAssume that a DVD loses 60 of its value every year it is in a video store Suppose the initial value of the DVD was 80 B 46 HW eTool Desmos Homework Help a What multiplier would you use to calculate the video s new values b What is the value of the DVD after one year After four years c Write a continuous function V t to model the value of a DVD after t years d When does the video have no value e Sketch a graph of this function Be sure to scale and label the axes
Math
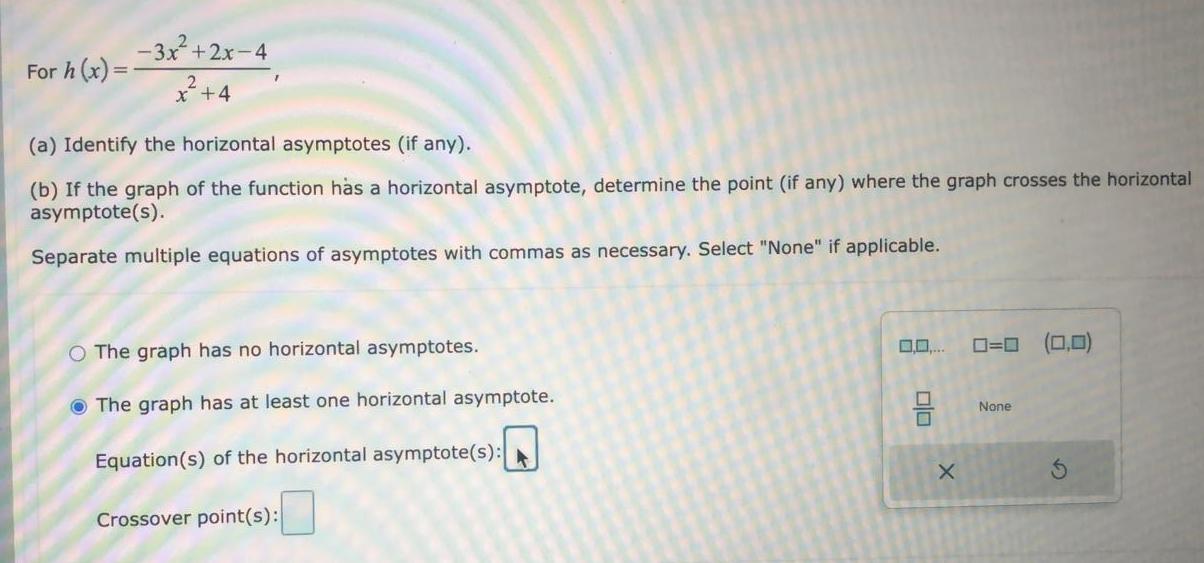
FunctionsFor h (x)=
-3x²+2x-4/x2 +4
(a) Identify the horizontal asymptotes (if any).
(b) If the graph of the function has a horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s).
Separate multiple equations of asymptotes with commas as necessary. Select "None" if applicable.
The graph has no horizontal asymptotes.
The graph has at least one horizontal asymptote.
Equation(s) of the horizontal asympt
Crossover point(s):

Math
FunctionsEvaluate f(x) for the given values for x. Then use the ordered pairs (x,f(x)) from the table to graph the function.
f(x) = (x - 1)²

Math
FunctionsFor s (x) = 5x-5 / 2x²-7x-1
(a) Identify the horizontal asymptotes (if any).
(b) If the graph of the function has a horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s).
Separate multiple equations of asymptotes with commas as necessary. Select "None" if applicable.
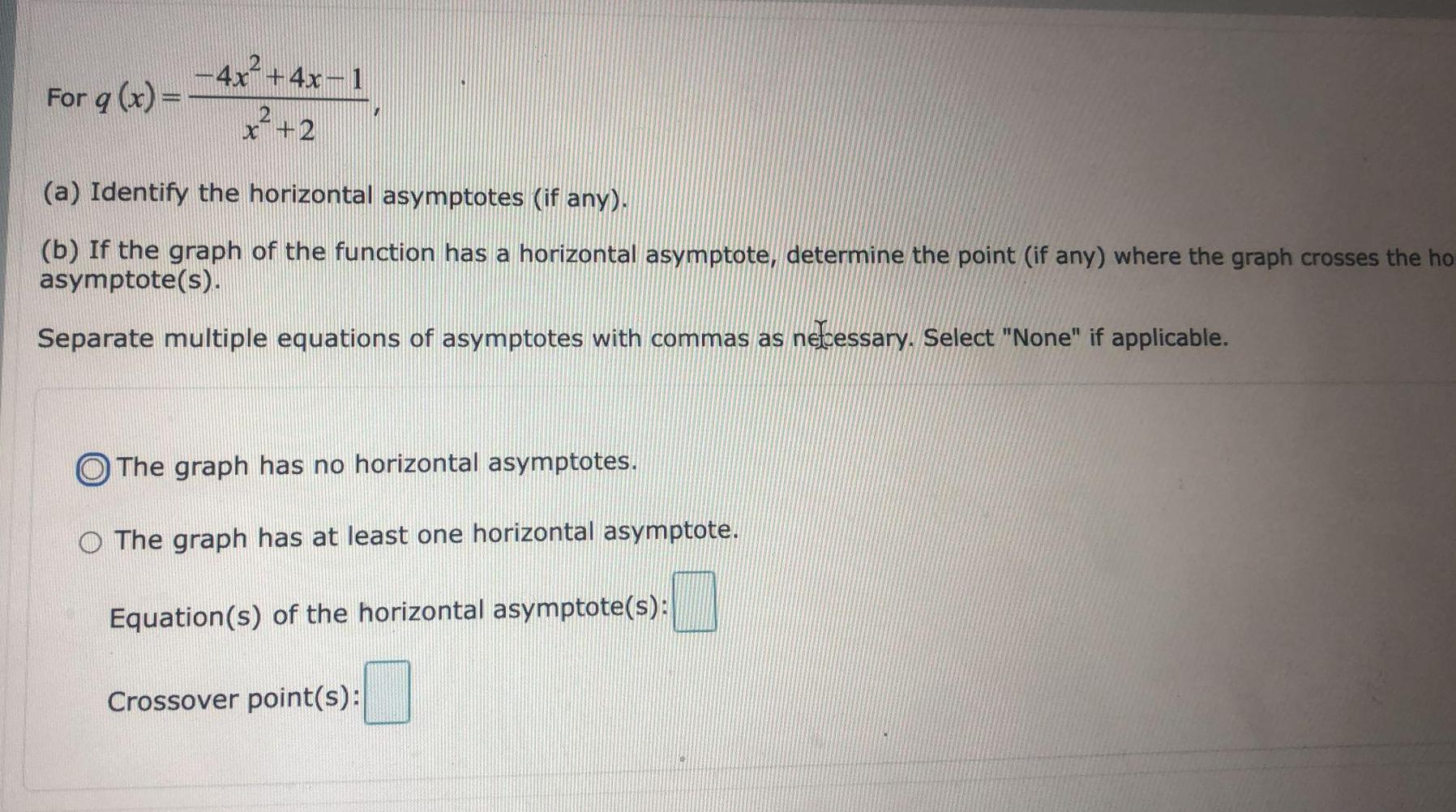
Math
FunctionsFor q (x) = -4x2+4x-1 / x²+2
(a) Identify the horizontal asymptotes (if any).
(b) If the graph of the function has a horizontal asymptote, determine the point (if any) where the graph crosses the horizontal asymptote(s).
Separate multiple equations of asymptotes with commas as necessary. Select "None" if applicable.
The graph has no horizontal asymptotes.
The graph has at least one horizontal asymptote.
Equation(s) of the horizontal asymptote(s):
Crossover point(s):

Math
FunctionsLet f(x) =5x+2 / x - 5
1) The domain of f(x) in interval notation is
2) The y intercept is the point
3) The x intercept(s) is/are the point(s)
4) The vertical asymptote is
5) The horizontal asymptote is
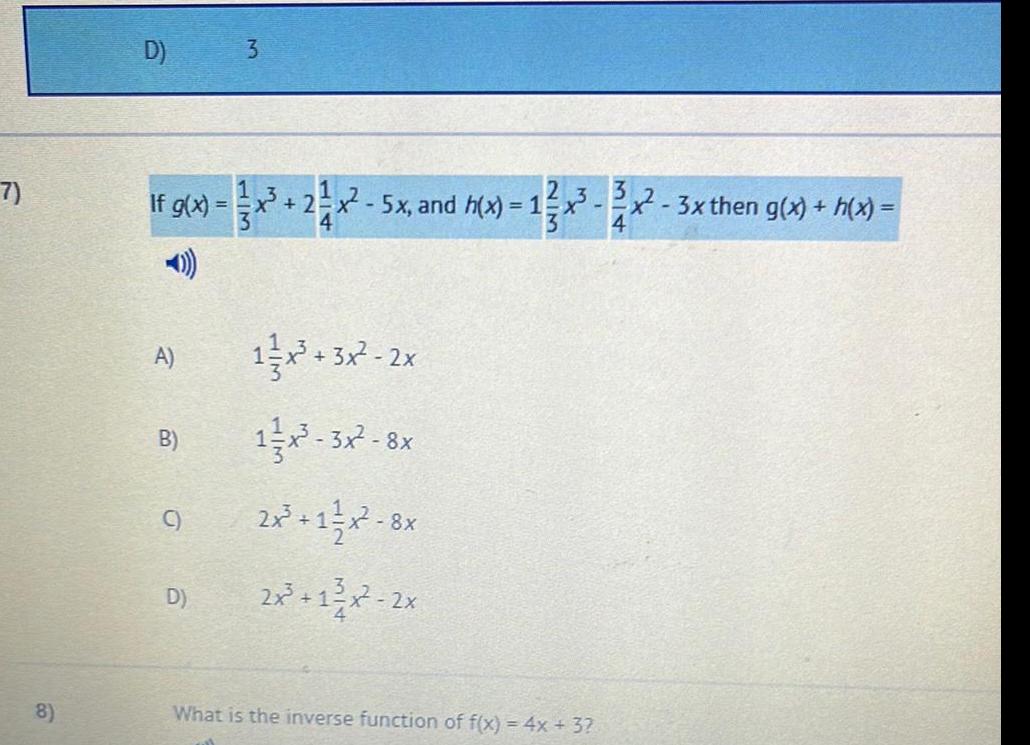
Math
FunctionsIf g(x) = 1/3 x3 + 2 1/4x²-5x and h(x) = 1 2/3x3 -3/4x2-3x then g(x) + h(x) =
A) 11/3x3+3x²-2x
B) 1 1/3x3-3x²-8x
C) 2׳ +1 1/2x²-8x
D) 2x³ + 1 3/4x² - 2x

Math
FunctionsMinimize the following objective function subject to the given constraints. Find the corner points and state the minimum.
Minimize: z = 10x + 4y
subject to 2x + y ≥ 8
x + 3y ≥ 9
x≥0, y≥0
A. Corner Points: (8, 0), (0, 9), (3, 2)
Minimum: 38
B. Corner Points: (0, 3), (4, 0), (3, 2), (0, 0)
Minimum: 0
C. Corner Points: (0, 8), (9, 0), (2, 3)
Minimum: 32
D. Corner Points: (8, 0), (0, 9), (2, 3)
Minimum: 32
E. Corner Points: (0, 8), (9, 0), (3, 2)
Minimum: 32

Math
FunctionsIn 2007, about 72% of US homes had Internet access. This percentage was expected to increase at an average of 1.7% per year for the next 4 years. Which of the following equations represents the given situation?
y=72x+1.7 where x is the number of years
y=0.017x+0.72 where x is the number of years
y=17x + 72 where x is the number of years