Solution of triangles Questions and Answers

Math
Solution of trianglesFrom Times Square in New York City you can see Central Park and the Empire State Building The approximate distance from Times Square to Central Park is 2 miles Central Park to the Empire State Building is 1 3 miles and Empire State Building to Times Square is 0 9 miles What is the approximate angle to the other tw landmarks from Times Square O 20 205 29 926 O 114 624

Math
Solution of trianglesonsider the triangle shown in the figure Let A 11 and B 3 in feet and the angle t A B Find the area of the triangle The angle involved is a special angle Give an exact answer Use symbolic notation and fractions where needed radians

Math
Solution of trianglesThe base of a triangle exceeds the height by 4 feet If the area is 142 5 square feet find the length of the base and the height of the triangle Answer How to enter your answer opens in new window Height k

Math
Solution of triangles11 A right triangle has a percent grade of 30 The slope of the triangle in lowest terms would be A 30 100 B 3 10 C 1 3 D Not enough information is given 12 Fill in the blanks The higher the percent grade is the of elevation is Therefore the higher lower the angle more less steep a ramp is

Math
Solution of triangles5 Jesse drew a perpendicular line in the triangle below from B to the opposite side What is the next step to prove the Law of Sines B A b Find the sines of B and C Find the sines of A and B Find the sines of A and C a Set the sine of A equal to the sine of C C

Math
Solution of trianglesOn a dogleg golf hole one golfer hits the ball 270 yards and then another 170 yards to reach the green The angle between the two hits is equal to 100 degrees How far would the golfer have to originally hit the ball for it to go directly to the same position on the green 150 463 yards 710

Math
Solution of triangles05 03 MC What is the area of AABC given mzB 83 a 25 feet and c 40 feet O 561 46 feet 496 27 feet 106 33 feet

Math
Solution of trianglesDetermine if the triangles can be Write your answer on the line provided If not congruent write not congruent 1 2 3 5 4 A Complete the proofs using the most appropriate method Some may require CPCTC 7 Given LBAC ZEDC BC EC Prove AABC ADEC 8 Given IKIM ZIKM LMK 6 D M B

Math
Solution of trianglesIn Texas the distance from Austin to Brownwood is 141 miles It is 171 miles from Brownwood to Corsicana and 157 miles from Corsicana to A Determine the angle between the routes from Brownwood Show your work

Math
Solution of trianglesThe map of a campground is shown below Campsite C first aid station F and supply station S lie along a straight path The path from the supply station to the tower T is perpendicular to the path from the supply station to the campsite The length of path FS is 400 feet The angle formed by path TF and path FS is 72 The angle formed by path TC and path CS is 55 Campground Map C 55 A Campsite F 72 Tower 400 ft First aid Supply station

Math
Solution of trianglesTriangle DEF is shown on the xy coordinate plane 10 9 the perimeter of AD E F 161 5 4 2 2 S 6 The triangle will be rotated 180 clockwise around point 4 8 to create AD E F Which characteristic of AD E F will NOT be the same for the corresponding characteristic of ADEF the coordinates of D O the coordinates of F O the area of AD E F

Math
Solution of trianglesUse the following information to determine if the triangles are congruent If the triangles are congruent choose the correct congruence statement and the postulate or theorem used If the triangles are not congruent choose Not Congruent Given BD AC AB CB

Math
Solution of trianglesThe Snoopy balloon in the Macy s Day parade has a 20 foot string that goes from the ground to the kite at a 27 degree angle of elevation How high off the ground is the balloon 27 20 feet

Math
Solution of trianglesA road crew uses the triangles shown in the diagram to measure the width of a sink hole across a highway from a safe distance away How wide is the sink hole 15 ft 13 ft 13 ft 15 ft A 18 ft B 15 ft C 13 ft D cannot be determined 18 ft

Math
Solution of trianglesTriangles ABE ADE and CBE are shown on the coordinate grid and all the vertices have co integers Which statement is true D No two triangles are congruent G ABE ADE and CBE are all congruent Only ABE and ADE are congruent Only AABE and ACBE are congruent

Math
Solution of trianglesThe city planning commission is looking to put in sidewalks where the three medians of the triangle are located What would be true about the sidewalks if the model of the city park is a equilateral triangle Select all that apply The sidewalks will meet in a single location A B C D E The sidewalks will bisect the angles of the park The length of one sidewalk will be shorter than the other sidewalks The total length of the sidewalks will be the same as the distance around the park The sidewalks divide the park into 6 smaller noncongruent triangles

Math
Solution of trianglesGeometry Formula Sheet Given the similar triangles below AEDF A BAC set up an equation that you would need to solve in order to find the missing side x Do not solve the equation E x D 22 F B Figure is not drawn to scale 45 A 99 C

Math
Solution of trianglesTal them Jeremy s drone is closer to him than to Leslie and Leslie s drone is closer to her than to Jeremy Jeremy s drone is 30 meters above the ground and he is located 50 meters to the left from the point directly below the drone The angle of elevation from Leslie s location on the ground to her drone is 55 and the distance between her location on the ground and her drone is 70 meters 1 2 3 Create a diagram of all the given information including calculated measurements make sure to add as you complete parts 2 4 Whose drone is higher show your work and make sure to update your drawing with your calculations What is the difference between the heights of the drones show your work and make sure to update your drawing with your calculations 4 The angle of elevation from the lower drone to the higher drone is 25 Use this information to calculate the distance between Jeremy s and Leslie s locations on the ground show your work and make sure to update your drawing with your calculations 5 Jeremy flies his drone vertically so that it is at the same height as Leslie s drone Draw a new diagram of the drones Fill in any information you know 6 Explain why the angle of elevation from Jeremy s location on the ground to his drone is different from the angle of elevation between Leslie s location on the ground and her drone given that both drones

Math
Solution of trianglesIn the figures pentagon ABCDE has been dilated to create pentagon LMNOP as shown Answer F 5 83 G 6 25 H 7 25 A J 15 5 18 20 E If pentagon ABCDE is similar to pentagon LMNOP what is the value of x 16 D 2x 1 L M 4y 2 N 12 O

Math
Solution of triangles7 Technology required What is the value of x D 3 40 X 50 E If necessary round your answer to the nearest tenth Do not include units units in your answer 2019 Illustrative Mathematics All Rights Reserved

Math
Solution of trianglesMelissa is sitting in a movie theater 8 meters from the screen The angle of elevation from her line of sight to the top of the screen is 11 and the angle of depression from her line of sight to the bottom of the screen is 51 Find the height of the entire screen Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 11 51 8 meters meters X S

Algebra
Solution of triangles7 pts Find c if a 2 57 b 3 83 and C 46 2 Round to two decimal places if needed Assume A is the angle opposite side a B is the angle opposite side b and Cis the angle opposite side c You must draw the triangle to get credit for this problem

Math
Solution of trianglesTriangle 1 has an angle measure 26° and an angle measures 53°. Triangle 2 has an angle that measures a where at # 53°. Based on the information, Frank claims that triangle 1 and triangle 2 cannot be similar. What value of will refute franks claim?

Math
Solution of trianglesThe triangle will be rotated by 180° clockwise around the point (3, 4) to create the triangle A'B'C'. Indicate whether each of the listed features of the image will or will not be the same as the corresponding feature in the original triangle by selecting the appropriate box in the table.

Math
Solution of trianglesSolve the triangle. Round to the nearest tenth.
In AEFD, f = 29, d = 21, e = 13
mZE = 25°, mZF = 131°, mZD = 24°
None of the other answers are correct
mZE = 30°, m≤F = 110º, m≤D = 40°
mZE=24°, mZF = 115°, mZD = 41°
mZE=25°, m<F = 111°, mZD=44°
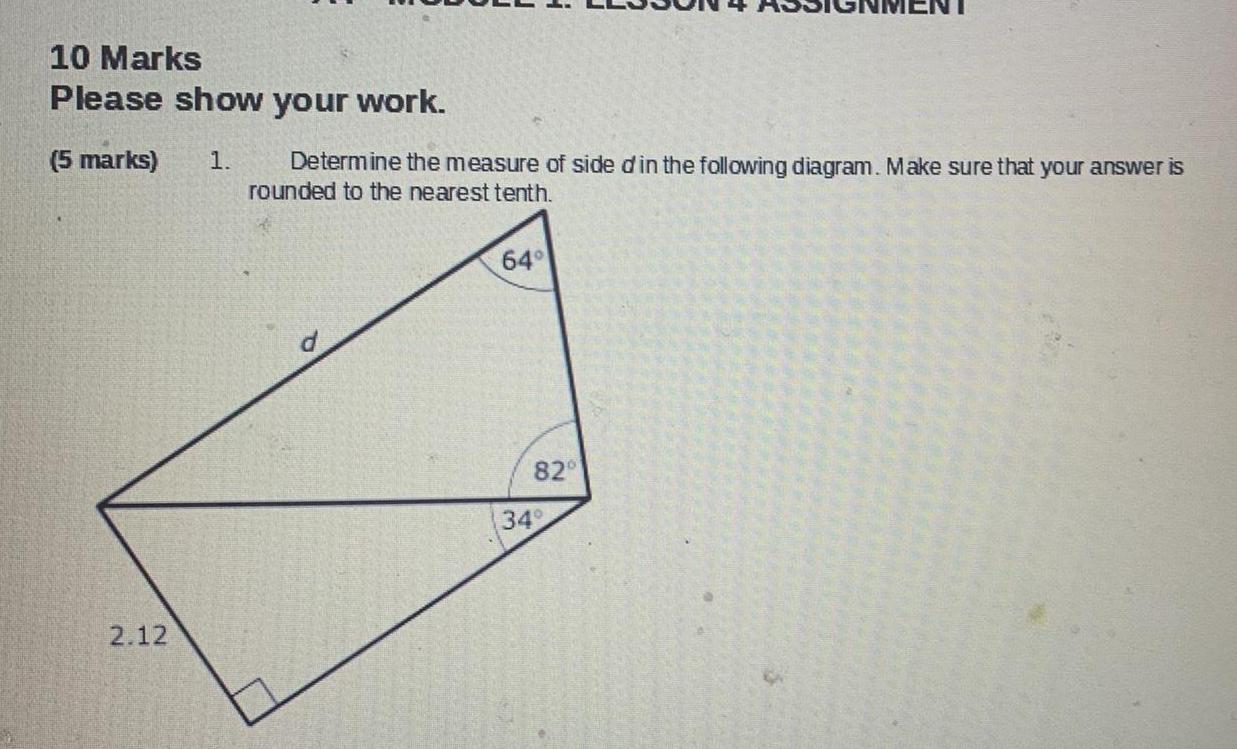
Math
Solution of trianglesDetermine the measure of side d in the following diagram. Make sure that your answer is rounded to the nearest tenth.
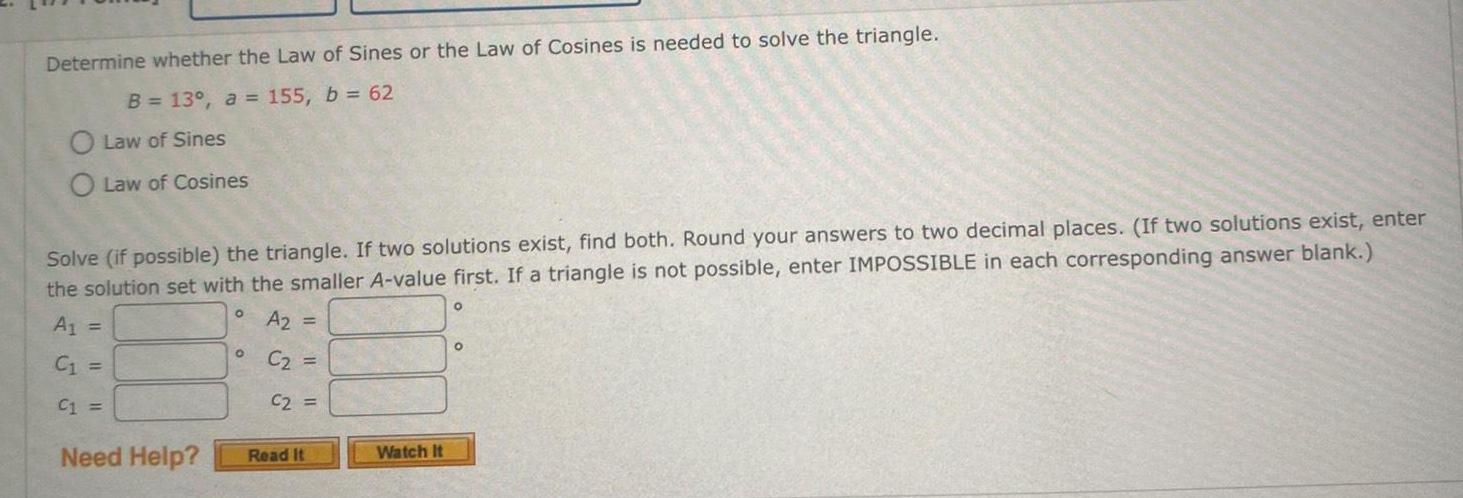
Math
Solution of trianglesDetermine whether the Law of Sines or the Law of Cosines is needed to solve the triangle.
B = 13°, a = 155, b = 62
Law of Sines
Law of Cosines
Solve (if possible) the triangle. If two solutions exist, find both. Round your answers to two decimal places. (If two solutions exist, enter
the solution set with the smaller A-value first. If a triangle is not possible, enter IMPOSSIBLE in each corresponding answer blank.)

Math
Solution of trianglesThink About the Process In AABC, mZB is 5
times mZA and mZC is 16° less than 4 times
mZA. What equation is used to solve for the
variable x? Find the measure of each angle.
The figure is not drawn to scale.
Which of the following is the correct equation used to solve for the measure of each angle?
A. MZA+mZB+mZC= 180°
B. MZA-mZB-m/C= 180°
C. MZA-mZB+mZC = 180°
D. MZA+mZB-mZC= 180°

Math
Solution of trianglesUse Heron's Area Formula to find the area of the triangle. (Round your answer to two decimal places.)
A = 80°, b = 74, c = 42

Math
Solution of trianglesIn the figure, m∠1 = (7x+7)°, m∠2 = (5x+14)°, and m∠4 = (13x +9)°. Your friend incorrectly says that m∠4 = 15°. What is m∠4? What mistake might your friend have made?

Math
Solution of trianglesDetermine whether the Law of Sines or the Law of Cosines is needed to solve the triangle.
A = 41°, B = 36°, c = 3.6
O Law of Sines
O Law of Cosines
Solve (if possible) the triangle. If two solutions exist, find both. Round your answers to two decimal places. (If a triangle is not possible, enter IMPOSSIBLE in each
corresponding answer blank.)
C=
a=
b=

Math
Solution of trianglesSolve ΔABC, given A=43°, a = 2.5 cm, and b= 3.6 cm. Begin by sketching and labeling a diagram. Account for all possible solutions. Express each angle to the nearest degree and each length to the nearest tenth of a unit.


Math
Solution of trianglesA farmer has a triangular field with sides that measure 40m (side AB), 35m (side BC),
and 38m (side CA). What are the measures of the angles A, B, and C in this field Provide a complete solution including a diagram.

Math
Solution of trianglesTriangle ABC is transformed to create AMNand APQR as described.
Triangle MNrepresents the translation 2 units left and 2 units down of AABC.
Triangle PQR represents the dilation of AABC by a scale factor of 2.
Which of these is correct?
The transformation of triangle ABC to triangle MNO preserves the angle measures but not the side lengths of the triangle.
The transformation of triangle ABC to triangle MNO preserves both the side lengths and angle measures of the triangle.
The transformation of triangle ABC to triangle PQR preserves both the side lengths and angle measures of the triangle.
The transformation of triangle ABC to triangle PQR preserves the side lengths but not the angle measures of the triangle.

Math
Solution of trianglesSolve the triangle, if possible. Determine the number of possible solutions.
A = 78.7° a = 11.2 b=9.7
Select the confect choice below and lite answer boxes wil Le choice.
(Round to the nearest tenth as needed.)
A. There are 2 possible solutions for the triangle.
The measurements for the solution with the longer side c are as follows.
m∠B=
m∠C=
The length of side c =
The measurements for the solution with the shorter side c are as follows.
m∠B=
mZC=
The length of side c =
B. There is only 1 possible solution for the triangle.
The measurements for the remaining angles A and C and side c are as follows.
m∠B=
m∠C=
The length of side c =

Math
Solution of trianglesUse the pythagorean theorem to find the length of TI.
(leg)2 + (leg) = (hypotemuse)"
Enter the answer in simplified form.
245

Math
Solution of trianglesIf AC has length 13 and BC has length 18, find:
• The length of AB:
• The measure of angle B (in degrees):
• The measure of angle C (in degrees):
If you use a calculator to find a decimal approximation, your answer must be accurate to at least 3 decimal places.
If you're using a calculator, be sure that your calculator is set to degrees, not radians.
You are also allowed to use the inverse trig functions in your answer instead of using a calculator. sin ¹(z) can be entered as arcsin(x) or asin(x).

Math
Solution of trianglesDarnell is constructing a rectangle window frame. He measured the length, the width, and the diagonal as 26 inches,
32 inches, and √1700 inches.
Use the drop-down menus to answer the following questions of Darnell's window frame.
(1)What is the longest side?
(2)What is the square of the longest side?
(3)What is the sum of the squares of the two shorter sides?
(4)Does the window frame form right triangles?

Math
Solution of trianglesThe map of a campground is shown below. Campsite C, first aid station F, and supply station S lie along a straight path. The path from the supply station to the tower, T, is perpendicular to the path from the supply station to the campsite. The length of path FS is 400 feet. The angle formed by path TF and path FS is 72º. The angle formed by path TC and path CS is 55°.
Determine and state, to the nearest foot, the distance from the campsite to the tower.

Math
Solution of trianglesWhat type of triangle has side lengths 2, √12, and √19?
A. not a triangle
B. acute
C. right
D. obtuse

Math
Solution of trianglesUnder a certain transformation ΔABC⇒ΔA'B'C' such that AB = A'B'. The triangles are:
A. neither congruent nor similar
B. congruent but not similar
C. similar but not congruent
D. both congruent and similar

Math
Solution of trianglesThe circumcenter of a triangle is also the center of
A. a circle inscribed inside the triangle
B. mass and balance
C. all of these
D. a circle circumscribing the triangle

Math
Solution of trianglesWhat point of concurrency in a triangle is always located inside the triangle?
A. orthocenter, only
B. Incenter, only
C. orthocenter and circumcenter
D. centroid and incenter

Math
Solution of trianglesIf three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
A Side-Side-Side (SSS) Congruence Postulate
B Side-Angle-Side (SAS) Congruence Postulate
C Angle-Angle-Angle (AAA) Congruence Postulate
DSide-Side-Angle (SSA) Congruence Postulate

Math
Solution of trianglesTriangle XYZ is a right triangle with the right angle at vertex Y.
Angle X must be
Angle Z must be
The sum of angles X and Z must be 90°.
![Complete the following statement with the correct number.
The sum of the three angles of any triangle is [?]°.](https://media.kunduz.com/media/sug-question/raw/52626974-1658418402.5552957.jpeg?w=256)
Math
Solution of trianglesComplete the following statement with the correct number.
The sum of the three angles of any triangle is [?]°.

Math
Solution of trianglesThe coordinates P(0, 1), Q(3, 2), R(5, -4) form a right triangle.
True
False

Math
Solution of trianglesIn slides 2-4, use the side lengths to determine if the triangle
is acute, obtuse, right, or not a triangle.
19, 6, 12

Math
Solution of trianglesIn triangle ABC, AC = 6, AB = 7, and BC = 5. Which is true?
The measure of ∠C is the least of the three angles.
The measure of ∠B is the greatest of the three angles.
The measure of ∠B is the least of the three angles.
The measure of ∠C is the greatest of the three angles.