Trigonometric equations Questions and Answers
Math
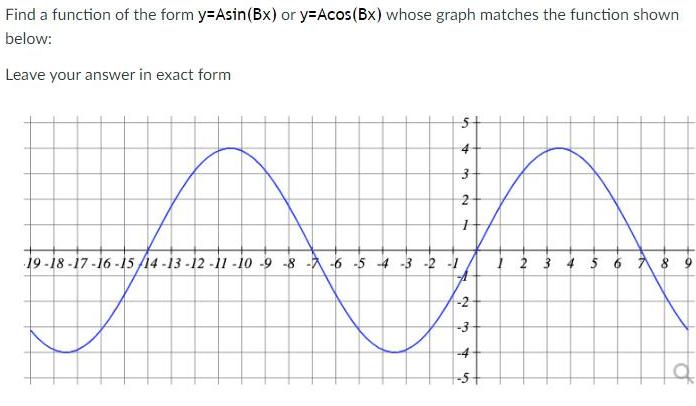
Trigonometric equationsFind a function of the form y Asin Bx or y Acos Bx whose graph matches the function shown below Leave your answer in exact form 5 A 3 2 M 19 18 17 16 15 14 13 12 11 10 986 54 3 2 1 2 3 5 1 2 3 4 5 6 7 8 C a

Math
Trigonometric equationsve the figure below 45 ft 60 ft the figure answer the questions on the right 9 10 1 point In the figure we see that the cherry picker can reach a height of 60 feet off the ground which includes the 8 feet from the base when it is inclined to its maximum angle of 48 degrees What is the length of the arm of the cherry picker Enter your answer to 2 decimal places Type your answer 1 point If the cherry picker does not move can the angle of the arm change in a way that it can reach the top of the building 17 00 D type your answer
Math
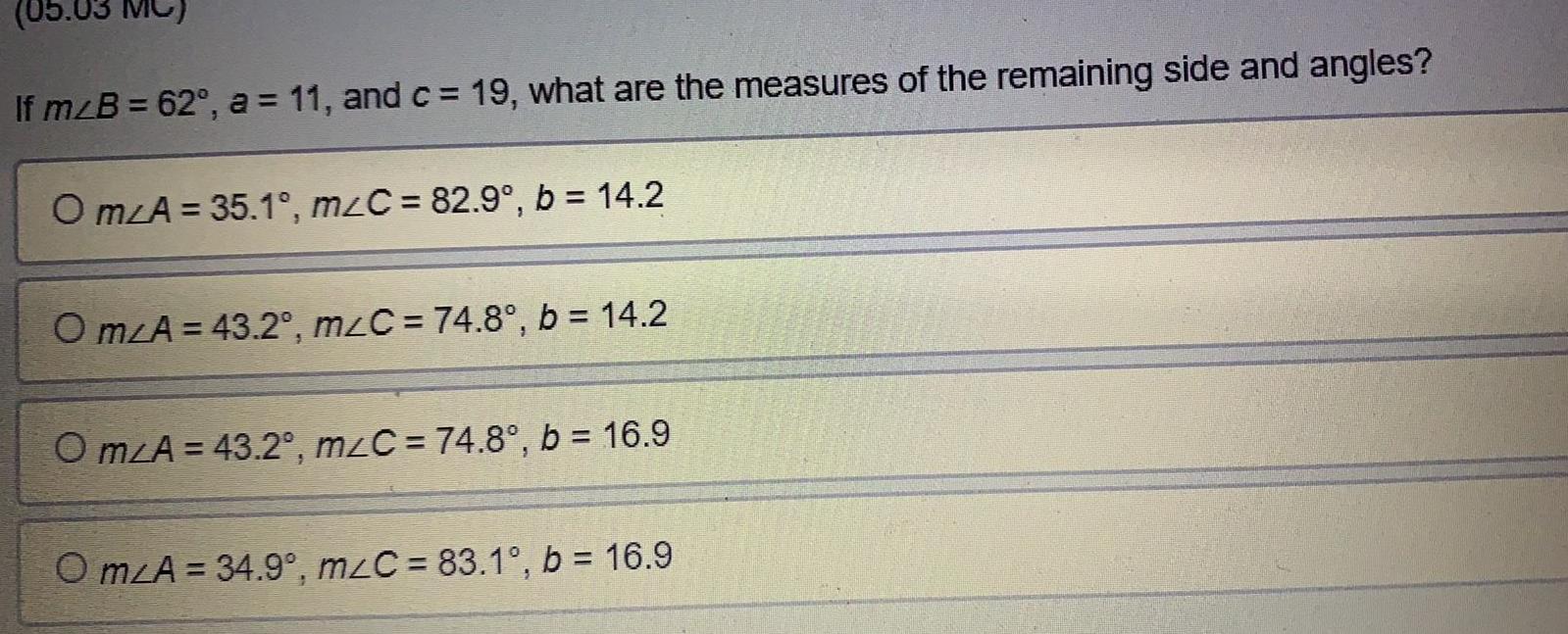
Trigonometric equationsIfm B 62 a 11 and c 19 what are the measures of the remaining side and angles O mA 35 1 m C 82 9 b 14 2 Om A 43 2 m C 74 8 b 14 2 Om A 43 2 mzC 74 8 b 16 9 Om A 34 9 m C 83 1 b 16 9
Math
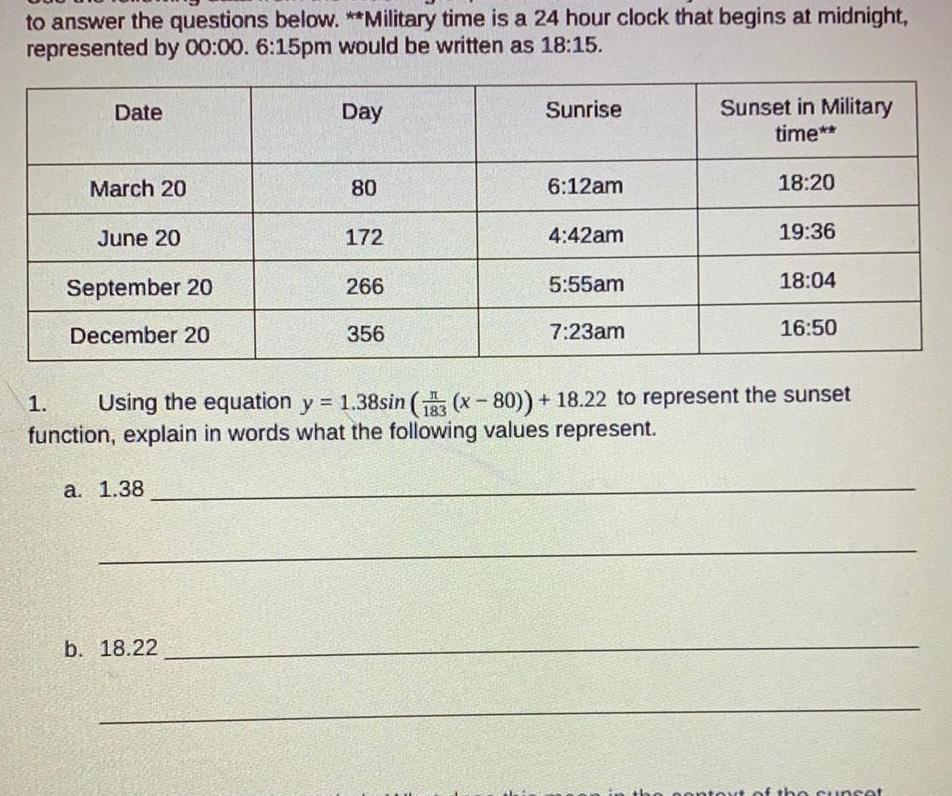
Trigonometric equationsto answer the questions below Military time is a 24 hour clock that begins at midnight represented by 00 00 6 15pm would be written as 18 15 Date March 20 June 20 September 20 December 20 a 1 38 Day b 18 22 80 172 266 356 Sunrise 6 12am 4 42am 5 55am 7 23am Sunset in Military time 18 20 19 36 18 04 1 Using the equation y 1 38sin 13 x 80 18 22 to represent the sunset function explain in words what the following values represent 16 50 context of the sunset

Math
Trigonometric equations2 Jada is riding on a Ferris wheel Her height in feet is modeled by the function 2am 10 h m 100 cos ride 110 where m is the number of minutes since she got on the a How many minutes does it take the Ferris wheel to make one full revolution Explain how you know b Sketch two cycles of a graph of h showing all of your thinking work 240 200 160 120 80 40

Calculus
Trigonometric equationsAt which values in the interval 0 2TT will the functions f x 2cos20 and g x 1 4cos 0 2cos20 intersect 4 3 3 00 O C 5x W H 2n 4x 3 2 5 1
Calculus
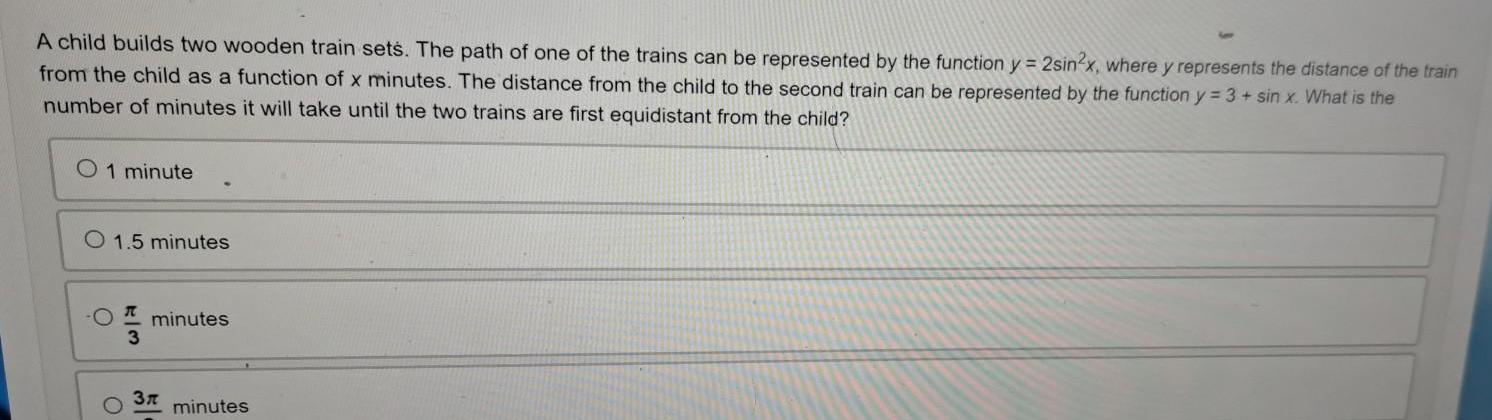
Trigonometric equationsA child builds two wooden train sets The path of one of the trains can be represented by the function y 2sin2x where y represents the distance of the train from the child as a function of x minutes The distance from the child to the second train can be represented by the function y 3 sin x What is the number of minutes it will take until the two trains are first equidistant from the child O 1 minute O 1 5 minutes O O W 3 minutes 3r minutes
Calculus
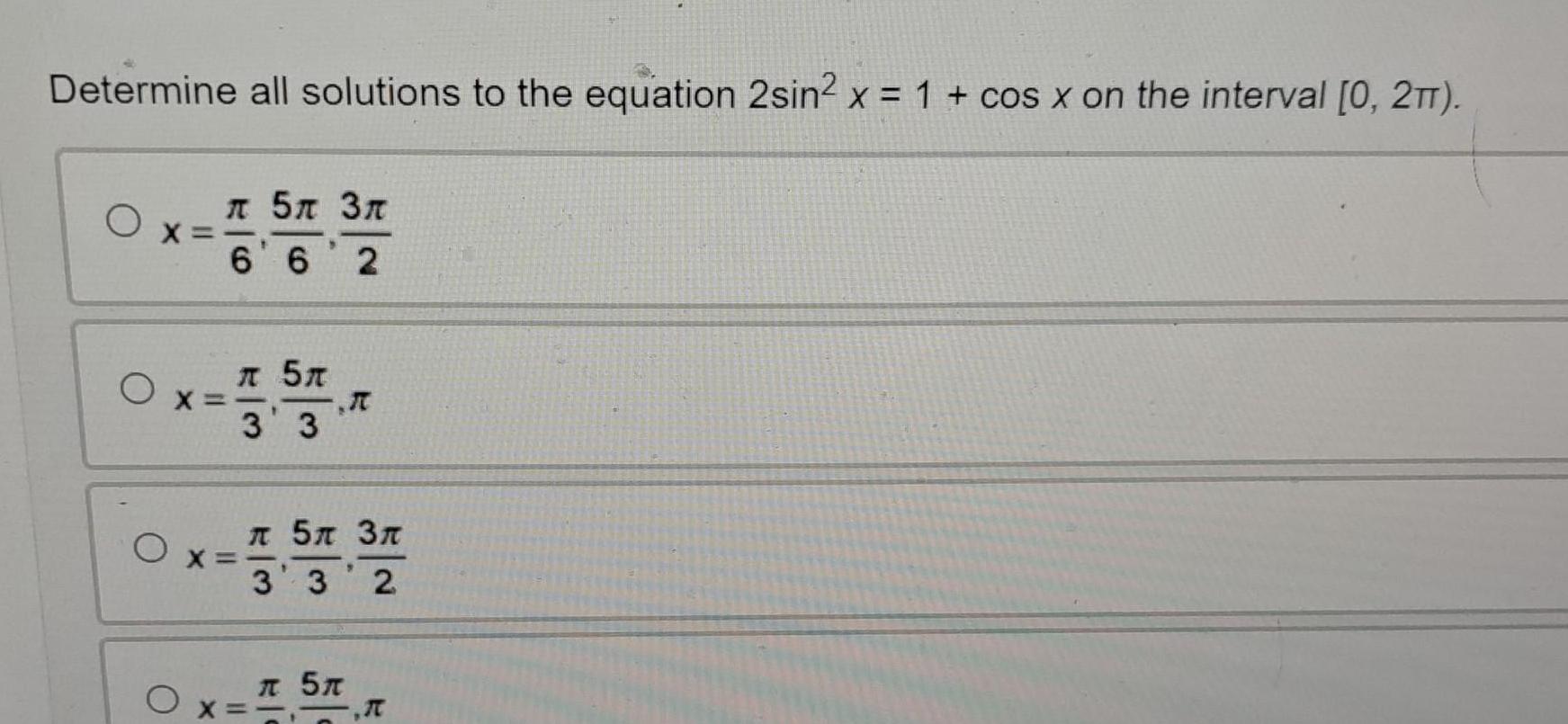
Trigonometric equationsDetermine all solutions to the equation 2sin x 1 cos x on the interval 0 2TT O Ox O 5 3 6 6 2 X 5 3 3 5x 3 332 5t x 7

![Consider the curve: y = 1-csc(2 (x-π))
(a) State the period of this curve.
(b) State the phase shift of this curve, and whether it is to the right or to the left.
(c) Sketch a sequence of 5 small separate graphs carefully labeled over a single period starting with y = sin(x) for x ∈[0,2π], moving one change at a time through 3 intermediate curves, and ending with the curve above, as we have done in class.](https://media.kunduz.com/media/sug-question/raw/77869161-1661533082.9264314.jpeg?w=256)
Math
Trigonometric equationsConsider the curve: y = 1-csc(2 (x-π))
(a) State the period of this curve.
(b) State the phase shift of this curve, and whether it is to the right or to the left.
(c) Sketch a sequence of 5 small separate graphs carefully labeled over a single period starting with y = sin(x) for x ∈[0,2π], moving one change at a time through 3 intermediate curves, and ending with the curve above, as we have done in class.

Math
Trigonometric equations12-35. For each of the following equations, list all of the solutions without using a calculator. Use the unit circle or a graph to check your answer. Then, predict the solution that your calculator will give, and use your calculator to check your prediction. a. 2cos(x) - 1 = 0 b. 4sin²(x) - 3 = 0 c. 2sin(x) = √3

Math
Trigonometric equationsSalina, Tamara, and Uma are working on their homework together. Salina tells her friends that she has θ = 52° for the inverse cosine problem she is working on and asks if they have the same answer. Tamara says she has θ = 128°, and Uma volunteers her answer of θ = 308°. Is it possible that these are all solutions to the same problem? Justify your answer.

Math
Trigonometric equationsSuppose sin(a)= 7/10, where 0 ≤ a ≤ π/2
Find all solutions in [0, 2π):
sin(2x) = 7/10
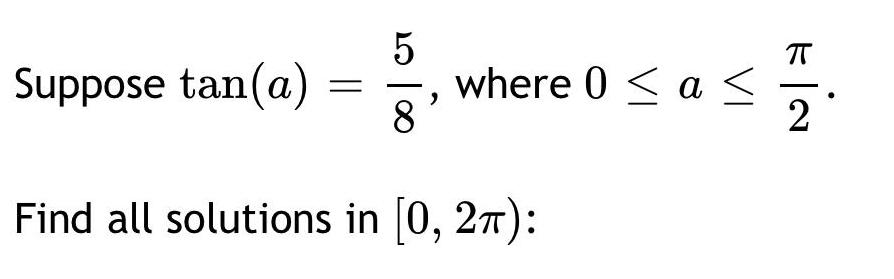
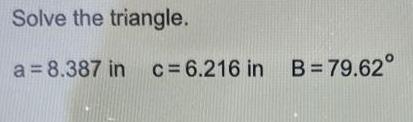
Math
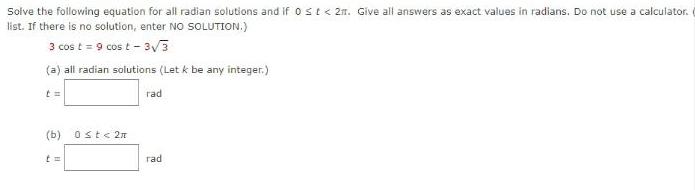
Trigonometric equationsSolve the following equation for all radian solutions and if 0 < t <2π. Give all answers as exact values in radians. Do not use a calculator. list. If there is no solution, enter NO SOLUTION.)
3 cos t = 9 cost t-3√3
(a) all radian solutions (Let k be any integer.)
t=rad
(b) 0≤t <2n
t= rad
Math
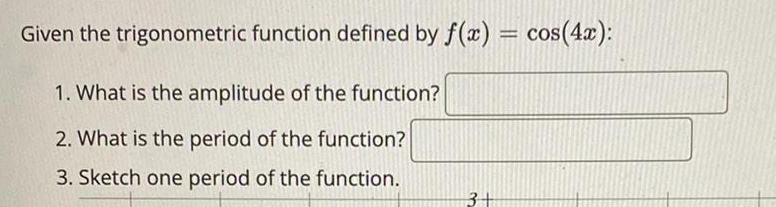
Trigonometric equationsGiven the trigonometric function defined by f(x) = cos(4x):
1. What is the amplitude of the function? _______
2. What is the period of the function? ______
3. Sketch one period of the function.
Math
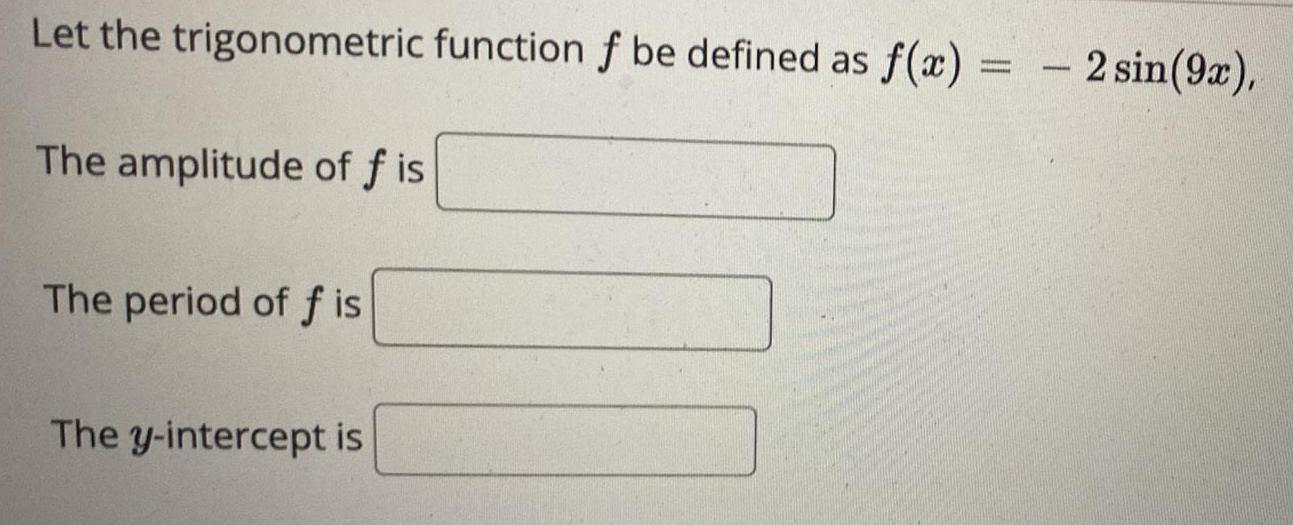
Trigonometric equationsLet the trigonometric function f be defined as f(x)= -2sin(9x),
The amplitude of f is _____
The period of f is ____
The y-intercept is ____

Math
Trigonometric equationsWhich expression below can be obtained from 10sin²x by using a power reducing formula?
Select the correct answer below:
5 - 10cos (5x)
5-5cos (2x)
10-5cos (2x)
5-10cos (x)
5-5cos (x)

Math
Trigonometric equationsFor sin 2x + cos x = 0, use a double-angle or half-angle formula to simplify the equation and then find all solutions of the equation in the interval [0, 2π).
The answers are
x1 =
12
x3 =
x4 =
Math
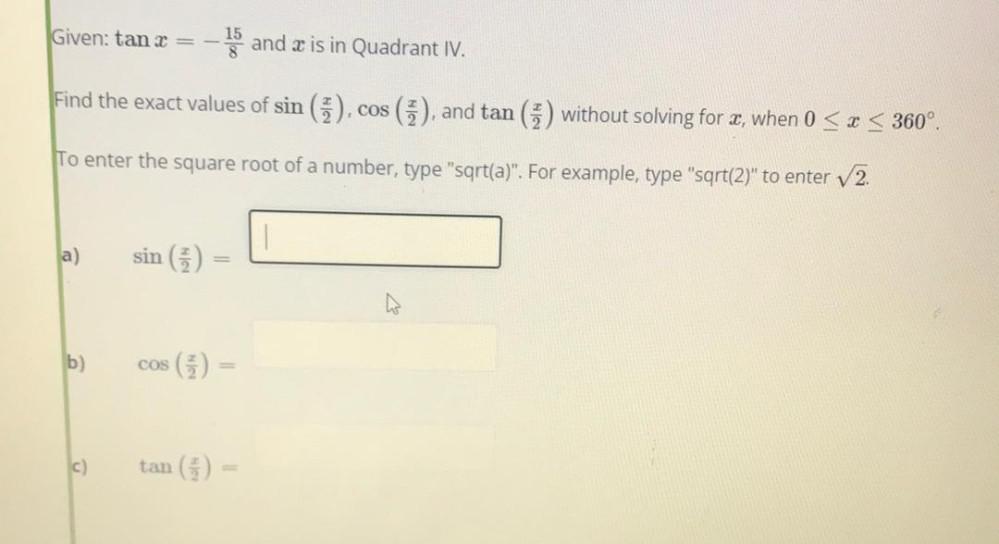
Trigonometric equationsGiven: tanx = -15/8 and x is in Quadrant IV.
Find the exact values of sin (x/2),cos (x/2), and tan (x/2) without solving for x, when 0 ≤ x ≤ 360°.
To enter the square root of a number, type "sqrt(a)". For example, type "sqrt(2)" to enter √2.
a)sin (x/2)= ___
b)cos (x/2)= ___
c)tan (x/2)= ___

Math
Trigonometric equationsLet P(x, y) be the terminal point on the unit circle determined by t. Then sin(t) = ___,
cos(t) = ___ , and tan(t) = ___.

Math
Trigonometric equationsEvaluating the cosine of a sum of two angles can be done using cos(A + B) = ?
a) sin(A) sin(B) – cos(A) cos(B)
b) None of these
c) cos(A) cos(B) + sin(A) sin(B)
d) cos(A) cos(B) – sin(A) sin(B)
Math
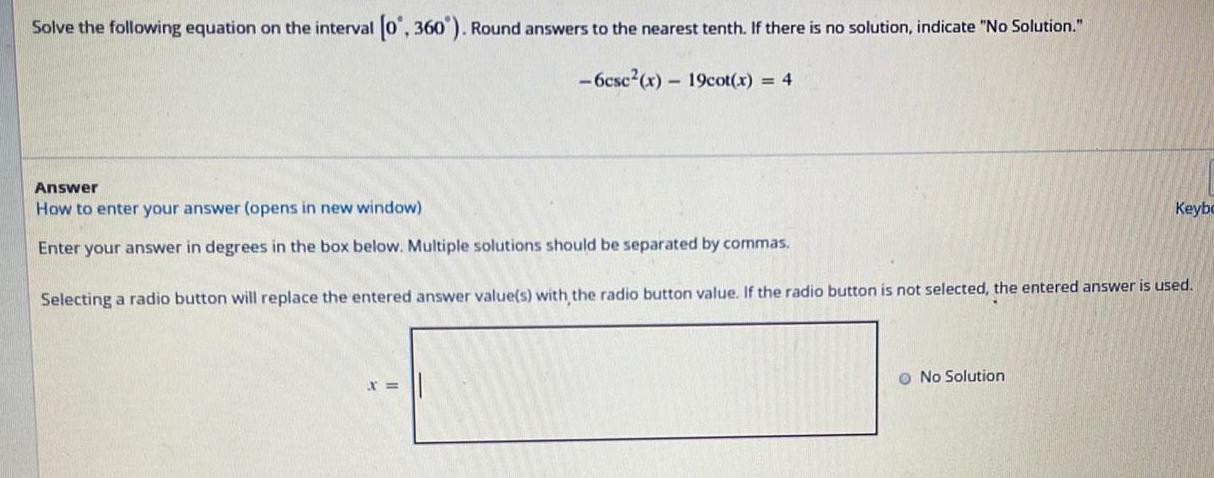
Trigonometric equationsSolve the following equation on the interval [0°, 360°). Round answers to the nearest tenth. If there is no solution, indicate "No Solution."
-6csc²(x) - 19cot(x) = 4
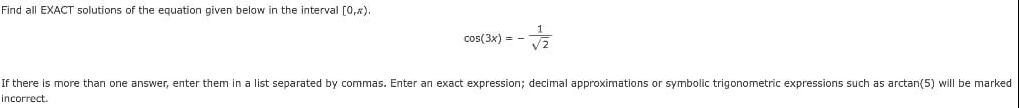
Math
Trigonometric equationsFind all EXACT solutions of the equation given below in the interval [0,π).
cos(3x)=-1/√2
If there is more than one answer, enter them in a list separated by commas. Enter an exact expression; decimal approximations or symbolic trigonometric expressions such as arctan (5) will be marked incorrect.

Math
Trigonometric equationsA complicated equation was simplified and factored into (tanx) (sin²x – a ) (sec x - a) = 0.
Determine the number of roots of the equation over the domain 0 <= x <= 2π if:
a) 0< a < 1
b) a > 1
Math
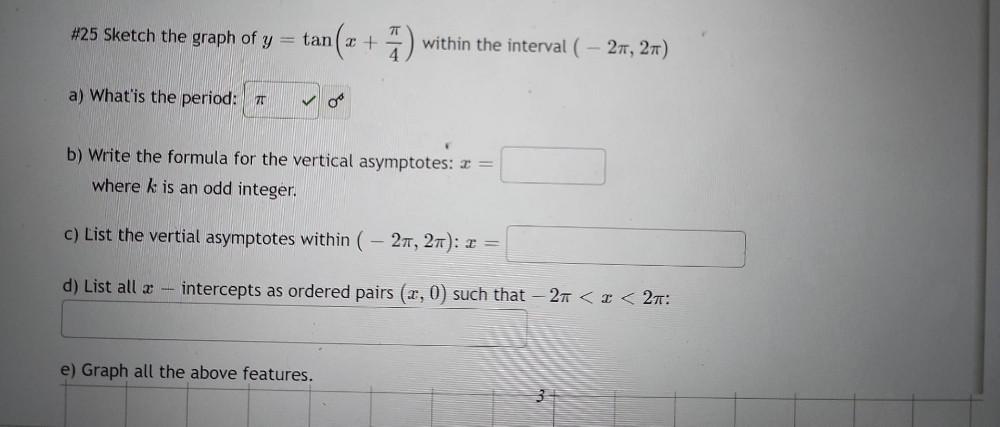
Trigonometric equationsSketch the graph of y = tan( x + π/4 ) within the interval ( – 2π, 2π)
a) What is the period?
b) Write the formula for the vertical asymptotes: x =
where k is an odd integer.
c) List the vertical asymptotes within ( - 2π, 2π ): x =
d) List all x intercepts as ordered pairs ( x,0) such that – 2π < x < 2π:
e) Graph all the above features.

Math
Trigonometric equationsThe amount of daylight in a town can be modelled by the sinusoidal function
d(t)= 4.37 cos 0.017t + 12.52
where d(t) represents the hours of daylight and t represents the number of days since June 20, 2012. How many hours of daylight should be expected on June 20, 2013?
a) 16.80 hr
c) 16.84 hr
b) 16.88 hr
d) 16.92 hr
Math
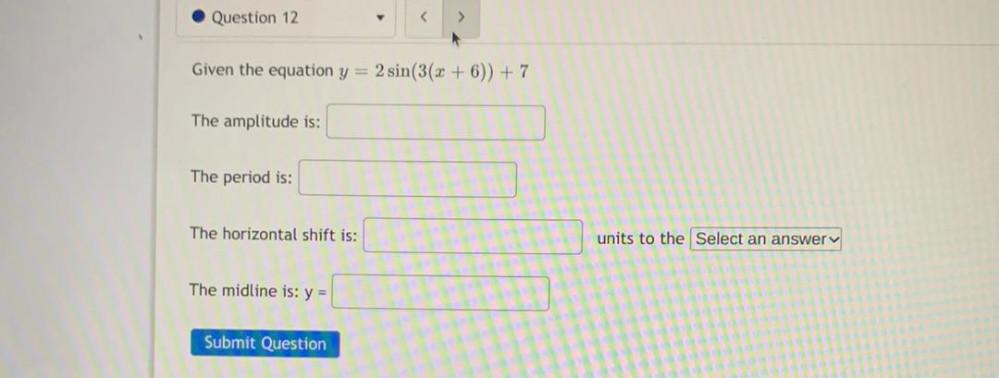
Trigonometric equationsGiven the equation y = 2 sin(3(x + 6)) + 7
The amplitude is:
The period is:
The horizontal shift is:
The midline is: y =


Math
Trigonometric equationsSuppose 0 ≤θ≤ π/2. Solve the equation: 2 cos(3θ) + cos(3θ) - 2 = 0 for θ.
Give your answer rounded to 2 places after the decimal point.

Math
Trigonometric equationsWrite 2 tan 17°/1 - tan² 17° as a trigonometric function of one number. You do NOT need to type in the degree symbol.
Math
Trigonometric equationsSolve 6 cos(2x)= 3 for the smallest positive solution.
Give your answer accurate to at least two decimal places.

Math
Trigonometric equationsSolve 7 sin(π 6)x = 4 for the four smallest positive solutions
Give your answers accurate to at least two decimal places, as a list separated by commas
![Find the maximum and minimum values of the function g(0) = 2θ - 7 sin(θ) on the interval [0, π/2]
Minimum value =
Maximum value: =](https://media.kunduz.com/media/sug-question/raw/51128461-1658398716.6813455.jpeg?w=256)
Math
Trigonometric equationsFind the maximum and minimum values of the function g(0) = 2θ - 7 sin(θ) on the interval [0, π/2]
Minimum value =
Maximum value: =

Math
Trigonometric equationsVerify the identity.
tan x csc 2x− tan x= cotx
Choose the sequence of steps below that verifies the identity.
Math
Trigonometric equationsFind all solutions of this equation in the interval [0, 2π):
2 cos(x) + 1 = 0

Math
Trigonometric equationsUse the definition or identities to find the exact value of each of the remaining five trigonometric functions of the acute angle θ.
cos θ = 1/11

Math
Trigonometric equationsFor each of the following, identify the amplitude, period, horizontal (phase) shift, vertical shift, domain, range, y-intercept and any x-intercepts.
f(x) = 4 - 2 sin 3 (x - 2π)
Amplitude:
Period:
Hor. Shift:
Vert Shift:
Domain:
Range:
y-int:
x-int:
Math
Trigonometric equationsSelect the correct answer from the drop-down menu.
Sam is flying a kite. The length of the kite string is 80 meters, and it makes an angle of 75° with the ground. The height of the kite from the ground is
meters.
Math
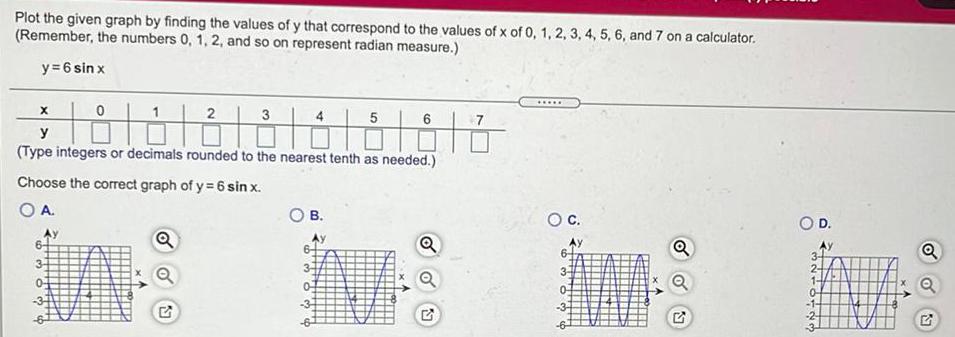
Trigonometric equationsPlot the given graph by finding the values of y that correspond to the values of x of 0, 1, 2, 3, 4, 5, 6, and 7 on a calculator.
(Remember, the numbers 0, 1, 2, and so on represent radian measure.)
y = 6 sin x

Math
Trigonometric equationsA ferris wheel is 45 meters in diameter and boarded from a platform that is 5 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. The function h-f(t) gives your height in meters above the ground t minutes after the wheel begins to turn.
What is the Amplitude? meters
What is the Midline? y= meters
What is the Period? minutes
How High are you off of the ground after 1 minutes? meters

Math
Trigonometric equationsA light source is located over the center of a circular table of diameter d = 12 feet (see figure). Find the height h of the light source such that the illumination I at the perimeter of the table is maximum when
I = k sin a / s²
where s is the slant height, a is the angle at which the light strikes the table, and k is a constant.
h =

Math
Trigonometric equationsSolve the following equation.
6 sin² θ-3=0,0 ≤θ<2π
What are the solutions in the interval 0 ≤θ<2π?
![A small aircraft starts its descent from an altitude of h = 4/5 miles, 4 miles west of the runway (see figure).
(a) Find the cubic function f(x) = ax³ + bx² + cx + d on the interval [-4, 0] that describes a smooth glide path for the
landing.
(b) The function in part (a) models the glide path of the plane. When would the plane be descending the greatest rate?](https://media.kunduz.com/media/sug-question/raw/54896663-1658071492.7540667.jpeg?w=256)
Math
Trigonometric equationsA small aircraft starts its descent from an altitude of h = 4/5 miles, 4 miles west of the runway (see figure).
(a) Find the cubic function f(x) = ax³ + bx² + cx + d on the interval [-4, 0] that describes a smooth glide path for the
landing.
(b) The function in part (a) models the glide path of the plane. When would the plane be descending the greatest rate?

Math
Trigonometric equationsFind the lengths of the sides of the given triangle.
The three sides of the triangle are units.
(Simplify your answers. Use a comma to separate answers as needed. Type integers or decimals rounded to the nearest tenth as needed.)

Math
Trigonometric equationsDetermine which law applies. Then solve the triangle, if possible. Round angles to the nearest
tenth when necessary, and round side lengths to the nearest hundredth when necessary.
C = 108.4°
a = 5.3
b = 10.53
Law of cosines; no solution
Law of cosines; c= 19, A = 20.4°, B = 51.2°
Law of sines; c= 16.1, A = 24.4°, B = 47.2°
Law of cosines; c= 13.2, A = 22.4°, B = 49.2°
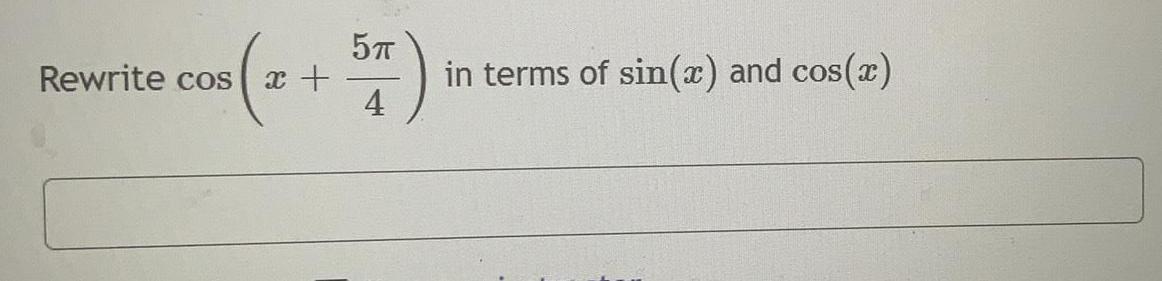

Math
Trigonometric equationsSolve 3tan² 0 + 1 = 4tan 9 for all positive angles less than 360°, to the nearest whole degree.
O 1.45°, 72°, 225°, 252°
02.
3.
26.6, 153.4°, 206.6°, 333.4°
45°, 18, 225°, 198
O 4.35.3°, 144.7°, 215.3°, 324.7%