Basic Math Questions and Answers
![The first 50 people who walk into a sporting event are polled on their television
preferences. [Select]
Simple Random
Stratified
Systematic
Cluster
Convenient](https://media.kunduz.com/media/sug-question/raw/54107099-1657999923.4551353.jpeg?w=256)
Math
Basic MathThe first 50 people who walk into a sporting event are polled on their television
preferences. [Select]
Simple Random
Stratified
Systematic
Cluster
Convenient
Math
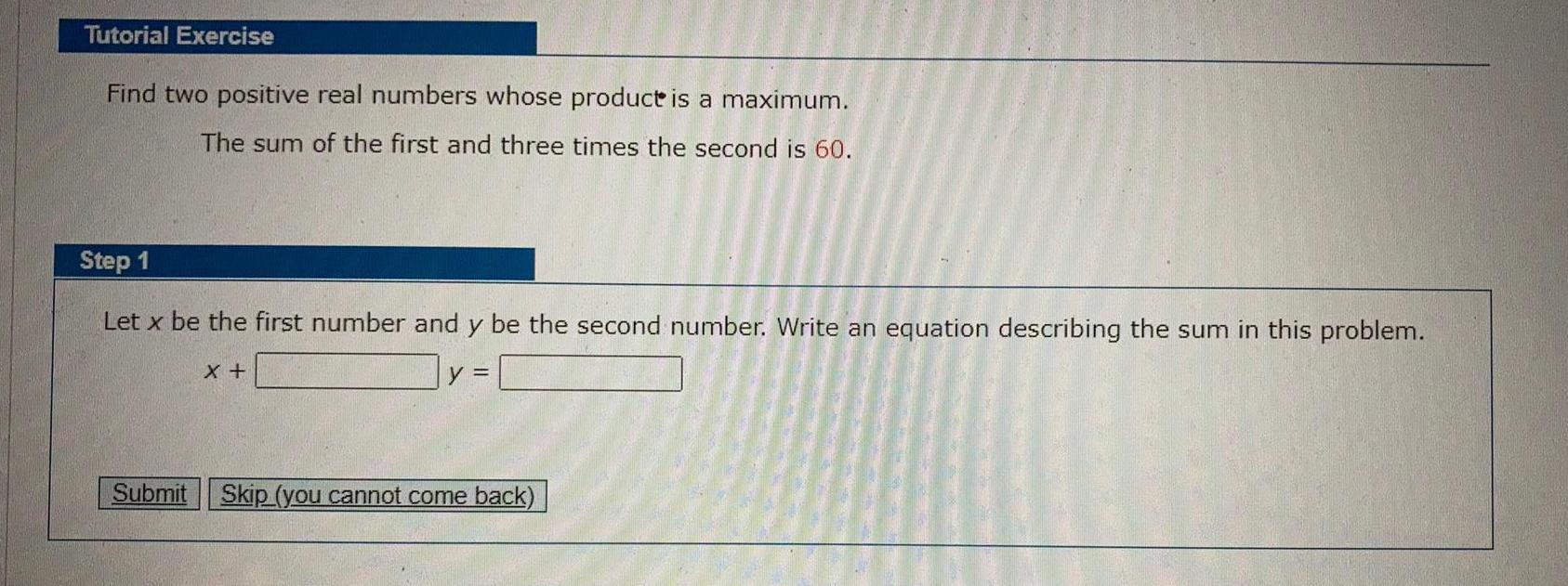
Basic MathTutorial Exercise
Find two positive real numbers whose product is a maximum.
The sum of the first and three times the second is 60.
Step 1
Let x be the first number and y be the second number. Write an equation describing the sum in this problem.
y =
X +
Submit Skip (you cannot come back)

Math
Basic MathBarbara sells iced tea for $1.49 per bottle and water for $1.25 per bottle. She wrote an equation to find the number
of bottles she needs to sell to earn $100.
1.25x + 1.49 = 100
What error did Barbara make in writing the equation?
O Barbara's equation did not consider the number of bottles of water.
O Barbara's equation did not consider the number of bottles of iced tea.
O Barbara's equation did not use the correct price for the bottles of iced tea.
O Barbara's equation did not use the correct total for sales.

Math
Basic MathPhoebe has a job singing in a café. Phoebe
makes an hourly rate of $4.25 plus tips. Last
week Phoebe worked 25 hours and made
$220.50. How much in tips did Phoebe earn
last week?

Math
Basic MathA shower uses 2.5 gal of water each minute. Yolanda wants to be sure each shower
she takes uses no more than 15 gal of water. She writes the inequality 2.5m ≤ 15,
where m is a number of minutes. Which values from 0 to 100 are solutions of the
inequality? What do the solutions tell you? Explain your reasoning.



Math
Basic MathAn airplane flying at an altitude of 30,000 feet flies up
to avoid a storm. Immediately after passing the storm,
the airplane returns to its original altitude.
a. What integer represents the airplane's change
in altitude to avoid the storm?
b. What integer represents the airplane's change
in altitude immediately after passing the storm?
c. Use Appropriate Tools Draw a number line to
represent the airplane's change in altitude.

Math
Basic MathJude worked at the student café. On Wednesday,
they worked for 3 hours and made their hourly rate
plus $7 in tips.
Write an expression that represents the
amount of money Jude made on Wednesday,
where x represents their hourly rate.

Math
Basic MathSolve the inequality algebraically Graph the solution set. Verify your results using a graphing utility.
|2x+1|-3≥-1
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Type your answer in interval notation. Use integers or fractions for any numbers in the expression.)
B. The solution is the empty set.

Math
Basic MathDetermine the value of n that makes the polynomial a perfect square trinomial. Then factor as the square of a binomial. Express numbers as integers or simplified fractions.
k²+16k+n
Math
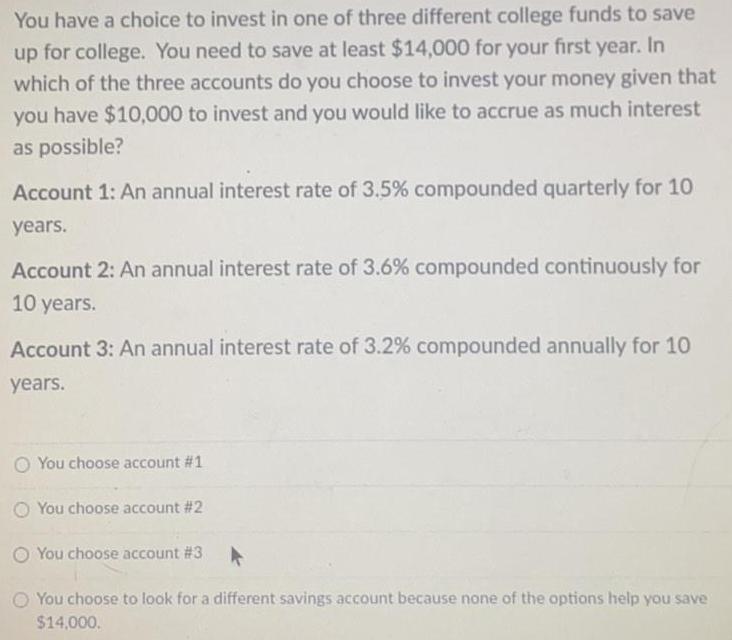
Basic MathYou have a choice to invest in one of three different college funds to save
up for college. You need to save at least $14,000 for your first year. In
which of the three accounts do you choose to invest your money given that
you have $10,000 to invest and you would like to accrue as much interest
as possible?
Account 1: An annual interest rate of 3.5% compounded quarterly for 10
years.
Account 2: An annual interest rate of 3.6% compounded continuously for
10 years.
Account 3: An annual interest rate of 3.2% compounded annually for 10
years.
You choose account #1
You choose account #2
You choose account # 3
You choose to look for a different savings account because none of the options help you save
$14,000.

Math
Basic MathMcKenna and Lara work for their uncle Eddie, who repairs
skateboards and bicycles. Uncle Eddie is leaving for a vacation to
the Amazon. He asks the girls to order 54 new wheels for the 21
skateboards and bicycles in his repair shop. How many bicycles and
how many skateboards are in Uncle Eddie's shop?
From the list of facts, circle those you need to solve Lara and
McKenna's problem.
McKenna and Lara's uncle is named Eddie.
There are 21 skateboards and bicycles in the shop.
Uncle Eddie went on a trip.
A bicycle has two wheels, and a skateboard has four wheels.
54 new wheels are needed.
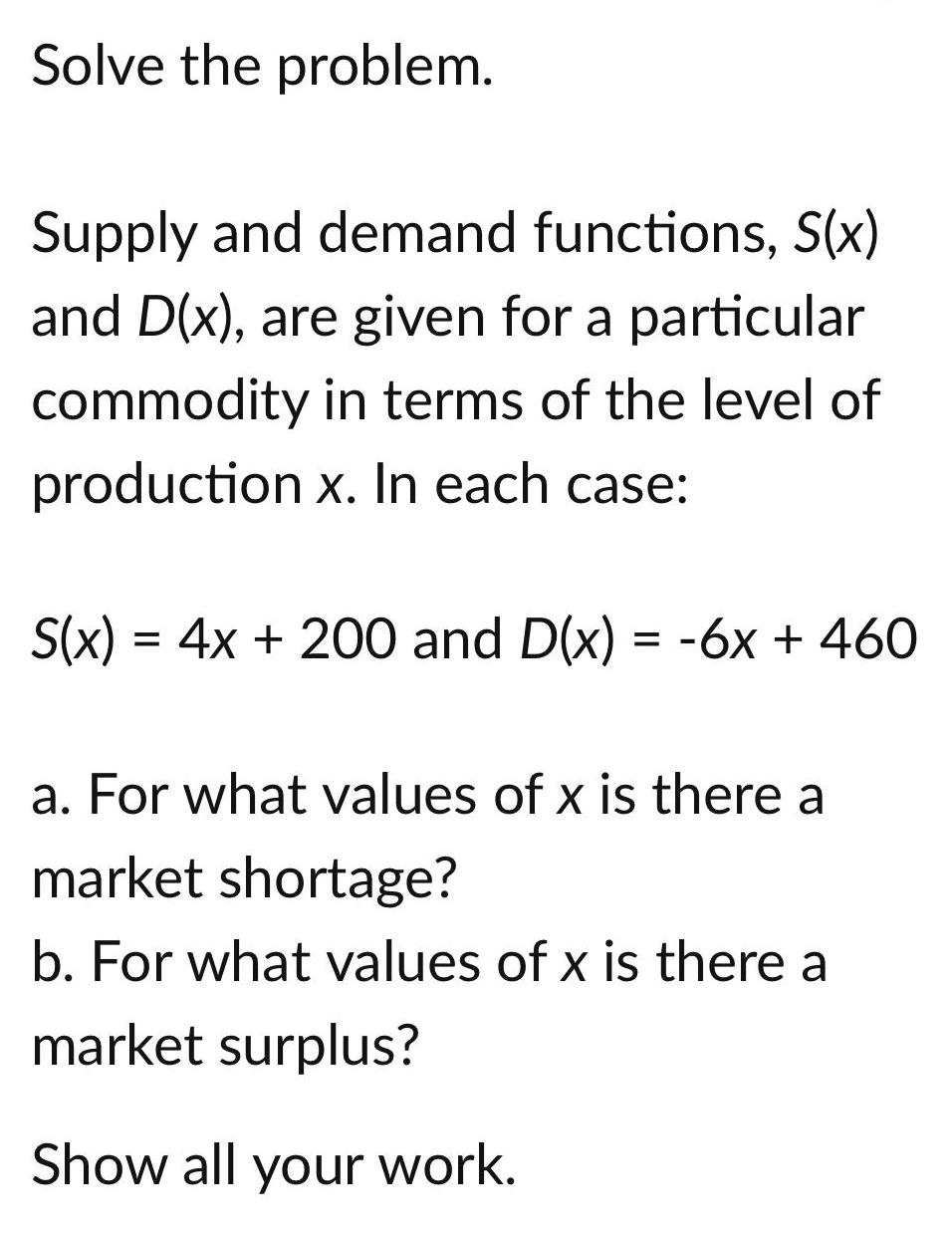
Math
Basic MathSolve the problem.
Supply and demand functions, S(x)
and D(x), are given for a particular
commodity in terms of the level of
production x. In each case:
S(x) = 4x + 200 and D(x) = -6x + 460
a. For what values of x is there a
market shortage?
b. For what values of x is there a
market surplus?
Show all your work.

Math
Basic MathA 1000 gram sample of radioactive matter will completely decay (be undetectable) in
10 hours. There exists a set of ordered pairs (t, m), where t is the amount of time in
hours that the substance has been decaying, and m is the mass in grams that has
decayed.
If t 0, what is the range of m?
Om 1000
OmER
Om 10
00 m 1000
Om > 0

Math
Basic MathA car enters an interstate highway 15 mi south of Youngstown. The car travels due south at an average speed of 62.5 mi/h. Write an equation to model the car's distance, d, from Youngstown after traveling h hours. How far south of Youngstown will the car be after 150 minutes?
Math
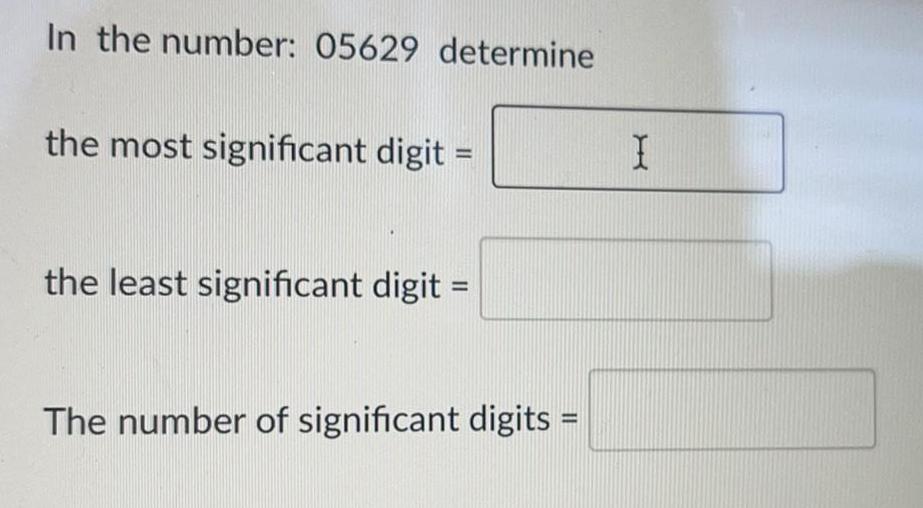
Basic MathIn the number: 05629 determine
the most significant digit =
the least significant digit =
The number of significant digits =
I

Math
Basic MathLuke invests $4200 in an account that has an annual interest rate of 2.8%
compounded semi-annually. Todd invests $3900 into an account that has
an annual interest rate of 3.3% and is compounded continuously. After 8
years what is the difference between the two accounts?
Todd has approximately $1.361 more in his account than Luke after 8 years.
Luke has approximately $168 more in his account than Todd after 8 years.
Luke has approximately $300 more in his account than Todd after 8 years.
Both Todd and Luke have the same amount of money in their accounts after 8 years.
Math
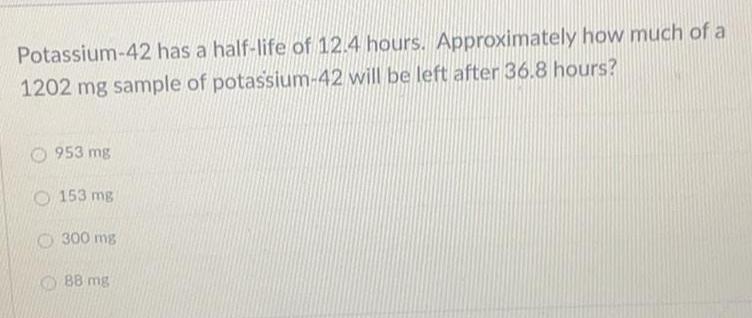
Basic MathPotassium-42 has a half-life of 12.4 hours. Approximately how much of a
1202 mg sample of potassium-42 will be left after 36.8 hours?
953 mg
153 mg
300 mg
88 mg

Math
Basic MathThe perimeter of the rectangular playing field is 370 yards. The length of the field is 7 yards less than triple the width. What are the dimensions of the playing field?

Math
Basic MathMaximum Capacity A delivery person uses a service elevator to bring boxes of
books up to an office. The delivery person weighs 160 lb and each box of books
weighs 50 lb. The maximum capacity of the elevator is 1000 lb. How many boxes of
books can the delivery person bring up at one time?

Math
Basic Math6
Write the equation of the line passing through the point (7, - 7) with slope 7
The equation of the line is
EE
H-R

Math
Basic MathWrite the equation of the line with slope 7 and y-intercept 1/8.
The equation of the line is

Math
Basic Math#10 i
The land area of the entire United States is 3,531,905 square miles. Use the current population of the United States to estimate the population per square mile. Explain.
-
T

Math
Basic MathSolve the problem.
When starting a new job at a production
facility, employees can be expected to
assemble n items per hour after t weeks of
work experience, where
n(t) = 75 -130/t+ 20.88
Employees are paid 30 cents for each item
they assemble.
a. Find an expression for the amount of
money A(t) earned per hour by an employee
with t weeks of experience.
b. How much money per hour should an
employee expect to earn in the long run
(as t→ ∞0)?

Math
Basic MathUse what you learned to solve these problems.
Aimee works up to 50 hours a month and earns $12 per hour. She wants to save
more than $240 to buy a computer. The inequality 12h 240, where h is the
number of hours Aimee works this month, models this situation. Which values
from 0 to 50 are solutions of the inequality? What do the solutions mean in this
situation? Explain your reasoning.

Math
Basic MathIn this Exercise, use what you've learned about linear functions and their
properties to model real-world situations.
1. In science class, you learned about converting temperatures between
degrees Celsius (°C) and Fahrenheit (°F), but recently you could not find a
reference with the correct formulas. You then remembered that the
relationship between °F and °C is linear.
(a) Using this and the knowledge that 32°F = 0°C and 212° F = 100°C, find
an equation that computes Celsius temperature in terms of
Fahrenheit; i.e. an equation of the form C = "an expression involving
only the variable F."
(b) Analogously, find an equation that computes Fahrenheit temperature
in terms of Celsius temperature; i.e. an equation of the form F = "an
expression involving only the variable C."

Math
Basic Math1 point
Final grades are often computed using weighted averages. Some college professors use complicated weighted averages. Your college professor tells you he will give a
33% -67% split on grades between tests and homework where whichever average is higher will be the 67%.
What will your final grade be if your homework average is 56 and your test average is 71?
Math
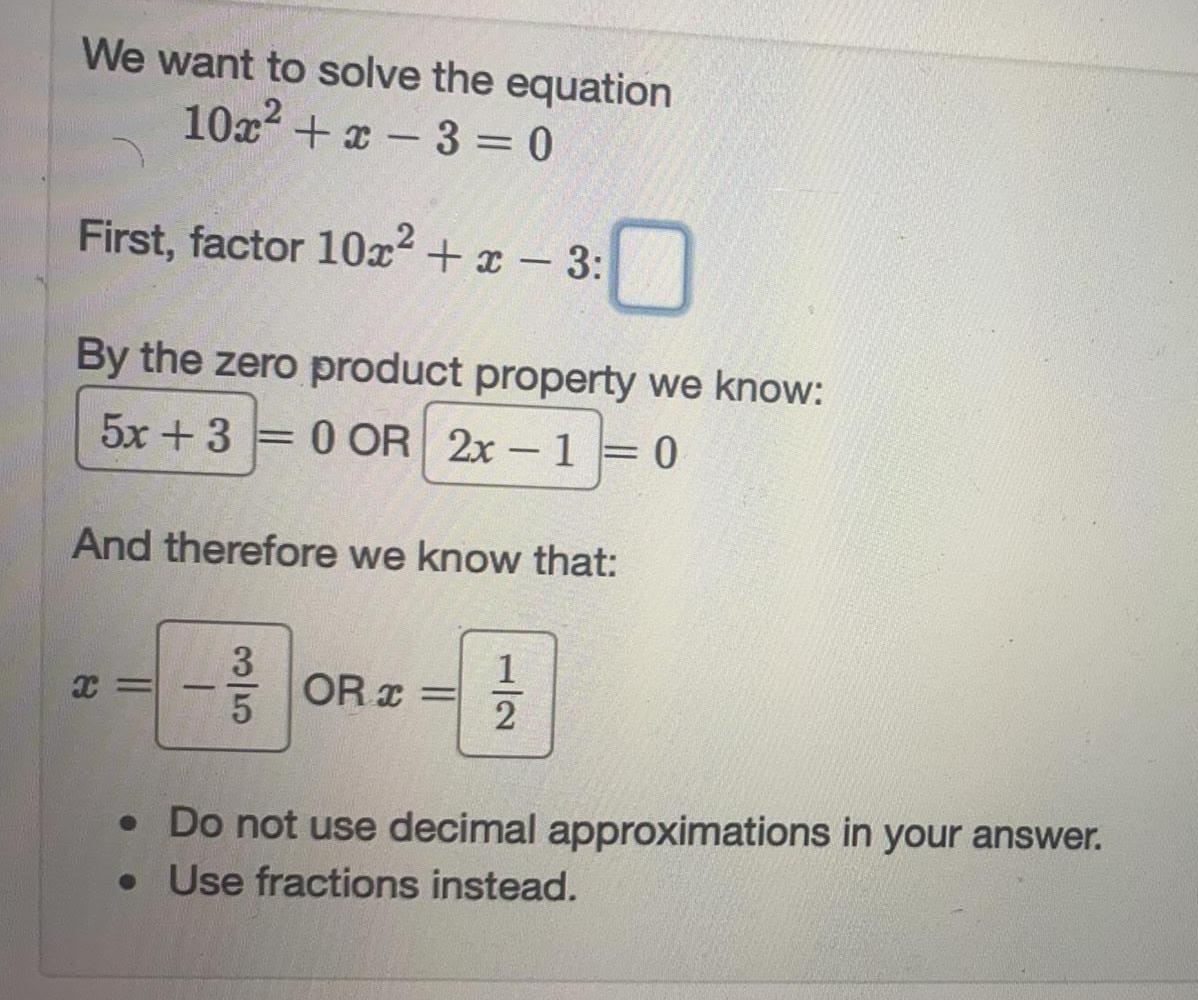
Basic MathWe want to solve the equation
10x² + x3 = 0
First, factor 10x² + x - 3:
By the zero product property we know:
5x+3
=
= 0 OR 2x-1=0
And therefore we know that:
X=
1
3/5
-B
2
OR=
• Do not use decimal approximations in your answer.
• Use fractions instead.
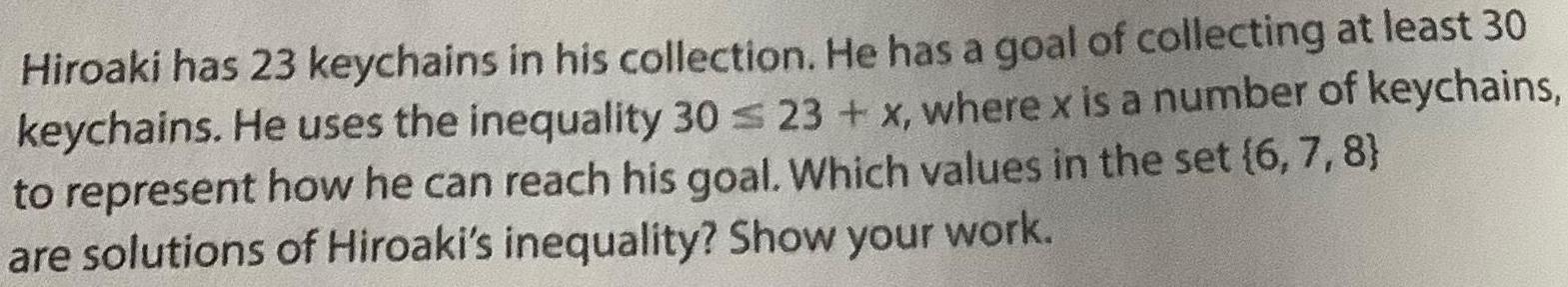
Math
Basic MathHiroaki has 23 keychains in his collection. He has a goal of collecting at least 30
keychains. He uses the inequality 30 ≤ 23 + x, where x is a number of keychains,
to represent how he can reach his goal. Which values in the set (6,7,8}
are solutions of Hiroaki's inequality? Show your work.

Math
Basic MathOn moving day, Guyton needs to rent a truck. The length of the cargo space is 11 ft, and the height is 2 ft less than the width. The brochure indicates that the
truck can hold 385 ft³. What are the dimensions of the cargo space? Assume that the cargo space is in the shape of a rectangular solid.
x-2
11 ft

Math
Basic MathFind the inverse of the one-to-one function f(x) = 5x/6 + 25.
(Use integers or fractions for any numbers in the expression.)

Math
Basic Math6. Ocean waves move in parallel lines toward the shore.
The figure shows Sandy Beaches windsurfing across
several waves. For this exercise, think of Sandy's wake
as a line. m/1 = (2x + 2y)° and m/2 = (2x + y)°.
Find x and y.
X =
y =



Math
Basic MathExpress the fact that x differs from 10 by less than 5 as an inequality involving absolute value. Solve for x.
Express the given sentence algebraically as an inequality involving absolute value.


Math
Basic MathThe land area of the entire United States is 3,531,905 square miles. Use the current population of the United States to estimate the population per square mile. Explain.

Math
Basic MathDraw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a
statement.
There were 22,869 children, 49,563 men, and 2,872 more women than men at the fair. How many
people were at the fair?

Math
Basic MathJenny is solving the equation 3x+5-4x42 using algebra tiles. She cannot decide if she should add 3 negative x-tiles or add 2 negative unit tiles to both sides first. Which explains which Jenny should do first?
She should add 3 negative x-tiles first because that is the only way to isolate the variable.
She should add 2 negative unit tiles first because that is the only way to get to the correct solution.
She can do either one first because zero pairs will be created to isolate the variable either way,
She should do neither one first because the first step is to add 4 negative tiles to both sides.
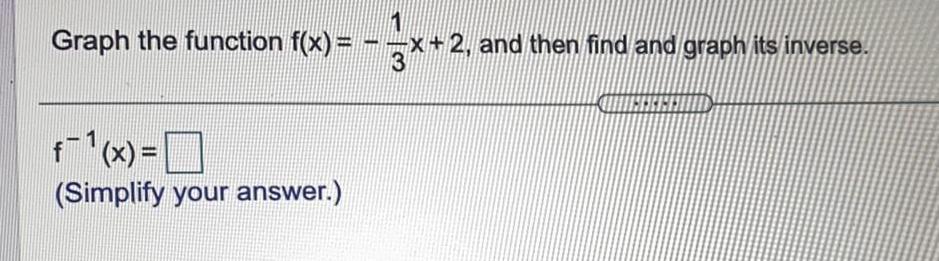
Math
Basic MathGraph the function f(x) = − −x+2, and then find and graph its inverse.
3
f-1(x) =
(Simplify your answer.)
Math
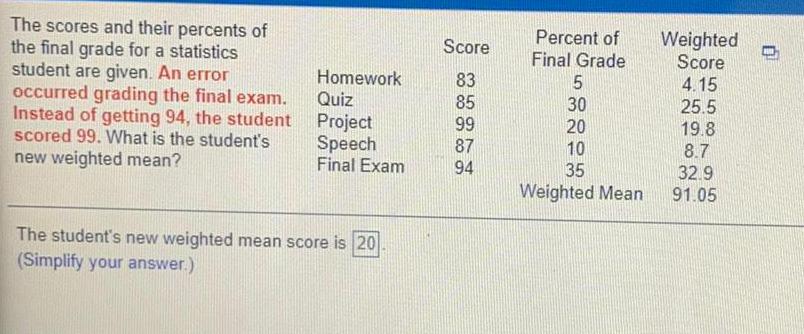
Basic MathThe scores and their percents of
the final grade for a statistics
student are given. An error
occurred grading the final exam.
Instead of getting 94, the student
scored 99. What is the student's
new weighted mean?
Homework
Quiz
Project
Speech
Final Exam
The student's new weighted mean score is 20
(Simplify your answer.)
Score
83
85
99
87
94
Percent of
Final Grade
5
30
20
10
35
Weighted Mean
Weighted
Score
4.15
25.5
19.8
8.7
32.9
91.05
0
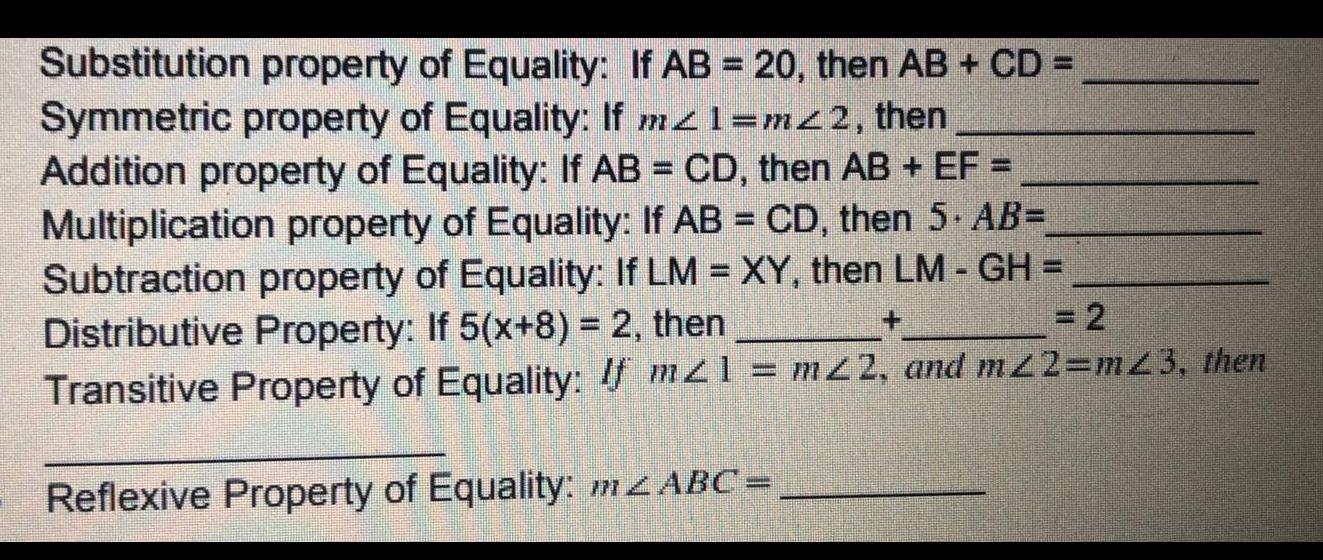
Math
Basic MathSubstitution property of Equality: If AB = 20, then AB + CD =
Symmetric property of Equality: If m1=m42, then
Addition property of Equality: If AB = CD, then AB + EF =
Multiplication property of Equality: If AB = CD, then 5. AB=
Subtraction property of Equality: If LM = XY, then LM - GH =
= 2
Distributive Property: If 5(x+8) = 2, then
Transitive Property of Equality: If mz1 = m22, and m22=m23, then
Reflexive Property of Equality: m<ABC=

Math
Basic MathBetsy, a recent retiree, requires $6,000 per year in extra income. She has $70,000 to invest and can invest in B-rated bonds paying 13% per year or in a certificate of deposit (CD) paying 3% per year. How much money should be invested in each to realize exactly $6,000 in interest per year?
The amount of money invested at 13% = $
The amount of money invested at 3% = $
Question 8, 1.6.19

Math
Basic MathA cell phone company charges $40 for a smart phone and $20 per month for its data package. Find the cost C(t) of operating a phone for t months. Use the function to find the cost of the plan for 2
months.
Find the cost C(t) of operating a phone for t months.

Math
Basic MathA credit card company estimates that
the average cardholder owed $7440
in the year 2005 and $9420 in 2010.
Suppose average cardholder debt D
grows at a constant rate.
a. Express D as a linear function of
time t, where t is the number of years
after 2005.
b. Draw the graph.
c. Use the function in part (a) to
predict the average cardholder debt
in the year 2015.

Math
Basic MathWhen drawing a card from a deck, the P(face card and hearts) is:
O 1/13
O 3/26
O 3/52
O 1/52

Math
Basic MathThe distance, d, of an object in free fall for an amount of time in seconds, t, is given by the equation d = 9.81². Write the distance d as a function of t, and find the distance an object falls after 5 seconds
The distance d as a function of t can be written as
