Definite Integrals Questions and Answers

Math
Definite IntegralsTo determine the size of the motor required to operate a press, a company must know the amount of work done when the press moves an object linearly 5 feet. The variable force to move the object is
F(x) = 100x√ 125 - x³,
where F is given in pounds and x gives the position of the unit in feet. Use Simpson's Rule with n = 12 to approximate the work W (in foot-pounds) done through one cycle when
-W = ∫F(x) dx.
(Round your answer to two decimal places.)

Math
Definite IntegralsA damping force affects the vibration of a spring so that the displacement of the spring is given by
y = e 3t(cos 6t + 5 sin 6t).
Find the average value of y on the interval from t = 0 to t = r. (Round your answer to three decimal places.)

Math
Definite IntegralsThe price-demand equation for a particular flashlight is given by p= 113 0.004x, where x is the number of flashlights demanded when the price is p dollars each. The flashlight manufacturers will produce no flashlights if the price is $75 or less, and they will market 6,000 flashlights when the price is $99 per flashlight. (Assume the price-supply equation is linear.)
(a) Find the consumers' surplus for this commodity.
(b) Find the producers' surplus for this commodity.

Math
Definite IntegralsFind the producers' surplus if the supply function for pork bellies is given by the following.
S(q) =q7/2+3q5/2 + 55
Assume supply and demand are in equilibrium at q = 9.
The producers' surplus is $
(Type an integer or decimal rounded to the nearest hundredth as needed.)
![The displacement (in centimeters) of a particle moving back and forth along a straight line is given by the equation of motion s= 3 sin(πt) + 4 cos(πt), where t is measured in seconds.
(Round your answers to two decimal places.)
(a) Find the average velocity during each time period.
[1, 2]
[1, 1.1]
[1, 1.01]
[1, 1.001]
(b) Estimate the instantaneous velocity of the particle when t = 1.](https://media.kunduz.com/media/sug-question/raw/72594226-1657478059.6320424.jpeg?w=256)
Math
Definite IntegralsThe displacement (in centimeters) of a particle moving back and forth along a straight line is given by the equation of motion s= 3 sin(πt) + 4 cos(πt), where t is measured in seconds.
(Round your answers to two decimal places.)
(a) Find the average velocity during each time period.
[1, 2]
[1, 1.1]
[1, 1.01]
[1, 1.001]
(b) Estimate the instantaneous velocity of the particle when t = 1.
![Which formula would be used to calculate the trapezoid approximation of ∫4x² dx using five subintervals?
T5 = 0.2/2 [4(0.0)² + 2(4)(0.2)² + 2(4)(0.4)² + 2(4)(0.6)² + 2(4)(0.8)² + 4(1.0)²]
T5 = 0.2/2 [4(0.0)² + (4)(0.2)² + (4)(0.4)² + (4)(0.6)² + (4)(0.8)² + 4(1.0)²]
T5 = 0.2/2 [2(0.0)² + 2(2)(0.2)² + 2(2)(0.4)² + 2(2)(0.6)² + 2(2)(0.8)² + 2(1.0)²]
T5 =0.2[4(0.0)22 + 2(4)(0.2)² + 2(4)(0.4)2 + 2(4)(0.6)² + 2(4)(0.8)² + 4(1.0)²]](https://media.kunduz.com/media/sug-question/raw/71067642-1657470301.1787038.jpeg?w=256)
Math
Definite IntegralsWhich formula would be used to calculate the trapezoid approximation of ∫4x² dx using five subintervals?
T5 = 0.2/2 [4(0.0)² + 2(4)(0.2)² + 2(4)(0.4)² + 2(4)(0.6)² + 2(4)(0.8)² + 4(1.0)²]
T5 = 0.2/2 [4(0.0)² + (4)(0.2)² + (4)(0.4)² + (4)(0.6)² + (4)(0.8)² + 4(1.0)²]
T5 = 0.2/2 [2(0.0)² + 2(2)(0.2)² + 2(2)(0.4)² + 2(2)(0.6)² + 2(2)(0.8)² + 2(1.0)²]
T5 =0.2[4(0.0)22 + 2(4)(0.2)² + 2(4)(0.4)2 + 2(4)(0.6)² + 2(4)(0.8)² + 4(1.0)²]

Math
Definite IntegralsLet R be the region in the first quadrant bounded by the graphs of y=√x, x = 4, and the x-axis. What is an integral expression for the volume of the solid generated when R is rotated about the y-axis? (1 point)
π∫(16-y²)dy
π∫(16-y²) dy
π∫(16-y)dy
π∫(16-y)dy
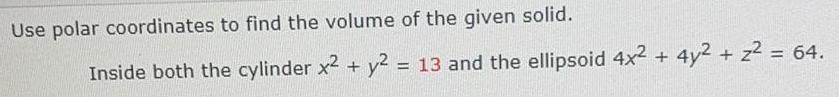
Math
Definite IntegralsUse polar coordinates to find the volume of the given solid.
Inside both the cylinder x2 + y2 = 13 and the ellipsoid 4x² +
+
4y2 + z² = 64.
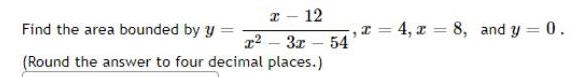
Math
Definite IntegralsFind the area bounded by y
x - 12/22-32-54, x=4, x=8, and y = 0.
(Round the answer to four decimal places.)

Math
Definite IntegralsLet Ω be the solid located above the plane z = 1 and below the hemisphere z = √5-x² - y². Using cylindrical coordinates, that is (z, r, θ coordinates), set up and calculate a triple integral for the volume of the solid Ω .
![Let f(x) = 1 / (x^2 - 2), and compute the Riemann sum of f over the interval [2, 5], using three subintervals of equal length (n = 3) and choosing the representative points to be the right endpoints of the subintervals.](https://media.kunduz.com/media/sug-question/raw/61269847-1657355703.6490326.jpeg?w=256)
Math
Definite IntegralsLet f(x) = 1 / (x^2 - 2), and compute the Riemann sum of f over the interval [2, 5], using three subintervals of equal length (n = 3) and choosing the representative points to be the right endpoints of the subintervals.

Math
Definite IntegralsConsider the following.
f(x) = {-5x, x ≤ 4
f(x) = {x2 - 4x + 7, x > 4
Find the x-value at which f is not continuous. Is the discontinuity removable? (Enter NONE in any unused answer blanks.)

Math
Definite IntegralsFor the function, do the following.
f(x)=√x from a = 3 to b = 6.
(a) Approximate the area under the curve from a to b by calculating a Riemann sum using 6 rectangles. Use the method
described in this example rounding to three decimal places.
square units
(b) Find the exact area under the curve from a to b by evaluating an appropriate definite integral using the Fundamental
Theorem.
square units

Math
Definite IntegralsUse a definite integral to find the area under the curve between the given x-values.
f(x) = ex/3 from x = 0 to x = 3
square units

Math
Definite IntegralsFind the area of the following region.
The region common to the circle r = 5 and the cardioid r= 5(1- cos 0)
The area shared by the circle and the cardioid is square units.
![Use left and right endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the x-axis over the given interval. (Round your answers to four decimal places.)
g(x) = 4x² + 4, [1, 3], 8 rectangles
< Area <](https://media.kunduz.com/media/sug-question/raw/60626079-1657265459.2165065.jpeg?w=256)
Math
Definite IntegralsUse left and right endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the x-axis over the given interval. (Round your answers to four decimal places.)
g(x) = 4x² + 4, [1, 3], 8 rectangles
< Area <

Math
Definite IntegralsA particle that moves along a straight line has velocity
v(t) = t²e-3t
meters per second after t seconds. How many meters will it travel during the first t seconds (from time=0 to time=t)?