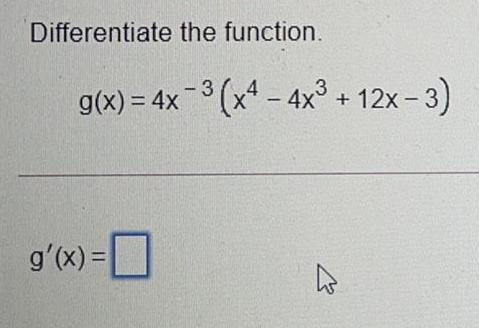
Differentiation Questions and Answers

Math
DifferentiationThe stock price for a certain corporation can be approximated for the years 2011 through 2016 by f(x) = 7.8x²-221x + 1586, where x = 11 corresponds to the year 2011. During what year did a local minimum stock price occur?
A local extremum occurs at a critical number of f. Because the derivative exists for every x, the only critical number(s) occur where the derivative is zero. Find the derivative of f(x).

Math
DifferentiationJesaki Water Sports incurs the following costs in producing a water ski vests in one day, for
0<x< 150:
fixed costs, $304;
unit production cost, $23 per vest;
equipment maintenance and repairs, 0.06 x² dollars.
Find the minimum average cost of a water ski vest. Round to the nearest cent.

Math
DifferentiationUse the First Derivative Test to find the location of all local extrema for the function given below. Enter an exact answer. If there is more than one local maximum or local minimum, write each value of x separated by a comma. If a local maximum or local minimum does not occur on the function, enter in the appropriate box. f(x) =5x/2x² +5

Math
DifferentiationA friend concludes that because y = In 6x and y = In x have the same derivative, namely dy/dx = 1/x'
these two functions must be the same. Explain why this is incorrect.
Choose the correct answer below.
A. A derivative shows the function at a certain point. Even though the function y = In 6x and y= In x have the same derivative, the derivative only shows that the functions are the same at a certain point.
B. A derivative shows the function's y-intercepts. Even though the function y = In 6x and y = In x have the same derivative, the derivative only shows that the functions have the same y-intercepts.
C. A derivative is a measure of how a function changes as its input changes. It is incorrect because the derivative shows how the functions change at an equal rate, not that the functions are the same.

Math
DifferentiationThe differential equation y' = 2y will produce which of the following? (6 points)
A slope field with parallel tangents along the diagonal
A slope field that does not have rows or columns of parallel tangents
A slope field with rows of parallel tangents
A slope field with columns of parallel tangents
![Find the derivative of the function.
y =1/2 [X√ 36 - x² + 36 arcsin(x/6)]
y'(x) =](https://media.kunduz.com/media/sug-question/raw/70510911-1657469070.2890024.jpeg?w=256)
Math
DifferentiationFind the derivative of the function.
y =1/2 [X√ 36 - x² + 36 arcsin(x/6)]
y'(x) =

Math
DifferentiationLet W(s, t) = F(u(s, t), v(s, t)), where F, u, and v are differentiable, and the following applies.
u(-6, 7) = 6
us(-6, 7) = -9
ut(-6, 7) = 0
Fu(6, 4) = 5
v(-6, 7) = 4
Vs(-6, 7) = -4
Vt(-6, 7) = 1
Fv(6, 4) = -2
Find Ws(-6, 7) and We(-6, 7).
Ws(-6, 7) =
W+(-6, 7) =
X

Math
DifferentiationKatie and Sarah are working on taking the derivative of f(x) = -
2x
3x + 4
Katie uses the quotient rule to get f'(x) =
product rule and the chain rule (shown below). Explain the discrepancies between the two answers.
-1
f(x) = 2x(3x+4)=1
f'(x) = 2x(-1)(3x+4)=2(3)+2(3x+4)-1
1
-2
= 2(3x + 4)¯¹ - 6x(3x+4) −²
(3x+4)2-2x(3)
(3x+4)²
8
(3x+4)²
Sarah converts it into a
Choose the correct answer below.
O A. In the first answer, using the quotient rule, the exponent in the denominator is positive. Whereas, in the second answer, using the product rule and the chain
rule, the exponents are negative and contain two terms. The two methods produce similar expressions.
OB. In the first answer, using the quotient rule, the exponent in the denominator is positive. Also, in the second answer, using the product rule and the chain rule,
the exponents are negative. The two methods produce different expressions that are not equivalent.
OC. In the first answer, using the quotient rule, the exponent in the denominator is positive. Whereas, in the second answer, using the product rule and the chain
rule, the exponents are negative and contain two terms. The answers are equivalent, just in different forms.

Math
DifferentiationThe students in a physics class are performing an experiment to determine the acceleration due to gravity. They drop water balloons from the top of a building and estimate the time at which the balloons hit the ground. After analyzing all of their data, the produce the model h(t) = -5² +30 to model the height of a balloon in metres 1 seconds after it has been dropped?
What is the best estimate for the instantaneous rate of change in the height of a ballon I s after it has been dropped?
a. -20 m/s
b. -10 m/s
c. -5 m/s
d. 5 m/s
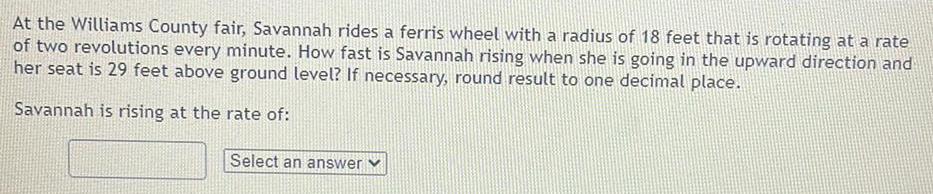
Math
DifferentiationAt the Williams County fair, Savannah rides a ferris wheel with a radius of 18 feet that is rotating at a rate of two revolutions every minute. How fast is Savannah rising when she is going in the upward direction and her seat is 29 feet above ground level? If necessary, round result to one decimal place.
Savannah is rising at the rate of:
Select an answer

Math
DifferentiationCreate DQ 5 Discussion Board in response to the following questions:
•What does the limit definition have to do with slopes of secant lines and the slope of a tangent line?
• How are the derivative rules helpful?
After posting, return to the board and read over the posts of your fellow classmates. Choose at least one classmate and create a post responding to his/her initial post on the

Math
DifferentiationThe monthly profit from the sale of a product is given by
P(x) = -1.5x² - 12x + 20
dollars.
25. What level of production maximizes profit?
a) x = 4.0 units
b) x = 0.25 units
c) x = -4.0 units
d) x = -88.00 units
26. What is the maximum possible profit?
a) $44.00
b) $22.90
c) $52.0
d) $12652.00
![Let f be a continuous function on the closed interval [-2, 5]. If f(-2) = -7 and f(5) = 1, then the Intermediate Value Theorem guarantees that
f (c) = -2 for some value c between -7 and 1
f' (c) = for at least one value c between -2 and 5
f(c) = -2 for some value c between -2 and 5.
There exists an absolute maximum value of f on [-2, 5].](https://media.kunduz.com/media/sug-question/raw/67201856-1657407626.2392037.jpeg?w=256)
Math
DifferentiationLet f be a continuous function on the closed interval [-2, 5]. If f(-2) = -7 and f(5) = 1, then the Intermediate Value Theorem guarantees that
f (c) = -2 for some value c between -7 and 1
f' (c) = for at least one value c between -2 and 5
f(c) = -2 for some value c between -2 and 5.
There exists an absolute maximum value of f on [-2, 5].

Math
DifferentiationA model rocket is launched from the roof of a building. Its flight path is modeled by h = -5t² +30t +10 where h is the height of the rocket above the ground in metres and t is the time after the launch in seconds.
What is the rocket's maximum height?
When did the rocket reach its maximum height?

Math
DifferentiationFind the function f given that the slope of the tangent line to the graph of f at any point (x, f(x)) is f'(x) and that the graph of f passes through the given point.
f'(x) = 7 + 3ex + 4/x
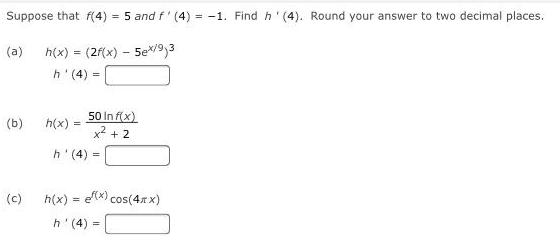
Math
DifferentiationSuppose that f(4) = 5 and f' (4) = -1. Find h'(4). Round your answer to two decimal places.
(a) h(x) = (2f(x) - 5e^x/9)3
h'(4) =
(b)h(x)= 50Inf(x)/x² + 2
h'(4) =
(c)h(x) = e^f(x) cos(4πx)
h'(4) =
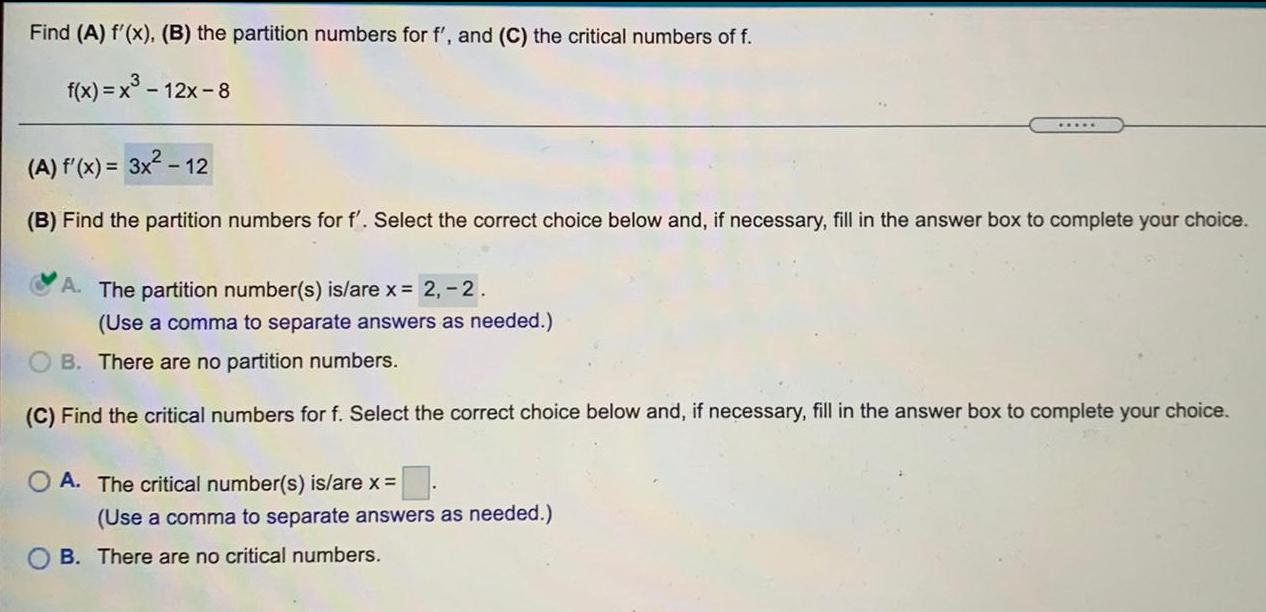
Math
DifferentiationFind (A) f'(x), (B) the partition numbers for f', and (C) the critical numbers of f.
f(x) = x³-12x-8
(A) f'(x) = 3x² - 12
(B) Find the partition numbers for f'. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The partition number(s) is/are x = 2,-2.
(Use a comma to separate answers as needed.)
B. There are no partition numbers.
(C) Find the critical numbers for f. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The critical number(s) is/are x =
(Use a comma to separate answers as needed.)
B. There are no critical numbers.

Math
DifferentiationThe radius of the base of a cylinder is decreasing at a rate of 12 kilometers per second.
The height of the cylinder is fixed at 2.5 kilometers.
At a certain instant, the radius is 40 kilometers.
What is the rate of change of the volume of the cylinder at that instant (in cubic kilometers per second)?
Choose 1 answer:
A -360π
B -2400π
C -4000π
D -1600π
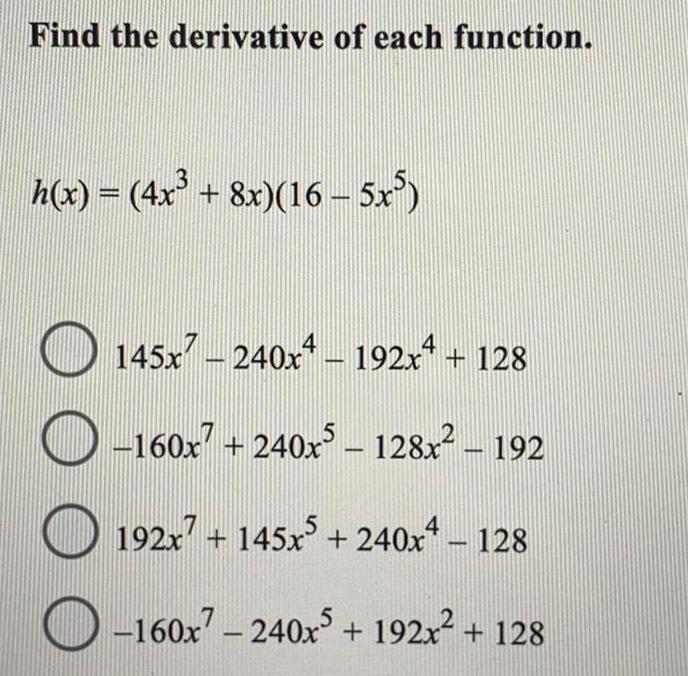
Math
DifferentiationFind the derivative of each function.
h(x) = (4x³ + 8x)(16 – 5x³)
OO
145x7 - 240x4 - 192xª + 128
-160x7+240x5 - 128x² - 192
192x7 + 145x5+240x4 - 128
-160x7 - 240x³ + 192x² + 128

Math
DifferentiationLet h be a differentiable function with a tangent line at x = n. The equation of the tangent line is y=-0.2x+0.5. What must be true about h and h' at x = n? (
I. h(n)= -0.1283
II. h'(n) = 0.3
III. h(0) = 0.5
I and II
II and III
I only
III only

Math
DifferentiationIn the function f(x) = 5.62 cos(0.7x) - 1.93, what is the first positive x value where the function has a minimum?
1.74
6.73
8.98
4.49
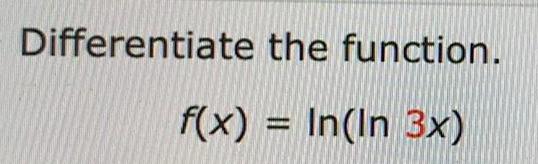
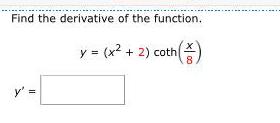
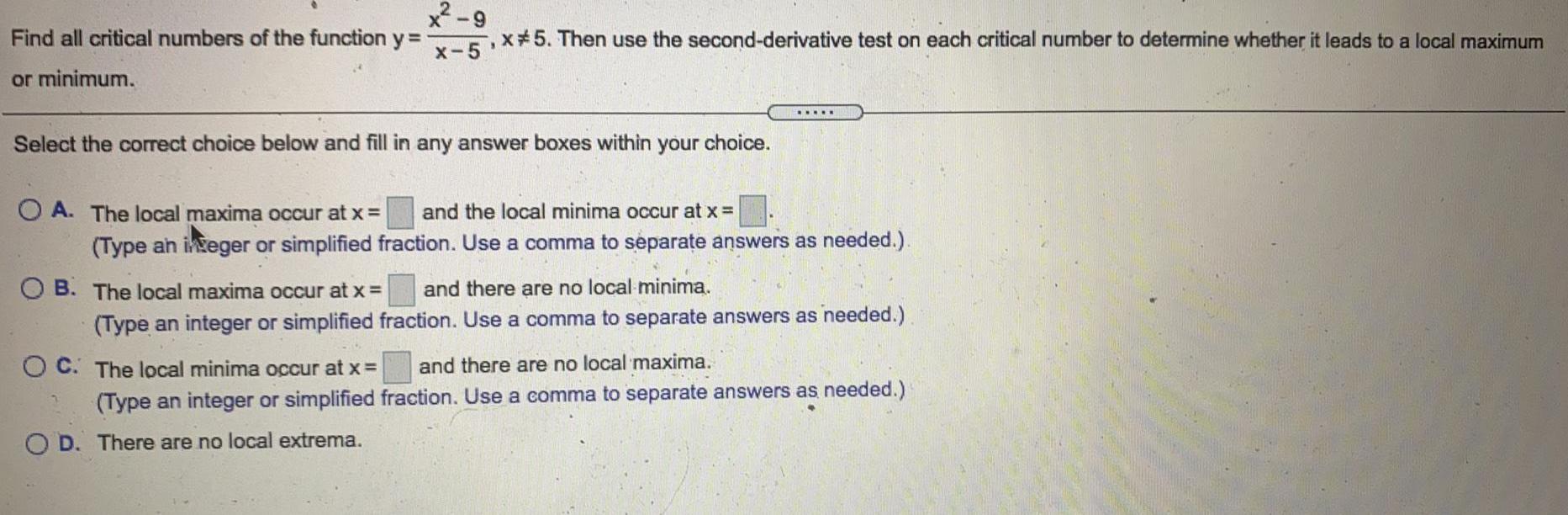
Math
DifferentiationFind all critical numbers of the function y =
or minimum.
x²-9/x-5, x≠5. Then use the second-derivative test on each critical number to determine whether it leads to a local maximum
Select the correct choice below and fill in any answer boxes within your choice.
A. The local maxima occur at x = and the local minima occur at x =
(Type an integer or simplified fraction. Use a comma to separate answers as needed.).
B. The local maxima occur at x = and there are no local minima.
(Type an integer or simplified fraction. Use a comma to separate answers as needed.)
C. The local minima occur at x = and there are no local maxima.
(Type an integer or simplified fraction. Use a comma to separate answers as needed.)
D. There are no local extrema.
![Differentiate the function.
g(x)=ln√[xcosx/(4x+5)^3]](https://media.kunduz.com/media/sug-question/raw/60982654-1657292494.7965693.jpeg?w=256)

Math
DifferentiationA retailer who sells backpacks estimates that by selling them for a dollars each, he will be able to sell 112 x backpacks a month. The quadratic function R(x) = 2² +112x is used to find the revenue, R, received when the selling price of a backpack is z. Find the selling price that will give him the maximum revenue and then find the amount of the maximum revenue. The maximum revenue is Answer: The selling price that will give maximum revenue is Select an answer Select an answer

Math
DifferentiationA rectangular playground is to be fenced off and divided in two by another fence parallel to one
side of the playground. Six hundred feet of fencing is used. Find the dimensions of the
playground that maximize the total enclosed area. What is the maximum area? Write the
function, in terms of x, used to maximize the enclosed region.

Math
DifferentiationFor the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing.
f(x) = (x+8) / (x + 3)
(a) Find the critical number(s). First, find f'(x).

Math
DifferentiationOn a particular day, the power used in a particular state (in thousands of megawatts) could be approximated by the function P(t)= -0.0068881³ +0.19181² -0.7085t+20.74, where t is the number of hours since midnight, for 0 ≤ t ≤ 24.
Find any relative extrema for power usage, as well as when they occurred.
Find the derivative of P(t).
P'(t)=

Math
DifferentiationFind an equation of the line tangent to the curve at the point corresponding to the given value of t.
x=t²-1, y=t³ +2t; t = 3
(Type an equation. Type your answer in slope-intercept form.)
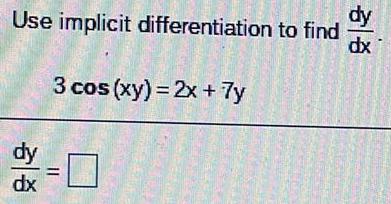

Math
DifferentiationAssume that x and y are both differentiable functions of t and find the required values of dy/dt and dx/dt.
x² + y² = 169
(a) Find dy/dt, given x = 5, y = 12, and dx/dt = 5.
dy/dt =
(b) Find dx/dt, given x = 12, y = 5, and dy/dt = -4.
dx/dt =

Math
DifferentiationDescribe the transformations we would expect to see to the toolkit function f(x) = |x| in the given function.
f(x) = -|x - 3| +2
Translate left 3 units, up 2 units, and reflect across the x-axis.
Translate right 3 units, up 2 units, and reflect across the y-axis.
Translate left 3 units, down 2 units, and reflect across the x-axis.
Translate right 3 units, up 2 units, and reflect across the x-axis.
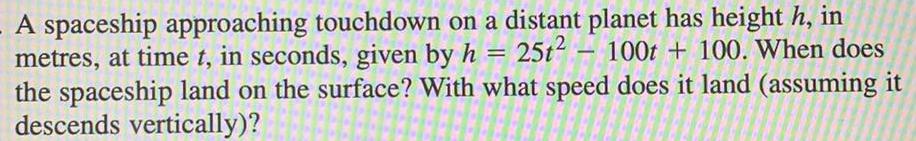
Math
DifferentiationA spaceship approaching touchdown on a distant planet has height h, in metres, at time t, in seconds, given by h = 25t² - 100t + 100. When does the spaceship land on the surface? With what speed does it land (assuming it descends vertically)?

Math
DifferentiationA particle moves in a straight line with the velocity function
v(t) = sin(wt)cos^8(wt). Find its position function
X = f(t) if f(0) = 0.

Math
DifferentiationGiven s(t)=t+2, where s(t) is in miles and t is in hours, find each of the following.
a) v(t)
b) a(t)
c) The velocity and acceleration when t = 2 hr
d) When the distance function is given by a linear function, there is uniform motion. What does uniform motion mean in terms of velocity and acceleration?

Math
Differentiation1. Consider the curve given by xy2 - x³y = 6.
a. Show that dy/dx = (3x²y-y²)/(2xy - x³)
b. Find all points on the curve whose x-coordinate is 1, and write an equation for the tangent line at each of these points.
C. Find the x-coordinate of each point on the curve where the tangent line is vertical.
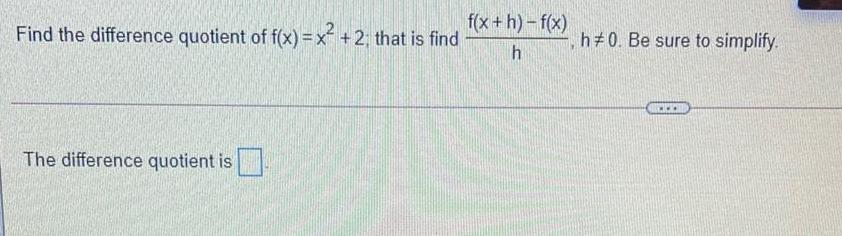
Math
DifferentiationFind the difference quotient of f(x)=x+2; that is find (f(x+h)-f(x))/h
Be sure to simplify.
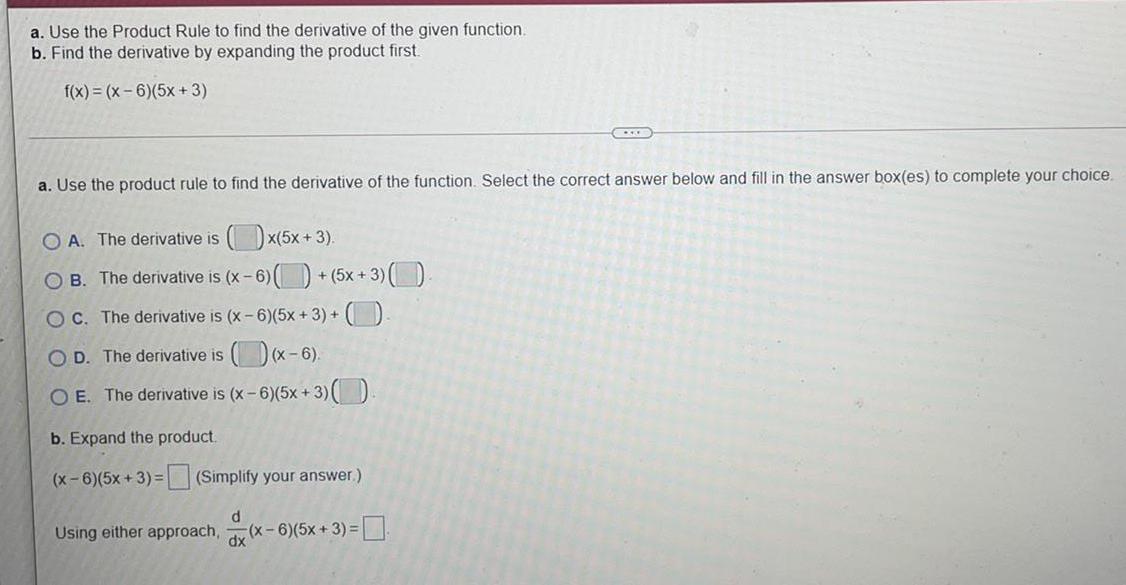
Math
Differentiationa. Use the Product Rule to find the derivative of the given function.
b. Find the derivative by expanding the product first.
f(x)=(x-6)(5x + 3)
a. Use the product rule to find the derivative of the function. Select the correct answer below and fill in the answer box(es) to complete your choice.
OA. The derivative is (x(5x+3).
OB. The derivative is (x-6)()+(5x+3)()-
OC. The derivative is (x-6)(5x+3)+(₁
OD. The derivative is ()(x-6).
O E. The derivative is (x-6)(5x+3)()
b. Expand the product.
(x-6)(5x+3)= (Simplify your answer.)
Using either approach, d/dx(x-6)(5x+3)=
Math
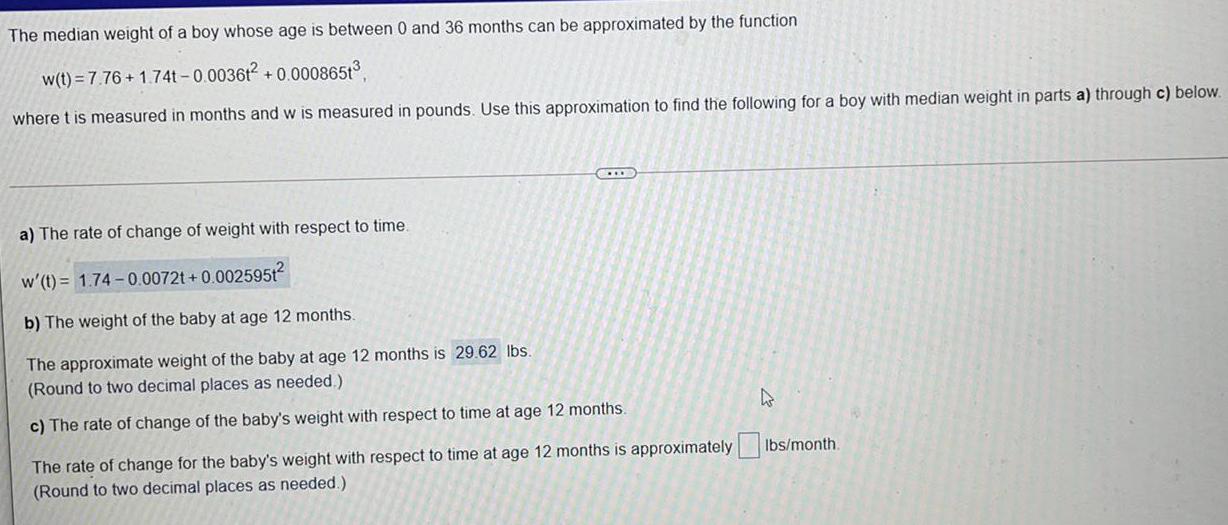
DifferentiationThe median weight of a boy whose age is between 0 and 36 months can be approximated by the function
w(t) = 7.76 +1.74t-0.003612 +0.0008651³
where t is measured in months and w is measured in pounds. Use this approximation to find the following for a boy with median weight in parts a) through c) below.
a) The rate of change of weight with respect to time.
w' (t) = 1.74 -0.0072t+0.002595t²
b) The weight of the baby at age 12 months.
The approximate weight of the baby at age 12 months is 29.62 lbs.
(Round to two decimal places as needed.)
c) The rate of change of the baby's weight with respect to time at age 12 months.
The rate of change for baby's weight with respect to time at age 12 months is approximately Ibs/month.
(Round to two decimal places as needed.)