Heights and Distances Questions and Answers

Math
Heights and DistancesAn object is sighted from a helicopter at an angle of depression of 54 After the helicopter has traveled 9 0km horizontally the angle of depression to the same side of the object is 68 Determine the direct line distance at that point from the helicopter to the object 5 marks

Math
Heights and DistancesRachel walked 2 0 meters south Then she made a right hand turn and walked 16 0 meters west She turned right again and walked 24 0 meters north Then she turned eft and walked 36 0 meters west What is the magnitude of the overall displacement O 50 2m O 53 7m O 56 5m 629m

Math
Heights and DistancesSolve the following problem Be sure to make a diagram of the situation with all the given information labeled If a 76 0 foot flagpole casts a shadow 54 0 feet long what is the angle of elevation of the sun to the nearest tenth of a degree

Math
Heights and DistancesA jewelry maker works 6 days a week makes 15 necklaces per day on average and charges 18 a necklace If she lowers her price to 10 a necklace by how many necklaces per day on average must she increase he production to make the same amount of money per 6 day workweek

Math
Heights and Distances5 A ladder is leaning against the side of an empty display pool at the local aquarium The top of the ladder is touching the 25 foot mark on the pool wall at a 59 angle a What is the angle of elevation from the foot of the ladder to the top of the ladder b Estimate the length of the ladder Round your answer to the nearest whole number if necessary

Math
Heights and Distances5 II Superman must stop a 120 km h train in 150 m to keep it from hitting a stalled car on the tracks If the train s mass is 3 6 105 kg how much force must he exert Compare to the weight of the train give as How much force does the train exert on Superman

Math
Heights and Distancesrelative to that acute angie Here are the approximate ratios for angle measures 55 65 and 75 Angle adjacent leg length hypotenuse length opposite leg length hypotenuse length opposite leg length adjacent leg length N 2 55 65 75 75 0 57 0 42 0 26 Use the table to approximate MO in the triangle below 0 82 0 91 0 97 1 43 2 14 3 73
Math
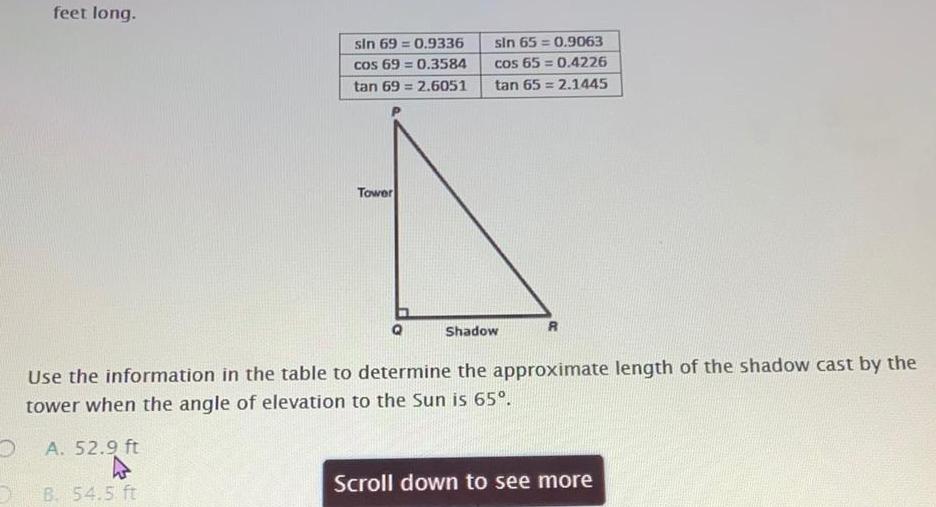
Heights and DistancesD feet long sin 69 0 9336 cos 69 0 3584 tan 69 2 6051 Tower sin 65 0 9063 cos 65 0 4226 tan 65 2 1445 Shadow R Use the information in the table to determine the approximate length of the shadow cast by the tower when the angle of elevation to the Sun is 65 A 52 9 ft B 54 5 ft Scroll down to see more
Math
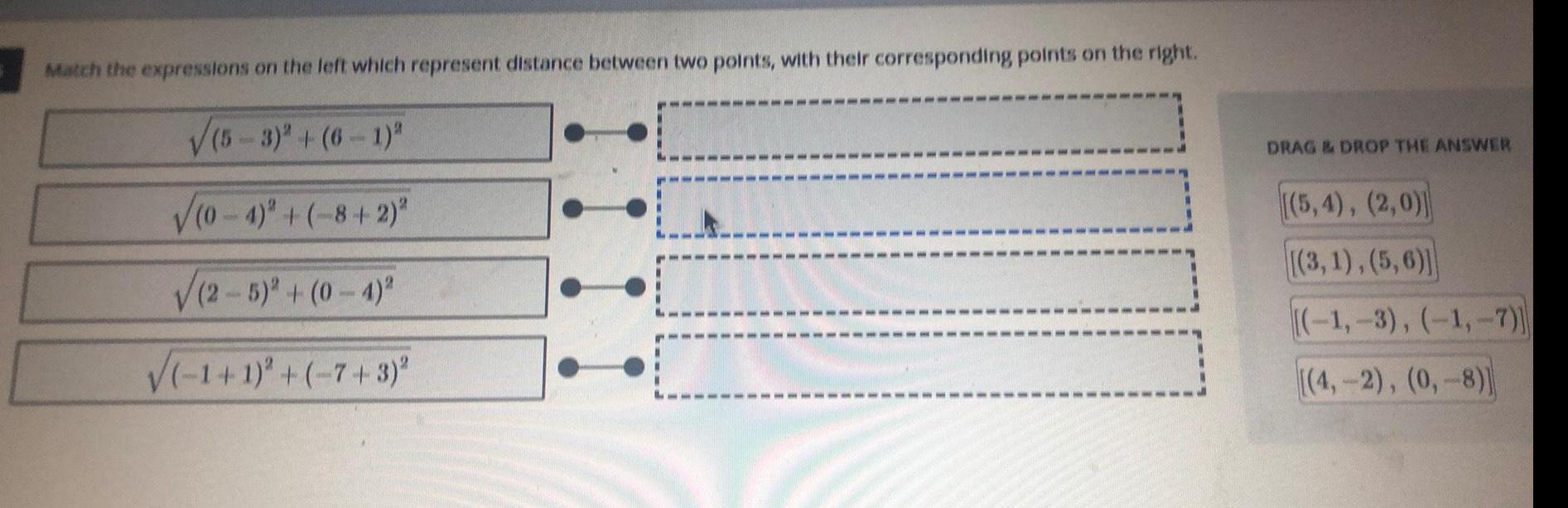
Heights and DistancesMatch the expressions on the left which represent distance between two points with their corresponding points on the right 5 3 6 1 2 0 4 8 2 2 5 0 4 1 1 7 3 DRAG DROP THE ANSWER 5 4 2 0 3 1 5 6 1 3 1 7 4 2 0 8
Math
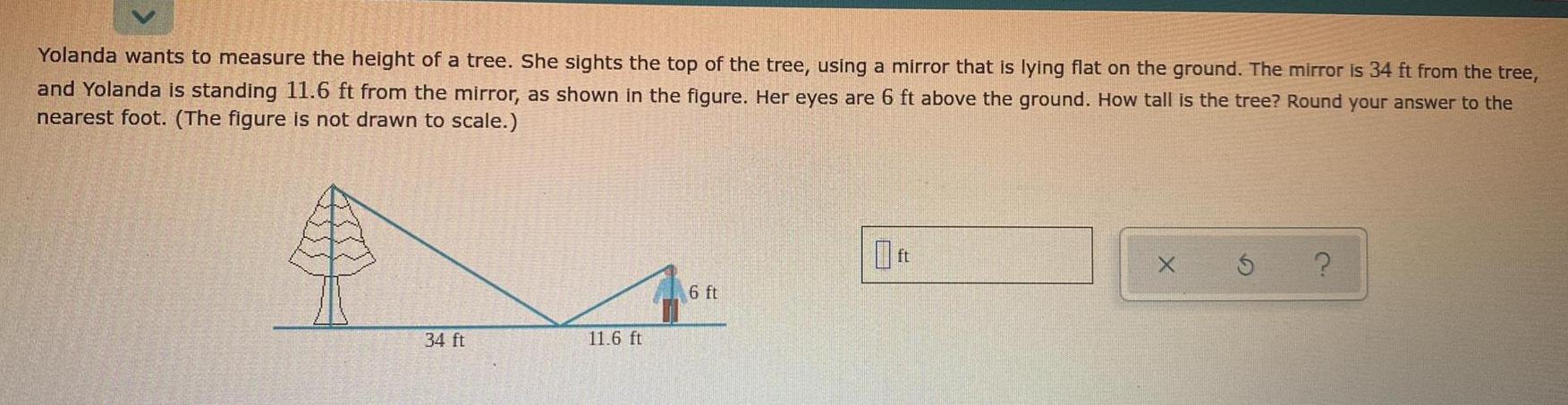
Heights and DistancesYolanda wants to measure the height of a tree She sights the top of the tree using a mirror that is lying flat on the ground The mirror is 34 ft from the tree and Yolanda is standing 11 6 ft from the mirror as shown in the figure Her eyes are 6 ft above the ground How tall is the tree Round your answer to the nearest foot The figure is not drawn to scale 34 ft 11 6 ft 6 ft

Math
Heights and DistancesSelect the correct answer Alice and Amy decide to meet at a party From a corner of the party hall Amy spots Alice at the corner of the hall diagonally opposite her If the party hall is a rectangle that measures 100 feet by 60 feet what is the shortest distance Amy has to walk to reach Alice Round your answer to the nearest foot OA O B O C O D 40 feet 80 feet 117 feet 160 feet

Math
Heights and DistancesThe shadow of a 16 ft tree is 20 ft long What is the angle of elevation from the ground to the sun Round to the nearest tenth of a degree 38 7 degrees O 25 9 degrees O 35 1 degrees 42 2 degrees

Math
Heights and Distances6 The surface area of a small toy ball is 18 square inches If the radius of the ball is tripled what will be the surface area of the new larger ball in square inches F 18 in H 54 in G 36 in 2 J 162 in 2

Math
Heights and Distances4 A company manufactures cylindrical containers that each have a volume of 6 cubic feet For a new container design the company plans to keep the same height for the container and double the radius Which statement best describes how this change will affect the volume of the container F The volume will be multiplied by a H The volume will be multiplied by a factor of 0 5 factor of 2 G The volume will be multiplied by a factor of 4 J The volume will be multiplied by a factor of 0 25
Math
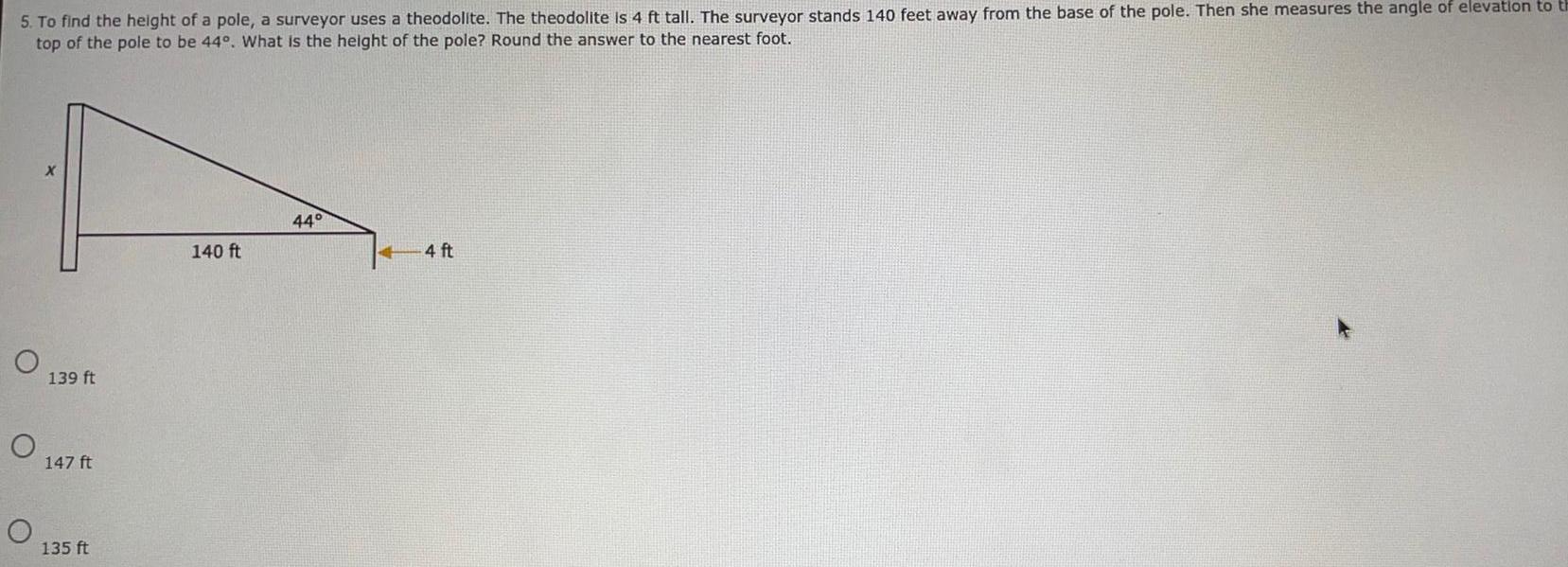
Heights and Distances5 To find the height of a pole a surveyor uses a theodolite The theodolite is 4 ft tall The surveyor stands 140 feet away from the base of the pole Then she measures the angle of elevation to th top of the pole to be 44 What is the height of the pole Round the answer to the nearest foot O O X 139 ft 147 ft 135 ft 140 ft 44 4 ft
Math
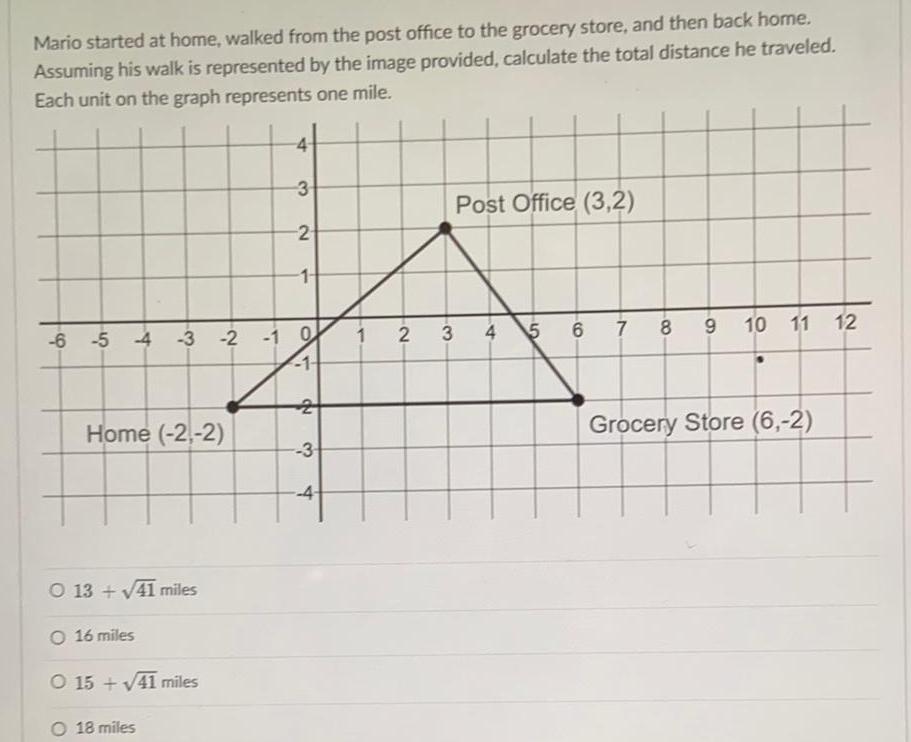
Heights and DistancesMario started at home walked from the post office to the grocery store and then back home Assuming his walk is represented by the image provided calculate the total distance he traveled Each unit on the graph represents one mile 6 5 4 Home 2 2 O 13 41 miles O 16 miles O 15 41 miles O 18 miles 4 3 3 2 1 0 1 2 1 ND 2 3 4 1 2 3 Post Office 3 2 4 5 6 7 8 9 10 11 Grocery Store 6 2 12

Math
Heights and DistancesYou are standing at the edge of a cliff You look down with an angle of depression of 20 degrees and see a a dog at the bottom that is 130 feet away from where you re standing What is the height of the cliff Round your answer to the nearest tenth and round only once

Math
Heights and DistancesFrom his eye which stands 1 62 meters above the ground Ar angle of elevation to the top of a prominent skyscraper to be 44 If he is standing at a horizontal distance of 164 meters from the base of the skyscraper what is the height of the skyscraper Round your answer to the nearest tenth of a meter if necessary

Math
Heights and DistancesThe expression 10 000 0 90 represents the population of a town t years after 2000 Select the value from each drop down menu that best completes the sentence The population of the town by each year
Math
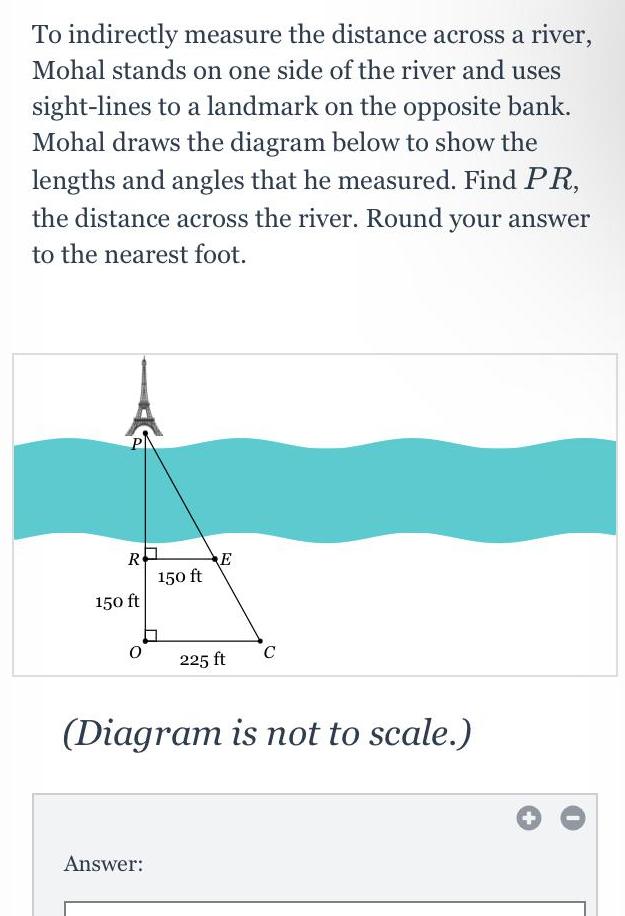
Heights and DistancesTo indirectly measure the distance across a river Mohal stands on one side of the river and uses sight lines to a landmark on the opposite bank Mohal draws the diagram below to show the lengths and angles that he measured Find PR the distance across the river Round your answer to the nearest foot R 150 ft 0 150 ft Answer 225 ft C Diagram is not to scale

Math
Heights and DistancesTwo buildings on level ground are 200 feet apart From the top edge of the shorter building the angle of depression to the bottom of the taller building is 35 How tall is the shorter building Round to the nearest foot Select one O a 229 ft Ob 286 ft c 140 ft O d 89 ft

Math
Heights and DistancesJeremy and Leslie are each flying their own drones in a flat field with their drones hovering between the two of them Jeremy s drone is closer to him than to Leslie and Leslie s drone is closer to her than to Jeremy Jeremy s drone is 30 meters above the ground and he is located 50 meters to the left from the point directly below the drone The angle of elevation from Leslie s location on the ground to her drone is 55 and the distance between her location on the ground and her drone is 70 meters 1 Create a diagram of all the given information including calculated measurements make sure to add as you complete parts 2 4

Math
Heights and DistancesTwo search teams spot a stranded climber between them on a mountain. The first team is 0.6 miles from the second team, and both teams are at an altitude of 0.2 miles. The angle of elevation from the first team to the stranded climber is 16 °. The angle of elevation from the second team to the climber is 24°. What is the altitude of the climber? Round to the nearest hundredth of a mile.
miles

Math
Heights and DistancesThe infield of a baseball field is a square with sides measuring 90 feet. A ball thrown from third to first base is caught in 1.2 seconds. Find the speed of the ball in feet per second. Round to the nearest tenth.
Math
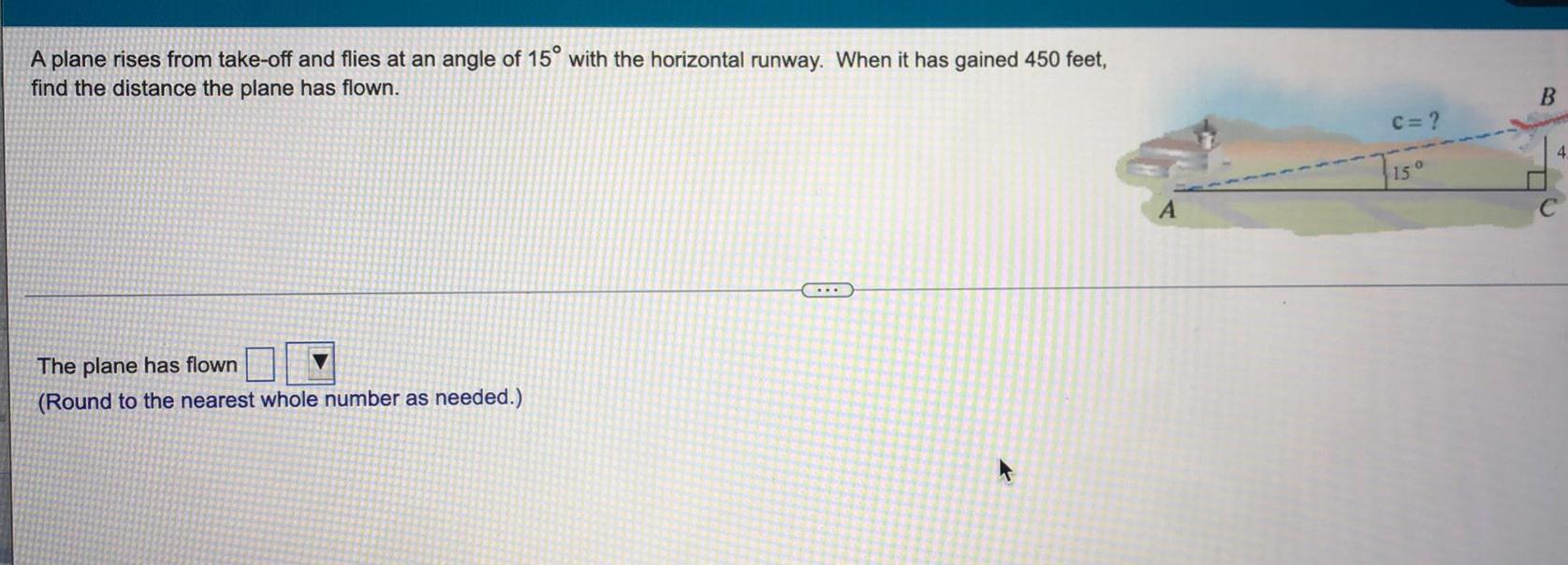
Heights and DistancesA plane rises from take-off and flies at an angle of 15° with the horizontal runway. When it has gained 450 feet, find the distance the plane has flown. The plane has flown
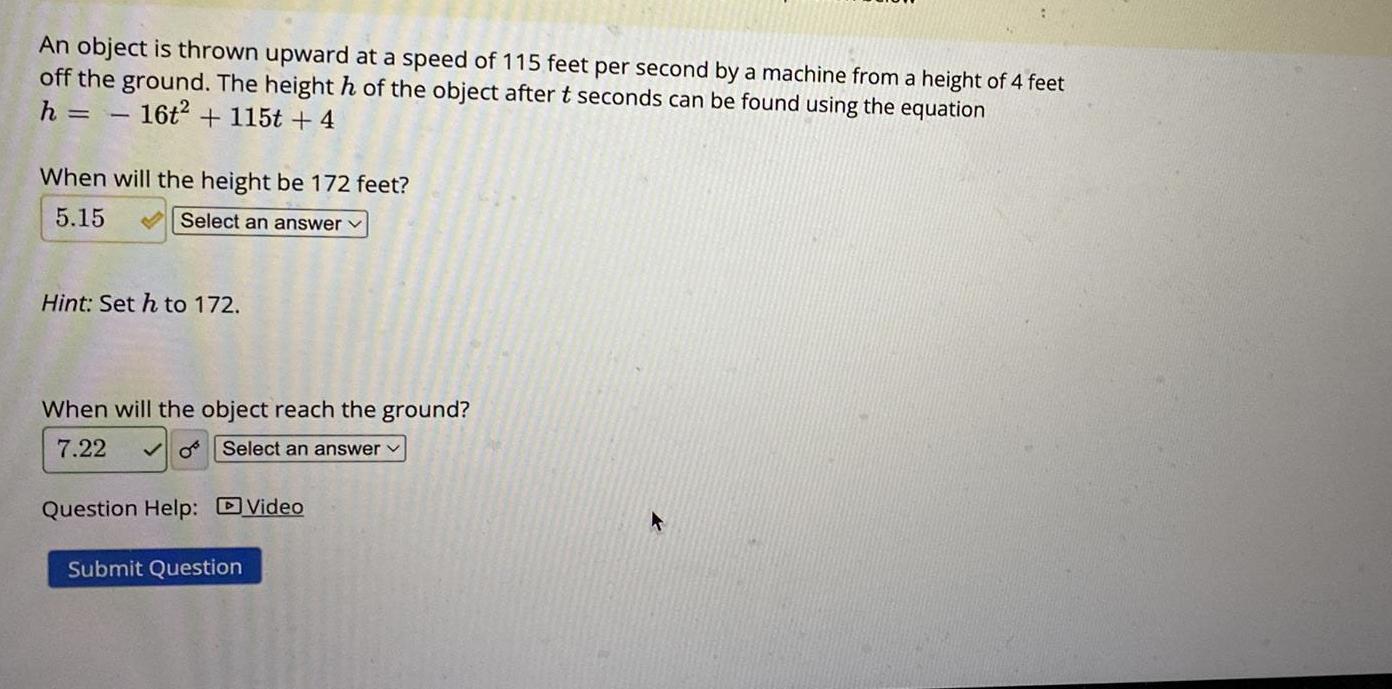
Math
Heights and DistancesAn object is thrown upward at a speed of 115 feet per second by a machine from a height of 4 feet off the ground. The height h of the object after t seconds can be found using the equation
h = 16t² + 115t +4
When will the height be 172 feet?
Hint: Set h to 172.
When will the object reach the ground?
7.22

Math
Heights and DistancesA plane flew for 5 hours heading west and for 4 hours heading south. If the total distance traveled was 3,444 miles, and the plane traveled 39 miles per hour faster heading west, at what speed was the plane traveling west? (Do not include the units in your response.)

Math
Heights and DistancesLily and William are both driving along
the same highway in two different cars to
a stadium in a distant city. At noon, Lily is
313 miles away from the stadium and
William is 334 miles away from the
stadium. Lily is driving along the highway
at a speed of 44 miles per hour and
William is driving at speed of 51 miles per
hour. Let L represent Lily's distance, in
miles, away from the stadium t hours
after noon. Let W represent William's
distance, in miles, away from the stadium
t hours after noon. Write an equation for
each situation, in terms of t, and
determine the interval of hours, t, for
which Lily is closer to the stadium than
William.

Math
Heights and DistancesThe New York Knicks play in Madison Square Garden, the Los Angeles Lakers play in the Staples Center, and the Miami Heat play in American Airlines Arena. Madison Square Garden is about 2.8 x 10³ miles from the Staples Center and Madison Square Garden is about 1.4 x 10³ miles from American Airlines Arena.
A. How many times of the distance the Knicks travel to play the Heat is the
distance the Knicks travel to play the Lakers?
B. How much further is the Staples Center than American Airlines Arena from
Madison Square Garden?

Math
Heights and DistancesSamantha goes on a road trip; she has to drive 1,311 miles and 20 hours to get to her destination but she can only drive 10 hours and 500 per day. Her rental car charges
$98 per day and the car goes 22 miles and requires 1 gallon to travel 22 miles. The car can hold 16 gallon of gas and gas costs $4.60 per gallon.
Now write an equation for the amount you will spend on the vehicle Rental and Gas. If C is the cost, x is the amount of days, and g is the number of gallons needed for your trip. Now include the cost of the gas in your equation - replace g.

Math
Heights and DistancesFind the distance between the pair of points. (2,3) and (-7, -24)
The distance is (Type an integer or a decimal rounded to three decimal places as needed.)

Math
Heights and DistancesThe surface areas of two similar solids are 441 cm² and 225 cm². If the approximate volume of the smaller solid is 250 cm³, what is the volume of the larger solid?
A. 466 cm³
B. 932 cm³
C. 686 cm³
D. 500 cm³

Math
Heights and DistancesSumalee wants to make a 23% saline solution. She has already poured 9 qt. of a 18% saline solution into a beaker. How many qt. of a 32% saline solution must she add to this to create the desired mixture?
5 qt.
6qt.
1 qt.
2 qt.
9 qt.
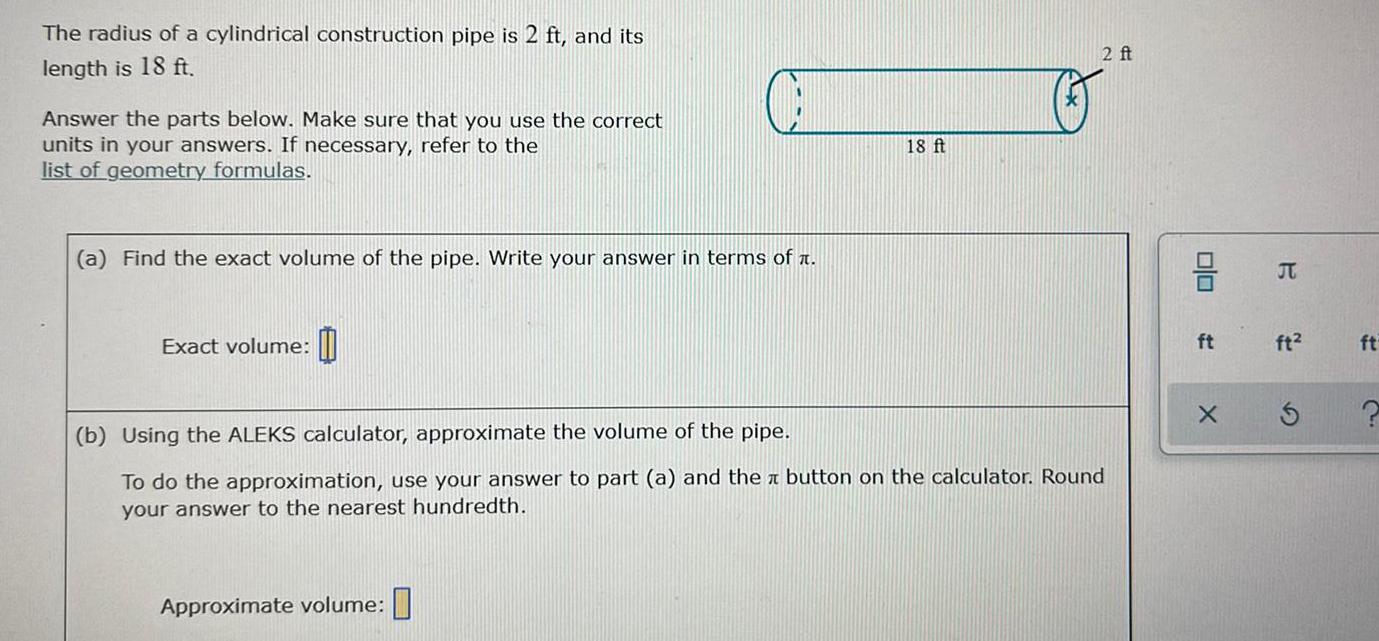
Math
Heights and DistancesThe radius of a cylindrical construction pipe is 2 ft, and its length is 18 ft.
Answer the parts below. Make sure that you use the correct units in your answers. If necessary, refer to the list of geometry formulas.
(a) Find the exact volume of the pipe. Write your answer in terms of .
Exact volume:
(b) Using the ALEKS calculator, approximate the volume of the pipe. To do the approximation, use your answer to part (a) and the button on the calculator. Round your answer to the nearest hundredth.
Approximate volume:

Math
Heights and DistancesA homeowner is going to build the raised bed garden shown in the plan, against an existing garden wall. The homeowner will build the new wall by stacking concrete blocks without mortar, and then fill in the walled space with garden soil. The concrete blocks have dimensions 8 inches x 8 inches x 16 inches. The wall will be capped by capstones that have dimensions 8 inches x 2 inches x 16 inches. Concrete blocks cost $1.50 each, capstones cost $1.00 each, and garden soil costs $36 per cubic yard. The homeowner will do all the work and will buy materials. How much will they cost?

Math
Heights and DistancesA jet and a passenger plane left Nairobi at the same time. The planes flew in opposite directions. The passenger plane flew 255 km/h faster than the jet. After seven hours they were 5005 km apart. Find the jet's speed.
340 km/h
240 km/h
230 km/h
80 km/h
210 km/h

Math
Heights and DistancesGrayson is flying a kite, holding his hands a distance of 3.25 feet above the ground and letting all the kite's string play out. He measures the angle of elevation from his hand to the kite to be 38°. If the string from the kite to his hand is 125 feet long, how many feet is the kite above the ground? Round your answer to the nearest tenth of a foot if necessary.

Math
Heights and DistancesA boat is heading towards a lighthouse, whose beacon light is 115 feet above the water. The boat's crew measures the angle of elevation to the beacon, 6º. What is the ship’s horizontal distance from the lighthouse (and the shore)? Round your answer to the nearest hundredth of a foot if necessary.

Math
Heights and DistancesA radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is 32° and that the angle of depression to the bottom of the tower is 24°. How tall is the tower?

Math
Heights and DistancesWhat is the angle of elevation of the sun if a 45 foot tall flag pole casts a 22 foot long shadow?
A. 26.1
B. 60.7
C. 63.9
D. 29.3

Math
Heights and DistancesThe angle of elevation to the top of a Building in New York is found to be 6 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building. Round to the tenths. Hint: 1 mile = 5280 feet

Math
Heights and DistancesKiara measured a swimming pool and made a scale drawing. The scale she used was
13 centimeters: 6 meters. In the drawing, the pool is 26 centimeters wide. What is the width
of the actual pool?

Math
Heights and DistancesJasper is taking an SAT prep class at the community center in Lakeside. The community center is 9 centimeters away from Jasper's house on a city map. If the map uses a scale of 3 centimeters: 1 kilometer, how far apart are Jasper's house and the community center in real life?
___kilometers
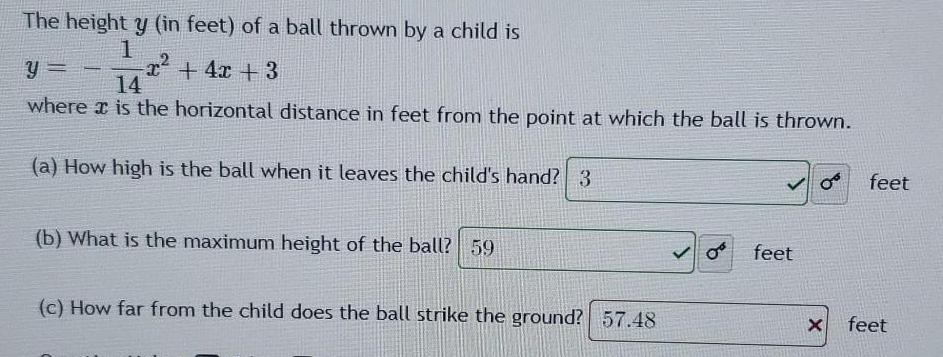
Math
Heights and DistancesThe height y (in feet) of a ball thrown by a child is
y = -1/14x² + 4x + 3
where is the horizontal distance in feet from the point at which the ball is thrown.
(a) How high is the ball when it leaves the child's hand? 3
(b) What is the maximum height of the ball? 59
(c) How far from the child does the ball strike the ground? 57.48
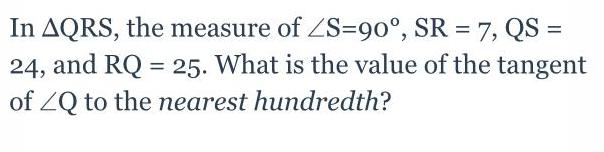
Math
Heights and DistancesIn AQRS, the measure of ∠S-90°, SR = 7, QS = 24, and RQ = 25. What is the value of the tangent of ∠Q to the nearest hundredth?

Math
Heights and DistancesA person is standing 40 ft from a light post and can see the top of the light at a 35° angle of elevation. The person's eye level is 5 feet from the ground. What is the height of the lightpost to the nearest foot.
The height of the light post is ---- feet.

Math
Heights and DistancesA baseball is travelling on a path given by the equation
y = -0.011x² + 1.15x + 1.22.
The profile of the bleachers in the outfield can be
modelled with the equation y = 0.6x - 72.
All distances are in metres.
a) Determine the maximum height of the ball.
b) Does the ball reach the bleachers for a home run?
Justify your answer.

Math
Heights and DistancesA model of a building is constructed using a scale of 1 inch: 4.5 feet. If the model is 12 inches tall, then the actual building is ___feet tall.

Math
Heights and DistancesMs. Pullara and Ms. Chng are both looking at the top of the school in the distance in the same line of sight, although Ms. Chng is 100 m ahead of Ms. Pullara. Ms. Pullara observes the school at an angle of 18 with the ground. If the top of the tower is 400 m from Ms. Chng, what is Ms. Chng's angle of sight with the ground? First make a sketch and then solve the problem to the nearest degree. /5

Math
Heights and DistancesTwo docks are located on an east-west line 2581 ft apart. From dock A, the bearing of a coral reef is 56°22'. From dock B, the bearing of the coral reef is 326°22'. Find the distance from dock A to the coral reef.