Limits and Continuity Questions and Answers
Math
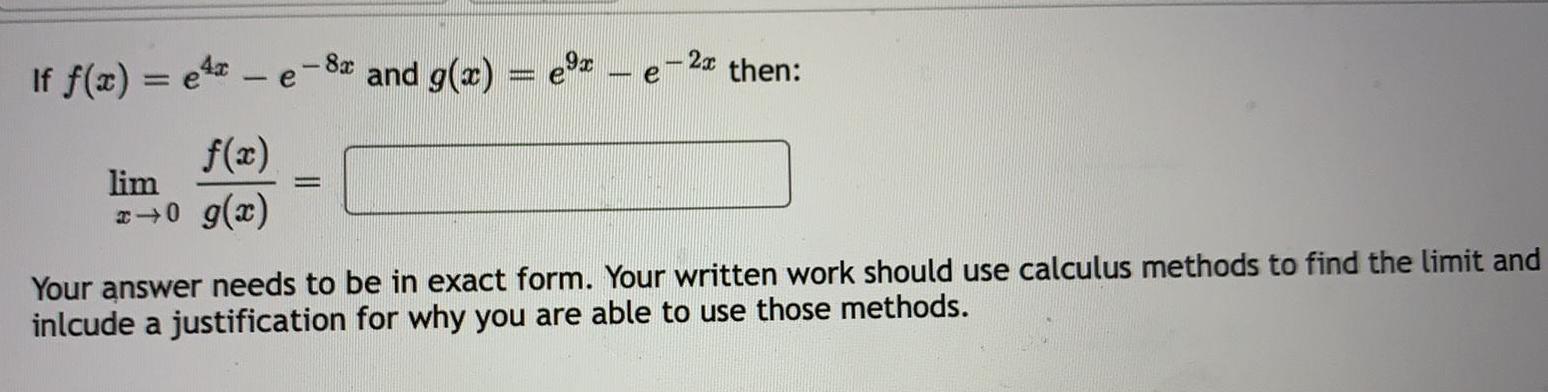
Limits and ContinuityIf f x exe 8 and g x f x lim x 0 g x 2x then Your answer needs to be in exact form Your written work should use calculus methods to find the limit and inlcude a justification for why you are able to use those methods
Math
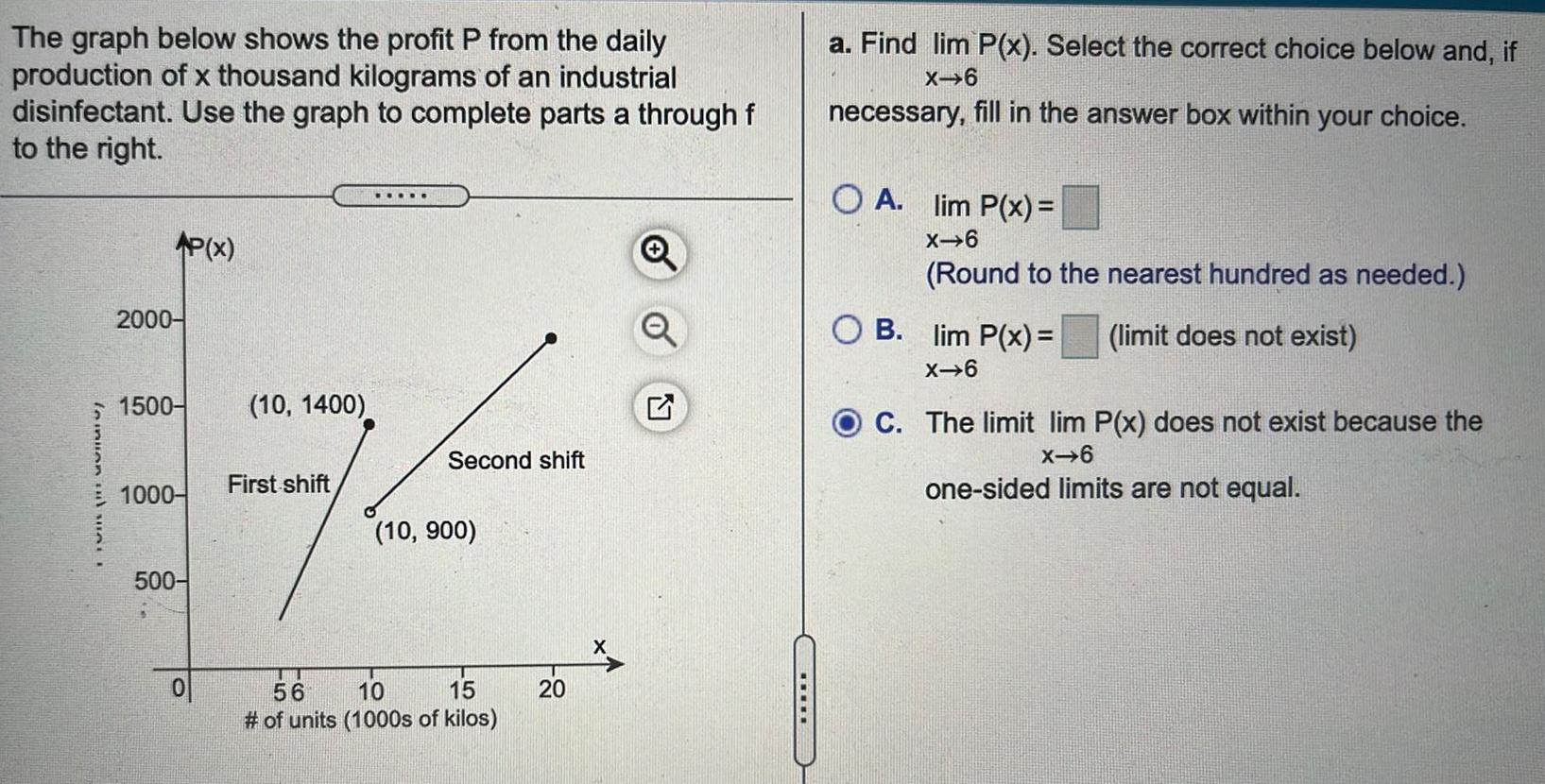
Limits and ContinuityThe graph below shows the profit P from the daily production of x thousand kilograms of an industrial disinfectant Use the graph to complete parts a through f to the right leinuen und unt 2000 1500 1000 P x 500 0 10 1400 First shift Second shift 10 900 56 10 15 of units 1000s of kilos 20 N a Find lim P x Select the correct choice below and if X 6 necessary fill in the answer box within your choice OA lim P x X 6 Round to the nearest hundred as needed limit does not exist OB lim P x X 6 C The limit lim P x does not exist because the X 6 one sided limits are not equal

Math
Limits and ContinuityThe amount of income tax t an individual owes is defined by piecewise function t and is based on the individual s income where is taxable income in dollar 0 10 t i 755 0 12 11000 4500 b i 35000 if Osis 12 000 if 12 000 32 000 if 32 000 Part A Show that the function t is not continuous at 12 000 10 points Part B Find the value of constant b that makes t i continuous at 32 000 20 points
Math
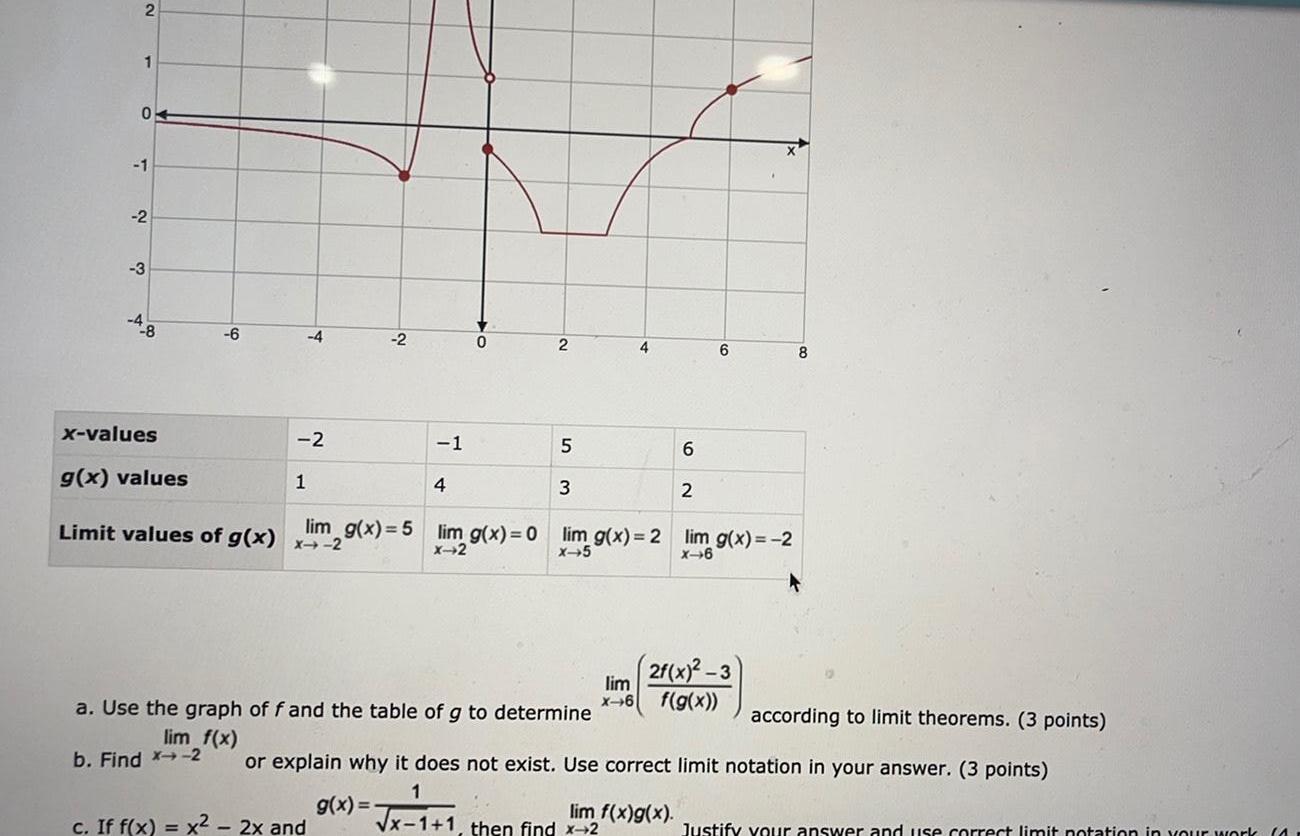
Limits and Continuity2 1 0 1 2 3 4 8 x values 6 b Find X 2 2 g x values Limit values of g x x 2 4 1 2 1 c If f x x 2x and 4 0 lim g x 5 lim g x 0 2 5 3 a Use the graph of f and the table of g to determine lim f x 4 lim X 6 lim g x 2 lim g x 2 x 6 x 5 x 1 1 then find x 2 6 2 lim f x g x 6 2f x 2 3 f g x according to limit theorems 3 points or explain why it does not exist Use correct limit notation in your answer 3 points g x 8 Justify your answer and use correct limit notation in your work 41
Math
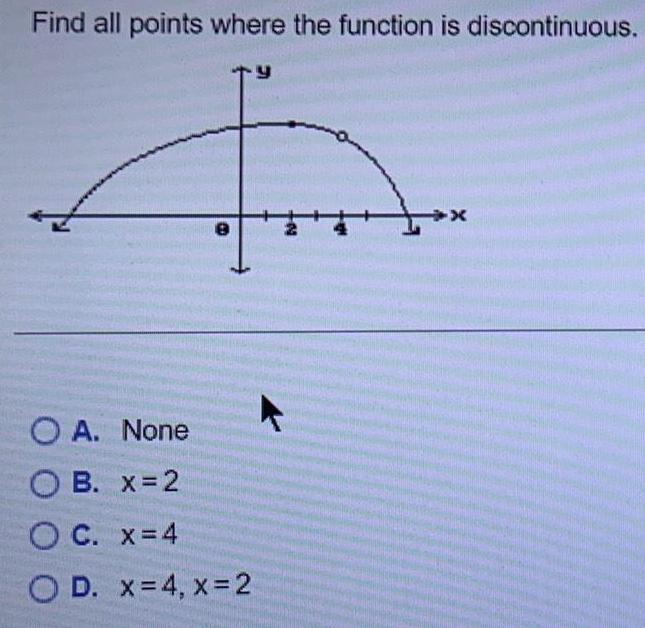
Limits and ContinuityFind all points where the function is discontinuous.
A. None
B. x=2
C. x = 4
D. x = 4, x = 2
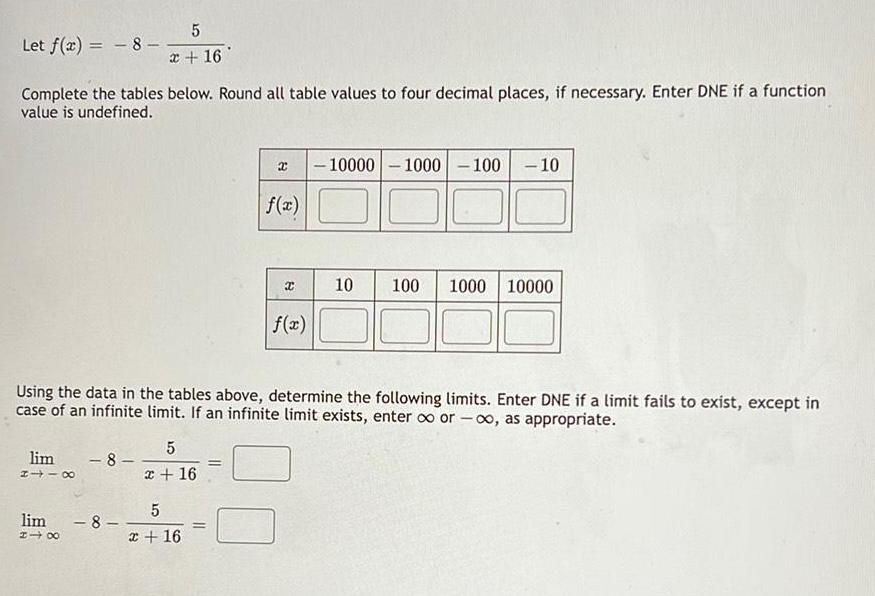
Math
Limits and ContinuityLet f(x) = -8 - 5/x+16
Complete the tables below. Round all table values to four decimal places, if necessary. Enter DNE if a function value is undefined.
Using the data in the tables above, determine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.

Math
Limits and ContinuityLet f(x)=√x6 +5x - x³ - 3.
Complete the tables below. Round all table values to four decimal places, if necessary. Enter DNE if a function value is undefined.
Using the data in the tables above, determine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.

Math
Limits and Continuity(1 point) Find an integer which is the limit of
tan(8x)/2x
as x goes to 0. (Enter I for infinity or DNE for does not exist.)

Math
Limits and ContinuityUse a graph or table of values near x =π/2 to estimate the value of this limit:
lim
x - 72
cos(7x)/x-π/2
i

Math
Limits and ContinuityLet f be the function defined as
f(x)= 3 for x<5
x+7 for x≥ 5
Which of the following statements is true?
f is not differentiable at x = 5 because f is not defined at x = 5.
f is not differentiable at x = 5 because fis not continuous at x = 5.
f is not differentiable at x = 5 because the graph off has a vertical tangent at x = 5.
f is not differentiable at x = 5 because the graph of f has a cusp at x = 5.
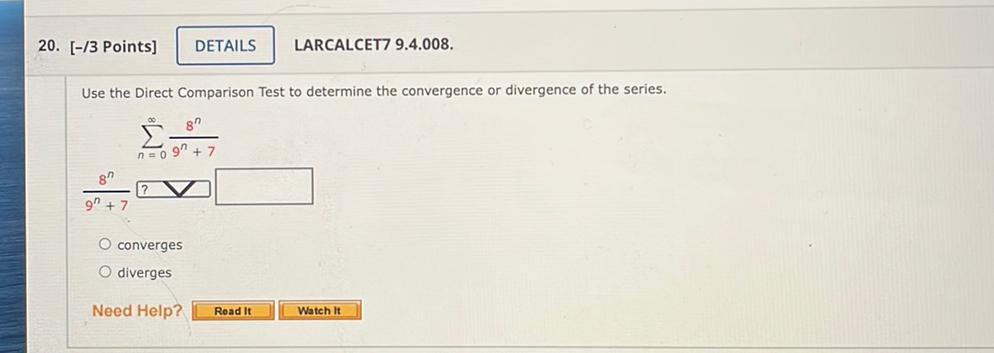
Math
Limits and ContinuityUse the Direct Comparison Test to determine the convergence or divergence of the series.
∞
Σ 8^n/(9^n) +7
n=0
a)converges
b)diverges

Math
Limits and ContinuityIn a study on the speed of muscle contraction in a certain species of frogs under various loads, researchers found that the speed of contraction decreases with increasing loads. In particular, they found that the relationship between speed of contraction v (in centimeters per second) and load x (in grams) is given approximately by v(x) = 29+0.05x/x, x≥5
(A) What does v(x) approach as x increases?
(B) Sketch a graph of the function v.
(A) As x increases, v(x) approaches

Math
Limits and ContinuityYou want to be able to withdraw $25,000 from your account each year for 25 years after you retire. You expect to retire in 30 years. If your account earns 5% interest, how much will you need to deposit each year until retirement to achieve your retirement goals?

Math
Limits and ContinuityGiven a continuous function f(x) with f(-5) = - 1 and f(9) = - 8:
There must be a number c with − 5 < c < 9 and f(c) = - 4.6.
There might be a number c with - 5 < c < 9 and f(c) = - 4.6.
There cannot be a number c with -5 < c < 9 and f(c) = - 4.6.
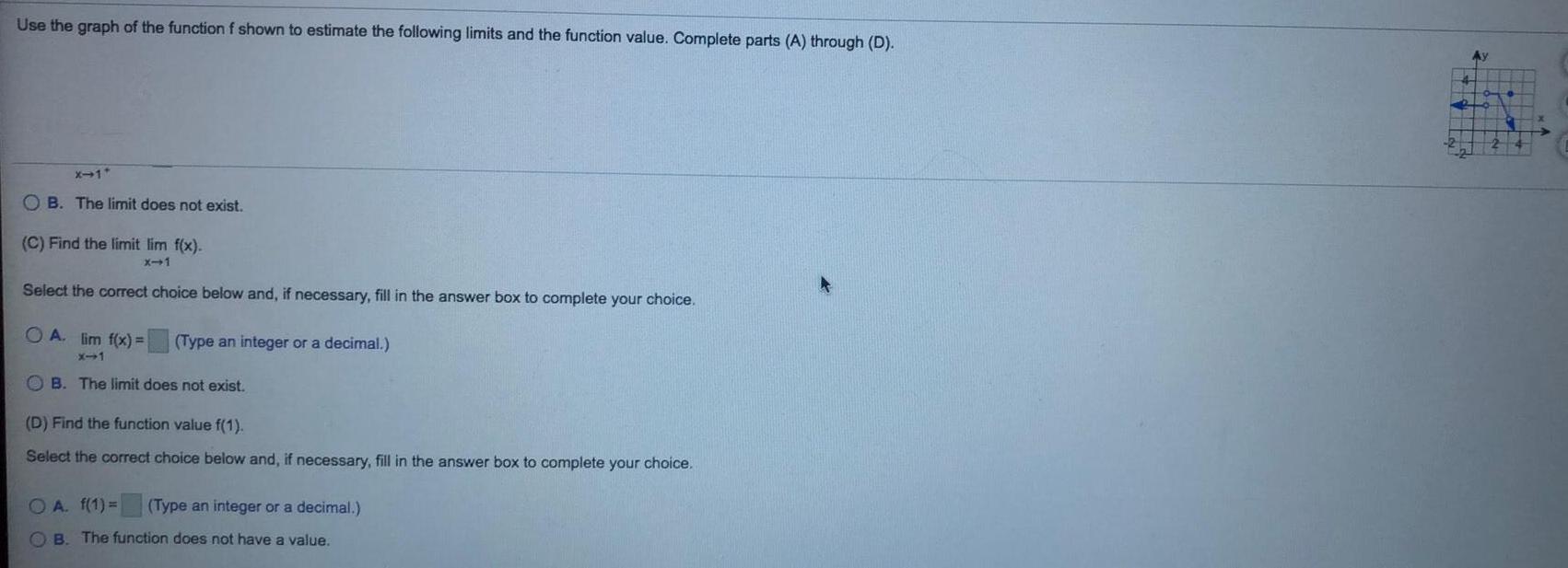
Math
Limits and ContinuityUse the graph of the function f shown to estimate the following limits and the function value. Complete parts (A) through (D).
(C) Find the limit lim x⇒1 f(x).
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. lim x⇒1 f(x)
B. The limit does not exist.
(D) Find the function value f(1).
A. f(1) =
B. The function does not have a value.

Math
Limits and ContinuityGiven a function f(x) with f(− 8) = 1 and f(9) ,m= 2:
There must be a number c with -8 < c < 9 and f(c) = 1.4.
There might be a number c with 8 < c < 9 and f(c) = 1.4.
There cannot be a number c with -8 < c < 9 and f(c) = 1.4.

Math
Limits and ContinuitySuppose that a ball is rolling down a ramp. The distance traveled by the ball is given by the function s(t), where t is the time, in seconds, after the ball is released, and s(t) is measured in feet. For the given function, find the ball's average velocity from t₁ to t₂.
s(t) = 12t²; t₁ = 5, t₂ = 5.001
A. 0.12 ft/sec
B. 12.012 ft/sec
C. 120.012 ft/sec
D. -120.012 ft/sec)

Math
Limits and ContinuityLet f be the function defined as
f(x)= 2 for x<4
f(x)= 4x-3 for x≥4
Which of the following statements is true?
f is not differentiable at x = 4 because fis not defined at x = 4.
f is not differentiable at x = 4 because the graph of f has a cusp at x = 4.
f is not differentiable at x = 4 because the graph of f has a vertical tangent at x = 4.
f is not differentiable at x = 4 because f is not continuous at x = 4,

Math
Limits and ContinuityFind the x-value of the removable discontinuity of the function.
Consider the graph of the function f(x) = x² - 121/x²+x-132
Provide your answer below:
The removable discontinuity occurs at x =
=

Math
Limits and ContinuityConsider the following function:
f(x)= x^2 - 5x - 24 / x^3 - 2x^2 - 15x
(A) Where is f discontinuous?
The function f is discontinuous at the following x-values:
Your answer must be a comma-separated list of numbers.
(B) At the leftmost x-value where f is discontinuous, what type of discontinuity does f have?
A. removable discontinuity
B. jump discontinuity
C. infinite discontinuity (vertical asymptote)
D. other type of discontinuity
(C) At the rightmost x-value where f is discontinuous, what type of discontinuity does f have?
A. removable discontinuity
B. jump discontinuity
C. infinite discontinuity (vertical asymptote)
D. other type of discontinuity
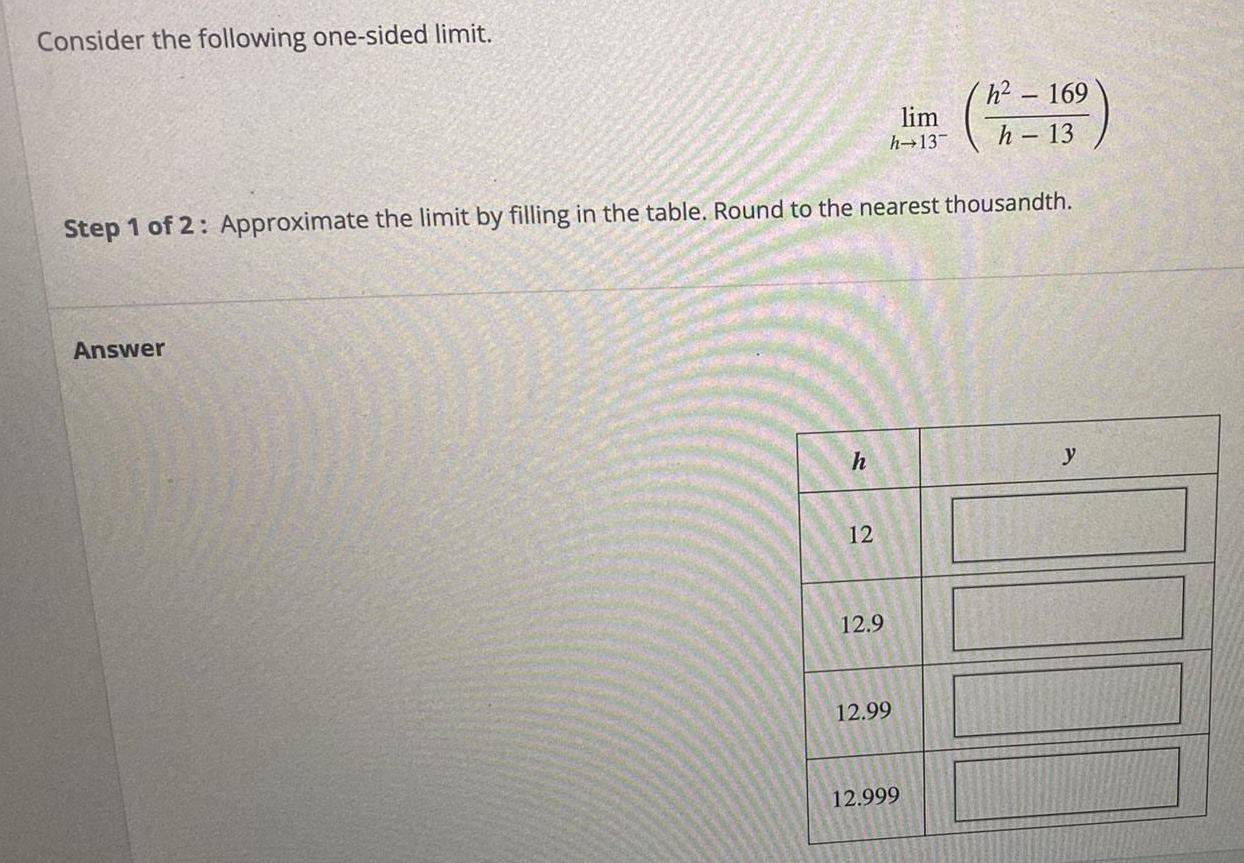
Math
Limits and ContinuityConsider the following one-sided limit.
lim h→13⁻ (h²- 169 / h - 13)
Approximate the limit by filling in the table. Round to the nearest thousandth.
h y
12
12.9
12.99
12.999

Math
Limits and ContinuityConsider the function p(x)= cos²x/sin 2x Which of the following accurately describes the limit as x approaches 0 of the function?
As x approaches 0, the limit of p(x) approaches a large negative y-value.
As x approaches 0, the limit of p(x) does not exist.
As x approaches 0, the limit of p(x) approaches 0.
As x approaches 0, the limit of p(x) approaches a large positive y-value.
![Find the limit of s(n) as n →∞.
s(n)=[n(n+1)/3]/n²](https://media.kunduz.com/media/sug-question/raw/55146281-1658076068.9006045.jpeg?w=256)
Math
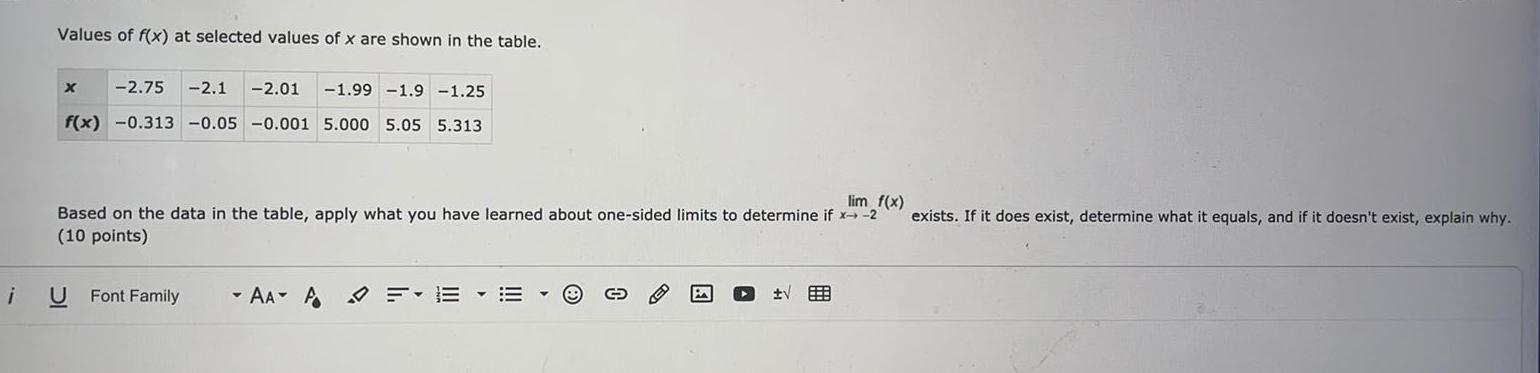
Limits and ContinuityValues of f(x) at selected values of x are shown in the table.
X -2.75 -2.1 -2.01 -1.99 -1.9 -1.25
f(x) -0.313 -0.05 -0.001 5.000 5.05 5.313
Based on the data in the table, apply what you have learned about one-sided limits to determine if lim x→-2 f(x) exists. If it does exist, determine what it equals, and if it doesn't exist, explain why.
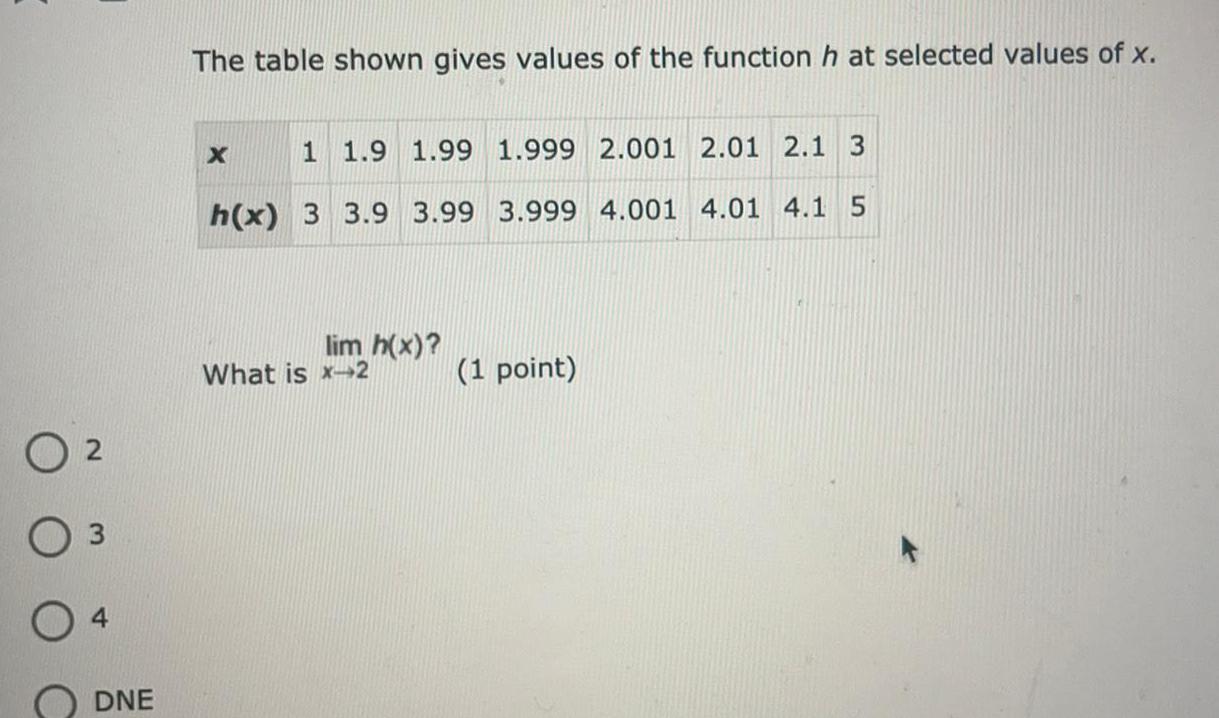
Math
Limits and ContinuityThe table shown gives values of the function h at selected values of x.
x 1 1.9 1.99 1.999 2.001 2.01 2.1 3
h(x) 3 3.9 3.99 3.999 4.001 4.01 4.1 5
lim x→2h(x)?
What is x-2
2
3
4
DNE

Math
Limits and ContinuityFast-Food Bills for Drive-Thru Customers A random sample of 44 cars in the drive-thru of a popular fast food restaurant revealed an average bill of $19.27 per car. The population standard deviation is $5.70. Estimate the mean bill for all cars from th drive-thru with 96% confidence. Round intermediate and final answers to two decimal places.
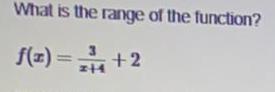
![Find the points of inflection of the graph of the function. (If an answer does not exist, enter DNE.)
f(x) = 4 sin x + 4 cos x,
[0, 2π]
(x, y) =
(x, y)
=
DNE
DNE
concave upward
Describe the concavity. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)
DNE
concave downward
(smaller x-value)
DNE
(larger x-value)](https://media.kunduz.com/media/sug-question/raw/54546850-1658053870.3581438.jpeg?w=256)
Math
Limits and ContinuityFind the points of inflection of the graph of the function. (If an answer does not exist, enter DNE.)
f(x) = 4 sin x + 4 cos x,
[0, 2π]
(x, y) =
(x, y)
=
DNE
DNE
concave upward
Describe the concavity. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)
DNE
concave downward
(smaller x-value)
DNE
(larger x-value)

Math
Limits and ContinuityA business has a cost of C = 0.5x + 500 for producing x units. The average cost per unit is given by the following.
Find the limit of the average cost as x approaches infinity.
![Use interval notation to indicate where on the interval [0,π/4] the function f(x) = 2x + 3 / cos 4x is continuous.](https://media.kunduz.com/media/sug-question/raw/54435716-1658051005.6372519.jpeg?w=256)
Math
Limits and ContinuityUse interval notation to indicate where on the interval [0,π/4] the function f(x) = 2x + 3 / cos 4x is continuous.
![Determine whether the Mean Value Theorem can be applied to f on the closed interval [a, b]. If the Mean
Value Theorem can be applied, find all values of c in the open interval (a, b) such that f '(c) the Mean Value Theorem cannot be applied, explain why not.
f(x) = x2/3, [0, 1]
To determine whether the Mean Value theorem can be applied on the given interval [0, 1], the following conditions must be satisfied.](https://media.kunduz.com/media/sug-question/raw/54366305-1658050212.998421.jpeg?w=256)
Math
Limits and ContinuityDetermine whether the Mean Value Theorem can be applied to f on the closed interval [a, b]. If the Mean
Value Theorem can be applied, find all values of c in the open interval (a, b) such that f '(c) the Mean Value Theorem cannot be applied, explain why not.
f(x) = x2/3, [0, 1]
To determine whether the Mean Value theorem can be applied on the given interval [0, 1], the following conditions must be satisfied.
![Mathematicians I. Perepelitsa and C. Douglas are having an argument. Professor Douglas claims that it is impossible for a function y = f(x) to have the following properties:
a) f(x) is continuous on [-4,4)
b) f(-4)= -2 and f(4) = 2
c) The Intermediate Value Theorem fails in that f(x) = -1 for any input r in [-4,4].
"If f(x) is continuous, then it has to achieve every intermediate value!" screams Professor Douglas. "No," responds Professor
Perepelitsa. "The Intermediate Value Theorem may not apply to this function. I think it is possible for conditions a)-c) to hold."
Who is correct, Professor Douglas or Professor Perepelitsa? If you think Professor Douglas is correct, explain why in the
space below the image. If you think Professor Perepelitsa is correct, use the image below to draw a graph of a function
y = f(x) with the stated properties.](https://media.kunduz.com/media/sug-question/raw/54388363-1658049887.5645201.jpeg?w=256)
Math
Limits and ContinuityMathematicians I. Perepelitsa and C. Douglas are having an argument. Professor Douglas claims that it is impossible for a function y = f(x) to have the following properties:
a) f(x) is continuous on [-4,4)
b) f(-4)= -2 and f(4) = 2
c) The Intermediate Value Theorem fails in that f(x) = -1 for any input r in [-4,4].
"If f(x) is continuous, then it has to achieve every intermediate value!" screams Professor Douglas. "No," responds Professor
Perepelitsa. "The Intermediate Value Theorem may not apply to this function. I think it is possible for conditions a)-c) to hold."
Who is correct, Professor Douglas or Professor Perepelitsa? If you think Professor Douglas is correct, explain why in the
space below the image. If you think Professor Perepelitsa is correct, use the image below to draw a graph of a function
y = f(x) with the stated properties.
![Determine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
f(x) = x²-3x - 10 /x + 7
Yes, Rolle's Theorem can be applied.
No, because f is not continuous on the closed interval [a, b].
No, because f is not differentiable in the open interval (a, b).
No, because f(a) = f(b).
[-2,5]
If Rolle's Theorem can be applied, find all values of c in the open interval (a, b) such that f'(c) = 0. (Enter your answers as a comma-separated list. If Rolle's Theorem cannot be applied, enter NA.)](https://media.kunduz.com/media/sug-question/raw/54366253-1658040542.0722342.jpeg?w=256)
Math
Limits and ContinuityDetermine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
f(x) = x²-3x - 10 /x + 7
Yes, Rolle's Theorem can be applied.
No, because f is not continuous on the closed interval [a, b].
No, because f is not differentiable in the open interval (a, b).
No, because f(a) = f(b).
[-2,5]
If Rolle's Theorem can be applied, find all values of c in the open interval (a, b) such that f'(c) = 0. (Enter your answers as a comma-separated list. If Rolle's Theorem cannot be applied, enter NA.)

Math
Limits and ContinuityState whether the graph of f(x)= x³+7x² + 10x / x +5 has infinite discontinuity, jump discontinuity, point discontinuity, or is continuous.
The function is continuous.
The function has jump discontinuity.
The function has infinite discontinuity.
The function has point discontinuity.
![Consider the following function and closed interval.
f(x) = x2/3
- 3, [-8, 8]
Is f continuous on the closed interval [-8, 8]?
Yes
No
If f is differentiable on the open interval (-8, 8), find f'(x). (If it is not differentiable on the open interval, enter DNE.)
f'(x) =
Find f(-8) and f(8).
f(-8) =
f(8) =
Determine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
Yes, Rolle's Theorem can be applied.
C =
No, because f is not continuous on the closed interval [a, b].
No, because f is not differentiable in the open interval (a, b).
No, because f(a) = f(b).
If Rolle's Theorem can be applied, find all values of in the open interval (a, b) such that f'(c) = 0. (Enter your answers as a comma-separated list. If Rolle's Theorem cannot be applied, enter NA.)](https://media.kunduz.com/media/sug-question/raw/54366256-1658039976.9539607.jpeg?w=256)
Math
Limits and ContinuityConsider the following function and closed interval.
f(x) = x2/3
- 3, [-8, 8]
Is f continuous on the closed interval [-8, 8]?
Yes
No
If f is differentiable on the open interval (-8, 8), find f'(x). (If it is not differentiable on the open interval, enter DNE.)
f'(x) =
Find f(-8) and f(8).
f(-8) =
f(8) =
Determine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
Yes, Rolle's Theorem can be applied.
C =
No, because f is not continuous on the closed interval [a, b].
No, because f is not differentiable in the open interval (a, b).
No, because f(a) = f(b).
If Rolle's Theorem can be applied, find all values of in the open interval (a, b) such that f'(c) = 0. (Enter your answers as a comma-separated list. If Rolle's Theorem cannot be applied, enter NA.)
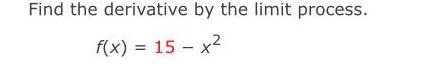

Math
Limits and ContinuityAlicia, the manager of a plant, determines
that when x% of the plant's capacity is being
used, the total cost of operation is C hundred
dollars, where
C(x) =
=
16x2-1240x - 3200
x² - 72x - 640
The company has a policy of rotating
maintenance in an attempt to ensure that
approximately 80% of capacity is always in
use. What cost should Alicia expect when
the plant is operating at this ideal capacity?

Math
Limits and ContinuityIn certain situations, it is necessary to weigh
the benefit of pursuing a certain goal against
the cost of achieving that goal. For instance,
suppose that to remove x% of the pollution
from an oil spill, it costs C thousands of
dollars, where
C(x) =
13x
100-x
What happens as x→ 100? Is it possible
remove all the pollution?

Math
Limits and ContinuityDetermine whether the function is differentiable at x = 3.
x² + 3, x ≤ 3
6x9,x>3
f(x) = {
The function
differentiable at x = 3.

Math
Limits and ContinuityFind the x-values (if any) at which f is not continuous. Which of the discontinuities are
enter DNE.)
f(x) = ln(x + 1),
12-x²,
x ≥ 0
x < 0

Math
Limits and ContinuityConsider the following.
f(x)=9|x - 71|/X-7
Find the x-value (if any) at which f is not continuous. Is the discontinuity removable? (Enter NONE in any unused answer blanks.)

Math
Limits and ContinuityConsider the following.
f(x)=x/x²-9
Find the x-values (if any) at which f is not continuous. Is the discontinuity removable? (Enter your answers from smallest to
largest. Enter NONE in any unused answer blanks.)
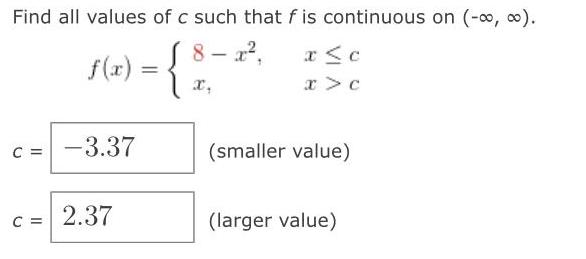
Math
Limits and ContinuityFind all values of c such that f is continuous on (-∞, ∞).
f(x)=8-x² , x≤c
x , x>c
c= (smaller value)
c=(larger value)

Math
Limits and ContinuityGiven the function f(x)=2x +3/x+1 Calculate the following values:
Note: Round the answer to two decimal places as needed. If the output does not exist, enter DNE
ƒ(-2)
f(-1)=
f(0)
ƒ(1)
ƒ(2)
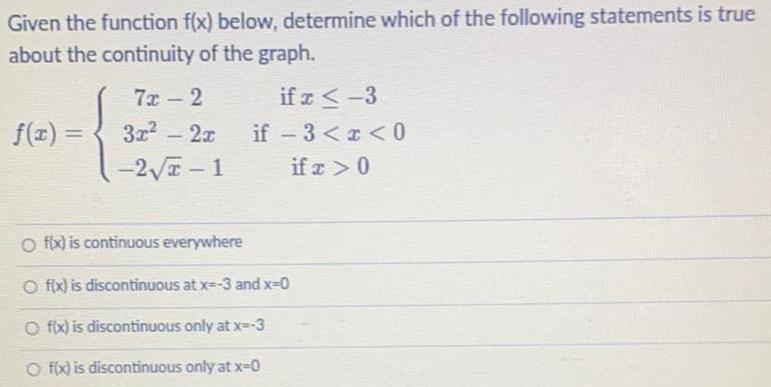
Math
Limits and ContinuityGiven the function f(x) below, determine which of the following statements is true
about the continuity of the graph.
f(x) =
7x-2
3x² - 2x
-2√x-1
if x ≤-3
if -3<x<0
if x > 0
O f(x) is continuous everywhere
Of(x) is discontinuous at x=-3 and x=0
O f(x) is discontinuous only at x=-3
O f(x) is discontinuous only at x-0
Math
Limits and Continuityse transformations to graph the following function. Determine the domain, range, horizontal asymptote, and y-intercept of the function.
x)=5* -3
se the graphing tool to graph the function.
Click to
enlarge
graph
For any answer boxes shown with the grapher, type an exact answer.)
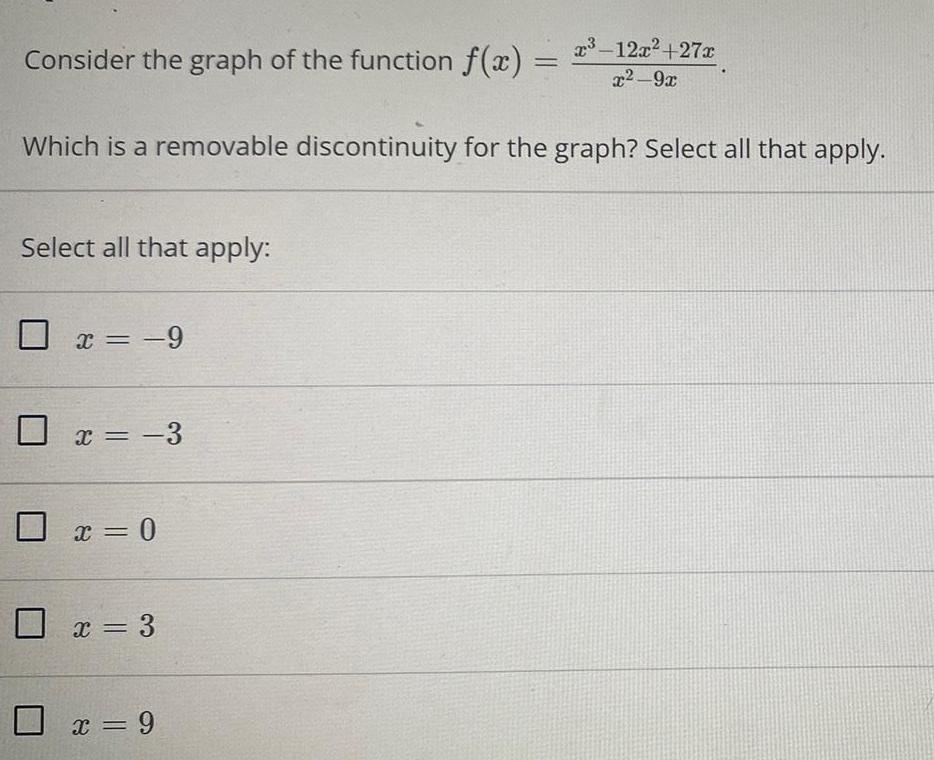
Math
Limits and ContinuityConsider the graph of the function f(x)=x³-12x² +27x/x²-9x
Select all that apply:
Which is a removable discontinuity for the graph? Select all that apply.
x = -9
x = -3
x = 0
x = 3
x = 9

Math
Limits and ContinuityA farmer was interested in determining how many grasshoppers were in his field. He knows that the distribution of grasshoppers may not be normally distributed in his
field due to growing conditions. As he drives his tractor down each row he counts how many grasshoppers he sees flying away. After several rows he figures the mean
number of flights to be 57 with a standard deviation of 12. What is the probability of the farmer will count 52 or fewer flights or 60 or more flights on average in the next 40
rows down which he drives his tractor?
0.0530
0.0612
0.9388
0.4959
![Given that
lim f(x) = 0
x-a
lim g(x) = 0
x→a
lim h(x) = 1
x-a
lim_p(x) = ∞
x-a
lim g(x) = ∞0,
x-a
evaluate if the following limits are not indeterminate forms. (If a limit is indeterminate, enter INDETERMINATE.)
(a) lim [f(x) - P(x)]
x-a
(b) lim [p(x) - q(x)]
x-a
(c) lim [p(x) + q(x)]
x→a](https://media.kunduz.com/media/sug-question/raw/58149734-1657717701.089779.jpeg?w=256)
Math
Limits and ContinuityGiven that
lim f(x) = 0
x-a
lim g(x) = 0
x→a
lim h(x) = 1
x-a
lim_p(x) = ∞
x-a
lim g(x) = ∞0,
x-a
evaluate if the following limits are not indeterminate forms. (If a limit is indeterminate, enter INDETERMINATE.)
(a) lim [f(x) - P(x)]
x-a
(b) lim [p(x) - q(x)]
x-a
(c) lim [p(x) + q(x)]
x→a

Math
Limits and Continuity3700t
The system of the population of a culture of tumor cells is given by p(t) =
t+5
Select the correct choice below, and fill in the answer box if necessary.
lim p(t)=
118
OB. The limit does not exist.
O A.
1.
Find and interpret lim p(t).
1-0
*****