Linear Programming Questions and Answers

Math
Linear ProgrammingHow does characterization support satire Select three options It pokes fun at characters by placing them in extreme situations O It makes fun of human weaknesses through humorous characters It exposes human flaws by exaggerating characters weaknesses It reveals a gap between belief and reality by making characters unaware of their weaknesses It ridicules socially acceptable behavior by showing how characters good intentions backfire
Math
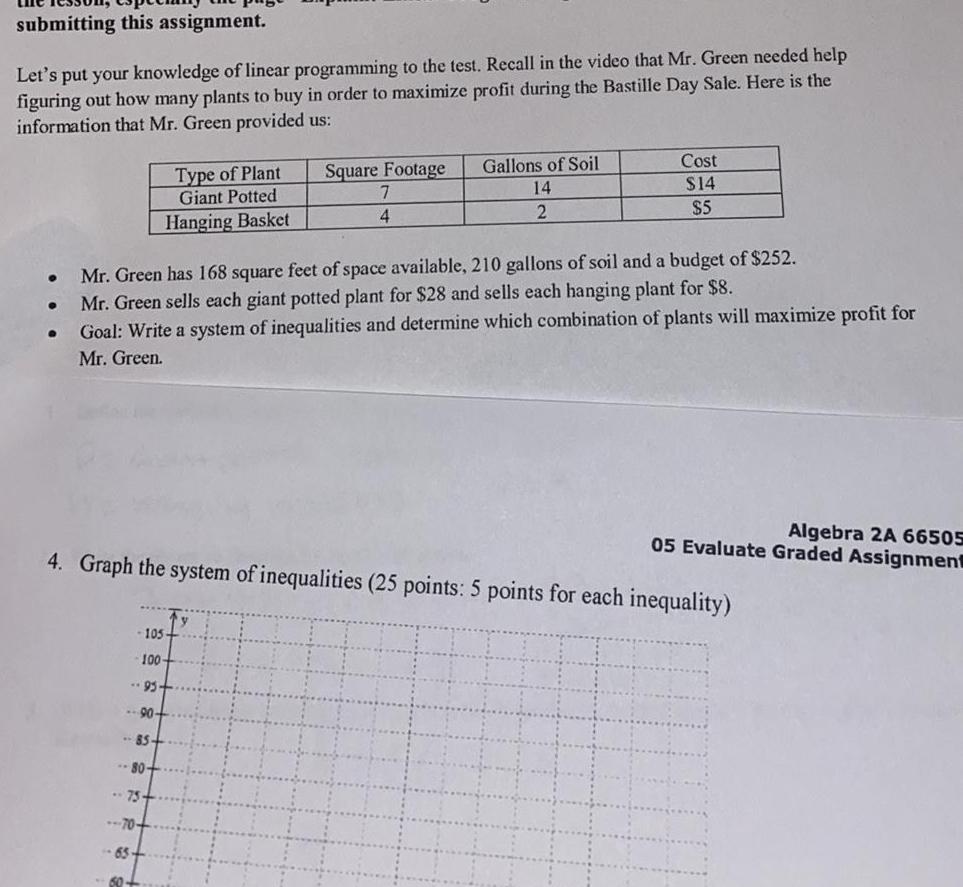
Linear Programmingsubmitting this assignment Let s put your knowledge of linear programming to the test Recall in the video that Mr Green needed help figuring out how many plants to buy in order to maximize profit during the Bastille Day Sale Here is the information that Mr Green provided us Type of Plant Giant Potted Hanging Basket 105 100 95 90 85 70 65 Square Footage 7 4 Mr Green has 168 square feet of space available 210 gallons of soil and a budget of 252 Mr Green sells each giant potted plant for 28 and sells each hanging plant for 8 Goal Write a system of inequalities and determine which combination of plants will maximize profit for Mr Green 60 Gallons of Soil 14 2 Cost 14 5 4 Graph the system of inequalities 25 points 5 points for each inequality Algebra 2A 66505 05 Evaluate Graded Assignment
Math
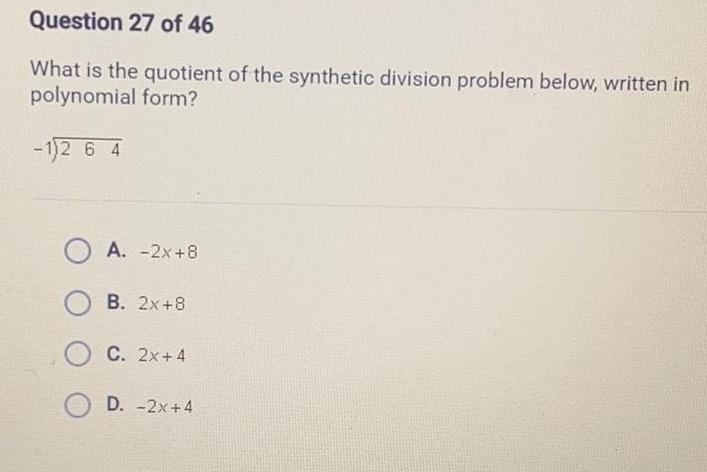
Linear ProgrammingQuestion 27 of 46 What is the quotient of the synthetic division problem below written in polynomial form 1 2 6 4 A 2x 8 OB 2x 8 OC 2x 4 OD 2x 4
Math
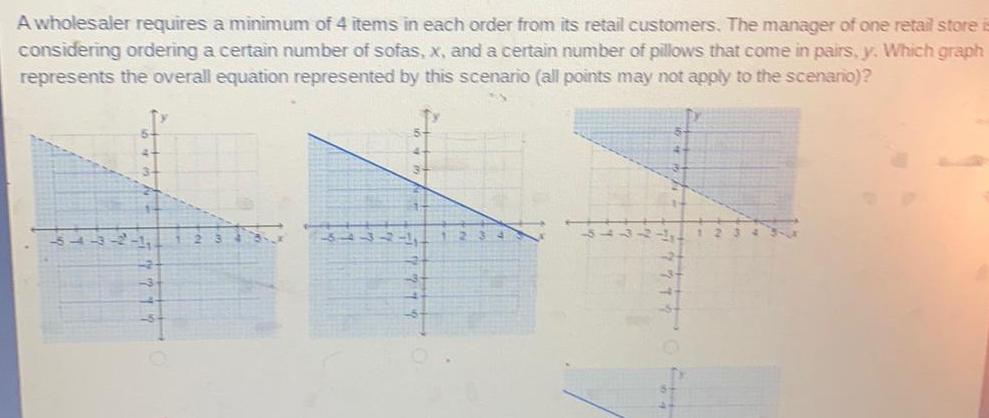
Linear ProgrammingA wholesaler requires a minimum of 4 items in each order from its retail customers The manager of one retail store considering ordering a certain number of sofas x and a certain number of pillows that come in pairs y Which graph represents the overall equation represented by this scenario all points may not apply to the scenario

Math
Linear ProgrammingSuppose in one year total revenues from digital sales of pop rock tropical salsa merengue cumbia bachata and urban reggaeton Latin music in a certain country amounted to 21 million Pop rock music brought in twice as much as the other two categories combined and 11 million more than tropical music How much revenue was earned from digital sales in each of the three categories pop rock music tropical music urban Latin music million million million

Math
Linear Programming6 CDs can be manufactured for 0 19 each The development cost is 210 000 The first 500 discs are samples and will not be sold a Write function for the average cost of a disc that is not a sample b What is the average cost if 5000 discs are produced Show work c How many discs must be produced to bring the average cost under 10 Show work

Math
Linear ProgrammingAnna wants to take fitness classes She compares two gyms to determine which would be the best deal for her Fit Fast charges a set fee per class Stepping Up charges a monthly fee plus an additional fee per class The system of equations models the total costs for each y 7 5x y 5 5x 10 1 Substitute 7 5x 5 5x 10 How many classes could Anna take so that the total cost for the month would be the same classes What is the total monthly cost when it is the same for both gyms
Math
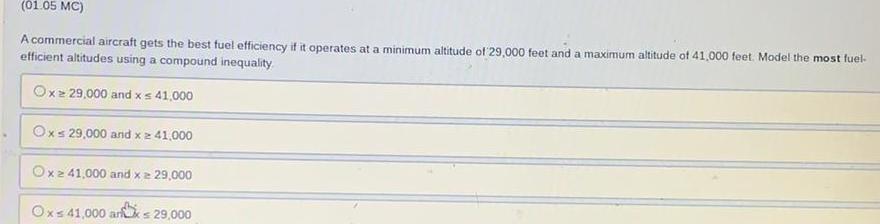
Linear Programming01 05 MC A commercial aircraft gets the best fuel efficiency if it operates at a minimum altitude of 29 000 feet and a maximum altitude of 41 000 feet Model the most fuel efficient altitudes using a compound inequality Oxz 29 000 and x 41 000 Oxs 29 000 and x 41 000 Ox 41 000 and x 29 000 the Ox 41 000 arx 29 000

Math
Linear ProgrammingA company manufactures two models of snowboards standard and deluxe Each deluxe model requires 26 hours to produce and 96 units of material Each standard model requires 13 hours to produce and 80 units of material The company has 858 production hours available and 4000 units of material in stock The deluxe model sells for 272 and the standard model sells for 170 What amount of each model should be produced and sold to obtain the maximum revenue Adeluxe models standard models

Math
Linear Programmingcarpool service has 2 000 daily riders A one way ticket costs 5 00 The service estimates that for each 1 00 increase to the one way fare 00 passengers will find other means of transportation Let x represent the number of 1 00 increases in ticket price Choose the inequality to represent the values of x that would allow the carpool service to have revenue of at least 12 000 Then use the nequality to select all the correct statements D W The price of a one way ticket that will maximize revenue is 7 50 100 2 1 500 10 000 1002 1 500 10 000 100x2 1 500 10 000 12 000 The maximum profit the company can make is 15 625 00 The maximum profit the company can make is 4 125 00 The price of a one way ticket that will maximize revenue is 12 50 12 000 12 000

Math
Linear ProgrammingUse the simplex method to maximize the following:
Maximize f = 7x1 + 9x2 subject to
4x1 +5x2 ≤ 15
5x1 + 4x2 ≤ 32
4x1+5x2 ≤ 30
x1 ≥ 0, x2 ≥ 0
If no solutions exist enter DNE in all answerboxes.
x1 =
x2 =
f =

Math
Linear ProgrammingUse the objective function z = 10x + 12y to determine the maximum profit subject to the constraints
{x20 2x + 3y≤6 5x + 7y≤35 6x + 4y224 y21
Graph the feasible region, determine the corner points, and compute the maximum profit.

Math
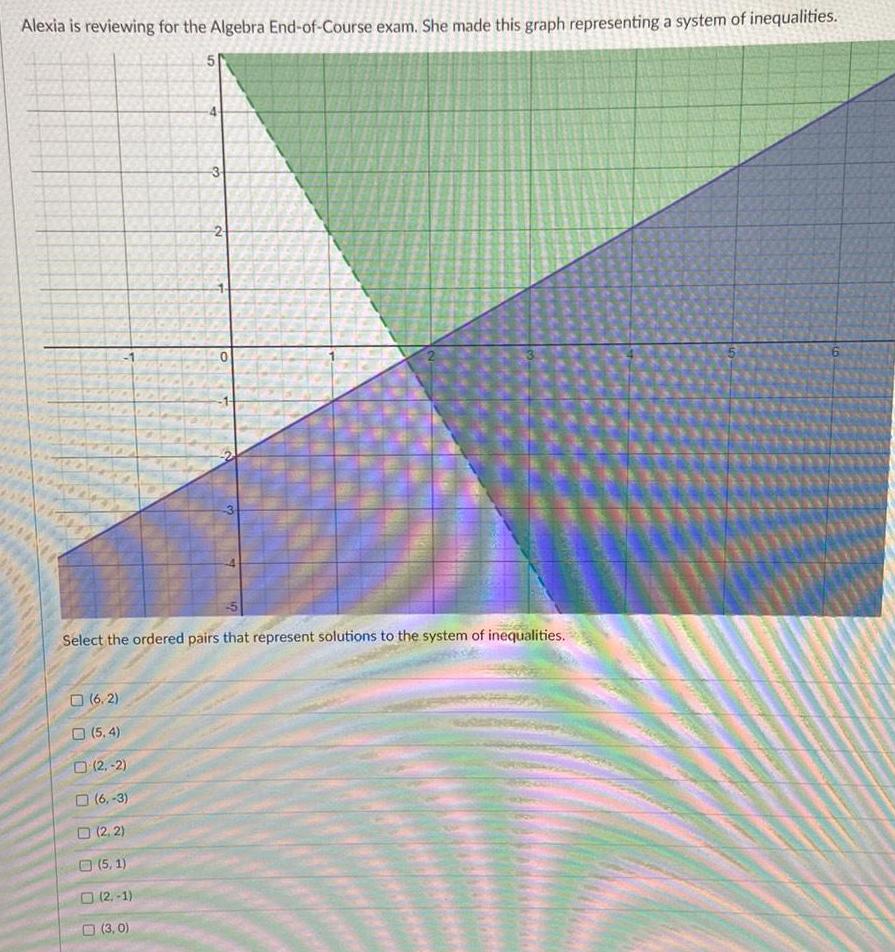
Linear ProgrammingAlexia is reviewing for the Algebra End-of-Course exam. She made this graph representing a system of inequalities.
(6.2)
(5.4)
(2,-2)
(6,-3)
(2, 2)
(5, 1)
(2.-1)
(3.0)

Math
Linear ProgrammingA high school band trip will require renting buses and trucks to transport no fewer than 150 students and 20 or more large instruments, Each bus can accommodate 60 students plus 3 large instruments; it costs $347 to rent. Each truck can accommodate 15 students plus 7 large instruments and costs $195 to rent. How many of each type of vehicle should be rented for the cost to be minimized?
Determine the minimum cost.
2 buses and 2 trucks: $1084
none of these
buses and 10 trucks: $1950
4 buses and 0 trucks: $1388
1 buses and 4 trucks: $1127
Math
Linear ProgrammingTwo artists make winter yard ornaments. They get $97 for each wooden snowman
they make and $77 for each wooden Santa Claus. On average, Nina must work 4
hours and Roberta 3 hours to make a snowman. Nina must work 2 hours and Roberta 4 hours to make a Santa Claus. If neither wishes to work more than 20 hours per week, how many of each ornament should they make each week to maximize their income?
3 snowmen an 4 ornaments of Santa Claus: $19
4 snowmen an 3 ornaments of Santa Claus: $19
4 snowmen an 2 ornaments of Santa Claus: $542
5 snowmen an no ornaments of Santa Claus: $485
2 snowmen an 5 ornaments of Santa Claus: $23
Math
Linear ProgrammingUse the simplex method to maximize f= 4x + 4y + z under the constraints
x + 2y + 4z ≤ 20
2x + 4y + 4z ≤ 60
3x + 4y + z ≤ 90
x ≥ 0, y ≥ 0, z ≥ 0.
Math
Linear ProgrammingTwo woodworkers, Tom and Carlos, earn a profit of $86 for making a table and $65
for making a chair. Tom must work 3 hours and Carlos 2 hours to make a chair. Tom
must work 2 hours and Carlos 6 hours to make a table. If neither wants to work more
than 42 hours per week, how many tables and chairs should they make to maximize
their profit?
3 tables and 12 chairs: $1038
13 tables and 2 chairs: $1227
notables and 15 chairs: $1806
12 tables and 3 chairs: $1227
none of these
Math
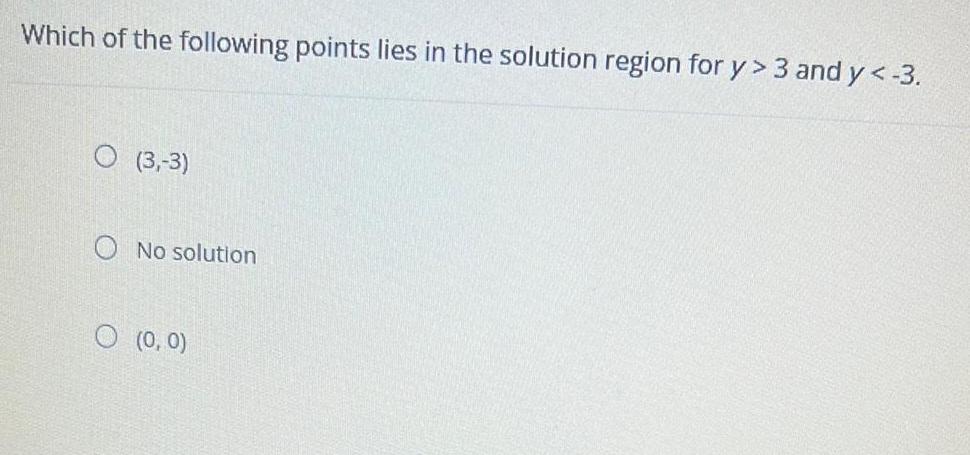
Linear ProgrammingWhich of the following points lies in the solution region for y> 3 and y < -3.
(3,-3)
No solution
(0, 0)

Math
Linear ProgrammingA company manufactures two models of snowboards, standard and deluxe. Each deluxe model requires 26 hours to produce, and 96 units of material. Each standard model requires 13 hours to produce and 80 units of material. The company has 858 production hours available and 4000 units of material in stock. The deluxe model sells for $272 and the standard model sells for $170. What amount of each model should be produced and sold to obtain the maximum revenue?
Adeluxe models
standard models
What is the maximum revenue? $

Math
Linear ProgrammingAntonio wants to invest $7600 in a savings account that pays 7.9% simple interest. How long will it take for this investment to double in value? Round your answer to the nearest tenth.
Math - Others
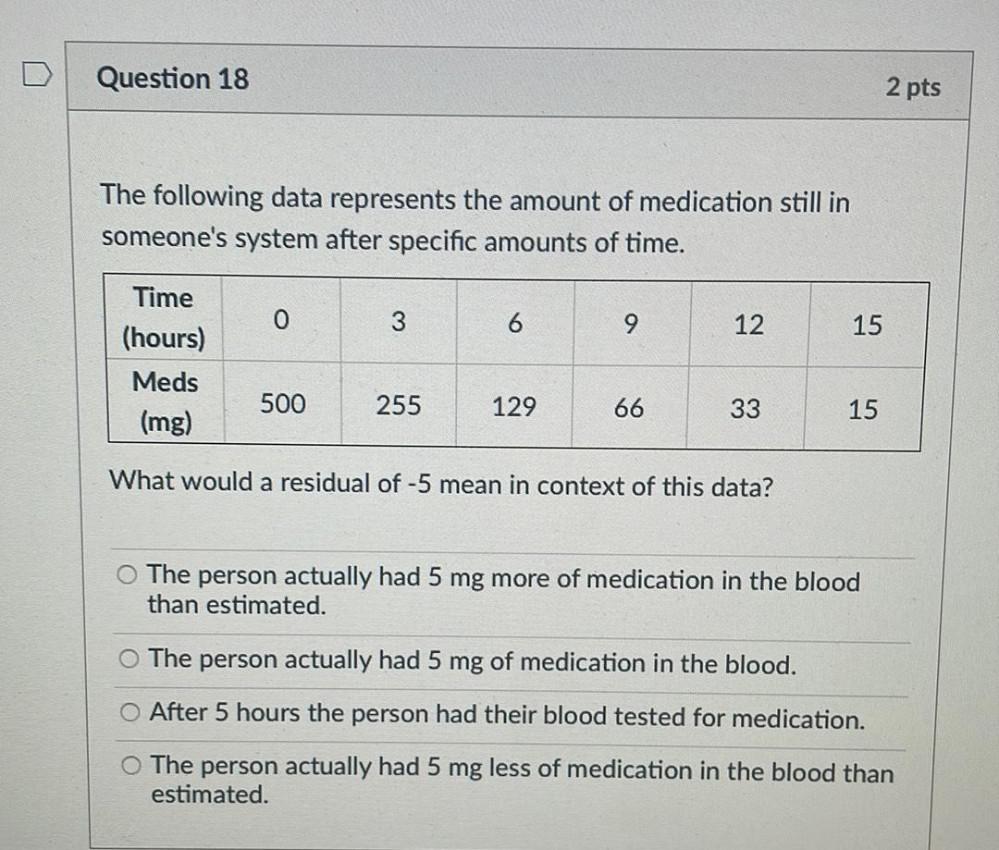
Linear ProgrammingThe following data represents the amount of medication still in someone's system after specific amounts of time.
Time
(hours) 0 3 6 9 12 15
Meds
(mg) 500 255 129 66 33 15
What would a residual of -5 mean in context of this data?
a)The person actually had 5 mg more of medication in the blood than estimated.
b)The person actually had 5 mg of medication in the blood.
c)After 5 hours the person had their blood tested for medication.
d)The person actually had 5 mg less of medication in the blood than estimated.
Math
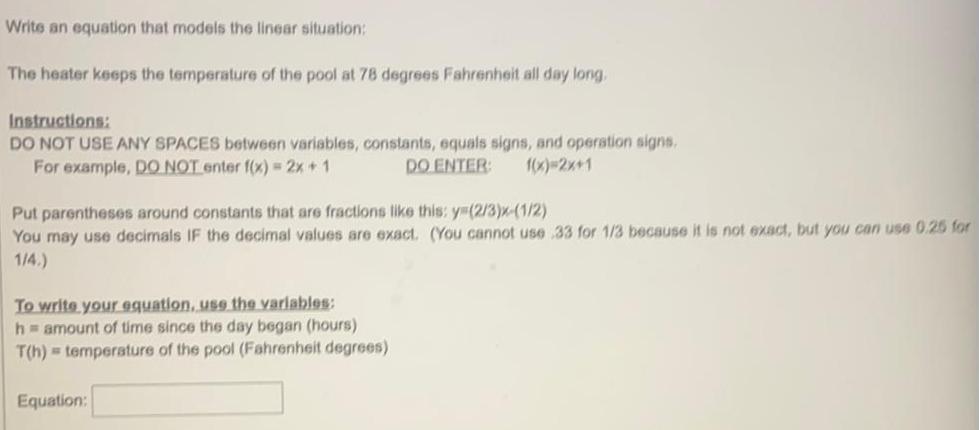
Linear ProgrammingWrite an equation that models the linear situation:
The heater keeps the temperature of the pool at 78 degrees Fahrenheit all day long.
Instructions:
DO NOT USE ANY SPACES between variables, constants, equals signs, and operation signs.
For example, DO NOT enter f(x) = 2x + 1
DO ENTER: f(x)=2x+1
Put parentheses around constants that are fractions like this: y=(2/3)x-(1/2)
You may use decimals IF the decimal values are exact. (You cannot use 33 for 1/3 because it is not exact, but you can use 0.25 for
1/4.)
To write your equation, use the variables:
h = amount of time since the day began (hours)
T(h) temperature of the pool (Fahrenheit degrees)
Equation:

Math
Linear ProgrammingWrite a program that uses a two-dimensional array to store the highest and lowest
temperatures for each month of the year. The program should output the average high,
average low, and the highest and lowest temperatures for the year. Your program must
consist of the following functions:
1. Function getData: This function reads and stores data in the two-dimensional array.
2. Function averageHigh: This function calculates and returns the aver- age high
temperature for the year.
3. Function averageLow: This function calculates and returns the average low
temperature for the year.
4. Function indexHighTemp: This function returns the index of the highest high
temperature in the array.
5. Function indexLowTemp: This function returns the index of the lowest low
temperature in the array.
These functions must all have the appropriate parameters.
Math
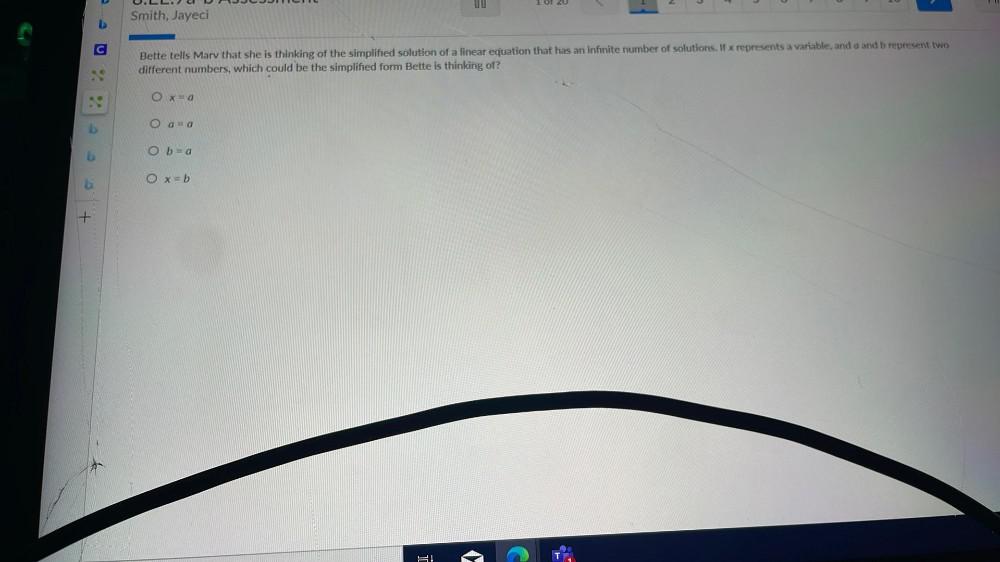
Linear ProgrammingBette tells Marv that she is thinking of the simplified solution of a linear equation that has an infinite number of solutions. If x represents a variable, and a and b represent two different numbers, which could be the simplified form Bette is thinking of?
x=a
a=a
b=a
x=b
![For the game, if a saddle point exists, find the strategies producing it and the value of the game. Identify whether the game is strictly determined
[-2 1]
[9 4]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A). The saddle point(s) is/are produced by the strategies described by the ordered pair(s)____ The value of the game is_____
B). There is no saddle point](https://media.kunduz.com/media/sug-question/raw/77323445-1658842248.256956.jpeg?w=256)
Math
Linear ProgrammingFor the game, if a saddle point exists, find the strategies producing it and the value of the game. Identify whether the game is strictly determined
[-2 1]
[9 4]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A). The saddle point(s) is/are produced by the strategies described by the ordered pair(s)____ The value of the game is_____
B). There is no saddle point

Math
Linear ProgrammingNettie's Bargain Clothing is having a huge sale. All shirts are $3 each and all pants are $5 each. You go to the sale and buy twice as many shirts as pants and spend $66.
a)Write a system of equations that models this situation where s = number of shirts and p = number of pants
Equation 1:
Equation 2:
b) Solve this system using substitution to determine how many of each item you bought. Write your answer in a complete sentence.
You bought ___pairs of pants and ______shirts.
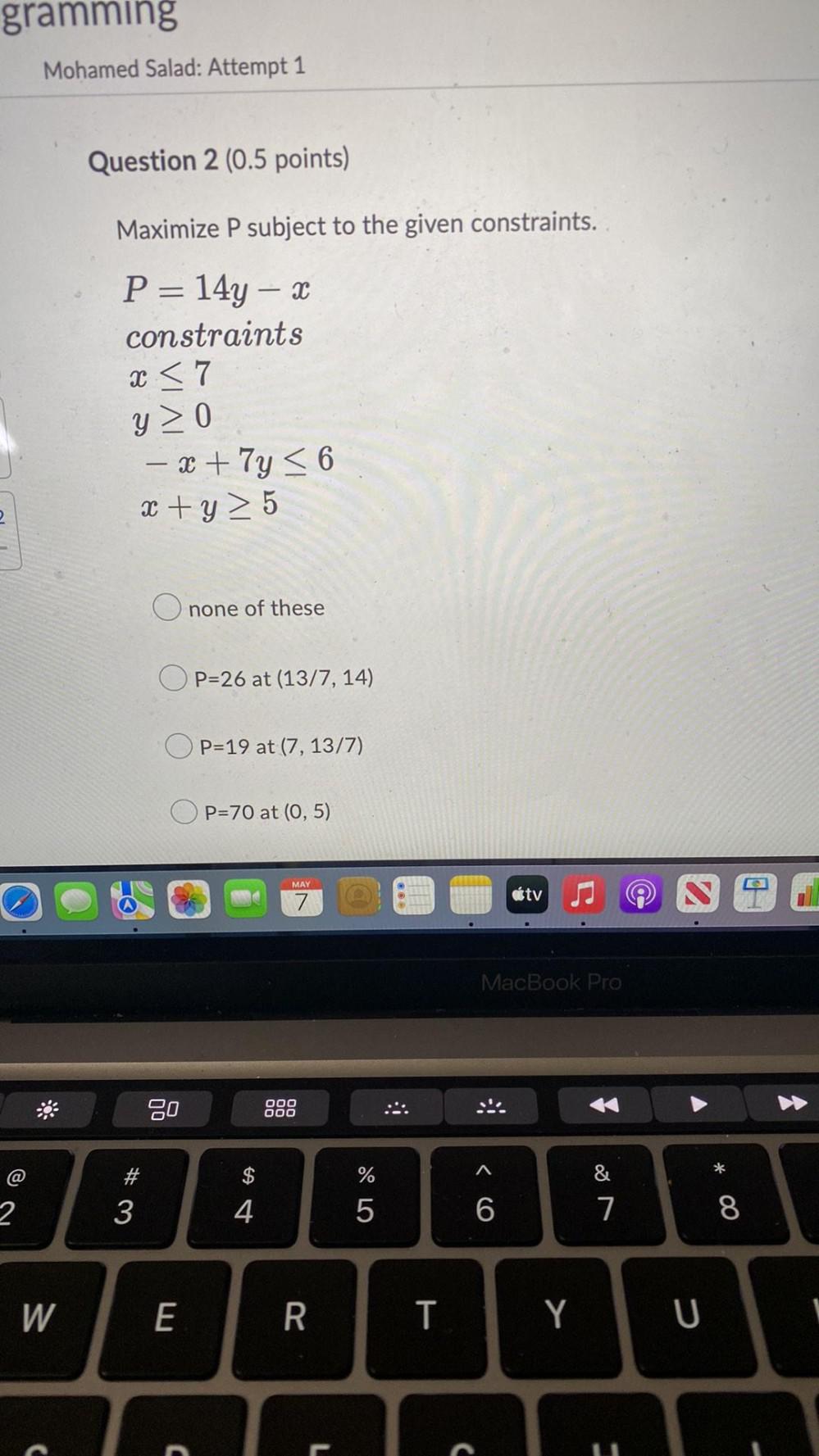
Math
Linear ProgrammingMaximize P subject to the given constraints. P= 14y – x constraints
x ≤ 7
y ≥ 0
-x + 7y ≤ 6
x +y ≥ 5
a. none of these
b. P = 26 at (13/7, 14)
c. P = 19 at (7, 13/7)
d. P = 70 at (0,5)

Math
Linear ProgrammingSweet-Fit jeans has a factory that makes two styles of jeans; Super-Fit and Super-Hug. Each pair of Super-Fit takes 12 minutes to cut and 15 minutes to sew and finish. Each pair of Super-Hug takes 12 minutes to cut and 40 minutes to sew and finish. The plant has enough workers to provide at most 12,599 minutes per day for cutting and at most 28,249 minutes per day for sewing and finishing. The profit on each pair of Super-Fit is $6.50 and the profit on each pair of Super-Hug is $8.50. How many pairs of each style should be produced per day to obtain maximum profit? Find the maximum daily profit.
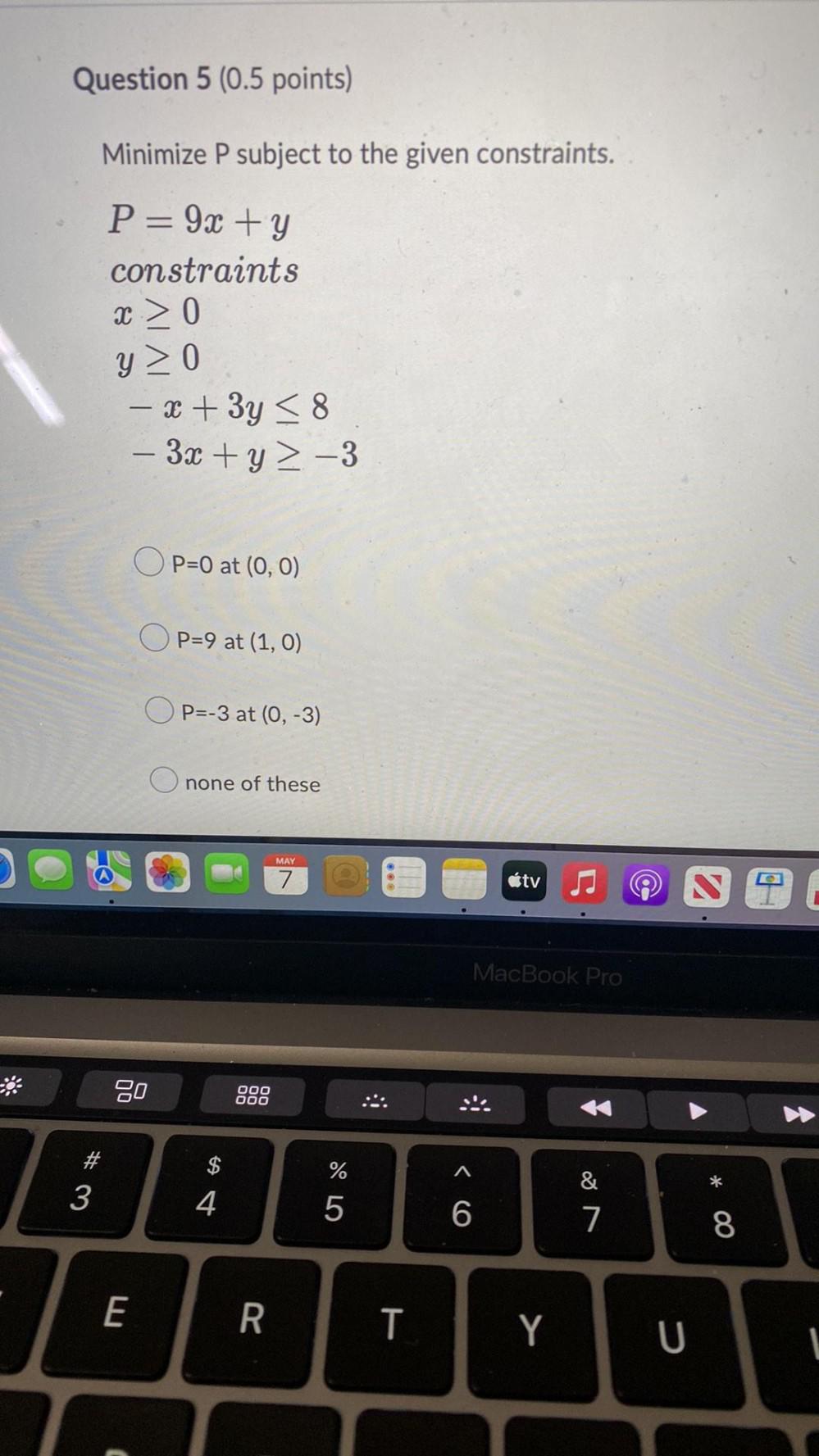
Math
Linear ProgrammingMinimize P subject to the given constraints.
P= 9x + y constraints
x ≥ 0
y ≥ 0
-x + 3y ≤ 8
-3x + y ≥ -3
a. P=0 at (0, 0)
b. P=9 at (1, 0)
c. P=-3 at (0, -3)
d. none of these

Math
Linear ProgrammingWrite a system of equations in two variables and solve. 1500 concert tickets were sold for a jazz festival. Tickets cost $25 for covered seats and $15 for lawn seats. Total receipts were $28,500. How many of each type of ticket were sold?
System of equations:
Number of tickets sold for covered seats:
Number of tickets sold for lawn seats:
Math
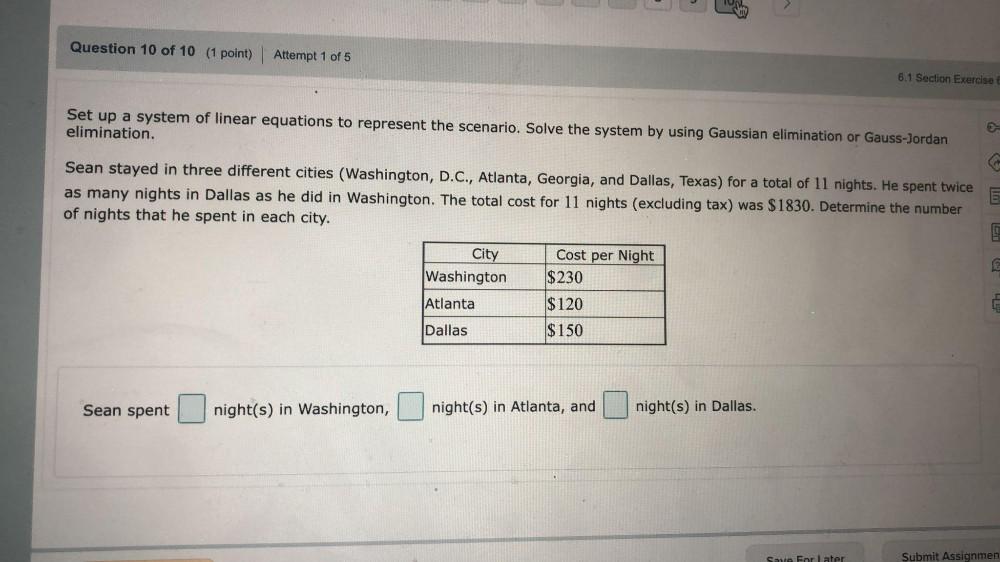
Linear ProgrammingSet up a system of linear equations to represent the scenario. Solve the system by using Gaussian elimination or Gauss-Jordan elimination. Sean stayed in three different cities (Washington, D.C., Atlanta, Georgia, and Dallas, Texas) for a total of 11 nights. He spent twice as many nights in Dallas as he did in Washington. The total cost for 11 nights (excluding tax) was $1830. Determine the number of nights that he spent in each city.
City Cost per Night
Washington $230
Atlanta $120
Dallas $150
Sean spent _____ night(s) in Washington, ______ night(s) in Atlanta, and ______ night(s) in Dallas.

Math
Linear ProgrammingGraph the following inequality.
4x + 2y > -4
Use the graphing tool to graph the inequality.

Math
Linear ProgrammingCDs can be manufactured for $0.19 each. The development cost is $210,000. The first 500 discs are samples and will not be sold. Write function for the average cost of a disc that is not a sample. What is the average cost if 5000 discs are produced? Show work. How many discs must be produced to bring the average cost under $10? Show work.

Math
Linear ProgrammingUse algebra to find the point at which the line g(x)= -4/5x+19/60
f(x)= 8/3x+469/36
Write the values of x and y as reduced fractions or integers. x= y=

Math
Linear ProgrammingThe bill for parts and labor for the repair of an automobile was $355. The cost for parts was II $285. The cost of labor was $35 per hour. Let x represent the number of hours of labor. Which of these equations is correctly setup if it took 2 hours of labor to repair the car?
285 = -355 +35x
35x+285 = -355
355 = 285 + 35x
285 = 35x +355

Math
Linear Programming24. Maggie wants to make at least $200 a week and can work no more than 30 hours a week. She works at the library for $8 an hour and babysits for $6 an hour. What system of inequalities shows the possible combination of hours and jobs she can work?

Math
Linear ProgrammingAn antique dealer stores her trunks in a shed that is 80 square feet. There are two sizes of trunks, trunk A takes up 6 square feet of space and trunk B takes up 5 square feet of space. The shed can hold a maximum of 10 trunks. If x is the number of trunk A and y is the number of trunk B, which constraint below shows the total number of trunks that the shed can hold?
Math
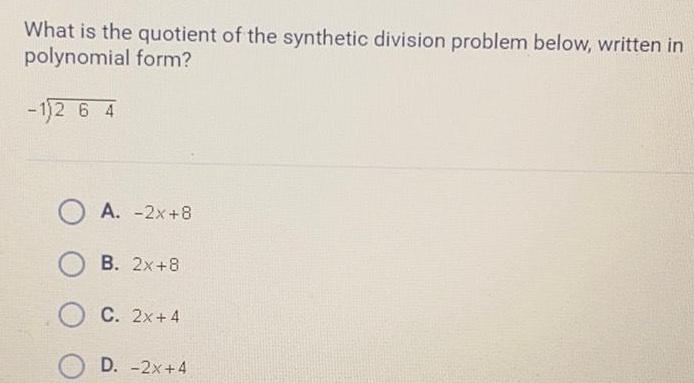
Linear ProgrammingWhat is the quotient of the synthetic division problem below, written in polynomial form?
-1√264
A. -2x+8
B. 2x+8
C. 2x+4
D. -2x+4
Math
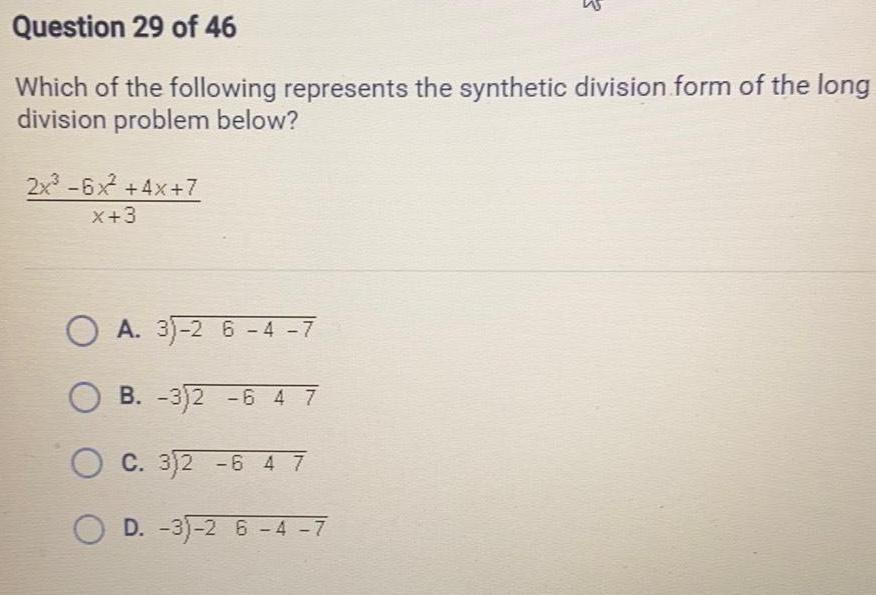
Linear ProgrammingWhich of the following represents the synthetic division form of the long division problem below?
2x³ -6x² +4x+7/x+3
A. 3√-2 6-4 -7
B. -3√2 -6 4 7
C. 3√2 -6 47
D. -3√-2 6-4 -7

Math
Linear ProgrammingWhen using the rational root theorem, which of the following is a possible root of the polynomial function below?
F(x) = 3x³x² + 4x +5
A. -5/3
B. -7
O C. 4/3
D. 6

Math
Linear ProgrammingSolve the quadratic equation using completing the square: x² - 12x + 23 = 0
x=-6+ √59 or x = -6-√√/59
x=6+ √13 or x = 6 - √13
x = 6 + √59 or x = 6 -√√59
x=-6+√13 or x = -6 -√13

Math
Linear ProgrammingA carpool service has 2,000 daily riders. A one-way ticket costs $5.00. The service estimates that for each $1.00 increase to the one-way fare 100 passengers will find other means of transportation. Let x represent the number of $1.00 increases in ticket price. Choose the inequality to represent the values of x that would allow the carpool service to have revenue of at least $12,000. Then, use the inequality to select all the correct statements.
The price of a one-way ticket that will maximize revenue is $7.50.
100x^2 + 1,500x - 10,000 ≤ 12,000
100x^2 - 1,500x - 10,000 ≥ 12,000
-100x^2 + 1,500x + 10,000 ≥ 12,000
The maximum profit the company can make is $15,625.00.
The maximum profit the company can make is $4,125.00.
The price of a one-way ticket that will maximize revenue is $12.50.

Math
Linear ProgrammingThe variables x and y. and y vary inversely, and y = 10 when z = 5.
Write an equation that relates x and y. y = k/x
Then find y when x = -2


Math
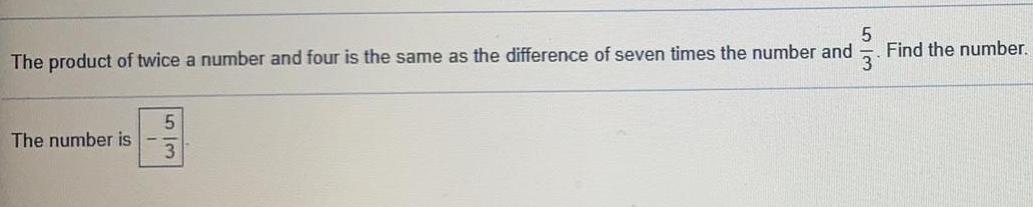
Linear ProgrammingThe product of twice a number and four is the same as the difference of seven times the number and 5/3 Find the number.
Math
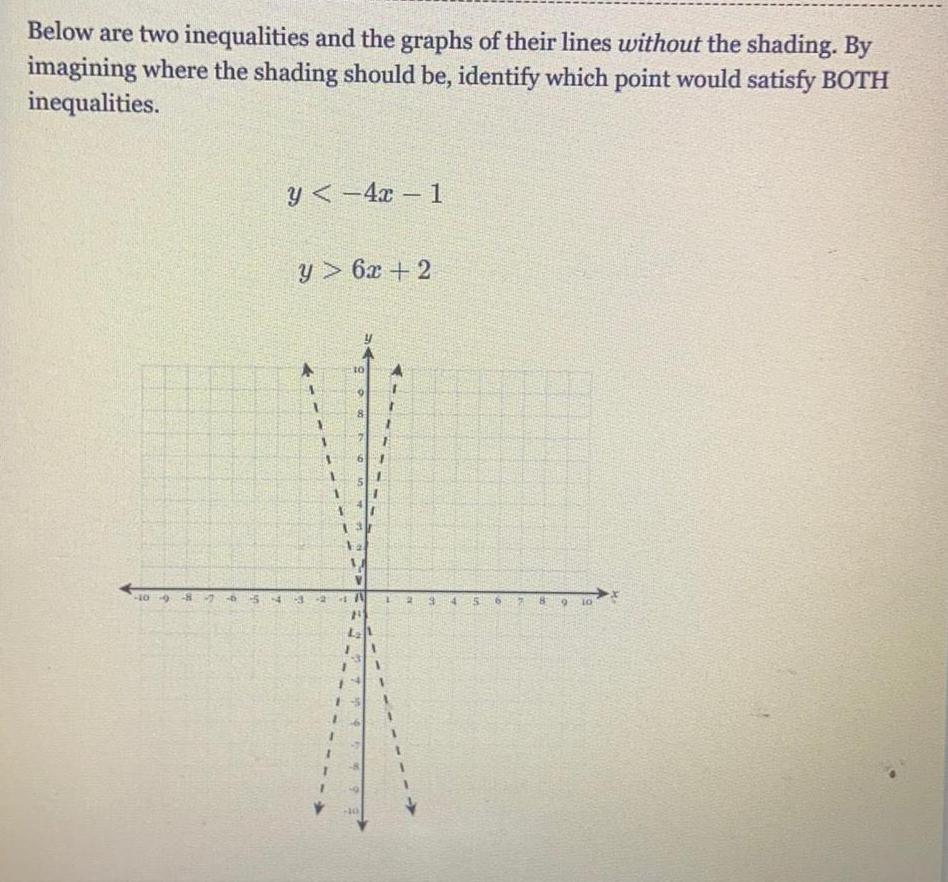
Linear ProgrammingBelow are two inequalities and the graphs of their lines without the shading. By imagining where the shading should be, identify which point would satisfy BOTH inequalities.

Math
Linear ProgrammingA new car worth $21,000 is depreciating in value by $3000 per year. Complete parts (a) through (6).
a. Write a formula that models the car's value, y, in dollars, after x years,
b. Use the formula from part (a) to determine after how many years the car's value will be 39,000.
6. Graph the formula from part (a) in the first quadrant of a rectangular coordinate system. Then, show your solution to part (b) on the graph.
a. A formula that models the car's value, y, in dollars, after years is
(Type an equation.)