Logarithms Questions and Answers

Math
LogarithmsGive the growth factor b, the starting value a, the growth rate r, and the value of k
whenQ is written in the form Q = a ekt. If there is exponential decay, then your
growth rate should be negative. For help entering logarithms, see help (logarithms)
Q = 250 (1.271)t has:

Math
LogarithmsRewrite the following statement using a natural logarithm. Fill
in each blank with the appropriate letter or number.
≈ 0.0183 is equivalent to In (

Math
LogarithmsThe sales of lawn mowers t years after a particular model is introduced is given by the function y = 5500 In (9t + 4), where y is the number of mowers sold. How many mowers will be sold 6 years after a model is introduced?
Round the answer to the nearest whole number.
21,943 mowers
43,939 mowers
22,332 mowers
9698 mowers
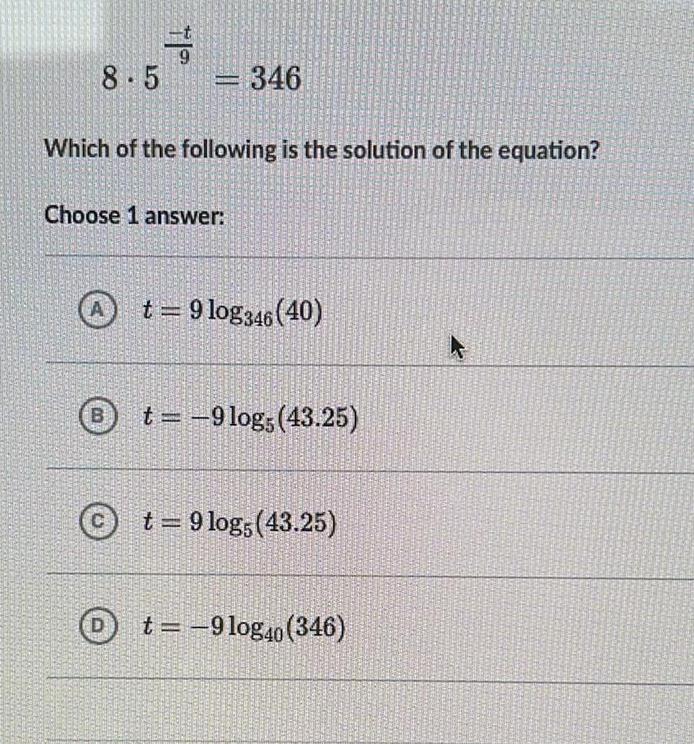
Math
Logarithms8.5^-t/9= 346
Which of the following is the solution of the equation?
Choose 1 answer:
A
t = 9 log346 (40)
t= -9 log5 (43.25)
t = 9 log5 (43.25)
t = -9 log40 (346)

Math
LogarithmsA 33 gram sample of a substance that's used to detect explosives has a k-value of 0.1473.
N= Noe^-kt
N0= initial mass (at time t = 0)
N= mass at time t
k=a positive constant that depends on the substance itself and on the units used to measure time
t=time, in days
Find the substance's half-life, in days.
Round your answer to the nearest tenth.

Math
LogarithmsA country's population in 1994 was 76 million. In 1998 it was 81 million. Estimate the population in 2016 using the exponential growth formula. Round your answer to the nearest million. P = Aekt

Math
LogarithmsA country's population in 1995 was 32 million. In 1997 it was 34 million, Estimate the population in 2003 using the exponential growth formula. Round your answer to the nearest million. P = Ae^kt

Math
LogarithmsThe decibel rating D is related to the sound intensity I by the formula D = 10 log10(I/10^-16)for the noise level in decibels.
(a) Let D and d represent the decibel ratings of sounds of intensity I and i, respectively. Using properties of logarithms, find a simplified formula for the difference between the two ratings, D-d, in terms of the two intensities I and i.
D-d=
(b) If a sound's intensity quadruples, how many decibels louder does the sound become?
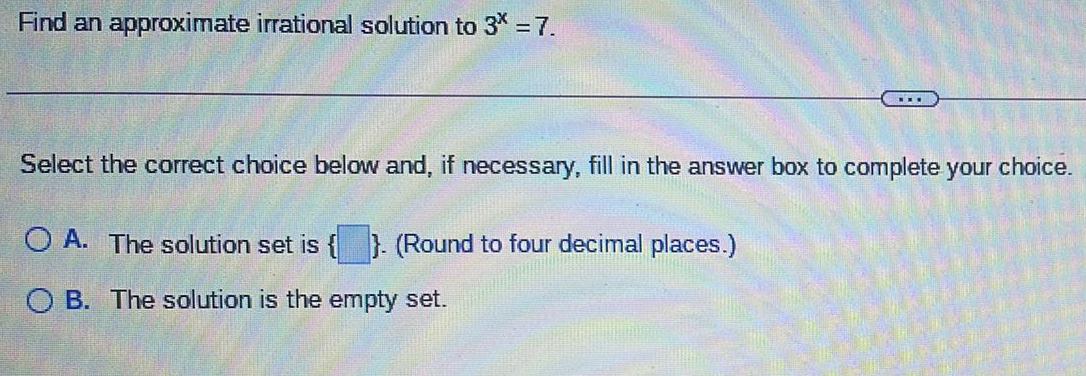
Math
LogarithmsFind an approximate irrational solution to 3* = 7.
...
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The solution set is }. (Round to four decimal places.)
OB. The solution is the empty set.

Math
LogarithmsA
Rewrite the logarithmic equation log(+2) = 2 in equivalent exponential form. There may be more than one correct answer
Az+2=e2²
B.z+2=100
DC. e²+2=²
D.z+2=10³²
DE 2+2 = log(2)
F. None of the above
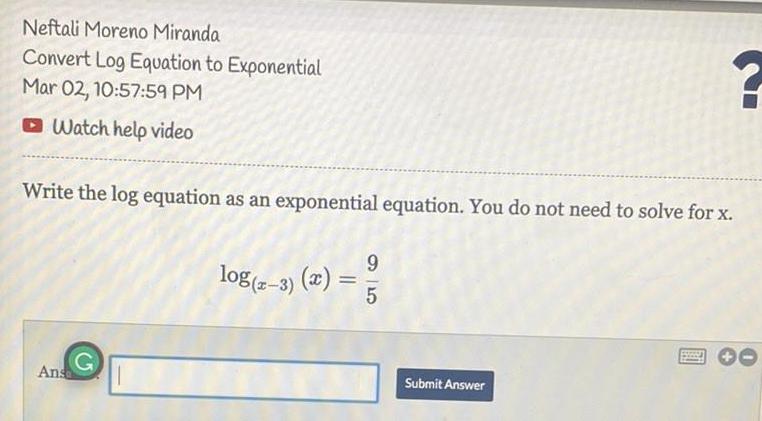
Math
LogarithmsWrite the log equation as an exponential equation. You do not need to solve for x.
log(x-3) (x)=9/5
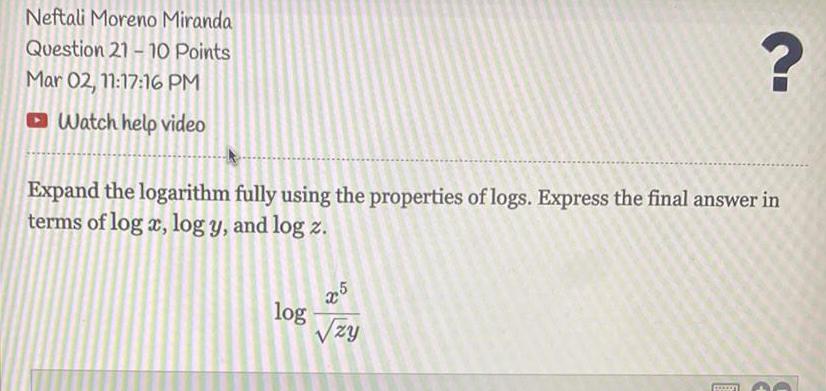
Math
LogarithmsExpand the logarithm fully using the properties of logs. Express the final answer in terms of log x, log y, and log z.
logx^5/√zy

Math
LogarithmsSuppose the supply of x units of a certain product at price p dollars per unit is given by
p = 12 + 6 In(4x + 1).
How many units of this product would be supplied when the price is $48 each? (Round your answer to the nearest whole number.)
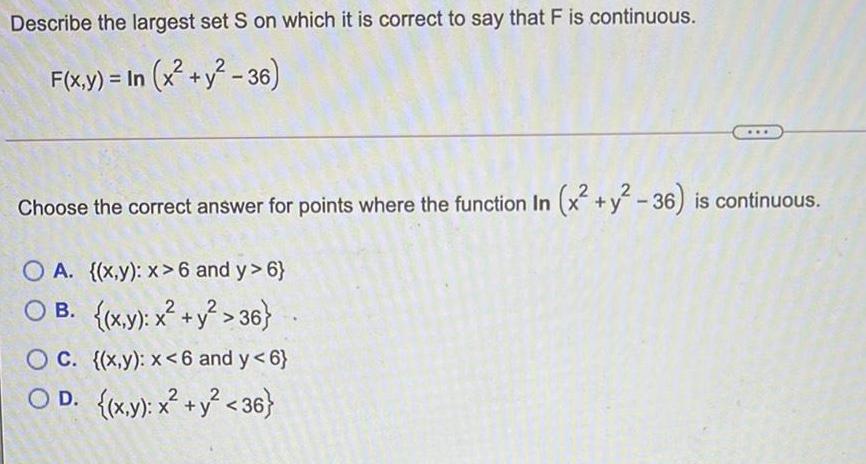
Math
LogarithmsDescribe the largest set S on which it is correct to say that F is continuous.
F(x,y)= In (x² + y²-36)
Choose the correct answer for points where the function In (x² + y² -36) is continuous.

Math
LogarithmsWhat is the meaning of the base of the function
y = log3(x)?
As y increases by 1, x increases by a factor of 3.
As y decreases by 1, x increases by a factor of 3.
As y increases by 1, x increases by 3.
As y decreases by 1, x increases by 3.

Math
LogarithmsA culture of 100 bacteria is started, and the number of bacteria will double every hour. In about how many hours will there be over 4,000,000 bacteria?
Hint: use a variation of the half-life formula
A = P(2)^1/h, where the value of h is 1.
10
4
14
16

Math
LogarithmsYour bank account is sitting on $14,000. You
started with a principal balance of $12,500. If the
interest rate was 4.5% compounded continuously,
how long was your money in the bank?
1.12 years
Less than a year
3.67 years
Approximately 2.5 years
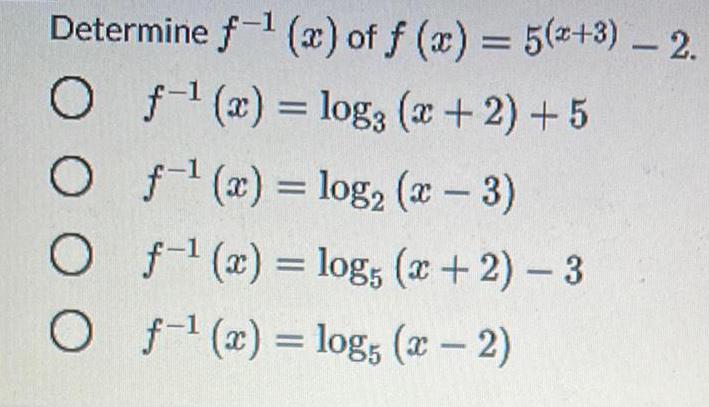
Math
LogarithmsDetermine f^-1(x) of f (x) = 5^(x+3) - 2.
f^-1(x)= log3 (x + 2) + 5
f^-1(x)= log₂ (x-3)
f^-1(x)= log5 (x+2) - 3
f^-1(x)= log5 (x - 2)
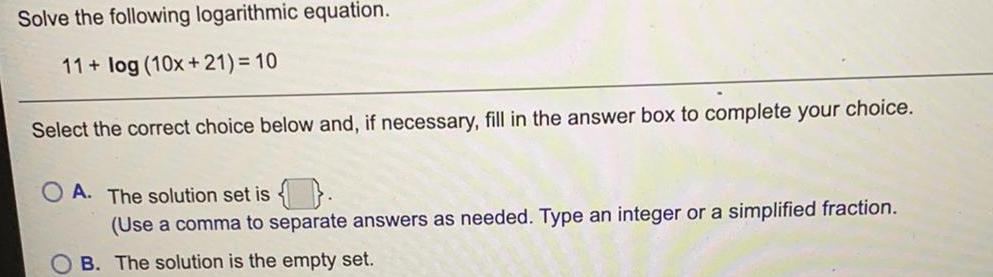
Math
LogarithmsSolve the following logarithmic equation.
11+ log (10x+21) = 10
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Use a comma to separate answers as needed. Type an integer or a simplified fraction.
B. The solution is the empty set.

Math
LogarithmsThe volume of a swimming pool being filled with water, in gallons, after t hours is modeled by the following function:
V(t) = 22,500 - 10,000e^(-0.2t)
Find the rate at which the volume of water in the pool is increasing after 10 hours.
270.6706 gal/hr
1,353.3528 gal/hr
21,146.6472 gal/hr
22,770.6706 gal/hr

Math
LogarithmsUse the properties of logarithms to completely expand ln 11y⁹/x
Do not include any parentheses in your answer.

Math
LogarithmsThe Parker family bought a house for $140,000. The value of the real estate in that town will increase by 3.1% each year.
If values continue at that rate, calculate how long it will take until the house is worth $300,000.
Round your answer to the nearest whole year when the house is worth at least $300, 000.
The house will be worth $300,000 after approximately
years.

Math
LogarithmsIn the beginning, the population of Antarctic Aardvarks was 8 million. Ever since, it has been decreasing by 8.5% every three thousand years. Write an exponential model P(t) for the population of Antarctic Aardvarks after t thousand years have passed.

Math
LogarithmsThe mass if Missy's megafis increases according to the exponential model:
M(t) = 12(1.24)^t/7+3
Where t is the number of days elapsed. By what percent does the mass of Missy's megafish increase each and every day? Express as a percent rounded to two decimal places.

Math
LogarithmsSuppose that $2060 is deposited into an account where the interest is compounded annually.
This situation can be modeled by the function
P (t) = 2060(1.018)^t where P(t) represent the value (in dollars) of the account at t years
after depositing the $2060.
In how many years will the money in the account double? {your final answer just number
without decimal}

Math
LogarithmsSuppose that a new employee starts working at $7.52 per hour, and receives a 4% raise each year. After time t, in years, his hourly wage is given by the function
P(t) = $7.52(1.04)t
a) Find the amount of time after which he will be earning $10.00 per hour.
b) Find the doubling time.
After what amount of time will the employee be earning $10.00 per hour?
(Round to the nearest tenth of a year.)
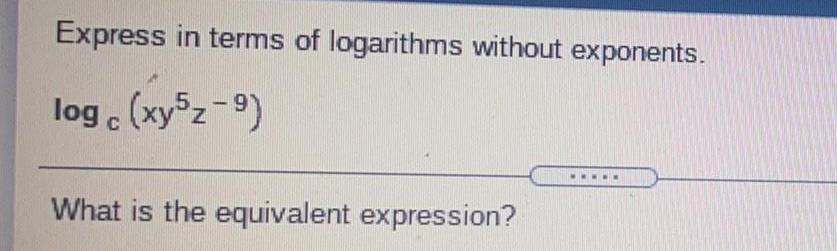
Math
LogarithmsExpress in terms of logarithms without exponents.
log c (xy5z-9)
What is the equivalent expression?


Math
LogarithmsA student was asked to determine the y-intercept for the logarithmic function f(x) = log3(x +2) + 1. Which of the following expressions would result in the correct y-intercept?
log2/log3+1
log3/log2+1
(3)-1-2
(-1)3-2

Math
LogarithmsPainful bone metastases are common in advanced prostate cancer. Physicians often order treatment with strontium-89 (89 Sr), a radionuclide with a strong affinity for bone tissue. A patient is given a sample containing 4 mCi of 89Sr
Part 1 of 2
(a) If 30% of the Sr remains in the body after 90 days, write a function of the form Q(t) = Q0e-kt to model the amount (t) of radioactivity in the body t days after the initial dose. Round the value of k to five decimal places. Do not round intermediate calculations.
Q (t) =
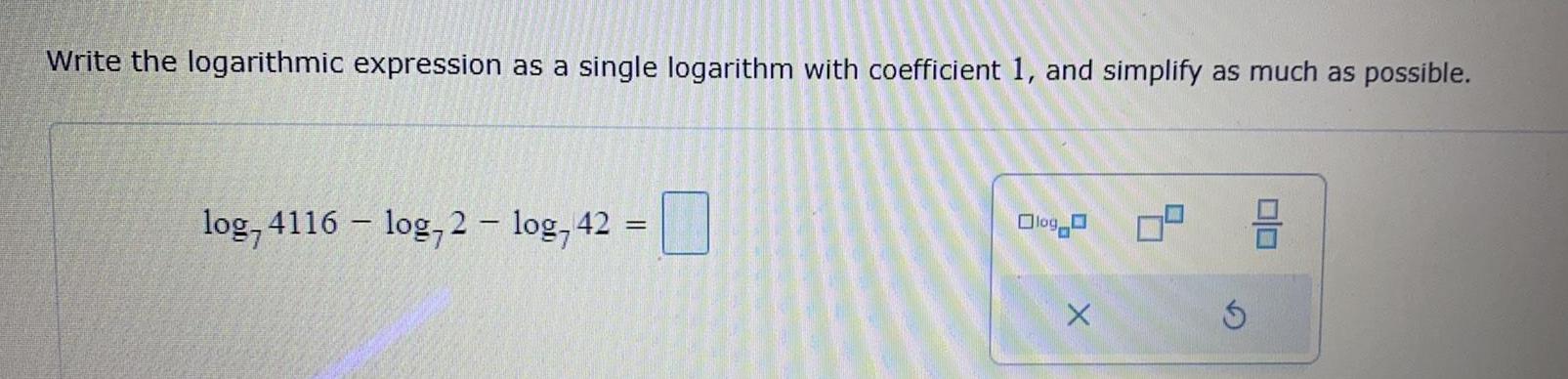
Math
LogarithmsWrite the logarithmic expression as a single logarithm with coefficient 1, and simplify as much as possible.
log7(4116 )-log7(2) - log,7(42) =

Math
LogarithmsA can of soda is placed inside a cooler. As the soda cools, its temperature 7(x) in degrees Celsius is given by the following function, where x is the number of
minutes since the can was placed in the cooler.
T(x)= 8+26e -0.038x
Find the initial temperature of the soda and its temperature after 18 minutes.
Round your answers to the nearest degree as necessary.
Initial temperature:
Temperature after 18 minutes:

Math
LogarithmsUsing the formula R = log ( x/0.001), where x is the seismographic reading in millimeters, and R is the magnitude of the earthquake on the Richter scale, determine the magnitude of an earthquake with a seismographic reading of 23,750 mm.

Math
LogarithmsThe count in a bacteria culture was 100 after 20 minutes
and 1800 after 40 minutes. Assuming the count grows
exponentially,
What was the initial size of the culture?
Find the doubling period.
Find the population after 110 minutes.
When will the population reach 10000.

Math
LogarithmsYou go to the doctor and he gives you 10 milligrams of radioactive dye. After 24 minutes, 6.5 milligrams of dye remain in your system. To leave the doctor's office, you must pass through a radiation detector without sounding the alarm. If the detector will sound the alarm if more than 2 milligrams of the dye are in your system, how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived? Give your answer to the nearest minute.
You will spend minutes at the doctor's office.
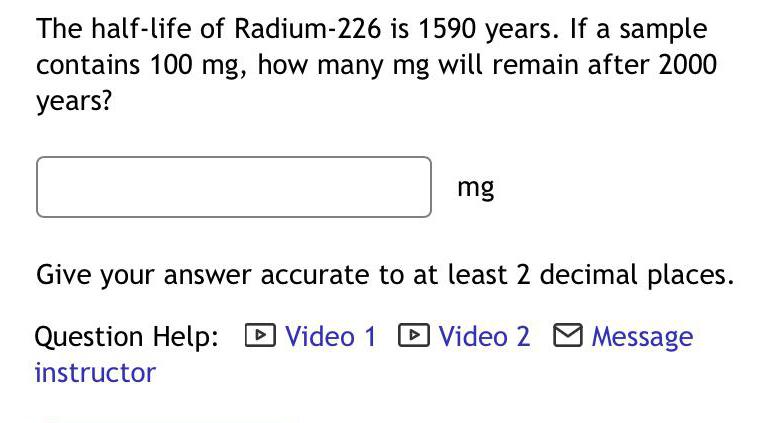
Math
LogarithmsThe half-life of Radium-226 is 1590 years. If a sample
contains 100 mg, how many mg will remain after 2000 years?
mg
Give your answer accurate to at least 2 decimal places.
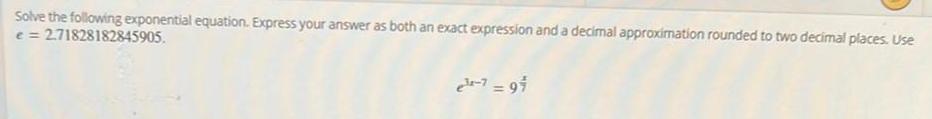
Math
LogarithmsSolve the following exponential equation. Express your answer as both an exact expression and a decimal approximation rounded to two decimal places. Use e = 2.71828182845905.
e 3x-7 = 9 x/7
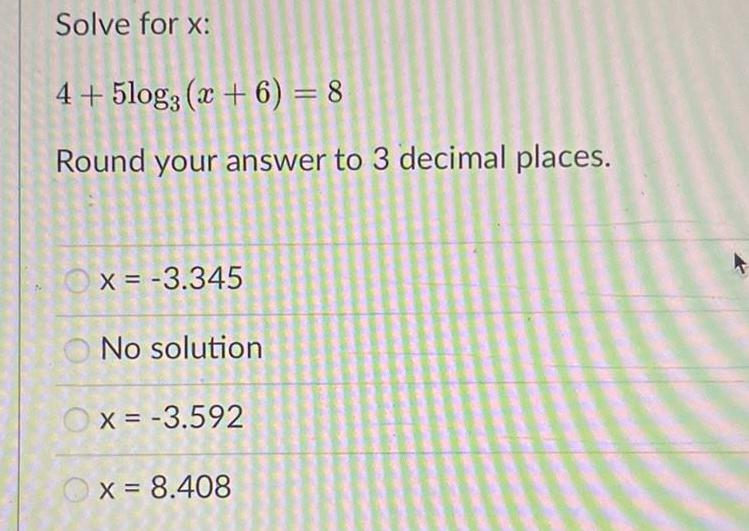
Math
LogarithmsSolve for x:
4 + 5log3(x + 6) = 8
Round your answer to 3 decimal places.
x = -3.345
No solution
x= -3.592
x = 8.408
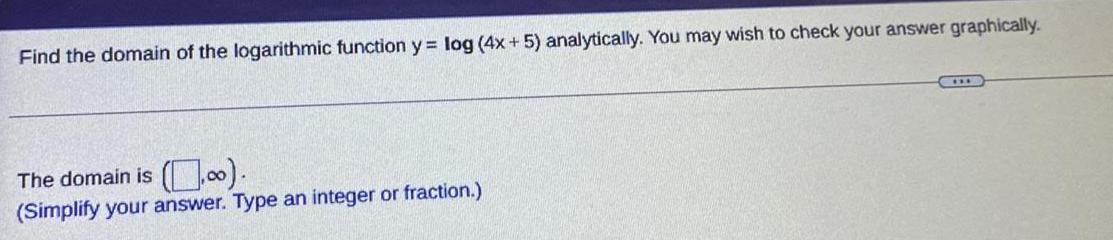
Math
LogarithmsFind the domain of the logarithmic function y = log (4x + 5) analytically. You may wish to check your answer graphically.
The domain is ( , ∞).
(Simplify your answer. Type an integer or fraction.)
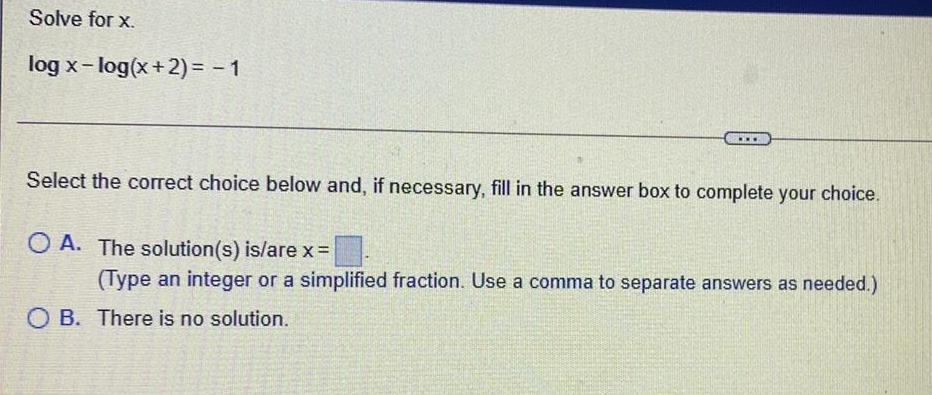
Math
LogarithmsSolve for x.
log x-log(x+2) = -1
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution (s) is/are x =
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)
B. There is no solution.
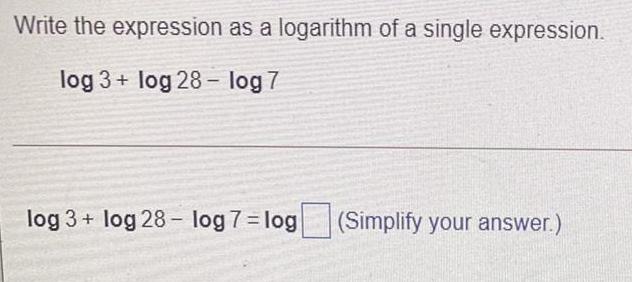
Math
LogarithmsWrite the expression as a logarithm of a single expression.
log 3+ log 28-log 7
log 3+ log 28 log 7 = log (Simplify your answer.)
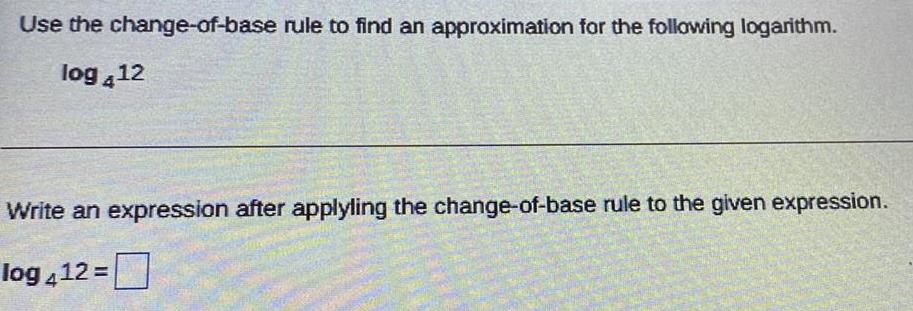
Math
LogarithmsUse the change-of-base rule to find an approximation for the following logarithm.
log 4 12
Write an expression after applyling the change-of-base rule to the given expression.
log 4 12=
![Tests show that the hydrogen ion concentration of a sample of apple juice is 0.0003 and that of ammonia is 1.3 x 10^(-9). Find the approximate pH of each liquid using the formula PH = -log [H+], where [H+] is the hydrogen ion concentration.](https://media.kunduz.com/media/sug-question/raw/65965101-1657090168.8946438.jpeg?w=256)
Math
LogarithmsTests show that the hydrogen ion concentration of a sample of apple juice is 0.0003 and that of ammonia is 1.3 x 10^(-9). Find the approximate pH of each liquid using the formula PH = -log [H+], where [H+] is the hydrogen ion concentration.
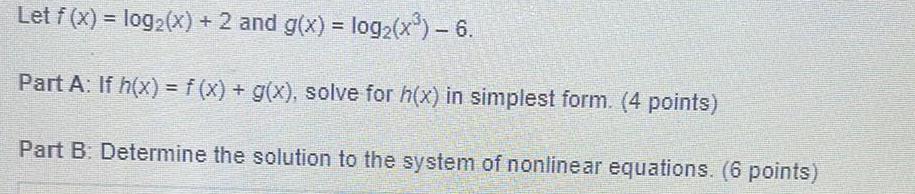
Math
LogarithmsLet f(x) = log₂ (x) + 2 and g(x) = log₂ (x³) - 6.
Part A: If h(x) = f(x) + g(x), solve for h(x) in simplest form. (4 points)
Part B: Determine the solution to the system of nonlinear equations. (6 points)
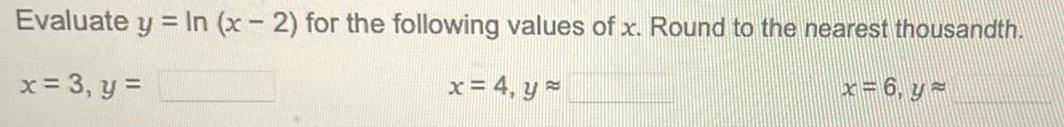
Math
LogarithmsEvaluate y = In (x-2) for the following values of x. Round to the nearest thousandth.
x = 3, y =
x = 4, y =
x = 6, y =