Parabola Questions and Answers

Math
ParabolaWrite the equation of the parabola in intercept form.
y = x² + 7x + 12
y=(x+4)(x+3)
y=(x-4)(x-3)
y=(x-6)(x-2)
y=(x+6)(x+2)

Math
ParabolaGraph the function. Label the vertex, axis of
symmetry, and x-intercepts.
y = 2(x + 2)(x+4)

Math
ParabolaConsider the quadratic function: f(x)
A) The line of symmetry:
B) The vertex:
=
- 2x² - 10x + 12. Find the following for this parabola.
C) The vertical intercept is the point
D) Find the coordinates of the two x intercepts of the parabola and write them as a list, separated by
commas:
Round your values to two decimal places for this part, if the roots are irrational.

Math
ParabolaA dolphin dives down into the ocean and resurfaces along a path that is modeled by x2 - 8x + 4y = 0, where the distances are in feet. How many feet is the dolphin from its
starting point along the water's surface?
8 feet
6 feet
4 feet
0 feet

Math
ParabolaLyra is designing a model of a solar system with a planet and a comet. The planet has a circular orbit, centered at the origin with a diameter of 140. The comet follows a
parabolic path with directrix x = 100 and vertex at (85, 0).
Part A: Write the equation of the planet's orbit in standard form. Show your work. (2 points)
Part B: Write the equation of the comet's path in standard form. Show your work. (4 points)
Part C: Identify all points where the planet's orbit intersects the path of the comet. Show your work and round answers to the hundredths place. (4 points)

Math
ParabolaThe quadratic function whose graph is a bar parabola that opens upward has a minimum value, and the quadratic function whose graph is a parabola that opens downward has a maximum value. The f(x)- or y-value of the vertex is the minimum, or maximum value of the function.

Math
ParabolaYou're at the aquarium, staring into a large exhibit, when
you look to your left and slightly downward and you see a
jellyfish. You notice that the jellyfish body looks like a very
wide, upside-down parabola. What is a possible equation
that models the jellyfish, assuming your eyes are at (0, 0)?
a) -2(x + 3)² + 4
-.3(x - 2)² - 1
2/5(x + 1)²-5
.3(x-4)² + 2
Answer is not there

Math
ParabolaGraph the quadratic function in standard form y = 2(x - 1)² - 8
A. Find the x-intercept(s).
B. Find the y-intercept.
C. Find the coordinates of the vertex.
D. Graph the equation and label the vertex, intercepts you found above, and the equation of the axis of symmetry.
E. Write the equation of the axis of symmetry.
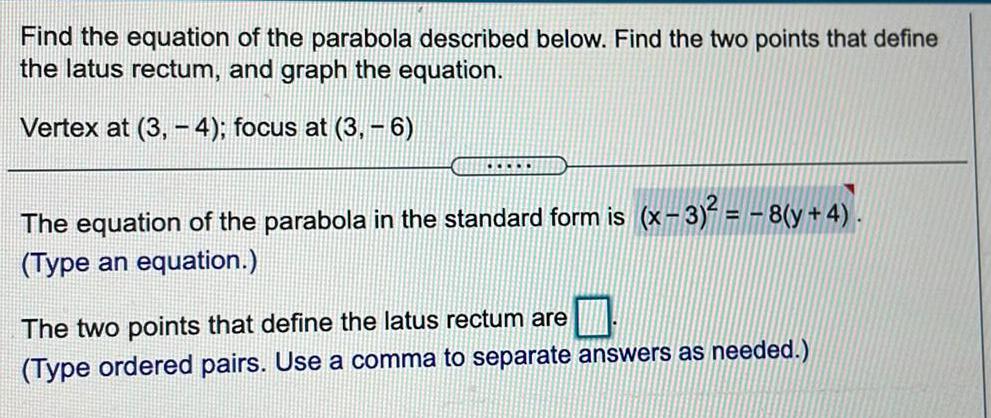
Math
ParabolaFind the equation of the parabola described below. Find the two points that define
the latus rectum, and graph the equation.
Vertex at (3, 4); focus at (3, −6)
CHICKE
The equation of the parabola in the standard form is (x − 3)² = − 8(y + 4).
(Type an equation.)
The two points that define the latus rectum are
(Type ordered pairs. Use a comma to separate answers as needed.)

Math
ParabolaFind the equation of the parabola described. Find the two points that define the
latus rectum, and graph the equation.
3
Directrix the line y=; vertex at (0,0)
2
.....
What is the equation of the parabola?
y=-6x²
(Use integers or fractions for any numbers in the equation.)
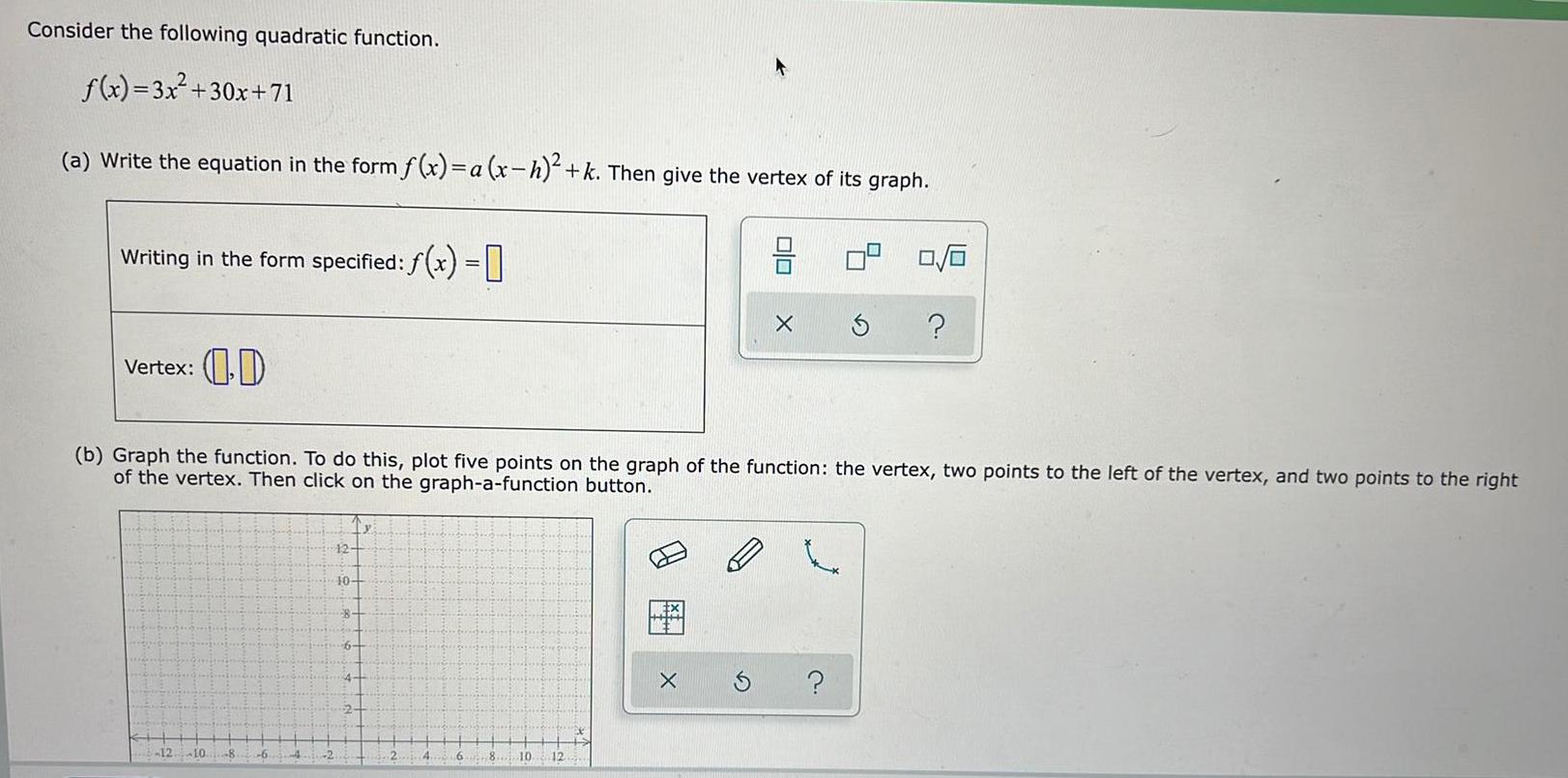
Math
ParabolaConsider the following quadratic function.
f(x)=3x²+30x+71
(a) Write the equation in the form f(x)= a (x-h)²+k. Then give the vertex of its graph.
(b) Graph the function. To do this, plot five points on the graph of the function: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function button.
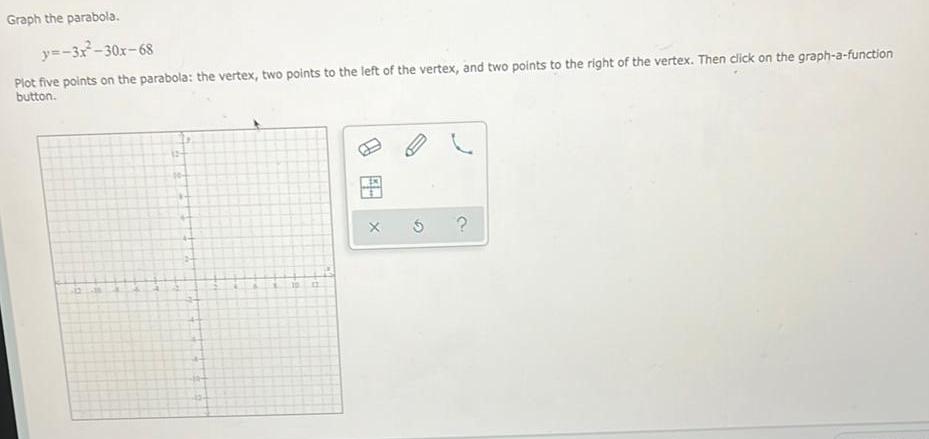
Math
ParabolaGraph the parabola. y=-3x²-30x-68
Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function button.

Math
ParabolaSketch the following parabolas, labeling the coordinates of the vertex and focus and equation of the directrix:
a. y + 2 = -1/4 (x - 1)²
Coordinates of vertex:
Coordinates of focus:
Equation of directrix:
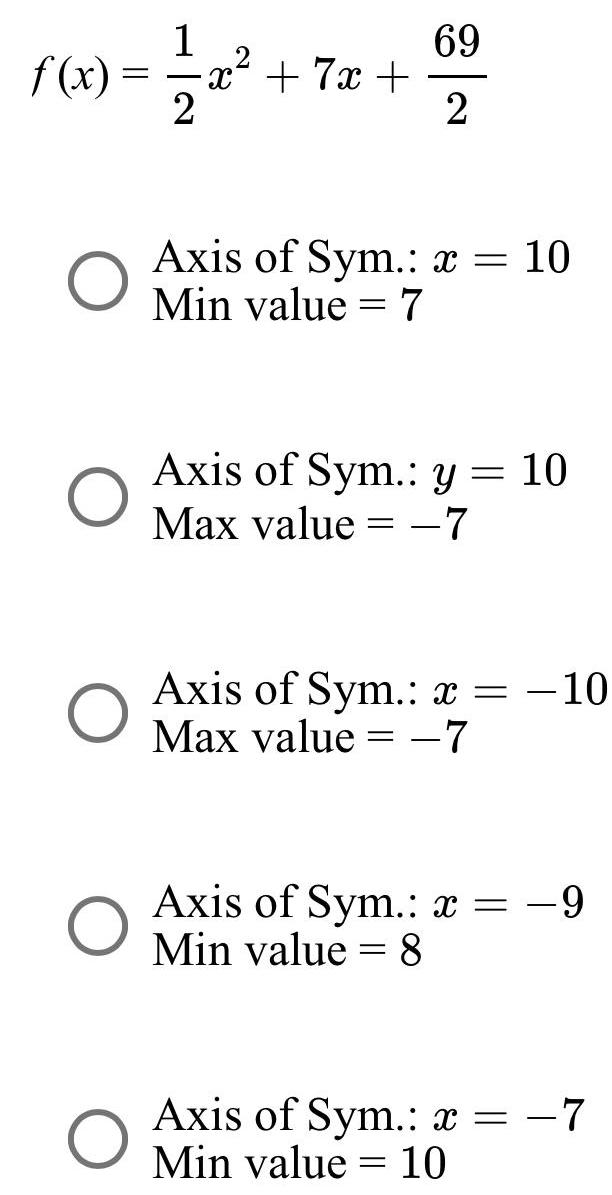
Math
Parabolaf (x)=1/2x² + 7x +69/2
Axis of Sym.: x = 10
Min value = 7
Axis of Sym.: y = 10
Max value = -7
Axis of Sym.: x = -10
Max value=—7
Axis of Sym.: x = -9
Min value = 8
Axis of Sym.: x = -7
Min value = 10
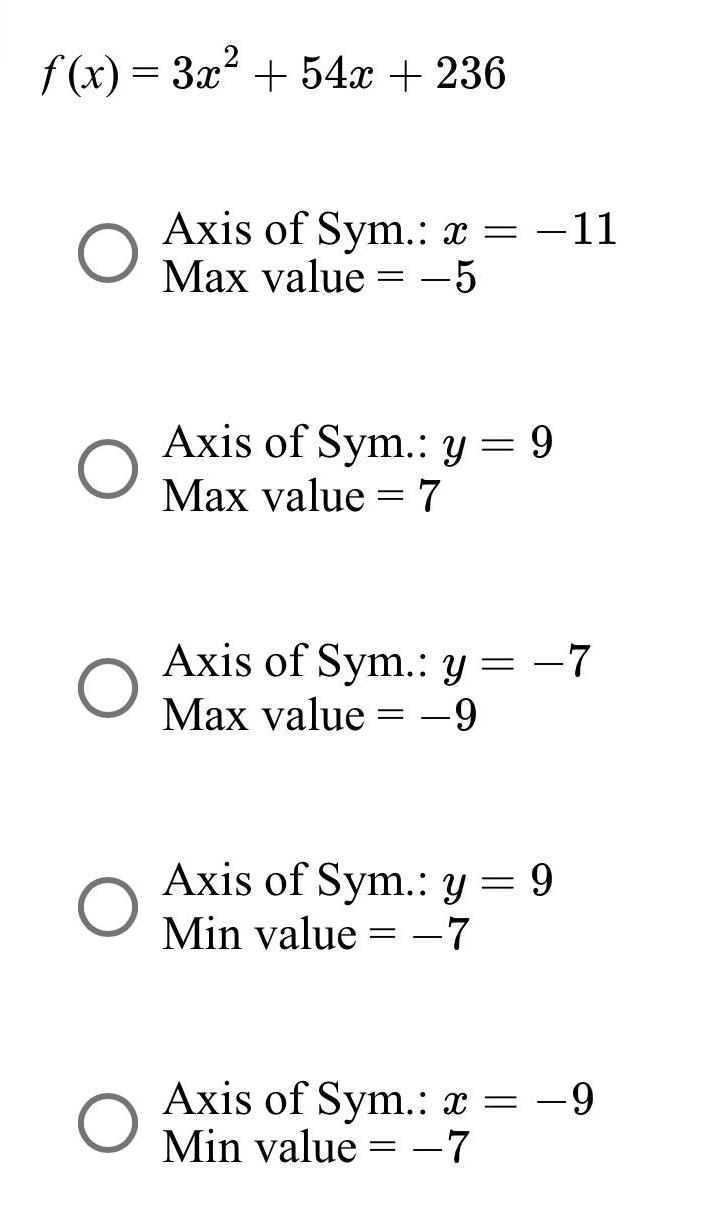
Math
Parabolaf(x) = 3x² + 54x +236
Axis of Sym.: x=-11
Max value = -5
Axis of Sym.: y = 9
Max value = 7
Axis of Sym.: y = -7
Max value = -9
Axis of Sym.: y = 9
Min value = -7
Axis of Sym.: x = -9
Min value = -7

Math
ParabolaUse the graph of the function to answer parts (a) through (1).
P(x) = -3(x+2)² +1
(a) Give the coordinates of the vertex.
The coordinates of the vertex are
(Type an ordered pair.)
(b) Give the domain and range. What is the domain of P(x)?
(Type your answer in interval notation.)
What is the range of P(x)?
(Type your answer in interval notation.)
(c) Give the equation of the axis of symmetry.
(Type an equation.)
Math
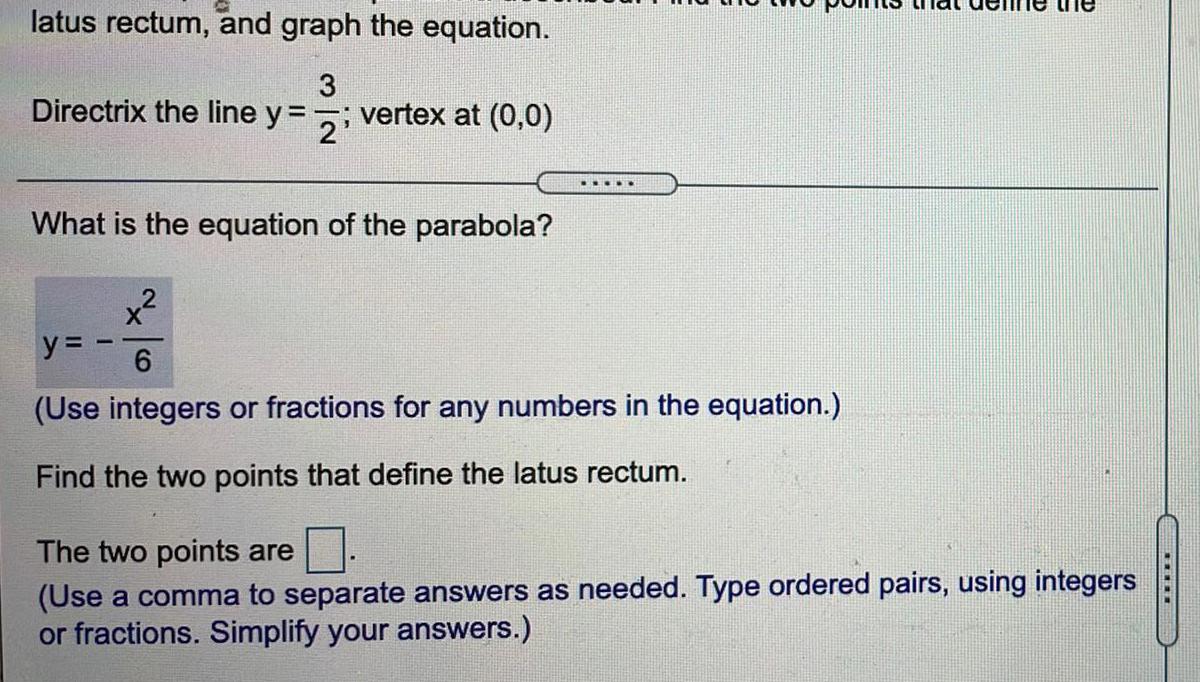
Parabolalatus rectum, and graph the equation.
3
==; vertex at (0,0)
2
Directrix the line y:
3
What is the equation of the parabola?
X
E.
y=
6
(Use integers or fractions for any numbers in the equation.)
Find the two points that define the latus rectum.
ne the
The two points are
(Use a comma to separate answers as needed. Type ordered pairs, using integers
or fractions. Simplify your answers.)

Math
ParabolaFor the following quadratic function, (a) write the function in the form P(x)= a(x-h)2 + k, (b) give the vertex of the parabola, and (c) graph the function.
P(x) = -2x² +10x
(a) P(x) =
(Use integers or fractions for any numbers in the expression.)

Math
ParabolaGiven a quadratic function
y = (x - 1)² -2
Complete the following tasks. (2 points each)
1. Find the vertex of the parabola.
2. Write the equation of the axis of symmetry.
3. Find the y-intercept.
4. Find the x-intercepts.
5. Show the graph of the quadratic function with at least two points on each sides of the axis of symmetry. Be sure to label the intercepts and the vertex on the graph and draw a dashed line for the axis of symmetry.

Math
ParabolaA jumping spider's movement is modeled by a parabola. The sider makes a single jump from the origin and reaches a maximum height of 20 mm halfway across a horizontal
distance of 160 mm.
Part A: Write the equation of the parabola in standard form that models the spider's jump. Show your work.
Part B: Identify the focus, directrix, and axis of symmetry of the parabola.

Math
ParabolaThe inside of a flashlight surrounding the bulb is shaped like a parabola in which the base of the bulb represents the vertex and the top of the bulb represents the focus. Which of the following standard equations represents the parabola in which the base of the bulb is at (4, 6) and top of the bulb is at (4, 3)?
(x-4)2 =-12(y-6)
(x-4)2 = -24(y - 6)
(x+4)2 = 12(y + 6)
(x+4)2 = 24(y + 6)
Math
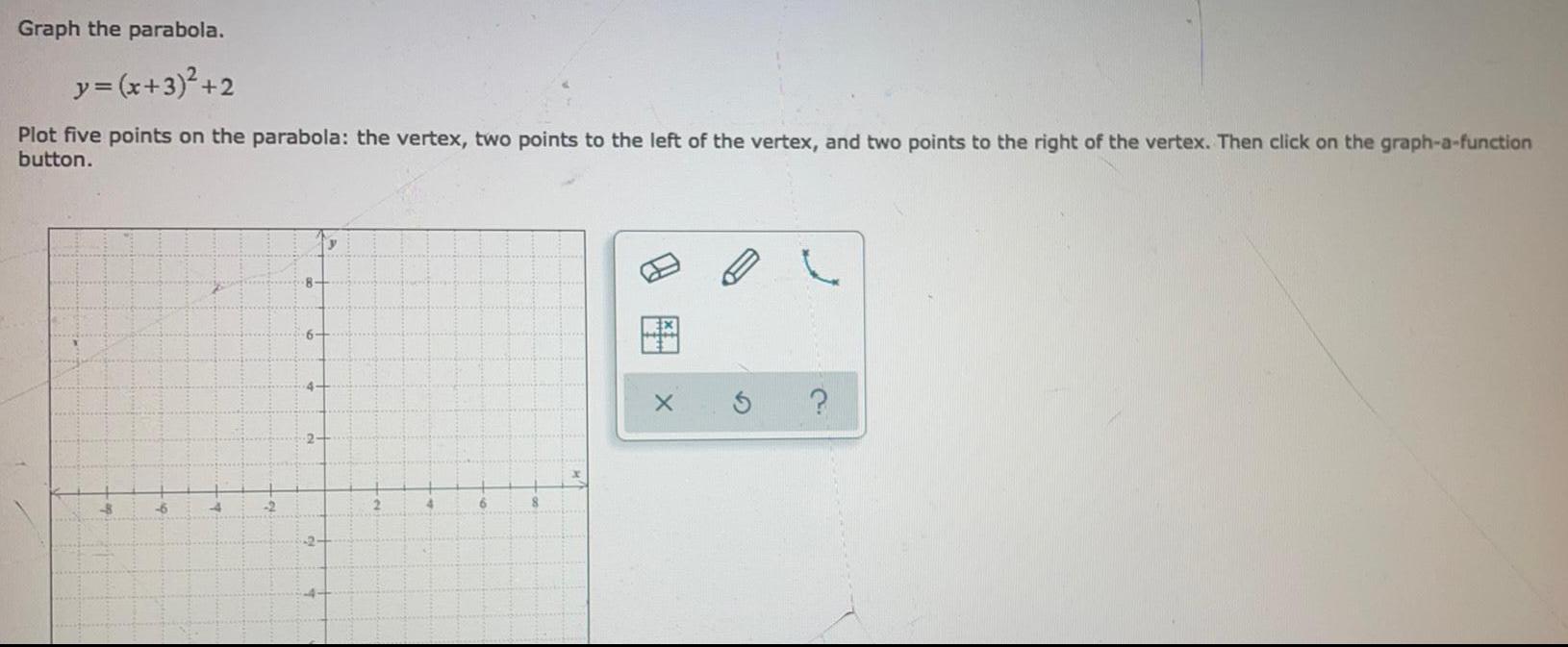
ParabolaGraph the parabola.
y = (x+3)² +2
Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex.
Math
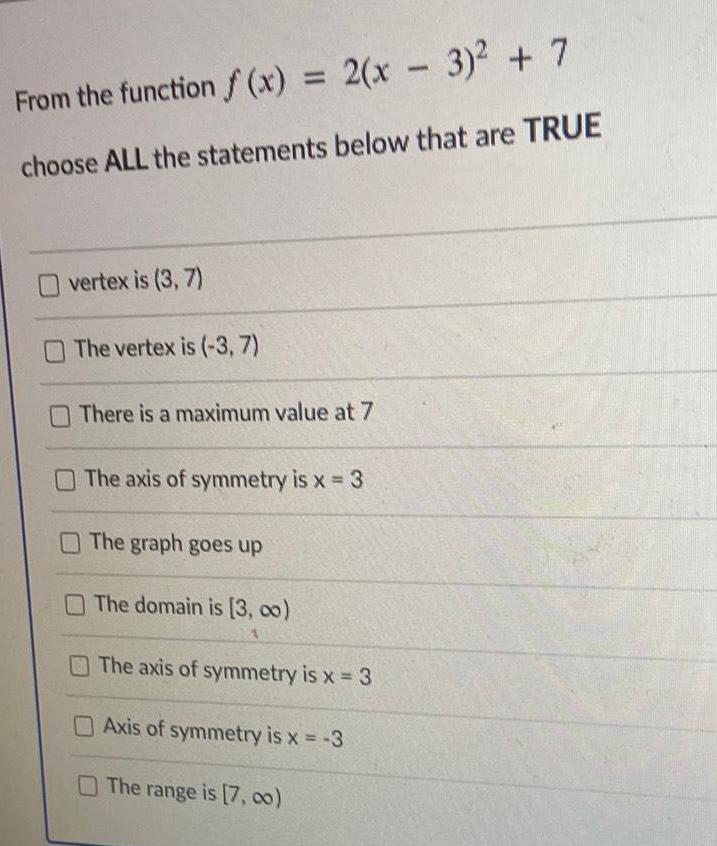
ParabolaFrom the function f(x) = 2(x - 3)² + 7
choose ALL the statements below that are TRUE
vertex is (3, 7)
The vertex is (-3,7)
There is a maximum value at 7
The axis of symmetry is x = 3
The graph goes up
The domain is [3,00)
The axis of symmetry is x = 3
Axis of symmetry is x = -3
The range is [7, 00)
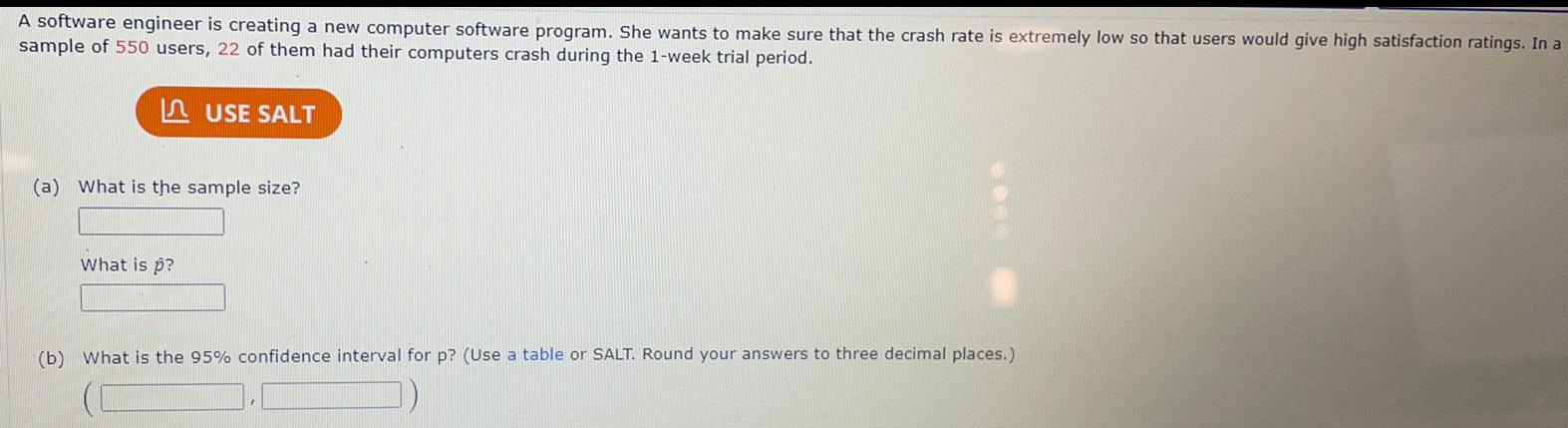
Math
ParabolaA software engineer is creating a new computer software program. She wants to make sure that the crash rate is extremely low so that users would give high satisfaction ratings. In a
sample of 550 users, 22 of them had their computers crash during the 1-week trial period.
USE SALT
(a) What is the sample size?
What is p?
(b) What is the 95% confidence interval for p? (Use a table or SALT. Round your answers to three decimal places.)

Math
ParabolaSelect the function that represents a parabola with vertex at (2,1) and y-intercept (0,3).
A) f(x) = 2(x - 2)² + 1
B) f(x) = 2(x + 2)² + 1
C) f(x) = ¹/2(x + 2)² + 1
D) f(x) = 1/₂(x - 2)² +1

Math
ParabolaSuppose the graph of y = ax² + 6x + c has x-intercepts at the points (-2, 0) and
(4,0).
(a) Find the coordinates of the vertex and the equation of the axis of symmetry.
(b) Find the coordinates of the y-intercept and tell whether the parabola opens
upward or downward.

Math
ParabolaTodd hit a golf ball 250 yards. The maximum height the golf ball reached was 35 yards. Assume the path of the ball is parabolic. Write an equation for the path of the ball.

Math
ParabolaFind the equation of the quadratic function whose graph is a parabola containing the points (0,1), (3,25), and (-2,15).The equation of the quadratic function whose graph is a parabola containing the given points is y=


Math
ParabolaConsider the following quadratic function.
f(x)=2x² + 4x+5
(a) Write the equation in the form f(x)= a (x-h)² + k. Then give the vertex of its graph.
(b) Graph the function. To do this, plot five points on the graph of the function: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function button.
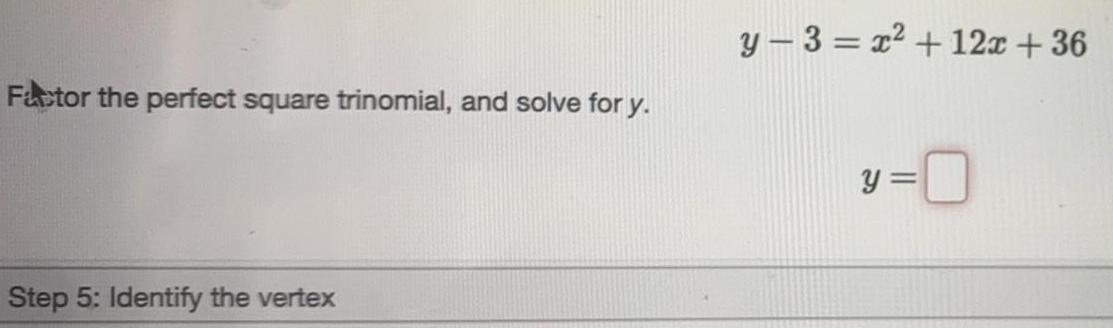

Math
ParabolaO
What is the directrix of the shape defined by the
equation (y - 3)2 = -12x?
x = -3
y = 0
Ox=1
O y = 6
x=3

Math
ParabolaWhich shape is defined by the equation y = 2x²
3?
-
O Circle
O Ellipse
Parabola
Hyperbola
None of the above.

Math
ParabolaWrite an equation for a parabola with x-intercepts (-3,0) and (4,0) which passes through the point (3,- 18).
Write the equation.
*****

Math
ParabolaA parabolic mirror to be used in a searchlight measures 40 centimeters tall and 80 centimeters wide. It's light bulb needs to be placed at the focus for the light to magnify properly. Find the distance from the vertex to the bulb. Hint: Assume the parabola opens downward and has its vertex at the origin.

Math
ParabolaA searchlight is shaped like a paraboloid of revolution. If the light source is located 1 feet from the base along the axis of symmetry and the opening is 6 feet across, how deep should the searchlight be?
The searchlight should be feet deep.
(Type an exact answer in simplified form.)
***

Math
ParabolaA parabolic flashlight reflector is to be 8 inches across and 2 inches deep. Where should the lightbulb be placed?
The lightbulb should be placed at inches from the vertex.

Math
ParabolaTrue and False. Determine if each statement is true (T) or false (F), if false correct the statement to make it true.
a. All quadratics have a degree of 2.
b. When the "a" value in a quadratic equation is negative, the parabola opens up.
c. Exponential functions have x as an exponent.
d. The axis of symmetry of a quadratic divides the parabola into mirror images.
e.
When the parabola opens down there is a minimum value.
f. Other names for the x-intercepts in a quadratic are roots, zeros and stems.
g. In y = ax² + bx + c, when the "c" value changes that changes the direction of opening of the quadratic.
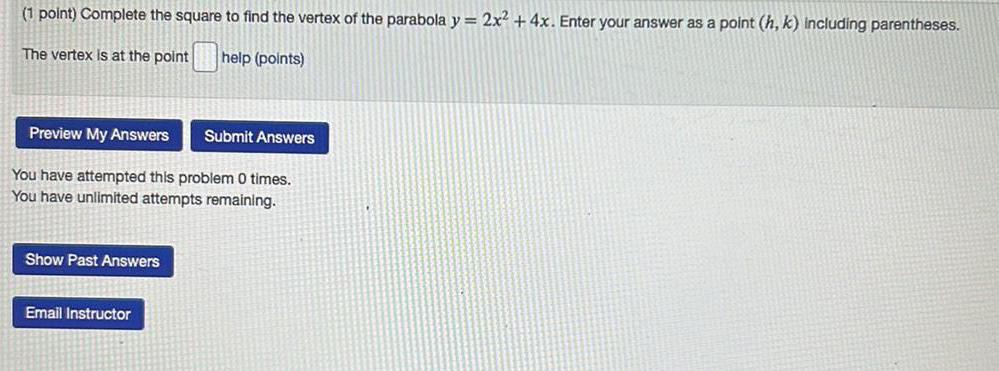
Math
ParabolaComplete the square to find the vertex of the parabola y = 2x² + 4x. Enter your answer as a point (h, k) including parentheses.
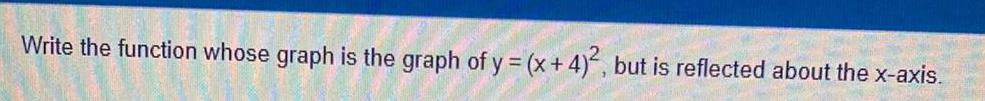
Math
ParabolaWrite the function whose graph is the graph of y = (x+4)², but is reflected about the x-axis.

Math
ParabolaFind the y-intercept and vertex for the following function: f(x) = 6x² - 6x + c
Express your answers in terms of c where appropriate.

Math
ParabolaConsider the solid S described below.
The base of S is the region enclosed by the parabola y = 4 - x² and the x-axis. Cross-sections perpendicular to the x-
axis are isosceles triangles with height equal to the base.
Find the volume V of this solid.
V =

Math
ParabolaIn mountainous areas, reception of radio and television is sometimes poor. Consider an idealized case where a hill is represented by the graph of the parabola y = x - x², a transmitter is located at the point (-3, 3), and a receiver is located on the other side of the hill at the point (x0, 0). What is the closest the receiver can be to the hill while still maintaining unobstructed reception? (Round your answer to three decimal places.)
![A ball is thrown vertically upward from ground level at a rate of 140 feet per second. Use the projectile formula h = - 16t² + vot + ho to find how long it will take the ball to reach its maximum height, and then find the maximum height the ball reaches. [Recall that vo is the initial velocity of the object and ho is the inital height of the object.]
Answer: The stone reaches its maximum height after after Select an answer
The maximum height the stone reaches is Select an answer
Note: Round any numerical responses to two decimal places. If there are multiple answers, separate them with commas.](https://media.kunduz.com/media/sug-question/raw/60977516-1657291571.6332226.jpeg?w=256)
Math
ParabolaA ball is thrown vertically upward from ground level at a rate of 140 feet per second. Use the projectile formula h = - 16t² + vot + ho to find how long it will take the ball to reach its maximum height, and then find the maximum height the ball reaches. [Recall that vo is the initial velocity of the object and ho is the inital height of the object.]
Answer: The stone reaches its maximum height after after Select an answer
The maximum height the stone reaches is Select an answer
Note: Round any numerical responses to two decimal places. If there are multiple answers, separate them with commas.

Math
ParabolaWhich is the focus and directrix of the parabola with equation (y + 2.5)² = 4(x-4)?
Focus (3,-2.5); directrix x = 3
Focus (5,-2.5); directrix y = 3.5
Focus (3,-2.5); directrix y = 3.5
Focus (5,-2.5); directrix x = 3

Math
ParabolaUse the ALEKS graphing calculator to find the x-intercept(s) and vertex for the quadratic function.
f(x) = -3x²+2x+3
Round to the nearest hundredth if necessary.
If there is more than one x-intercept, separate them with commas.
If applicable, click on "None".

Math
ParabolaA searchlight uses a parabolic mirror to cast a beam of light in parallel rays where the light bulb is located at the focus of the parabola in order to give the best illumination. The mirror is modeled by y² = 20(x - 10), where the measurements are in cm. What is the location of the light bulb?
(10,0)
(20, 0)
(12, 0)
(15, 0)