Statistics Questions and Answers

Math
StatisticsConsider the case of a male student who has three beers and weighs 120 pounds. Simplify the Widmark equation as much as possible for this case, rounding any constants to 3 decimal places.

Math
StatisticsThe activity on Marny Zell's MasterCard account for one billing period is shown below. Find the average daily balance and the finance charge if the billing period is June 26 through July 25, the previous balance was $396.63, and the annual interest rate is 19.5%.
Math
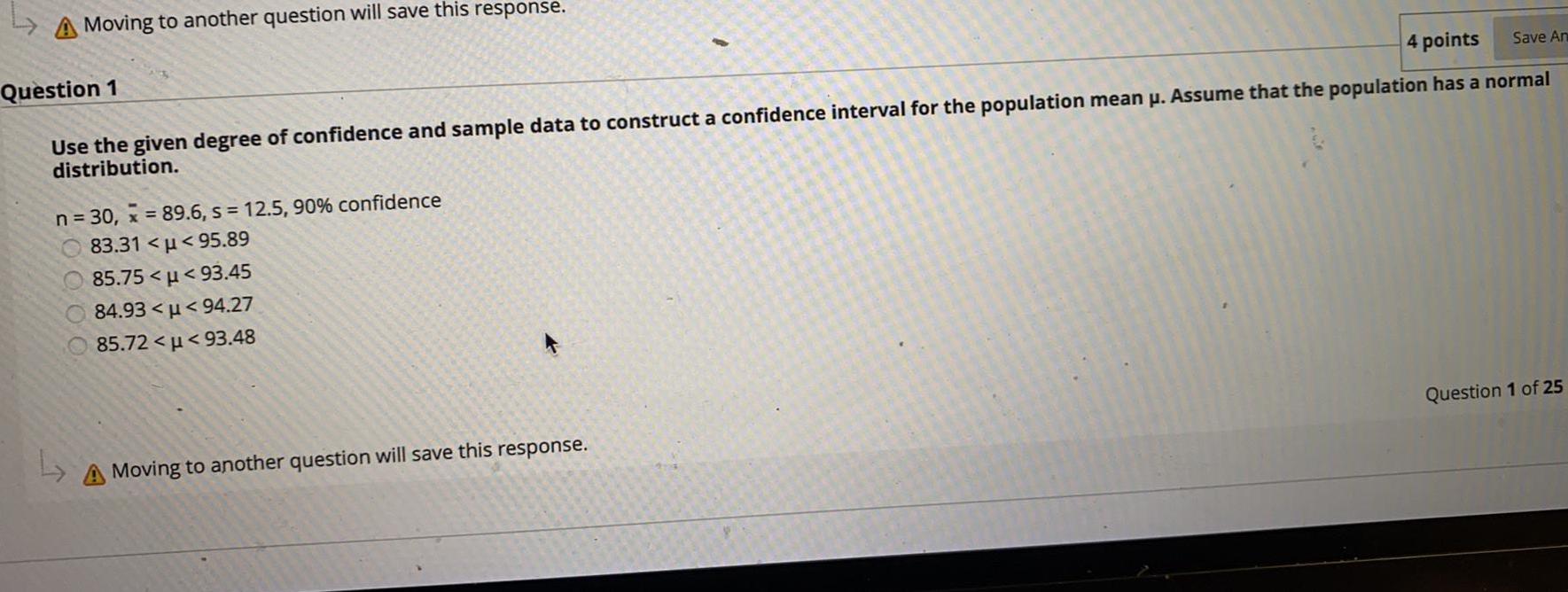
StatisticsUse the given degree of confidence and sample data to construct a confidence interval for the population mean μ. Assume that the population has a normal distribution.
n = 30, x = 89.6, s = 12.5, 90% confidence
83.31 <µ< 95.89
85.75 <µ< 93.45
84.93 <μ< 94.27
85.72 <µ< 93.48

Math
StatisticsYour grade point average (GPA) is a form of a weighted average. That is, 4 units of A counts more than 4 units of B. The most common weight for grades is A, 4 points;
B, 3 points; C, 2 points; D, 1 point; and F, 0 points. To find a GPA,
1. Multiply the points for each grade by the number of units for the course.
2. Find the sum of these products.
3. Divide this sum by the total number of units taken.
Find the GPA for 4 units of F in astronomy, 3 units of D in geometry, 2 units of A in sociology, and 3 units of B in biology. Round your answer to the nearest tenth.

Math
StatisticsA simple random sample is taken from a population and yields the following data for a variable of the population.
9 34 38 37 19
24 11 19 21 32
Find a point estimate for the population standard deviation (that is, the standard deviation of the variable).
A point estimate for the population standard deviation is
Math
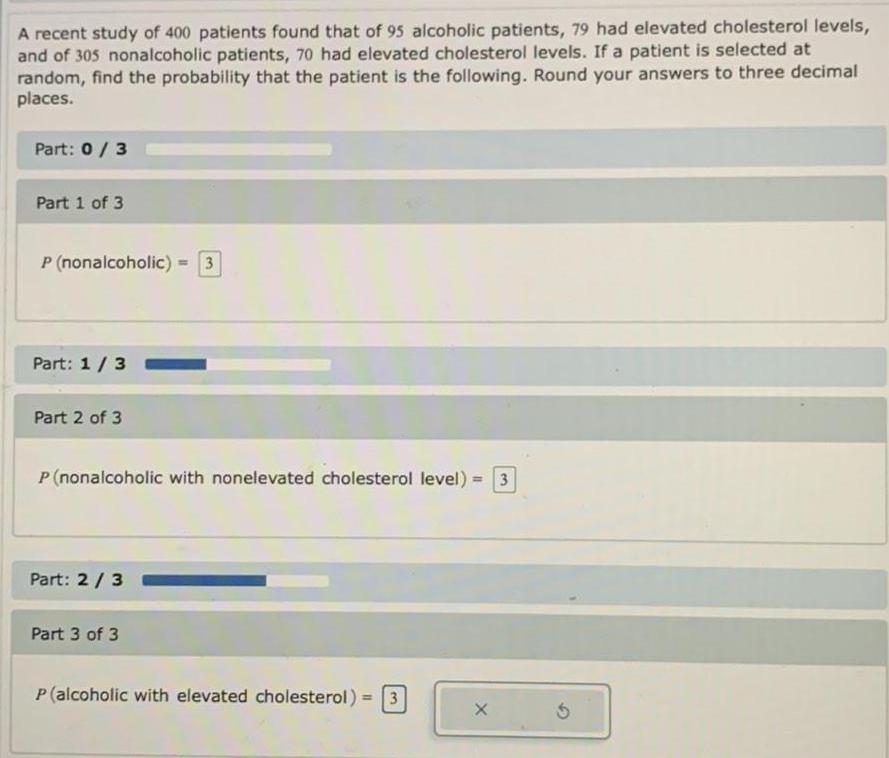
StatisticsA recent study of 400 patients found that of 95 alcoholic patients, 79 had elevated cholesterol levels, and of 305 nonalcoholic patients, 70 had elevated cholesterol levels. If a patient is selected at random, find the probability that the patient is the following. Round your answers to three decimal places.
P (nonalcoholic) =
P (nonalcoholic with nonelevated cholesterol level) =
P (alcoholic with elevated cholesterol) =
Math
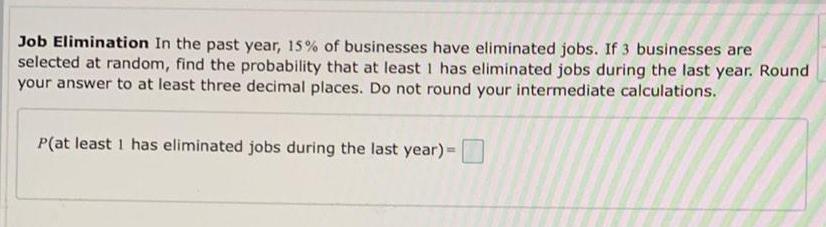
StatisticsJob Elimination In the past year, 15% of businesses have eliminated jobs. If 3 businesses are selected at random, find the probability that at least 1 has eliminated jobs during the last year. Round your answer to at least three decimal places. Do not round your intermediate calculations.
P(at least 1 has eliminated jobs during the last year) =

Math
StatisticsFor an outdoor concert by the city orchestra, concert organizers estimate that 10,000 people will attend if it is not raining. If it is raining, concert organizers estimate
that 3000
people will attend. On the day of the concert, meteorologists predict a 35% chance of rain. Determine the expected number of people who will attend this concert.
Enter your answer in the space provided using number keys only.
Math
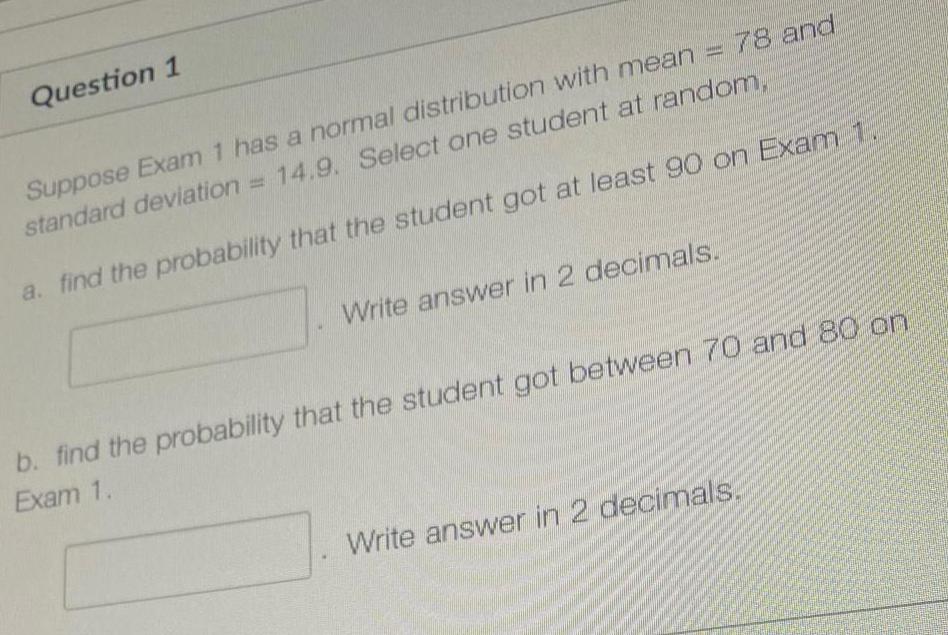
StatisticsSuppose Exam 1 has a normal distribution with mean = 78 and
standard deviation = 14.9. Select one student at random,
a. find the probability that the student got at least 90 on Exam 1.
Write answer in 2 decimals.
b. find the probability that the student got between 70 and 80 on
Exam 1.

Math
StatisticsA farmer is growing a type of apple with a known mean
weight of 0.3 lbs. and a standard deviation of 0.05 lbs.
After looking through his orchard, he believes his apples
might weigh less on average. He selects a random sample
of 35 apples and finds the mean weight to be 0.28 lbs.
Write null and alternative hypotheses to describe this
situation.

Math
StatisticsKari is purchasing a home for $260,000. The down payment is 25% and the balance will be financed with a 15 year mortgage at 8% and 4 discount points. Kari made a deposit of $20,000 (applied to the down payment) when the sales contract was signed. Kari also has these expenses: credit report, $70; appraisal fee, $110; title insurance premium, 1% of amount financed; title search, $200; and attorney's fees, $500. Find the closing costs (in $).

Math
StatisticsA baseball supply store has many inexpensive baseball gloves. In fact, over half of the gloves in stock cost less than $50. However, there are also a few high-end, more expensive gloves in stock. Some of those gloves cost over $300. The store owner wants to advertise her store. She wants to advertise to local children's baseball teams. She wants to advertise that her store is a place to buy reasonably priced items. Which number should she use in the advertisement for the gloves?
Median baseball glove price
Mean baseball glove price
Mode baseball glove price

Math
StatisticsThe amount of water consumed each week by Montana residences is normally distributed. A simple random sample of 25 residences was taken with a sample mean of 120.3 gallons and a standard deviation of 10.0 gallons. Test the claim at the 0.10 SL that the average amount of water consumed is less than 125 gallons. Make sure to give the test-statistic and the p-value.

Math
StatisticsThirty-nine different video games showing violence were observed. The duration times of violence (in seconds) were recorded. When using this sample for a t test of the claim that the population mean is greater than 90 sec, what does df denote, and what is its value? What does df denote?

Math
StatisticsAssume that a sample is used to estimate a population mean μ. Use the given confidence level and sample data to find the margin of error. Assume that the
sample is a simple random sample and the population has a normal distribution. Round your answer to one more decimal place than the sample standard
deviation.
95% confidence; n = 51; x = 240; s = 242
143.0
61.3
88.5
68.1

Math
StatisticsSuppose Robbie is the educational director for a group of teen test
prep programs in Nevada. He knows that the mean score on Nevada's
mathematics exam is 114 points with a standard deviation of 18 points. Robbie
thinks the teens in his program score differently than the population mean on
Nevada's mathematics exam. To test his claim, he randomly selects 250 of his
students and finds the mean test score of the sample to be 117 points.
a. What are Robbie's null (Ho) and alternative (H₁) hypotheses?
A. Ho: u 114 pts and H₁: u 114 pts
B. Ho: u
114 pts and H₁: u>
114 pts
C. Ho: x=
114 pts and H₁: x # 114 pts
D. Ho: u 117 pts and H₁: u 117 pts
E. Ho: x= 117 pts and H₁:x> 117 pts
b. What is the z-statistic? Give your answer precise to two decimal places.
c. What is the positive critical value z for a significance level of a= 0.05? Give
vour answer precise to at least two decimal places.

Math
StatisticsThe number of breakfast drive thru customers per day is normally distributed with a mean of 44 and a standard deviation of 6.
A. What precent of days have between 38 and 50 breakfast drive thru customers?
B. What precent of days have MORE than 50 breakfast drive thru customers?
(include percent signs in your answers)

Math
StatisticsSome species of eagles have been fighting extinction due to environmental hazards such as DDT, PCBS, and dioxin. The problem is with the food chain. Fish or rodents consume contaminated food and/or water. Then the eagles ingest the poison, which in turn affects the durability of the eagles' eggs. It takes only 44 parts per million of certain chemicals to ruin an eagle egg; write this number as a fraction in lowest terms.

Math
StatisticsYour alpha level is 0.05. The probability of observing two sample means that you have gathered if the means of the population are the same is 0.04. Which statement below is true?
You will accept that the null hypothesis that the means of the populations are the same.
You will reject the null hypothesis that the means of the population are the same.
There is no conclusion you can make in this situation.
Reject both the null and the alternate hypothesis.

Math
StatisticsAssume SAT Math scores are normally distributed with a mean of 500 and standard deviation of 100.
A) Find the probability that a student scores lower than 575
B) Find the probability that a student scores higher than 393.

Math
StatisticsFrom recent survey data, its known that the proportion of adults in the United States who are smokers is 18%. For a random sample of size 150, what is the standard deviation for the sampling distribution of the sample proportions, rounded to three decimal places?

Math
StatisticsA random number generator picks a number from 13 to 38 in a uniform manner. Round answers to 4 decimal places when possible.
a. The mean of this distribution is
b. The standard deviation is
c. The probability that the number will be exactly 24 is P(x = 24) =
d. The probability that the number will be between 22 and 29 is P(22 < x < 29) =
e. The probability that the number will be larger than 28 is P(x> 28) =
f. P(x> 16 | x < 32) =
g. Find the 22nd percentile.
h. Find the minimum for the upper quartile.
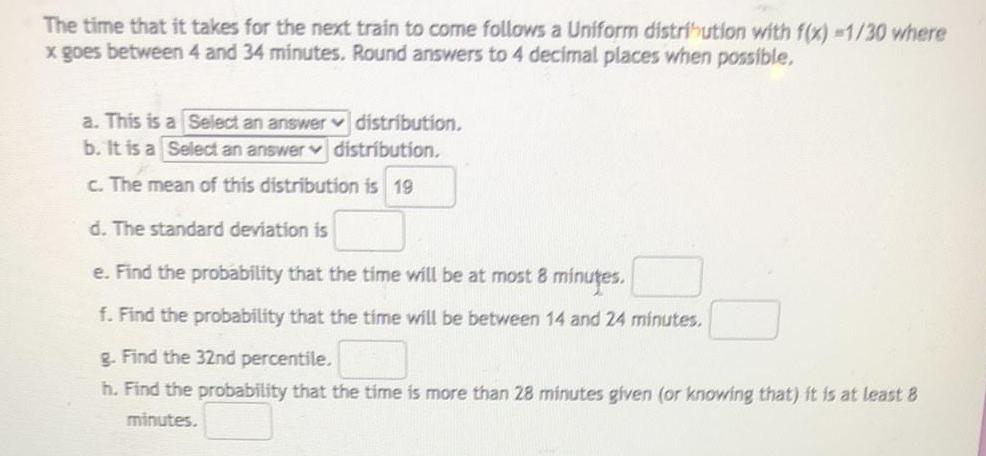
Math
StatisticsThe time that it takes for the next train to come follows a Uniform distribution with f(x) =1/30 where x goes between 4 and 34 minutes. Round answers to 4 decimal places when possible.
a. This is a Select an answer distribution.
b. It is a Select an answer distribution.
c. The mean of this distribution is 19
d. The standard deviation is
e. Find the probability that the time will be at most 8 minutes.
f. Find the probability that the time will be between 14 and 24 minutes.
g. Find the 32nd percentile.
h. Find the probability that the time is more than 28 minutes given (or knowing that) it is at least 8 minutes.

Math
StatisticsFill in the blanks to correctly complete the sentence below.
Suppose a simple random sample of size n is drawn from a large population with mean μ and standard deviation σ. The sampling distribution of x has mean µx= and standard deviation σx=

Math
StatisticsThe round off errors when measuring the distance that a long jumper has jumped is uniformly distributed between 0 and 5.6 mm. Round values to 4 decimal places when possible.
a. The mean of this distribution is
b. The standard deviation is
c. The probability that the round off error for a jumper's distance is exactly 2.3 is P(x = 2.3) =
d. The probability that the round off error for the distance that a long jumper has jumped is
between 0 and 5.6 mm is P(1.4 < x < 4.6) =
e. The probability that the jump's round off error is greater than 1.32 is P(x > 1.32) =
f. P(x> 4.7 x > 0.6) =
g. Find the 92nd percentile.
h. Find the minimum for the upper quartile.

Math
StatisticsSuppose that the weight of an newborn fawn is Uniformly distributed between 1.5 and 3.6 kg. Suppose that a newborn fawn is randomly selected. Round answers to 4 decimal places when possible.
a. The mean of this distribution is
b. The standard deviation is
c. The probability that fawn will weigh exactly 2.6 kg is P(x = 2.6) =
d. The probability that a newborn fawn will be weigh between 1.6 and 2.9 is P(1.6 < x < 2.9) =
e. The probability that a newborn fawn will be weigh more than 3.12 is P(x > 3.12) =
f. P(x> 1.91 x < 2.6) =
g. Find the 91st percentile.
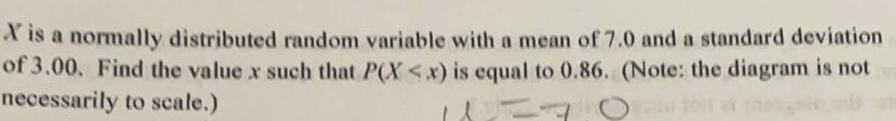
Math
StatisticsX' is a normally distributed random variable with a mean of 7.0 and a standard deviation of 3.00. Find the value x such that P(X<x) is equal to 0.86. (Note: the diagram is not necessarily to scale.)

Math
StatisticsAssuming the population has a bell-shaped distribution, if a sample size n = 19 has a sample mean x̄ = 33 with a sample standard deviation s = 7, find the margin of error at a 95% confidence level. Round the answer to two decimal places.

Math
StatisticsAssuming the population has a bell-shaped distribution, if a sample size n 12 has a sample mean x= 35 with a sample standard deviation s = 7, find the margin of error at a 95% confidence level. Round the answer to two decimal places.

Math
StatisticsSuppose that in a large population of students, the mean amount of sleep the previous night was μ = 6.9 hours and the standard deviation was σ = 1.55 hours. Consider randomly selected samples of n = 220 students.
(a) What is the value of the mean of the sampling distribution of possible sample means?
Mean = 6.9
(b) Calculate the standard deviation, s.d., of the sampling distribution of possible sample means. (Round your answer to three decimal places.)
s.d.(x) = 105
(c) Use the Empirical Rule to find values that fill in the blanks at the end of the following sentence. (Round your answers to three decimal places.)
For 68% of all randomly selected samples of n = 220 students, the mean amount of sleep the previous night will be between 219.895 and 220.105 hours.
(d) Use the Empirical Rule to fill in the blanks at the end of the following sentence. (Round your answers to three decimal places.)
For 95% of all randomly selected samples of n = 220 students, the mean amount of sleep will be between 219.790 and 220.210 hours.

Math
StatisticsWe want to obtain a sample to estimate a population mean. Based on previous evidence, researchers believe the population standard deviation is approximately σ = 1.3. We would like to be 90% confident that the esimate is within 0.5 of the true population mean. How large of a sample size is required?

Math
StatisticsWhich of the following is NOT involved in the process of interpreting pictures?
Determine what type of picture it is.
Form an opinion on the quality of work.
Analyze the author's intentions.
Observe the elements of the picture.

Math
StatisticsThe average height of young adult males has a normal distribution with standard deviation of 2.4 inches. You want to estimate the mean height of students at your college or university to within one inch with 99% confidence. How many male students must you measure?
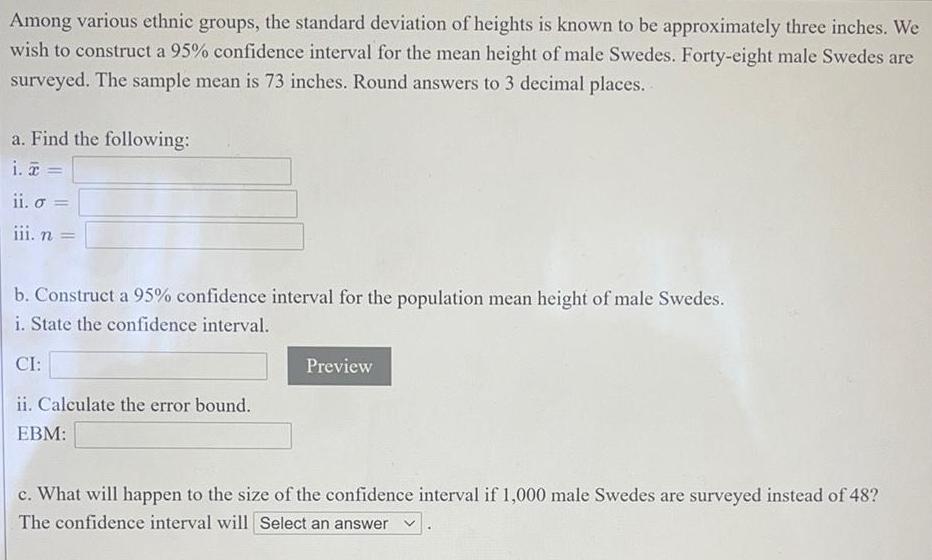
Math
StatisticsAmong various ethnic groups, the standard deviation of heights is known to be approximately three inches. We wish to construct a 95% confidence interval for the mean height of male Swedes. Forty-eight male Swedes are surveyed. The sample mean is 73 inches. Round answers to 3 decimal places.
a. Find the following:
i. =
ii. o =
iii. n =
b. Construct a 95% confidence interval for the population mean height of male Swedes.
i. State the confidence interval.
ii. Calculate the error bound.
c. What will happen to the size of the confidence interval if 1,000 male Swedes are surveyed instead of 48?
The confidence interval will

Math
StatisticsIf the average price of a television in my store is $900 with stock is morally a standard deviation of $50. Assuming my distributed where is:
A. 68% of the computers prices
B. 95% of the computers prices
C. 99.7% of the computers prices
Assuming the data is not normal Chebyshev's states:
D. at least 75% of data is between
E. at least 88.87% of data is between
F. at least 94% of data is between

Math
StatisticsThe offensive line of a football team is larger than in previous years. The program will list a statistic to show this fact. Which statistic (mean, median, or mode) might be most appropriate in this situation?
Mean
Median
Mode

Math
StatisticsRabies is an often-fatal disease, which is typically transmitted through the bite of an infected animal. The state of Florida has been recording all known cases of rabies for the past 20 years, with data indicating an average rate of 3.6 cases of rabies per week. Let X be the count of rabies cases reported in a given week.
(a) Find the mean of X. (Enter your answer rounded to one decimal place.)
mean of X:
Find the standard deviation of X. (Enter your answer rounded to three decimal places.)
standard deviation of X:

Math
StatisticsA reporter is doing a story on the falling prices of homes in a large neighborhood. The reporter wants to demonstrate how the prices have fallen for all homes, not just the most expensive houses. Which statistic (mean, median, or mode) is most appropriate in this situation?
Mean
Median
Mode

Math
StatisticsTables in the dining hall are numbered 1-12 for students who eat there. The principal calls out a number for the table that will go through the buffet line first. The other tables follow in order of the table numbers. One student is sure the principal calls certain tables more often. She keeps track of which numbers are called over a 21-day period. Which statistic (mean, median, or mode) is this student using?
Mean Median Mode

Math
StatisticsA sports psychologist tests a new coaching method and finds that of the 43 novice athletes who were trained under the new method, they only froze/choked when in high stakes competition 3.5% of the time. If it is known that all novice athletes tend to freeze/choke 6% of the time when in high stakes competition (with a 3.2% average variation from the mean), what would the expected rate of all novice athletes trained using the new coaching method with 92% confidence?
Question
What is the lower bound estimate for how often all novice athletes would choke if trained under the new method?
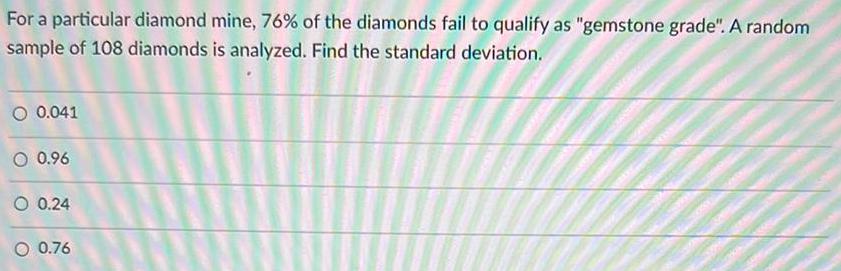
Math
StatisticsFor a particular diamond mine, 76% of the diamonds fail to qualify as "gemstone grade". A random sample of 108 diamonds is analyzed. Find the standard deviation.
0.041
0.96
0.24
0.76
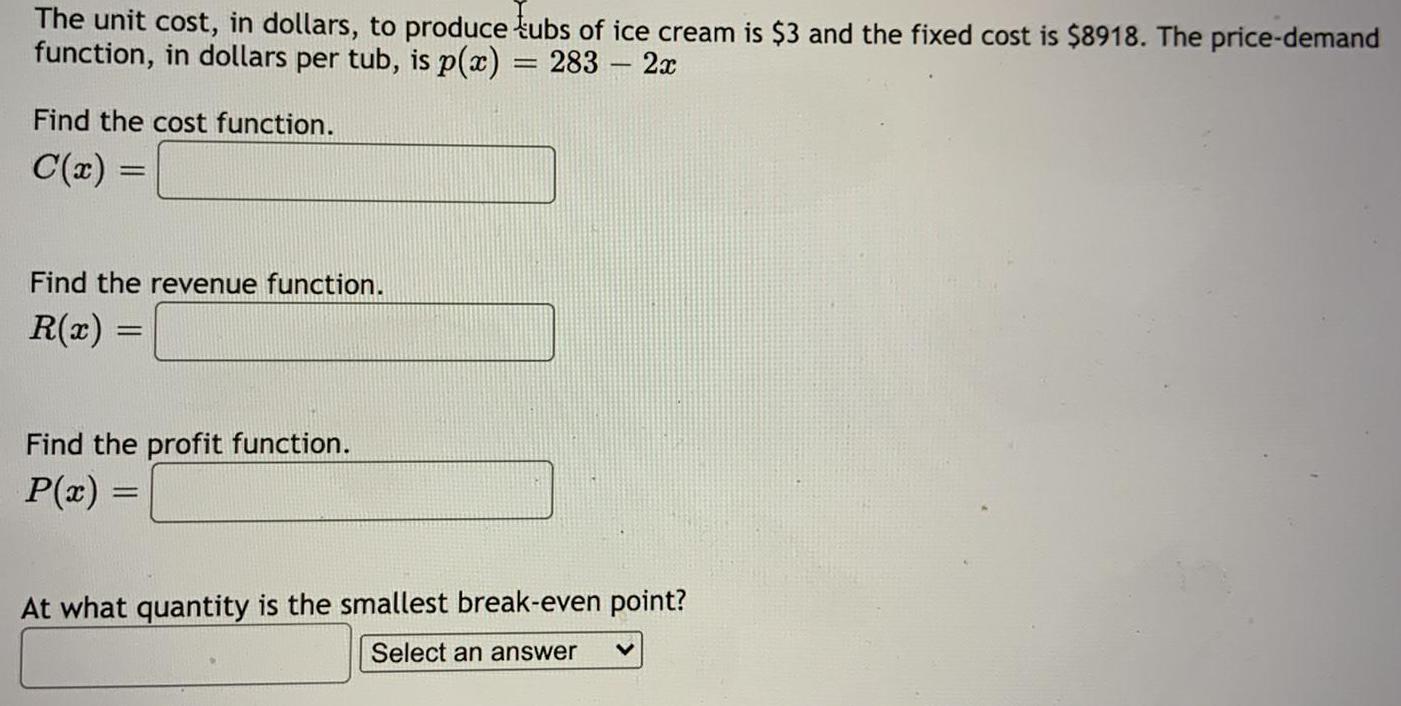
Math
StatisticsThe unit cost, in dollars, to produce tubs of ice cream is $3 and the fixed cost is $8918. The price-demand function, in dollars per tub, is p(x) = 283 - 2x
Find the cost function.
C(x) =
Find the revenue function.
R(x) =
Find the profit function.
P(x) =
At what quantity is the smallest break-even point?

Math
StatisticsEngineers must consider the diameters of heads when designing helmets. The company researchers
have determined that the population of potential clientele have head diameters that are normally
distributed with a mean of 7-in and a standard deviation of 1-in. Due to financial constraints, the
helmets will be designed to fit all men except those with head diameters that are in the smallest
3.8% or largest 3.8%.
What is the minimum head diameter that will fit the clientele?
What is the maximum head diameter that will fit the clientele?

Math
StatisticsFind the area under the standard normal curve within three standard deviations of the mean. Round the
solution to four decimal places, if necessary.

Math
StatisticsWhat percentage of the general U.S. population are high-school dropouts? The Statistical Abstract of the United States, 120th Edition, gives the percentage of high- school dropouts by state. For convenience, the data are sorted in increasing order.

Math
StatisticsCollege students average 7.1 hours of sleep per night with a standard deviation of 45 minutes. If the amount of sleep is normally distributed, what proportion of college students sleep for more than 8.1 hours?

Math
StatisticsThe residents of a city voted on whether to raise property taxes. The ratio of yes votes to no votes was 4 to 5. If there were 6417 total votes, how many yes votes were there?

Math
StatisticsA Food Marketing Institute found that 30% of households spend more than $125 a week on groceries. Assume the population proportion is 0.3 and a simple random sample of 481 households is selected from the population. What is the probability that the sample proportion of households spending more than $125 a week is less than 0.31?

Math
StatisticsInvestors buy a studio apartment for $150,000. Of this amount, they have a down payment of $37,500. Their down payment is what percent of the purchase price? What percent of the purchase price would a $60,000 down payment be?
Their down payment is% of the purchase price.
(Type a whole number.)
A. $60,000 down payment would be % of the purchase price.
(Type a whole number.)

Math
StatisticsA population of values has a normal distribution with µ=68.9 and σ= 34.3.
A random sample of size n = 239 is drawn. Find the probability that a
sample of size n = 239 is randomly selected with a mean less than 75.1.
Round your answer to four decimal places.
P(M<75.1):