Application of derivatives Questions and Answers

Math
Application of derivativesCountry Motorbikes Incorporated finds that it costs $200 to produce each motorbike, and that fixed costs are $1300 per day. The price function is p(x) = 500 - 5x, where p is the price (i dollars) at which exactly x motorbikes will be sold. Find the quantity Country Motorbikes should produce and the price it should charge to maximize profit. Also find the maximum profit.
Math
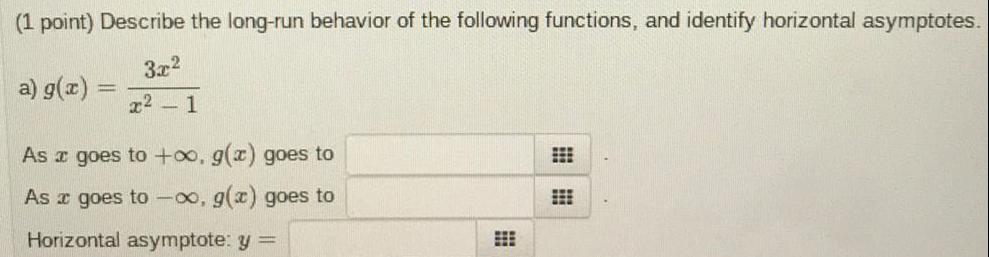
Application of derivativesDescribe the long-run behavior of the following functions, and identify horizontal asymptotes.
a) g(x)=3x²/x² - 1
As a goes to +∞, g(x) goes to
As a goes to -∞, g(x) goes to
Horizontal asymptote: y =

Math
Application of derivatives4. Choose the appropriate answer for each of these questions:
A. The derivative of a function measures:
a. How steep its graph is
b. What value it takes for a given x
c.Where its graph crosses the x-axis
B. The derivative of a function at a given point is a:
a.An equation
b.A number
c.A function
C. The derivative of a function is closely related to the
a. Set of solutions of an equation
b. Slope of a line
c. Zero of a function
![Find the derivative of the function.
y = 5(2-x²)4
Step 1
Apply the general power rule which states that if y = [u(x)], where u is a differentiable function of x and n is a rational number, then
dy/dx = n[u(x)]n-¹du/dx
Let u = 2x² and substitute u for 2x² in the original equation.
y = 5(2-x²)4
= 5 4(-2x) (2-x²) ³](https://media.kunduz.com/media/sug-question/raw/54203517-1658997247.8931298.jpeg?w=256)
Math
Application of derivativesFind the derivative of the function.
y = 5(2-x²)4
Step 1
Apply the general power rule which states that if y = [u(x)], where u is a differentiable function of x and n is a rational number, then
dy/dx = n[u(x)]n-¹du/dx
Let u = 2x² and substitute u for 2x² in the original equation.
y = 5(2-x²)4
= 5 4(-2x) (2-x²) ³

Math
Application of derivativesA rocket is fired from a building 240 ft tall. The height of the rocket with respect to time (in
seconds) is modeled by f (t) = -161² +32t + 240. What is the maximum height?
32 ft
240 ft
256 ft
120 ft

Math
Application of derivativesGiven the function f(x) =1/x^2
a. Find the average rate of change between x=__and x= (choose two consecutive negative
Integers)
b. Find the instantaneous rate of change at x=_______ (choose a negative integer value for x)
c. Find the equation of the tangent line at your chosen point
d. Prove that f(x) is continuous at your chosen point
Math
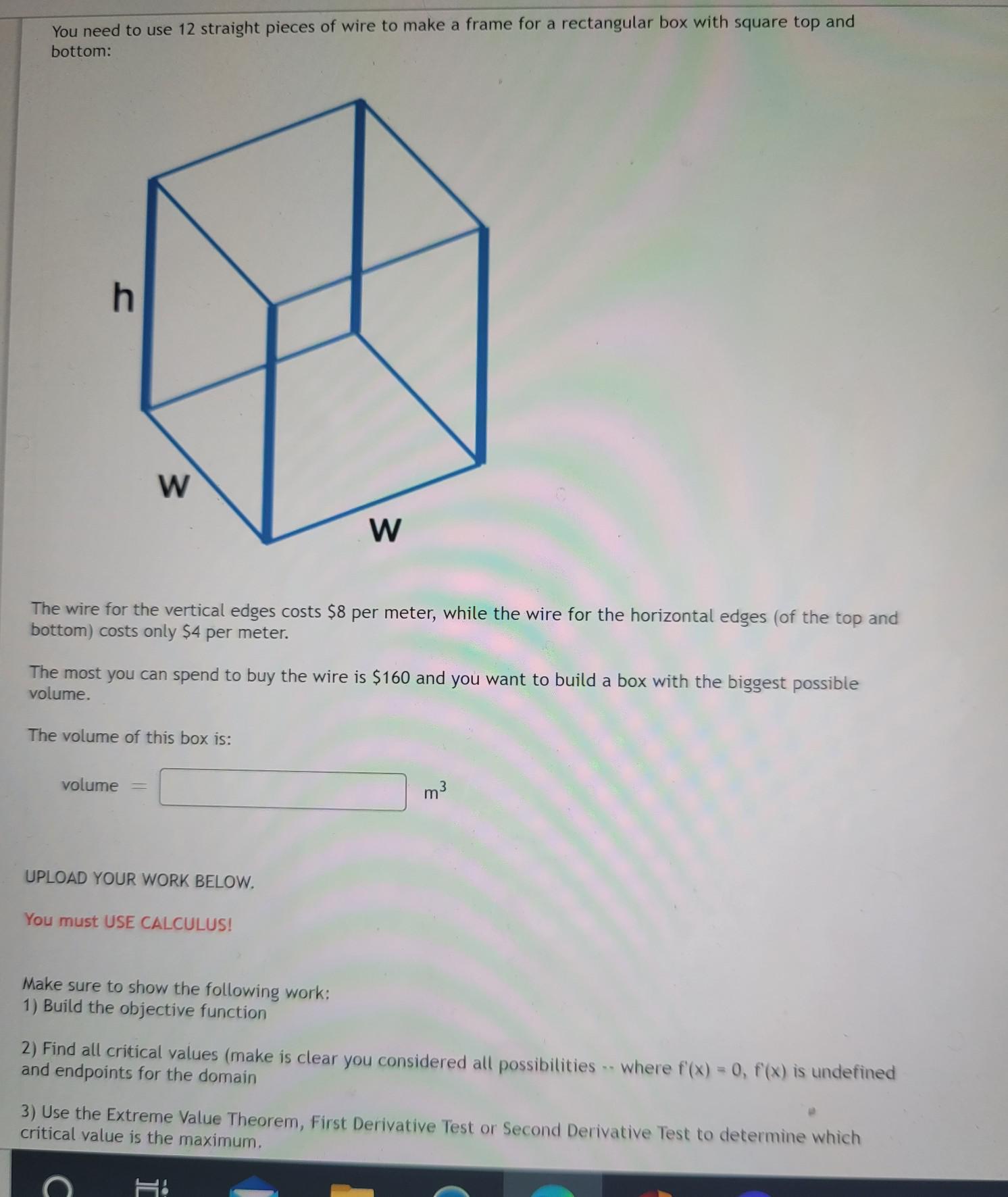
Application of derivativesYou need to use 12 straight pieces of wire to make a frame for a rectangular box with square top and bottom:
The wire for the vertical edges costs $8 per meter, while the wire for the horizontal edges of the top and bottom) costs only $4 per meter.
The most you can spend to buy the wire is $160 and you want to build a box with the biggest possible

Math
Application of derivativesConsider the differential equation dy/dx=x^2(y + 1).
Sketch a slope field for the given differential equation on your paper for the domain (-3, 3) and the range (-3, 3).
A): List five coordinates and the corresponding slope of their segments.
B): Using the slope field that you drew, describe all points in the xy-plane for which the slopes are negative.
Math
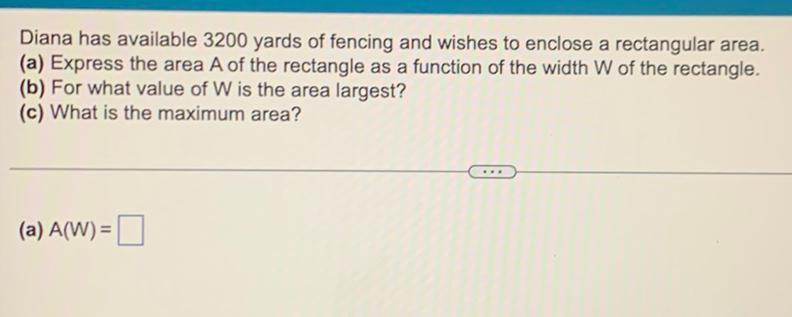
Application of derivativesDiana has available 3200 yards of fencing and wishes to enclose a rectangular area.
(a) Express the area A of the rectangle as a function of the width W of the rectangle.
(b) For what value of W is the area largest?
(c) What is the maximum area?
(a) A(W)= ▢
Math
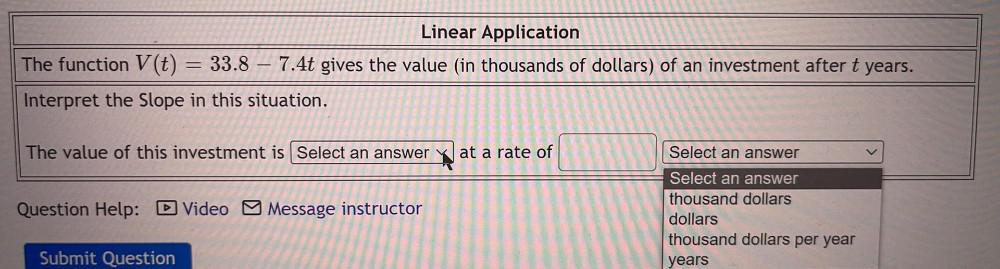
Application of derivativesThe function V(t) =33.8 – 7.4t gives the value (in thousands of dollars) of an investment after t years. Interpret the Slope in this situation. The value of this investment is_______ at a rate of_______
![Consider the differential equation dy/dx = x²(y + 1).
Sketch a slope field for the given differential equation on your paper for the domain [-3, 3] and the range [-3, 3].
(A) List five coordinates and the corresponding slope of their segments.
(B) Using the slope field that you drew, describe all points in the xy-plane for which the slopes are negative.](https://media.kunduz.com/media/sug-question/raw/77435223-1658835743.4339602.jpeg?w=256)
Math
Application of derivativesConsider the differential equation dy/dx = x²(y + 1).
Sketch a slope field for the given differential equation on your paper for the domain [-3, 3] and the range [-3, 3].
(A) List five coordinates and the corresponding slope of their segments.
(B) Using the slope field that you drew, describe all points in the xy-plane for which the slopes are negative.
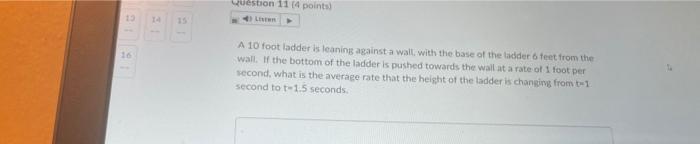
Math
Application of derivativesA 10 foot ladder is leaning against a wall with the base of the ladder 6 feet from the wall. If the bottom of the ladder is pushed towards the wall at a rate of 1 foot per second, what is the average rate that the height of the ladder is changing from t=1 second to t=1.5 seconds

Math
Application of derivativesWhat is the maximum vertical distance between the line y = x + 12 and the parabola y = x² for -3 ≤ x ≤ 4?

Math
Application of derivativesA company found that new employees prefer training sessions of moderate length, shorter training sessions provided too little instruction to complete a task, while longer training sessions contain too much instruction to remember. For a training session on a particular task, the company determined that the ratings new employees gave for the training session could be approximated
by R(t)=32t/t²+256 where t is the length of the training session in minutes. Find the training session length that received the highest rating
The training session length that received the highest rating is____minutes
(Simplify your answer.)

Math
Application of derivativesFind all relative extrema and saddle points of the function. Use the Second Partials Test where applicable. (If an answer does not exist, enter DNE.)
f(x, y) = -8x² - 5y^2 + 8x - 10y + 8
relative minimum.
relative maximum
saddle point

Math
Application of derivativesThe radius r of a sphere is increasing at a rate of 2 inches per minute.
(a) Find the rate of change of the volume when r = 11 inches.
in.3/min
(b) Find the rate of change of the volume when r = 36 inches.
in.3/min
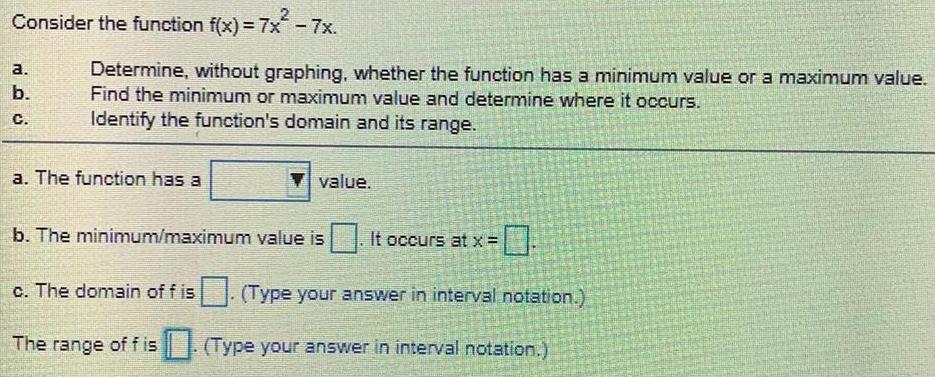
Math
Application of derivativesConsider the function f(x) = 7x² - 7x.
a.Determine, without graphing, whether the function has a minimum value or a maximum value.
b.Find the minimum or maximum value and determine where it occurs.
c.Identify the function's domain and its range.
a. The function has a
value.
b. The minimum/maximum value is It occurs at x =
c. The domain off is. (Type your answer in interval notation.)
(Type your answer in interval notation.)
The range of fis
![Approximate the area under the graph of F(x) = 0.9x³ +9x² -0.9x-9 over the interval [-6, -1] using 5 subintervals. Use the left endpoints to find the heights of the rectangles.
The area is approximately square units.](https://media.kunduz.com/media/sug-question/raw/53109592-1658489278.4091115.jpeg?w=256)
Math
Application of derivativesApproximate the area under the graph of F(x) = 0.9x³ +9x² -0.9x-9 over the interval [-6, -1] using 5 subintervals. Use the left endpoints to find the heights of the rectangles.
The area is approximately square units.

Math
Application of derivativesA cylinder shaped can needs to be constructed to hold 600 cubic centimeters of soup. The material for the sides of the can costs 0.03 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.08 cents per square centimeter. Find the dimensions for the can that will minimize production cost.
Helpful information:
h: height of can, r: radius of can
Volume of a cylinder: V = r²h
Area of the sides: A = 2πrh
Area of the top/bottom: A = ²

Math
Application of derivativesNASA launches a rocket at t= 0 seconds. Its height, in meters above sea-level, as an equation of time is given by h=- 4.9ť² + 139t + 269.
How many seconds does it take for the rocket to reach its maximum height?

Math
Application of derivativesFind the equation of the tangent line to the curve (a lemniscate) 2 (z² + y²)² = 25 (x² - y²) at the point
(3, 1). The equation of this tangent line can be written in the form y = mx + b where m is:
and where b is:
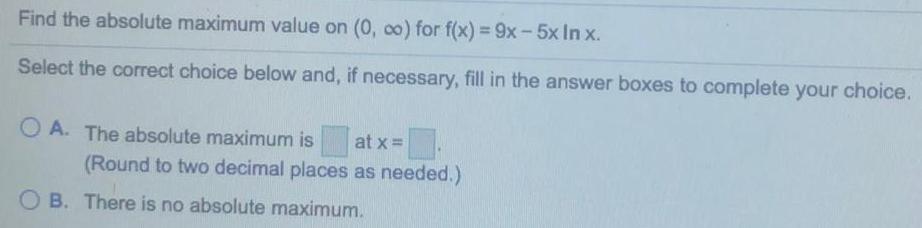
Math
Application of derivativesFind the absolute maximum value on (0, co) for f(x) = 9x - 5x In x.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The absolute maximum is at x =
(Round to two decimal places as needed.)
B. There is no absolute maximum.

Math
Application of derivativesYou're flying from Joint Base Lewis-McChord (JBLM) to an undisclosed location 73 km south and 200 km east. Mt. Rainier is located approximately 56 km east and 40 km south of JBLM. If you are flying at a constant speed of 800 km/hr, how long after you depart JBLM will you be the closest to Mt. Rainier?

Math
Application of derivativesThe expression f(x+h)-f(x)/h for h#0 is called the difference quotient. Find and simplify the difference quotient for the following function.
f(x)=3x² +5x+6

Math
Application of derivativesA rock is thrown into a still pond. The circular ripples move outward from the point of impact of the rock so that the radius of the circle formed by a ripple increases at the rate of 5 feet per minute. Find the rate at which the area is changing at the instant the radius is 15 feet.
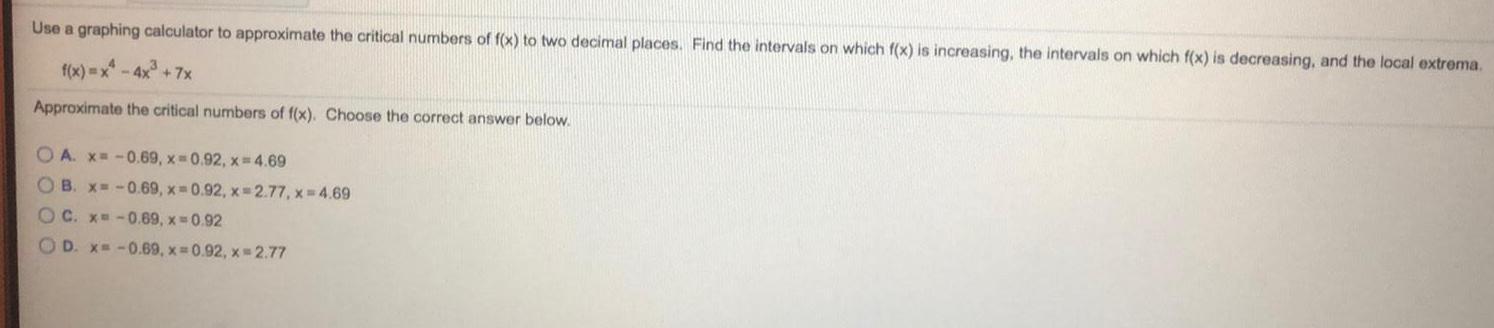
Math
Application of derivativesUse a graphing calculator to approximate the critical numbers of f(x) to two decimal places. Find the intervals on which f(x) is increasing, the intervals on which f(x) is decreasing, and the local extrema.
f(x)=x² - 4x³ +7x
Approximate the critical numbers of f(x). Choose the correct answer below.
A. x=-0.69, x=0.92, x= 4.69
B. x=-0.69, x=0.92, x=2.77, x=4.69
C. x=-0.69, x=0.92
D. x= -0.69, x=0.92, x=2.77
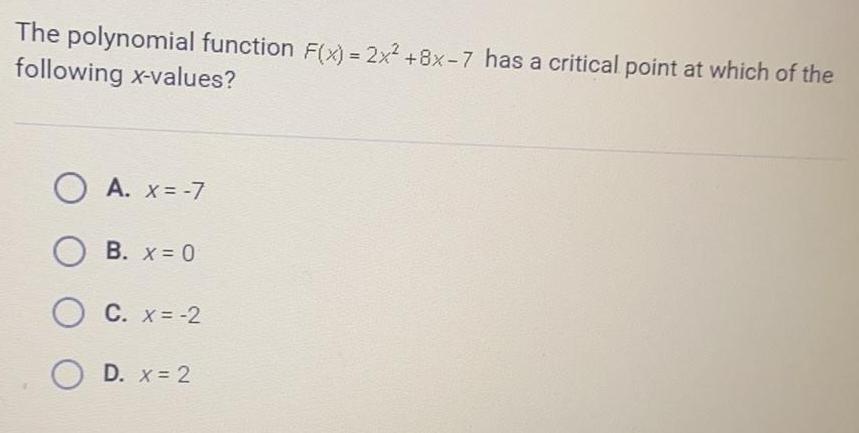
Math
Application of derivativesThe polynomial function F(x) = 2x² +8x-7 has a critical point at which of the following x-values?
A. x = -7
B. x = 0
C. x = -2
D. x = 2

Math
Application of derivativesA rice producer fills boxes with the same weights of different rice varieties to produce rice blends. The machinery filling each box is designed to put 42 ounces of rice in each box. But the machinery is imperfect. The actual weight of each box varies by a certain number of ounces.
What mathematical model could the manufacturer use to represent the weights of the boxes?

Math
Application of derivativesA ball is thrown from the top of the school. The height of the ball (in feet) written in terms of the time (in seconds) is modeled by f(t) = -16r² + 32 + 48. What is the maximum height of the
ball?
6 feet
64 feet
48 feet
112 feet
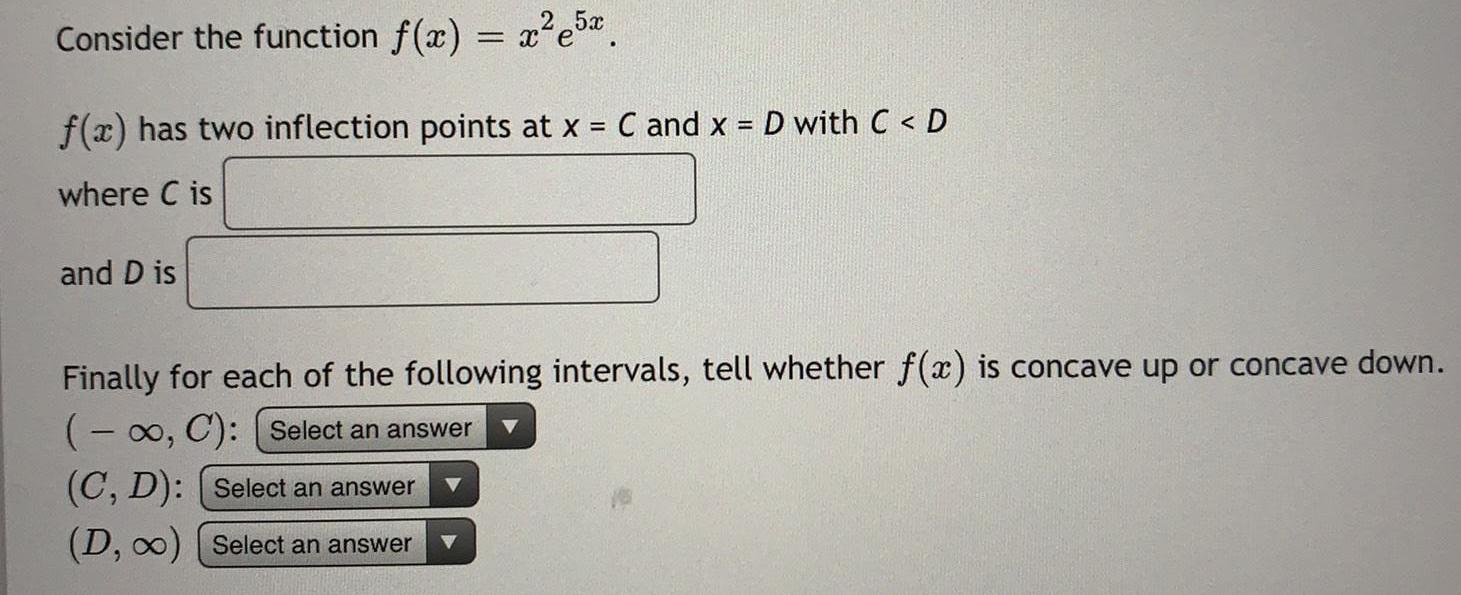
Math
Application of derivativesConsider the function f(x) = x²e^5x
f(x) has two inflection points at x = C and x = D with C < D
where C is
and D is
Finally for each of the following intervals, tell whether f(x) is concave up or concave down.
(-∞, C):
(C, D):
(D, ∞):

Math
Application of derivativesAt noon, ship A is 20 nautical miles due west of ship B. Ship A is sailing west at 18 knots and ship B is sailing north at 24 knots. How fast (in knots) is the distance between the ships changing at 7 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)

Math
Application of derivativesA basketball is thrown and the path can be modeled by ƒ (x) = −16x² + 15x + 6 where x
represents time in seconds and f (x) represents height of the ball in feet. In how many seconds
will the basketball hit the ground if no one catches it?
about 1.2 seconds
about 0.6 seconds
about 0.3 seconds
about 2.4 seconds
![Consider the function f(x) = 2 - 5x² on the interval [ - 3, 7].
The average rate of change of f(x) on this interval is:
f(7) - f(-3) / 7-(-3) =
The Mean Value Theorem says that there is at least one number c in the open interval (,) so that f'(c) equals this average rate of change. Find the value(s) of c that work for f(x) on ( - 3, 7):](https://media.kunduz.com/media/sug-question/raw/51014664-1658398914.4256885.jpeg?w=256)
Math
Application of derivativesConsider the function f(x) = 2 - 5x² on the interval [ - 3, 7].
The average rate of change of f(x) on this interval is:
f(7) - f(-3) / 7-(-3) =
The Mean Value Theorem says that there is at least one number c in the open interval (,) so that f'(c) equals this average rate of change. Find the value(s) of c that work for f(x) on ( - 3, 7):
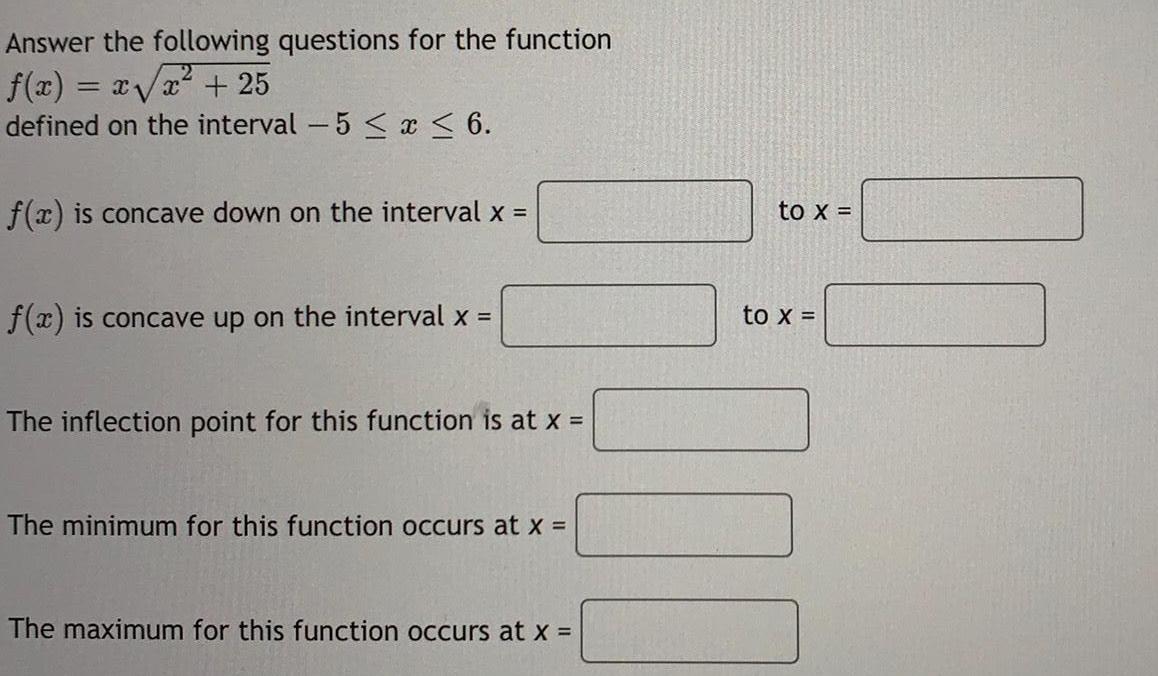
Math
Application of derivativesAnswer the following questions for the function
f(x)=x√x² + 25
defined on the interval -5 ≤ x ≤ 6.
f(x) is concave down on the interval x =
f(x) is concave up on the interval x =
The inflection point for this function is at x =
The minimum for this function occurs at x =
The maximum for this function occurs at x =

Math
Application of derivativesConsider the function f(x) = 8(x - 2)^2/3. For this function there are two important intervals: (-∞, A)
and (A, ∞) where A is a critical number.
A is
For each of the following intervals, tell whether f(x) is increasing or decreasing.
(-∞, A):
(A, ∞):
For each of the following intervals, tell whether f(x) is concave up or concave down.
(-∞, A):
(A, ∞):
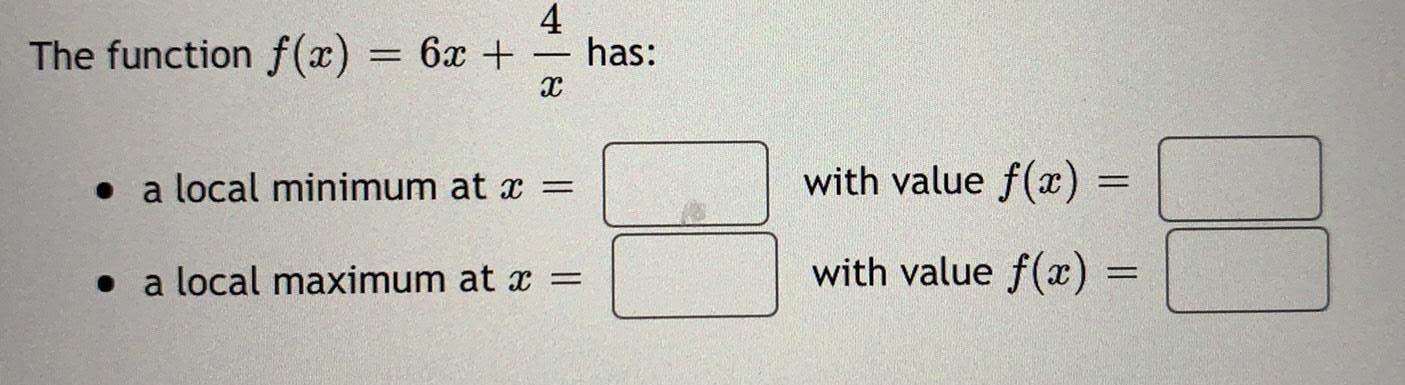
Math
Application of derivativesThe function f(x) = 6x + (4/x) has:
• a local minimum at x = with value f(x) =
• a local maximum at x = with value f(x) =

Math
Application of derivativesYou know that the following information about f(x):
f(3) = 14
f(14) = 2
f'(14) = 2
f'(3) = 13
If F(x) = f(f(x)) and G(x) = (F(x))² then:
F'(3) =
G'(3) =
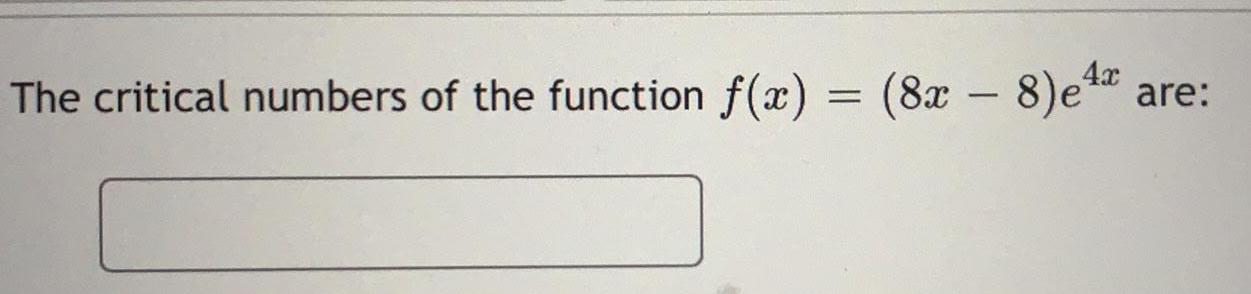

Math
Application of derivativesThe circumference of a sphere was measured to be 75 cm with a possible error of 0.5 cm. Use linear
approximation to estimate the maximum error in the calculated surface area.
Estimate the relative error in the calculated surface area.
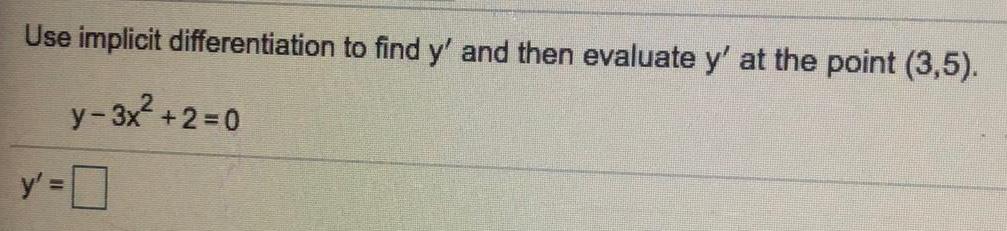
Math
Application of derivativesUse implicit differentiation to find y' and then evaluate y' at the point (3,5).
y - 3x² +2=0

Math
Application of derivativesFor the polynomial function f(x) = -0.02x4+.36x2 - 1.62, find all local and global extrema.
No local extrema exist.
The only extrema point is (-1.62, 0).
The only extrema point is (9, 0).
The local and global extrema are: (-3, 0), (0, -1.62) and (3, 0).

Math
Application of derivativesA rectangular bird sanctuary is being created with one side along a straight riverbank. The remaining three sides are to be enclosed with a protective fence. If there are 16 km of fence available, find the dimension of the rectangle to maximize the area of the sanctuary.
(Give your answer as a whole or exact number.)
length of fencing perpendicular to the riverbank:
length of fencing parallel to the riverbank:
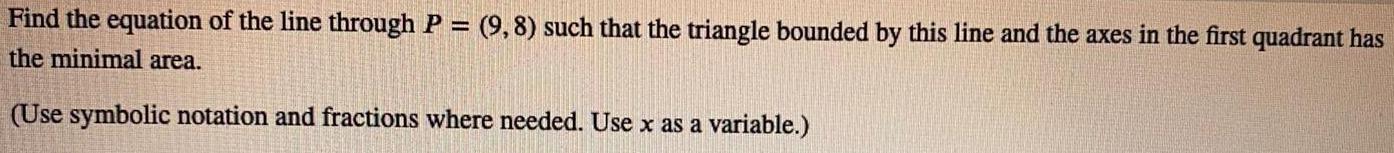
Math
Application of derivativesFind the equation of the line through P = (9,8) such that the triangle bounded by this line and the axes in the first quadrant has the minimal area.
(Use symbolic notation and fractions where needed. Use x as a variable.)

Math
Application of derivativesA poster of area 6000 cm² has blank margins of 10 cm wide on the top and bottom and cm wide on the sides. Find the dimensions that maximize the printed area.
(Use decimal notation. Give your answers as whole or exact numbers.)
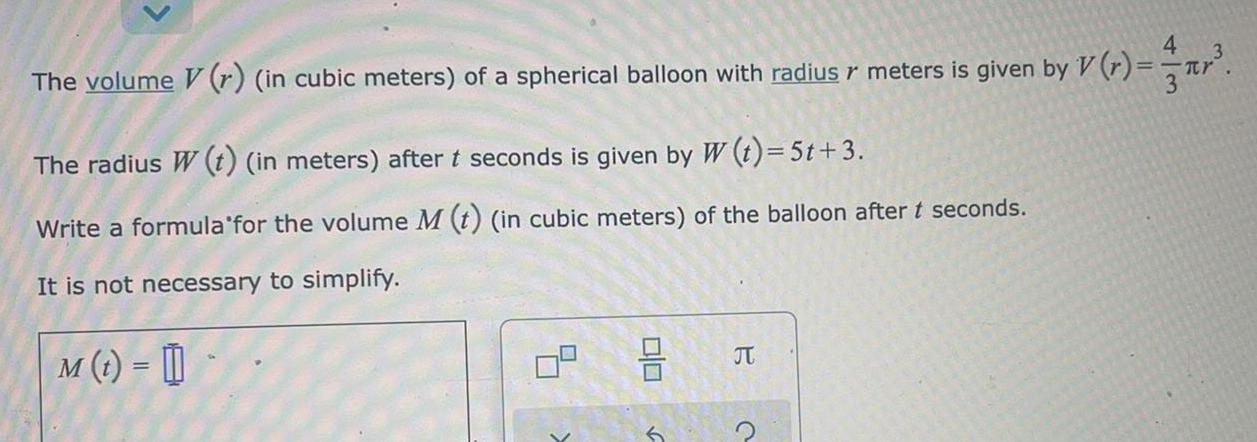
Math
Application of derivativesThe volume (r) (in cubic meters) of a spherical balloon with radius r meters is given by V(r) = 4/3πr³.
The radius W (t) (in meters) after t seconds is given by W (t) = 5t+3.
Write a formula for the volume M (t) (in cubic meters) of the balloon after t seconds.
It is not necessary to simplify.
M(t) =

Math
Application of derivativesGiven this function: f(x)=35+arcsin(x/11) an equation for the line tangent to the graph of y = f(x) at the point where x=11/2 is:
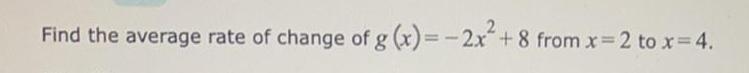

Math
Application of derivativesA cardboard box without a lid is to have a volume of 5,324 cm³. Find the dimensions that minimize the amount of cardboard used.
(Let x, y, and z be the dimensions of the cardboard box.)
(x, y, z) =

Math
Application of derivativesIn Problems 3-6, find the slope msec of the secant
line through the two given points and then calculate
mtan = lim h→0 msec.
3. f(x) = x²
(a) (-2,4), (-2+h, (-2+h)2)
(b) (0.5, 0.25), (0.5+h, (0.5+h)²)
4. f(x) = 3+x²
(a) (1,4), (1+h,3 + (1 + h)²)
(b) (x,3+x²), (x+h,3 + (x + h)²)
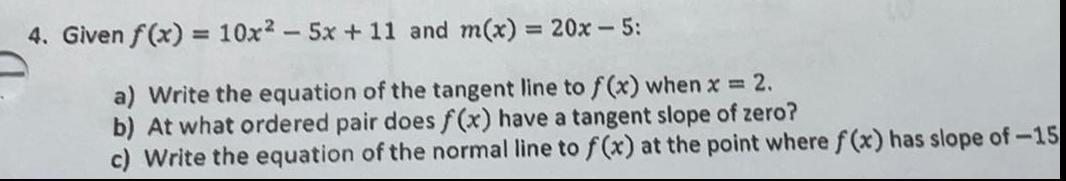
Math
Application of derivativesGiven f(x) = 10x² - 5x + 11 and m(x) = 20x - 5:
a) Write the equation of the tangent line to f(x) when x = 2.
b) At what ordered pair does f(x) have a tangent slope of zero?
c) Write the equation of the normal line to f(x) at the point where f(x) has slope of -15