Application of derivatives Questions and Answers

Math
Application of derivativesThe ideal gas law states that for an ideal gas PV=nRT, where P,V, and T are the pressure, volume, and absolute temperature, n is the number of moles of gas, and R is the ideal gas constant (0.0821). Suppose that currently the P = 8.0 atm (atmospheres) and is increasing at a rate of 0.15 atm/min and V = 9L and is decreasing at a rate of 0.1 L/min.
Find the rate of change of T with respect to time at this instant if n = 20 mol. (Hint: You will need implicit differentiation for this problem.)

Math
Application of derivativesIf 1400 square centimeters of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
Volume= (include units)
Math
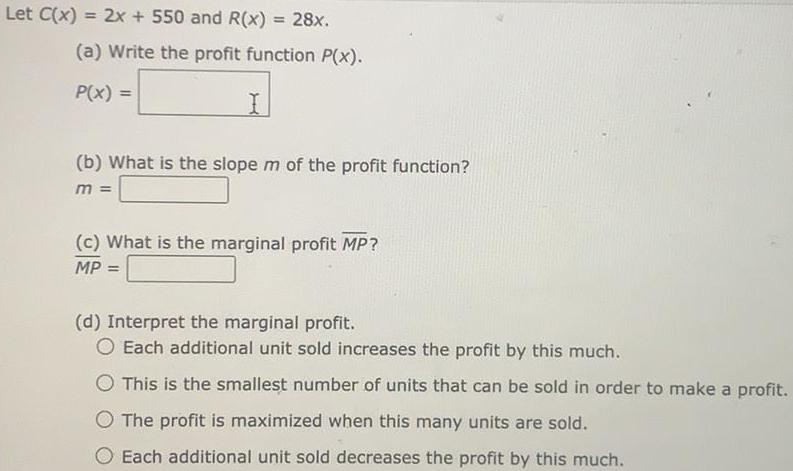
Application of derivativesLet C(x) = 2x + 550 and R(x) = 28x.
(a) Write the profit function P(x).
P(x) =
(b) What is the slope m of the profit function?
m=
(c) What is the marginal profit MP?
MP =
(d) Interpret the marginal profit.
Each additional unit sold increases the profit by this much.
This is the smallest number of units that can be sold in order to make a profit.
The profit is maximized when this many units are sold.
Each additional unit sold decreases the profit by this much.
Math
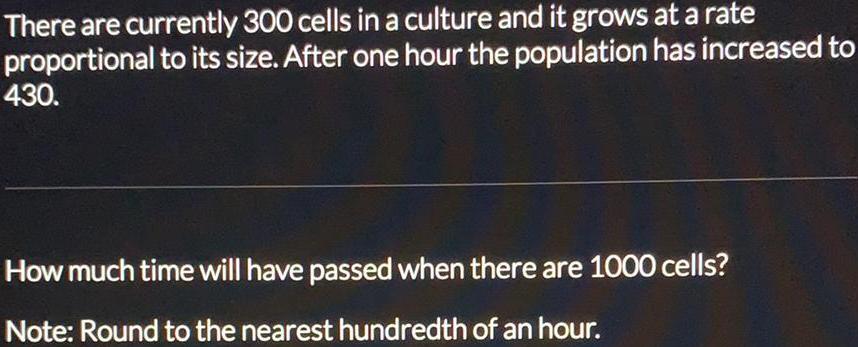
Application of derivativesThere are currently 300 cells in a culture and it grows at a rate
proportional to its size. After one hour the population has increased to
430.
How much time will have passed when there are 1000 cells?
Note: Round to the nearest hundredth of an hour.

Math
Application of derivativesA ball is thrown upward from the top of a building 340 feet tall. The height of the ball is described by the function h(t) = -16t² +320t + 340, where t is in seconds and t = 0 corresponds to the moment the ball is thrown.
Determine for what value of t the ball reaches the maximum height and determine this maximum height t=__ and maximum height=___

Math
Application of derivatives8) A cylindrical can without a top is to be made to contain 150 cubic centime- ters of liquid. Find the dimensions that will minimize the cost of the metal to make the can. (Recall that the volume formula for a cylinder is: V = r²h.)

Math
Application of derivativesIf a stone is thrown vertically upward from the surface of the moon with a velocity of 10 m/s, its height (in meters) after t seconds is h(t) = 10t - 0.83²
(a) What is the velocity of the stone after 4 seconds?
(b) What is the velocity of the stone after it has risen 25 m?


Math
Application of derivativesSand is poured onto a surface at 20 cm³/s, forming a conical pile whose
base diameter is always equal to its altitude.
How fast (in cm/s) is the altitude of the pile increasing when the pile is 3 cm high? Remember, the volume of a cone is V =πr ².
Note: Round to the nearest hundredth.
Math
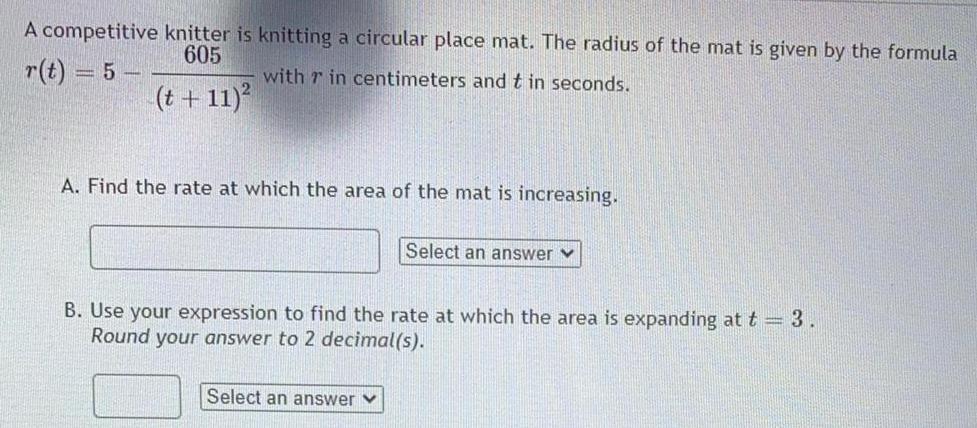
Application of derivativesA competitive knitter is knitting a circular place mat. The radius of the mat is given by the formula
r(t) = 5- 605/(t + 11)²
with 7 in centimeters and t in seconds.
A. Find the rate at which the area of the mat is increasing.
Select an answer
B. Use your expression to find the rate at which the area is expanding at t = 3.

Math
Application of derivativesThe length of a rectangle is increasing at a rate of 8 cm/s and its width is increasing at a rate of 3 cm/s. When the length is 11 cm and the width is 5 cm, how fast is the area of the rectangle increasing? cm²/s
![A function f(x) and interval [a, b] are given. Check if the Mean Value Theorem can be applied to f on [a, b]. If so, find all values c in [a, b] guaranteed by the Mean Value Theorem
Note, if the Mean Value Theorem does not apply, enter DNE for the c value.
f(x) = 4 sin-1x on [-1,1]
(Separate multiple answers by commas.)](https://media.kunduz.com/media/sug-question/raw/44722078-1658253976.644671.jpeg?w=256)
Math
Application of derivativesA function f(x) and interval [a, b] are given. Check if the Mean Value Theorem can be applied to f on [a, b]. If so, find all values c in [a, b] guaranteed by the Mean Value Theorem
Note, if the Mean Value Theorem does not apply, enter DNE for the c value.
f(x) = 4 sin-1x on [-1,1]
(Separate multiple answers by commas.)

Math
Application of derivativesConsider the function f(x)=-42+2 on the interval (0, 4) Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval
Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0 Find all such values c and enter them as a comma-separated list.
Values of c
Math
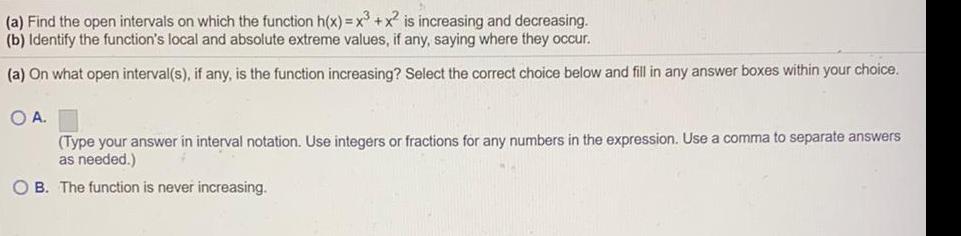
Application of derivativesFind the open intervals on which the function h(x)= x³ + x² is increasing and decreasing.
Identify the function's local and absolute extreme values, if any, saying where they occur.
(a) On what open interval(s), if any, is the function increasing? Select the correct choice below and fill in any answer boxes within your choice.
A.
(Type your answer in interval notation. Use integers or fractions for any numbers in the expression. Use a comma to separate answers
as needed.)
B. The function is never increasing.

Math
Application of derivativesA management consultant estimates that the number h of hours per day that employees will work and their daily pay of p dollars are related by the equation 90h5 + 18,000,000 = p³. Find dh/ dp at p = 300 and interpret your answer.
![Find the absolute maximum and minimum values of f(z) = (x²+x)^2/3 over the interval [-2, 3].
absolute maximum is
and it occurs at x =
absolute minimum is
and it occurs at x =
Notes: If there is more than one z value, enter as a comma separated list.](https://media.kunduz.com/media/sug-question/raw/43672145-1658251935.5916944.jpeg?w=256)
Math
Application of derivativesFind the absolute maximum and minimum values of f(z) = (x²+x)^2/3 over the interval [-2, 3].
absolute maximum is
and it occurs at x =
absolute minimum is
and it occurs at x =
Notes: If there is more than one z value, enter as a comma separated list.
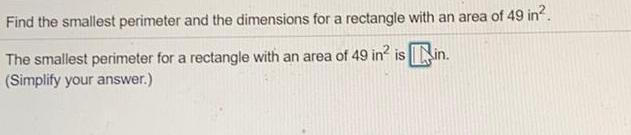
Math
Application of derivativesFind the smallest perimeter and the dimensions for a rectangle with an area of 49 in².
The smallest perimeter for a rectangle with an area of 49 in² is in. (Simplify your answer.)

Math
Application of derivativesAt 2:00pm a car's speedometer reads 50mph, and at 2 10pm it reads 70mph. Use the Mean Value Theorem to find an acceleration the car must achieve Answer( in mi/h²)

Math
Application of derivativesMarine ecologists estimate the reproduction curve for swordfish in a fishing ground to be f(p) = -0.01p² + 8p, where p and f(p) are in hundreds. Find the population that gives the maximum sustainable yield, and the size of the yield.
population size of the yield
X hundred swordfish
X hundred swordfish
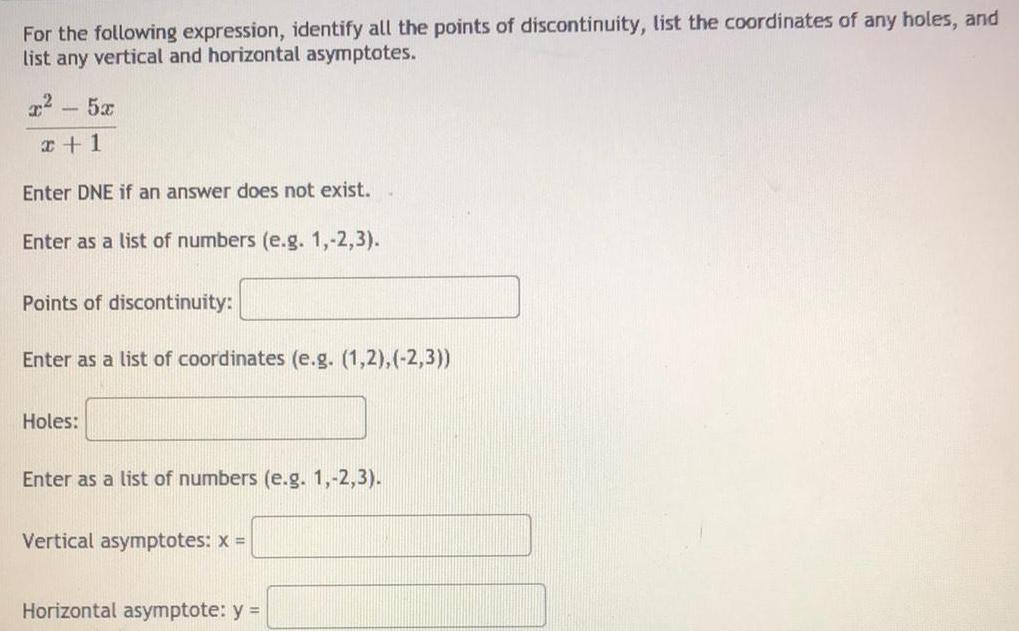
Math
Application of derivativesFor the following expression, identify all the points of discontinuity, list the coordinates of any holes, and list any vertical and horizontal asymptotes.
x² - 5x / x+1
Enter DNE if an answer does not exist.
Enter as a list of numbers (e.g. 1,-2,3).
Points of discontinuity:
Enter as a list of coordinates (e.g. (1,2), (-2,3))
Holes:
Enter as a list of numbers (e.g. 1,-2,3).
Vertical asymptotes: x =
Horizontal asymptote: y =

Math
Application of derivativesFind the coordinates of any local extreme points and inflection points. Use these to graph the function y=x- sin(-x) on the interval 0≤x≤2R.
Choose the correct answer regarding local extreme points.
A. The function as no local extreme points.
B. Local minimum: (0,0)
Local maximum: (2x,2x)
C. Local maximum: (0,0)
Local minimum: (21,2x)
D. The function has a local maximum at (x,x).
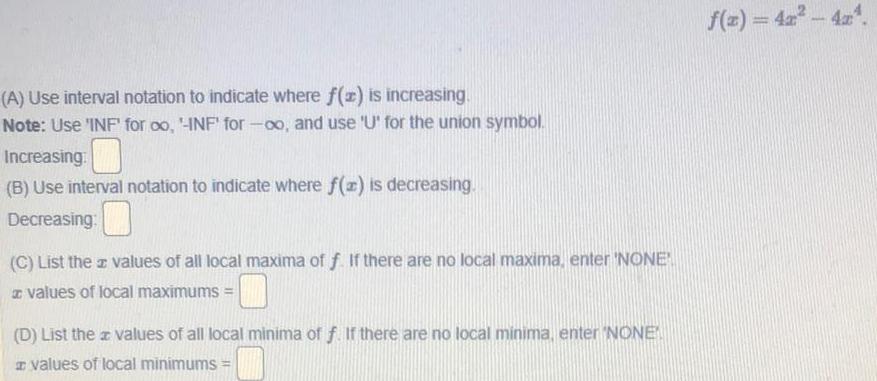
Math
Application of derivatives(A) Use interval notation to indicate where f(x) is increasing.
Note: Use 'INF' for oo, '-INF' for -oo, and use 'U' for the union symbol.
Increasing:
(B) Use interval notation to indicate where f(x) is decreasing.
Decreasing:
(C) List the values of all local maxima of f. If there are no local maxima, enter 'NONE'
values of local maximums =
(D) List the values of all local minima of f. If there are no local minima, enter "NONE"
values of local minimums =
f(x) = 4x² - 4x
![f(x)=32-15 ln(3x)
on the interval [3,9].
Enter DNE for any absolute extrema that does not exist.
Absolute maximum =
Absolute minimum
=](https://media.kunduz.com/media/sug-question/raw/43672134-1658249900.7889009.jpeg?w=256)
Math
Application of derivativesf(x)=32-15 ln(3x)
on the interval [3,9].
Enter DNE for any absolute extrema that does not exist.
Absolute maximum =
Absolute minimum
=

Math
Application of derivativesA landscape architect wished to enclose a rectangular garden on one side by a brick wall costing $60/ft and on the other three sides by a metal fence costing $50/fL. If the area of the garden is 182 square
feet, find the dimensions of the garden that minimize the cost.
Length of side with bricks x =
Length of adjacent side y =

Math
Application of derivativesA stone dropped in a pond sends out a circular ripple whose radius increases at a constant rate of 4 ft/sec. After 12 seconds, how rapidly is the area inclosed by the ripple increasing? Recall the area of a circle is given by A= πr².

Math
Application of derivativesA girl flies a kite at a height of 300 ft, and the wind carries the kite horizontally away from her at a rate of 25 ft/sec. How fast must she let out the string when the kite is 500 ft away from her?

Math
Application of derivativesThe length, width, and height of a box are measured as 8 ft, 7 ft, and 6 ft, respectively, with an error in measurement of at most 0.1 ft in each. Use differentials to estimate the maximum error (in feet) in the calculated volume of the box.

Math
Application of derivativesThe original 24 m edge length x of a cube decreases at the rate of 5 m/min.
a. When x = 5 m, at what rate does the cube's surface area change?
b. When x = 5 m, at what rate does the cube's volume change?
a. When x = 5 m, the surface area is changing at a rate of m²/min.
(Type an integer or a decimal.)

Math
Application of derivativesWater is dropped at the rate of 2cm³/sec into a cone of semivertical angle 45°. The rate at which periphery of water surface changes when height of the water in the cone is 2 cm, is :-
1 cm/sec
2 cm/sec
3 cm/sec
4 cm/sec

Math
Application of derivativesA rectangular piece of cardboard, 100 cm by 40 cm, is going to be used to make a rectangular box with an open top by cutting congruent squares from the corners. Calculate the dimensions (to one decimal place) for a box with the largest volume.
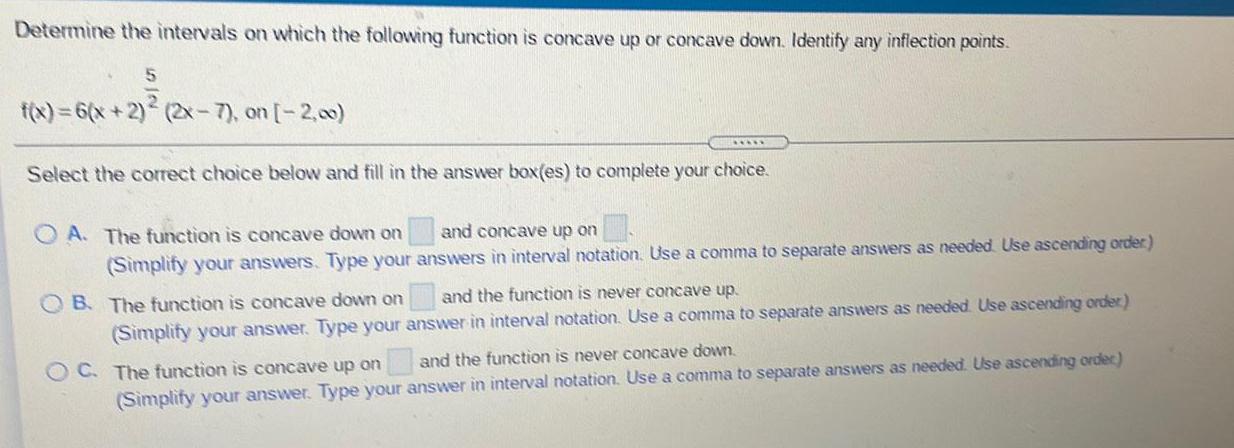
Math
Application of derivativesDetermine the intervals on which the following function is concave up or concave down. Identify any inflection points.
f(x) = 6(x + 2)5/2 (2x-7), on [-2,00)

Math
Application of derivativesA company sells x ribbon winders per year at $p per ribbon
winder. The demand function for ribbon winders is given by p = 250
- 0.04x. Determine the elasticity of demand when the price is $75
apiece.
Round your answer to the nearest hundredth.
0.21
0.22
0.23
0.24
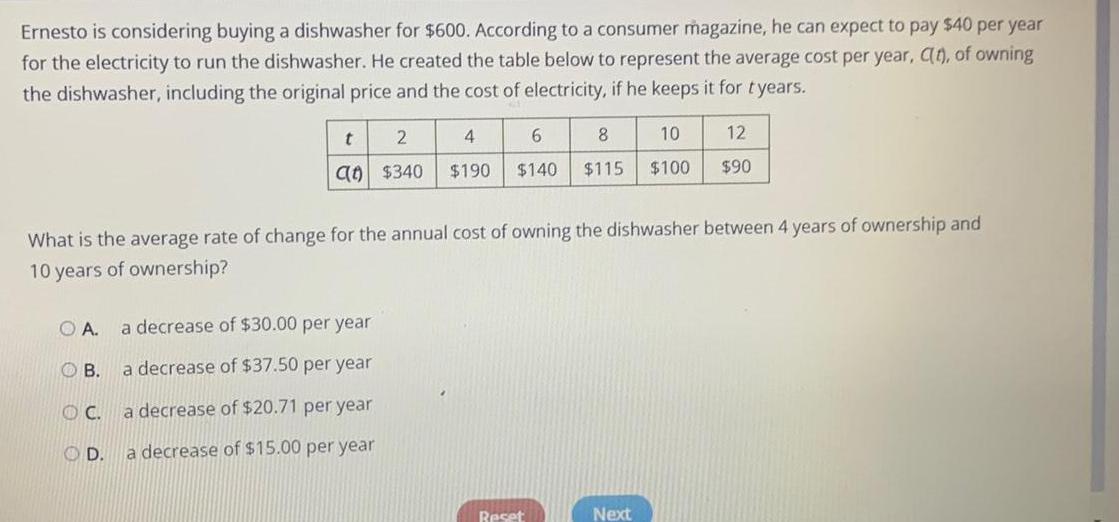
Math
Application of derivativesErnesto is considering buying a dishwasher for $600. According to a consumer magazine, he can expect to pay $40 per year for the electricity to run the dishwasher. He created the table below to represent the average cost per year, C(t), of owning the dishwasher, including the original price and the cost of electricity, if he keeps it for tyears.
What is the average rate of change for the annual cost of owning the dishwasher between 4 years of ownership and 10 years of ownership?

Math
Application of derivativesA rain gutter is formed by bending up the sides of a 52-in.-wide rectangular metal sheet as shown in the figure
(a) Find a function that models the cross-sectional area of the gutter in terms of x.
(b) Find the value of x that maximizes the cross-sectional area of the gutter.
(c) What is the maximum cross-sectional area for the gutter?

Math
Application of derivativesa. Write the equation of the line that represents the linear approximation to the following function at the given point a.
b. Use the linear approximation to estimate the given quantity.
c. Compute the percent error in the approximation, 100.|approximation - exact|/|exact|
where the exact value is given by a calculator.
f(x) = 6-x² at a = 1; f(0.9)
![Which of the following is true about the graph of f(x) = 2 sin³(x) + 3 sin(x) + 2 on the interval [0, π]?
a) f(x) has a local minimum at the point (π,7).
b) f(x) has points of inflection at the points (π/4,2√2+2) and (3π/4, 2√2+2).
c) f(x) is concave down on the interval (0, π).
d) f(x) is concave up on the interval (0, π).
e) f(x) is increasing on the interval (π/2, π).](https://media.kunduz.com/media/sug-question/raw/56487952-1658174257.3880801.jpeg?w=256)
Math
Application of derivativesWhich of the following is true about the graph of f(x) = 2 sin³(x) + 3 sin(x) + 2 on the interval [0, π]?
a) f(x) has a local minimum at the point (π,7).
b) f(x) has points of inflection at the points (π/4,2√2+2) and (3π/4, 2√2+2).
c) f(x) is concave down on the interval (0, π).
d) f(x) is concave up on the interval (0, π).
e) f(x) is increasing on the interval (π/2, π).

Math
Application of derivativesA toy manufacturer determines that the daily cost, C, for producing x units of a dump truck can be approximated by the function C(x) = 0.01x²-x+104.
a. How many toy dump trucks must the manufacturer produce per day in order to minimize the cost?
b. What is the minimum daily cost?

Math
Application of derivativesThe profit for a product can be described by the function P(x)=202x-5000-x² dollars, where x is the number of units produced and sold. To maximize profit, how many units must be produced and sold? What is the maximum possible profit?
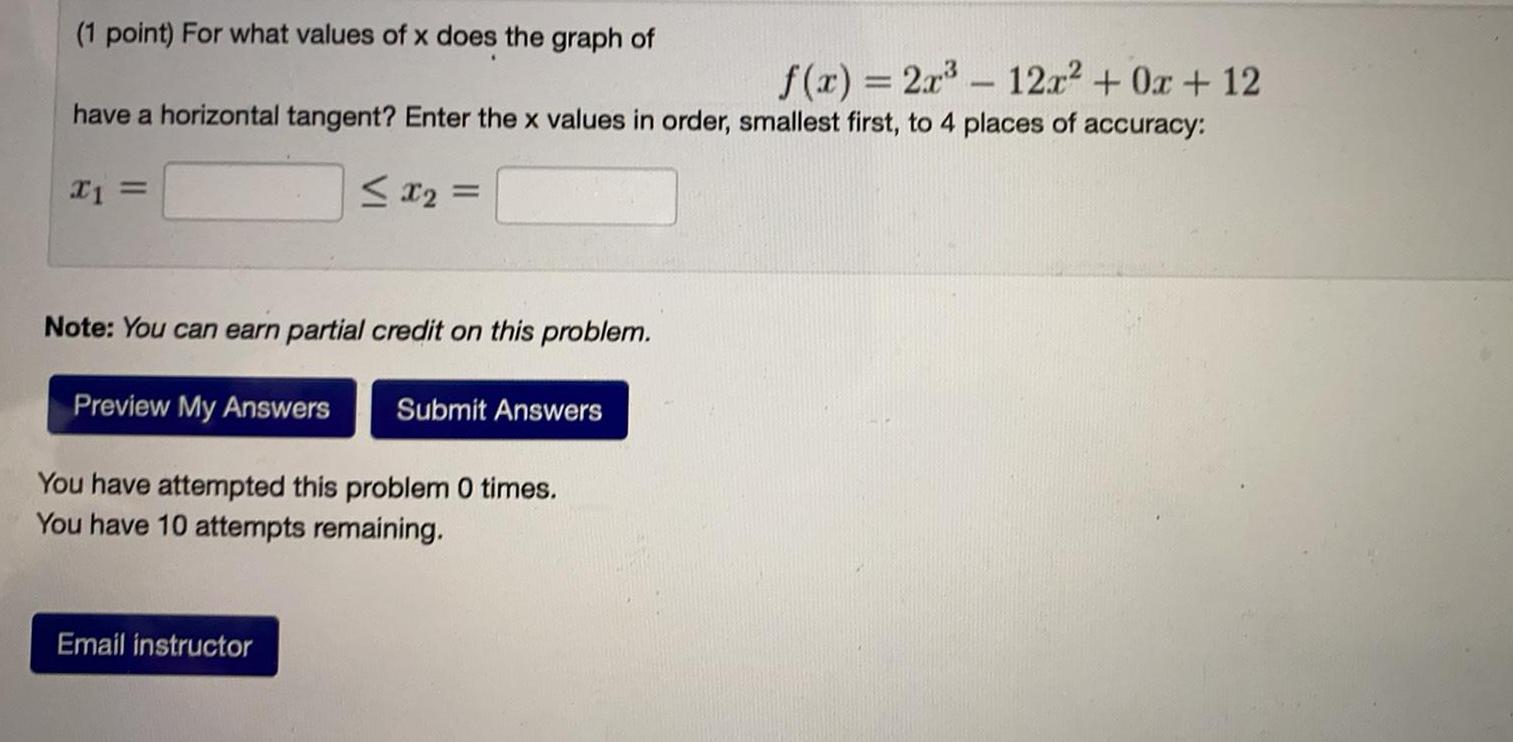
Math
Application of derivativesFor what values of x does the graph of
f(x) = 2x³ - 12x² + 0x + 12
have a horizontal tangent? Enter the x values in order, smallest first, to 4 places of accuracy:
x1 = ≤ x₂ =

Math
Application of derivativesA rock is thrown off of a 100 foot cliff with an upward velocity of 50 m/s. As a result its height after t seconds is given by the formula:
h(t) = 100+ 50t - 5t²
What is its height after 3 seconds?
What is its velocity after 3 seconds?
(Positive velocity means it is on the way up, negative velocity means it is on the way down.)

Math
Application of derivativesIf a person's temperature after x hours of strenuous exercise is T(x) = x²(7-x²) + 98.6 degrees Fahrenheit (for 0 ≤ x ≤ 2), find the rate of change of the temperature after 2 hours.
°F/hr
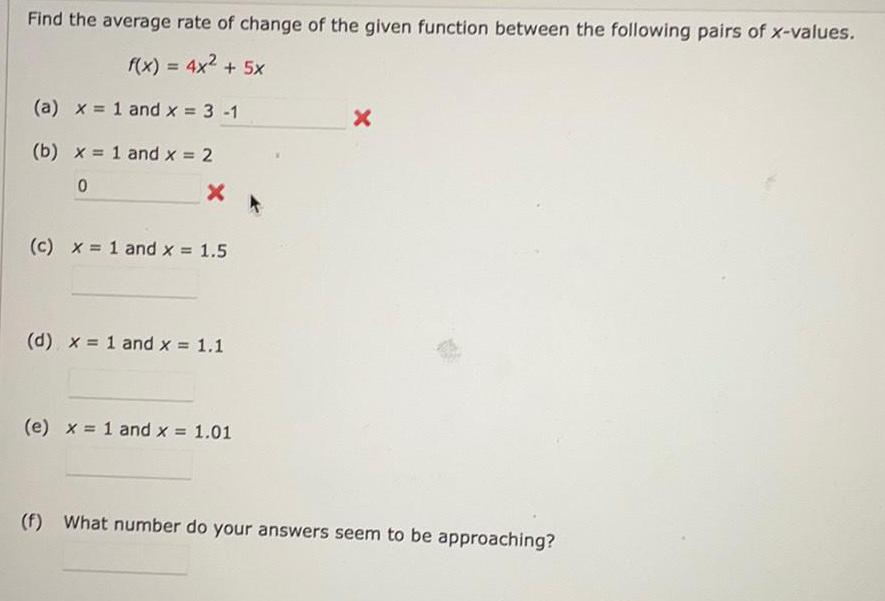
Math
Application of derivativesFind the average rate of change of the given function between the following pairs of x-values.
f(x) = 4x² + 5x
(a) x = 1 and x = 3
(b) x = 1 and x = 2
(c) x = 1 and x = 1.5
(d) x = 1 and x = 1.1
(e) x = 1 and x = 1.01
(f) What number do your answers seem to be approaching?

Math
Application of derivativesUse the Generalized Power Rule to find the derivative of the function.
f(x) = (3x + 1)^4 (3x - 1)^5
f'(x) =
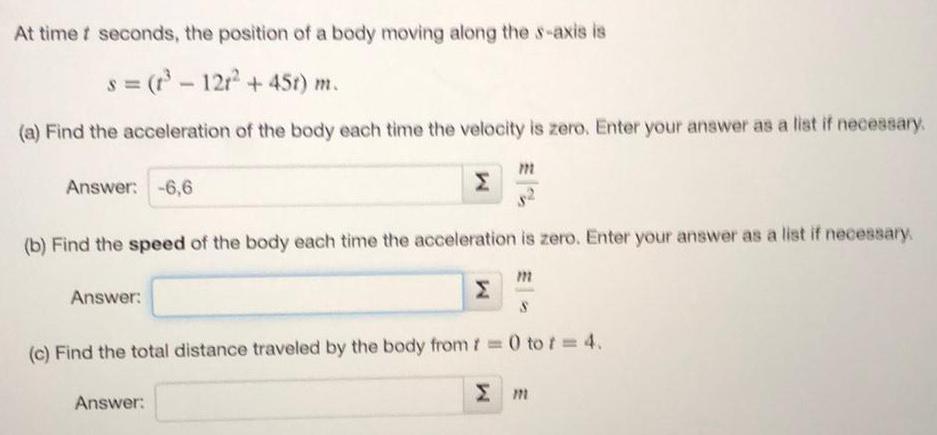
Math
Application of derivativesAt time t seconds, the position of a body moving along the s-axis is
s = (³-12t² + 45t) m.
(a) Find the acceleration of the body each time the velocity is zero. Enter your answer as a list if necessary.
Answer: -6,6
(b) Find the speed of the body each time the acceleration is zero. Enter your answer as a list if necessary.
(c) Find the total distance traveled by the body from t=0 tot = 4.
Σm

Math
Application of derivatives1. (5 pts) Graph one continuous function f(x) such that all of the following hold:
a. f(x) is increasing on (-∞, -4)
b. f(x) is constant on (-4,2)
c. f(x) is decreasing on (2,5)
d. f(x) is increasing on (5,0)

Math
Application of derivativesA Kite 50 feet above the ground moves horizontally at a speed of 9 ft/sec. At what rate is the angle between the string and the ground decreasing when 140 feet of string is out?

Math
Application of derivativesBert is going to claim a depreciation tax credit for his business car. The car costs $28,000 when new, and Bert anticipates it will be worth $16,000 three years later.
(d) How long does it take for the car to lose all of its value?
(c) Express the value V of the car as linear function of time t, the number of years after the car was purchased.
(e) In the context of this problem, what is the range of the linear function?
Math
Application of derivativesFor what values of x does the graph of f(x) = x³ + 2x² + x + 16 have a horizontal tangent?
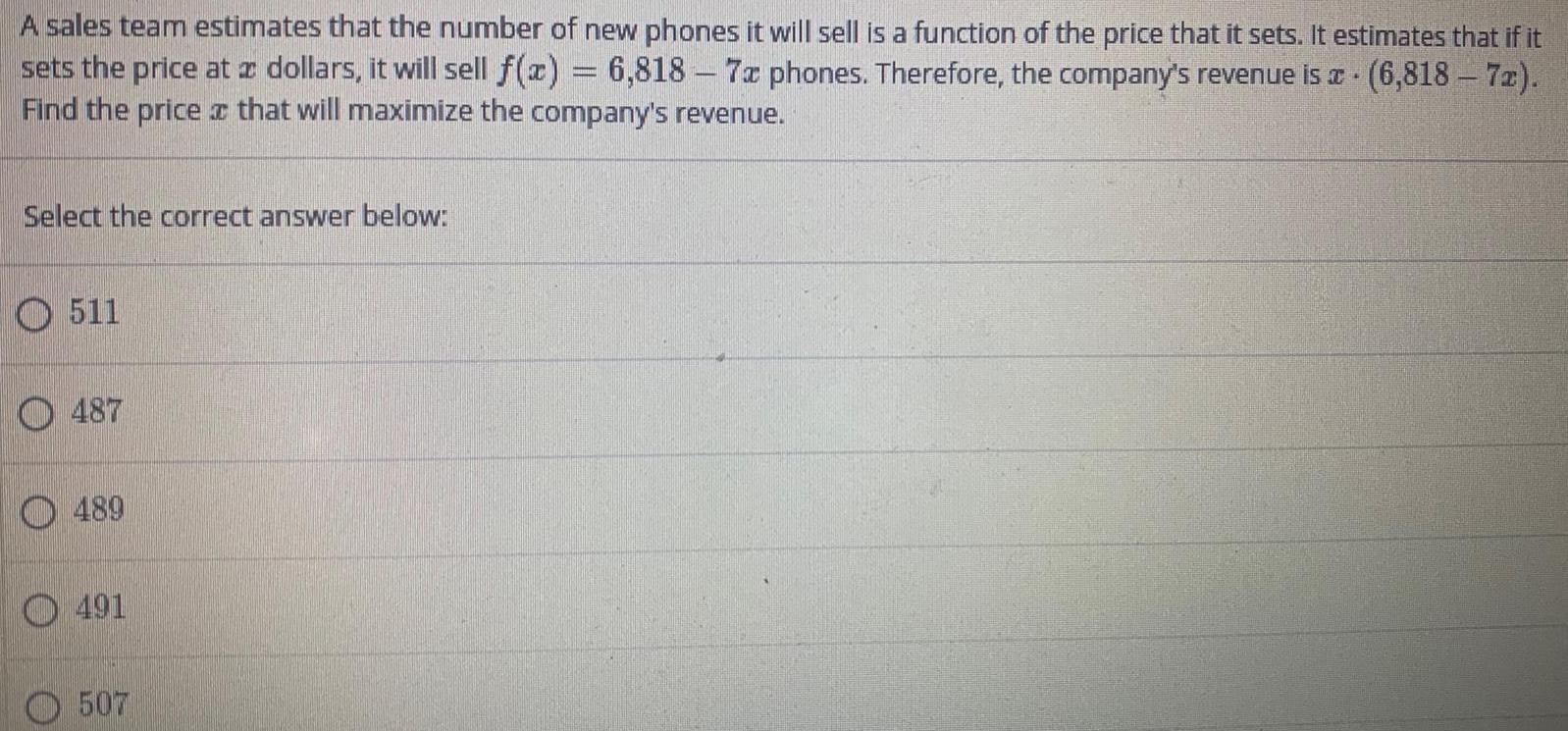
Math
Application of derivativesA sales team estimates that the number of new phones it will sell is a function of the price that it sets. It estimates that if it sets the price at a dollars, it will sell f(x) = 6,818 - 7x phones. Therefore, the company's revenue is x(6,818 - 7x).
Find the price that will maximize the company's revenue.
Select the correct answer below:
511
487
489
491
507
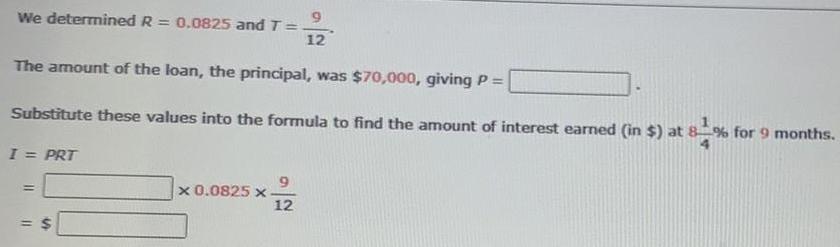
Math
Application of derivativesWe determined R = 0.0825 and T = 9/15
The amount of the loan, the principal, was $70,000, giving P =
Substitute these values into the formula to find the amount of interest earned (in $) at 8 1/4 % for 9 months.
I = PRT