Application of derivatives Questions and Answers

Math
Application of derivativesThe weekly sales of Honolulu Red Oranges is given by q = 960-10p. Calculate the price elasticity of demand when the price is $32 per orange (yes, $32 per oranget).
Interpret your answer.
The demand is going by % per 1% increase in price at that price level.
Also, calculate the price that gives a maximum weekly revenue.
$
Find this maximum revenue..
$
Math
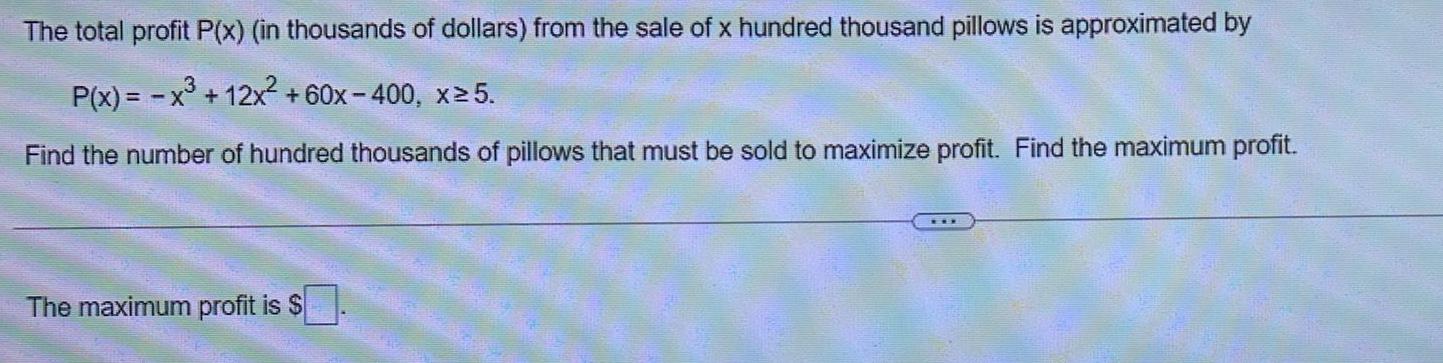
Application of derivativesThe total profit P(x) (in thousands of dollars) from the sale of x hundred thousand pillows is approximated by
P(x)= x³ + 12x²+60x-400, x≥5.
Find the number of hundred thousands of pillows that must be sold to maximize profit. Find the maximum profit.
Math
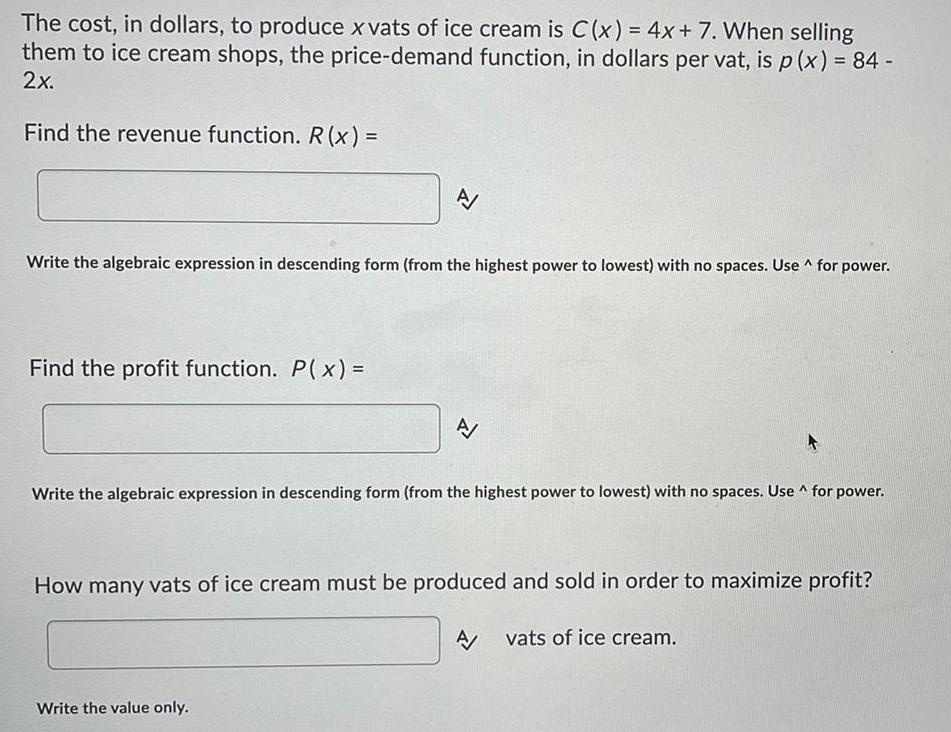
Application of derivativesThe cost, in dollars, to produce x vats of ice cream is C(x) = 4x + 7. When selling them to ice cream shops, the price-demand function, in dollars per vat, is p(x) = 84 - 2x.
Find the revenue function. R(x) =
Find the profit function. P(x) =
How many vats of ice cream must be produced and sold in order to maximize profit?

Math
Application of derivativesA ball is thrown vertically upward. After t seconds, its height / (in feet) is given by the function h (t) = 961-167. What is the maximum height that the ball
will reach?
Do not round your answer.
Height: fe
feet
X

Math
Application of derivativesIf 1,200 cm² of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
cm³

Math
Application of derivativesA rectangular piece of land is to be fenced using two kinds of fencing. Two
opposite sides will be fenced using standard fencing that costs $6/m, while
the other two sides will require heavy-duty fencing that costs $9/m. What are
the dimensions of the rectangular lot of greatest area that can be fenced for a
cost of $9000?

Math
Application of derivatives(a) Find an equation of the tangent plane to the surface at the given point.
x2 + y2 + z² = 19, (1, 3, 3)

Math
Application of derivativesFind the point(s) on the surface at which the tangent plane is horizontal.
z = 9-x² - y² + 4y
(x, y, z) = (
)

Math
Application of derivativesA sociologist determines that a foreign-language student has learned N(t) = 20t - 2 vocabulary terms after t hours of uninterrupted study.
a. How many terms are learned between times t = 2 and t = 3?
b. What is the rate, in terms per hour, at which the student is learning at time t = 2?
c. What is the maximum rate, in terms per hour, at which the student is learning?

Math
Application of derivativesConsider h(x) = 5x² +7-x³ +7x
Determine the intervals on which h is concave down.
h is concave down on:
h is concave down nowhere.
Determine the intervals on which his concave up.
h is concave up on:
h is concave up nowhere.
Determine the value and location of any inflection point of h. Enter the solution in (x, h(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has an inflection point at:
h has no inflection point.
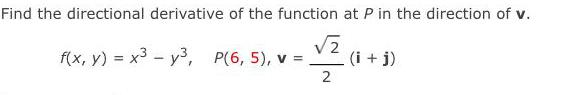
Math
Application of derivativesFind the directional derivative of the function at P in the direction of v.
f(x, y) = x³-y³, P(6, 5), v =√2/2(i+j)

Math
Application of derivativesArchaeologists used pieces of burned wood, or charcoal, found at the site to date prehistoric paintings and drawings on walls and ceilings of a cave in Lascaux, France. Use the information in Example 3 of Section 3.1 to determine the appropriate age of a piece of burned wood, if it was found that 83.5% of the C-14 found in living trees of the same type had decayed. (Round your answer to the nearest hundred years.)
![Which of the following functions of x is guaranteed by the Extreme Value Theorem to have an absolute maximum on the interval [0, 4]?
y = sinx
y = sin-¹x
y=tanx
y =x²-16/x²+x-20](https://media.kunduz.com/media/sug-question/raw/69716443-1657462831.3632874.jpeg?w=256)
Math
Application of derivativesWhich of the following functions of x is guaranteed by the Extreme Value Theorem to have an absolute maximum on the interval [0, 4]?
y = sinx
y = sin-¹x
y=tanx
y =x²-16/x²+x-20
Math
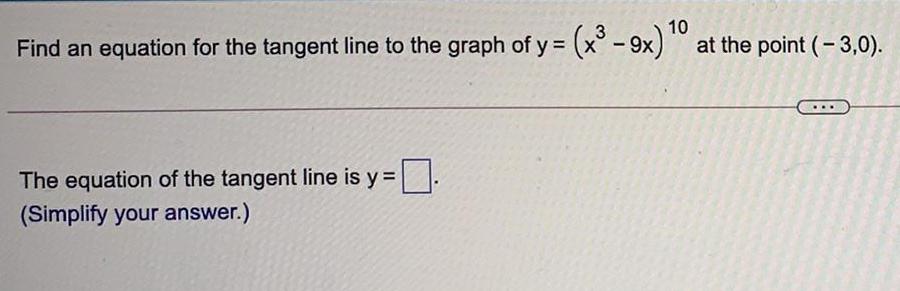
Application of derivativesFind an equation for the tangent line to the graph of y = (x³ - 9x) ^10 at the point ( – 3,0).
The equation of the tangent line is y=.
(Simplify your answer.)

Math
Application of derivativesA thermometer is removed from a room where the temperature is 70° F and is taken outside, where the air temperature is 30° F. After one-half minute the thermometer reads 50° F. What is the reading of the thermometer at t = 1 min? (Round your answer to
two decimal places.)
How long will it take for the thermometer to reach 35° F? (Round your answer to two decimal places.)
min

Math
Application of derivativesThe radioactive isotope of lead, Pb-209, decays at a rate proportional to the amount present at time t and has a half-life of 3.3 hours. If 1 gram of this isotope is present initially, how long will it take for 85% of the lead to decay? (Round your answer to two decimal places.) hr
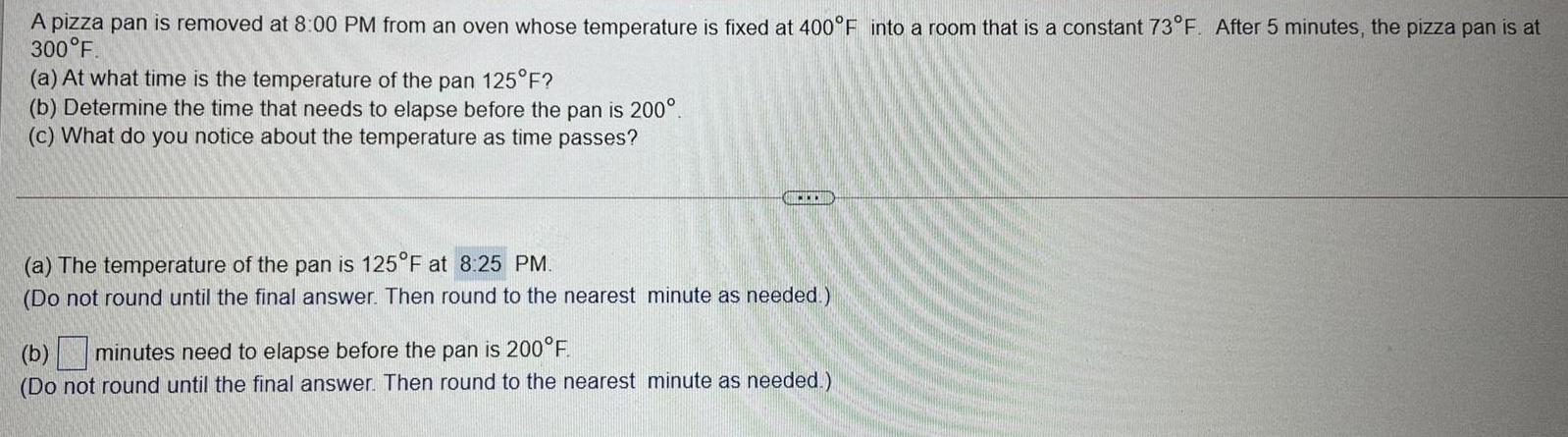
Math
Application of derivativesA pizza pan is removed at 8:00 PM from an oven whose temperature is fixed at 400°F into a room that is a constant 73°F. After 5 minutes, the pizza pan is at 300°F.
(a) At what time is the temperature of the pan 125°F?
(b) Determine the time that needs to elapse before the pan is 200°.
(c) What do you notice about the temperature as time passes?
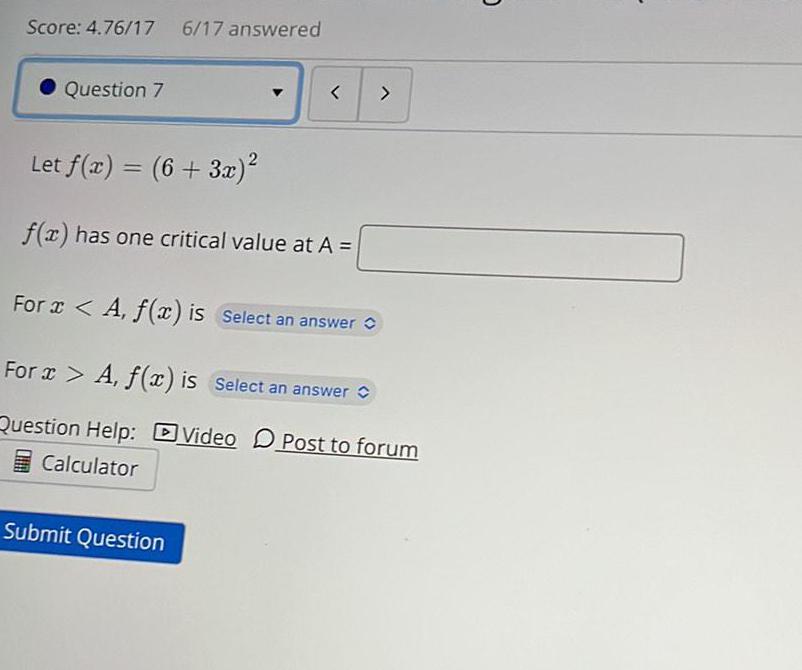
Math
Application of derivativesLet f(x) = (6 + 3x)²
f(x) has one critical value at A =
For x < A, f(x) is
For x> A, f(x) is
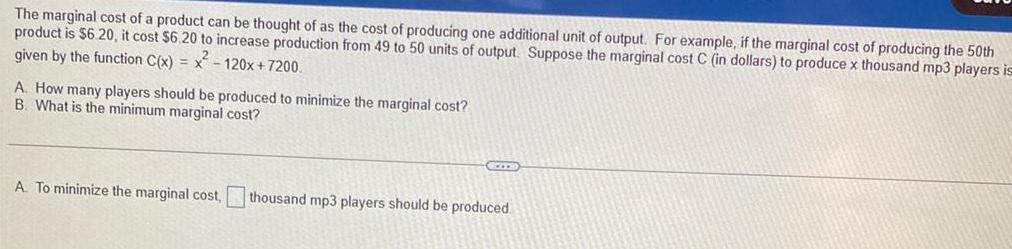
Math
Application of derivativesThe marginal cost of a product can be thought of as the cost of producing one additional unit of output. For example, if the marginal cost of producing the 50th product is $6.20, it cost $6.20 to increase production from 49 to 50 units of output. Suppose the marginal cost C (in dollars) to produce x thousand mp3 players is given by the function C(x) = x²- 120x+7200.
A. How many players should be produced to minimize the marginal cost?
B. What is the minimum marginal cost?

Math
Application of derivativesThe depth of a rain puddle D(t) is given in inches, and t is given in minutes. If the depth is changing with respect to time, which expression gives the rate of change at which the depth is changing at 1 minute?
D"(1)
D"(0) - D"(2)
D'(1)
D(0)-D(2)

Math
Application of derivativesConsider the surface z=f(x,y) = 3x² + 5y² +1 and the curve C in the xy-plane given parametrically as x= cost and y=sint where Osts2.
a. Find z'(t).
b. Imagine that you are walking on the surface directly above the curve C in the direction of positive orientation. Find the values of t for which you are walking uphill
(that is, z is increasing).
a. Find the intermediate derivatives.
dz/ax
(Type an expression using x and y as the variables.)
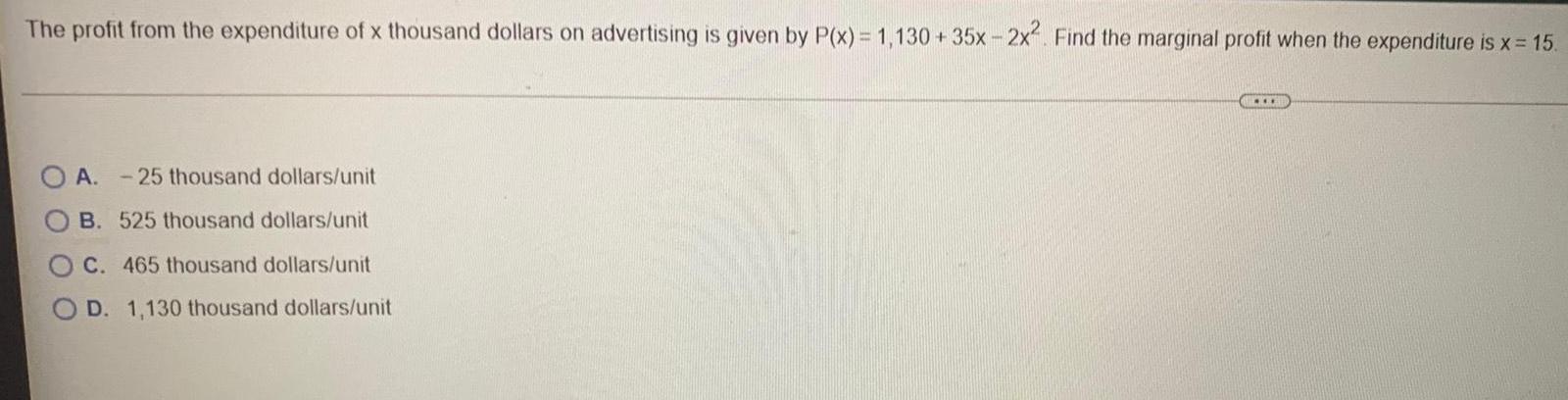
Math
Application of derivativesThe profit from the expenditure of x thousand dollars on advertising is given by P(x) = 1,130+35x-2x². Find the marginal profit when the expenditure is x = 15.
A. -25 thousand dollars/unit
B. 525 thousand dollars/unit
C. 465 thousand dollars/unit
D. 1,130 thousand dollars/unit

Math
Application of derivatives3. A dairy farmer plans to fence in a rectangular
pasture adjacent to a river. The river serves as one
border to the pasture, so the farmer does not need a
fence along that part. The pasture must contain
180,000 square meters in order to provide enough
grass for the herd. What dimensions would require
the least amount of fencing?
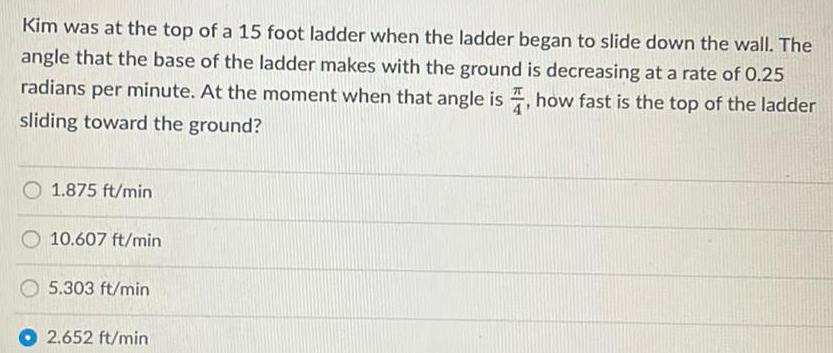
Math
Application of derivativesKim was at the top of a 15 foot ladder when the ladder began to slide down the wall. The angle that the base of the ladder makes with the ground is decreasing at a rate of 0.25 radians per minute. At the moment when that angle is, how fast is the top of the ladder sliding toward the ground?
1.875 ft/min
10.607 ft/min
5.303 ft/min
2.652 ft/min

Math
Application of derivativesA manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.4x² +9,000. How fast is the cost per month changing when production is changing at the rate of 13 units per month and the production level is 80 units?

Math
Application of derivativesYour company wants to make the largest and most luxurious rectangular dog kennels possible with 72 feet of fencing. The design of the kennel is to use the back side of the dog owner's house as one side of the kennel. The other three sides of the kennel must be made from the fencing. What is the largest area your company can make for these new kennels?

Math
Application of derivativesConsider the function on the interval (0, 2π).
f(x) = √3 sin x + cosx
(a) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation.)
increasing
decreasing
(b) Apply the First Derivative Test to identify the relative extrema.
relative maximum
relative minimum

Math
Application of derivativesFind a, b, c, and d such that the cubic function f(x) = ax³ + bx² + cx + d satisfies the given conditions.
Relative maximum: (3, 15)
Relative minimum: (5, 13)
Inflection point: (4, 14)
a=
b =
C=
d =

Math
Application of derivatives(5) A straight piece of wire of 28 cm is cut into two pieces. One piece is bent into a square (ie., dimensions x times x.) The other piece is bent into a rectangle with aspect ratio three (ie., dimensions y times 3y.) What are dimensions, in centimeters, of the square and the rectangle such that the sum of their areas is minimized? (6 points)

Math
Application of derivativesSuppose the velocity v of a motorboat coasting in water satisfies the differential equation dv/dt=kv². The initial speed of the motorboat is v(0) = 1 m/s. The speed at 2 seconds is 5 m/s. Find the speed at t = 1 second.

Math
Application of derivativesFind all the zeros of f(x) = x^3 + 2x^2 - 5x - 6 given that x = -3 is one of its zeros.

Math
Application of derivativesThe length of a rectangle is increasing at a constant rate of 3 cm/s, and its width is increasing at a constant rate of 0.5 cm/s. At the time the length is 5 cm and the width is 1.2 cm, how fast is the area of the rectangle increasing? (1 point)
15.6 cm²/s
6.1 cm²/s
6 cm²/s
1.5 cm²/s

Math
Application of derivativesA manufacturing plant calculates its Cost function, C(x), to be C(x) = x³ - 4x² + 50/x and its Revenue
function, R(x), to be R(x) = 50x. Construct the Profit function, P(x), and determine the x-value when
dP/dt is 4.544 and dx/dt = 0.05.

Math
Application of derivativesYour new house sits at a perpendicular distance of 6 miles from the county highway across a flat
parcel of land. The town where you work is 15 miles down the highway from that point P. You are
going to build a gravel road that will connect somewhere to the county highway. The maximum speed
on your gravel road will be 25 mph and the maximum speed on the county highway is 50 mph. You
would like to be able to drive to town in the shortest time.
a. Write the equation you will be working with in this problem.
b.
Use Calculus to determine how far down the highway from the point P you should connect your
road to the county highway.
C. How much time can be saved by constructing the road as you indicated in part b.

Math
Application of derivativesTwo rows of three cattle pens are going to be built using 400 meters of fencing. Each pen will be rectangular, the same size and the pens will form a single larger rectangle.
(a) Find a function A(l) that models the total area of the entire enclosure in terms of the length l of one of the sides of the larger enclosure.
(b) What are the dimensions of the entire enclosure that maximize the total area?

Math
Application of derivativesA company manufactures and sells x television sets per month. The monthly cost and price-demand equations are C(x) = 73,000 + 70x and p(x) = 250--
(A) Find the maximum revenue.
(B) Find the maximum profit, the production level that will realize the maximum profit, and the price the company should charge for each television set.
(C) If the government decides to tax the company $4 for each set it produces, how many sets should the company manufacture each month to maximize its profit? What is the maximum profit? What should the company charge
for each set?
(A) The maximum revenue is $312500
(Type an integer or a decimal.)
(B) The maximum profit is $ when
(Type integers or decimals.)
sets are manufactured and sold for $ each.
20
, 0≤x≤ 5000.

Math
Application of derivativesIn 1958, you could buy an Edsel Citation convertible for $3800. Cars often depreciate in value rapidly, but one of these convertibles in "winning-show" condition could sell for up to $62,000 today. Suppose the value of this car could be modeled by the quadratic expression, v(t) = 23t - 450t + $3800, where t is the number of years since 1958.
a. Since this car was always kept in mint condition, what year would have been the worst year to sell the car?

Math
Application of derivativesSince 1915, the infant mortality rate (in number of deaths per 1000 live births) could be approximated by the equation r(t) = 0.01t² - 2t + 97, where t is the number of years since 1915.
In what year does your model predict when the minimum number of deaths per 1000 live births would occur? Does this make sense?

Math
Application of derivativesYou regularly pay your nephew to drive a semi hauling hay a distance of 170 miles. You have just learned that the stretch of highway that he drives no longer has a speed limit. The semi can do 90 miles/hour for the entire trip, and of course you want the trip to go quickly since you are paying your nephew $100/hour during the drive. However, the cost of fuel varies directly with the square of the speed of the truck and is calculated by taking 0. 1v². If your desire is to minimize cost...
a. Write the equation you will be working with in this problem.
b. Use Calculus to determine the speed (to the nearest mile per hour) you should tell your nephew to drive to minimize the total (overall) cost per trip.

Math
Application of derivatives11
A 5-foot ladder is leaning against a vertical wall. If the bottom of the ladder is being pulled away from the wall at the rate of 2 feet per second,
at what rate is the area of the triangle formed by the wall, the ground, and the ladder changing, in square feet per second, at the instant the
bottom of the ladder is 4 feet from the wall?
b)
O
O
e) 07/3
7
14
3
Review La
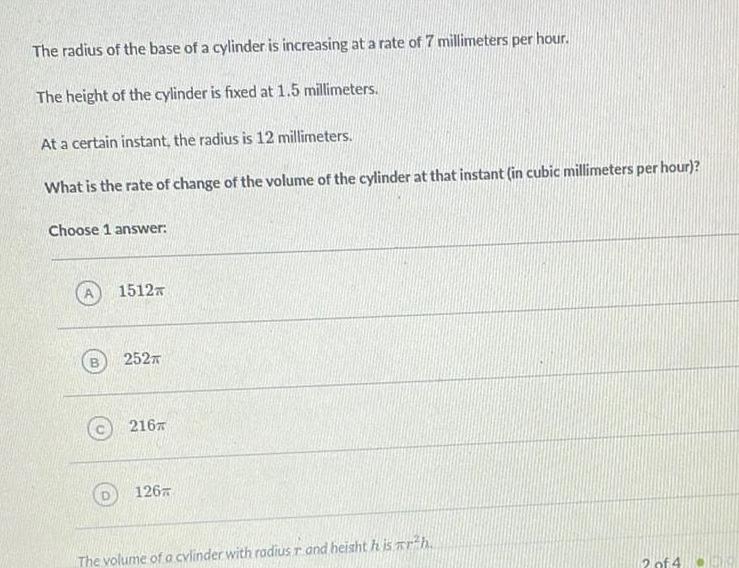
Math
Application of derivativesThe radius of the base of a cylinder is increasing at a rate of 7 millimeters per hour.
The height of the cylinder is fixed at 1.5 millimeters.
At a certain instant, the radius is 12 millimeters.
What is the rate of change of the volume of the cylinder at that instant (in cubic millimeters per hour)?
Choose 1 answer:
1512
252
216
126
The volume of a cylinder with radius r and height his wrh.
2 of 4

Math
Application of derivatives9. Suppose that a product has a revenue function given by R(x) = 2500x - 2x³ and a cost function given by C(x) = x² + 2x + 1000. Find the level of rounded to the nearest production, is for which marginal profit unit, equal to 80.
A)17
B) 20
C) 23
D) 26
E) 29

Math
Application of derivativesA ball is thrown vertically upward. After f seconds, its height / (in feet) is given by the function h(t)-1161-167. What is the maximum height that the ball
will reach?
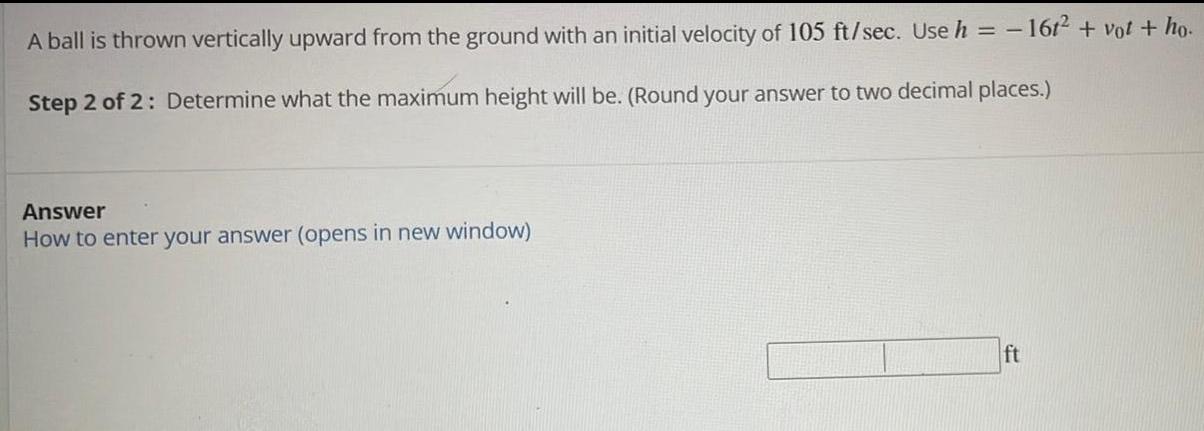
Math
Application of derivativesA ball is thrown vertically upward from the ground with an initial velocity of 105 ft/sec. Use h = -16t² + vot + ho.
Step 2 of 2: Determine what the maximum height will be. (Round your answer to two decimal places.)

Math
Application of derivativesA rectangle has a length of 11 inches and a width of 2 inches whose sides are changing. The length is increasing by 5 in/sec and the width is growing at 7 in/sec. What is the rate of change of the perimeter?
![Find the absolute maximum and minimum, if either exists, for the function on the indicated interval.
f(x) = 2x³-36x² +210x+4
(A) [-2, 10] (B) [-2,7] (C) [6, 10]
(A) Find the absolute maximum. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The absolute maximum is at x =
(Use a comma to separate answers as needed.)
B. There is no absolute maximum.](https://media.kunduz.com/media/sug-question/raw/61275607-1657322418.4735038.jpeg?w=256)
Math
Application of derivativesFind the absolute maximum and minimum, if either exists, for the function on the indicated interval.
f(x) = 2x³-36x² +210x+4
(A) [-2, 10] (B) [-2,7] (C) [6, 10]
(A) Find the absolute maximum. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The absolute maximum is at x =
(Use a comma to separate answers as needed.)
B. There is no absolute maximum.

Math
Application of derivativesSusan throws a softball upward into the air at a speed of 32 feet per second from a 40-foot platform. The height of the ball after seconds is given by the function h(t)= -16t² + 32t + 40 What is the maximum height reached by the softball and at what time does this maximum height occur?

Math
Application of derivativesFind dy/dx and d²y/dx2, and find the slope and concavity (if possible) at the given value of the parameter. (If an answer does not exist, enter DNE.)
Parametric Equations Point
x = 6 cos θ, y = 6 sin θ θ = π / 4
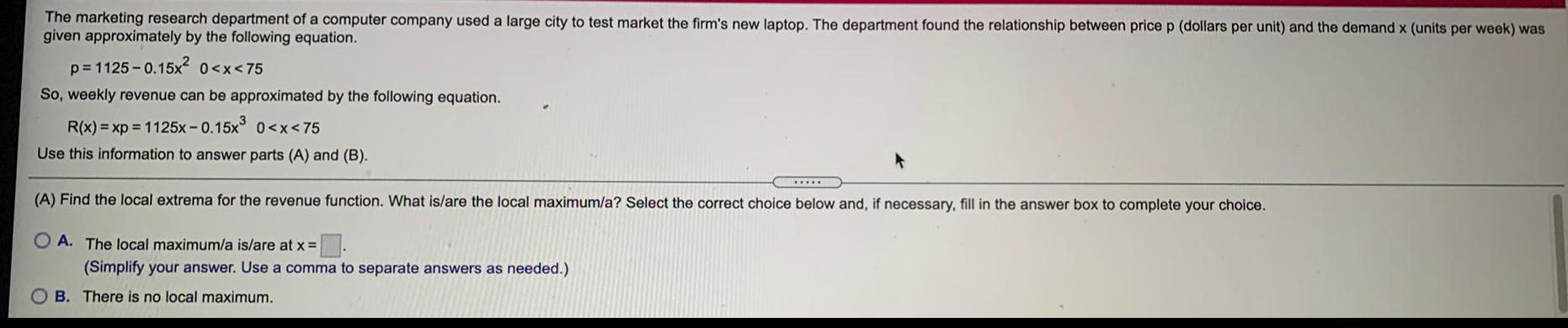
Math
Application of derivativesThe marketing research department of a computer company used a large city to test market the firm's new laptop. The department found the relationship between price p (dollars per unit) and the demand x (units per week) was given approximately by the following equation.
p=1125-0.15x² 0<x<75
So, weekly revenue can be approximated by the following equation.
R(x) = xp = 1125x-0.15x³ 0<x<75
Use this information to answer parts (A) and (B).
(A) Find the local extrema for the revenue function. What is/are the local maximum/a? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The local maximum/a is/are at x =
(Simplify your answer. Use a comma to separate answers as needed.)
B. There is no local maximum.
Math
Application of derivativesA rectangular plot of farmland will be bounded on one side by a river and on the other three sides by a single-strand electric fence. With 500 m of wire at your disposal, what is the largest area you can enclose, and what are its dimensions?