Application of derivatives Questions and Answers

Math
Application of derivativesFind dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
tan (5x + y) = 5x, (0, 0)
dy
dx
=
At (0, 0): y'=

Math
Application of derivativesEvaluate f(8) and f(8.1) and use the results to approximate f '(8). (Round your answer to one decimal place.)
f(x) = x(1-x)
f'(8) = -15

Math
Application of derivativesThe function r(t) = 1,000 πcos(πt/2) gives the rate of change in the deer population in a certain area after t months.
The net change in the deer population between t = 0 and t = 3 is
-2,000.
-2,000.
2,000.
2,000.

Math
Application of derivativesA projectile is shot upward from the surface of Earth with an initial velocity of 123 meters per second. Use the position function below for free-falling objects. What is its velocity after 3 seconds? After 15 seconds? (Round your answers to one decimal place.)
s(t) =-4.9t² + vot + 50
3 s
15 s

Math
Application of derivativesAn 8-foot ladder is leaning against a building. If the bottom of the ladder is sliding along the pavement directly away from the building at 1 ft/sec, how fast is the top of the ladder moving down when the foot of the ladder is 3 feet from the wall?
![Water is leaking out the bottom of a hemispherical tank of radius 8 feet at a rate of 2 cubic feet per hour. The tank was full at a certain time. How fast is the water level
changing when its height h is 3 feet? Note: the volume of a segment of height h in a hemisphere of radius r is xh [r-(h/3)]
The water level is changing at a rate of t/hr when its heighth is 3 feet.](https://media.kunduz.com/media/sug-question/raw/53953390-1657990185.2832336.jpeg?w=256)
Math
Application of derivativesWater is leaking out the bottom of a hemispherical tank of radius 8 feet at a rate of 2 cubic feet per hour. The tank was full at a certain time. How fast is the water level
changing when its height h is 3 feet? Note: the volume of a segment of height h in a hemisphere of radius r is xh [r-(h/3)]
The water level is changing at a rate of t/hr when its heighth is 3 feet.

Math
Application of derivativesA spherical balloon is inflating with helium at a rate of 400π ft3/min.
How fast is the balloon's radius increasing at the instant the radius is 5 ft?
at the instant the radius is 5 ft.

Math
Application of derivativesRachel is a stunt driver, and she's escaping from a building that is about to explode!
The variable d models Rachel's distance from her exit (in meters) t seconds after the cameras began recording the stunt.
d=-38t+ 220
What is Rachel's speed?

Math
Application of derivativesUse a graphing utility to graph the function to approximate (to two decimal places) any relative minima or maxima of the function. (If an answer does not exist, enter DNE.)
h(x)=x² - 6x² + 11
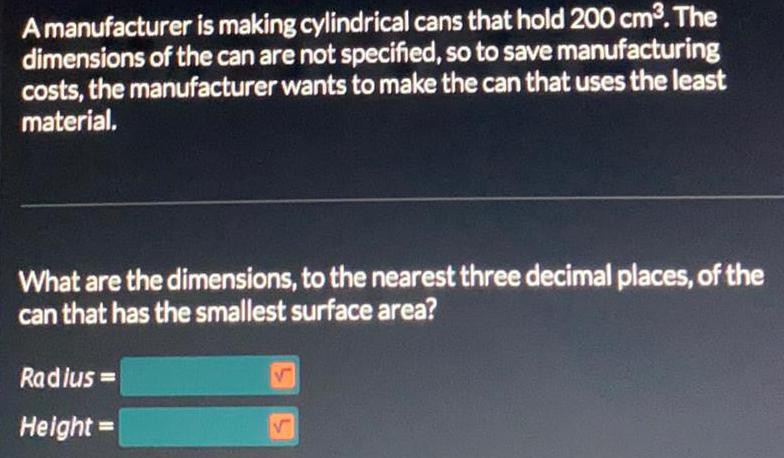
Math
Application of derivativesA manufacturer is making cylindrical cans that hold 200 cm³. The
dimensions of the can are not specified, so to save manufacturing
costs, the manufacturer wants to make the can that uses the least
material.
What are the dimensions, to the nearest three decimal places, of the
can that has the smallest surface area?
Radius=
Height =

Math
Application of derivativesThe
frequency of an ambulance siren f heard by an individual standing on
, where is the velocity of
a street corner can be modeled as f:
121400
330-v
the approaching ambulance.
What is the rate of change of f with respect to when the ambulance is
moving at 25 m/s.
Note: Round to the nearest hundreth.

Math
Application of derivativesA cup of coffee is poured when its temperature is 150 Fahrenheit and is placed on a table in a room where
the temperature is 75 Fahrenheit. Give answers accurate to at least 2 decimal places.
If the temperature of the coffee is 96 Fahrenheit after 5 minutes, what is its temperature after 8 minutes?
Fahrenheit

Math
Application of derivativesA street light is at the top of a 11 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 7
ft/sec along a straight path. How fast is the tip of her shadow moving when she is 45 ft from the base of
the pole?
ft
sec

Math
Application of derivativesThe average number of vehicles waiting in a line to enter a parking ramp can be modeled by the function
f(x) =x²/5(4-x)
where x is a quantity between 0 and 1 known as the traffic intensity. Find the rate of change of the number of vehicles in line with respect to the traffic intensity for x = 0.2.
The rate of change for x = 0.2 is.
(Simplify your answer. Type an integer or decimal rounded to four decimal places as needed.)
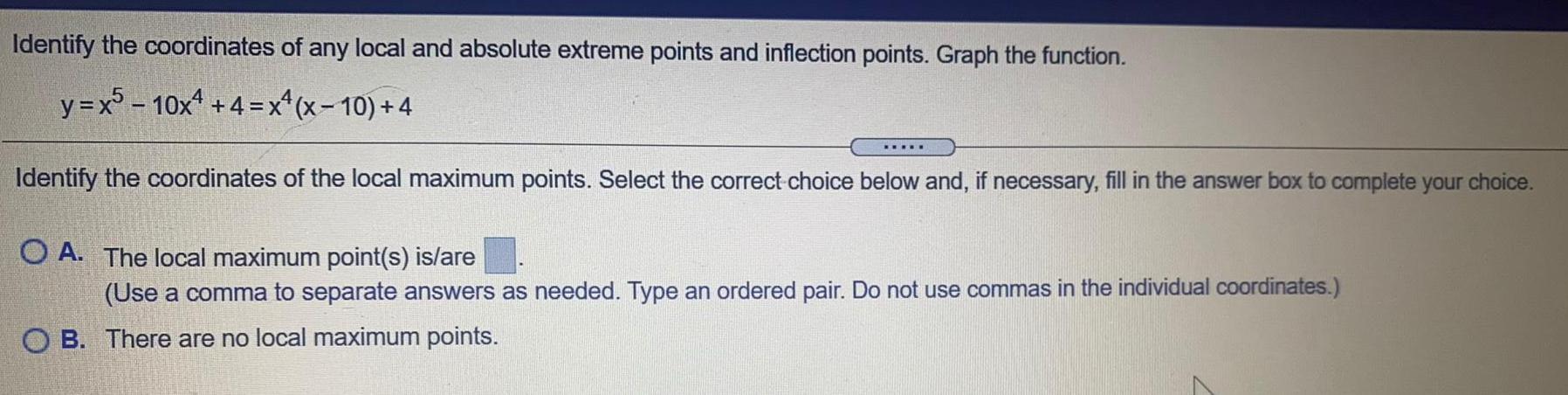
Math
Application of derivativesIdentify the coordinates of any local and absolute extreme points and inflection points. Graph the function.
y=x^5-10x^4 + 4 = x^4(x-10)+4
Identify the coordinates of the local maximum points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The local maximum point(s) is/are
B. There are no local maximum points.

Math
Application of derivativesA company that makes bicycles has determined that a new employee can assemble M(d), where M(d) = 102d²/5d²+7
(a) Find the rate of change function for the number of bicycles assembled with respect to time.
(b) Find and interpret M'(2) and M'(5).
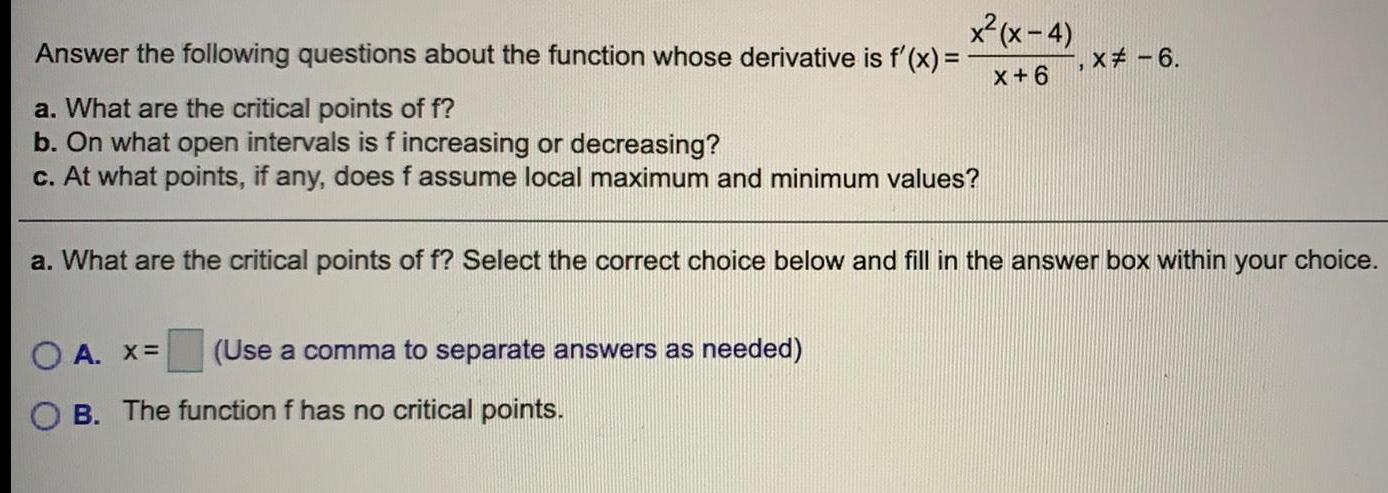
Math
Application of derivativesAnswer the following questions about the function whose derivative is f'(x) = x^2(x-4) / x+6, x ≠ -6
a. What are the critical points of f?
b. On what open intervals is f increasing or decreasing?
c. At what points, if any, does f assume local maximum and minimum values?
Math
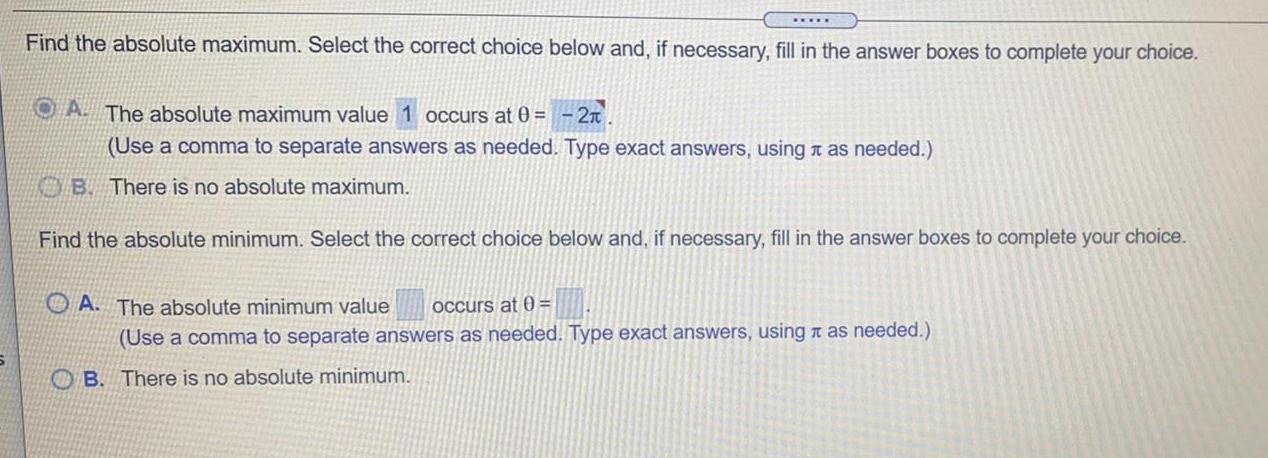
Application of derivativesFind the absolute maximum. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
OA. The absolute maximum value 1 occurs at 0 = 2π
(Use a comma to separate answers as needed. Type exact answers, using it as needed.)
B. There is no absolute maximum.
Find the absolute minimum. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The absolute minimum value
occurs at 0=
(Use a comma to separate answers as needed. Type exact answers, using * as needed.)
OB. There is no absolute minimum.
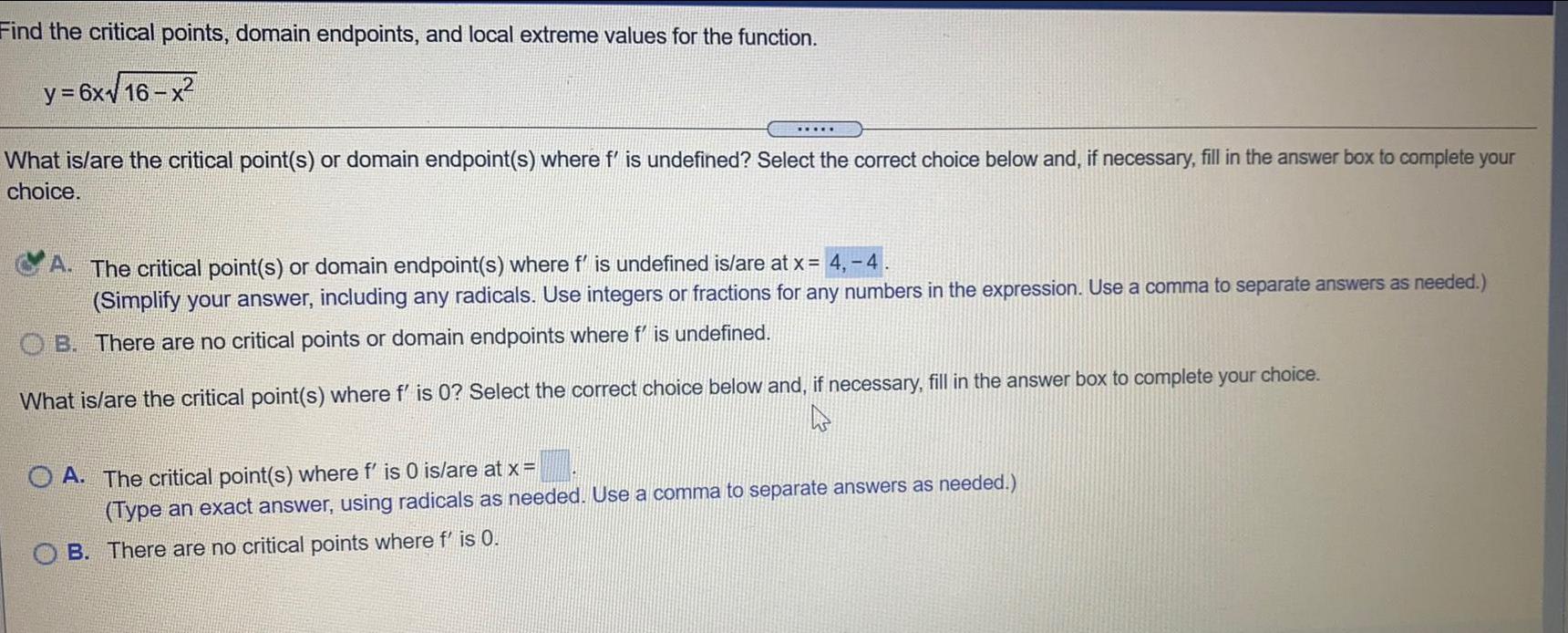
Math
Application of derivativesFind the critical points, domain endpoints, and local extreme values for the function.
y=6x√16-x²
What is/are the critical point(s) or domain endpoint(s) where f' is undefined? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The critical point(s) or domain endpoint(s) where f' is undefined is/are at x = 4,- 4
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)
B. There are no critical points or domain endpoints where f' is undefined.
What is/are the critical point(s) where f' is 0? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The critical point(s) where f' is 0 is/are at x =
(Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.)
B. There are no critical points where f' is 0.
![Find the absolute extrema of the function f(x)=x²-18x² +81 on the interval [-4,4].
The function has an absolute minimum at x = .
(Simplify your answer. Use a comma to separate answers as needed.)
The function has an absolute maximum at x =
(Simplify your answer. Use a comma to separate answers as needed.)](https://media.kunduz.com/media/sug-question/raw/59503103-1657885611.7115319.jpeg?w=256)
Math
Application of derivativesFind the absolute extrema of the function f(x)=x²-18x² +81 on the interval [-4,4].
The function has an absolute minimum at x = .
(Simplify your answer. Use a comma to separate answers as needed.)
The function has an absolute maximum at x =
(Simplify your answer. Use a comma to separate answers as needed.)
![Find the absolute extrema of the function f(x)=x4-72x² + 1296 on the interval [-7,7].
Find the second derivative of the function.](https://media.kunduz.com/media/sug-question/raw/59507795-1657884795.3742256.jpeg?w=256)
Math
Application of derivativesFind the absolute extrema of the function f(x)=x4-72x² + 1296 on the interval [-7,7].
Find the second derivative of the function.

Math
Application of derivativesA farmer has 2100 m of fencing and wants to enclose a rectangular field bordering a river, with no fencing needed along the river. Let x represent the width of the field.
Complete parts (a) through (d) below.
*****
(a) Write an expression for the length of the field. Let the length of the field be the distance along the river.
L(x) =

Math
Application of derivativesA rectangular tank that is 8788 ft³ with a square base and open top is to be constructed of sheet steel of a given thickness. Find the dimensions of the tank with minimum weight.
![Consider the function
3-x²/2 if x ≤ 1
f(x) =
1/x if x > 1.
Show that f satisfies the conditions of the mean value theorem on the interval [0, 2] and
determine all the values of c that satisfy the condition of the mean value theorem.](https://media.kunduz.com/media/sug-question/raw/59423215-1657880834.8115938.jpeg?w=256)
Math
Application of derivativesConsider the function
3-x²/2 if x ≤ 1
f(x) =
1/x if x > 1.
Show that f satisfies the conditions of the mean value theorem on the interval [0, 2] and
determine all the values of c that satisfy the condition of the mean value theorem.

Math
Application of derivatives(a) Construct a 95% confidence interval for the mean lifetime of this type of drill. Use tables or technology. Round your answers to at least two decimal
places.
The confidence interval is
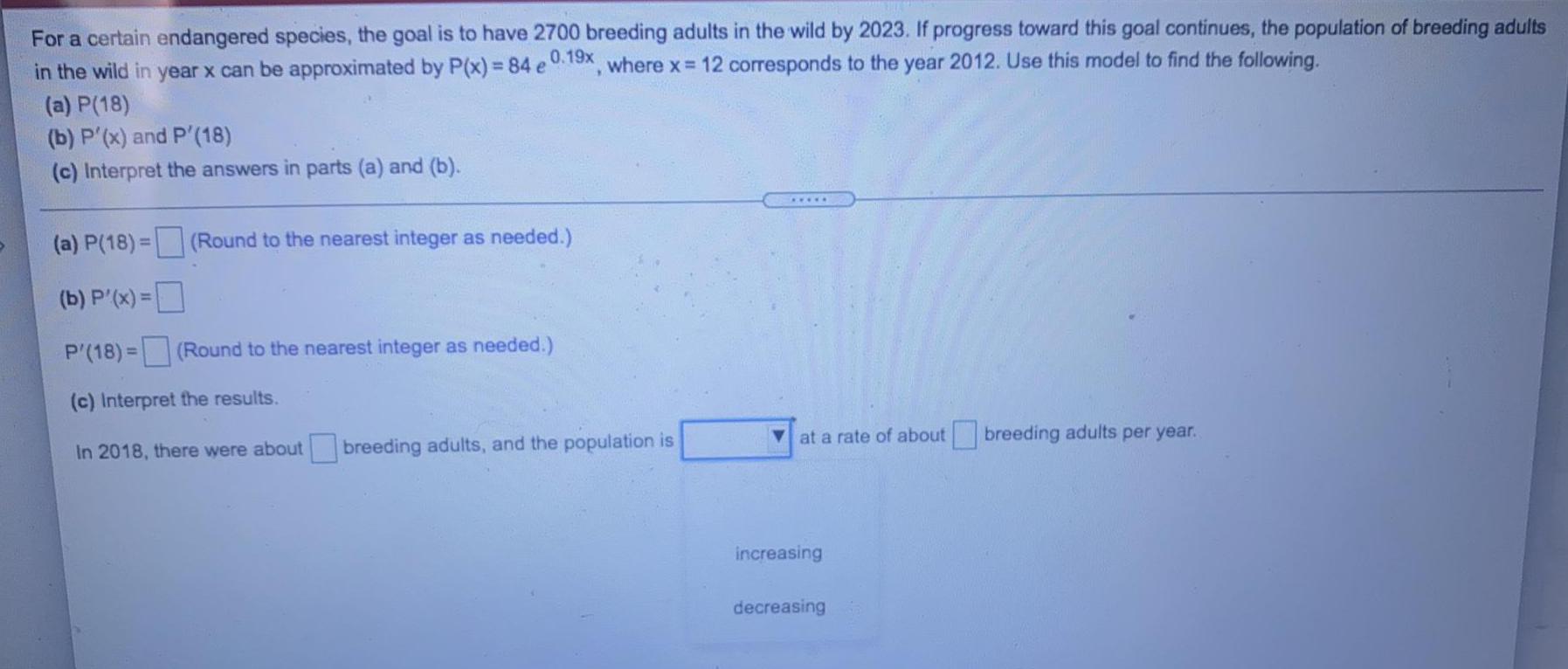
Math
Application of derivativesFor a certain endangered species, the goal is to have 2700 breeding adults in the wild by 2023. If progress toward this goal continues, the population of breeding adults
in the wild in year x can be approximated by P(x) = 84 e 0.19x, where x = 12 corresponds to the year 2012. Use this model to find the following.
(a) P(18)
(b) P'(x) and P'(18)
(c) Interpret the answers in parts (a) and (b).
(a) P(18)= (Round to the nearest integer as needed.)
(b) P'(x) =
P'(18)=
(c) Interpret the results.
In 2018, there were about breeding adults, and the population is
(Round to the nearest integer as needed.)
*****
at a rate of about breeding adults per year.
increasing
decreasing

Math
Application of derivativesA private shipping company will accept a box for domestic shipment only if the sum of its length and
girth (distance around) does not exceed 120 in. Suppose you want to mail a box with square sides so
that its dimensions are h by h by w and it's girth is 2h+2w. What dimensions will give the box its largest
volume?
40 in. x 20 in. x 40 in.
80
in. x 20 in.
20 in. x 20 in. x 40 in.
20 in. x 20 in. x 100 in.
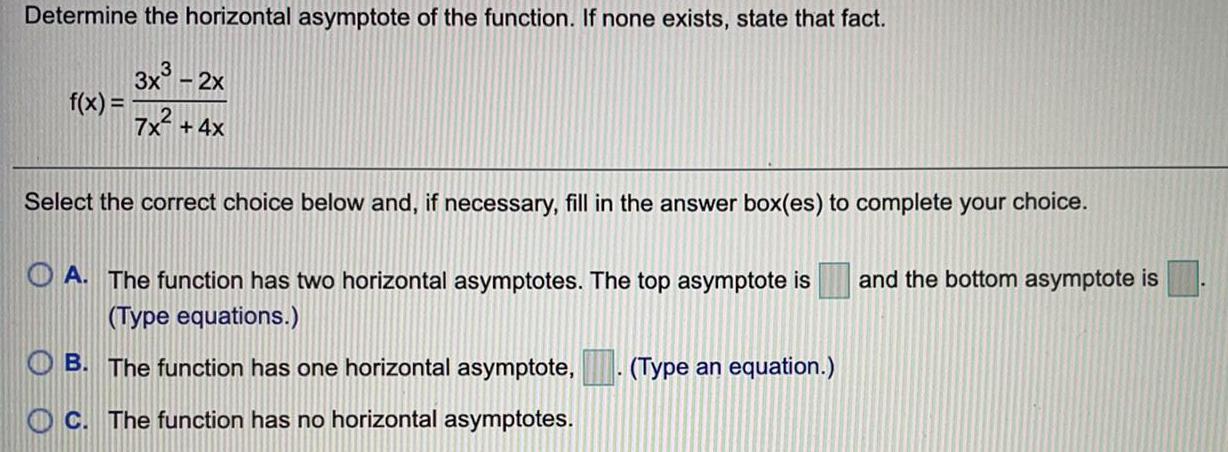
Math
Application of derivativesDetermine the horizontal asymptote of the function. If none exists, state that fact.
3x³ - 2x
2
7x + 4x
f(x) =
Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
A. The function has two horizontal asymptotes. The top asymptote is
(Type equations.)
B. The function has one horizontal asymptote,
C. The function has no horizontal asymptotes.
(Type an equation.)
and the bottom asymptote is

Math
Application of derivativesThe number of online buyers in Western Europe grew steadily over the past decade. The function
P(t) = 27.1 + 14.79 In t (1 st≤7)
gives the number of online buyers as a percent of the total population, where t is measured in years, with t = 1 corresponding to
2001.
(a) What was the percentage of online buyers in 2004? (Round your answer to two decimal places.)
---Select---
(b)
How fast was it changing in 2004? (Round your answer to two decimal places.)
---Select--

Math
Application of derivativesFind the point of diminishing returns (x,y) for the function R(x), where R(x) represents revenue (in thousands of dollars) and x represents the amount spent on advertising (in thousands o
dollars).
R(x) = 10,000-x³+45x² +600x, 0≤x≤ 20
The point of diminishing returns is. (Type an ordered pair.)

Math
Application of derivativesThus, the relative maximum of f(x) = arctan(x) - arctan(x - 8) is
(x, y) =

Math
Application of derivativesFind the relative extrema of the function. Use a graphing utility to confirm your results. (Order your answers from smallest to largest
x, then from smallest to largest y.)
f(x) = sin(x) sinh(x) cos(x) cosh(x), -4≤x≤4
maxima (x, y) =
(x, y) =
minimum (x, y) =

Math
Application of derivativesConsider the function.
f(x) = 2x³ + 12x² - 24x + 15
Step 2 of 2: Determine the open intervals on which the function is increasing and on which the function is decreasing. Enter Ø to indicate the interval is empty.
Answer
Separate multiple entries with commas.
Increasing:
Decreasing:
1
Keyboard S
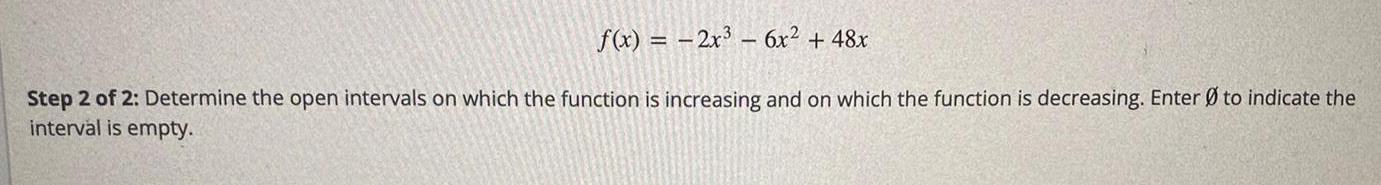
Math
Application of derivativesf(x) = 2x³ - 6x² + 48x
Determine the open intervals on which the function is increasing and on which the function is decreasing. Enter Ø to indicate the interval is empty.

Math
Application of derivativesLena is driving to Chicago. Let y represent her distance from Chicago (in miles). Let x represent the time she has been driving (in hours). Suppose that x and y
are related by the equation y-325-60x.
Answer the questions below.
Note that a change can be an increase or a decrease.
For an increase, use a positive number. For a decrease, use a negative number.
What was Lena's distance from Chicago when she began her drive?
miles
What is the change in Lena's distance from Chicago for each hour she drives?
miles

Math
Application of derivativesA rock is thrown vertically upward from the surface of an airless planet. It reaches a height of s= 120t- 12t² meters in t
seconds. How high does the rock go? How long does it take the rock to reach its highest point?
A. 595 m, 5 sec
B. 600 m, 10 sec
C. 1,080 m, 10 sec
D. 300 m, 5 sec

Math
Application of derivativesA rectangular garden 98 square feet in area is to be fenced off against rodents. Find the dimensions that will require the least amount of fencing if one side of the ga already protected by a barn.
Math
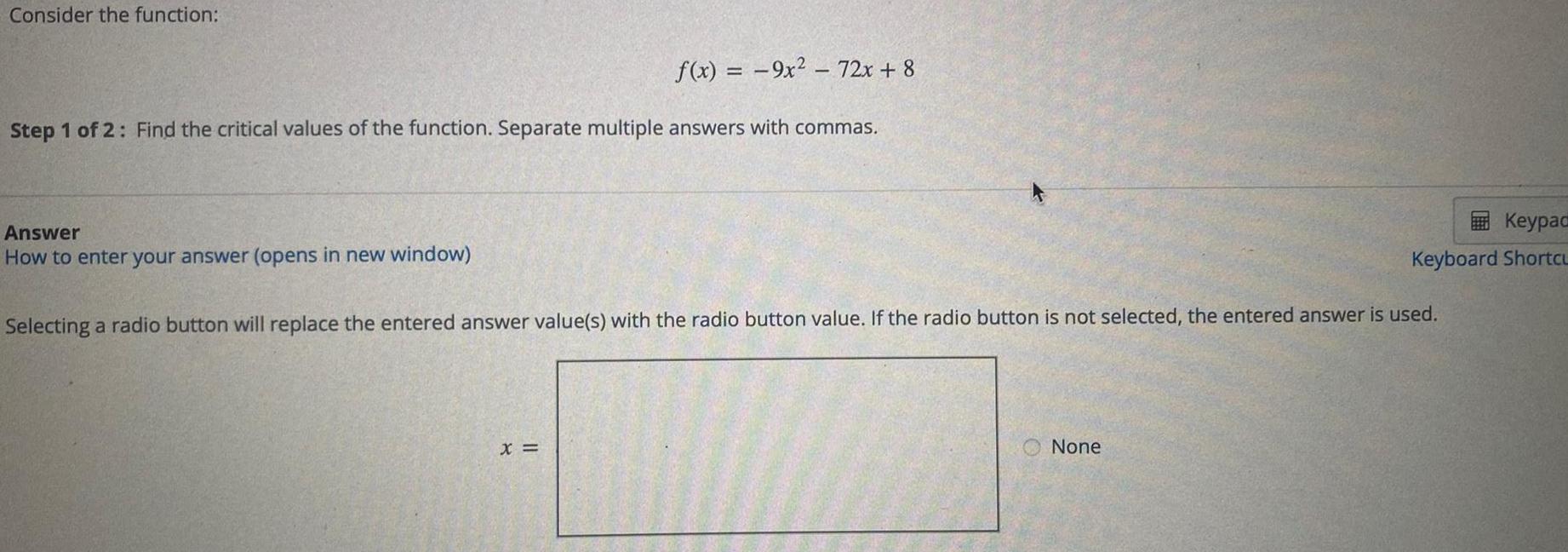
Application of derivativesConsider the function:
f(x) = -9x² - 72x+8
Step 1 of 2: Find the critical values of the function. Separate multiple answers with commas.
Answer
How to enter your answer (opens in new window)
Selecting a radio button will replace the entered answer value(s) with the radio button value. If the radio button is not selected, the entered answer is used.
x =
Keypac
Keyboard Shortcu
None
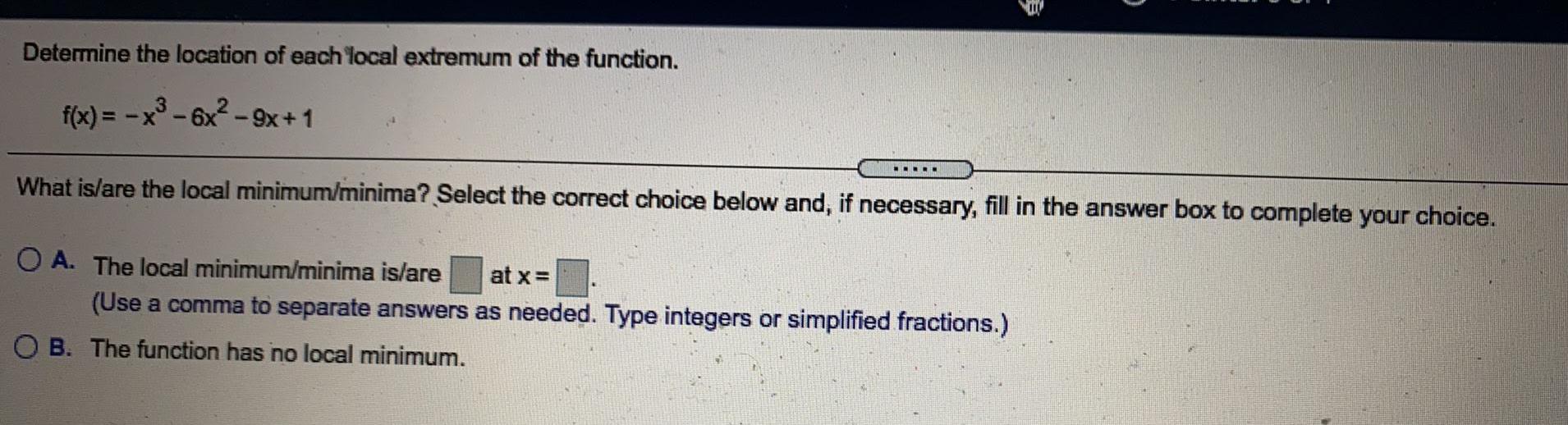
Math
Application of derivativesDetermine the location of each local extremum of the function.
f(x) = -x³-6x²-9x+1

Math
Application of derivativesf(x) = -x² - 8x - 18
Find all values of x that correspond to horizontal tangent lines. Select "None" if the function does not have any values of x that correspond to horizontal tangent lines.
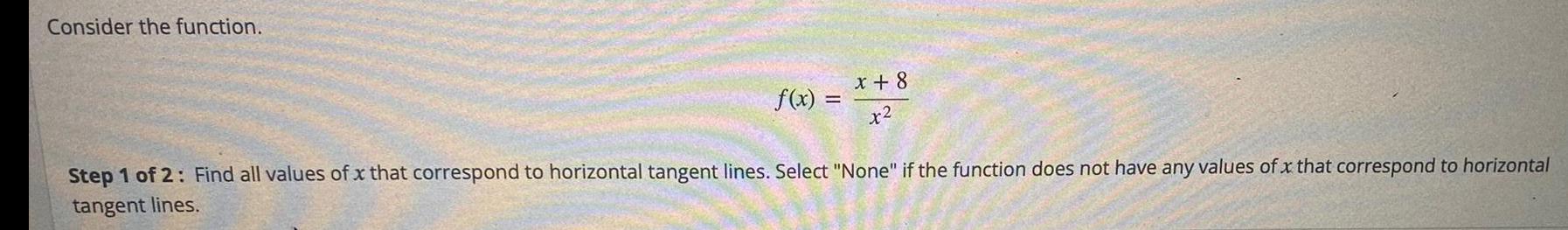
Math
Application of derivativesConsider the function.
f(x) = x+8/x2
Step 1 of 2: Find all values of x that correspond to horizontal tangent lines. Select "None" if the function does not have any values of x that correspond to horizontal tangent lines.
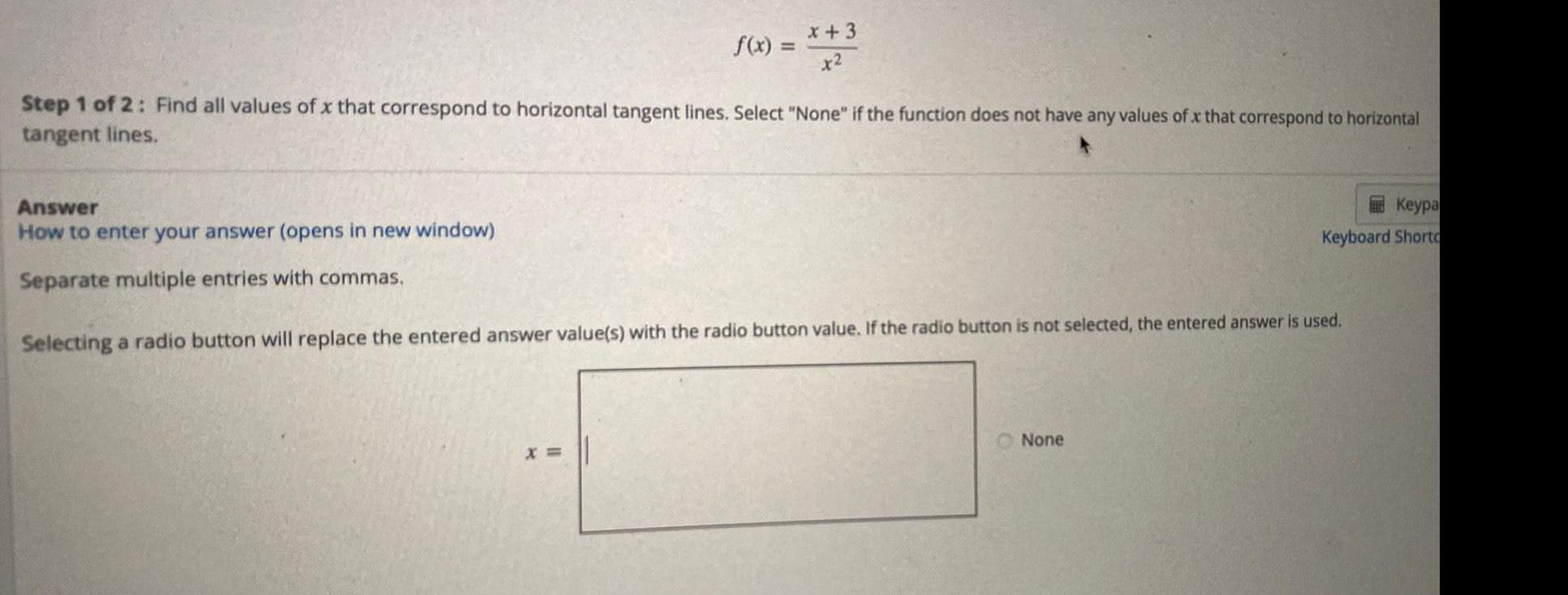
Math
Application of derivativesf(x) = x+3/x²
Step 1 of 2: Find all values of x that correspond to horizontal tangent lines. Select "None" if the function does not have any values of x that correspond to horizontal
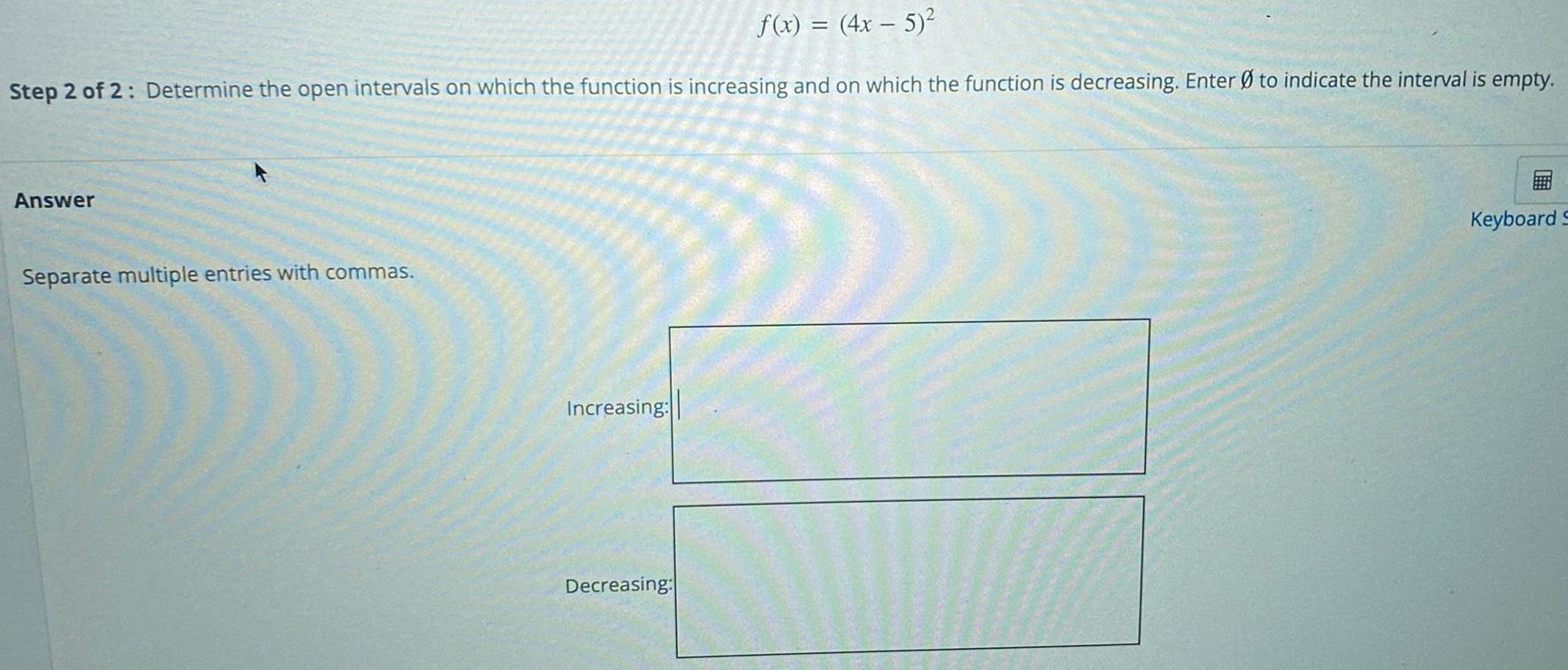
Math
Application of derivativesf(x) = (4x - 5)²
Step 2 of 2: Determine the open intervals on which the function is increasing and on which the function is decreasing. Enter Øto indicate the interval is empty.
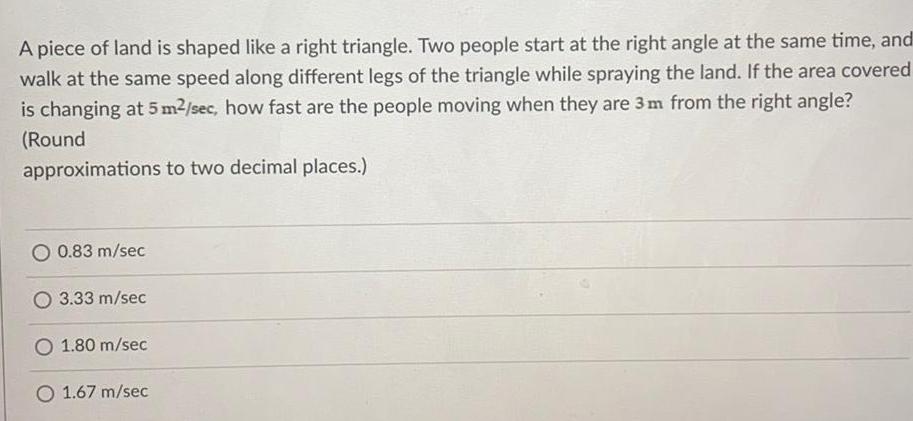
Math
Application of derivativesA piece of land is shaped like a right triangle. Two people start at the right angle at the same time, and walk at the same speed along different legs of the triangle while spraying the land. If the area covered is changing at 5 m²/sec, how fast are the people moving when they are 3 m from the right angle?
(Round approximations to two decimal places.)
0.83 m/sec
3.33 m/sec
1.80 m/sec
1.67 m/sec
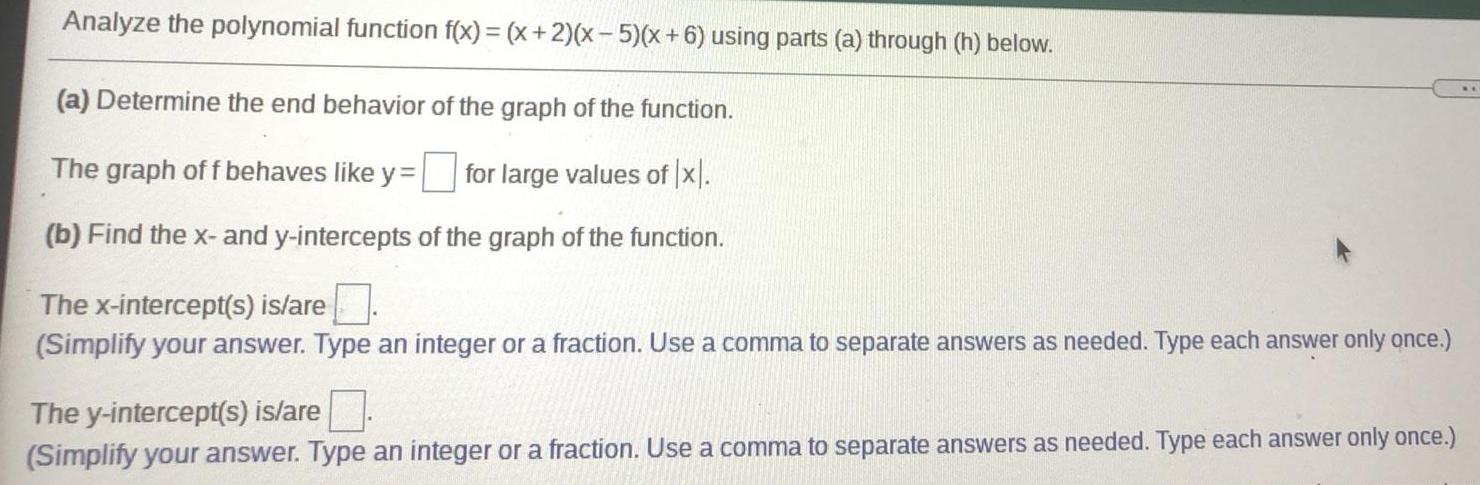
Math
Application of derivativesAnalyze the polynomial function f(x) = (x+2)(x - 5)(x+6) using parts (a) through (h) below.
(a) Determine the end behavior of the graph of the function.
The graph off behaves like y = for large values of |x|.
(b) Find the x- and y-intercepts of the graph of the function.
The x-intercept(s) is/are
(Simplify your answer. Type an integer or a fraction. Use a comma to separate answers as needed. Type each answer only once.)
The y-intercept(s) is/are
(Simplify your answer. Type an integer or a fraction. Use a comma to separate answers as needed. Type each answer only once.)
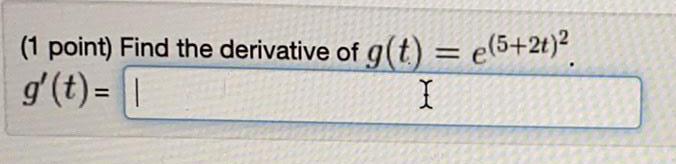

Math
Application of derivativesA sales team estimates that the number of new phones they will sell is a function of the price that they set. They estimate
that if they set the price at a dollars, they will sell f(x) = 2160 - 9x phones. Therefore, the company's revenue is
x (2160-9x). Find the price x which will maximize the company's revenue.
•
Provide your answer below:

Math
Application of derivativesGraph the equation shown below. Find the coordinates of any local and absolute extreme points and inflection points.
y=x4-6x²-4.
Find the local extreme points. Select the correct choice below and, if necessary, fill in any answer box(es) to complete your ch
A. Local minimum(s): (); Local maximum(s): ()
(Type ordered pairs. Type exact answers, using radicals as needed. Use a comma to separate answers as needed.)
B. Local minimum(s) only:
(Type ordered pairs. Type exact answers, using radicals as needed. Use a comma to separate answers as needed.)
C. Local maximum(s) only:
(Type ordered pairs. Type exact answers, using radicals as needed. Use a comma to separate answers as needed.)
D. No local extreme points


Math
Application of derivativesWhen a circular plate of metal is heated in an oven, its radius increases at a rate of 0.02 cm/min. At what rate is the plate's area increasing when the radius is 50 cm?
Write the equation that relates the rate of change in area to the rate of change in radius.