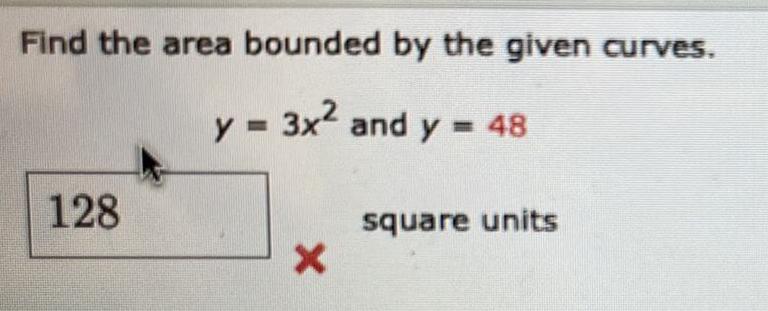
Area Questions and Answers

Math
AreaA carpenter is framing a wall that is 8 feet high and 15 feet long. If the carpenter wants to be sure that
the sides of the wall meet at right angles, then what should the diagonal measurement of the wall be?
13 feet
19 feet
17 feet

Math
AreaTom is fertilizing his garden. The garden is in the shape of a rectangle. Its length is 12 feet and its width is 10 feet. Suppose each bag of fertilizer covers 30 square feet. How many bags will he need to cover the garden?

Math
AreaYou have a circular mirror in your house that desperately needs cleaning. The diameter of the mirror is 3 feet. How many square feet of the mirror will need cleaning?

Math
AreaA rectangle is to be inscribed in an isosceles right triangle in such a way that one vertex of the rectangle is the intersection point of the legs of the triangle and the opposite vertex lies on the hypotenuse. Find the largest area (in cm²) of the rectangle and its dimensions (in cm) given that the two equal legs of the triangle have length 6.

Math
AreaThe surface area of a sphere, S is
equal to 4r², where is the radius of
the sphere.
What is the surface area of a sphere with
a radius of 6.5 meters?
52π cubic meters
169π cubic meters
169π square meters
52π square meters

Math
AreaA company sells orange juice in spherical containers that look like oranges. Each container has a surface area of approximately 113 in². Use 3.14 for π.
Part 1 out of 2
What is the volume of the container? Round to the nearest tenth.
The volume of the container is approximately

Math
AreaThe Pyramid Arena in Memphis, Tennessee, is a square pyramid with base edge lengths of 200 yd and a height of 32 stories. Estimate the area of the glass on the sides of the pyramid by rounding the slant height of the building to the nearest 10 feet. (Hint: 1 story = 10 ft) The area of the glass on the sides of the pyramid is approximately.

Math
AreaFind the area of a rhombus with a perimeter of 100 meters and one diagonal with a length of 48 meters.

Math
AreaFind the area of a sector with a central angle of 200° and a diameter of 5.3 cm. Round to the nearest tenth.
2.3 cm²
49 cm²
5.9cm²
12.3cm²

Math
AreaA parallelogram has a base of 12 feet, sides of 15 feet, and a height of 13 feet.
a) Find the perimeter and area of the parallelogram.
b) Suppose the base of the parallelogram is reduced to three-fourths of the original. Find the new perimeter and area.
c) Compare your answers in parts a and b for perimeter and area of the original parallelogram.
Math
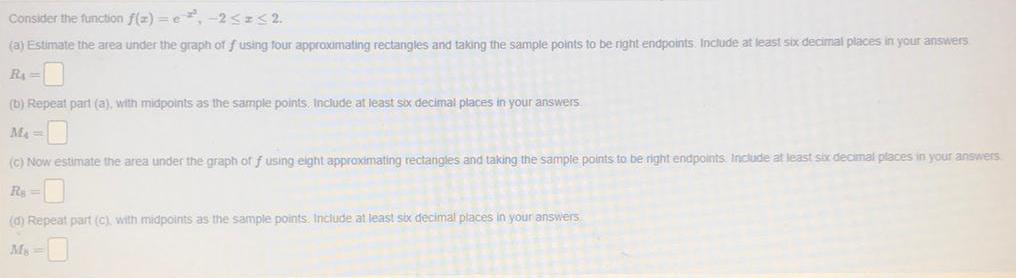
AreaConsider the function f(x) = e, -2 ≤ ≤ 2.
(a) Estimate the area under the graph of fusing four approximating rectangles and taking the sample points to be right endpoints. Include at least six decimal places in your answers
(b) Repeat part (a), with midpoints as the sample points, Include at least six decimal places in your answers
(c) Now estimate the area under the graph of f using eight approximating rectangles and taking the sample points to be right endpoints. Include at least six decimal places in your answers
(d) Repeat part (c), with midpoints as the sample points. Include at least six decimal places in your answers
Math
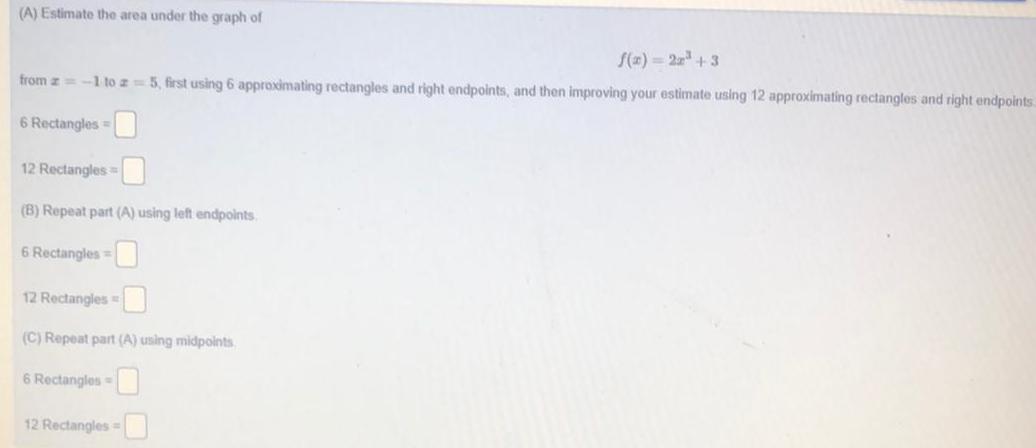
Area(A) Estimate the area under the graph of
f(x)=2x³ +3
from x = -1 to x=5, first using 6 approximating rectangles and right endpoints, and then improving your estimate using 12 approximating rectangles and right endpoints
6 Rectangles =
12 Rectangles
(B) Repeat part (A) using left endpoints.
6 Rectangles =
12 Rectangles =
(C) Repeat part (A) using midpoints
6 Rectangles
12 Rectangles =

Math
AreaA grocery store wants to paint 6 concrete spheres that are in their parking lot in front of the store. If the diameter of each sphere is 3.5 feet, which value is closest to the total surface area that will be painted in square inches? Show your work.
A. 22,170 in.²
B. 5,540 in.2
C. 33,250 in.2
D.17,600 in.2

Math
AreaA rectangular prism has a height of 12 feet. The cross section at 8 feet has an area of 45.5 square feet. A triangular prism shares the same parallel planes as the rectangular prism and also has a height of 12 feet. If the volumes of the prisms are equal, what is the area of a cross section in the triangular prism at 8 feet?
72.25 square feet
45.5 square feet
52.6 square feet
22.75 square feet

Math
AreaThe area of the base of a cylinder is 52 cm², and the height is 8 cm. Which equation can be used to find the volume of the cylinder?
Vcylinder = (π) (52²) (8)
Vcylinder = (52) (8)
Vcylinder = (52π) (8)
Vcylinder = (52²) (8)

Math
AreaThe formulas for the volume of which of the following shapes were used in order to determine the formula for the volume of a sphere? Select all that apply.
triangular prism
cube
cone
cylinder

Math
AreaDetermine the volume of the solid generated by rotating the region bounded by y = x², y = 0 and y = 5 around the line y = 5.

Math
AreaConstellation Party Supplies makes different types of cylindrical glow sticks. A
regular glow stick has a volume of 26.5 cubic centimeters. A thin glow stick for
bracelets has 1/4 the volume of a regular one and a diameter of 0.64 centimeters.
What is the length of a thin glow stick?

Math
AreaTwo similar solids have volumes of 576 in³ and 1125 in³. If the smaller solid has a side length of 12 inches, how long is the corresponding side in the larger solid (in inches)?
![Consider the function f(x) = 1/16 x² + 2x + 4.
What is the maximum approximation of the area under the curve of f on the interval [-1, 3] with four equal subintervals?](https://media.kunduz.com/media/sug-question/raw/46577277-1658300946.7176647.jpeg?w=256)
Math
AreaConsider the function f(x) = 1/16 x² + 2x + 4.
What is the maximum approximation of the area under the curve of f on the interval [-1, 3] with four equal subintervals?
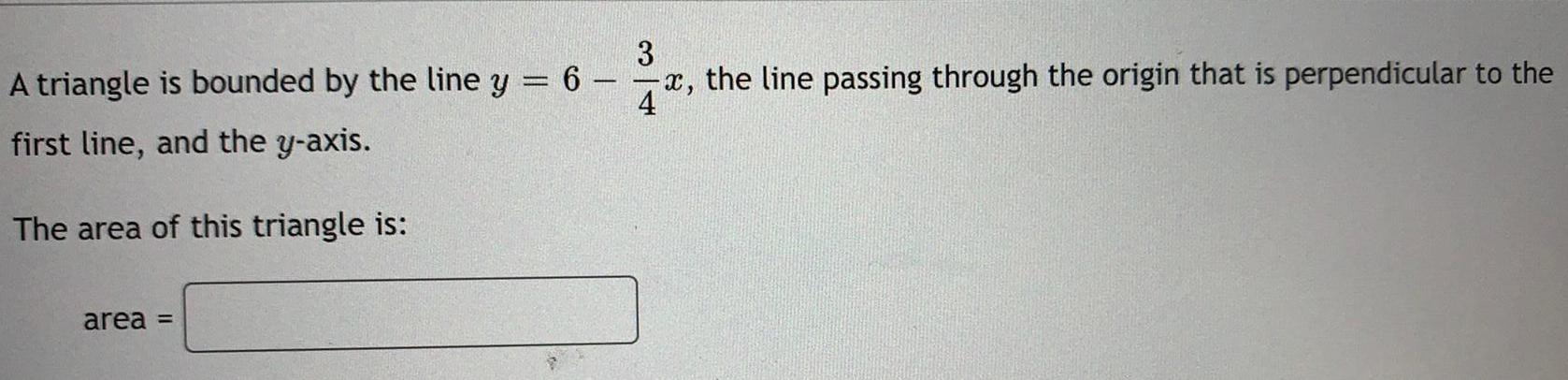
Math
AreaA triangle is bounded by the line y = 6 -3/4 x, the line passing through the origin that is perpendicular to the first line, and the y-axis.

Math
AreaPhoenix has a population density of 3,349 people per square mile. If the current population of the city is 1,733,630 people, what land area (in square miles) does Phoenix cover? Round to the tenths of a square mile. Show all work.
Math
AreaSuppose the area of square A is 15 cm² and the area of square C is 42 cm². What is the area of square
B if the three squares create a right triangle?
A 27 cm²
B 39 cm²
C 52 cm²
D 57 cm²

Math
AreaJohn does a weekly exercise program consisting of cardiovascular work and weight training. Each week, he exercises for at least 10 hours. He spends at most 6 hours on weight training. He spends at most 12 hours doing cardiovascular work. Let x denote the time (in hours) that John spends doing cardiovascular work. Let y denote the time (in hours) that he spends on weight training. Shade the region corresponding to all values of x and y that satisfy these requirements.
![Consider the function f(x) = -1/2 x² + 3x + 9.
What is the overestimate of the area under the curve of f using rectangular approximations on the interval [-2, 3] with five equal subintervals?](https://media.kunduz.com/media/sug-question/raw/45615053-1658262023.156044.jpeg?w=256)
Math
AreaConsider the function f(x) = -1/2 x² + 3x + 9.
What is the overestimate of the area under the curve of f using rectangular approximations on the interval [-2, 3] with five equal subintervals?

Math
AreaSuppose an open box with a rectangular base is to be constructed from a rectangular piece of cardboard 12 inches wide and 24 inches long by cutting congruent squares from each corner and then bending up the sides.
What is the maximum possible volume of the box, in cubic inches?

Math
AreaA wire of length 15 is cut into two pieces which are then bent into the shape of a circle of radius r and a square of side a. Then the total area enclosed by the circle and square is the following function of sand r
If we solve for s in terms of r. we can reexpress this area as the following function of r alone
Thus we find that to obtain maximal area we should let r
To obtain minimal area we should let r

Math
AreaUse finite approximations to estimate the area under the graph of the function f(x) = 24-x² - 2x between x = -6 and x = 4 for each of the following cases.
a. Using a lower sum with two rectangles of equal width
b. Using a lower sum with four rectangles of equal width
c. Using an upper sum with two rectangles of equal width
d. Using an upper sum with four rectangles of equal width

Math
AreaKalesha has a statue that is in the shape of a square pyramid. One of the side of the square base is 17 in. long and the volume of the pyramid is 2023 in³.
What is the height of the pyramid?
Enter your answer in the box.
in.
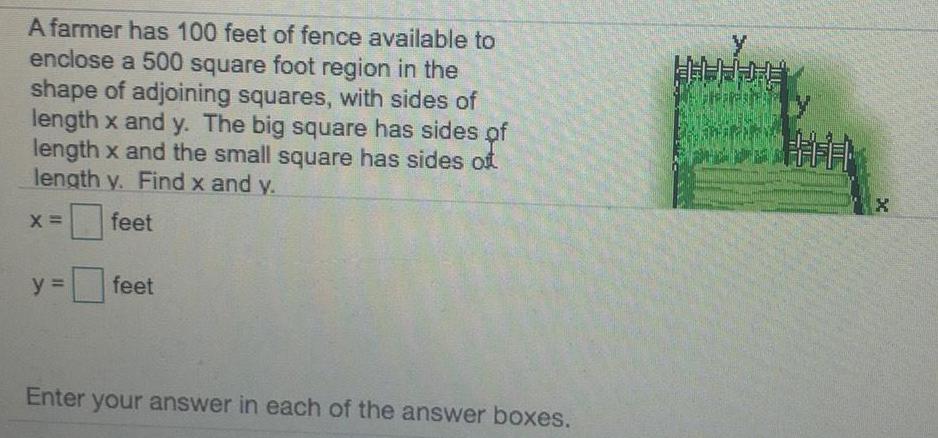
Math
AreaA farmer has 100 feet of fence available to
enclose a 500 square foot region in the
shape of adjoining squares, with sides of
length x and y. The big square has sides of
length x and the small square has sides oft
length y. Find x and y.
Math
Areaa) Approximate the area under the curve of f(x) = -x³ + 20 from x = 1 to x = 4 to using 3 right approximating rectangles.
b) The answer from part "a" is Select an answer

Math
AreaThe perimeter of a rectangle is 20 inches and its area is 16 square inches. What are its dimensions? What are the dimensions?
inches (Use a comma to separate answers as needed.)
Math
AreaFind the area of a regular octagon circumscribed about a circle with radius of 6 inches. Hint:
Draw a diagram.
Round the final answer to the nearest hundredth.

Math
AreaA square pyramid measuring 6 km along each edge of the base with a height of 9 km.
123 km³
108 km³
324 km³
106 km³

Math
AreaA cylindrical cup is 8 centimeters in height. When filled to the very top, it holds 480 cubic centimeters of water. What is the radius of the cup, rounded to the nearest tenth?
a 4.4
b 19.1
c 8.5
d 15.6

Math
AreaGiven a soda can with a volume of 36 and a diameter of 4, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank). (4 points)

Math
AreaA piece of cardboard is being used to make a container that will have no lid. Four square cutouts of side length h will be cut from the corners of the cardboard. The container will have a square base of side s, height h, and a volume of 80 in³. Which is the correct order of steps for finding minimum surface area A of the container?
s²h = 80 and A = s² + 4sh
I. A'=2s - 320/s²
II. 0=2s - 320/s²
III. A = s² + 320/s²
s = 5.429 in and h = 2.714 in
I, III, II
III, I, II
III, II, I
I, II, III

Math
AreaA company that manufactures and ships canned vegetables is designing boxes in the shape of square prisms to meet specific requirements. The vegetables are packed into cans that are 2.5 inches in diameter and 4 inches in height. Company regulations state that boxes must be filled with two layers of 16 cans each, and be completely closed with no overlapping material. What is the smallest amount of cardboard needed to meet the company's requirements.
They will need at least inches of cardboard. square
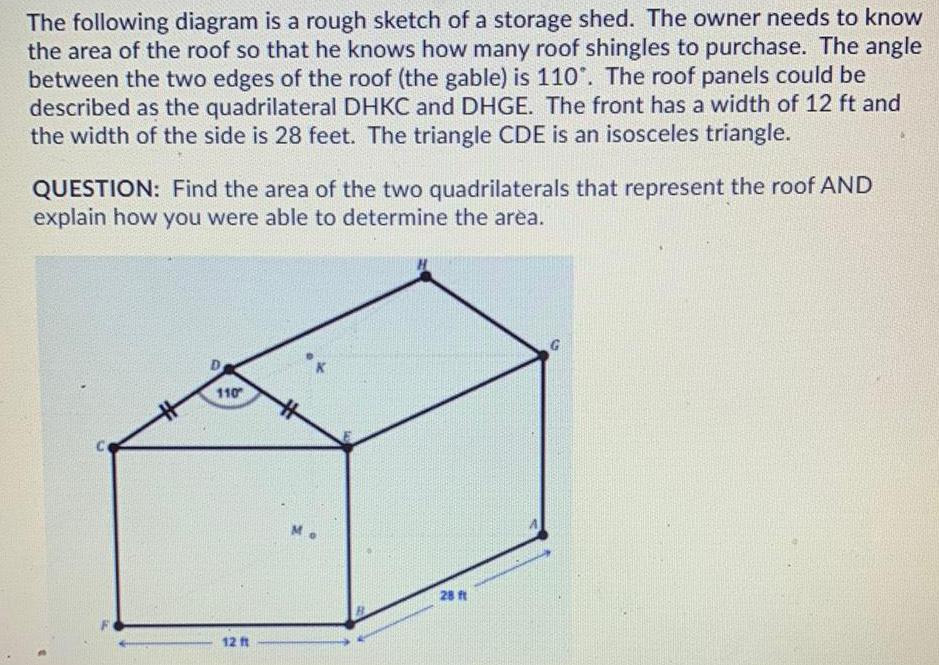
Math
AreaThe following diagram is a rough sketch of a storage shed. The owner needs to know the area of the roof so that he knows how many roof shingles to purchase. The angle between the two edges of the roof (the gable) is 110°. The roof panels could be described as the quadrilateral DHKC and DHGE. The front has a width of 12 ft and the width of the side is 28 feet. The triangle CDE is an isosceles triangle.
QUESTION: Find the area of the two quadrilaterals that represent the roof AND explain how you were able to determine the area.

Math
AreaAn ice-cream cone has a radius of 2.8 cm and a height of 6.7 cm. The cone is filled with ice-cream and one additional scoop in the shape of a sphere with the same radius as the cone is placed on top. What is the amount of ice cream in cubic cm? Round to the nearest hundredth.
Math
AreaAn architect is making a model of a building she is designing. The kitchen will be 8 feet by 14 feet. The scale she is using for the model is 3 inches = 2 feet.
How many 1 inch x 1 inch tiles are needed to cover the floor of the model kitchen?
Tiles needed:

Math
AreaA carpenter is creating two new templates for his designs. One template will be in the shape of a right triangle, where the longer leg is three inches more than three times the shorter leg. The second template will be in the shape of a rectangle, where one side length is one inch less than three times the length of the triangle's shorter leg, and the other side length is one inch more than twice the width.
The carpenter needs the lengths of both diagonals to be the same. Write a system of equations to represent this situation, where y is the length of the diagonals, and x is the shorter leg of the triangle. Which statement describes the number and viability of the system's solutions?
A. The system has two solutions, and both are viable because they result in figures with only positive side lengths.
B. The system has two solutions, but only one is viable because the other results in a figure with negative side lengths.
C. The system has only one solution, and it is viable because it results in a figure with only positive side lengths.
D. The system has only one solution, but it is not viable because it it results in a figure with a negative side length.
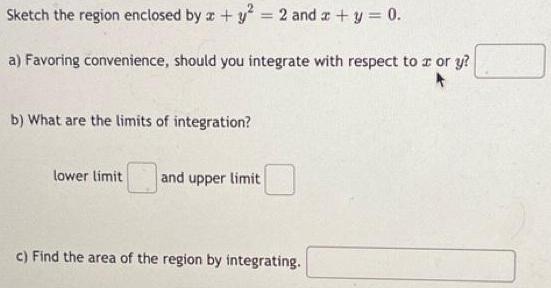
Math
AreaSketch the region enclosed by x + y² = 2 and x + y = 0.
a) Favoring convenience, should you integrate with respect to x or y?
b) What are the limits of integration?
lower limit and upper limit
c) Find the area of the region by integrating.

Math
AreaFor studying the electric current that is induced in wire rotating through a magnetic field, a piece of wire 88 cm long is cut into two pieces. One of these is bent into a circle and the other into a square. Express the total area A of the two figures as a function of the perimeter of the square. Use p for the perimeter of the square.
A=
(Simplify your answer. Do not factor. Type an exact answer, using as needed. Use integers or fractions for any numbers in the expression.)

Math
AreaThe area of a rectangle is equal to x² +10x+16 square units. If the length of the
rectangle is equal to x+8 units, what expression represents its width?
DIVIDE
x-2
x+2
x + 4.00
x+8
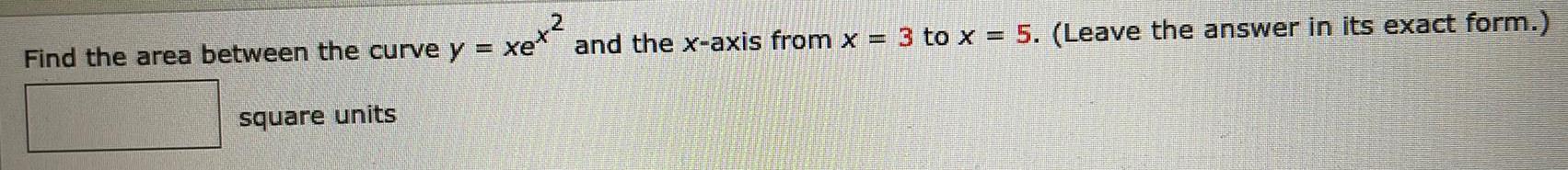
Math
AreaFind the area between the curve y = x e x 2 and the x-axis from x = 3 to x = 5. (Leave the answer in its exact form.)

Math
AreaWally Beige has painted a rectangular mural that is 8 ft tall and 10 ft wide. He plans to paint a border of equal width all the way around the outside of the mural. To end up with a border that has an area of 144 square ft, find the width of the border.
Answer: ft

Math
AreaA rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals (see figure). What dimensions should be used so that the enclosed area will be a maximum?

Math
AreaThis problem illustrates the typical approach for creating a model. Use lower case letters.
(a) We want to express the area of a circle, A, as a function of its circumference, c.
Start with the basic formula we know for the area of a circle in terms of its radius.
A=
Because we want this area formula in terms of circumference and not radius, we need another formula that will allow us to replace in terms of c. The formula that has both r and c in it is the circumference formula for a circle.
c=
Solve this equation for r.
r=
Use this to replace r in terms of c in our area formula. Note the function notation also reminds us that the independent variable should be c when we are done.
A(C)=
Now try this approach on the following problem. Don't forget, if you need, there is a reference sheet of geometry formulas in the description of this assignment.
(b) Express the diagonal of a rectangle, D, in terms of its width, w, if the area of the rectangle is 13 square feet.
D(w) =