Area Questions and Answers

Math
AreaYou are designing a rectangular swimming pool to be set into the ground. The width of the pool is 5 feet less than the length, and the depth is 40 feet less than the length. The pool holds 9000 cubic feet of water. What are the dimensions of the pool?

Math
AreaA tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹500 per m². (Note that the base of the tent will not be covered with canvas.)

Math
AreaThe lengths of the sides of a rectangular prism are made, twice as long to create a new prism. How does the surface area of the new, larger prism compare to the surface area of the original prism?
The surface area of the new prism is twice as large as the surface area of the original prism.
The surface area of the new prism is four times as large as the surface area of the original prism.
The surface area of the new prism is six times as large as the surface area of the original prism.
The surface area of the new prism is eight times as large as the surface area of the original prism.
![HAPPULO
Box A: 7.5 in. by 6.25 in. by 10 in.
Box B: 8 in. by 5.25 in. by 11.5 in.
[]
They need to decide which box will be less expensive for them to use. That is what you will
figure out in # 1-5 below." (Note: The amount of cardboard needed to make a box is determined
by the surface area of the box since the cardboard covers each surface. This is not a volume
problem because we are not interested in the amount of space contained in the box.)
1. How much cardboard does it take to make Box A? (Ignore any overlapping of flaps.)
2. How much cardboard does it take to make Box B? (Ignore any over pping of flaps.)
3. The cardboard costs $0.04 per square inch. How much will it cost to make Box A?](https://media.kunduz.com/media/sug-question/raw/72361788-1657476139.9544203.jpeg?w=256)
Math
AreaHAPPULO
Box A: 7.5 in. by 6.25 in. by 10 in.
Box B: 8 in. by 5.25 in. by 11.5 in.
[]
They need to decide which box will be less expensive for them to use. That is what you will
figure out in # 1-5 below." (Note: The amount of cardboard needed to make a box is determined
by the surface area of the box since the cardboard covers each surface. This is not a volume
problem because we are not interested in the amount of space contained in the box.)
1. How much cardboard does it take to make Box A? (Ignore any overlapping of flaps.)
2. How much cardboard does it take to make Box B? (Ignore any over pping of flaps.)
3. The cardboard costs $0.04 per square inch. How much will it cost to make Box A?

Math
AreaEvaluate the integral, where E is the solid that lies within the cylinder x² + y2 = 9, above the plane z = 0, and below the cone z² = 9x² +9y^2. Use cylindrical coordinates.
∫∫∫E x² dv

Math
AreaSam wants to fence his rectangular garden plot along its length on the front side. The perimeter of the plot is 24 meters, and its length is 3 times its width.
If x is the length and y is the width of the plot, set the equations of the system.
Solve and determine the values of x and y.
If the cost of fencing is $25 per meter, how much does Sam need to spend on fencing?

Math
AreaThe width of a rectangle is two-thirds of its length, and its area is 216 square meters. What is the length?
27 m
12 m
18 m

Math
AreaTracy needs to find the length and width of the equipment storage room where she works. The room is 4 meters longer than it is wide. Its perimeter is 24 meters. Find the width in meters.

Math
AreaWater is leaking out of an inverted conical tank at a rate of 10,000 cm³/min at the same time that water is being pumped into the tank at a constant rate. The tank has height 6 m and the diameter at the top is 4 m. If the water level is rising at a rate of 20 cm/min when the height of the water is 2 m, find the rate at which water is being pumped into the tank.

Math
AreaDirections: Design an ice cream cone and a scoop of ice
cream so that if the ice cream melts completely:
1) It fits exactly in the cone. Show the picture with the
dimensions. Justify that it satisfies the condition.
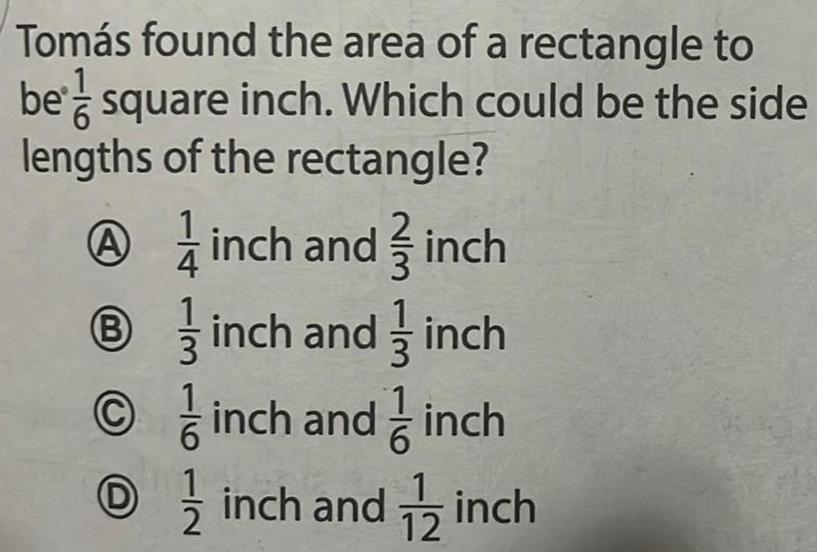
Math
AreaTomás found the area of a rectangle to
be square inch. Which could be the side
lengths of the rectangle?
A
inch and inch
3
4
Ⓡinch and inch
C inch and inch
Ⓒinch and inch
1
12

Math
AreaYou read online that a 15 ft by 20 ft brick patio would cost about $2,275 to have professionally installed.
Estimate the cost of having a 27 by 30 ft brick patio installed.
Math
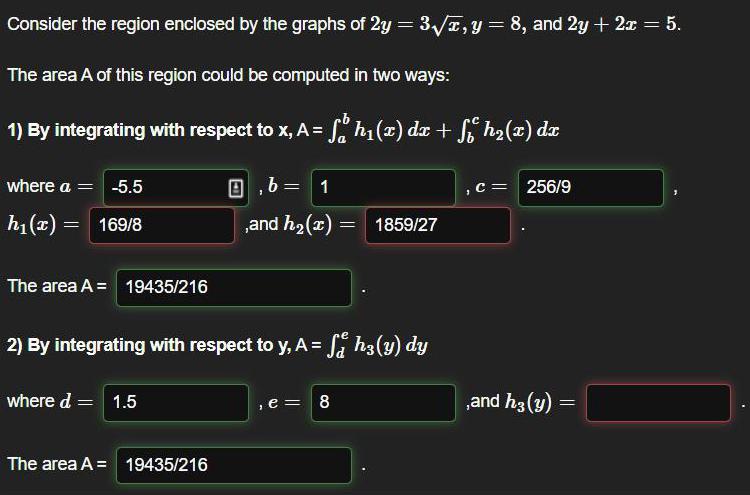
AreaConsider the region enclosed by the graphs of 2y = 3√, y = 8, and 2y + 2x = 5.
The area A of this region could be computed in two ways:
1) By integrating with respect to x, A = ∫h₁(x) dx + ∫h₂(x) dx
where a = ,b = , c = , h₁(x) = ,and h₂(x)=
The area A = .
2) By integrating with respect to y, A = ∫h3(y) dy
where d = ,e = ,and h3(y)=
The area A =

Math
AreaA rectangular field is 380 yards in length and 157 yards in width. Find the area of the field in ACRES (1 acre = 43,560 square feet). Round to the nearest tenth of an acre

Math
AreaAn interior decorator needs border trim for a home she is wallpapering. She needs 36 feet of border trim for the living room, 33 feet of border trim for the bedroom, and 45 feet of border trim for the dining room. How many yards of border trim does she need?

Math
AreaNon-calculator: Consider a circle with a radius of k. Explain and show why there must be a square that has a diagonal with a length between k and 2k and an area that is half the area of the circle.

Math
AreaThe campus of a college has plans to construct a rectangular parking lot on land bordered on one side by a highway. There are 640 ft of fencing available to fence the other three sides. Let x represent the length of each of the two parallel sides of fencing.
(a) Express the length of the remaining side to be fenced in terms of x.
(b) What are the restrictions on x?
(c) Determine a function A that represents the area of the parking lot in terms of x.
(d) Determine the values of x that will give an area between 30,000 and 40,000 ft².
(e) What dimensions will give a maximum area, and what will this area be?

Math
AreaSketch the following to help answer the question. Kite QRST has a short diagonal of QS and a long diagonal of RT. The diagonals intersect at point P. Side QR = 17 m, diagonal QS = 30 m, and segment PT = 25 m. Find the area of kite QRST.
8m²
33 m²
495 m²
990 m²

Math
AreaYou have 200 feet of fencing to enclose a rectangular plot that borders on a river. If you do not fence the side along the river, find the length and width of the plot that will maximize the area. What is the largest area that can be contained by the fencing?

Math
AreaA high school is building a new gymnasium in the shape of a pyramid. Its base is a square with each side 500 feet long and has a slant height of 60 feet. What is closest to the surface area of this pyramid?
310,000 ft²
265,000 ft²
490,000 ft²
280,000 ft²
![Use the Fundamental Theorem of Calculus to find the area of the region between the graph of the function 5/7 x(2/7) + 1/2 x(4/9) + 6 and the x-axis on the interval [4,8]. Round off your answer to the nearest integer.
52 units²
40 units²
33 units²
34 units²](https://media.kunduz.com/media/sug-question/raw/61691691-1657386182.309029.jpeg?w=256)
Math
AreaUse the Fundamental Theorem of Calculus to find the area of the region between the graph of the function 5/7 x(2/7) + 1/2 x(4/9) + 6 and the x-axis on the interval [4,8]. Round off your answer to the nearest integer.
52 units²
40 units²
33 units²
34 units²

Math
AreaSketch the region enclosed by the curves given below. Decide whether to integrate with respect to x or y. Then find the area of the region.
9y+ x = 9, y² − x = 1
Area =
M
Math
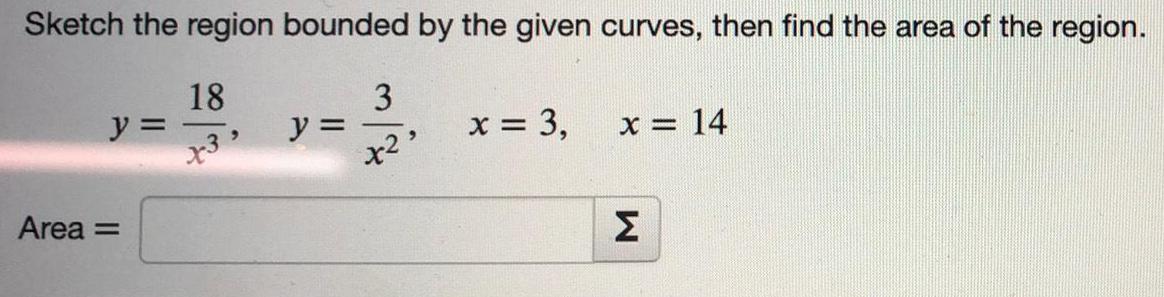
AreaSketch the region bounded by the given curves, then find the area of the region.
y=18/x^3 , y= 3/x^2 , x=3 , x=4

Math
AreaWe spent a bit of time working with parallelograms, trapezoids and triangles. Suppose that a shape has an area of 30 square units. Draw and label it if it is a ... and show how you know.
a) parallelogram
b) trapezoid
c) triangle

Math
AreaA farmer wants to make a rectangular pen for his sheep. He has
120m fencing material to cover three sides with the other side
being a brick wall. What dimensions would maximize the space for
his sheep?
width 20, length 50
width 30, length 60
width 3, length 150
width 40, length 40

Math
AreaYour company wants to make the largest and most luxurious rectangular dog kennels possible with 56 feet of fencing. The design of the kennel is to use the back side of the dog owner's house as one side of the kennel. The other three sides of the kennel must be made from the fencing. What is the largest area your company can make for these new kennels?
• Write answer as a number only.
• Round answer to two decimal places if necessary.

Math
AreaJorge wants to make an open top box from a flat rectangular piece of cardboard measuring 12 inches by 24 inches. To do this Jorge will cut identical squares out of the corners of the cardboard and then fold up the sides. Jorge wants to use this box to store some of his card collection. He calculated that he will need the area of the base of the box to be 100 square inches to fit all the cards he has in mind. What is the length of the sides of the squares Jorge needs to cut out of his original cardboard to get the size of box he wants? . Write your answer as a number only. Round your answer to 2 decimal places if necessary.
Math
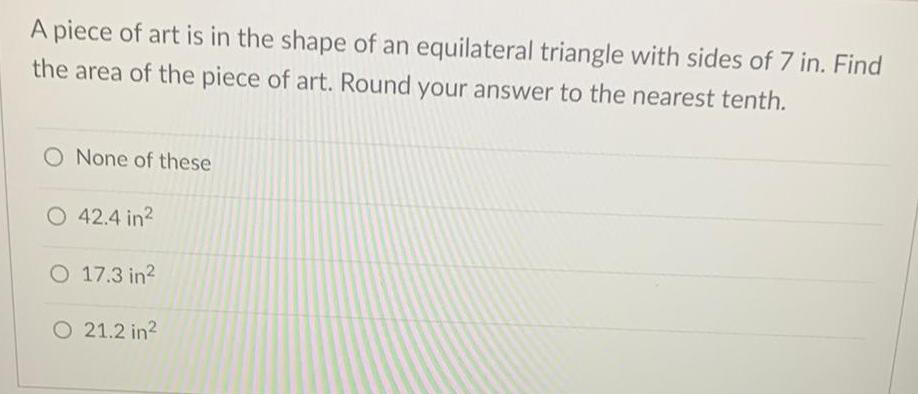
AreaA piece of art is in the shape of an equilateral triangle with sides of 7 in. Find
the area of the piece of art. Round your answer to the nearest tenth.
None of these
42.4 in²
17.3 in2
21.2 in2
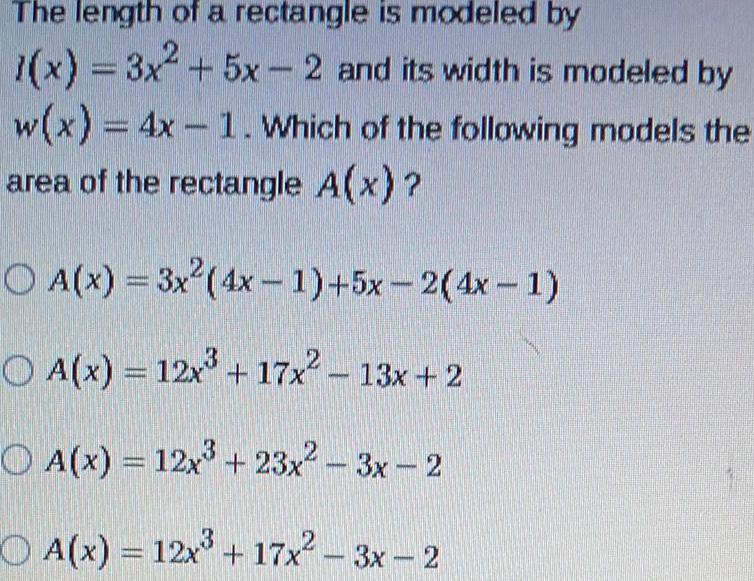
Math
AreaThe length of a rectangle is modeled by l(x) = 3x² + 5x - 2 and its width is modeled by
w(x) = 4x 1. Which of the following models the area of the rectangle A(x)?
A(x) = 3x² + (4x-1) + 5x - 2(4x-1)
A(x) = 12x³ + 17x² - 13x + 2
A(x) = 12x³ + 23x² - 3x - 2
A(x) = 12x³ + 17x² - 3x - 2

Math
AreaThe base of a triangle is eight more than twice the height. The area of the triangle is 285 square feet. Find the measures of the base and
height of the triangle.
The base measures
The height measures
feet
square feet

Math
AreaA regular heptagon with 7 sides is inscribed in a circle with radius 9 millimeters. What is the area of
the figure? (3 points)
260.262 mm.
221.649 mm.²
189.985 mm.2
31.664 mm.²

Math
AreaMateo uses 94.5 feet of fence for a rectangular pen alongside his house. He only needs to fence three sides such that the pen's width is % of its length. He decides to put the shorter side (width) along the house as shown.
What is the area inside the pen?
Enter the value of the answer in the first blank and enter the units in the second.
Enter your answer in decimal form. Round to the nearest tenth if rounding is necessary.
Enter units as ft., square ft., or cubic ft.
The area inside the pen is (about)
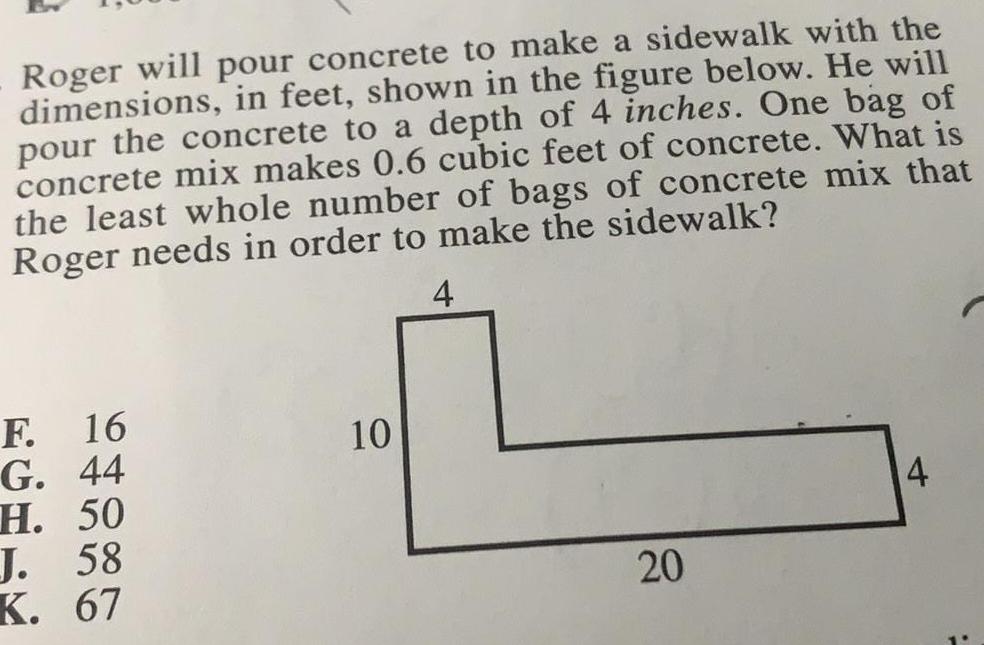
Math
AreaRoger will pour concrete to make a sidewalk with the dimensions, in feet, shown in the figure below. He will pour the concrete to a depth of 4 inches. One bag of concrete mix makes 0.6 cubic feet of concrete. What is the least whole number of bags of concrete mix that Roger needs in order to make the sidewalk?
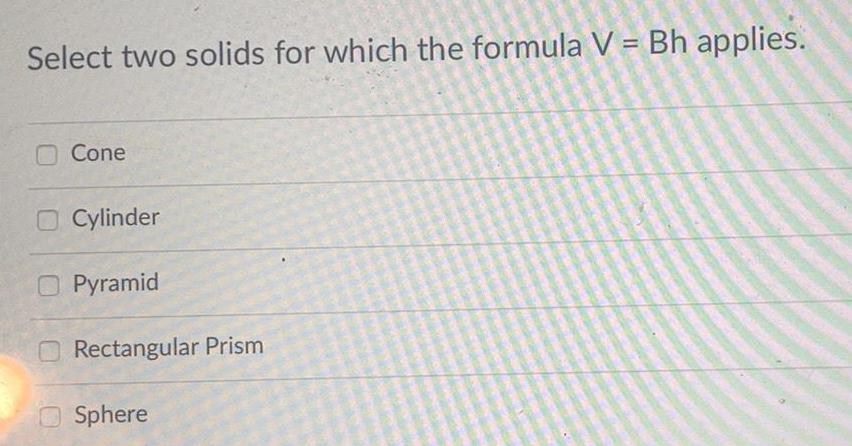
Math
AreaSelect two solids for which the formula V = Bh applies.
Cone
Cylinder
Pyramid
Rectangular Prism
Sphere

Math
AreaA basketball court measures 1012 inches on the sides while the baseline stretches 695 inches. There is a circle in the middle of the cour
that has a diameter of 72 inches. The team can fit 13 people in the circle at one time. How many people can fit on a court?
Helpful Formulas:
A = lw
A=πr²
O 698,600 people
50,000 people
2245 people
2405 people
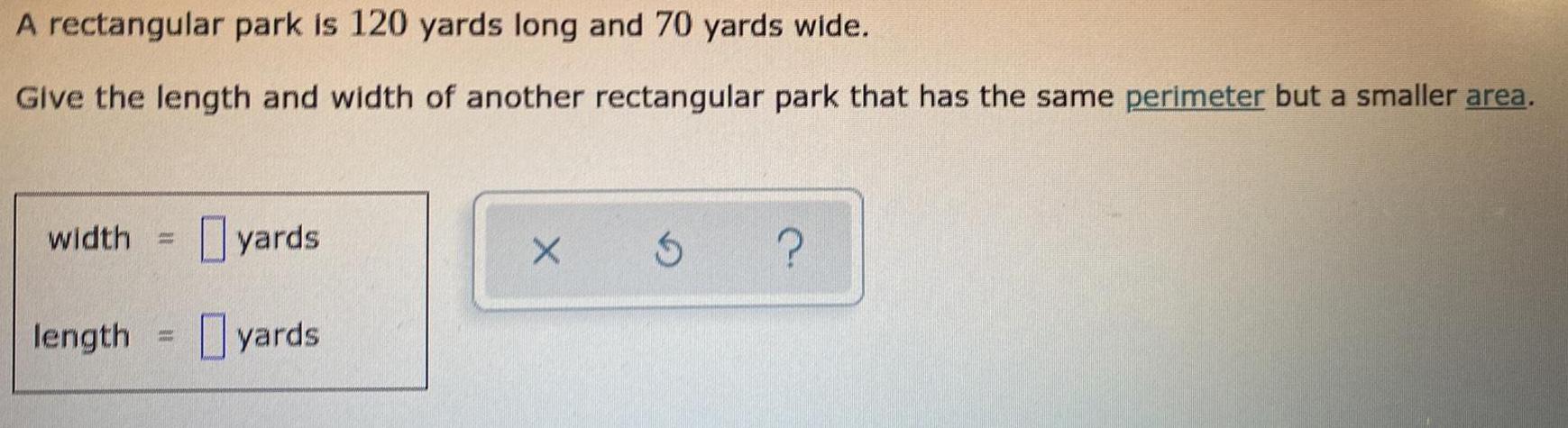
Math
AreaA rectangular park is 120 yards long and 70 yards wide. Give the length and width of another rectangular park that has the same perimeter but a smaller area.
Math
Areacontractor is designing a rectangular room that will have a pool table. The length of the pool table is twice its width. The contractor wishes to have 3 ft of open space between each wall and the pool table as
hown to the right. Express the area of the room in terms of the width w of the pool table. Then perform the indicated operations.
Express the area of the room as the product of two polynomials in terms of the width w of the pool table.
(Do not multiply.)
The area of the room in terms of the width w of the pool table is
(Simplify your answer.)
units.
(...)

Math
AreaHow much wrapping paper would you need to wrap a cylindrical gift with a height of 12.6 inches and
a radius of 4.5 in? Round your answer to the nearest tenth.
O 431.2 in²
O 345.8 ft²
O 483.5 in²
O 510.6 in²

Math
AreaCoach Smith wants to paint his classroom walls red. Each wall is 25 feet long and 9 feet tall. The janitor says he can only order the paint in boxes that contain 3 small cans. One box is used to paint a 125 square foot on the wall.
How many boxes does he need to order?
How many paint cans will he have ordered in total?
How many cans will be used to paint all the walls in the room?
How many paint cans will not be opened?

Math
AreaThe volumes of two similar solids are 729 m³ and 125 m³. The surface area of the larger solid is
324 m³. What is the surface area of the smaller solid?"
100 m²
56 m²
500 m²
200 m²

Math
AreaCarmen wants to tile the floor of his house. He will need 1,000 square feet of tile. He will do most of the
floor with a tile that costs $1.50 per square foot, but also wants to use an accent tile that costs $9.00 per square foot. How many square feet of each tile should he plan to use if he wants the overall cost to be $3 per
square foot?
![Sketch the graph of y = x³ + 3. Estimate the area under the curve
in the interval [0, 4] divided into n = 4 subintervals using:
(a) Lower rectangles
(b) Upper rectangles](https://media.kunduz.com/media/sug-question/raw/65289955-1657007233.7018723.jpeg?w=256)
Math
AreaSketch the graph of y = x³ + 3. Estimate the area under the curve
in the interval [0, 4] divided into n = 4 subintervals using:
(a) Lower rectangles
(b) Upper rectangles
Math
AreaConsider the solid S whose base is the triangular region with vertices (0, 0), (1, 0), and (0, 1). Cross-sections perpendicular to the y-axis are rectangles with height 5.
Volume of S=