Probability Questions and Answers

Math
ProbabilityA survey of 100 Mercy students revealed 20 freshmen of which 4 had student debt; 25 sophmores of which 10 had student debt; 15 juniors of which 8 had student debt and 40 seniors of which 30 had student debt. A. What is the probability of selecting a student at random from this group who is a freshman or has student debt? B. What is the probability of selecting a student at random from this group who has no student debt? C. What is the probability of selecting a student at random from this group who is a sophmore or a senior?

Math
ProbabilitySelect the correct definition of an experiment from the choices below.
An official survey given to every member of a population in order to collect information about each individual.
A study where subjects are given treatments and their responses are measured and recorded.
A study where data are collected and recorded by observing subjects, but no treatments are given to the subjects in
the study.
A group drawn from a population that is used in studies to gather information about the population.

Math
ProbabilityAfter becoming sick, a patient sees a doctor, who determines the most likely cause is an allergic reaction; the doctor prescribes
an antihistamine. The patient returns home and stops burning candles and incense for the next week while taking the medication.
By the end of the week, the patient is feeling better and is telling all his friends how wonderful the medication was at relieving
his symptoms.
What is the best description of this situation?
It is an example of convenience sampling since the patient stopped burning candles and incense only because it was
easy.
It is an example of bias because the patient wanted to feel better and would have reported relief of symptoms even if
they had not improved.
It is an example of confounding, as there is no way to tell whether it was the medication that alleviated the patient's
symptoms.
It is an example of an experiment because the doctor prescribed the antihistamine to the patient, rather than letting the
patient choose his medication.

Math
ProbabilityWhich choice best describes a simple random sample?
when a population is first sorted into comparable groups, groups are randomly chosen, and all of the individuals
from those groups are chosen
a selection of members chosen from a population beginning at a random point and then chosen at set intervals from
that point
a selection of members from a population in such a way that every possible sample of the same size has an equal
chance of being chosen
when a population is first sorted into groups that share a similar characteristic and individuals are randomly chosen
from each of the groups
a selection of members of a population chosen because of their convenient accessibility and proximity
Math
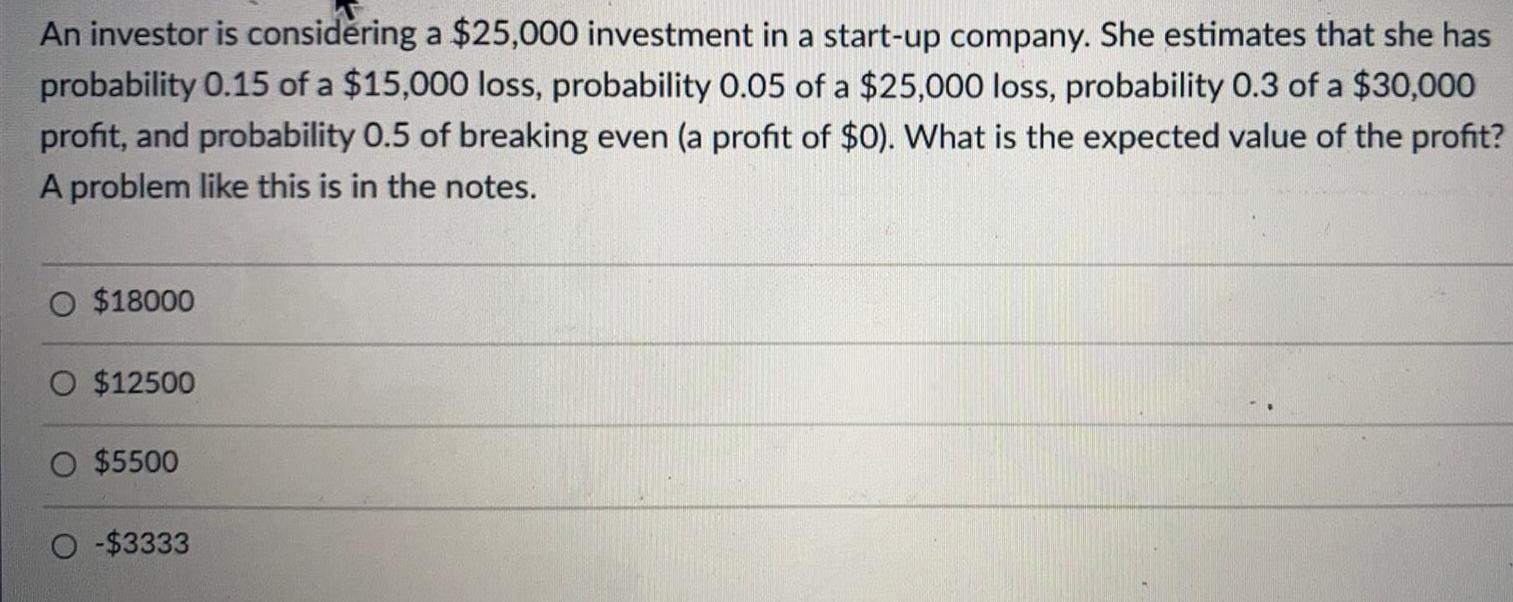
ProbabilityAn investor is considering a $25,000 investment in a start-up company. She estimates that she has
probability 0.15 of a $15,000 loss, probability 0.05 of a $25,000 loss, probability 0.3 of a $30,000
profit, and probability 0.5 of breaking even (a profit of $0). What is the expected value of the profit?
A problem like this is in the notes.
$18000
$12500
$5500
-$3333

Math
ProbabilityA certain system can experience three different types of defects. Let A (i = 1,2,3) denote the event that the
system has a defect of type i. Suppose that
(a) Find the probability that the system has exactly 2 of
the 3 types of defects.
(b) Find the probability that the system has a type 1 defect given that it does not have a type 2 defect and does not have a type 3 defect.

Math
ProbabilityA lot of 101 semiconductor chips contains 16 that are
defective.
(a) Two are selected, one at a time and without
replacement from the lot. Determine the probability
that the second one is defective.
(b) Three are selected, one at a time and without
replacement. Find the probability that the first one
is defective and the third one is not defective.

Math
ProbabilityHeart failures are due to either natural occurrences
(83%) or outside factors (17%). Outside factors are
related to induced substances (69%) or foreign objects
(31%). Natural occurrences are caused by arterial
blockage (52%), disease (31%), and infection (17%).
(a) Determine the probability that a faliure is due to an
induced substance.
(b) Determine the probability that a failure is due to
disease or infection.

Math
ProbabilityAn automobile manufacturing plant produced 36 vehicles today: 17 were vans, 13 were trucks, and 6 were sedans. Plant managers are going to select two of these vehicles for a thorough inspection. The first vehicle will be selected at random, and then the second vehicle will be selected at random from the remaining vehicles. What is the probability that two vans will be selected? Do not round your intermediate computations. Round your final answer to three decimal places.

Math
ProbabilityA company that makes crayons is trying to decide which 4 colors to include in a promotional
mini-box of 4 crayons. The company can choose the 4 mini-box colors from its collection of 65
colors. How many mini-boxes are possible?
A company has 31 salespeople. A board member at the company asks for a list of the top 5
salespeople, ranked in order of effectiveness. How many such rankings are possible?

Math
ProbabilityA parucular disease is tested for and the results determine that it occurs in about 1 of every 525 Chinese baby births and about 1 of every 149,000 non-Chinese baby births. Find the empirical probability that a randomly selected Chinese baby will have this disease.
The probability is
(Type an integer or decimal rounded to three decimal places as needed.)

Math
ProbabilityA university class has 29 students: 14 are nursing majors, 9 are history majors, and 6 are business majors. The professor is planning to select two of students for a demonstration. The first student will be selected at random, and then the second student will be selected at random from the remaining students. What is the probability that the first student selected is a history major and the second student is a business major? Do not round your intermediate computations. Round your final answer to three decimal places. (If necessary, consult a list of formulas.)

Math
ProbabilityAt a local college, 155 of the male students are smokers and 155 are non-smokers. Of the female students, 60 are smokers and 140 are non-smokers. A male student and a female student from the college are randomly selected for a survey. What is the probability that both are smokers? Do not round your answer. (If necessary, consult a list of formulas.)

Math
ProbabilityIf we denote a cystic fibrosis gene with a c and a disease-free gene with a C (since the disease is recessive), then only a cc person will actually have the disease. Such persons would ordinarily die before parenting children, but a child can also inherit the disease from two Cc parents (who themselves are healthy-that is, have no symptoms but are "carriers" of the disease). Suppose a child is born to one cystic fibrosis carrier parent and one non-carrier parent. Find the probability that that the child will be a carrier. The probability is (Type an integer or a simplified fraction.) *****

Math
ProbabilityA poker hand consisting of 6 cards is dealt from a standard deck of 52 cards. Find the probability that the hand contains exactly 2 face cards.
The probability is
(Give your answer as a decimal rounded to 3 places.)

Math
ProbabilityAt a particular restaurant, 42% of all customers order an appetizer and 36% of all customers order dessert. If 52% of all customers order an appetizer or
dessert (or both), what is the probability a randomly selected customer orders both an appetizer and dessert?

Math
ProbabilityIf you randomly select a card from a well-shuffled standard deck of 52 cards, what is the probability that the card you select is a club or 3?
(answer as a fraction or decimal rounded to three places)

Math
ProbabilityA bag has ten marbles. Five green, three blue, two red. What is the probability of
drawing two green and one red in that order without replacement?

Math
ProbabilityKristina buys a bag of cookies that contains 7 chocolate chip cookies, 4 peanut butter cookies, 9 sugar cookies and 8 oatmeal cookies. What is the probability that Kristina reaches in the bagland randomly selects 2 sugar cookies from the bag?

Math
ProbabilityInside the box of every cereal box contains a surprise gift. The store manager assures employees that 21 of the 65 boxes on the shelf have a secret decoder ring and inside the other 44 boxes on the shelf contain a different gift. If two cereal boxes are randomly selected from the shelf to purchase, what is the probability that both of them have the secret decoder ring?

Math
ProbabilityUse a normal approximation to find the probability of the indicated number of voters. In this case, assume that 183 eligible voters aged 18-24 are randomly selected. Suppose a previous study showed that among eligible voters aged 18-24, 22%
of them voted.
Probability that exactly 46 voted
The probability that exactly 46 of 183 eligible voters voted is
(Round to four decimal places as needed.)

Math
ProbabilityUsing a standard 52-card deck, find the following probabilities. Leave your answer as a reduced fraction.
a. If a card is randomly selected, what is the probability that the card is any one suit, e.g., a diamond, heart, spade, or club?
b. If two cards are randomly selected, what is the probability of drawing a face card first, followed by
drawing a numbered card?
c. If two cards are randomly selected, what is the probability of drawing any one suit first, followed by drawing a face card?

Math
ProbabilityThe waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 9 minutes. Find at a randomly selected passenger has a waiting time greater than 1.25 minutes.
Find the probability that a randomly selected passenger has a waiting time greater than 1.25 minutes.
(Simplify your answer. Round to three decimal places as needed.)
![Bianca and Carlos play a game using a bag of marbles. The bag contains 12 blue, 14 green, 8 red, and 6 yellow marbles. A marble is drawn. If
the marble is red or yellow, Bianca wins. If the marble is green, Carlos wins. If the marble is blue, neither player wins.
Is the game fair? Select one choice from the set to answer the question.
The game is [ fair / not fair].
Enter a percent in each box to explain why the game is fair or unfair.
% chance of winning and Carlos has a
Blanca has a
% chance of winning.](https://media.kunduz.com/media/sug-question/raw/53824162-1657977532.6170409.jpeg?w=256)
Math
ProbabilityBianca and Carlos play a game using a bag of marbles. The bag contains 12 blue, 14 green, 8 red, and 6 yellow marbles. A marble is drawn. If
the marble is red or yellow, Bianca wins. If the marble is green, Carlos wins. If the marble is blue, neither player wins.
Is the game fair? Select one choice from the set to answer the question.
The game is [ fair / not fair].
Enter a percent in each box to explain why the game is fair or unfair.
% chance of winning and Carlos has a
Blanca has a
% chance of winning.

Math
ProbabilityThe positions on a lacrosse team are called defenders (D), midfielders (M), and attackers (A). One player is chosen at random to lead the tearn In
exercises before each game. The letters MDD mean that a midfielder was chosen at the first game and a defender was chosen at the next two
games. The list of all possible outcomes is shown, where each outcome has equal probability of occurring.
What is the probability that a defender is chosen at least once, given that a midfielder is chosen at the first game?
Math
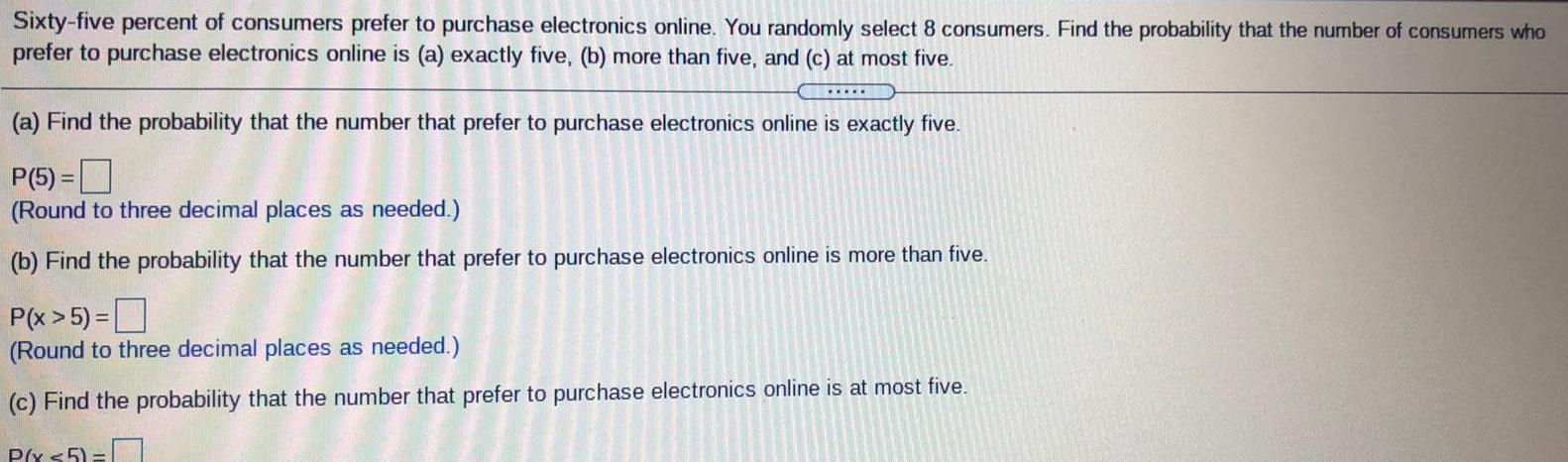
ProbabilitySixty-five percent of consumers prefer to purchase electronics online. You randomly select 8 consumers. Find the probability that the number of consumers who
prefer to purchase electronics online is (a) exactly five, (b) more than five, and (c) at most five.
(a) Find the probability that the number that prefer to purchase electronics online is exactly five.
P(5) =
(Round to three decimal places as needed.)
(b) Find the probability that the number that prefer to purchase electronics online is more than five.
P(x > 5) =
(Round to three decimal places as needed.)
(c) Find the probability that the number that prefer to purchase electronics online is at most five.
P(x 55) =

Math
ProbabilityIdentify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram.
Determining a person's favorite steak (rib-eye (R), filet (F), T-bone (T), sirloin (S)) and doneness (rare (R), medium (M), well done (W))
Identify the sample space.
A. (RR, RM, FR, FM, TR, TM, SR, SM}
B. (RR, RM, FR, FM, TR, TM}
C. {RR, RM, FR, FM, TR, TM, SR, SM, FR, FM}
D. (RR, RM, RW, FR, FM, FW, TR, TM, TW, SR, SM, SW}
There are outcomes in the sample space.

Math
ProbabilityA spinner has 8 equally sized sections, 2 of which are gray and 6 of which are blue. The spinner is spun twice. What is the probability that the first spin lands on blue and the second spin lands on gray ?
Write your answer as a fraction in simplest form.

Math
ProbabilityCan two events with nonzero probabilities be both independent and mutually exclusive?
Choose the correct answer below.
.....
OA. Yes, two events with nonzero probabilities can be both independent and mutually exclusive when their probabilities are equal.
OB. No, two events with nonzero probabilities cannot be independent and mutually exclusive because if two events are mutually exclusive, then when one of
them occurs, the probability of the other must be zero.
OC. Yes, two events with nonzero probabilities can be both independent and mutually exclusive when their probabilities add up to one.
OD. No, two events with nonzero probabilities cannot be independent and mutually exclusive because independence is the complement of being mutually
exclusive.
Math
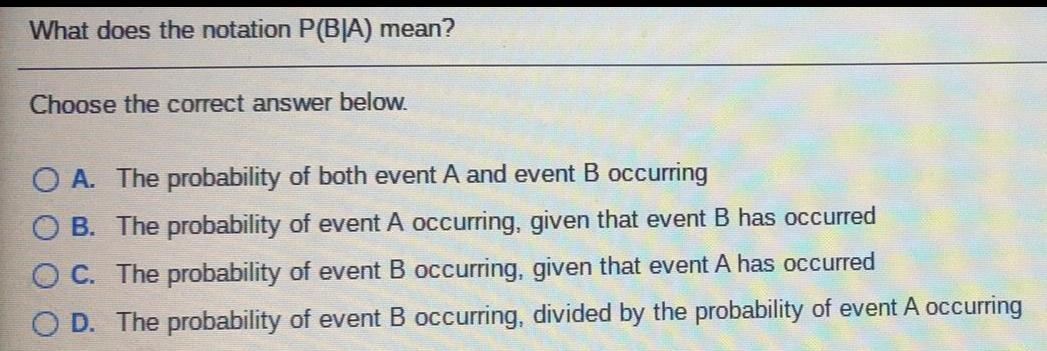
ProbabilityWhat does the notation P(BIA) mean?
Choose the correct answer below.
O A. The probability of both event A and event B occurring
OB. The probability of event A occurring, given that event B has occurred
OC. The probability of event B occurring, given that event A has occurred
OD. The probability of event B occurring, divided by the probability of event A occurring

Math
ProbabilityExplain how the complement can be used to find the probability of getting at least one item of a particular type.
Choose the correct answer below.
*****
OA. The complement of "at least one" is "all." So, the probability of getting at least one item is equal to P(all items) - 1.
OB. The complement of "at least one" is "all." So, the probability of getting at least one item is equal to 1-P(all items).
OC. The complement of "at least one" is "none." So, the probability of getting at least one item is equal to 1-P(none of the items).
D. The complement of "at least one" is "none." So, the probability of getting at least one item is equal to P(none of the items) - 1.

Math
ProbabilityA coin is tossed and an eight-sided die numbered 1 through 8 is rolled. Find the probability of tossing a tail and then rolling a number greater than 6.
The probability of tossing a tail and then rolling a number greater than 6 is
(Round to three decimal places as needed.)
*****

Math
ProbabilityDecide whether the events shown in the accompanying Venn diagram are mutually exclusive. Explain your reasoning.
Click the icon to view the Venn diagram.
The events
mutually exclusive, since there are
*****
movies that are rated PG and

Math
ProbabilityA factory claims a 4% defective rate on items produced. If a quality control engineer samples 25 items, what is the probability that 3 are defective? Express your answer to four decimal places.
01. 0.078
O2.0.0600
O 3. 0.1397
O4.0.01198
Math
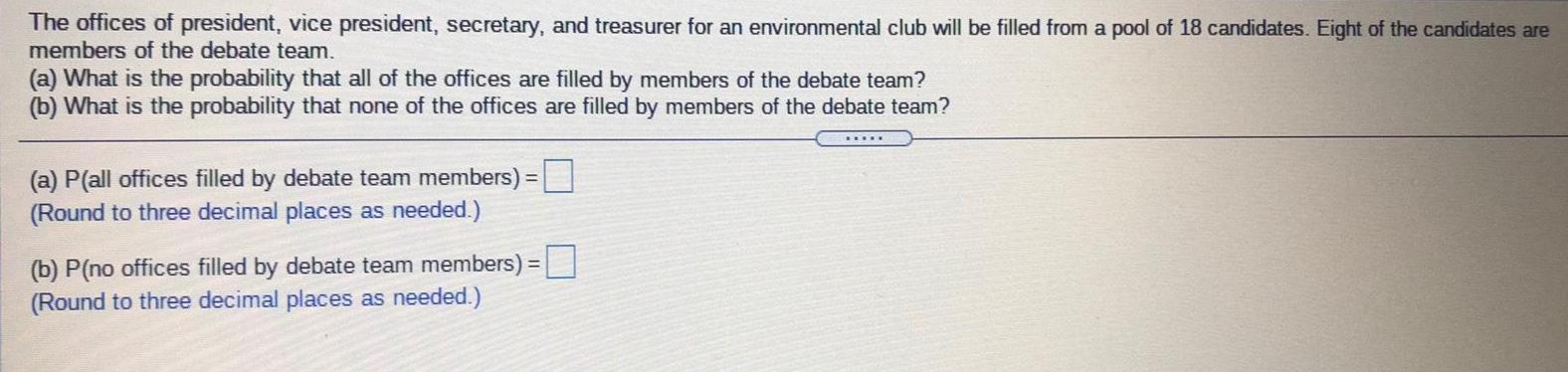
ProbabilityThe offices of president, vice president, secretary, and treasurer for an environmental club will be filled from a pool of 18 candidates. Eight of the candidates are
members of the debate team.
(a) What is the probability that all of the offices are filled by members of the debate team?
(b) What is the probability that none of the offices are filled by members of the debate team?
(a) P(all offices filled by debate team members) =
(Round to three decimal places as needed.)
(b) P(no offices filled by debate team members) =
(Round to three decimal places as needed.)
*****

Math
ProbabilityThe data collected for new students enrolled at a community college show that 23 are under the age of eighteen, 375 are between the ages of eighteen and twenty-two, 259 are between the ages of twenty-three and twenty-seven, 124 are between the ages of
twenty-eight and thirty-two, and 219 are over age thirty-two. What is the probability distribution for these data?
Construct a probability distribution for the data.
Age when Enrolled
Probability
under 18
18-22
23-27
28-32
over 32

Math
ProbabilityA
music collection includes 16 rock CDs, 14 country CDs, 7 classical CDs, and 5 hip hop CDs.
a. What is the probability that a CD randomly selected from the collection is a classical CD?
b. What is the probability that a CD randomly selected from the collection is not a classical CD?
1
that a randomly selected CD is a classical CD.
6
a. The probability is
(Simplify your answer.)
b. The probability is that a randomly selected CD is not a classical CD.
(Simplify your answer.)

Math
ProbabilityA bag contains letter tiles that spell the name of the state Arizona. Find the theoretical probability of drawing one tile at random for P(a).
What is the probability that the letter "a" is selected?
P(a) = (Type an integer or a simplified fraction.)
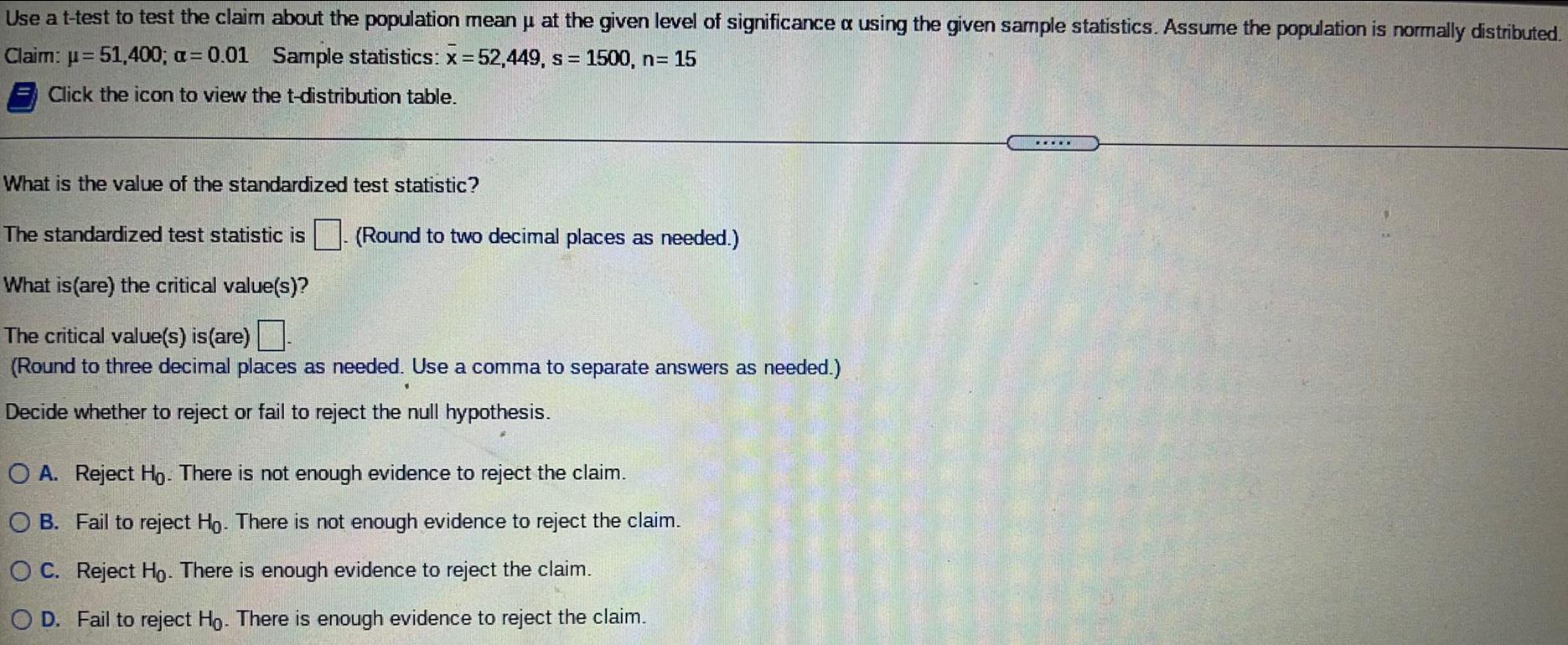
Math
ProbabilityUse a t-test to test the claim about the population mean μ at the given level of significance a using the given sample statistics. Assume the population is normally distributed.
Claim: μ = 51,400; a= 0.01 Sample statistics: x=52,449, s = 1500, n= 15
Click the icon to view the t-distribution table.
What is the value of the standardized test statistic?
The standardized test statistic is. (Round to two decimal places as needed.)
What is (are) the critical value(s)?
The critical value(s) is (are).
(Round to three decimal places as needed. Use a comma to separate answers as needed.)
Decide whether to reject or fail to reject the null hypothesis.
A. Reject Ho. There is not enough evidence to reject the claim.
B. Fail to reject Ho. There is not enough evidence to reject the claim.
C. Reject Ho. There is enough evidence to reject the claim.
D. Fail to reject Ho. There is enough evidence to reject the claim.
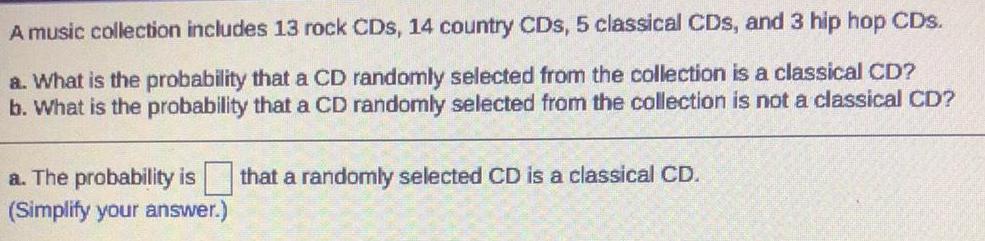
Math
ProbabilityA music collection includes 13 rock CDs, 14 country CDs, 5 classical CDs, and 3 hip hop CDs.
a. What is the probability that a CD randomly selected from the collection is a classical CD?
b. What is the probability that a CD randomly selected from the collection is not a classical CD?

Math
Probability38% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit cards. Use the binomialpdf function in the calculator to find the probability that the number of college students who say they use credit cards because of the rewards program is exactly 7.
A. 0.242
B. 0.033
C. 0.468
D. 0.202

Math
Probability8. Based on their history, a hockey team has a 40% chance of winning any random game.
a. What is the probability that this team will win both of their next two games?
b. What is the probability that this team will win exactly two out of their next three
games?

Math
ProbabilityThe amounts of time per workout an athlete uses a stair climber are normaly distributed, with a mean of 23 minutes and a standard deviation of 7 minutes. Use the normalcdf function in the calculator to find the probability that the time a randomly selected athlete uses a stair climber is less than 19 minutes.
A 0.716
B. 0.498
C. 0.284
D. 0.103

Math
ProbabilityA private detective figures that he has a one in ten chance of recovering stolen property for his client. The expenses for the investigation will cost him $10,000, but the recovery fee is $80,000.
Based ONLY on this information, should the private detective take the job?
The expected value is $1,000, so the detective should take the job.
The expected value is -$2,000, so the detective should not take the job.
The expected value is $2,000, so the detective should take the job.
The expected value is -$8,000, so the detective should not take the job.

Math
ProbabilityGiven A, B and C are events with P(A)= 0.33, P(B)=0.25, P(C)=0.5, P(A ∩ B)=0.17, P(A∩C)= 0.11, P(B∩C)= 0.15, and P(A∩B∩C)=0.02, find P(A∪B ∪C).

Math
ProbabilityAn airline claims that there is 0.25 probability a randomly selected business traveler will check baggage. An agent at the check-in counter records whether each business traveler checks baggage. Explain what probability 0.25 means in this setting.

Math
ProbabilityIn a math class with 21 students, a test was
given the same day that an assignment
was due. There were 14 students who
passed the test and 16 students who
completed the assignment. There were 12
students who passed the test and also
completed the assignment. What is the
probability that a student chosen
randomly from the class passed the test or
completed the homework

Math
ProbabilityA bag contains 10 white, 12 blue, 13 red, 7 yellow, and 8 green wooded balls. A ball is selected from the bag, its color noted, then replaced. You then draw a second ball,
note its color and then replace the ball. What is the probability of selecting one white ball and one blue ball? Round to the nearest ten-thousandth.
0.2200
0.4400
0.0088
0.0480

Math
Probability2. Given A, B and C are mututally exclusive and exhaustive events with p(A)=0.3, p(B)=0.5, and p(C)=0.2.
For an event G, we know that p(G|A)=0.8, p(G|B)=0.7, and p(G|C)=0.9. Find p(G).

Math
ProbabilityA group consists of 6 men and 5 women. Four people are selected to attend a
conference. In how many ways can 4 people be selected from this group of 11? In
how many ways can 4 men be selected from the 6 men? Find the probability that the
selected group will consist of all men.