Probability Questions and Answers
Math
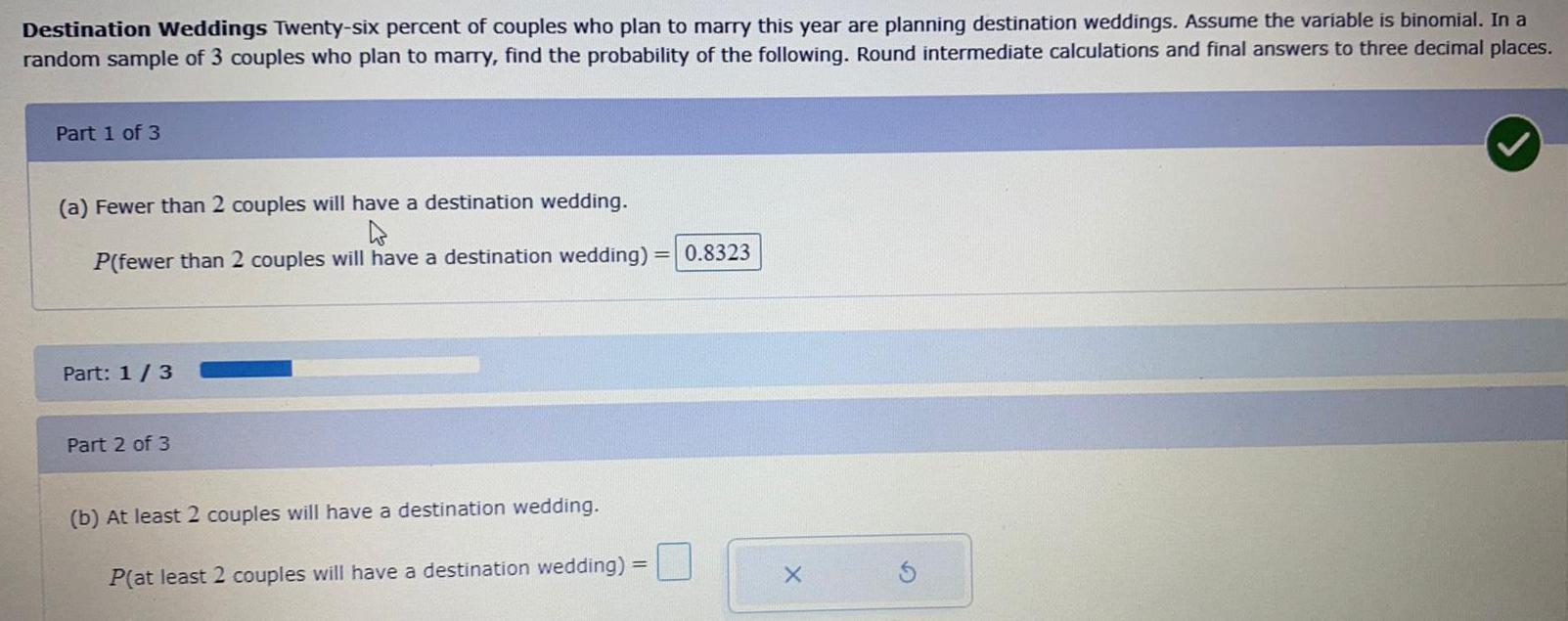
ProbabilityDestination Weddings Twenty-six percent of couples who plan to marry this year are planning destination weddings. Assume the variable is binomial. In an andom sample of 3 couples who plan to marry, find the probability of the following. Round intermediate calculations and final answers to three decimal places.
(a) Fewer than 2 couples will have a destination wedding.
(b) At least 2 couples will have a destination wedding.
Math
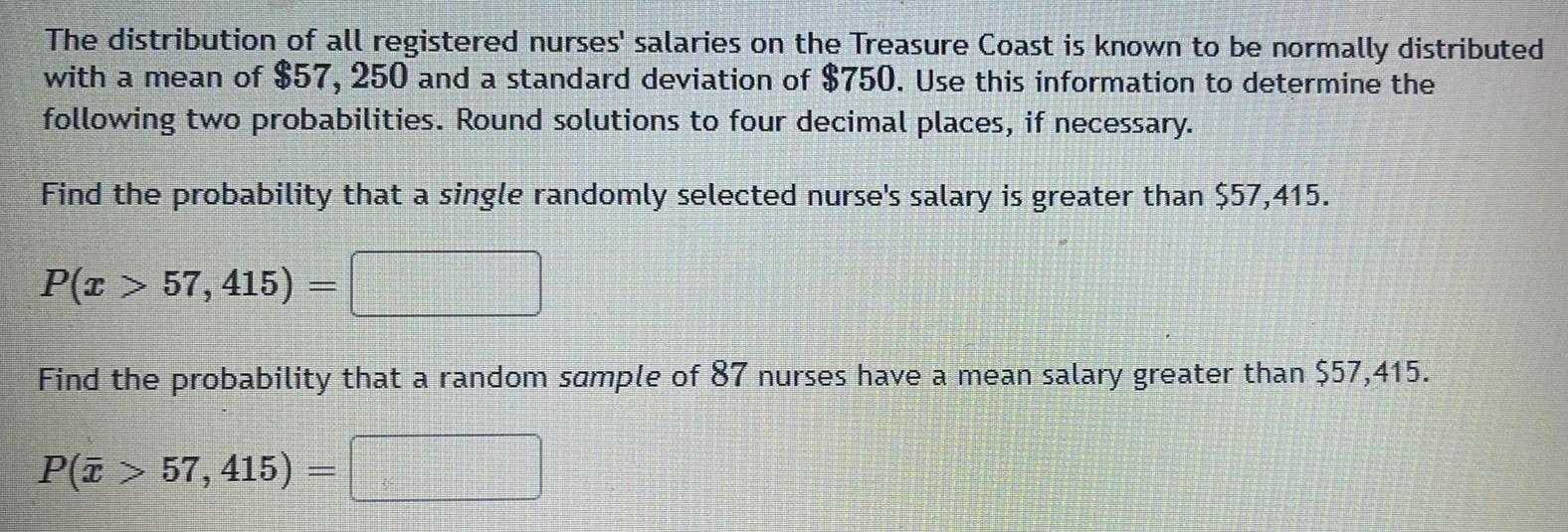
ProbabilityThe distribution of all registered nurses' salaries on the Treasure Coast is known to be normally distributed with a mean of $57, 250 and a standard deviation of $750. Use this information to determine the following two probabilities. Round solutions to four decimal places, if necessary.
Find the probability that a single randomly selected nurse's salary is greater than $57,415.
P(x > 57, 415) =
Find the probability that a random sample of 87 nurses have a mean salary greater than $57,415.
P(x > 57, 415) =

Math
ProbabilityAssume that a national fitness study reports that 15% of millenials exercise daily. Suppose that a researcher surveys a random sample of 200 millenials regarding their daily exercise habits. Assume that X is a binomial random variable that represents the number of millenials in the sample who exercise daily.
Compute the mean μ and standard deviation o of the sampling distribution of X. Report μ as a whole number and o as a decimal precise to two decimal places.

Math
ProbabilitySuppose Kristen is researching failures in the restaurant business. In the city where she lives, the probability that an independent restaurant will fail in the first year is 67%. She obtains a random sample of 98 independent restaurants that opened in her city more than one year ago and determines if each one had closed within a year.
What are the mean and standard deviation of the number of restaurants that failed within a year? P

Math
ProbabilityThe Wechsler Adult Intelligence Scale (WAIS) is the most common IQ test. The distribution of scores for adults taking the WAIS is approximately Normal with a mean of 100 and a standard deviation of 15.
Use the 68-95-99.7 rule to answer the questions about WAIS scores.
What percentage of adults score above 100?
68%
32%
84%
2.5%
50%
0.3%

Math
ProbabilityThe distribution of heights of both five-year old boys and seven-year old boys is approximately Normal. The mean height of a five-year old boy is 43 inches and the standard deviation is 1.8 inches. The mean height of a seven-year old boy is 48 inches and the standard deviation is 2.1 inches. John's height was 44 inches on his fifth birthday, and today, on his seventh birthday, he measures 49 inches tall. What can you conclude about the rate of John's growth when compared to other boys his age?

Math
ProbabilityIn the country of United States of Heightlandia, the height measurements of ten-year-old children are approximately normally distributed with a mean of 53 inches, and standard deviation of 6.8 inches.
What is the probability that the height of a randomly chosen child is between 39.9 and 54.9 inches? Do not round until you get your your final answer, and then round to 3 decimal places.
Math
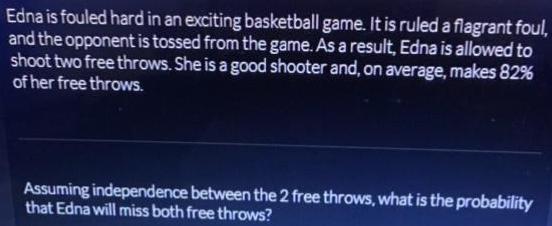
ProbabilityEdna is fouled hard in an exciting basketball game. It is ruled a flagrant foul, and the opponent is tossed from the game. As a result, Edna is allowed to shoot two free throws. She is a good shooter and, on average, makes 82% of her free throws.
Assuming independence between the 2 free throws, what is the probability that Edna will miss both free throws?

Math
ProbabilityYour college is having a housing lottery. The probability that you will get a single room all to yourself next year is 0.2, the probability of getting a double is 0.6, and the probability of getting a triple is 0.2. All of the triples have air conditioning, half of the doubles have air conditioning, and only 10% of the singles have air conditioning.
What is the probability that your dorm room next year will have air conditioning?

Math
ProbabilityA random variable X can take on three possible values: 0, 8, or 20. Each of these values is associated with the following probabilities:
P(X= 0) = 0.25, P (X= 8) = 0.25, and
P(X= 20) = 0.5.
What is the expected value of X?

Math
ProbabilityA manufacturer knows that their items have a normally distributed lifespan, with a mean of 11.6 years, and standard deviation of 1.8 years If you randomly purchase one item, what is the probability it will last longer than 10 years? Round answer to three decimal places
Enter your answer as an integer or decimal number. Examples: 3, -4,
Enter DNE for Does Not Exist, oo for Infinity

Math
ProbabilityAccording to Masterfoods, the company that manufactures M&M's, 12% of peanut M&M's are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. (Round your answers to 4 decimal places where possible)
a. Compute the probability that a randomly selected peanut M&M is not red.
b. Compute the probability that a randomly selected peanut M&M is red or blue.
c. Compute the probability that three randomly selected peanut M&M's are all green.
d. If you randomly select five peanut M&M's, compute that probability that none of them are brown.
e. If you randomly select five peanut M&M's, compute that probability that at least one of them is brown.
Math
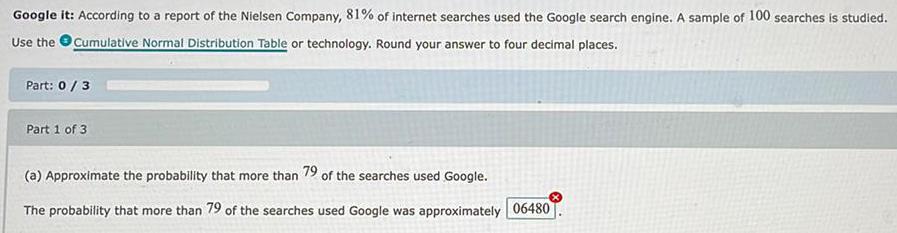
ProbabilityGoogle it: According to a report of the Nielsen Company, 81% of internet searches used the Google search engine. A sample of 100 searches is studied.
Use the Cumulative Normal Distribution Table or technology. Round your answer to four decimal places.
(a) Approximate the probability that more than 79 of the searches used Google.
The probability that more than 79 of the searches used Google was approximately 06480
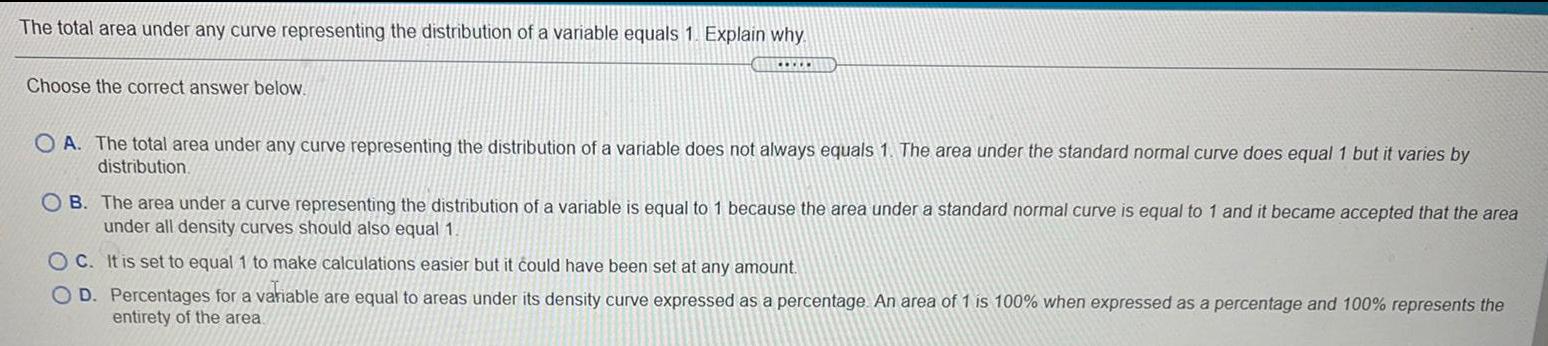
Math
ProbabilityThe total area under any curve representing the distribution of a variable equals 1. Explain why.
.
A. The total area under any curve representing the distribution of a variable does not always equals 1. The area under the standard normal curve does equal 1 but it varies by distribution.
B. The area under a curve representing the distribution of a variable is equal to 1 because the area under a standard normal curve is equal to 1 and it became accepted that the area under all density curves should also equal 1.
C. It is set to equal 1 to make calculations easier but it could have been set at any amount.
D. Percentages for a variable are equal to areas under its density curve expressed as a percentage. An area of 1 is 100% when expressed as a percentage and 100% represents the entirety of the area.
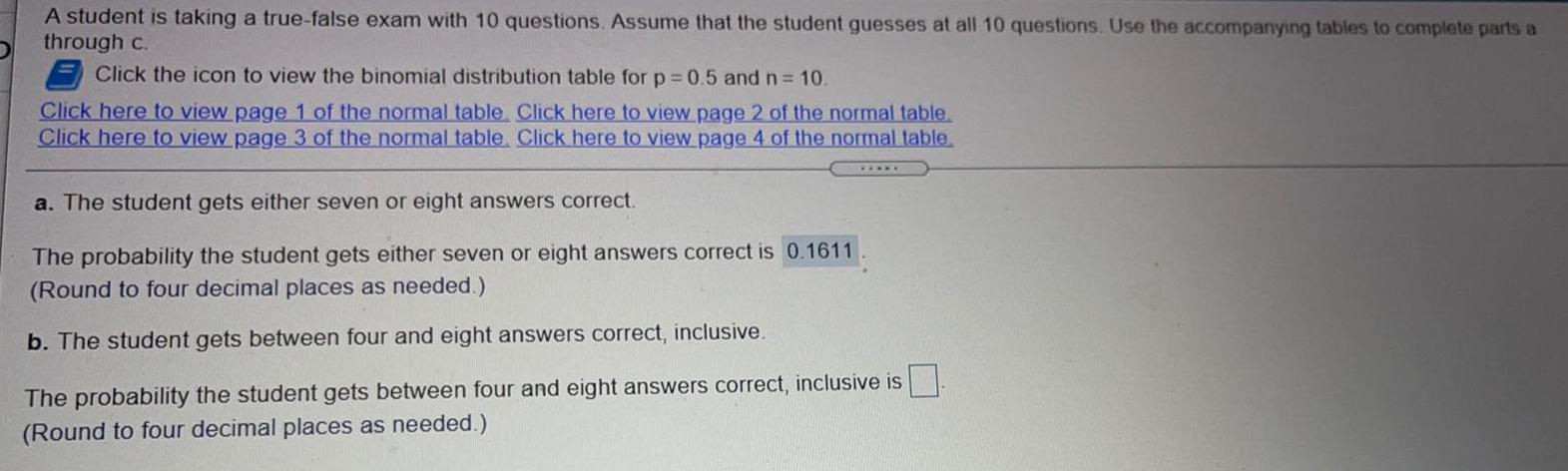
Math
ProbabilityA student is taking a true-false exam with 10 questions. Assume that the student guesses at all 10 questions. Use the accompanying tables to complete parts a
through c.
a. The student gets either seven or eight answers correct.
The probability the student gets either seven or eight answers correct is _____
b. The student gets between four and eight answers correct, inclusive.
The probability the student gets between four and eight answers correct, inclusive is _____

Math
ProbabilityThe population of weights of a particular fruit is normally distributed, with a mean of 228 grams and a standard deviation of 12 grams. If 26 fruits are picked at random, then 7% of the time, their mean weight will be greater than how many grams? Round your answer to the nearest gram.

Math
ProbabilityYou own 18 CDs. You want to randomly arrange 5 of them in a CD rack. What is the probability that the rack ends up in alphabetical order?
The probability that the CDs are in alphabetical order is
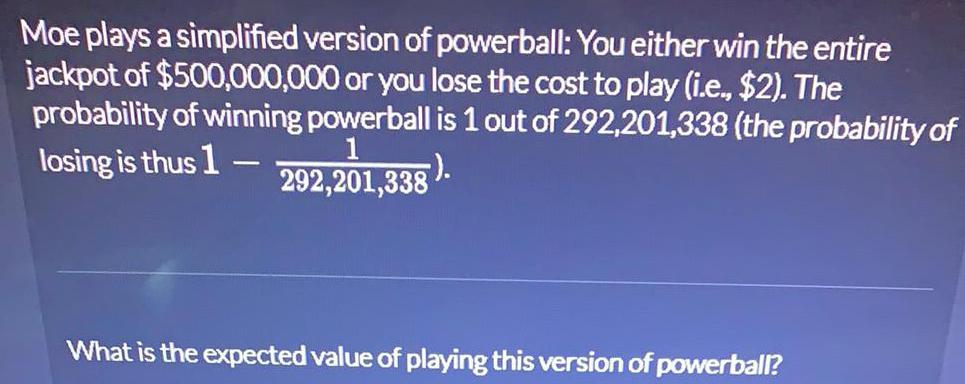
Math
ProbabilityMoe plays a simplified version of powerball: You either win the entire jackpot of $500,000,000 or you lose the cost to play (i.e., $2). The probability of winning powerball is 1 out of 292,201,338 (the probability of losing is thus 1-
1- 1/292,201,338).What is the expected value of playing this version of powerball?

Math
ProbabilityA particular stock is currently trading at $1. An expert market analyst determines that in one year, the price of the stock will be: $2 with a probability of 0.5; $3 with a probability of 0.1; and nothing ($0) with a probability of 0.4.
f the random variable X represents the gain or loss in the stock price in one year, what is the expected value of X?

Math
Probabilitya. The student gets either seven or eight answers correct.
The probability the student gets either seven or eight answers correct is
(Round to four decimal places as needed.)
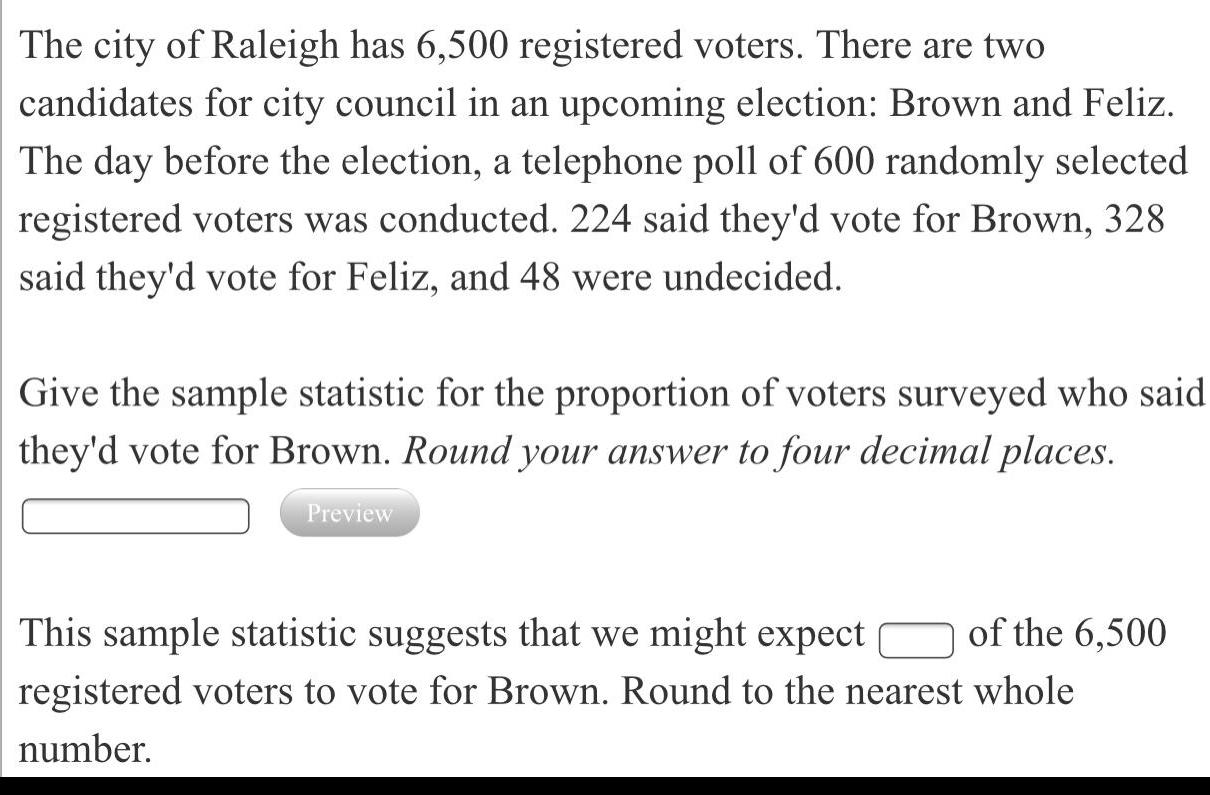
Math
ProbabilityThe city of Raleigh has 6,500 registered voters. There are two candidates for city council in an upcoming election: Brown and Feliz. The day before the election, a telephone poll of 600 randomly selected registered voters was conducted. 224 said they'd vote for Brown, 328 said they'd vote for Feliz, and 48 were undecided.
Give the sample statistic for the proportion of voters surveyed who said they'd vote for Brown. Round your answer to four decimal places.
This sample statistic suggests that we might expect of the 6,500 registered voters to vote for Brown. Round to the nearest whole number.

Math
ProbabilityA criminologist developed a test to measure recidivism, where low scores indicated a lower probability of repeating the undesirable behavior. The test is normed so that it has a mean of 140 and a standard deviation of 40. What is the percentile rank of a score of 172, please round to a whole number?
Math
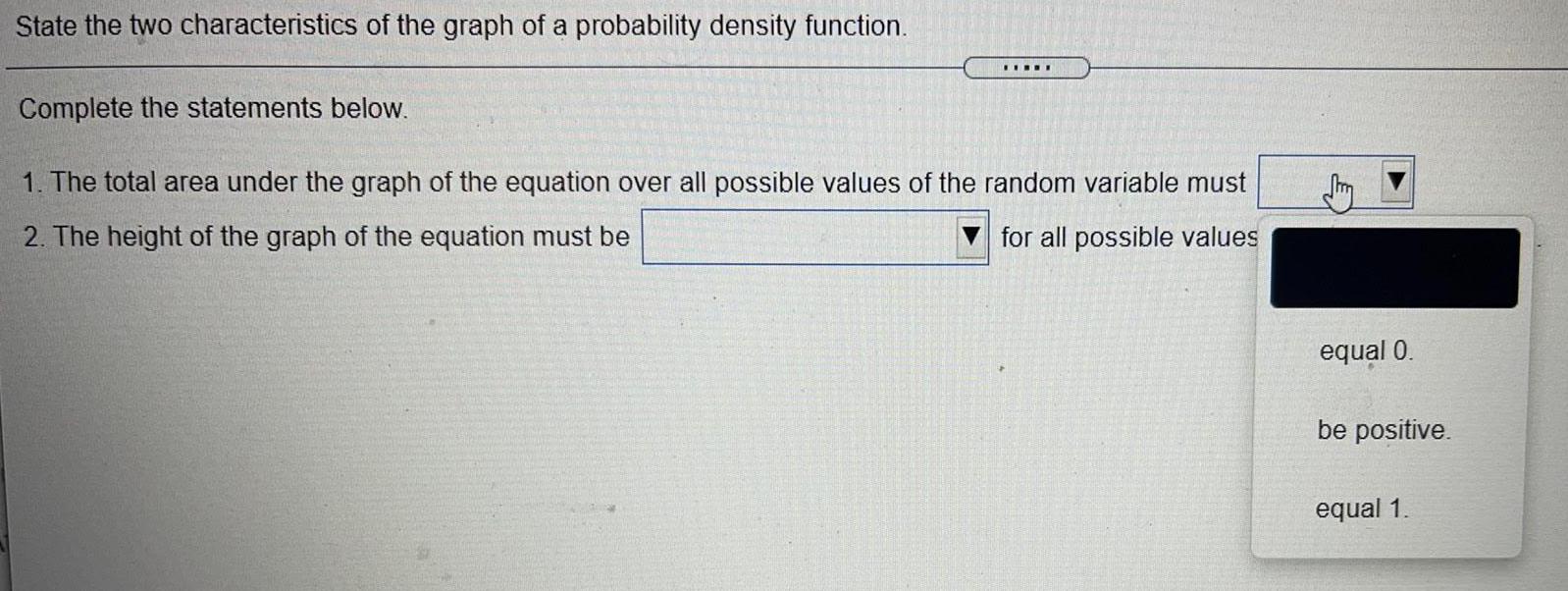
ProbabilityState the two characteristics of the graph of a probability density function.
Complete the statements below.
1. The total area under the graph of the equation over all possible values of the random variable must
2. The height of the graph of the equation must be
for all possible values
equal 0.
be positive.
equal 1.
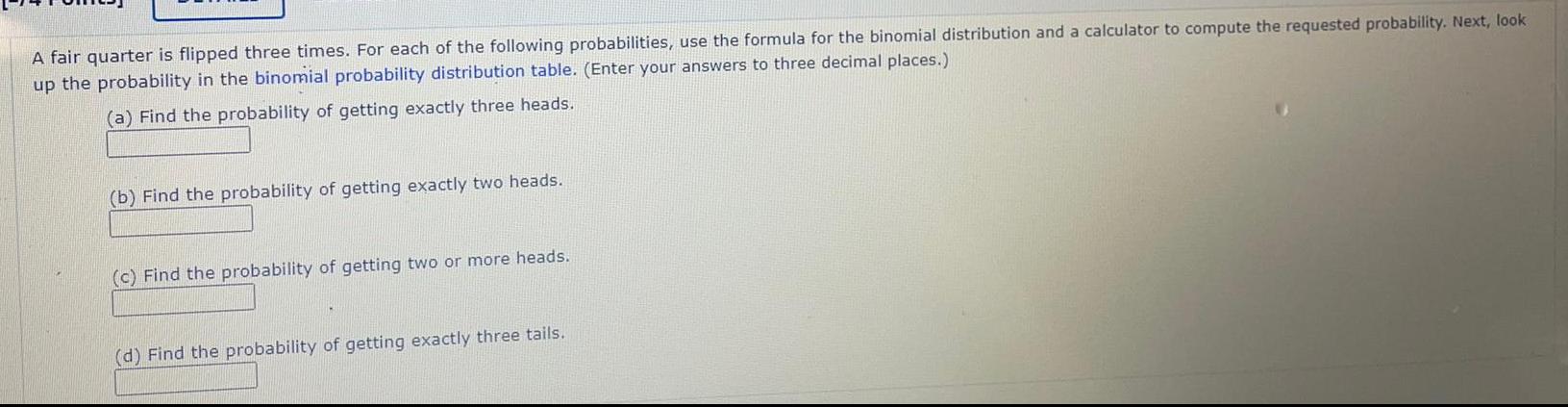
Math
ProbabilityA fair quarter is flipped three times. For each of the following probabilities, use the formula for the binomial distribution and a calculator to compute the requested probability. Next, look up the probability in the binomial probability distribution table. (Enter your answers to three decimal places.)
(a) Find the probability of getting exactly three heads.
(b) Find the probability of getting exactly two heads.
(c) Find the probability of getting two or more heads.
(d) Find the probability of getting exactly three tails.
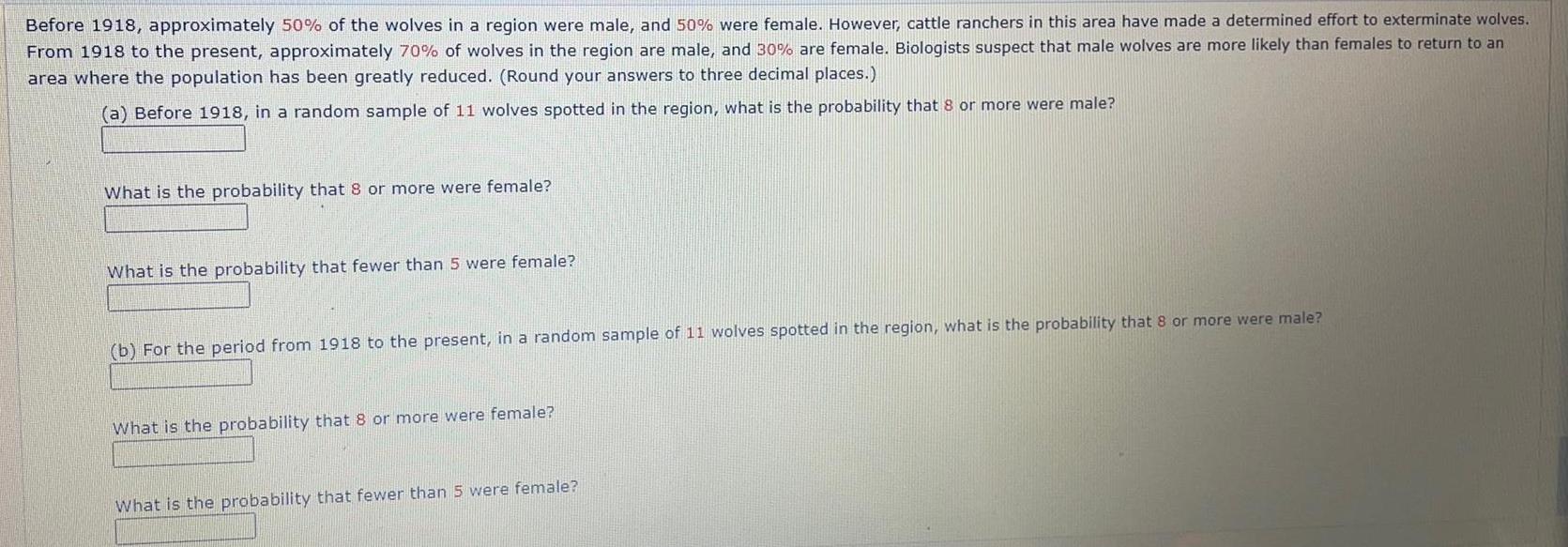
Math
ProbabilityBefore 1918, approximately 50% of the wolves in a region were male, and 50% were female. However, cattle ranchers in this area have made a determined effort to exterminate wolves.
From 1918 to the present, approximately 70% of wolves in the region are male, and 30% are female. Biologists suspect that male wolves are more likely than females to return to an
area where the population has been greatly reduced. (Round your answers to three decimal places.)
(a) Before 1918, in a random sample of 11 wolves spotted in the region, what is the probability that 8 or more were male?
What is the probability that 8 or more were female?
What is the probability that fewer than 5 were female?
(b) For the period from 1918 to the present, in a random sample of 11 wolves spotted in the region, what is the probability that 8 or more were male?
What is the probability that 8 or more were female?
What is the probability that fewer than 5 were female?
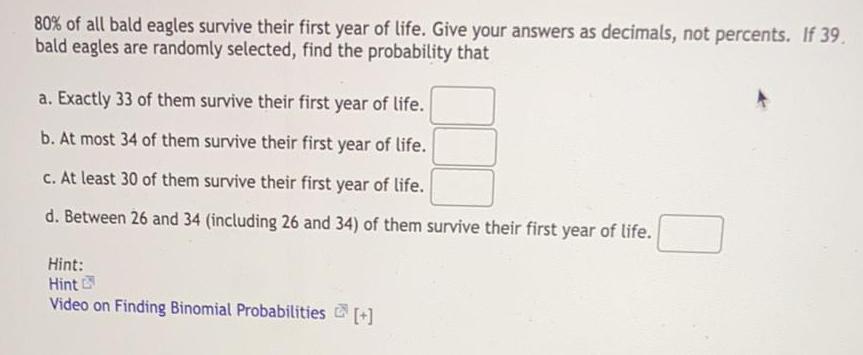
Math
Probability80% of all bald eagles survive their first year of life. Give your answers as decimals, not percents. If 39.
bald eagles are randomly selected, find the probability that
a. Exactly 33 of them survive their first year of life.
b. At most 34 of them survive their first year of life.
c. At least 30 of them survive their first year of life.
d. Between 26 and 34 (including 26 and 34) of them survive their first year of life.
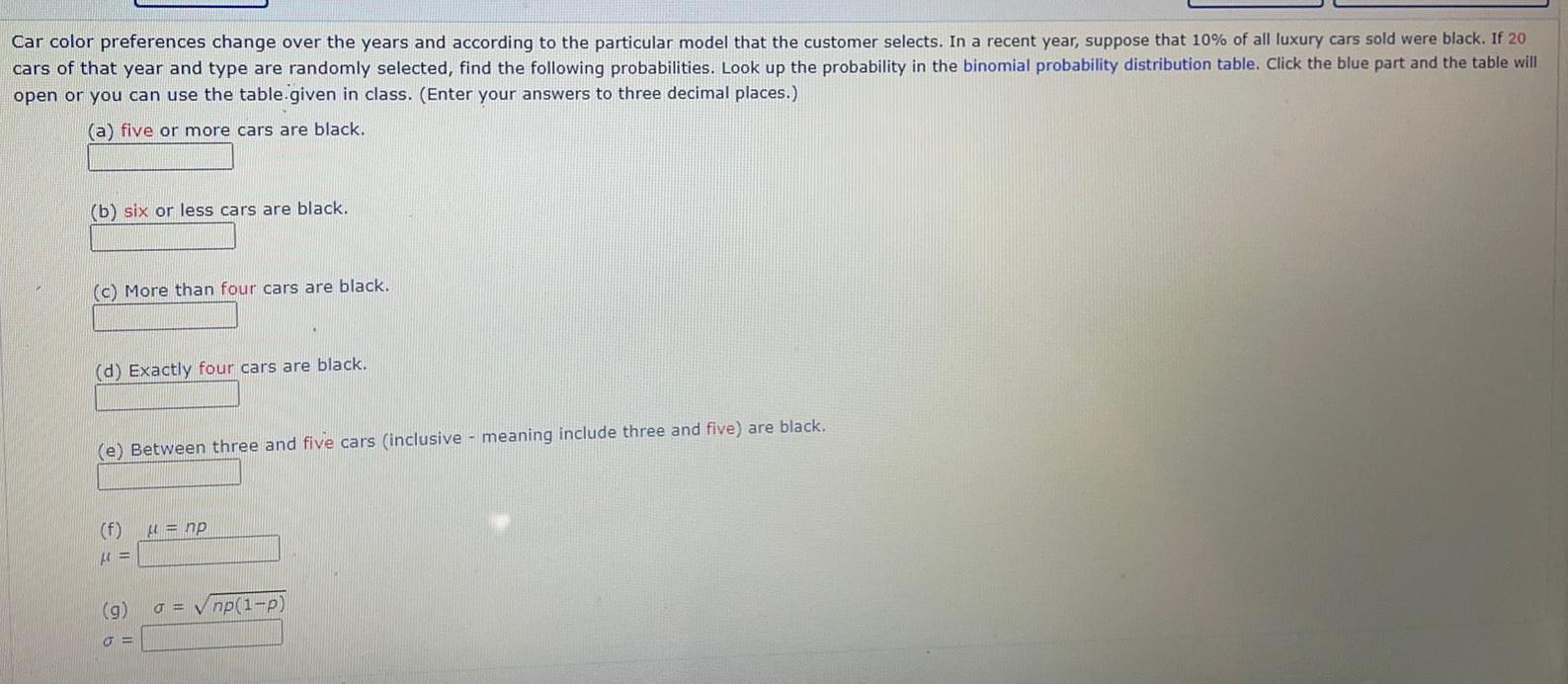
Math
ProbabilityCar color preferences change over the years and according to the particular model that the customer selects. In a recent year, suppose that 10% of all luxury cars sold were black. If 20 cars of that year and type are randomly selected, find the following probabilities. Look up the probability in the binomial probability distribution table. Click the blue part and the table will open or you can use the table.given in class. (Enter your answers to three decimal places.)
(a) five or more cars are black.
(b) six or less cars are black.
(c) More than four cars are black.
(d) Exactly four cars are black.
(e) Between three and five cars (inclusive - meaning include three and five) are black.
(f) μ = np
μ =
(g) σ = √(np(1-P))
σ =

Math
ProbabilityAn experiment consists of first rolling a die and then tossing a coin:
a. How many elements are there in the sample space?
b. Let A be the event that either a 2, 3 or 4 is rolled first, followed by landing a head on the coin toss.
P(A) = Present your answer as a decimal rounded to four decimal places.
c. Let B be the event that a number less than 2 is rolled, followed by landing a head on the coin toss. Are
the events A and B mutually exclusive?
Yes, they are Mutually Exclusive
No, they are not Mutually Exclusive
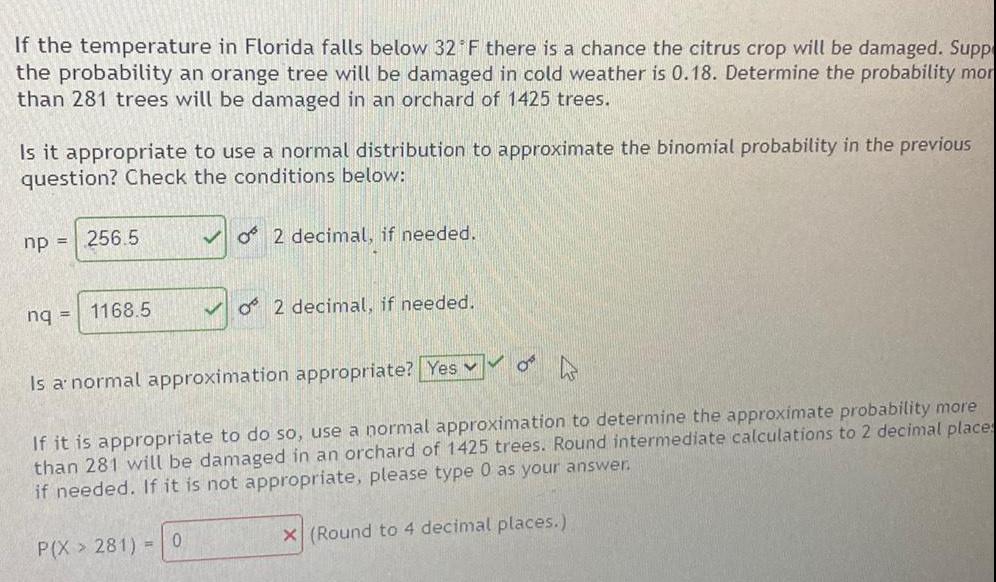
Math
ProbabilityIf the temperature in Florida falls below 32°F there is a chance the citrus crop will be damaged. Supp the probability an orange tree will be damaged in cold weather is 0.18. Determine the probability more than 281 trees will be damaged in an orchard of 1425 trees. Is it appropriate to use a normal distribution to approximate the binomial probability in the previous question? Check the conditions below:
np = 256.5
nq =
1168.5
✓ 2 decimal, if needed.
Is a normal approximation appropriate? Yes
P(X> 281) =
✓ 2 decimal, if needed.
If it is appropriate to do so, use a normal approximation to determine the approximate probability more than 281 will be damaged in an orchard of 1425 trees. Round intermediate calculations to 2 decimal places if needed. If it is not appropriate, please type 0 as your answer. x (Round to 4 decimal places.)

Math
ProbabilityAt a large high school outside of Chicago, there are two students running for class president, Ronald and Bo. 60% of the students in the school support Bo and the remaining 40% support Ronald. If you randomly sampled 12 students, what is the probability that more than half of your sample is comprised of Ronald supporters? Assume independence between students. Note: Round to the nearest thousandth.

Math
ProbabilityA drug test is accurate 98% of the time. If the test is given to 2400 people who have not taken drugs, what is the probability that at most 50 will test positive, in other words, the test was inaccruate? Round intermediate calculations to two decimal places.
Probability = Give your answers to 4 decimal places.

Math
ProbabilityAndre plays baseball for his university and has a batting average, the probability of successfully hitting the ball, of 0.310. If Andre has 42 turns at bat, what is the probability he successfully hits the ball between 11 and 20 times?

Math
ProbabilityA venture capitalist, willing to invest $1,000,000, has three investments to choose from. The first investment, a software company, has a 11% chance of returning $10,000,000 profit, a 45% chance of returning $2,500,000 profit, and a 44% chance of losing the million dollars. The second company, a hardware company, has a 10% chance of returning $10,000,000 profit, a 44% chance of returning $1,000,000 profit, and a 46% chance of losing the million dollars. The third company, a biotech firm, has a 12% chance of returning $6,000,000 profit, a 29% of no profit or loss, and a 59% chance of losing the million dollars.
Order the expected values from smallest to largest.
third, first, second
second, third, first
third, second, first
first, third, second
second, first, third
first, second, third

Math
ProbabilityNinety percent of individuals have brown/black hair, 8% of individuals have blond hair, and 2% of individuals have red hair. Suppose that of those with black/brown hair, 70% have blue eyes. Of those with blond hair, 85% have blue eyes. Of those with red hair, 60% have blue eyes.
What is the probability that a randomly chosen individual does not have
blue eyes?
Note: Enter your answer in decimals and not percentages. Do not round
your answer.

Math
ProbabilityThe Magazine Mass Marketing Company has received 12 entries in its latest sweepstakes. They know that the probability of receiving a magazine subscription order with an entry form is 0.5. What is the probability that more than 8 of the entry forms will include an order? Round your answer to four decimal places.

Math
ProbabilityA light bulb factory finds that 5 out of every 200 light bulbs are defective. If 5 bulbs are sampled, what's the probability of observing at most 1 defective bulbs? Note: Round to the nearest thousandth.

Math
ProbabilityArrows An Olympic archer is able to hit the bull's-eye 80% of the time. Assume each shot is
independent of the others. If she shoots 6 arrows, what's the probability of each of the following
results?
a) Her first bull's-eye comes on the third arrow.
b) She misses the bull's-eye at least once.
c) Her first bull's-eye comes on the fourth or fifth arrow.
d) She gets exactly 4 bull's-eyes.
e) She gets at least 4 bull's-eyes.
f) She gets at most 4 bull's-eyes.
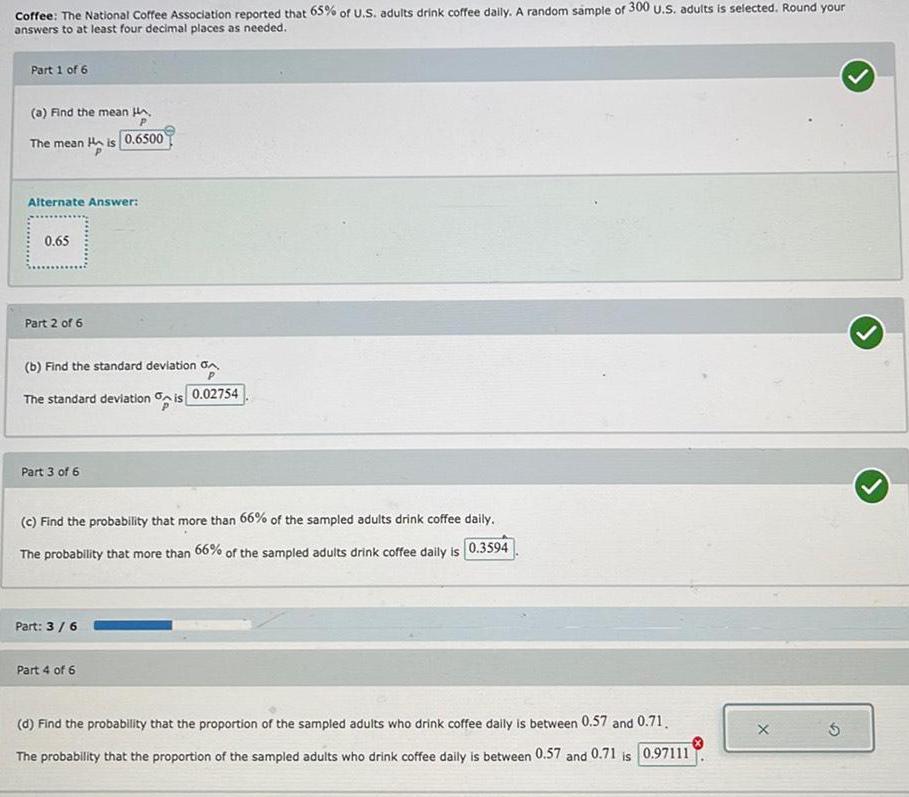
Math
ProbabilityCoffee: The National Coffee Association reported that 65% of U.S. adults drink coffee daily. A random sample of 300 U.S. adults is selected. Round yourmanswers to at least four decimal places as needed.
(a) Find the mean µp?
The mean is µp
(b) Find the standard deviation σp
PThe standard deviation σp is
(c) Find the probability that more than 66% of the sampled adults drink coffee daily.
The probability that more than 66% of the sampled adults drink coffee daily is
(d) Find the probability that the proportion of the sampled adults who drink coffee daily is between 0.57 and 0.71.
The probability that the proportion of the sampled adults who drink coffee daily is between 0.57 and 0.71 is
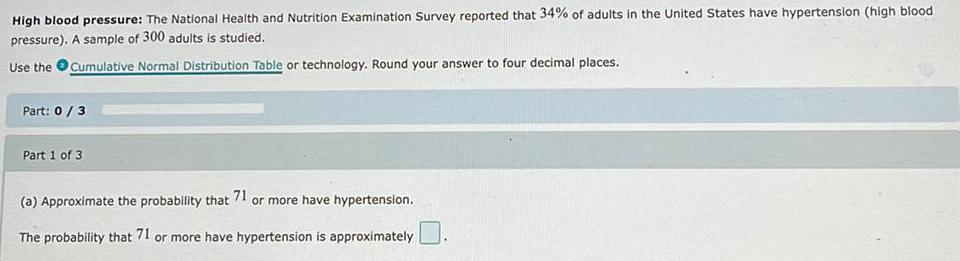
Math
ProbabilityHigh blood pressure: The National Health and Nutrition Examination Survey reported that 34% of adults in the United States have hypertension (high blood
pressure). A sample of 300 adults is studied.
Use the Cumulative Normal Distribution Table or technology. Round your answer to four decimal places.
Part: 0 / 3
Part 1 of 3
(a) Approximate the probability that 71 or more have hypertension.
The probability that 71 or more have hypertension is approximately

Math
ProbabilityA ball is drawn randomly from a jar that contains 2 red balls, 7 white balls, and 8 yellow balls. Find the
probability of the given event, and show your answers rounded to 4 decimal places when possible.
a. A red ball is drawn. P(red) =
b. A white ball is drawn. P(white) =
c. A yellow ball or red ball is drawn. P(yellow or red) =

Math
ProbabilityFrogs A wildlife biologist examines frogs for a genetic trait he suspects may be linked to
sensitivity to industrial toxins in the environment. Previous research had established that this trait is
usually found in 1 of every 8 frogs. He collects and examines a dozen frogs. If the frequency of the trait
has not changed, what's the probability he finds the trait in
a) none of the 12 frogs?
b) at least 2 frogs?
c) 3 or 4 frogs?
d) no more than 4 frogs?
Math
ProbabilityA hospital has 5 doctors (Dr. A, Dr. B, Dr. C, Dr. D and Dr. E). An administrator is going to randomly choose 2 of them to be on a committee. Write out the sample space (all the possible outcomes) for this random phenomenon.

Math
ProbabilityThe last time Brea played softball, she hit the ball 35% of the times she was at bat. Based on this information, how many times will Brea hit the ball the next time she plays softball if she is at bat 20 times?
F 4
G 7
H 15
J 6

Math
ProbabilityAccording to a survey, 10% of Americans are afraid to fly. Suppose 1,100 Americans are sampled.
a. What is the probability percentage that 121 or more Americans in the survey are afraid to fly?
b. What is the probability percentage that 165 or more Americans in the survey are afraid to fly?
c. What is the probability percentage that 8% or less of the Americans surveyed answered they were afraid to fly?

Math
ProbabilityA school counts the number of students taking AMDM and find 205 students taking AMDM. They also count the number of students taking Physics and find 217 students taking the Physics. When they compare the two lists they find 86 student taking AMDM and Physics. What is the probability of a student taking AMDM given they are taking Physics. (Answer in decimal form rounded to the thousandth)

Math
ProbabilityA store has three employees who all work independently. Each employee has a 2% rate The store can't open if at of absenteeism. least 1 employee doesn't show up, what is the probability that the store cannot open?

Math
ProbabilitySuppose the probability that an American owns a dog is 0.44, the probability that an American owns a cat is 0.29, and the probability that an American owns a cat and a dog is 0.19.
What is the probability that an American owns a dog GIVEN THAT they own a cat?
Note: Round to the nearest thousandth if necessary.

Math
ProbabilityThe National Coffee Association reported that 65% of U.S. adults drink coffee daily. A random sample of 300 U.S. adults is selected. Round your answers to at least four decimal places as needed.

Math
ProbabilityCoffee: The National Coffee Association reported that 61% of U.S. adults drink coffee daily. A random sample of 275 U.S. adults is selected. Round your answers to at least four decimal places as needed.
(a) Find the mean .

Math
ProbabilityIn a certain Algebra 2 class of 28 students, 23 of them play basketball and 12 of them play baseball. There are 3 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?