Probability Questions and Answers

Math
ProbabilityConsider a political discussion group consisting of 5 Democrats, 7 Republicans, and 4 Independents. Suppose that two group members are randomly selected, in
succession, to attend a political convention. Find the probability of selecting a Republican and then a Democrat.
(Type an integer or a simplified fraction.)
*****

Math
Probability1
The probability that a certain state will be hit by a major tornado (category F4 or F5) in any single year is Complete parts (a) through (d) below.
17
*****
a. What is the probability that the state will be hit by a major tornado two years in a row?
(Simplify your answer. Round to five decimal places as needed.)

Math
ProbabilityMrs. Tyler rolls a die each day to see how many
points the homework will be worth that day.
What is the probability that she rolls a 6 on
Monday and a number less than 3 on Tuesday?

Math
Probability5.2.7-T
In a recent study on world happiness, participants were asked to evaluate their current lives on a scale from 0 to 10, where 0 represents the worst possible life and 10
represents the best possible life. The responses were normally distributed, with a mean of 5.9 and a standard deviation of 2.6. Answer parts (a)-(d) below.
(a) Find the probability that a randomly selected study participant's response was less than 4.
The probability that a randomly selected study participant's response was less than 4 is. (Round to four decimal places as needed.)

Math
ProbabilityThe mathematics faculty at a college consists of 12 professors, 5 associate professors, 10 assistant professors, and 11 instructors. If one faculty member is randomly
selected, find the probability of choosing a professor or an instructor.
The probability is (Type an integer or a fraction. Simplify your answer.)

Math
ProbabilityAccording to a study conducted by an organization, the proportion of Americans who were afraid to fly in 2006 was 0.10. A random sample of 1,300 Americans results in 143 indicating that they are afraid to fly. Explain why this is not necessarily evidence that the proportion of Americans who are afraid to fly has increased.

Math
ProbabilityI select two cards from a deck of 52 cards and observe the color of each (26 cards in the deck are
red and 26 are black). Which of the following is the most appropriate sample space S for the
possible outcomes?
Os= ((red,red), (red,black), (black,red), (black,black)}
Os={0, 1, 2}
Os = {red,black}
O none of the above

Math
ProbabilityIt is equally probable that the pointer on the spinner shown will land on any one of the eight regions, numbered 1 through 8. If the pointer lands on a borderline, spin again. Find the probability that the pointer will stop on an odd number or a number greater than 3.

Math
ProbabilityA bag of sweets contains 5 chocolates (C), 10 toffees(T) and 7 licorice(L). Amy takes a
sweet from the bag and eats it, then selects a second one and eats that. What is the
probability that she eats one toffee and one chocolate? Give your answer as a decimal
correct to three significant figures.

Math
ProbabilityThe mathematics department of a college has 5 male professors, 9 female professors, 13 male teaching assistants, and 9 female teaching assistants. If a person is selected at random from the group, find the probability that the selected person is a teaching assistant or a female.

Math
ProbabilityEvents A and B are independent, P(A) = 0.49 and P(AUB) = 0.83.
Find P(An B). Give an exact answer as a fraction in fully simplified form or an
approximate answer as a decimal rounded to three significant figures.

Math
ProbabilitySuppose the body mass index (BMI) of a group of athletes has a population mean of 24.98 and a standard deviation of 4.18. If a random sample of 150 athletes is chosen for a study, compute the standard deviation of the sampling distribution of the mean.
Give your answer to two decimal places.
Standard deviation of the sampling distribution of the mean:

Math
ProbabilityAn experiment is given together with an event. Find the (modeled) probability of each event, assuming that the dice are distinguishable and fair, and that what is observed are the numbers
uppermost.
Two dice are rolled; the numbers add to 13.


Math
ProbabilityYour manufacturing plant produces air bags, and it is known that 10% of them are defective. Five air bags are tested.
(a) Find the probability that three of them are defective. (Round your answer to four decimal places.)
P(X= 3) =
(b) Find the probability that at least two of them are defective. (Round your answer to four decimal places.)
P(X ≥ 2) =

Math
ProbabilityOf the 44 plays attributed to a playwright, 14 are comedies, 19 are tragedies, and 11 are histories. If one play is selected at random, find the odds in favor of selecting a history or a comedy.
The odds in favor are
(Simplify your answer.)
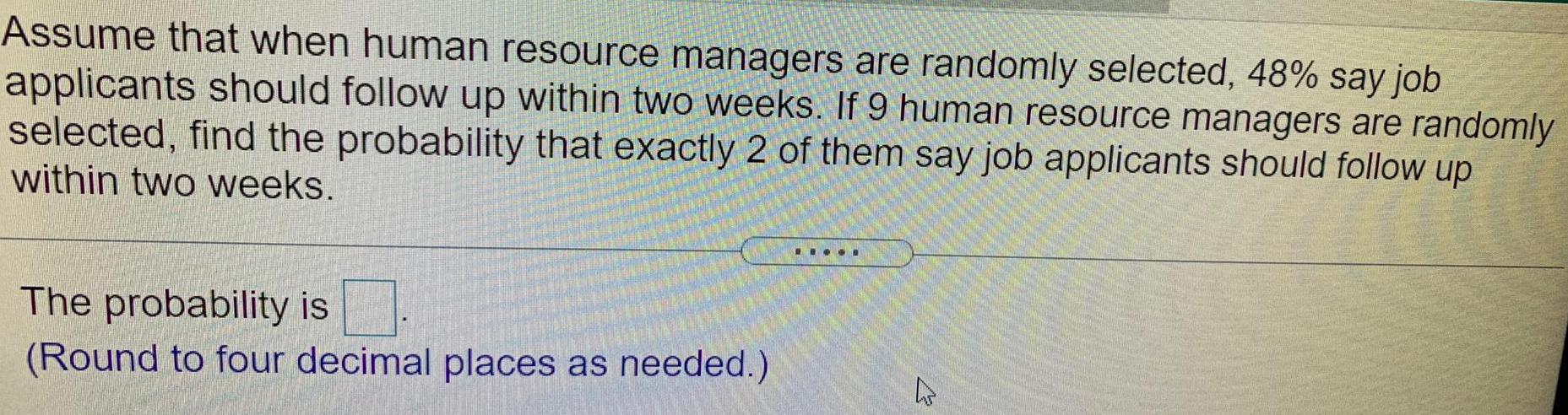
Math
ProbabilityAssume that when human resource managers are randomly selected, 48% say job
applicants should follow up within two weeks. If 9 human resource managers are randomly
selected, find the probability that exactly 2 of them say job applicants should follow up
within two weeks.
The probability is
(Round to four decimal places as needed.)

Math
ProbabilityA student takes a multiple choice test with 5 choices in each question out of which only one is correct. The student knows the correct choice for 80% of the questions. In all other cases the student makes a random guess. A question is chosen randomly. What is the probability that the student gets the correct answer?


Math
ProbabilityYou use software to run an hypothesis test. The program tells you that the P-value is P = 0.031.
This result is
significant at both the 5% level and 1% level.
significant at the 5% level but not at the 1% level.
not significant at the 5% level.
significant at the 1% level.

Math
ProbabilityIn an IB school 47 students study biology, 53- students study chemistry and 34 students do not study either of these two subjects. There are 109 students in this school. A student is selected at random. Find the probability that this student studies exactly one of these two subjects. Give an exact answer as a fraction in fully simplified form, or an approximate answer as a decimal rounded to three significant figures.

Math
ProbabilityUse the "at least once" rule to find the probability of the following event. Purchasing at least one winning lottery ticket out of 7 tickets when the probability of winning is 0.06 on a single ticket

Math
ProbabilityA regular six sided dice is thrown and a card is drawn at random from a pack of 52. What is the probability that the dice shows a 6 and the card is an ace? Give your answer as a decimal, correct to 3 significant figures.
![According to a poll by The New York Times/CBS, 61% of those polled ranked neither Iraq nor North Korea as the top foreign policy issue. What is the probability that a randomly selected person polled ranked either Iraq or North Korea as the top foreign policy issue? HINT [See Example 5.] (Enter your answer to two decimal places.)](https://media.kunduz.com/media/sug-question/raw/57999681-1657694950.016797.jpeg?w=256)
Math
ProbabilityAccording to a poll by The New York Times/CBS, 61% of those polled ranked neither Iraq nor North Korea as the top foreign policy issue. What is the probability that a randomly selected person polled ranked either Iraq or North Korea as the top foreign policy issue? HINT [See Example 5.] (Enter your answer to two decimal places.)
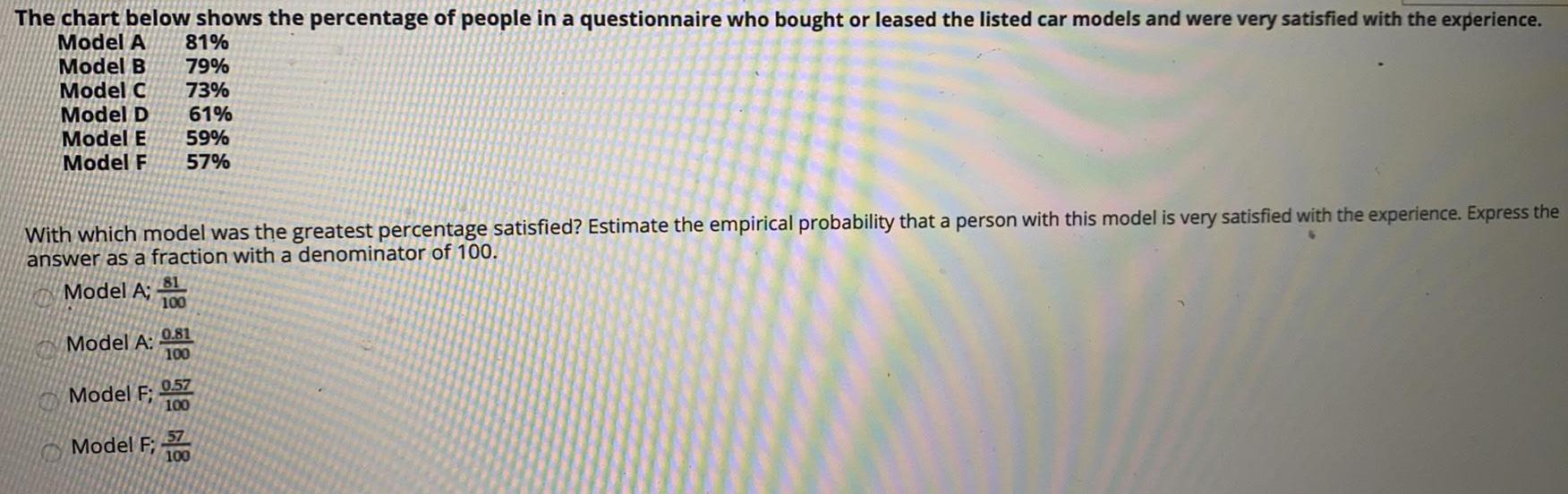
Math
ProbabilityThe chart below shows the percentage of people in a questionnaire who bought or leased the listed car models and were very satisfied with the experience.
Model A 81%
Model B 79%
Model C 73%
Model D 61%
Model E 59%
Model F 57%
With which model was the greatest percentage satisfied? Estimate the empirical probability that a person with this model is very satisfied with the experience. Express the answer as a fraction with a denominator of 100.
Model A; 81/100
Model A: 0.81/100
Model F: 0.57/100
Model F: 57/100

Math
ProbabilityGiven events A and B with probabilities P(A) = 0.5, P(B) = 0.4, and P(A and B) = 0.2, are A and B independent?
yes
cannot be determined
no

Math
ProbabilityAccording to an article, 14.9% of Internet stocks that entered the market in 1999 ended up trading below their initial offering prices. If you were an investor who purchased three Internet stocks at their initial offering prices, what was the probability that at least two of them would end up trading at or above their initial offering price? (Round your answer to four decimal places.)
P(X ≥ 2) =

Math
ProbabilityClassify the statement as an example of classical probability, empirical probability, or subjective probability. It is known that the probability of hitting a pothole while driving on a certain road is 1%.
classical probability
subjective probability
empirical probability

Math
ProbabilitySuppose a brewery has a filling machine that fills 12-ounce bottles of beer. It is known that the amount of beer poured by this filling machine follows a normal distribution with a mean of 12.23 ounces and a standard deviation of 0.04 ounce. The company is interested in reducing the amount of extra beer that is poured into the 12 ounce bottles. The company is seeking to identify the highest 1.5% of the fill amounts poured by this machine. For what fill amount are they searching? Round to the nearest thousandth.
11.913 oz
12.087 oz
12.317 oz
12.143 oz

Math
ProbabilitySuppose a bag contains a set of 10 tiled letters: M, T, O, A, T, P.J.A.K.A You draw a tile from the bag, and record the letter and leave it on the table. You shake up the bag, and draw another tile out of the bag. Calculate the probability you will select the letter M on the first draw and the Letter T on the second draw?
2/45.
3/19
2/19
1/50

Math
ProbabilityThe average number of gallons of Gatorade consumed by the football team
during a game is 20 with a standard deviation of 3. Assume the variable is
normally distributed. When a game is played, find the probability of using
a) Between 20 and 25 gallons.
b)
Less than 19 gallons
c)
More than 21 gallons
d)
Between 26 and 28 gallons

Math
ProbabilityWe are given that a die is weighted in such a way that each of 1 and 2 is three times as likely to come up as 3, 4, 5, or 6. We are asked to find the probability distribution associated with this die. The probability of each outcome is unknown, so the first step is to use the properties of probability distributions to write an equation that we can solve for the probability of one or more of the outcomes. Assign the variable x to the probability of rolling a 3, and compute the probabilities of the other outcomes, in terms of x. 6

Math
ProbabilityThe top five countries for movie
releases for a specific year are the United States with
471 releases, United Kingdom with 386, Japan with 79,
Germany with 316, and France with 132. Choose 1 new
release at random. Find the probability that it is
a. European
b. From the United States
c. German or French
d. German given that it is European
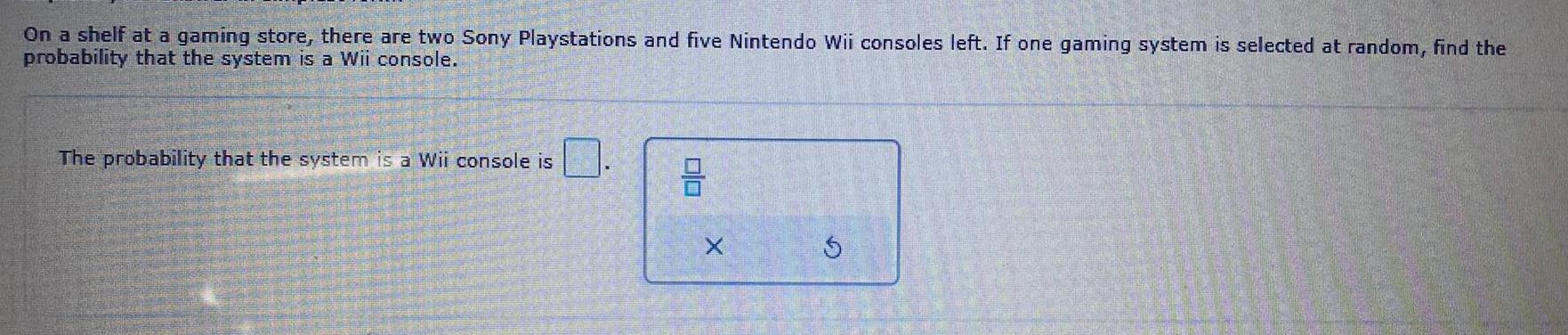
Math
ProbabilityOn a shelf at a gaming store, there are two Sony Playstations and five Nintendo Wii consoles left. If one gaming system is selected at random, find the probability that the system is a Wii console.
The probability that the system is a Wii console is

Math
ProbabilitySuppose you work for a company that
manufactures electronics. The development
analysts estimate that 1% of their flagship product
will fail within 2 years of the purchase date, with a
replacement cost of $ 1600.
A newly hired associate at the company proposes to
charge $6 for a 2 year warranty.
a. Compute the expected value of this proposal. Let
X be the amount profited or lost (by the company)
on the warranties and P(X) is the probability. E =
b. Interpret the expected value in complete
sentences. (See Example 4.3 in the textbook for an
example of this)

Math
ProbabilityFind the probability that of 25 randomly selected students, at least two share the same birthday. Round to the nearest thousandth.
0.068
0.995
0.432
0.569

Math
ProbabilityThe time it takes to preform a task has a continuous uniform distribution between 43 min and 57 min. What is the the probability it takes between 52.1 and 54.9 min. Round to 4 decimal places.
P(52.1<X<54.9) =
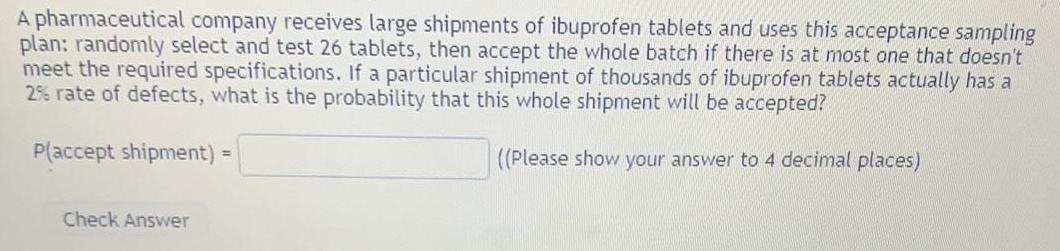
Math
ProbabilityA pharmaceutical company receives large shipments of ibuprofen tablets and uses this acceptance sampling plan: randomly select and test 26 tablets, then accept the whole batch if there is at most one that doesn't meet the required specifications. If a particular shipment of thousands of ibuprofen tablets actually has a 2% rate of defects, what is the probability that this whole shipment will be accepted?
P(accept shipment) ((Please show your answer to 4 decimal places)
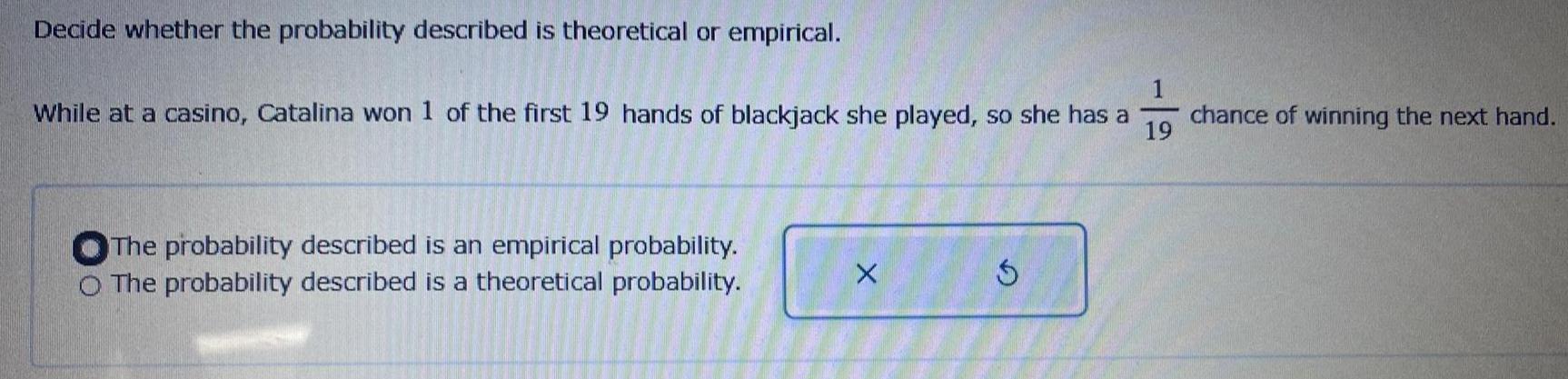
Math
ProbabilityDecide whether the probability described is theoretical or empirical.
While at a casino, Catalina won 1 of the first 19 hands of blackjack she played, so she has a 1/9 chance of winning the next hand.
The probability described is an empirical probability.
The probability described is a theoretical probability.
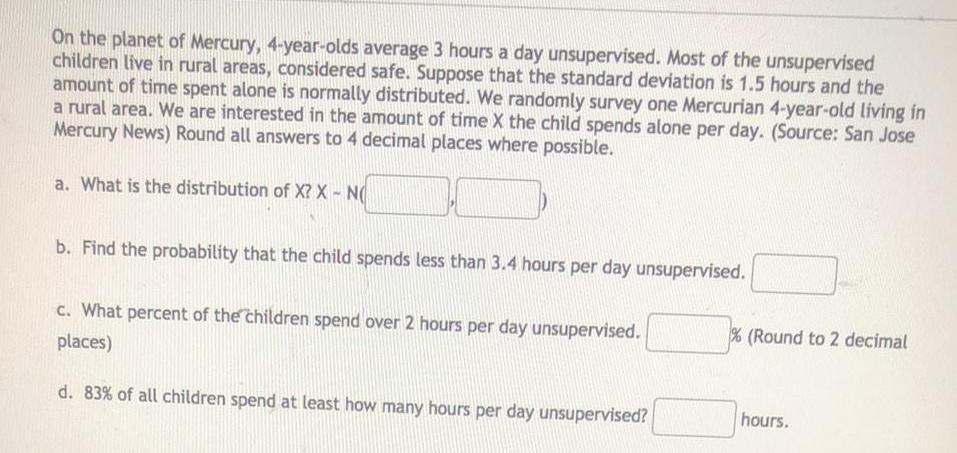
Math
ProbabilityOn the planet of Mercury, 4-year-olds average 3 hours a day unsupervised. Most of the unsupervised children live in rural areas, considered safe. Suppose that the standard deviation is 1.5 hours and the amount of time spent alone is normally distributed. We randomly survey one Mercurian 4-year-old living in a rural area. We are interested in the amount of time X the child spends alone per day. (Source: San Jose Mercury News) Round all answers to 4 decimal places where possible.
a. What is the distribution of X? X - N(
b. Find the probability that the child spends less than 3.4 hours per day unsupervised.
c. What percent of the children spend over 2 hours per day unsupervised. places)
d. 83% of all children spend at least how many hours per day unsupervised? % (Round to 2 decimal hours.

Math
ProbabilityThe average THC content of marijuana sold on the street is 9.6%. Suppose the THC content is normally distributed with standard deviation of 1%. Let X be the THC content for a randomly selected bag of marijuana that is sold on the street. Round all answers to 4 decimal places where possible,
a. What is the distribution of X? X - N(
b. Find the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 10.7.
c. Find the 63rd percentile for this distribution.

Math
ProbabilityJorge has a standard deck of 52 cards and a six-sided number cube. What is the probability that he will draw a diamond from the deck of cards and roll a number greater than two? Write your answer as a simplified fraction.

Math
ProbabilityFind the indicated area under the standard normal curve.
Between z = -2.39 and z = 2.39

Math
ProbabilityThe number of ants per acre in the forest is normally distributed with mean 43,000 and standard deviation 12,354. Let X = number of ants in a randomly selected acre of the forest. Round all answers to 4 decimal places where possible.
a. What is the distribution of X? X - N
b. Find the probability that a randomly selected acre in the forest has fewer than 46,282 ants.
c. Find the probability that a randomly selected acre has between 41,412 and 50,234 ants.
d. Find the first quartile.
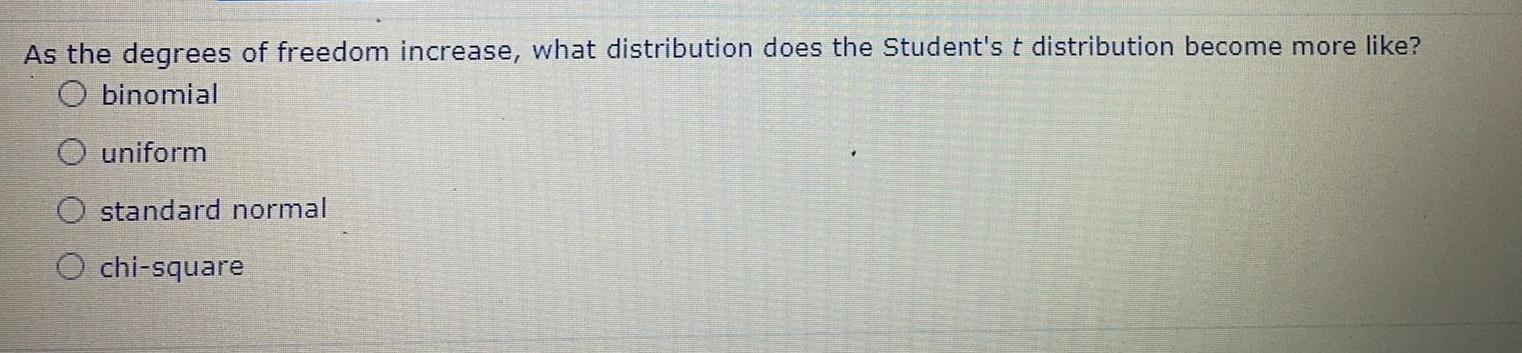
Math
ProbabilityAs the degrees of freedom increase, what distribution does the Student's t distribution become more like?
binomial
uniform
standard normal
chi-square

Math
ProbabilityThere were 25 horses performing at a dressage exhibition. Of these, 13 were of Westphalian breed and 2/3 of the remaining horses were of Andalusians breed. -
If a horse is chosen at random, find the probability that it is neither Andalusian nor Westphalian.

Math
ProbabilityThe average height of a certain age group of people is 53 inches. The standard deviation is 4 inches. If the variable is normally distributed, find the probability that a selected individual's height will be
a. Greater than 59 inches.
b. Less than 45 inches
c. Between 50 and 55 inches.
d. Between 58 and 62 inches.
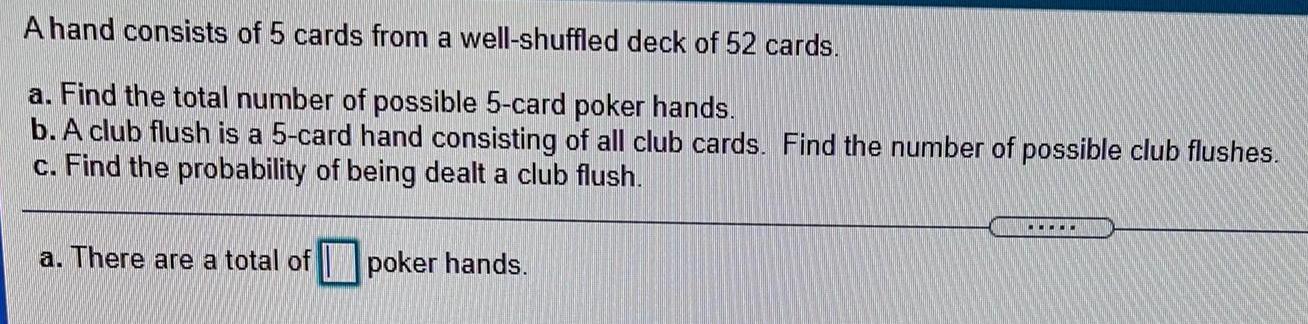
Math
ProbabilityA hand consists of 5 cards from a well-shuffled deck of 52 cards.
a. Find the total number of possible 5-card poker hands.
b. A club flush is a 5-card hand consisting of all club cards. Find the number of possible club flushes.
c. Find the probability of being dealt a club flush..

Math
ProbabilityWhen rolling a six-sided die, of which all sides are equally likely, it can be shown that the probability of rolling a multiple of 3 is:
2/6 = 1/3 ≈ 0.3333
Explain the meaning of the event having a probability of 0.3333.
Math
ProbabilityThe names of 3 boys and 5 girls are written on cards. The cards are placed in a bowl. Two cards are drawn, one at a time, without replacement. What is the probability that the first card is a girl's name and the second card is a boy's name?
A. 1/56
B. 5/15
C. 15/56
D. 1/15